BADANIA SYSTEMU POJAZDÓW

PRZEZNACZONYCH DO REALIZACJI LOSOWEJ

LICZBY ZADAŃ TRANSPORTOWYCH

Wprowadzenie

Pojęcie systemu pojazdów przewidywanego
do realizacji losowej liczby zadań i pojęcie
zadania dla tego systemu pojazdów

Schemat problemu decyzyjnego metody
modelowania systemu pojazdów – idea,
parametry systemu, zmienna decyzyjna,
funkcja celu

Heurystyczny algorytm realizacji metody

Symulator cyfrowy realizujący algorytm metody
Sym_Sys_Poj_1

Przykład realizacji metody i zastosowania
symulatora

Podsumowanie

[e-mail]

Plik: BO_FT_Badania_Sys_Poj_2007_[v1].doc

Plik:

AK_Badanie_Sys_Poj_2007_[v1].doc

1

BADANIA SYSTEMÓW POJAZDÓW

PRZEZNACZONYCH DO REALIZACJI LOSOWEJ

LICZBY ZADAŃ TRANSPORTOWYCH

1. Wprowadzenie

W okresie rosnącej konkurencji na rynku transportowym, zarówno wewnątrzgałęziowym

jak i między różnymi gałęziami transportu, niezbędne są skuteczne narzędzia do ocen

efektywności techniczno-ekonomicznej przedsięwzięć i systemów transportowych.

Określenie efektywności przedsięwzięć transportowych i efektywności funkcjonowania

systemów transportowych wymaga znajomości składowych kosztów (oraz relacji między

nimi) i ich sumy. Koszty działalności ponoszone przez operatora transportu działającego na

rynku usług publicznych, związane są m.in. z użytkowaniem taboru. Taborem dysponuje

najczęściej świadczący usługę na zasadzie własności lub wynajmu.

Dalej rozpatrywany jest problem operatora transportu, który świadczy usługi na rynku

usług publicznych. Do realizacji usług operator dysponuje m.in. systemem pojazdów. Rynek

usług transportowych świadczonych przez operatorów transportu może być określany za

pomocą liczby zadań transportowych.

Niech zadanie transportowe jest to usługa realizowana przez operatora (system) za

pomocą jednego pojazdu w ciągu pewnego okresu czasu (np. jednego dnia kalendarzowego).

Zapotrzebowanie na tak określone zadania transportowe może być losowe. W takiej

sytuacji, u operatorów transportu, zaistnieć może potrzeba racjonalizacji parku własnych

pojazdów gotowych do realizacji zadań transportowych.

W procesie racjonalizacji liczności parku własnych pojazdów, można wykorzystać

kryterium minimum średnich kosztów funkcjonowania systemu pojazdów w długim okresie

czasu.

Dalej pokazane zostanie zastosowanie tego kryterium do oceny dokonywanych zmian w

systemie. W tym celu zbudowane zostaną modele matematyczne systemu pojazdów i za ich

pomocą przedstawiony zostanie przykład badania możliwości realizacji losowej liczby

zadań transportowych przez system pojazdów o określonych parametrach.

2. Modele matematyczne

1

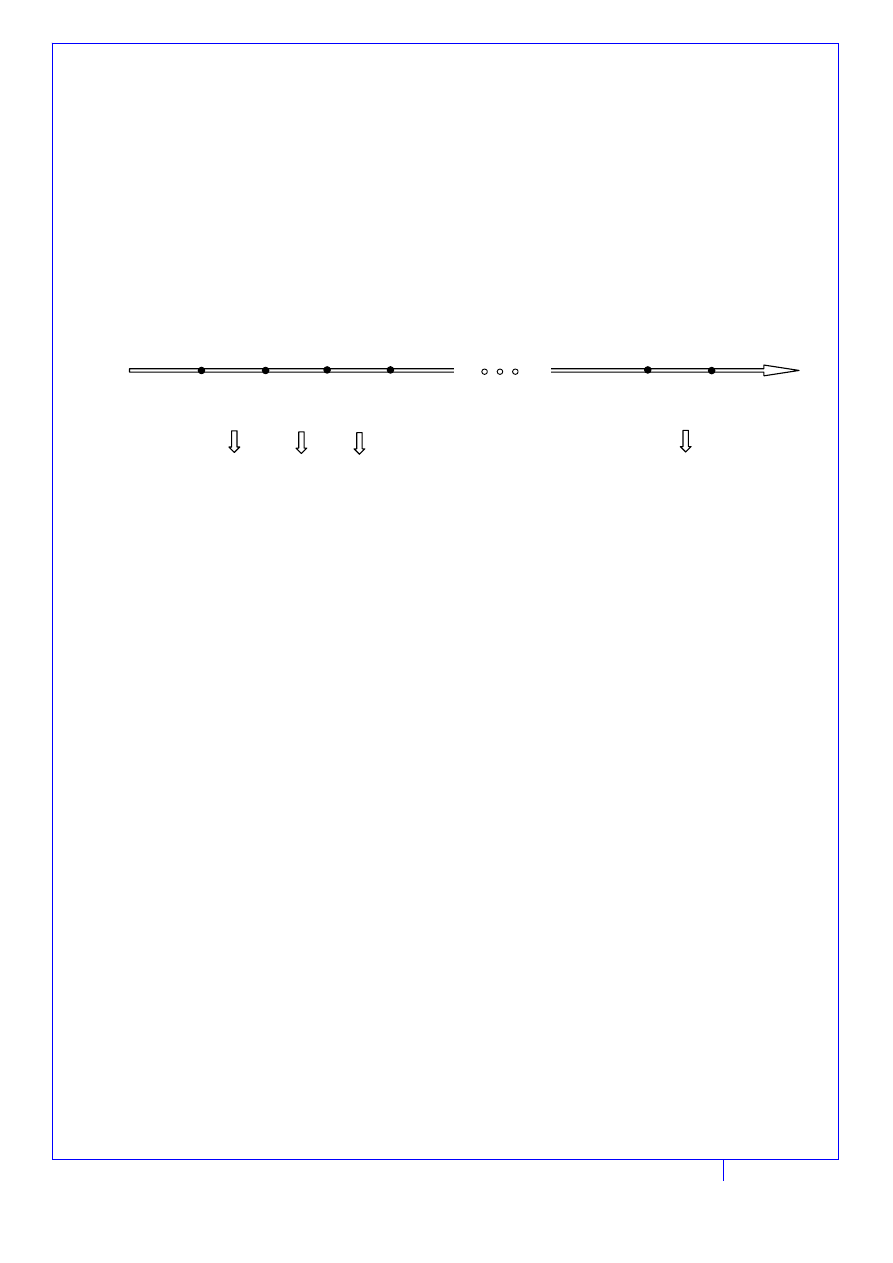
. System pojazdów pracuje w czasie ciągłym, ale wszystkie możliwe zmiany stanu systemu

dokonywane są w określonych chwilach czasu t

1

, t

2

, ... . W stałych przedziałach czasu

T

i

= < t

i

, t

i+1

) pomiędzy kolejnymi chwilami t

i

( i = 1,2, ... ) stan systemu nie zmienia się.

Długość wszystkich T

i

okresów pracy systemu jest taka sama

Δ

t = t

i+1

- t

i

i wynosi np. 1 dzień kalendarzowy (rys. 1).

T

i-1

T

i

T

i+1

t

i-1

t

i+1

t

i

t

i+2

t

M

t

M+1

T

M

S(T

i

) S(T

i+1

)

S(T

i-1

)

S(T

M

)

K(T

i-1

)

K

śr

(T)

i-1

K

śr

(T)

i

K

śr

(T)

i+1

K

śr

(T)

M

K(T

i

) K(T

i+1

)

K(T

M

)

Rys. 1. Schemat wybranych oznaczeń stosowanych w formułach modeli matematycznych

2

. W okresie T

i

, system (rys. 2) dysponuje losową liczbą L

poj

(T

i

) własnych pojazdów

(gotowych do realizacji zadań transportowych) o rozkładzie dyskretnym postaci:

( )

( )

{

}

( )

1

=

∈

=

=

∑

l

i

poj

i

poj

i

poj

l,

T

p

,

l,

l

T

L

P

l,

T

p

N

. (1)

3.

W chwili t

i

określane jest zadanie systemu pojazdów, wyrażające się liczbą pojazdów z,

które są potrzebne do realizacji tego zadania. Rozkład określający liczbę pojazdów, które

realizują zadanie systemu w okresie T

i

, przedstawia zależność:

( )

( )

{

}

( )

1

=

∈

=

=

∑

z

i

popyt

i

popyt

i

popyt

z

,

T

p

,

z

,

z

T

L

P

z

,

T

p

N

. (2)

System pojazdów realizuje wszystkie zgłoszenia zadań transportowych, nawet wtedy gdy

do wykonania ich części istnieje konieczność wynajęcia pojazdu z innego systemu.

4.

Stan systemu pojazdów w okresie T

i

określa wektor:

( )

( )

( )

[

]

i

popyt

i

poj

i

T

L

,

T

L

T

S

=

.

(3)

Plik:

AK_Badanie_Sys_Poj_2007_[v1].doc

2

1

1

2

3

2

k

L

popyt

(T

i

)

L

poj

(T

i

)

j

L

nad

(T

i

)

L

poj

(T

i

)+1

F

popyt

(l)=?

L

poj

(T

i

)=?

K

śr

(T)

M

=?

k

wł

, k

wy

, k

ut

Zadania do realizacji

Pojazdy do realizacji zadań

L

poj

(T

i

)+2

L

wy

(T

i

)

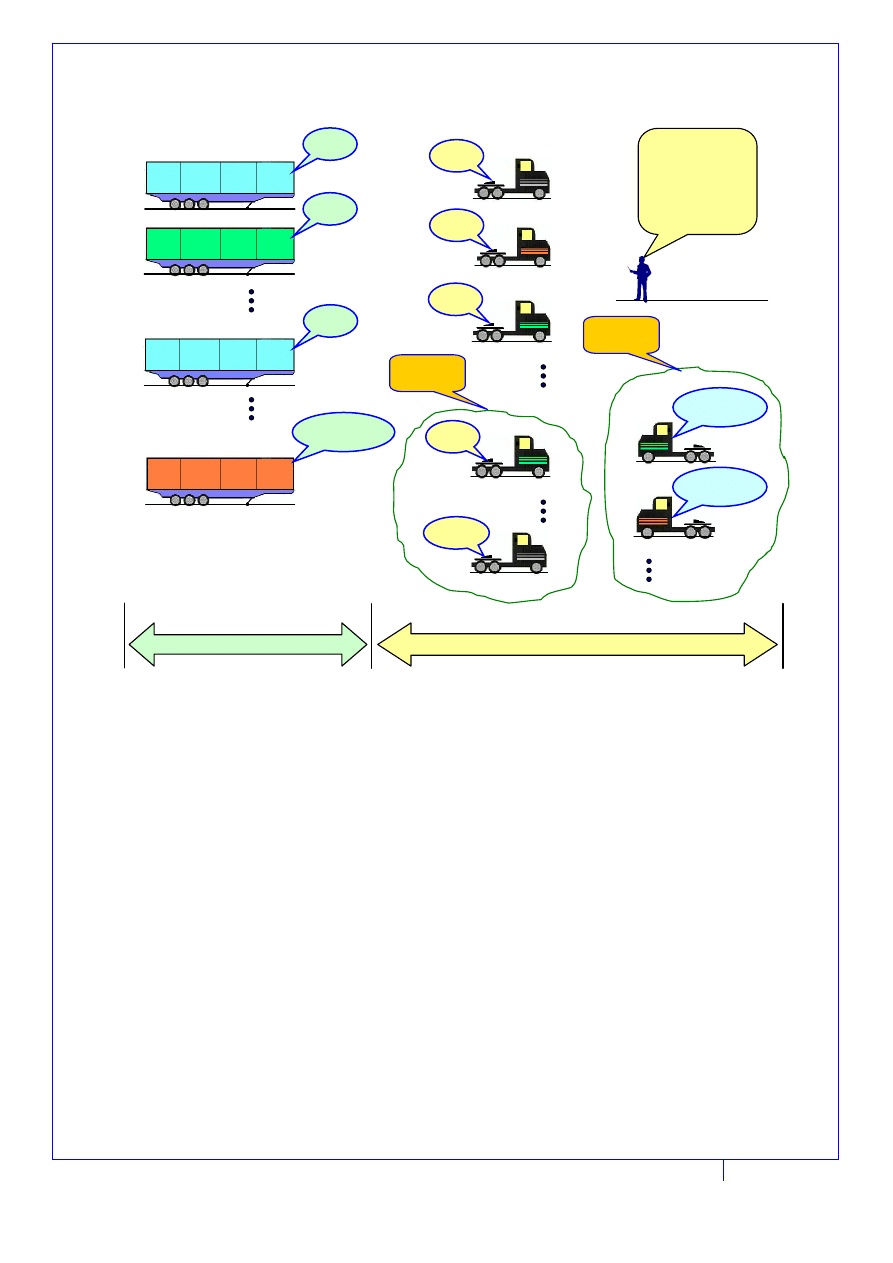
Rys. 2. Schemat ideowy modelu problemu decyzyjnego realizacji zadań transportowych przez system

pojazdów firmy transportowej (objaśnienie oznaczeń zawarto w tekście)

Plik:

AK_Badanie_Sys_Poj_2007_[v1].doc

3

5.

Koszty działalności systemu pojazdów wynikają z następujących kosztów jednostkowych

(przypadających na ustalony okres czasu T

i

):

i) k

wl

- jednostkowy średni koszt wykonania zadania transportowego

własnym pojazdem;

ii) k

wy

- jednostkowy średni koszt realizacji zadania transportowego

wynajętym pojazdem;

iii) k

ut

- jednostkowy średni koszt utrzymania własnego pojazdu bez względu na to

czy są dla niego zadania transportowe czy też nie.

W warunkach losowej liczby własnych pojazdów i losowego zapotrzebowania na nie,

generowane są określone całkowite koszty K(T

i

) funkcjonowania systemu w okresie czasu

T

i

. Koszty te przedstawiają następujące modele matematyczne:

a) gdy L

poj

(T

i

)

≥ L

popyt

(T

i

), tzn., że liczba własnych pojazdów gotowych do realizacji

zadań transportowych jest większa lub co najmniej równa zapotrzebowaniu na nie, to

wtedy

( ) (

)

( )

( )

( )

(

)

i

popyt

i

poj

ut

i

popyt

ut

wl

i

T

L

T

L

k

T

L

k

k

T

K

−

⋅

+

⋅

+

=

, (4)

b) gdy L

poj

(T

i

) < L

popyt

(T

i

), tzn., że liczba pojazdów własnych gotowych do realizacji

zadań transportowych jest mniejsza od zapotrzebowania na nie, to wtedy

( ) (

)

( )

( )

( )

(

)

i

poj

i

popyt

wy

i

poj

ut

wl

i

T

L

T

L

k

T

L

k

k

T

K

−

⋅

+

⋅

+

=

. (5)

6.

Rozpatrując funkcjonowanie systemu w długim okresie czasu T takim, że jest on wielokrotnością

okresów T

i

o długości

Δ

t

N

∈

⋅

=

M

,

Δt

M

T

, (6)

lub

, (7)

∑

=

=

M

i

i

T

T

1

można w następujący sposób przedstawić model matematyczny średnich kosztów

funkcjonowania systemu pojazdów w czasie T:

( )

( )

∑

=

⋅

=

M

i

i

M

śr

T

K

M

T

K

1

1

. (8)

Plik:

AK_Badanie_Sys_Poj_2007_[v1].doc

4

3. Symulator do badania możliwości realizacji losowej liczby zadań

transportowych przez system pojazdów

Modele matematyczne kosztów funkcjonowania systemu pojazdów odwzorowano w

symulatorze cyfrowym Sym_Sys_Poj_1.Xls . Jest to aplikacja komputerowa składająca się z

arkuszy kalkulacyjnych opracowanych w formacie programu Excel. Podstawą symulatora

jest arkusz szablonu do symulacji. Na podstawie tego szablonu tworzone są arkusze do

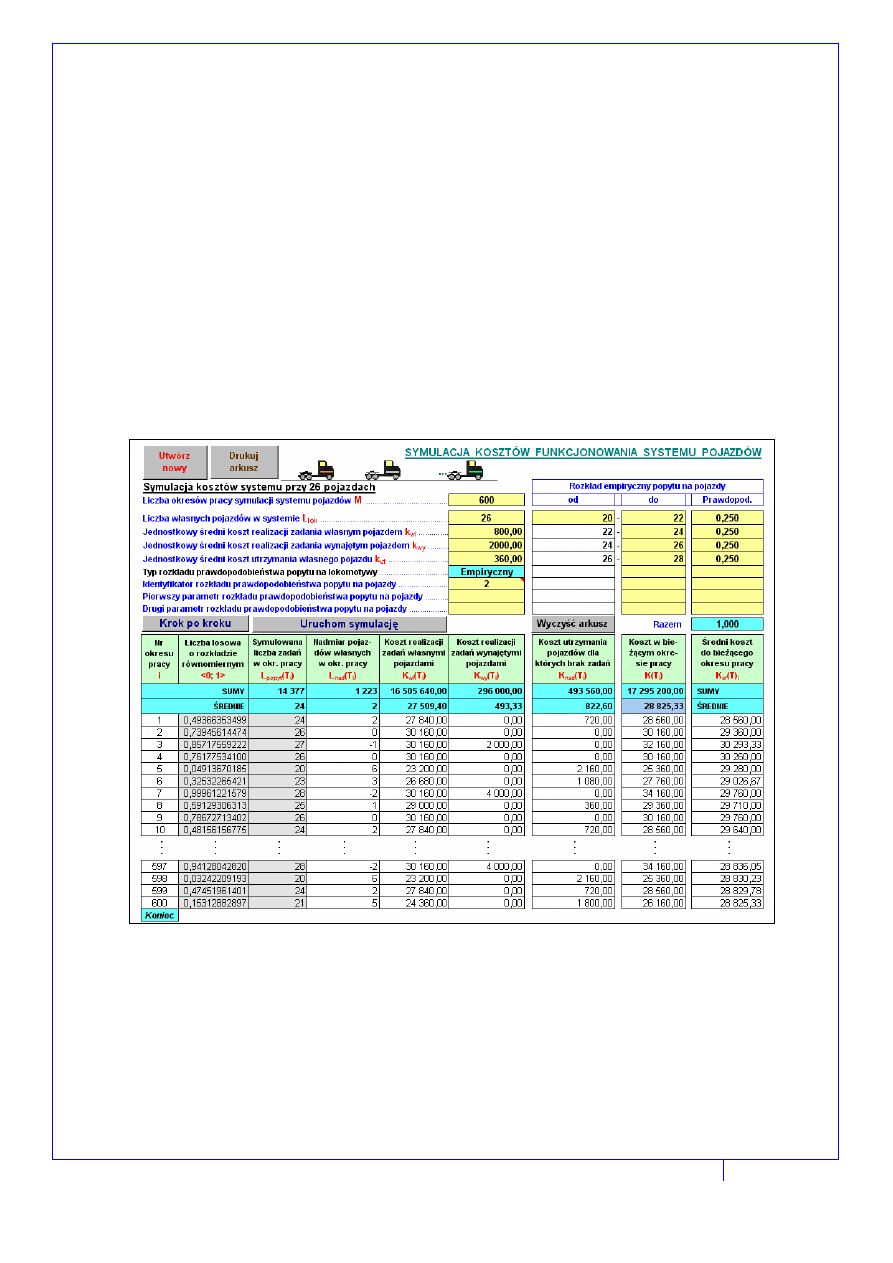
przeprowadzania kolejnych eksperymentów symulacyjnych. Widok ekranów monitora

przedstawiających początkową i końcową fazę przeprowadzania przykładowej symulacji

kosztów funkcjonowania systemu pojazdów, pokazano na rys. 3.

Rys. 3. Widok arkusza z danymi i fragmentem wyników symulacji kosztów funkcjonowania

systemu pojazdów dysponującego 26 własnymi pojazdami

Na ekranie zawsze widoczny jest formularz do wprowadzania danych opisujących

warunki eksperymentu symulacyjnego przeprowadzanego w ramach systemu pojazdów. W

formularzu należy zadeklarować:

− liczbę okresów pracy (czas) prowadzenia symulacji,

Plik:

AK_Badanie_Sys_Poj_2007_[v1].doc

5

− liczbę własnych pojazdów w systemie,
− jednostkowe średnie koszty: realizacji zadań własnym pojazdem, realizacji zadań

wynajętym pojazdem, utrzymania własnego pojazdu,

− identyfikator i parametry rozkładu zapotrzebowania na pojazdy.

Wyniki symulacji po kolejnych doświadczeniach eksperymentu symulacyjnego

zapisywane i zapamiętywane są w bazie danych w układzie kolumnowym (rys. 3). W

kolejnych kolumnach tabeli rejestrowane lub obliczane są następujące wielkości:

− numer i-tego symulowanego okresu pracy odpowiadający numerowi doświadczenia

eksperymentu symulacyjnego,

− liczba losowa o rozkładzie równomiernym na przedziale <0;1> będąca podstawą

generowania zapotrzebowania na pojazdy w kolejnych doświadczeniach eksperymentu

symulacyjnego (z wyłączeniem przypadku, w którym zapotrzebowanie na pojazdy opisuje

rozkład normalny),

− symulowana liczba zadań do realizacji L

popyt

(T

i

) w i-tym okresie pracy eksperymentu

symulacyjnego (odpowiada popytowi na pojazdy),

− nadmiar własnych pojazdów L

nad

(T

i

) = L

poj

(T

i

) - L

popyt

(T

i

) w systemie w stosunku do

symulowanej liczby zadań do realizacji,

− całkowity koszt realizacji zadań własnymi pojazdami, obliczany według zależności:

a) gdy L

poj

(T

i

)

≥ L

popyt

(T

i

), to wtedy

( ) (

)

( )

i

popyt

ut

wl

i

wl

T

L

k

k

T

K

⋅

+

=

, (9)

b) gdy L

poj

(T

i

) < L

popyt

(T

i

), to wtedy

( ) (

)

( )

i

poj

ut

wl

i

wl

T

L

k

k

T

K

⋅

+

=

. (10)

− całkowity koszt realizacji zadań wynajętymi pojazdami, obliczany według zależności:

a) gdy L

poj

(T

i

)

≥ L

popyt

(T

i

), to wtedy

( )

0

=

i

wy

T

K

, (11)

b) gdy L

poj

(T

i

) < L

popyt

(T

i

), to wtedy

( )

( )

( )

(

)

i

poj

i

popyt

wy

i

wy

T

L

T

L

k

T

K

−

⋅

=

. (12)

− całkowity koszt utrzymania pojazdu dla których brak jest zadań, obliczany według

zależności:

Plik:

AK_Badanie_Sys_Poj_2007_[v1].doc

6

a) gdy L

poj

(T

i

) > L

popyt

(T

i

), to wtedy

( )

( )

( )

(

)

i

popyt

i

poj

ut

i

nad

T

L

T

L

k

T

K

−

⋅

=

, (13)

b) gdy L

poj

(T

i

)

≤ L

popyt

(T

i

), to wtedy

( )

0

=

i

nad

T

K

. (14)

− całkowity koszt funkcjonowania systemu pojazdów w bieżącym (tzn. i-tym) okresie pracy,

obliczany według zależności:

( )

( )

( )

( )

i

nad

i

wy

i

wl

i

T

K

T

K

T

K

T

K

+

+

=

, (15)

− średni koszt funkcjonowania systemu pojazdów do bieżącego (tzn. i-tego) okresu pracy,

obliczany według zależności:

( )

(

∑

=

⋅

=

i

j

j

i

śr

T

K

i

T

K

1

1

)

. (16)

Użytkownik symulatora Sym_Sys_Poj_1.Xls ma do dyspozycji szereg przycisków, które

pozwalają w wygodny sposób prowadzić badania symulacyjne. Do przycisków przypisano

następujące procedury operacyjne (rys. 3):

− tworzenie arkusza roboczego do przeprowadzenia nowego eksperymentu symulacyjnego

na podstawie arkusza szablonu (przycisk »Utwórz nowy«),

− realizacja kolejnego doświadczenia eksperymentu symulacyjnego (przycisk

»Krok po kroku«),

− pełna realizacja (od doświadczenia bieżącego do doświadczenia odpowiadającego

zadeklarowanej liczbie okresów pracy) eksperymentu symulacyjnego (przycisk

»Uruchom symulację«).

− drukowanie wyników eksperymentu symulacyjnego (przycisk »Drukuj arkusz«).
− całkowite czyszczenie bazy danych z wynikami doświadczeń eksperymentu

symulacyjnego (przycisk »Wyczyść arkusz«),

Plik:

AK_Badanie_Sys_Poj_2007_[v1].doc

7

4. Przykładowy eksperyment symulacyjny

Niech losowy popyt na pojazdy jaki musi zaspokoić system pojazdów określa empiryczny

rozkład prawdopodobieństwa postaci:

⎪

⎪
⎩

⎪⎪

⎨

⎧

≤

<

≤

<

≤

<

≤

≤

=

28

26

25

0

26

24

25

0

24

22

25

0

22

20

25

0

z

.

z

.

z

.

z

.

)

z

,

T

(

p

i

popyt

dla

dla

dla

dla

.

(17)

System wykonuje zadania za pomocą własnych pojazdów i pojazdów wynajętych.

Realizacja w taki sposób zadań transportowych wiąże się z określonymi kosztami.

Jednostkowy średni koszt wykonania zadania własnym pojazdem wynosi 800 zł, zaś

jednostkowy średni koszt wykonania zadania wynajętym pojazdem wynosi 2000 zł.

Dodatkowo, jednostkowy średni koszt utrzymania własnego pojazdu, niezależnie od tego czy

realizuje ona zadania czy też brak dla niego zadań do realizacji, wynosi 360 zł.

Należy wyznaczyć średnie koszty funkcjonowania systemu pojazdów (wyznaczane na

podstawie wzoru (8)) działającego w opisanych warunkach przy różnej liczbie własnych

pojazdów. Na tej podstawie należy ustalić jaką liczbą pojazdów własnych winien

dysponować system aby średnie koszty jego funkcjonowania były jak najmniejsze.

W celu odpowiedzi na postawione pytania przeprowadzono szereg eksperymentów za

pomocą symulatora Sym_Sys_Poj_1.Xls . Sposób przygotowania danych do eksperymentów

symulacyjnych pokazano już na rys. 2. Proces symulacji prowadzono przez M = 600 okresów

pracy – aż do stabilizacji wartości funkcji kryterialnej K

śr

(T)

i

.

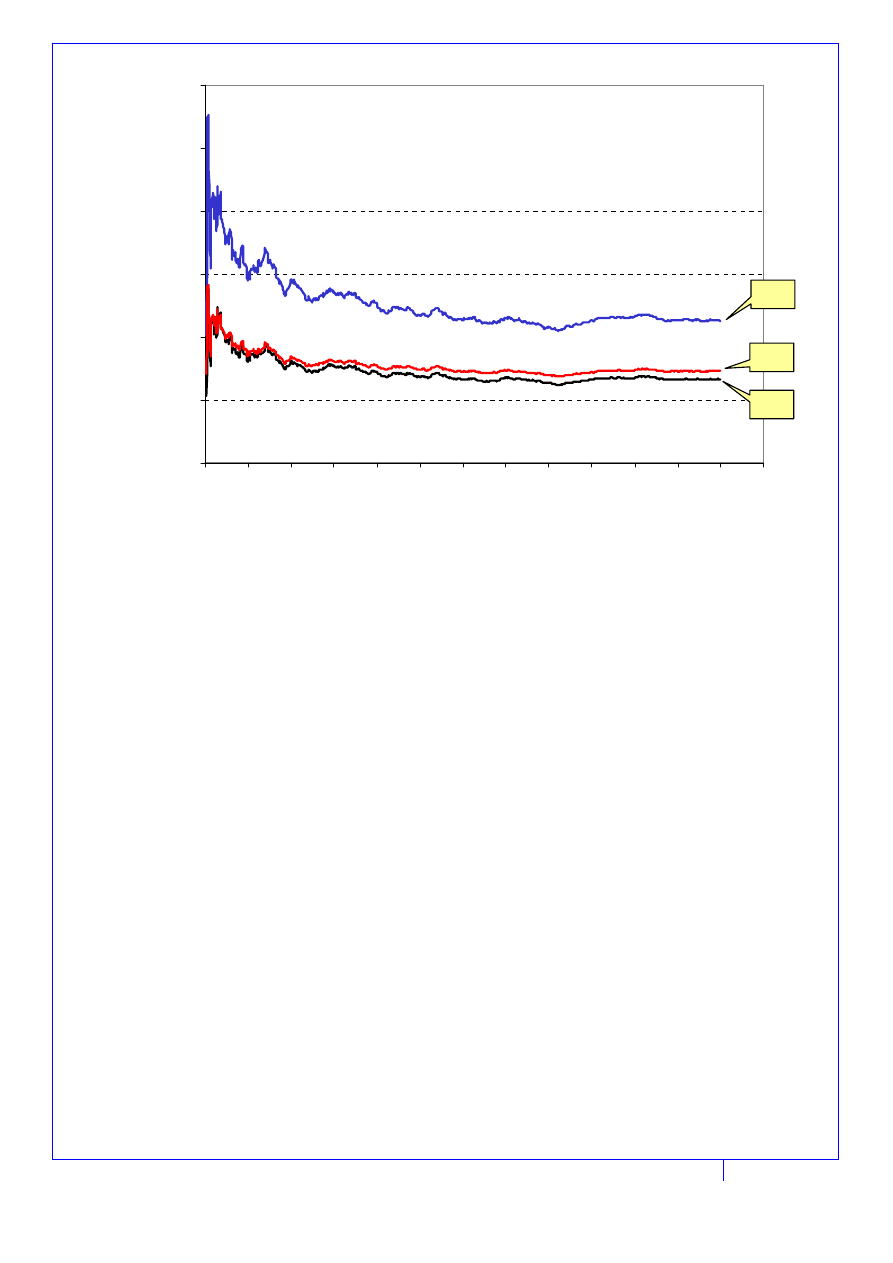
Przykład wyników symulacji kosztów funkcjonowania systemu pojazdów, przeznaczonego

do wykonywania w kolejnych okresach pracy liczby zadań określonej rozkładem

przedstawionym za pomocą formuły (17) a dysponującego do ich realizacji różnymi liczbami

własnych pojazdów, pokazano na rys. 4. Z przeprowadzonych badań symulacyjnych wynika,

że najmniejszą średnią wartością funkcji kryterialnej K

śr

(T)

600

oceny systemu charakteryzuje

się system dysponujący 26 własnymi pojazdami.

Plik:

AK_Badanie_Sys_Poj_2007_[v1].doc

8

27 500

28 500

29 500

30 500

31 500

32 500

33 500

0

50

100

150

200

250

300

350

400

450

500

550

600

650

Czas symulacji - liczba okresów pracy - i

Ś

redni koszt funkcjonowania systemu - K

śr

(T)

i

22

27

26

Rys. 4. Wybrane wyniki symulacji kosztów funkcjonowania systemu pojazdów przeznaczonego

do realizacji losowej liczby zadań a dysponującego różnymi liczbami własnych pojazdów

5. Uwagi końcowe

Operatorzy transportu, zarówno już działający na rynku, jak i nowo wchodzący i/lub

pragnący poszerzyć swoją ofertę

− swój udział w rynku, narażeni są na duże ryzyko

niepowodzenia. Toteż kluczową sprawą jest określenie sposobu dobrego wykorzystania

istniejącego taboru oraz w przypadku wymiany lub rozbudowy parku pojazdów

− umiejętne i

korzystne dokonywanie zakupów inwestycyjnych.

Wychodząc naprzeciw spodziewanym potrzebom dokonywania analiz funkcjonowania

systemów pojazdów w warunkach losowo określonego zbioru zadań przewozowych,

opracowano modele matematyczne i symulator komputerowy. Główną trudnością jednak jest,

nie budowa poprawnych modeli i symulatorów, ale dotarcie do wiarygodnych źródeł

potrzebnych danych do ich weryfikacji. Z tego względu zaprezentowany w tym opracowaniu

przykład obliczeniowy należy traktować jako pokazanie potencjalnych możliwości

opracowanych modeli. Istnieje uzasadniona nadzieja, że w przypadku zainteresowania

prezentowaną tu problematyką operatorów transportowych, będzie łatwiej skłonić ich do

zbierania i udostępniania odpowiednich danych.

Plik:

AK_Badanie_Sys_Poj_2007_[v1].doc

9