13
5. Metodyka doboru obudowy wyrobiska korytarzowego i połączenia
wyrobisk korytarzowych
5.1 Ustalenie
parametrów
wytrzymałościowych
skał
otaczających
projektowane wyrobisko
a) Określenie profilu charakterystycznego.
Najważniejszymi danymi w projektowaniu wyrobisk korytarzowych jest ustalenie
parametrów wytrzymałościowych skał otaczających projektowane wyrobisko. Żeby
określić właściwości wytrzymałościowe masywu, trzeba najpierw ustalić jaki jest profil
geologiczny, charakteryzujący ten rejon, w którym prowadzone będzie wyrobisko.
Określenie tego profilu obejmuje masyw skalny w stropie na 1 wysokości
projektowanego wyrobiska(W
w
) lub szerokości(S
w
), jeśli jest ona większa od
wysokości, i skał spągowych na głębokość połowy wysokości lub szerokości w
zależności od tego co jest większe.
b) Określenie średniej ważonej wartości wskaźnika zwięzłości skał
Po określeniu charakterystycznego profilu geologicznego wylicza się średnią ważoną
wskaźnika zwięzłości skał, a za wagę przyjmuje się grubość i-tej warstwy. Określa się
ją wzorem:
∑
∑
(w. 5.1)
f
i
– wartość wskaźnika zwięzłości w i-tej warstwie
m
i
– grubość i-tej warstwy
c) Określenie średniej-ważonej modułu sprężystości
Wylicza się średnią ważoną modułu sprężystości skał :
∑
∑
(w. 5.2)
Wskaźniki zwięzłości skał i moduły sprężystości przyjmuje się z wyników badań
laboratoryjnych lub wyników z badań penetrometrycznych. Jeśli w rejonie nie były
przeprowadzone takowe badania, można przyjąć właściwości skał z rejonu o podobnej
budowie geologicznej.[10]
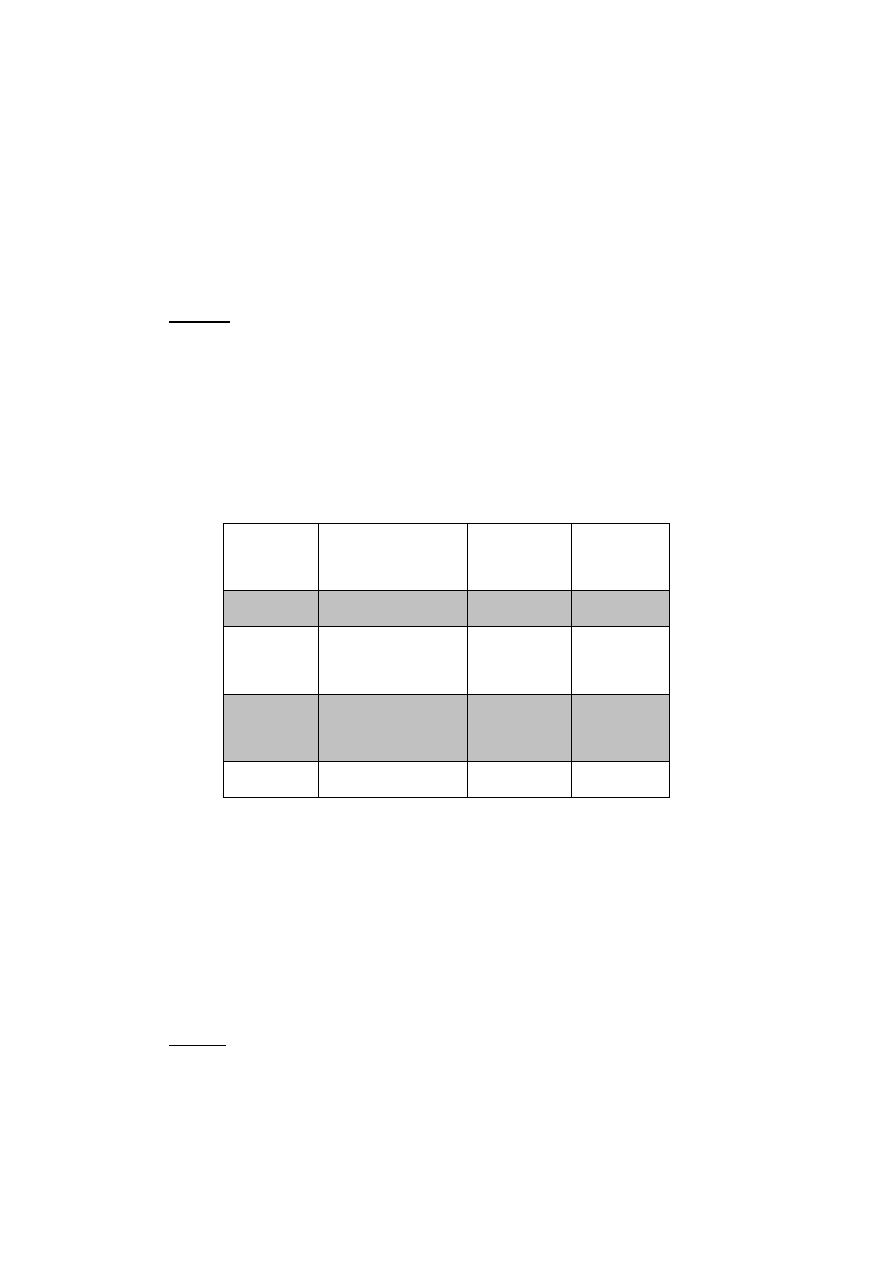
14
5.1.1 Czynniki wpływające na wytrzymałość masywu skalnego w rejonie
projektowanego chodnika odstawczego Aw
a) Określenie podzielności masywu skalnego
Współczynnik podzielności masywu skalnego określa się poprzez współczynniki
osłabienia masywu skalnego ze wzoru :
∑
∑
(w. 5.3)
– wartość współczynnika osłabienia skały w i-tej warstwie, przyjmujemy
z tabeli 5.1.
– miąższość i-tej warstwy.
L
min
– odległości powierzchni płaszczyzny o zmniejszonej wytrzymałości.
Tab. 5.1 Klasyfikacja ze względu na podzielność masywu.
Lp.
Nazwa
klasy
L
min
[m]
d
1
1
Masywna
>2,0
1,0
2
Blokowa
0,5-
2,0
0,9
3
Płytowa
0,1-
0,5
0,7
4
Kostkowa
<0,1
0,5
Jeżeli f jest przyjęte z badań penetrometru to wartość d
1
= 1
b) Określenie współczynnika na działanie wody
Negatywny wpływ wody na właściwości wytrzymałościowe górotworu uwzględnia się
poprzez współczynnik d
2
zwany współczynnikiem rozmakalności. Współczynnik ten
określa się średnią ważoną wyrażoną wzorem:
∑
∑
(w. 5.4)
Jeżeli pomiary penetrometryczne zastaną przeprowadzone w zawodnionym masywie,
wtedy wartość współczynnika wynosi d
2
= 1.
15
c) Określenie wpływu zaburzeń tektonicznych
Wpływ uskoku tektonicznego na jakość masywu skalnego wyraża się za pomocą:
√
(w. 5.5)
h
u
– wysokość zrzutu uskoku, m
α
u
– kąt nachylenia płaszczyzny uskoku.
d) Określenia wpływu zaszłości eksploatacyjnych
Zaszłości poeksploatacyjne maja duży wpływ na wytrzymałość skał, uwzględnia się to
poprzez zmniejszenie wytrzymałości skał.
Gdy wyrobisko znajduje nad zrobami w odległości mniejszej niż pięciokrotna
miąższość wyeksploatowanego pokładu traktuje się go jako zniszczony. Można przyjąć
że współczynnik d
3
= 1,0 ÷ 0,5.
Gdy wyrobisko lokalizowane będzie w odległości większej niż pięciokrotna
wysokość eksploatacyjna ale mniejsza niż 8 krotna wysokość wyeksploatowanego
pokładu, przyjmuje się, że górotwór jest plastyczny, a wartość współczynnika d
3
= 0,5.
Gdy wyrobisko znajduje się w odległości przekraczającej 8 krotną wysokość
wydobytego pokładu można uznać za masyw skalny w strefie uskoku więc
współczynnik d
3
= 1 ale współczynnik d
1
ulega zmniejszeniu o jeden w tabeli.
W przypadku, gdy badanie penetrometryczne wykonane było w rejonie przyszłego
wyrobiska korytarzowego, można uznać, że wyniki badań uwzględniły ten wpływ na
właściwości skał w masywie. Współczynnik d
3
= 1,0.
5.1.2 Określenie wartości wskaźnika zwięzłości skał
Ostateczna wartość wskaźnika zwięzłości skał wyraża się zależnością :
(w. 5.6) [10]
16
5.2 Określenie stanu naprężenia w górotworze w rejonie projektowanego
wyrobiska korytarzowego
5.2.1 Określenie naprężenia w
.
górotworze w rejonie projektowanego wyrobiska
Naprężania pierwotne masywu w rejonie przyszłego wyrobiska wyraża się poprzez:
(w. 5.7)
γ – ciężar objętościowy skał nadległych.
H – głębokość zalegania wyrobiska
5.2.2.
Określenie współczynnika koncentracji naprężeń wynikających z
odziaływania dodatkowych czynników
A. Wpływ zaburzeń tektonicznych.
Wpływ uskoku tektonicznego na jakość masywu skalnego wyraża się za pomocą:
√
(w. 5.8)
h
u
– wysokość zrzutu uskoku, m
α
u
– kąt nachylenia płaszczyzny uskoku.
Jeśli odległość minimalna, jest mniejsza niż wyliczona ze wzoru 5.8 to współczynnik
k
1
= 1,2 w innym przypadku k
1
= 1.
B. Wpływ oddziaływania innych wyrobisk korytarzowych
Istniejące wyrobiska w rejonie projektowanego chodnika wpływają na stan naprężeń
i ten wpływ uwzględnia się poprzez współczynnik koncentracji naprężeń wyrażony
wzorem:
(w. 5.9)
n – ilość wyrobisk korytarzowych oddziałujących na górotwór w rejonie
projektowanego wyrobiska.
k
2
j
– współczynnik koncentracji naprężeń od j-tego wyrobiska .
C. Wpływ oddziaływania krawędzi eksploatacyjnych i resztek pokładów.
Na wielkość naprężenia pionowego w skałach otaczających projektowane wyrobisko
mają wpływ krawędzie eksploatacji oraz resztki pokładów i właśnie ten wpływ wyraża
się poprze współczynnik koncentracji naprężeń k
3
. Aby określić wartość tego
17
współczynnika trzeba przeprowadzić dokładną analizę stanu naprężeń górotworu,
dokonuje się jej różnymi sposobami np.: metoda numeryczna lub analityczna.
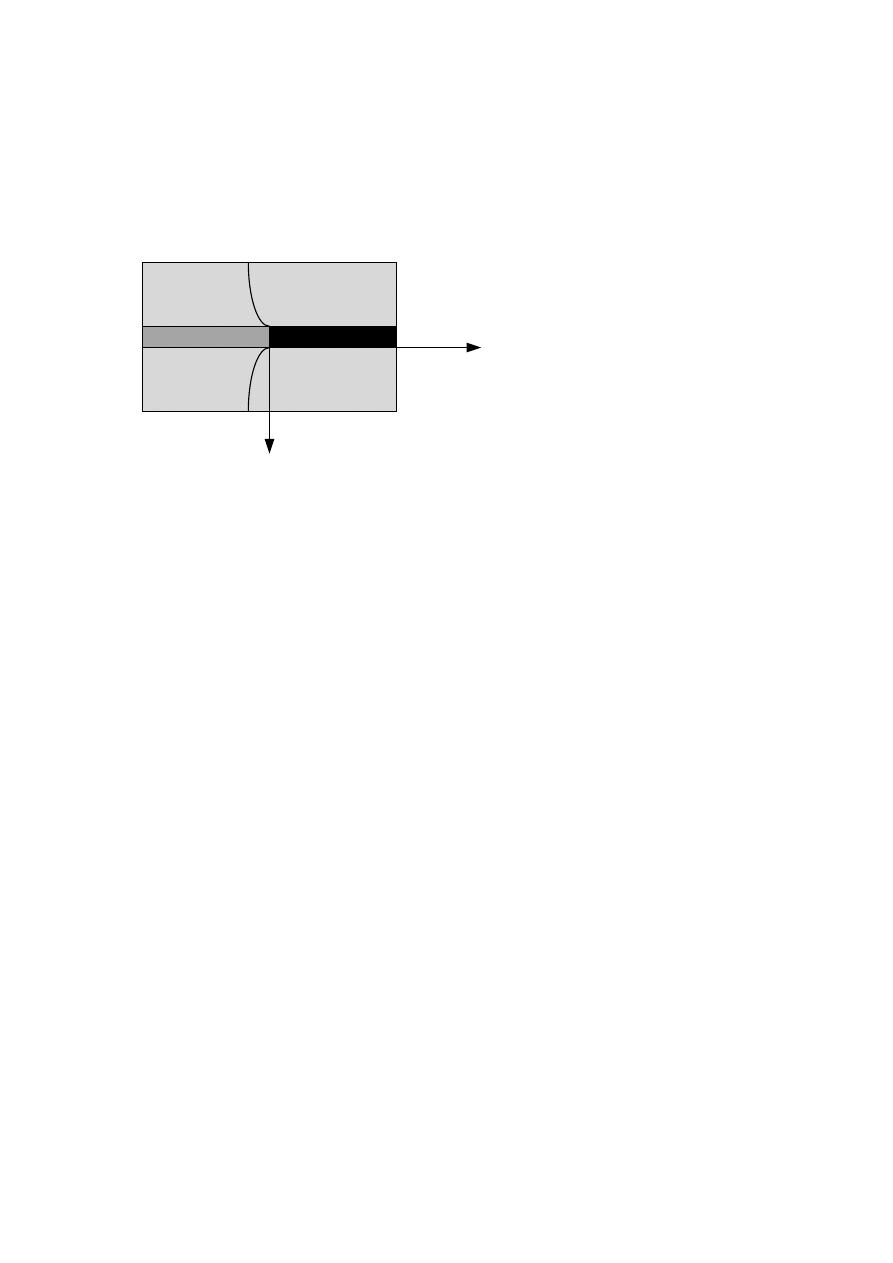
a) Wpływ krawędzi eksploatacji
Jeżeli w rejonie występują krawędzie eksploatacyjne mamy do czynienia z powstaniem
dwóch stref : jedna jest to strefa
odprężona a druga jest to strefa
koncentracji naprężeń.
x – położenie analizowanego punktu względem krawędzi lub brzegu krawędzi lub
resztki.
z – pionowa odległość między projektowanym wyrobiskiem a krawędzią lub resztką
Dla strefy odprężonej:
Dla:
( | |
) (w. 5.10)
Współczynnik koncentracji naprężeń przyjmuje wartość k
3
=1.
Dla strefy koncentracji naprężeń:
Dla:
( | |
) ( | |
) (w. 5.11)
To współczynnik k
3
przyjmuje wartość:
| |
(w. 5.12)
Dla:
( | |
) (w. 5.13)
Współczynnik k
3
przyjmuje wartość:
k
3
=1
Strefa koncentracji
naprężeń
Stefa
odprężona
x
z
Rys. 5.1 schemat obliczeniowy
oddziaływanie krawędzi eksploatacyjnek
18
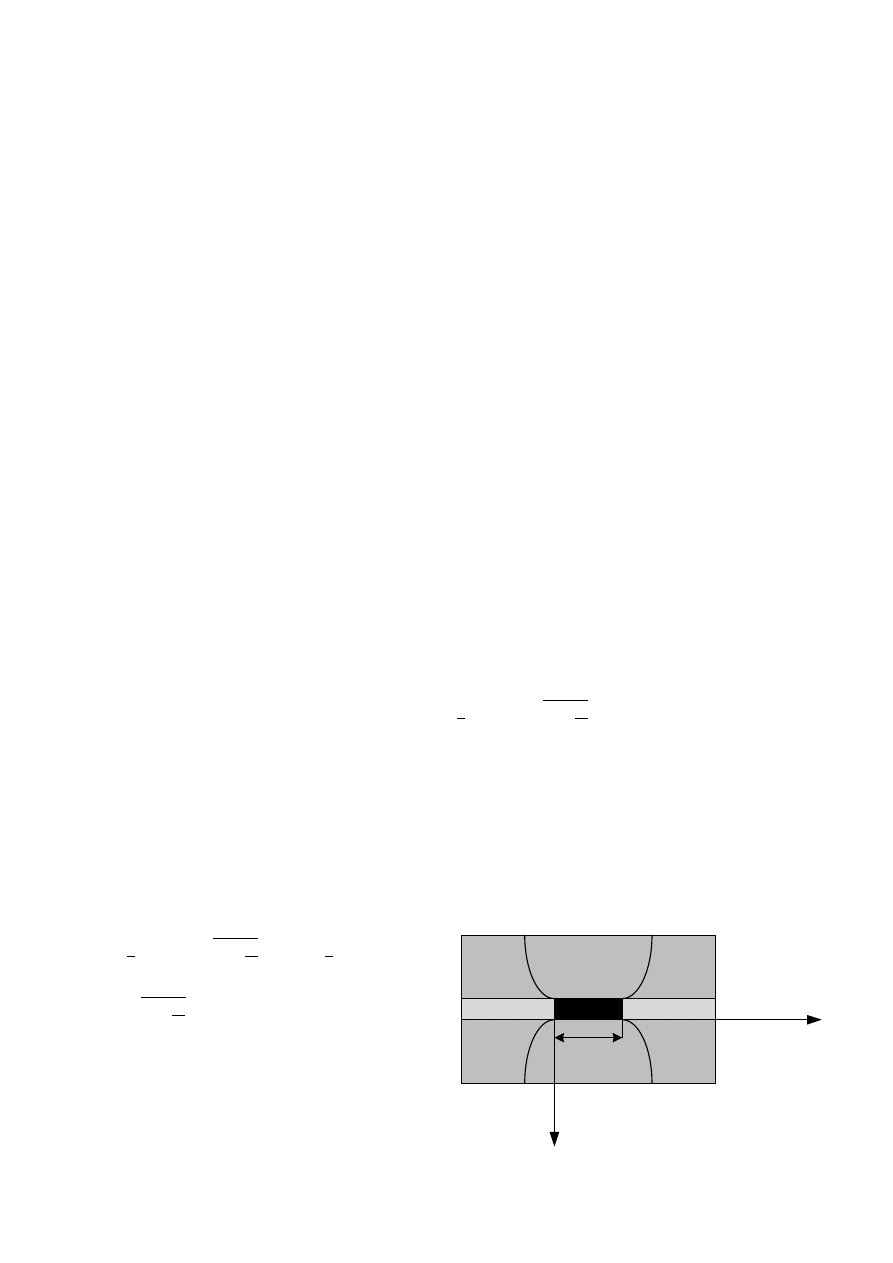
b) Wpływ filarów i resztek
W przypadku występowania filaru lub resztki pokładu powstaje strefa koncentracji
naprężeń i strefy odprężone.
L
f
– szerokość resztki łub pokładu.
x – położenie analizowanego punktu względem krawędzi lub brzegu krawędzi lub
resztki.
z – pionowa odległość między projektowanym wyrobiskiem a krawędzią lub resztką.
Strefy odprężone:
Dla:
(
)
( | |
)[ ] (w. 5.14)
Oraz:
(
)
( | |
) [ ] (w. 5.15)
Spółczynnik k
3
przyjmuje wartość 1
Strefa koncentracji naprężeń:
- jeśli:
(
)
(w. 5.16)
to:
(
)
( | |
)[ ]
( √
) (w. 5.17)
gdzie:
(
)
(w. 5.18)
wartość współczynnika naprężeń wynosi:
(
)| |
(w. 5.19)
Natomiast dla wyrażenia:
( √
)
(
√
) (w. 5.20)
- jeżeli:
(
)
(w. 5.21)
Strefa
koncentracji
naprężeń
Strefa
odprężona
Strefa
odprężona
x
z
L
f
Rys. 5.2 Schemat obliczeniowy oddziaływania
filara lub resztki pokładu
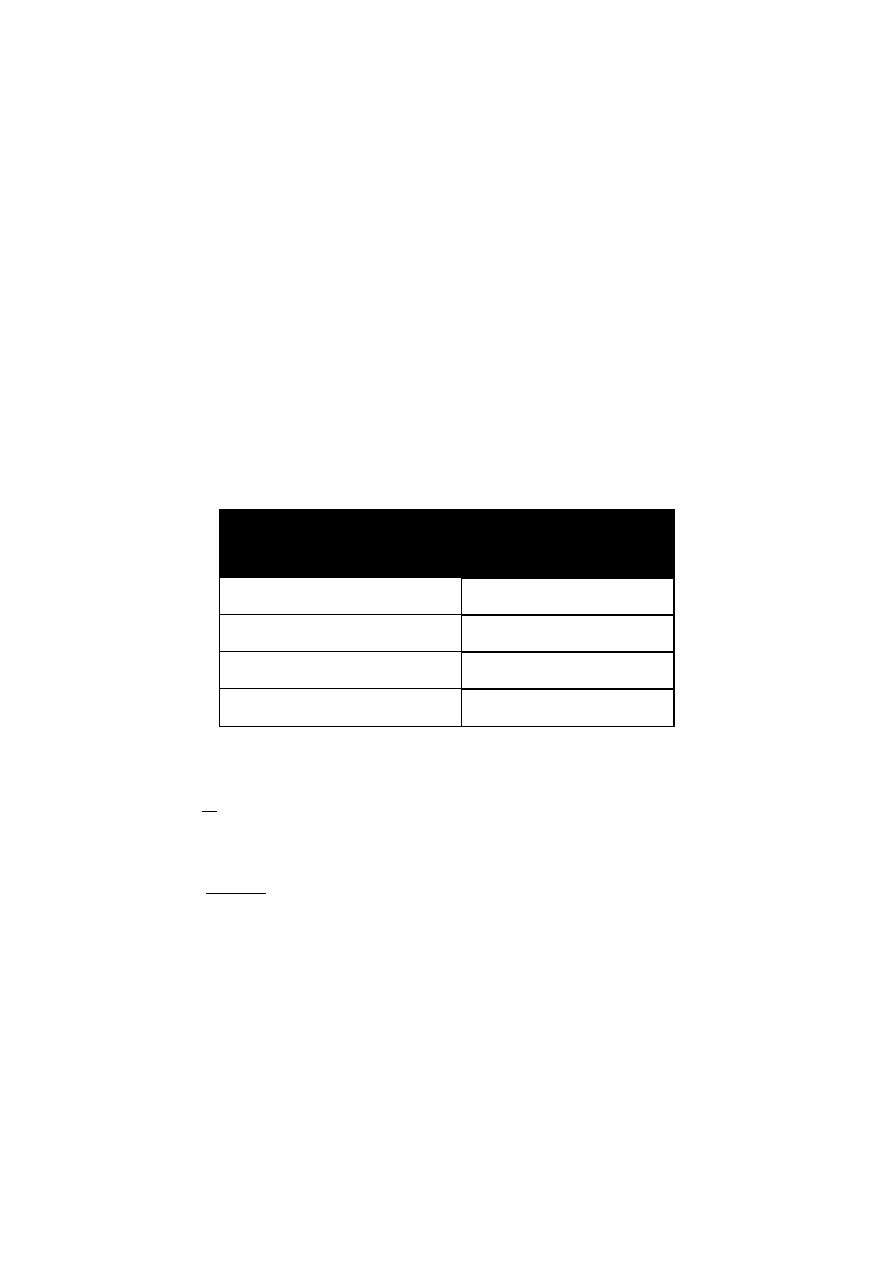
19
to dla:
(
)
( | |
)
(
)
( | |
)
(w. 5.22)
wartość k
3
wynosi:
(
)| |
(w. 5.23)
D. Wpływ oddziaływania nachylenia warstw
Na wielkość i rozłożenie naprężeń w górotwór w rejonie projektowanego wyrobiska
korytarzowego ma kąt zalegania warstw. Wpływ ten uwzględnia się poprzez
współczynnik koncentracji naprężeń k
4
. I przyjmuje on wartości przedstawione w tabeli
5.2.
Tab. 5.2 Wpływ nachylenia warstw na koncentracje naprężeń. [10]
Nachylenie
warstw
w
masywie skalnym [
o
]
Wartość k
4
0 – 15
1,00
15 – 30
1,15
30 – 45
1,25
45<
-
E. Wpływ oddziaływania wstrząsów górotworu
Współczynnik odziaływania wstrząsów górotworu wylicza się ze wzoru:
(w. 5.24)
Gdzie:
(
)
[ ] (w. 5.25)
A
s
– prognozowana energia sejsmiczna wstrząsu ( jeżeli nie ma prognozy wstrząsów
można przyjąć max. wartość energii wstrząsu, który nastąpił w tym rejonie).
r – odległość prawdopodobnego ogniska od wyrobiska.[9]
5.2.3.
Określenie naprężeń górotworu w rejonie projektowego wyrobiska wraz z
uwzględnieniem współczynników koncentracji naprężeń.
W rejonie projektowanego wyrobiska korytarzowego wielkość naprężeń oblicza się z
zależności:
20
(w. 5.26)
Wartość poszczególnych współczynników uzyskujemy z powyżej opisanych operacji
obliczeniowych.
5.3. Określenie oddziaływania górotworu na obudowę wyrobiska
5.3.1. Określenie wielkości oddziaływania górotworu na obudowę ze względu na
stan wytężenia masywu skalnego
Obciążenie stateczne obudowy zależne jest od wielu czynników, a do podstawowych
zaliczają się: gabaryty wyrobiska, zwięzłość skał f , moduł sprężystości E, głębokość
zalegania H, natężenia dodatkowe wynikające z oddziaływania czynników naturalnych i
górniczych. Wielkość obciążenia statycznego górotworu na obudowę wyrobiska można
wyznaczyć za pomocą monogramów, zamieszczonych dalej, które pozwalają
wyznaczyć obciążenia obudowy w oparciu o wartość współczynnika wytężenia
górotworu. Współczynnik wytężenia górotworu wylicza się ze wzoru:
(w. 5.27)
Można też skorzystać z nomogramu do określenia współczynnika wytężenia górotworu,
wykres 5.1, przedstawiającego korelacje współczynnika wytężania górotworu,
naprężenia w górotworze oraz współczynnika zwięzłości skał f.
Gabaryty wyrobiska uwzględnia się poprze zastosowanie współczynnika szerokości
zastępczej:
(w. 5.28)
k
p
– współczynnik kształtu przekroju.
Dla wyrobiska w kształcie obudowy ŁP k
p
= 1,0
Dla wyrobiska w kształcie prostokąta k
p
= 1,25
W celu określenia obciążenia obudowy q
o
, należy obliczyć parametr charakteryzujący
stan górotworu:
(w. 5.29)
gdzie:
n
sg
– parametr charakteryzujący stan górotworu
n
e
– parametr charakteryzujący właściwości odkształceniowe górotworu
n
w
– współczynnik wytężenia górotworu
21
Wartość parametru charakteryzującego właściwości odkształceniowe górotworu n
e
wyznacza się z, nomogramu do określenia wartości parametru charakteryzującego
własności odkształceniowe górotworu, wykres 5.2, w oparciu o wartości modułu
sprężystości E
śr
( jeżeli wartości wykorzystywane są z badań penetrometrycznych wtedy
wykorzystujemy zależność 0,7 E
śr
) oraz wskaźnika zwięzłości skał f
śr
.
Po wyznaczeniu parametru charakteryzującego stan górotworu n
sg
oraz zastępczej
szerokości wyrobiska S
w
, z nomogramów, wykresy 5.3 – 5.6, możemy wyznaczyć
wartość współczynnika obciążenia statycznego obudowy wyrobiska(q
0
). W naszym
przypadku wyznaczamy go z nomogramu do określenia obciążenia obudowy dla
parametru charakteryzującego stan górotworu od 0,5 do 1,0, wykres 5.4.
5.3.2. Określenie dynamicznego oddziaływania na obudowę spowodowane
wstrząsem tektonicznym
Dynamiczne oddziaływanie górotworu na obudowę projektowanego chodnika można
określić za pomocą:
Odziaływanie wstrząsu przejawia się poprzez zwiększenie naprężeń wywołującym
zwiększenie strefy spękań oraz nadanie skałom znajdującym się w strefie odprężonej
prędkości początkowej.
a) Wzrost naprężeń wywołujący wzrost strefy spękań opisuje się poprzez
współczynnik k
d
:
(w. 5.30)
gdzie:
(
)
(w. 5.31)
A
s
– prognozowana energia sejsmiczna [J]
R – odległość prawdopodobnego ogniska
b) Nadanie skałom dodatkowej energii wyraża się poprzez obciążenie dynamiczne q
d
:
(w. 5.32)
gdzie:
(
)
(w. 5.33)
22
Całkowite obciążenie obudowy wyrobiska korytarzowego w warunkach gdy występują
wstrząsy górotworu, wyraża się następującym wzorem:[10]
(w. 5.34)
5.4. Określenie parametrów wytrzymałościowych obudowy projektowanego
wyrobiska
Parametry wytrzymałościowe obudowy projektowanego wyrobiska określa się na
podstawie wytężenia górotworu i ze względu na dynamiczne oddziaływanie wstrząsów
górotworu.
Dla typowych warunków obciążenia obudowy oraz obliczonej wartości obciążenia
statycznego obudowy wymaganą odległość pomiędzy odrzwiami d
o1
dla profilu V-29
oraz dla gabarytów projektowanego wyrobiska wyznaczamy z nomogramu do
określenia odległości pomiędzy odrzwiami obudowy ŁP ze względu na wytrzymałości
profilu, wykres 5.8 , typ wykładki dobry, opinka ciągła. Na podstawie nomogramu do
określenia odległości pomiędzy odrzwiami obudowy ŁP ze względu na nośność
zamka, wykres 5.9. Z nomogramu odczytuje się odległość zastępczą d
zast
, na
podstawie której oblicza się odległość d
o2
z wzoru:
(w. 5.35)
gdzie:
N
z
– nośność złącza odrzwi odczytujemy z tabeli 5.3.
d
zast
– zastępcza odległość między odrzwiami obliczona dla nośności zamka wynoszącej
100 kN.
23
Tab. 5.3 Wartość nośności najczęściej stosowanych złączy obudowy ŁP. [10]
Typ
złącza
N
z
[kN] dla wartości momentu dokręcenia śrub M
d
[Nm]
200
300
350
400
450
500
550
600
K25
160
220
K29
200
ZS25
160
250
300
ZS29
160
270
350
400
425
ZS36
295
345
350
470
SD25
170
SD29
240
SD36
295
345
350
470
Wymagana minimalna odległość pomiędzy odrzwiami obudowy ŁP wynosi:
(
) (w. 5.36) [10]
5.5. Zasady ustalenia parametrów wytrzymałościowych skał otaczających
projektowanego połączenia wyrobisk
Dla projektowanego połączenia wyrobisk ustala się charakterystyczny profil
geologiczny górotworu tak sama jak zrobiono to dla wyrobiska korytarzowego oraz
określa się też wskaźnik zwięzłości skał oraz moduł sprężystości skał. Obliczenia
przeprowadza się tak jak w punkcie 5.1 tego rozdziału. [10]
5.6. Określenie stanu naprężenia w górotworze w rejonie projektowanego
połączenia wyrobisk korytarzowych
Dla projektowanego połączenia wielkość naprężeń oblicza się tak jak dla wyrobiska
korytarzowego, zgodnie z punktem 5.2 tego rozdziału.[10]
5.7. Określenie oddziaływania górotworu na obudowę rozgałęzienia pod
kątem prostym ze względu na stan wytężenia masywu skalnego
W przypadku odgałęzienia pod kątem prostym wielkość oddziaływania na obudowę
tego rozgałęzienia określona jest dla trzech stref:
- I strefa – to przestrzeń wspólna dla obydwóch chodników.
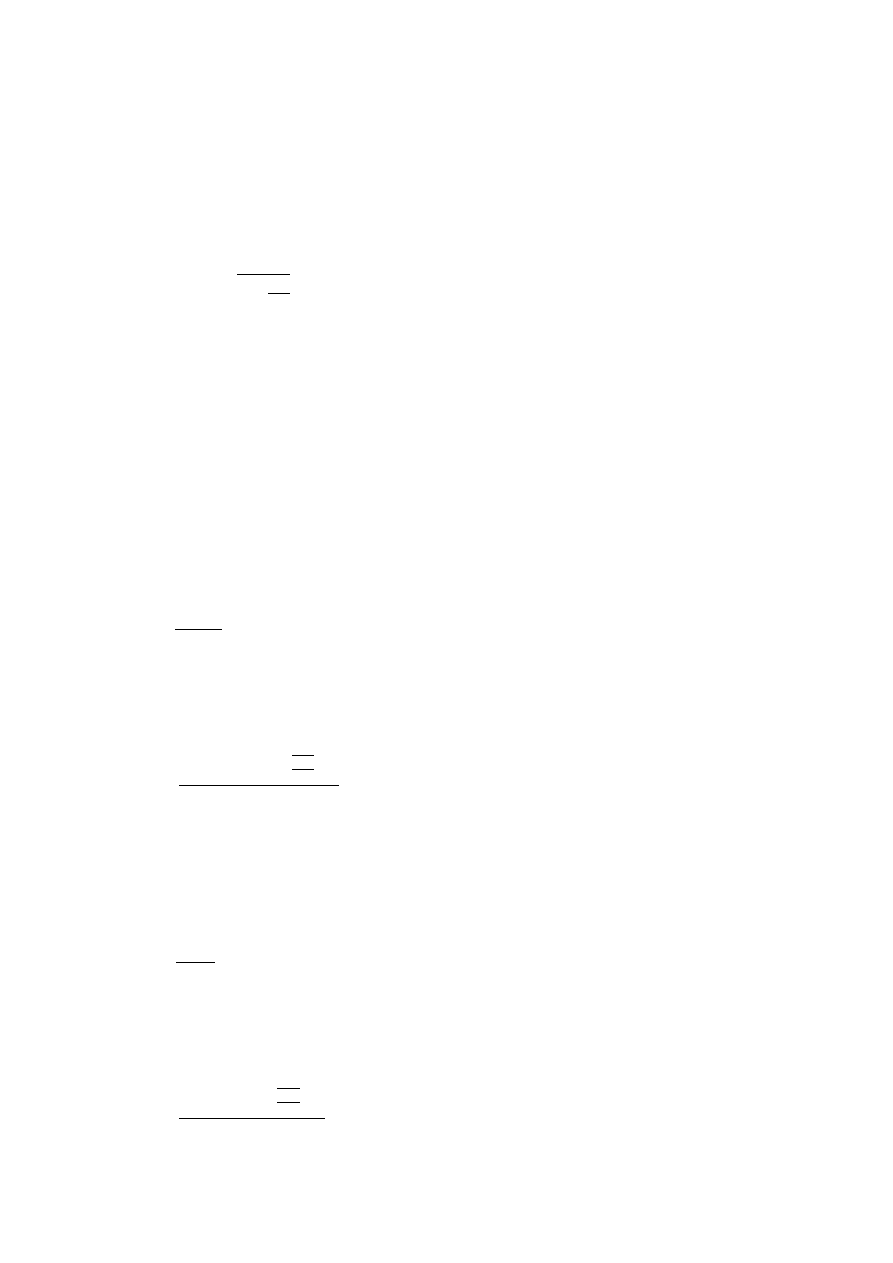
24
- II strefa – to części chodnika głównego z którego odchodzi rozgałęzienie,
- III strefa – obejmuje początek wyrobiska odgałęziającego się, część ta przylega do
chodnika głównego.
Strefa I
Dla strefy I wyznacza się maksymalną szerokość wyrobiska:
√
(w. 5.37)
W oparciu o tę szerokość oraz wyliczone i określone wcześniej parametry
wytrzymałości i stanu naprężeń masywu w rejonie projektowanego wyrobiska.
Obciążenie statyczne obudowy dla tego odcinka odgałęzienia wyznacza się jak dla
wyrobiska korytarzowego. Wyznaczając współczynnik koncentracji naprężeń
korzystamy z wzoru, jak dla strefy II. W tym celu korzystamy z nomogramów,
wykresy 5.3-5.6.
Strefa II
W strefach II i III występuje wzrost naprężeń co jest spowodowane wzajemnym
odziaływaniem wyrobisk na siebie. Wyliczamy zasięg strefy II:
(w. 5.38)
Dla tej strefy obciążenie obliczeniowe q
o
określa się jak dla pojedynczego wyrobiska
biorąc pod uwagę średnią wielkość koncentracji naprężeń dla tego odcinka, wytężenie
górotworu określa się wzorem:
[ ( √
)]
(w. 5.39)
Następnie określa się obciążenie statyczne obudowy. W tym celu korzystamy z
nomogramów, wykresy 5.3-5.6.
Strefa III
Zasięg strefy III wyliczamy z:
(w. 5.40)
Tak jak poprzednio, obciążenie obliczeniowe q
o
określa się jak dla pojedynczego
chodnika. Uwzględniając średnią wartość koncentracji naprężeń dla tego odcinka,
wytężenie górotworu określa się wzorem:
[ ( √
)]
(w. 5.41)
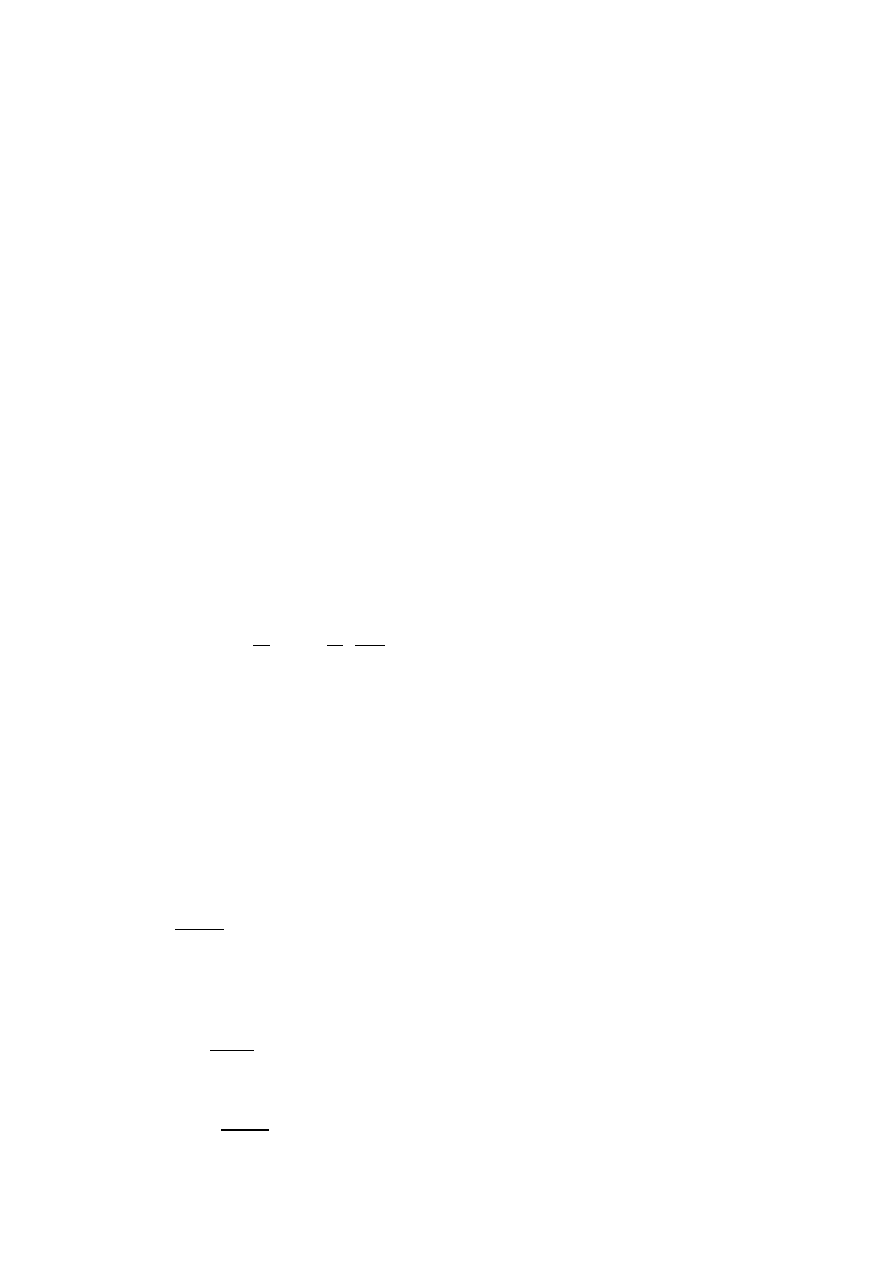
25
Następnie określa się obciążenie statyczne obudowy. W tym celu korzystamy z
nomogramów, wykresy 5.3-5.6. [10]
5.8. Określenie wymaganej nośności obudowy połączenia
Odległości pomiędzy odrzwiami obudowy, w strefach I ,II i III, wylicza się tak jak dla
wyrobiska korytarzowego przyjmując:
- obciążenie obudowy wyliczone q
o
wyznaczone, dla poszczególnych stref, w
podpunkcie 5.3 tego rozdziału.
- szerokość wyrobiska S
w
określona jest jak w podpunkcie 5.7.
Wymagany krok obudowy określany jest za pomocą nomogramów, wykresy 5.7-5.8
Następnym krokiem w obliczeniach statycznych odrzwi jest określenie obciążenia
pozostałych elementów konstrukcyjnych, w tym przypadku podciągów.
Podciągi oblicza się jako belki podparte, w miejscach zamocowania ich do odrzwi
obudowy, obciążonymi siłami skupionymi w miejscach, w których oparte na nich są
odrzwia.
Obliczono wielkość siły skupionej która obciąża i-ty podciąg:
(
)
(w. 5.42)
P
Oi
– wielkość siły skupionej obciążający i-ty podciąg, [kN]
q
o
– wartość obciążenia statycznego oddziałującego na obudowę, [kPa]
S
w
– szerokość wyrobiska, [m]
x
p
– odległość podciągu od środka wyrobiska, [m]
n
pod
– liczba podciągów zastosowanych do wzmocnienia obudowy.
d – krok odrzwi obudowy wyrobiska, [m]
Przeliczono obciążenie punktowe sił skupionych na obciążenie ciągłe;
∑
(w. 5.43)
L
pod
– długość podciągu.
Następnie wyliczono maksymalny moment zginający :
(w. 5.44)
Wielkość reakcji w miejscach podparcia podciągów wyliczono z wzoru:
∑
(w. 5.45)
26
Zaprojektowany projekt musi spełniać zależność:
(w. 5.46)
M
g dop
– dopuszczalna wartość momentu zgniatającego dla profilu stropnicy
odczytujemy z tabeli 5.4.
Tab.5.4 Zestawienie parametrów wytrzymałościowych dla niektórych kształtowników
stosowanych jako stropnice.
Lp.
Rodzaj kształtownika
W
x
[cm
3
]
M
g
dop
[kNm]
1
V-29
93,7
64,28
2
V-44
173,6
119,09
3
s-149
241,0
172,00
4
I-260
442,0
303,3
Odrzwia podtrzymujące podciągi zabudowane są w rejonie naroży odgałęzienia. Są
one szczególnie narażone na deformacje jest to spowodowane tym że na te odrzwia
oddziałuje obciążenia q
o
obliczonym dla strefy I ale także dodatkowej siłami
skupionymi pochodzącymi od podciągów. Wielkość sił skupionych jest zależna od
ilości podciągów, a miejsce występowania sił skupionych jest zależne od miejsca
podwieszenia podciągów. Aby wyliczyć jak obciążony są odrzwia obudowy
zamieniamy obciążenia punktowego siły skupionej na obciążenia ciągłe:
∑
(w. 5.47)
q
o
– wartość obciążenia obudowy wynikające z wytężenia górotworu,
P
oi
– wielkość siły skupionej w miejscu utwierdzenia i-tego podciągu,
Parametry wytrzymałościowe odrzwi obudowy określa się tak jak dla wyrobiska
korytarzowego. Jeżeli wyznaczona tą drogą odległość jest mniejsza niż odległość
planowana w pozostałej części strefy, odrzwia podtrzymujące podciągi należy
wykonać jako odrzwia podwójne. [10]