Obliczanie zwarć symetrycznych
Obliczanie zwarć symetrycznych
2 / 31
Wiadomości wstępne
Wiadomości wstępne
Klasyfikacja zwarć:
symetryczne i niesymetryczne
trwałe i przemijające
metaliczne (bezpośrednie) i oporowe (występujące
za pośrednictwem impedancji np. łuku elektrycznego)
jednoczesne i niejednoczesne
pojedyncze i wielomiejscowe
Częstość występowania zwarć:
Zwarcie jednofazowe – średnio 65% (od 30% do 97%)
Podwójne zwarcie z ziemią i zwarcie dwufazowe z ziemią –
średnio 20% (od 0% do 55%)
Dwufazowe – średnio 10% (od 0% do 55%)
Trójfazowe - średnio 5% (od 0% do 35%)
3 / 31
Przyczyny zwarć
Przyczyny zwarć
Przyczyny elektryczne:
Przepięcia atmosferyczne
Przepięcia łączeniowe
Omyłki łączeniowe
Długotrwałe przeciążenia prądowe
Przyczyny nieelektryczne:
Zawilgocenie izolacji linii, urządzeń
Zanieczyszczenie izolatorów
Uszkodzenia mechaniczne kabli, słupów, izolatorów
Wady fabryczne urządzeń
Ingerencja zwierząt np. ptaki, gryzonie
Przewracające się lub nadmiernie wysokie drzewa, itp.
4 / 31
Przyczyny zwarć
Przyczyny zwarć
-
-
przykłady
przykłady
5 / 31
Przyczyny zwarć
Przyczyny zwarć
-
-
przykłady
przykłady
6 / 31
Przyczyny zwarć
Przyczyny zwarć
-
-
przykłady
przykłady
7 / 31
Skutki prądów zwarciowych
Skutki prądów zwarciowych
Działanie cieplne i dynamiczne
•
Zwarcie powoduje znaczne przetężenia prądowe, którym towarzyszy
energia cieplna proporcjonalna do kwadratu prądu i czasu trwania
zwarcia. Czas trwania zwarcia zależy od czasu działania zabezpieczeń
zwarciowych.
Zagrożenie porażeniowe
•
Spowodowane przepływem prądu do ziemi i powstawaniem napięć
dotykowych i krokowych o dużej wartości.
Zapady napięcia i przepięcia
•
Duża wartość prądu zwarciowego powoduje duży spadek napięcia na
elementach sieci, czego efektem jest obniżenie napięcia w węzłach
odbiorczych, tzw. zapad. Przepięcia towarzyszą zwarciom doziemnym.
Zagrożenia spowodowane łukiem elektrycznym
Skutki sieciowe i systemowe
•
Związane z wyłączeniem fragmentów sieci objętych zakłóceniem
8 / 31
Przypadkowe dotknięcie przewodów linii
napowietrznej przez dźwig.
Skutki zwarć
Skutki zwarć
-
-
przykład
przykład
9 / 31
Skutki zwarć
Skutki zwarć
-
-
przykład
przykład
10 / 31
(
)
ω + γ = +
0
di
2 Esin t
Ri L
dt
( )
(
)
(
)
−
=
ω + γ − ϕ −
⋅
⋅
γ − ϕ
R
t
L
0
z
0
z
2 E
2 E
i t
sin t
e
sin
Z
Z
( )
2
2
Z
R
L
=
+ ω
ω
ϕ =
z
L
arctg
R
Przebieg
Przebieg
prądu zwarciowego
prądu zwarciowego
–
–
zwarcia odległe
zwarcia odległe
Zwarcie ze stanu
jałowego
Warunek początkowy:
−
=
=
i(t 0 ) 0
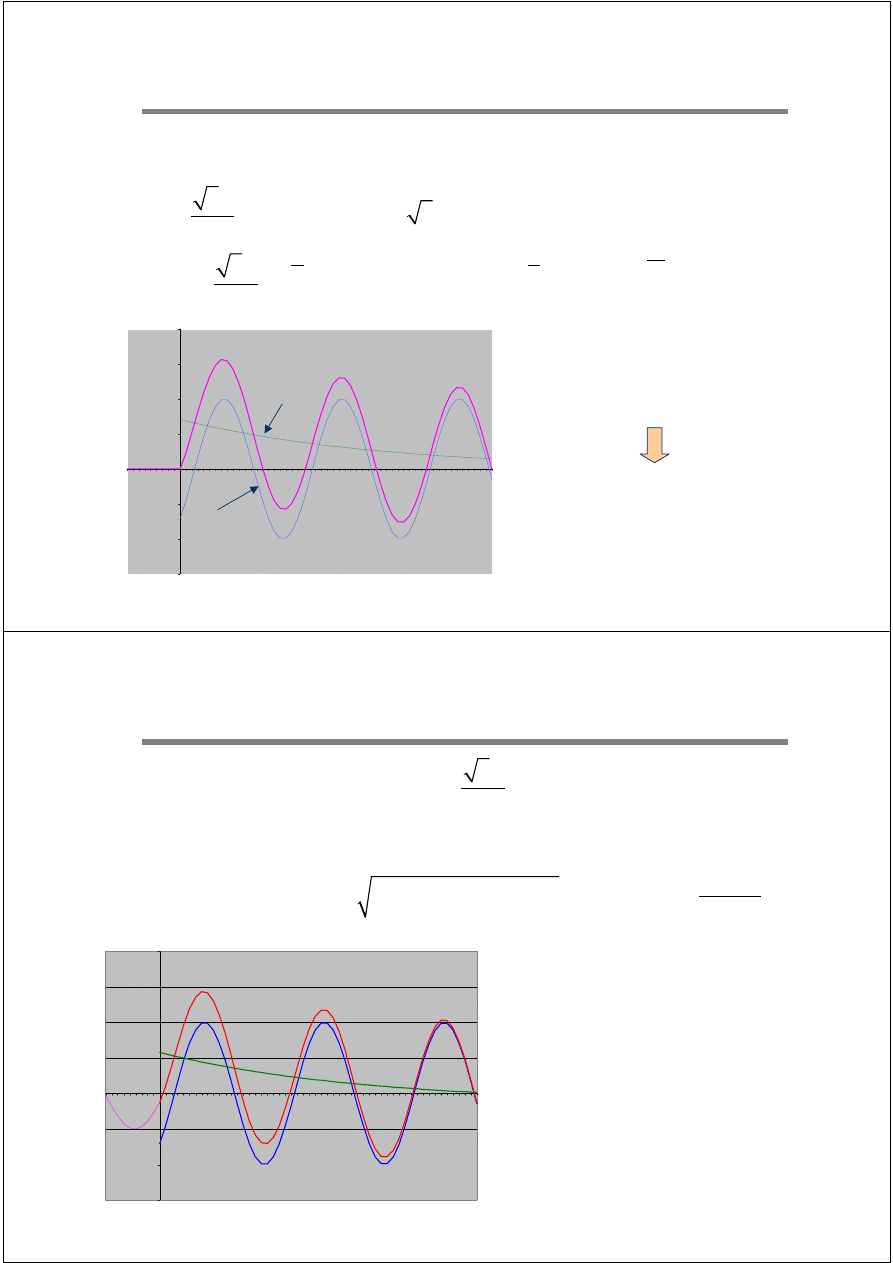
11 / 31
( )
( )
( )
ok
nok
i t
i
t
i
t
=
+
( )
(
)
(
)
=
ω + γ − ϕ =
ω + γ − ϕ
ok
0
z
ok
0
z
2 E
i
t
sin t
2I sin t
Z
( )
(
)
−
−
−
= −
⋅
⋅
γ − ϕ =
⋅
=
⋅
a
t
R
R
t
t
T
L
L
nok
0
z
nokm
nokm
2 E
i
t
e
sin
i
e
i
e
Z
Dla czasu t=0:
i
ok
(0)= - i
nok
(0)
Przebieg
Przebieg
prądu zwarciowego
prądu zwarciowego
–
–
zwarcia odległe
zwarcia odległe
−
= = =
i(0) 0 i(t 0 )
-1,5
-1
-0,5
0
0,5
1
1,5
2
i
ok
i
onk
12 / 31
( )
(
)
ob
0
ob
ob
2 E
i
t
sin t
Z
=
⋅
ω + γ − ϕ
(
) (
)
=
+
+
+
2
2
ob
o
o
Z
R R
X X
+
ϕ =
+
o
ob
o
X X
arctg
R R
( )
( )
( )
( )
−
=
=
=
=
+
ob
ok
nok
i 0
i(0 ) i
0
i
0
i
0
( )
( )
( )
=
=
= −⎡
−
⎤
⎣
⎦
nok
nokm
ok
ob
i
0
i
i
0
i
0
-1,5
-1
-0,5
0
0,5
1
1,5
2
Przebieg
Przebieg
prądu zwarciowego
prądu zwarciowego
–
–
zwarcia odległe
zwarcia odległe
Zwarcie ze stanu
obciążenia
Warunek początkowy:
−
=
=
ob
i(t 0 ) i
13 / 31
Przebieg
Przebieg
prądu zwarciowego
prądu zwarciowego
–
–
zwarcia odległe
zwarcia odległe
Przebiegi prądu zwarciowego w trzech
fazach układu trójfazowego,
przy
0
=0, φ
z
=90°
Faza R
Faza T
Faza S
14 / 31
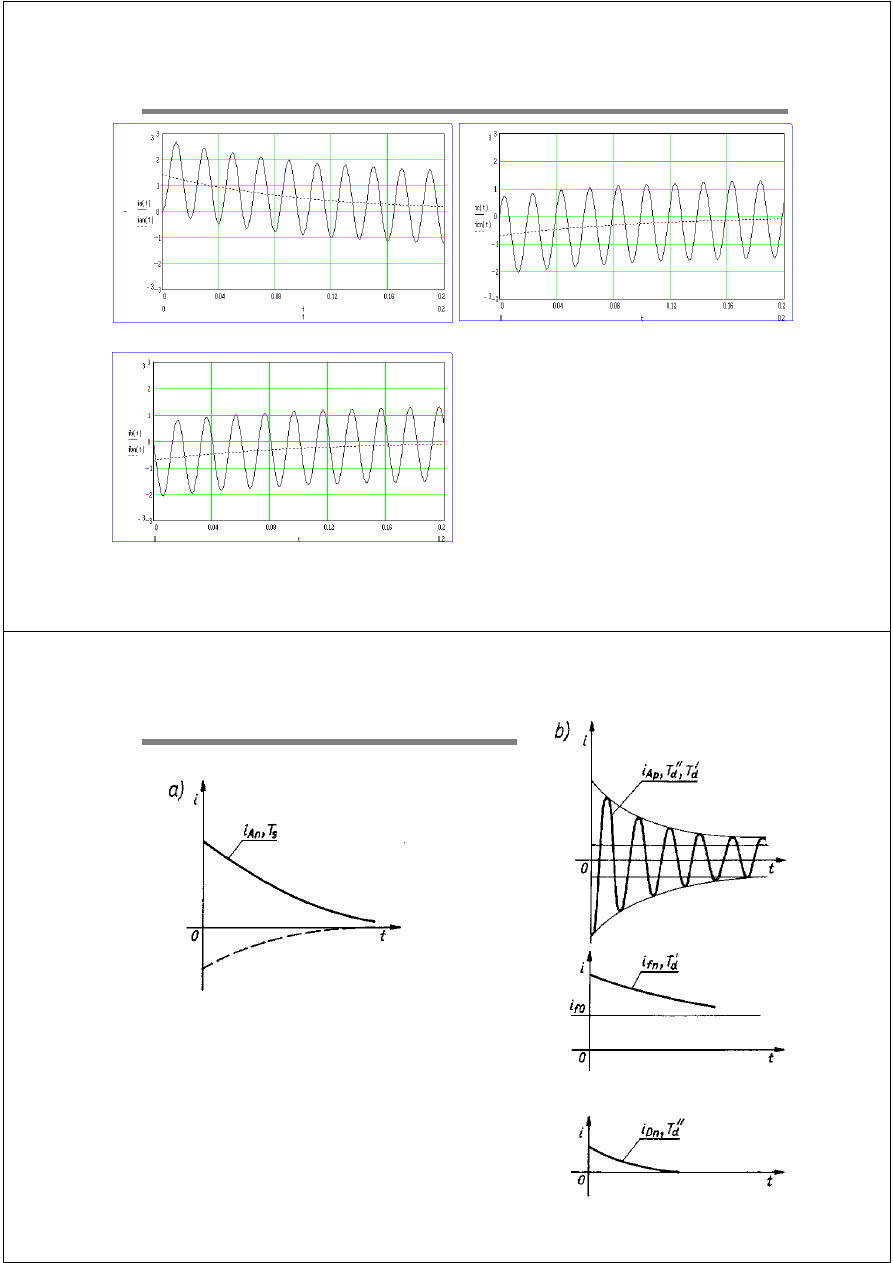
a) Składowa aperiodyczna prądu
stojana
b) Składowa okresowa prądu stojana
oraz prądy wirnika, które ją wywołały
Zwarcie w pobliżu generatora
Zwarcie w pobliżu generatora
Prąd w
uzwojeniu
wzbudzającym
Prąd w
uzwojeniu
tłumiącym
15 / 31
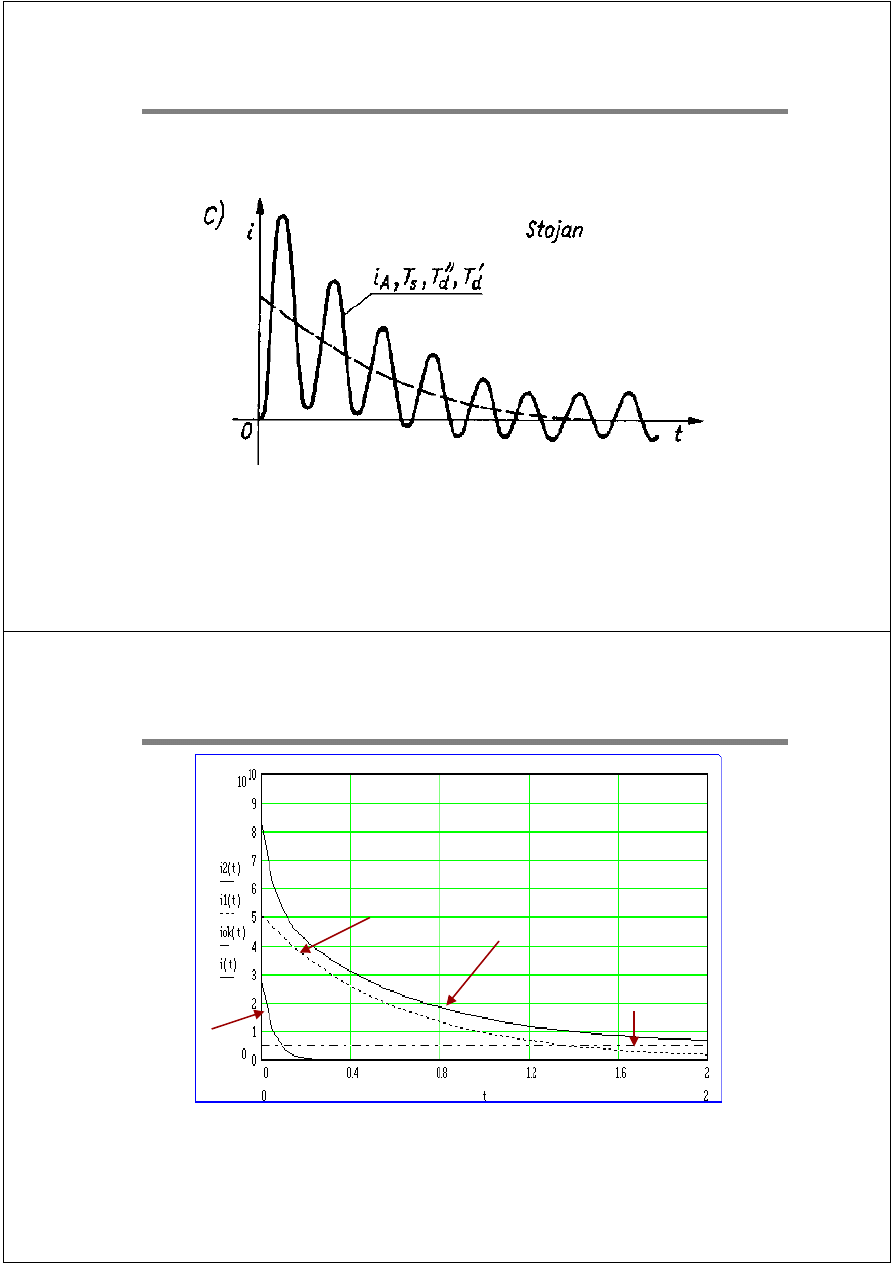
Całkowity prąd stojana
Zwarcie w pobliżu generatora
Zwarcie w pobliżu generatora
16 / 31
Zwarcia pobliskie
Zwarcia pobliskie
Przebieg wartości skutecznych składowych okresowych prądu zwarciowego;
zwarcie na zaciskach generatora nieobciążonego.
Składowa
nadprzejściowa
Składowa
przejściowa
Prąd okresowy
Składowa
ustalona
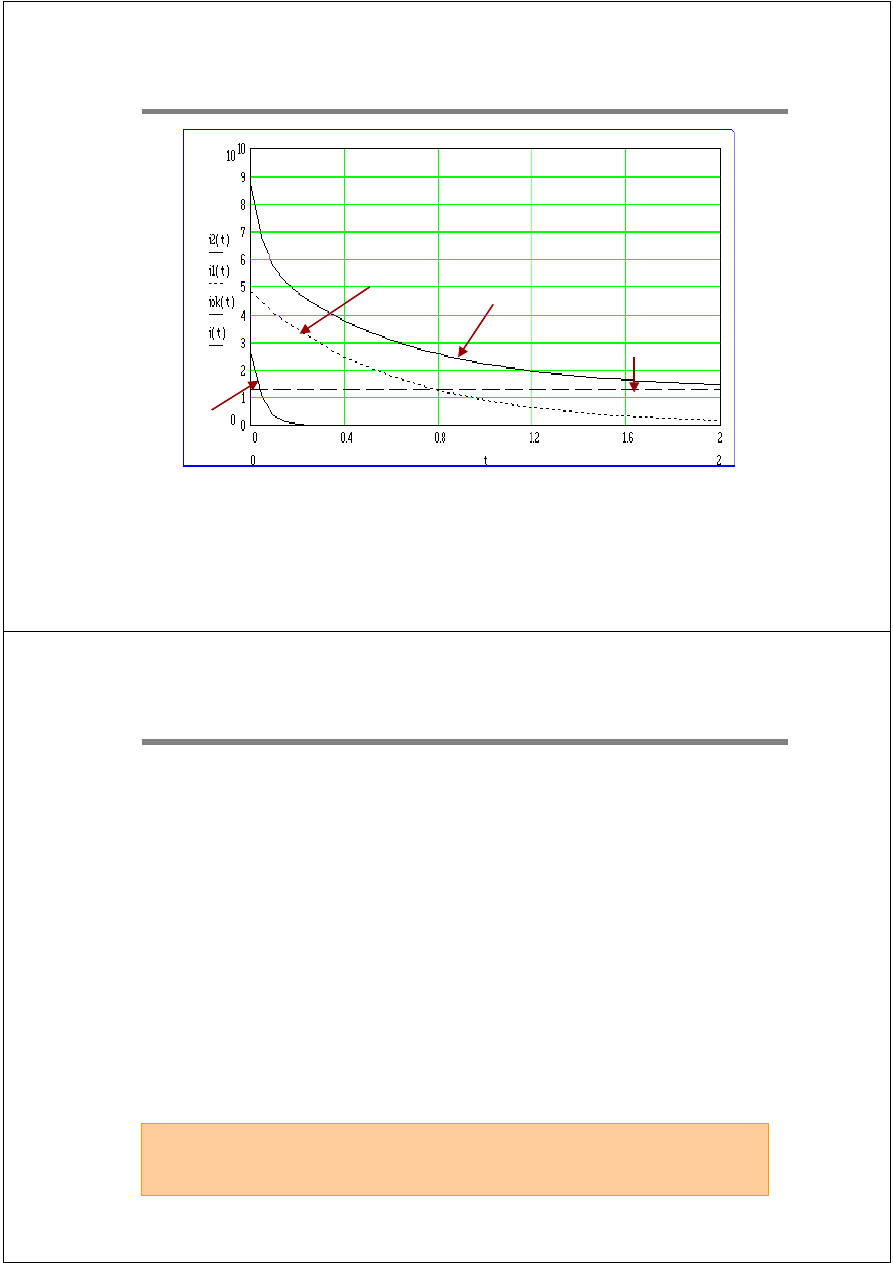
17 / 31
Zwarcia pobliskie
Zwarcia pobliskie
Przebieg wartości skutecznych składowych prądu zwarciowego;
zwarcie na zaciskach generatora obciążonego znamionowo.
Składowa
nadprzejśiowa
Składowa
przejśiowa
Prąd okresowy
Składowa
ustalona
18 / 31
Obowiązuje norma PN /E-05002, będąca tłumaczeniem dokumentu
IEC 909/1988
U podstaw metody leży podstawowe twierdzenie teorii obwodów –
twierdzenie Thevenina.
Normatywna metoda obliczania prądu zwarciowego
Normatywna metoda obliczania prądu zwarciowego
Cel obliczeń zwarciowych:
Dobór urządzeń elektroenergetycznych ze względu na
wytrzymałość cieplną i mechaniczną
Dobór przekrojów przewodów i kabli
Zaprojektowanie konfiguracji sieci elektroenergetycznych
Dobór szyn zbiorczych w rozdzielniach
Dobór nastawień zabezpieczeń elektroenergetycznych
Ocena skuteczności ochrony przeciwporażeniowej
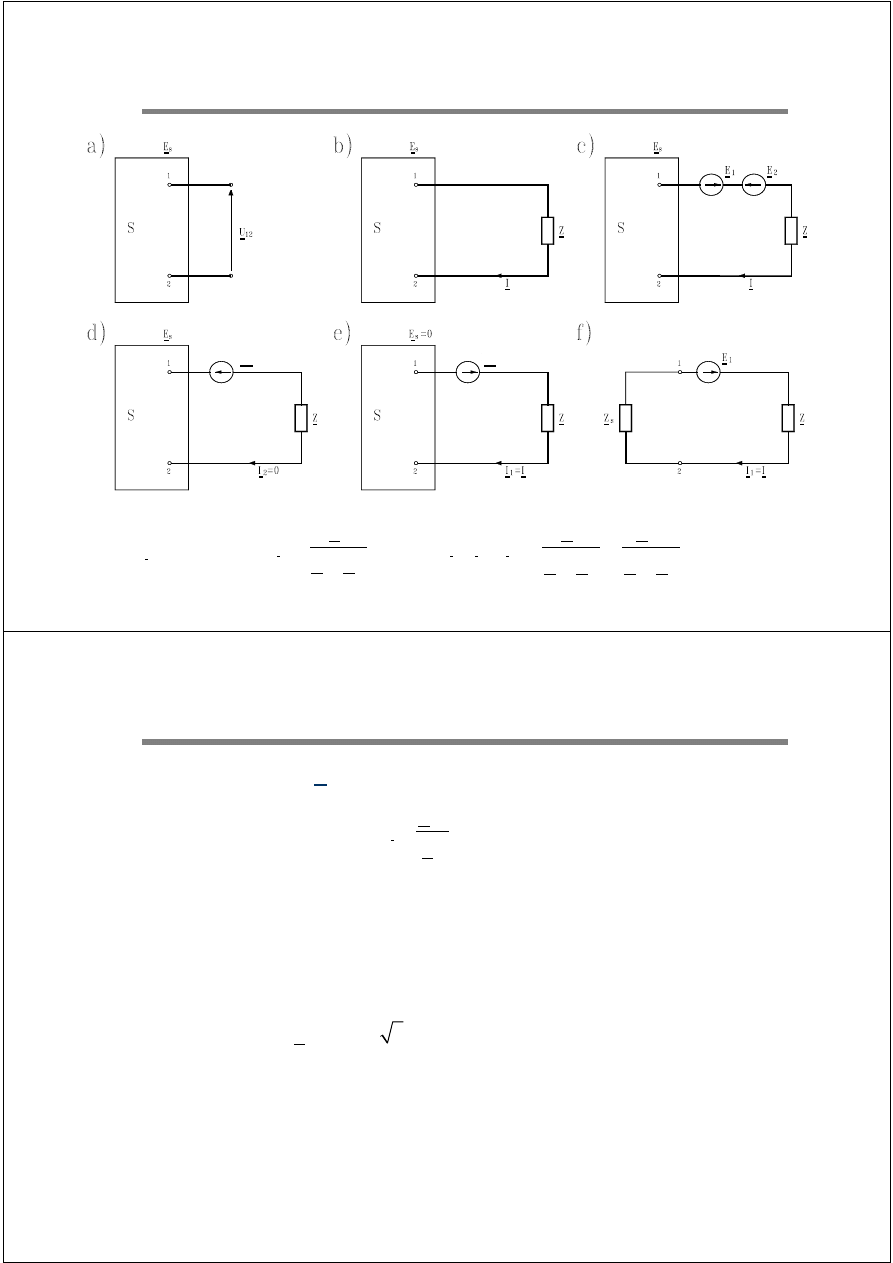
19 / 31
Ilustracja twierdzenia
Ilustracja twierdzenia
Thevenina
Thevenina
2
I
0
=
E
2
E
1
1
1
s
E
I
Z Z
=
+
1
12
1
2
s
s
U
E
I I I
Z Z
Z Z
= + =
=
+
+
20 / 31
12
s
U
I
Z
=
Przy założeniu, że Z=0 (przypadek zwarcia bezoporowego):
gdzie:
U
12
jest napięciem fazowym w miejscu zwarcia przed zwarciem,
a Z
s
impedancją widzianą z miejsca zwarcia.
Idea metody
Idea metody
Uproszczenia:
Jako napięcie przed zwarciem przyjmuje się napięcie źródła
zastępczego:
n
12
U
cU / 3
=
Pomija się obciążenia niewirujące
Pomija się gałęzie poprzeczne w schematach zastępczych elementów
W obliczeniach można pominąć rezystancje elementów,
jeśli R
k
< 0,3 X
k
21 / 31
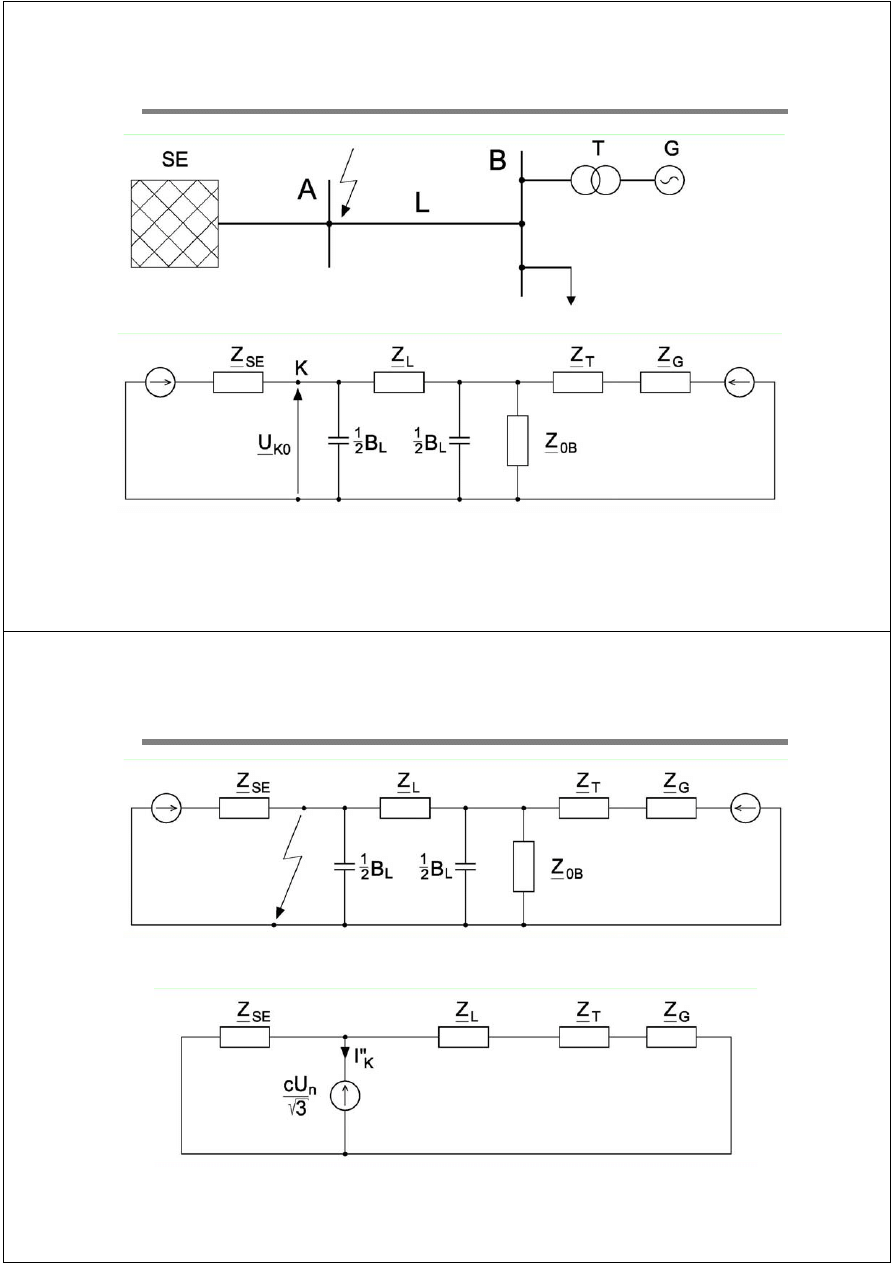
Schemat zastępczy sieci w stanie poprzedzającym zwarcie
Ilustracja metody obliczeniowej IEC
Ilustracja metody obliczeniowej IEC
22 / 31
Schemat sieci w stanie zwarcia
Schemat sieci po dokonaniu uproszczeń
Ilustracja metody obliczeniowej IEC
Ilustracja metody obliczeniowej IEC
23 / 31
Modelowy przebieg prądu
Modelowy przebieg prądu
W metodzie IEC/PN oblicza się pewne charakterystyczne parametry
modelowego przebiegu prądu zwarciowego:
Prąd początkowy
Prąd udarowy
Prąd wyłączeniowy symetryczny
Prąd nieokresowy
24 / 31
"
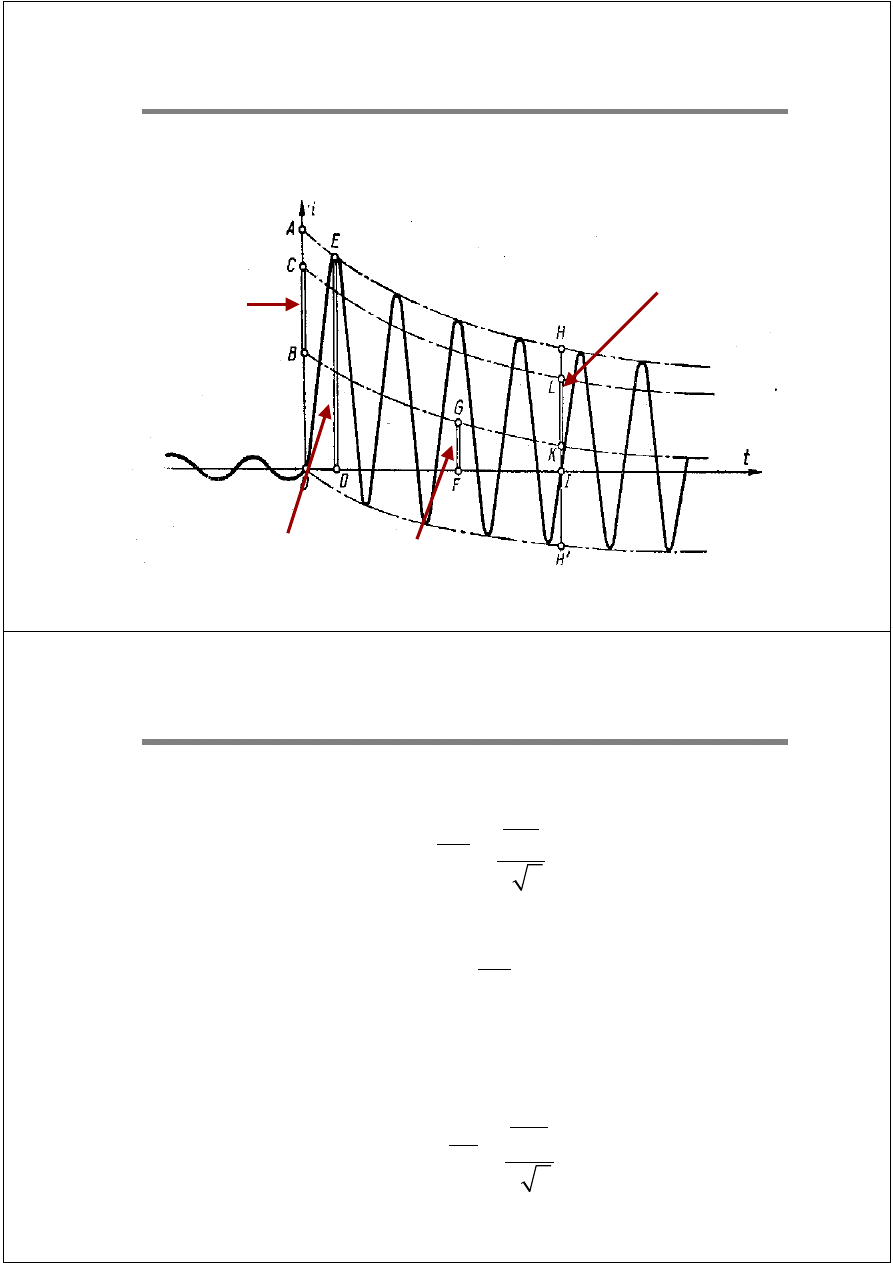
k
OA
I
BC
2 2
=
=
p
i
DE
=
'
b
HH
I
KL
2 2
=
=
Prąd początkowy
Jest to wartość skuteczna składowej okresowej prądu zwarciowego
w chwili t = 0.
Prąd udarowy
Jest to największa chwilowa wartość prądu zwarciowego.
Prąd wyłączeniowy symetryczny
Jest to wartość skuteczna składowej okresowej prądu zwarciowego
w chwili rozdzielenia styków łącznika t. Dla t = 0I:
Parametry prądu zwarciowego
Parametry prądu zwarciowego
25 / 31
Parametry prądu zwarciowego
Parametry prądu zwarciowego
2
2
basym
b
DC
I
I
i
=
+
DC
i
KI
=
Prąd zwarciowy nieokresowy i
DC
Dla chwili 0I:
Prąd wyłączeniowy niesymetryczny
Jest to prąd Ib uzupełniony o składową nieokresową
Prąd zwarciowy ustalony I
k
Jest to wartość skuteczna prądu zwarciowego po wygaśnięciu zjawisk
przejściowych
Prąd zwarciowy cieplny I
th
Jest to wartość skuteczna prądu powodującego takie same skutki
cieplne, jak prąd zwarciowy podczas zwarcia trwającego T
k
sek.
26 / 31
W metodzie IEC:
¾
rozróżnia się dwa przypadki obliczeniowe:
1. Zwarcia odległe
od generatorów (prąd zwarciowy zawiera
składową przemienną o stałej amplitudzie)
2. Zwarcia w pobliżu generatorów
(prąd zwarciowy zawiera
składową o amplitudzie malejącej)
¾
Wyznacza dwa rodzaje prądów zwarciowych:
1. Maksymalny
– do doboru urządzeń elektroenergetycznych,
2. Minimalny
– do doboru nastawień zabezpieczeń
elektroenergetycznych
Metoda IEC
Metoda IEC
27 / 31
"
n
k
k
cU
I
3 Z
=
Obliczanie prądów zwarciowych symetrycznych przy
zwarciach odległych
gdzie Z
k
jest wypadkową impedancją obwodu zwarciowego widzianą
z miejsca zwarcia
Podstawą obliczeń jest
prąd zwarciowy początkowy
:
Metoda IEC
Metoda IEC
28 / 31
Współczynnik napięciowy c
1,0
1,1
WN
(35-220) kV
1,0
1,1
SN
(1-35) kV
0,95
1,0
1,0
1,05
nN
a)
230/400 V
b)
inne napięcia
Obliczany prąd zw.
minimalny
Obliczany prąd zw.
maksymalny
Napięcie
znamionowe U
n
Dobór współczynnika c zastępczego źródła napięciowego
Metoda IEC
Metoda IEC
29 / 31
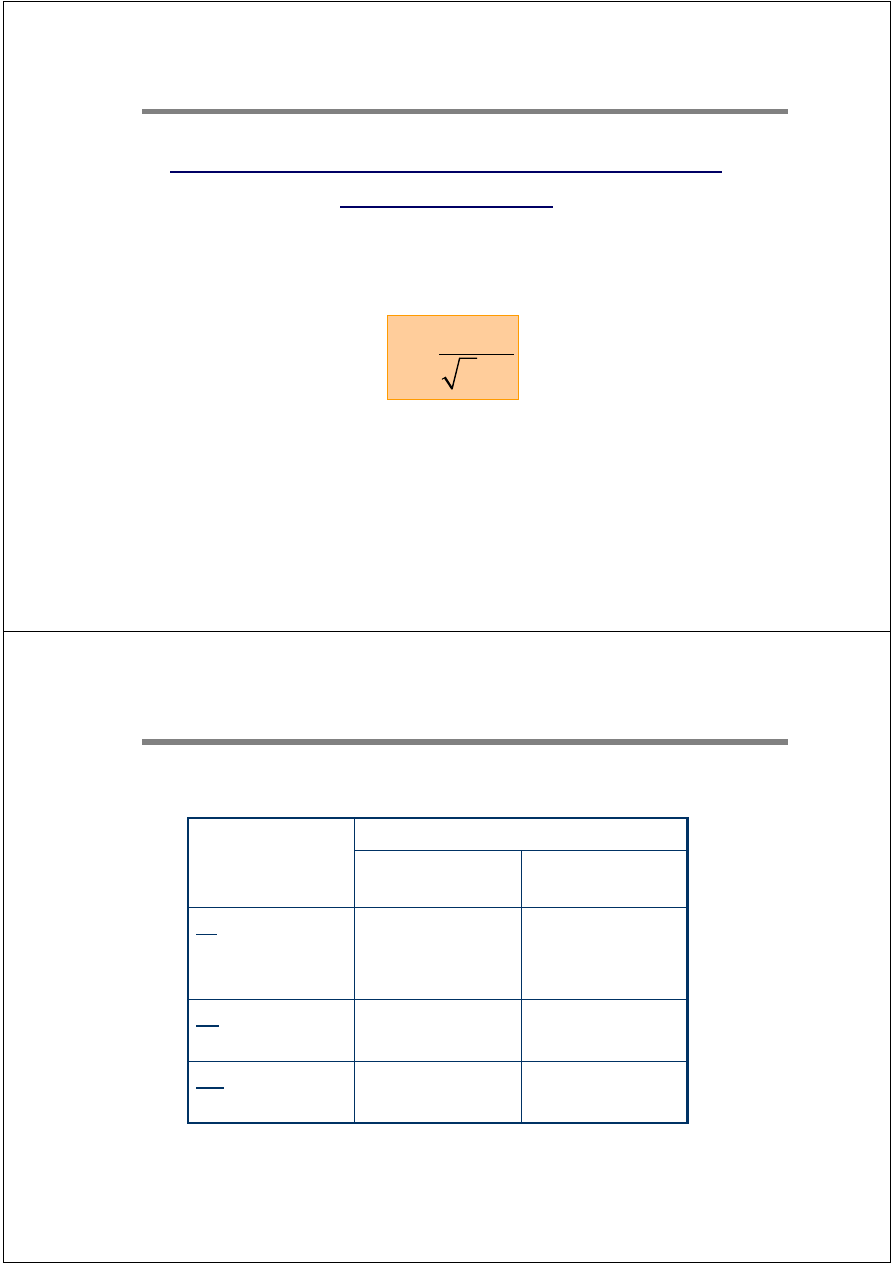
Zwarcie w sieci promieniowej:
Przy zbliżonych wartościach R/X poszczególnych źródeł prąd udarowy jest równy
sumie prądów w poszczególnych gałęziach.
Zwarcie w sieci zamkniętej
Współczynnik k wyznacza się dla impedancji zwarciowej Z
k
=R
k
+jX
k
. Prąd udarowy
wyznacza się ze wzoru:
=
∑
p
pi
i
i
i
=
κ
"
p
k
i
2 I
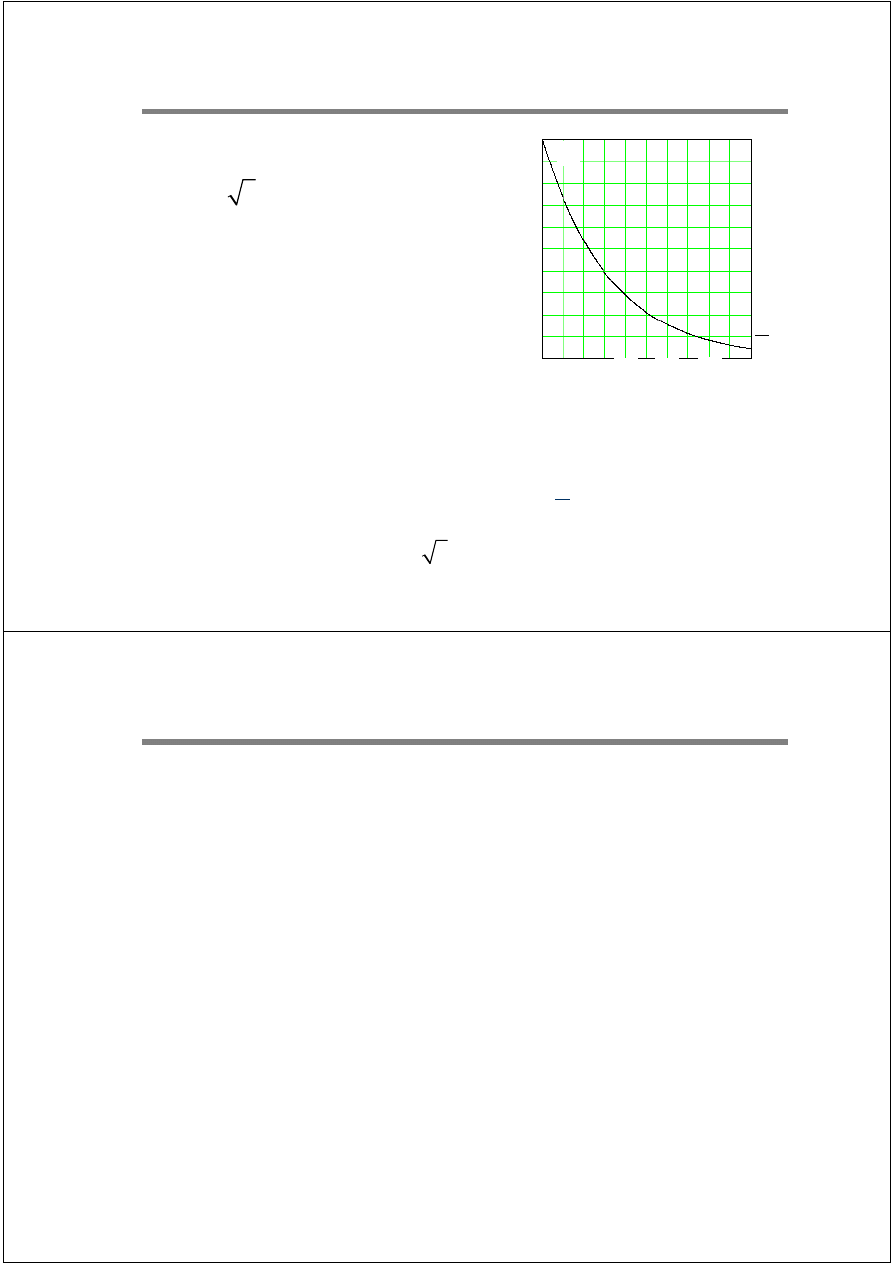
Prąd udarowy
χ jest współczynnikiem zależnym od stosunku
R/X obwodu zwarciowego, zgodnie ze wzorem
lub z wykresem podanym na rysunku:
−
κ =
+
3R / X
1,02 0,98 e
Metoda IEC
Metoda IEC
X
R
u
k
2.0
1.8
1.6
1.4
1.2
1.0
1.0
0.2
0.4
0.6
0.8
=
κ
"
p
k
i
1,15
2I
30 / 31
Z uwagi na usytuowanie miejsca zwarcia – odległe od źródeł
rzeczywistych (generatorów, silników) –
wartości prądów
początkowego, ustalonego i wyłączeniowego są równe.
I
k
= I
b
= I”
k
Lokalizacja zwarć w pobliżu generatorów i silników powoduje
konieczność skorygowania metody obliczeniowej z uwagi na:
1. Pominięcie stanu obciążenia przedzwarciowego
2. Przybliżone oszacowanie napięcia źródła zastępczego
Ponadto, inny przebieg stanu nieustalonego powoduje, że oprócz
prądu początkowego i udarowego konieczne jest wyznaczenie prądu
wyłączeniowego i ustalonego
Metoda IEC
Metoda IEC
31 / 31
=
"
"
k
n k
S
3 U I
k
2
"
"
n
n
k
n
n
k
k
cU
cU
S
3 U I
3 U
Z
3Z
=
=
⋅
=
2
n
k
"
k
cU
Z
S
=
Moc zwarciowa
Z mocy zwarciowej oblicza się zastępczą reaktancję systemu
elektroenergetycznego.
Ponieważ:
Stąd:
Metoda IEC
Metoda IEC