Zadanie 4: Rozciąganie mimośrodowe

:

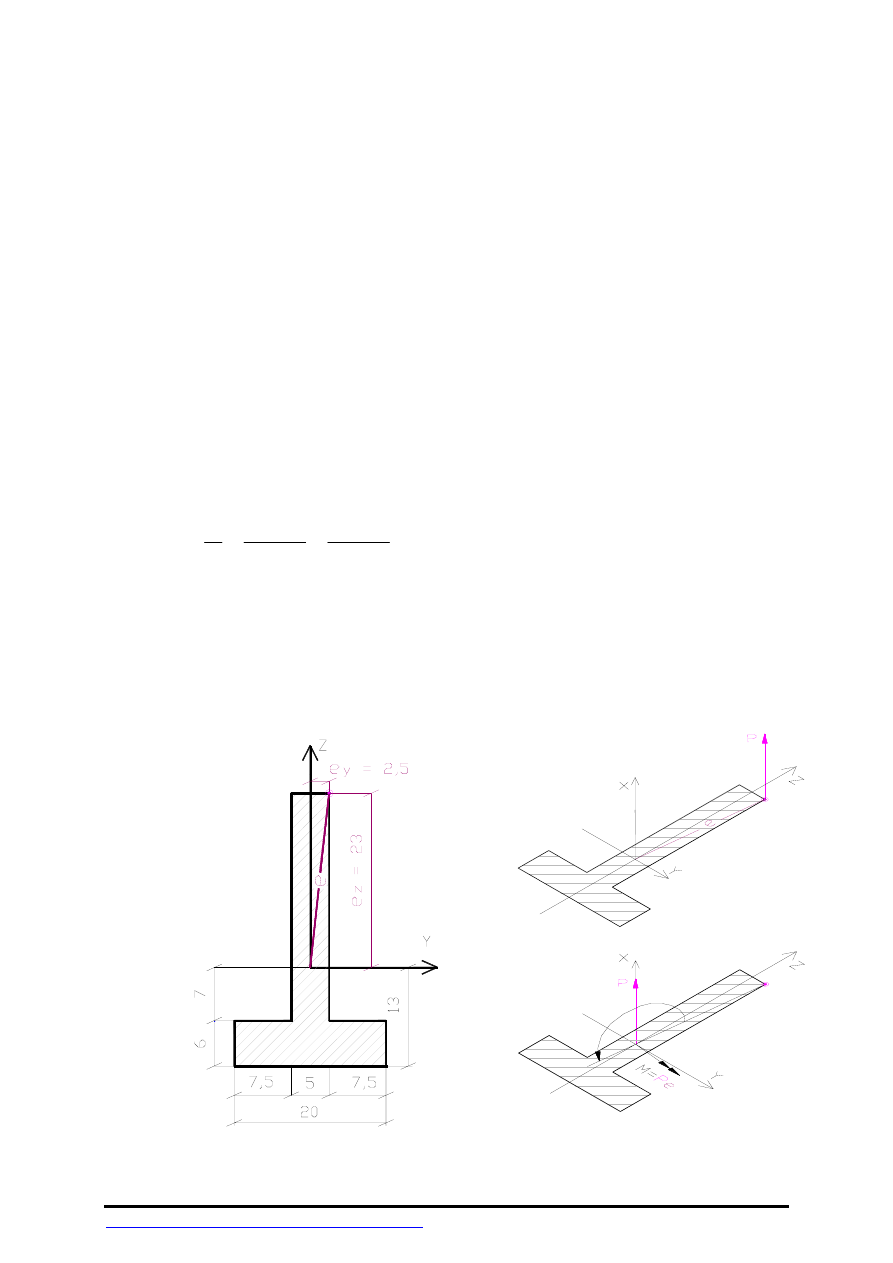
Dla słupa o przekroju jak na

Rys.1

wyznaczyć:

•

bryłę naprężeń

,

•

oś obojętną

,

•

rdzeń przekroju

.

Oznaczenia:

P -

siła normalna (rozciągająca) w przekroju

e ( e

y

, e

z

)

- mimośród

M =

P

∗

e

- moment zginający w płaszczyźnie obciążenia

M

y

=

P

∗

e

z

- moment zginający w płaszczyźnie głównej xz

M

z

=

P

∗

e

y

- moment zginający w płaszczyźnie głównej xy

J

y

, J

z

-

główne centralne momenty bezwładności

i

,

i

- promienie bezwładności

2

y

2

z

Naprężenie normalne

σ

x

z

z

y

y

x

J

y

M

J

z

M

A

P

∗

+

∗

+

=

σ

1.

Dane

:

wymiary przekroju słupa podane są w centymetrach,

e

y

=2,5

cm,

e

z

=23

cm

P=540 KN

http://www.pk.edu.pl/~iwroblew/dydaktyka

1/5

Rys.1

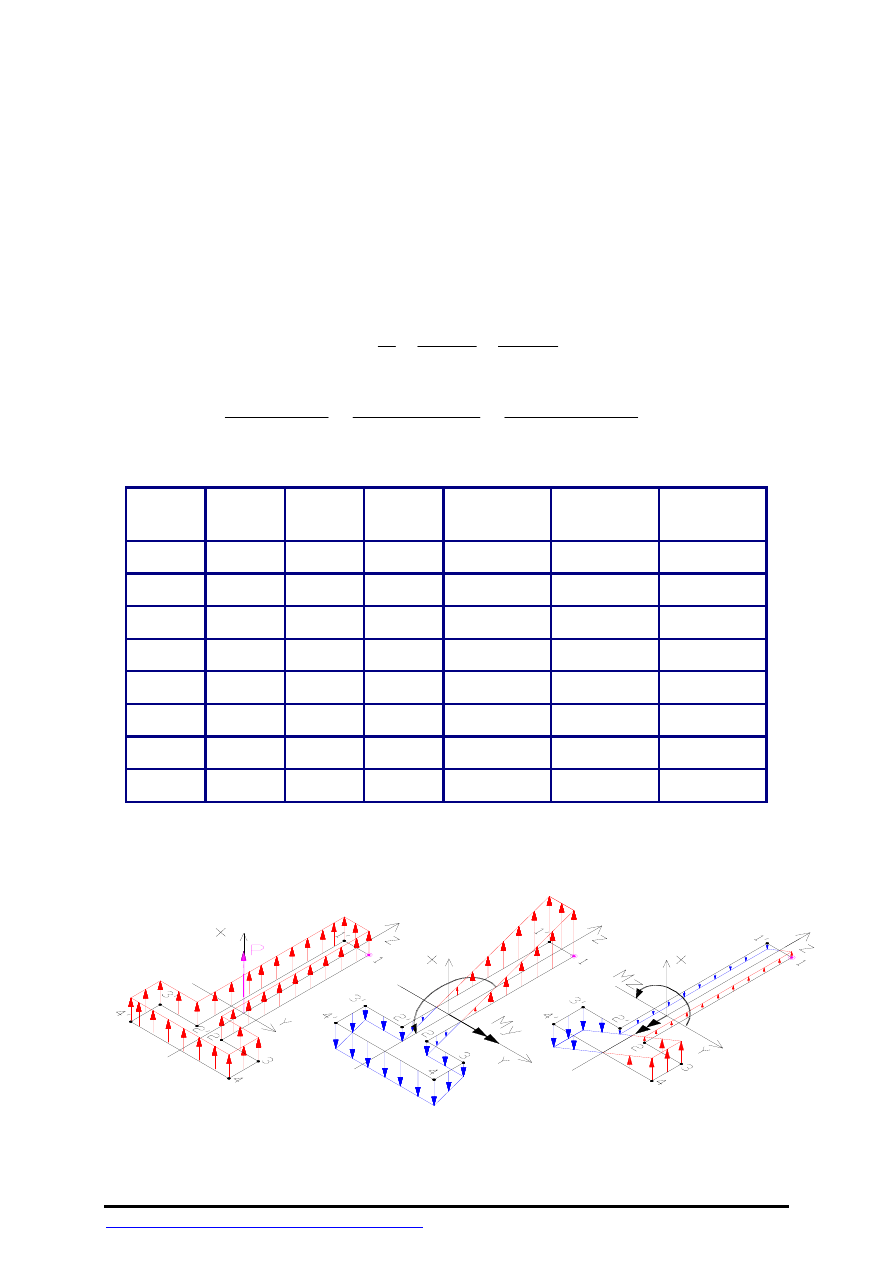
2.

Bryła naprężeń

-

Rys.3

Obliczenia (

tab.1

,

tab.2

):

pole przekroju: A=270

∗10

-4

m

2

mimośród: e

y

=2,5

∗ 10

-2

m

e

z

= 23

∗ 10

-2

m

M

y

=

P

∗

e

z

=

540

∗

23

∗ 10

-2

= 124,2 [KNm]

J

y

= 33210

∗ 10

-8

m

4

M

z

=

P

∗

e

y

=

540

∗

2,5

∗ 10

-2

= 13,5 [KNm]

J

z

= 4312,5

∗ 10

-8

m

4

z

z

y

y

x

J

y

M

J

z

M

A

P

∗

+

∗

+

=

σ

8

8

4

x

10

5

,

4312

y

5

,

13

10

33210

z

2

,

124

10

270

540

−

−

−

∗

∗

+

∗

∗

+

∗

=

σ

[KN/m

2

]

+ naprężenia rozciągające

− naprężenia ściskające

σ

x

=

P

/ A

σ

x

= M

y

∗

z / J

y

σ

x

= M

z

∗ y / J

z

Rys.2

http://www.pk.edu.pl/~iwroblew/dydaktyka

2/5

tab.1

Punkt

z

[m]

y

[m]

P

/ A

[MPa]

M

y

∗z / J

y

[MPa]

M

z

∗y / J

z

[MPa]

σ

x

[MPa]

1 0,23

0,025

20

86,475

7,826

114,301

2 -0,07

0,025

20

-26,319

7,826

1,507

3 -0,07 0,1

20

-26,319

31,304

24,985

4 -0,13 0,1

20

-48,877

31,304

2,427

1' 0,23

-0,025

20

86,475

-7,826

98,649

2' -0,07

-0,025

20

-26,319

-7,826

-14,145

3' -0,07 -0,1

20

-26,319

-31,304

-37,623

4' -0,13 -0,1

20

-48,877

-31,304

-60,181

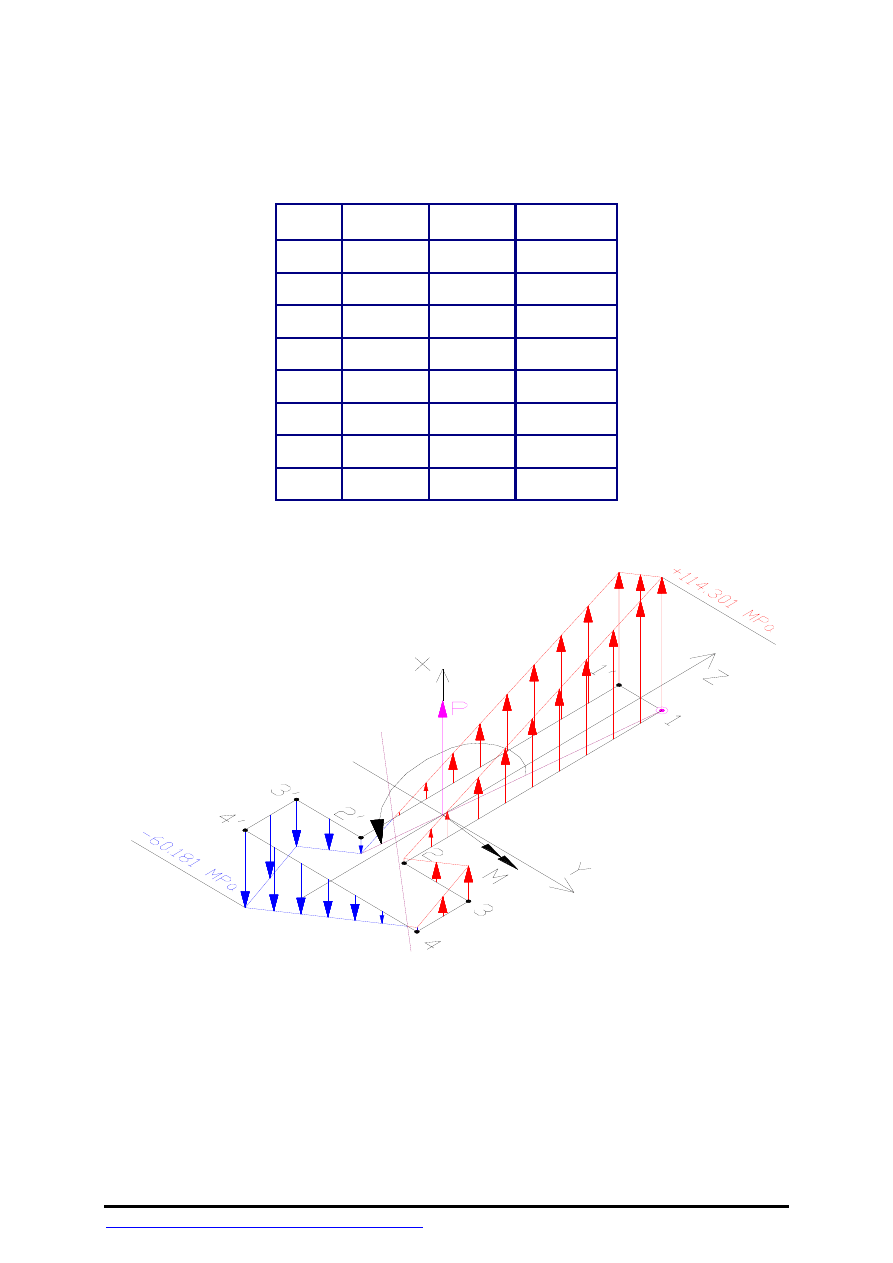
σ

x

=

P

/ A + M

y

∗

z / J

y

+ M

z

∗ y / J

z

tab.2

Punkt

z [m]

y [m]

σ

x

[MPa]

1 0,23 0,025

114,301

2 -0,07 0,025

1,507

3 -0,07 0,1

24,985

4 -0,13 0,1

2,427

1' 0,23 -0,025

98,649

2' -0,07 -0,025

-14,145

3' -0,07 -0,1

-37,623

4' -0,13 -0,1

-60,181

− naprężenia ściskające

+ naprężenia rozciągające

Rys.3

http://www.pk.edu.pl/~iwroblew/dydaktyka

3/5

Bryła naprężeń

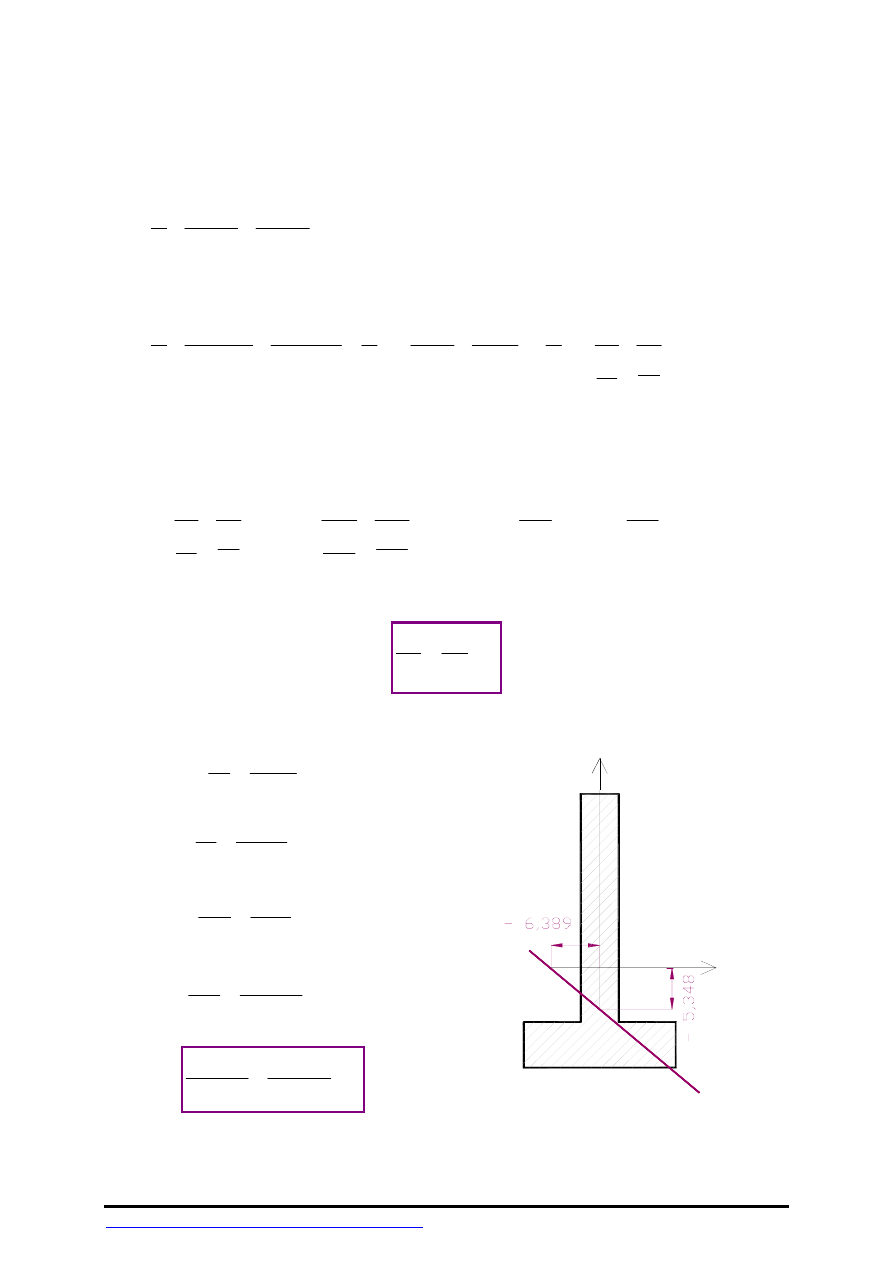
3.

Równanie osi obojętnej

-

Rys.4

Wyprowadzenie wzoru:

z

z

y

y

x

J

y

M

J

z

M

A

P

∗

+

∗

+

=

σ

2

y

y

i

A

J

∗

=

2

z

z

i

A

J

∗

=





























+

+

=















∗

+

∗

+

=

∗

∗

∗

+

∗

∗

∗

+

=

σ

y

2

z

z

2

y

2

z

y

2

y

z

2

z

y

2

y

z

x

e

i

y

e

i

z

1

A

P

i

y

e

i

z

e

1

A

P

i

A

y

e

P

i

A

z

e

P

A

P

Równanie odcinkowe osi obojętnej

σ

x

= 0

0

e

i

y

e

i

z

1

y

2

z

z

2

y

=

+

+

1

e

i

y

e

i

y

2

z

z

2

y

=

−

+

−

z

z

2

y

z

e

i

a

−

=

y

2

z

y

e

i

a

−

=

1

a

y

a

z

y

z

=

+

2

y

2

y

cm

123

270

33210

A

J

i

=

=

=

2

z

2

z

cm

972

,

15

270

5

,

4312

A

J

i

=

=

=

cm

348

,

5

23

123

e

i

a

z

2

y

z

−

=

−

=

−

=

cm

389

,

6

5

,

2

972

,

15

e

i

a

y

2

z

y

−

=

−

=

−

=

1

389

,

6

y

348

,

5

z

=

−

+

−

oś oboj

ętn

a

Y

Z

Rys.4

http://www.pk.edu.pl/~iwroblew/dydaktyka

4/5

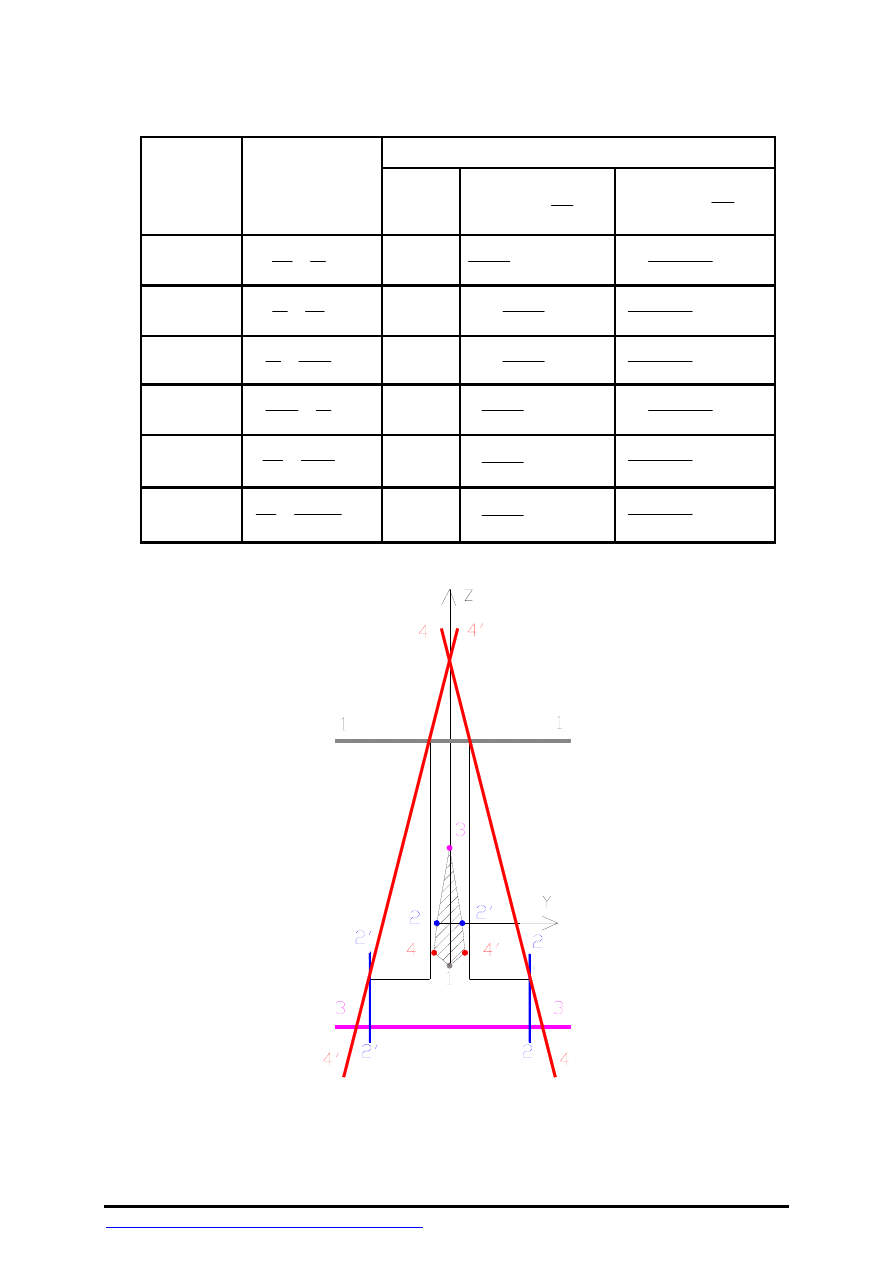
4.

Rdzeń przekroju

-

Rys.5

Współrzędne punktów rdzenia e(e

y

, e

z

)

Oznaczenie

danej osi

obojętnej

Równanie danej

osi obojętnej

Punkt

rdzenia

z

2

y

z

a

i

e

−

=

y

2

z

y

a

i

e

−

=

1 – 1

1

y

23

z

=

∞

+

1

348

,

5

23

123

−

=

−

0

972

,

15

=

∞

−

2 - 2

1

10

y

z

=

+

∞

2

0

123 =

∞

−

597

,

1

10

972

,

15

−

=

−

2’ – 2’

1

10

y

z

=

−

+

∞

2’

0

123 =

∞

−

597

,

1

10

972

,

15

+

=

−

−

3 - 3

1

y

13

z

=

∞

+

−

3

462

,

9

13

123

+

=

−

−

0

972

,

15

=

∞

−

4 – 4

1

25

,

8

y

33

z

=

+

4

727

,

3

33

123

−

=

−

936

,

1

25

,

8

972

,

15

−

=

−

4’ – 4’

1

25

,

8

y

33

z

=

−

+

4’

727

,

3

33

123

−

=

−

936

,

1

25

,

8

972

,

15

+

=

−

−

Rys.5

http://www.pk.edu.pl/~iwroblew/dydaktyka

5/5