Szeregi potęgowe

Dla potomnych

Artur Ślączka

Definicja

Niech

Y ,∥⋅∥ -przestrzeń unormowana nad ciałem K ,

a

n

∈Y , x , x

0

∈ K .

Szereg funkcyjny postaci

∑

n

=0

∞

a

n

 x−x

0



n

nazywamy szeregiem potęgowym o środku w punkcie x

0

.

Umowa

∀ x , x

0

∈K a

n

 x−x

0



0

:

=1

czyli

∑

n

=0

∞

a

n

 x−x

0



n

=a

0

a

1

 x−x

0

a

2

 x−x

0



2



Uwaga

Wystarczy badać zbieżność szeregów potęgowych o środku w punkcie 0 , bo

podstawiając t :=x−x

0

, otrzymujemy

∑

n

=0

∞

a

n

t

n

-szereg potęgowy o środku w punkcie 0.

Lemat Abela

Jeśli

∑

n

=0

∞

a

n

x

n

jest zbieżny w punkcie

∈K ∖ { 0 } , to szereg ten jest zbieżny bezwzglednie

w kuli K

0,∣∣ oraz jest zbieżny jednostajnie w każdej kuli domkniętej K 0,  ,

gdzie 0

∣∣.

Dowód

∑

n

=0

∞

a

n

x

n

− zbieżny w ∈ K ⇒

WK

lim

n

∞

a

n



n

=0 ⇒ a

n



n



n

∈ℕ

−ciąg ograniczony ⇒

⇒∃ M 0: ∥a

n



n

∥M dla n∈ℕ.

Niech x

∈K 0,∣∣. Wtedy ∣x∣∣∣⇒

∥a

n

x

n

∥=

∥

a

n



n



x





n

∥

=

∥

a

n



n

∥

⋅

∣

x



∣

n

M

∣

x



∣

n

Ponieważ

∑

n

=0

∞

M

∣

x



∣

n

-zbieżny jako szereg geometryczny o ilorazie q=

∣

x



∣

1

zatem

∑

n

=0

∞

M

∣

x



∣

n

- zbieżna majoranta szeregu

∑

n

=0

∞

∥a

n

x

n

∥. Stąd na podstawie kryterium

porównawczego

∑

n

=0

∞

∥a

n

x

n

∥−zbieżny ∀ x∈K 0,∣∣ ⇒

- 1 -

⇒

∑

N

=0

∞

a

n

x

n

-zbieżny bezwzględnie w K

0,∣∣.

Niech x

∈ K 0,  , gdzie

0

∣∣ . Wtedy

∥a

n

x

n

∥=

∥

a

n



n



x





n

∥

=∥a

n



n

∥⋅

∣

x



∣

n

M

∣

x



∣

n

M





∣∣



n

∑

n

=0

∞

M





∣∣



n

−zbieżna majoranta szeregu

∑

a

n

x

n

}

⇒

Tw.Weierstrassa

∑

n

=0

∞

a

n

x

n

−zbieżny

jednostajnie w 

K

0, .

Definicja

Definiujemy promień zbieżności szeregu potęgowego R w następujący sposób :

R :

= sup { r :

∑

n

=0

∞

a

n

x

n

−zbieżny w kuli K 0, r}

oraz dodatkowo

R :

=0 , jeśli

∑

n

=0

∞

a

n

x

n

zbieżny tylko w x

=0 ,

R :

=∞ , jeśli

∑

n

=0

∞

a

n

x

n

zbieżny

∀ x∈K .

Ponadto, jeśli

R

0 ⇒ K 0, r

-nazywamy kołem zbieżności szeregu,

K

=ℝ ⇒ K 0, R=−R , R -przedział zbieżności szeregu.

Uwaga

Szereg

∑

n

=0

∞

a

n

x

n

w K

/ K 0, R - jest rozbieżny.

Wniosek

Niech R -promień zbieżności szeregu

∑

n

=0

∞

a

n

x

n

.

Wtedy

1

˚

∑

n

=0

∞

a

n

x

n

- zbieżny bezwzględnie i niemal jednostajnie w K

0, R

2

˚

∑

n

=0

∞

a

n

x

n

-rozbieżny w K

/ K 0, R.

Jeżeli

∣x∣=R

, to aby rozstrzygnąć zbiezność szeregu dla tych x , należy szereg zbadać

inaczej.

- 2 -

Twierdzenie Cauchy'ego-Hadamarda

Niech

:=lim sup

n

 ∞

n



∥a

n

∥

.

Wtedy promień zbieżności szeregu potęgowego

∑

n

=0

∞

a

n

x

n

wynosi:

R

=

{

0

, gdy

=∞ ,

1


, gdy 0

∞ ,

∞ , gdy =0 .

Dowód

Wystarczy zbadać, kiedy szereg

∑

n

=0

∞

a

n

x

n

jest zbieżny bezwzględnie. Na podstawie

kryterium Cauchy'ego szereg

∑

n

=0

∞

∥a

n

x

n

∥ jest zbieżny, jeśli lim sup

n

∞

n



∥a

n

x

n

∥1 ,czyli

lim sup

n

∞

n



∥a

n

x

n

∥=lim sup

n

∞

n



∥a

n

∥⋅∣x

n

∣=lim sup

n

∞

∣x∣

n



∥a

n

∥=∣x∣lim sup

n

∞

n



∥a

n

∥=∣x∣⋅1 .

Jeśli 1

˚ =0 ⇒ ∀ x∈K : ∣x∣⋅1 ⇒ R=∞ ,

2

˚ =∞ ⇒ tylko dla x=0 : ∣x∣⋅1 ⇒ R=0

3

˚ ≠0

≠∞

}

⇒∣x∣

1



□

Przykład

Obliczyć promień i przedział zbieżności szeregu

∑

n

=0

∞

−2

n

1

x

n

.

=:lim sup

n

∞

n



∣−2

n

1

∣=lim sup

n

∞

n



∣2 ⋅2

n

∣=2

⇒

Tw.Cauchy ' ego

−Hadamarda

R

=

1
2

⇒ ~dla ∣x∣

1
2

szereg jest zbieżny .
sprawdzimy zbieżność na końcach przedziału zbieżności

dla x

=

1
2

:

∑

n

=0

∞

−2

n

1

⋅



1
2



n

=

∑

n

=0

∞

−1

n

1

⋅2 −szereg rozbieżny

dla x

=−

1
2

:

∑

n

=0

∞

−2

n

1

⋅



−

1
2



n

=

∑

n

=0

∞

−2−szereg rozbieżny

czyli

∑

n

=0

∞

−2

n

1

⋅x

n

-zbieżny w



−

1
2

,

1
2



.

- 3 -

Twierdzenie

Jeśli istnieje granica lim

n

∞

∥

a

n

1

a

n

∥

= oraz a

n

≠0  , to promień zbieżności szeregu

potegowego

∑

n

=0

∞

a

n

x

n

wynosi

R

=

{

0

, gdy

=∞

1


, gdy 0

∞

∞ , gdy =0

Przykład

Obliczyć promień zbieżności R szeregu

∑

n

=1

∞

2 n!

n

!⋅n

n

⋅z

n

, z

∈ℂ.

=lim

n

∞

∥

a

n

1

a

n

∥

=lim

n

∞

∥

2 n22 n12 n!n!⋅n

n

n1n!⋅n1n1

n

2 n!

∥

=lim

n

∞

4 n

2

n

1

⋅



n

n

1



n

=

4
e

⇒ R=

e
4

Twierdzenie (o różniczkowaniu szeregu potęgowego)

Niech R – promień zbieżności szeregu

∑

n

=0

∞

a

n

x

n

,

f – suma tegoż szeregu,

f

 x=

∑

n

=0

∞

a

n

x

n

,

x

∈K O , R.

Wtedy

f

∈C

∞

 K O , R

-tzn. f posiada pochodną dowolnego rzędu

oraz

∀ x∈K O , R

f

k 

 x=

∑

n

=k

∞

k

!



n
k



a

n

x

n

−k

.

Dowód
Na podstawie twierdzenia o różniczkowaniu szeregu funkcyjnego

f

'

 x=

∑

n

=0

∞

a

n

x

n



'

=

∑

n

=0

∞

a

n

x

n



'

=

∑

n

=1

∞

n a

n

x

n

−1

,

jeśli

∑

n

=0

∞

a

n

x

n



'

jest zbieżny jednostajnie.

Ponieważ lim sup

n

∞

n



∥na

n

∥=R ⇒

∑

n

=1

∞

n a

n

x

n

−1

-zbieżny niemal jednostajnie w K

0, R ⇒

∀  , 0R :

∑

na

n

x

n

−1

jest zbieżny jednostajnie w K

O , (czyli można go

różniczkować “wyraz po wyrazie”)
Analogicznie

- 4 -

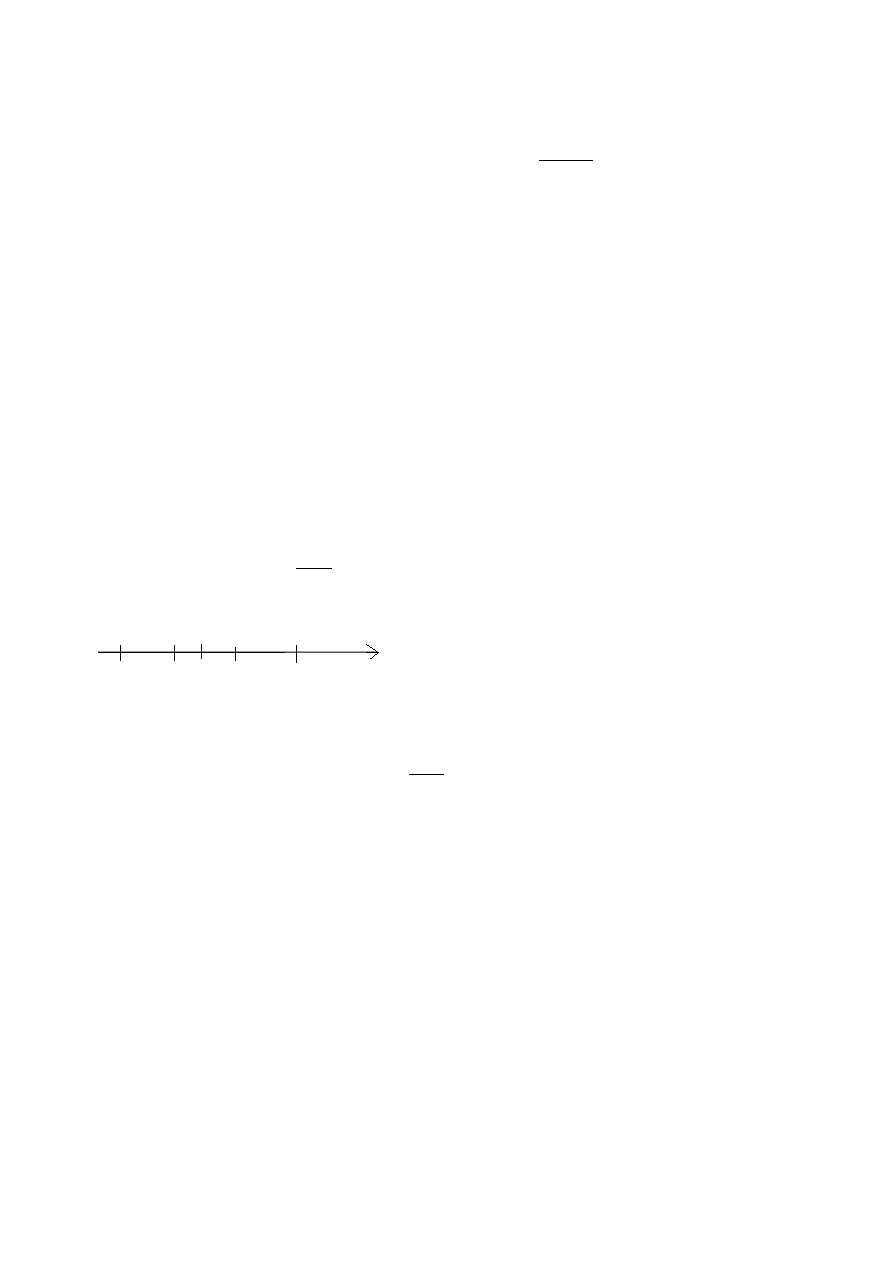
f

' '

 x=

∑

n

=1

∞



n a

n

x

n

−1



'

=

∑

n

=2

∞

n

n−1a

n

x

n

−2

f

k 

 x=

∑

n

=k

∞

n

n−1n−2⋅⋅n−k1a

n

x

n

−k

=

∑

n

=k

∞

n

!

n−k !

a

n

x

n

−k

=

∑

n

=k

∞

k

!



n
k



a

n

x

n

−k

□

Uwaga

Dla x

=0 teza twierdzenia przyjmuje postać

f

k 

0=k!



k
k



a

k

=k!a

k

.

Twierdzenie o całkowaniu szeregu potęgowego

Niech

∑

n

=0

∞

a

n

x

n

− szereg rzeczywisty, to znaczy a

n

∈ℝ , x∈ℝ ,

R -promień zbieżności szeregu

∑

n

=0

∞

a

n

x

n

.

Wtedy

∫

0

x



∑

n

=0

∞

a

n

x

n



dx

=

∑

n

=0

∞

a

n

n

1

x

n

1

∀ x∈−R , R.

Dowód

−R − 0  R

W przedziale

[− , ] , dla 0R , szereg można całkować wyraz po wyrazie (jest

jednostajnie zbieżny)

Zatem dla x

∈−R , R

∫

0

x



∑

n

=0

∞

a

n

x

n



dx

=

∑

n

=0

∞



∫

0

x

a

n

x

n

dx



=

∑

n

=0

∞

a

n

n

1

x

n

1

.

□

- 5 -

Twierdzenie (Abela)

Niech

∑

n

=0

∞

a

n

x

n

-szereg rzeczywisty.

Jeśli

∑

n

=0

∞

a

n

x

n

jest zbieżny w punkcie końcowym przedziału zbieżności, to jego suma jest

funkcją jednostronnie ciągłą w tym punkcie, to znaczy:

jeśli R -promień zbieżności szeregu

∑

n

=0

∞

a

n

x

n

,

f -suma tegoż szeregu

oraz szereg jest zbieżny w punkcie x

0

=R ⇒ lim

x

 x

0

-

f

 x=

∑

n

=0

∞

a

n

x

0

n

lub szereg jedt zbieżny w punkcie x

0

=−R szereg jest zbieżny ⇒ lim

x

 x

0

+

f

 x=

∑

n

=0

∞

a

n

x

0

n

.

Przykład

Dla x

∈[−1,1]

funkcję

f

 x=arctg x zapisz w postaci szeregu potęgowego.

Następnie oblicz sumę szeregu liczbowego

∑

n

=0

∞

−1

n

1

2 n

1

.

Ponieważ

f

'

 x=

1

1

x

2

=

a

1

=1

∣−x

2

∣1

=−x

2

x

2

1

x

∈−1,1

=

∑

n

=0

∞

−x

2



n

=

∑

n

=0

∞

−1

n

x

2 n

dla x

∈−1,1

zatem

f

 x=

∫

0

x

1

1

x

2

dx

=

∫

0

x



∑

n

=0

∞

−1

n

x

2 n



dx

=

tw.

∑

n

=0

∞



∫

0

x

−1

n

x

2 n

dx



=

−1

n

2 n

1

x

2 n

1

dla x

∈−1,1.

Ponadto

dla x

0

=1 otrzymujemy szereg

∑

n

=0

∞

−1

n

2 n

1

-zbieżny (z kryterium Leibniza) ,

dla x

0

=−1 otrzymujemy szereg

∑

n

=0

∞

−1

n

2 n

1

-zbieżny (z kryterium Leibniza) .

Ponieważ funkcja

arctg

∈C ℝ ⇒ arctg x=

∑

n

=0

∞

−1

n

2 n

1

x

2 n

1

dla x

∈[−1,1].

Stąd dla x

=1

∑

n

=0

∞

−1

n

2 n

1

=arctg1=


4

czyli



4

=1−

1

3



1
5

−

1

7

 (wzór Leibniza).

- 6 -

Przypomnienie: Twierdzenie Taylora

f :

ℝ ℝ

f

∈C

n

U  , U ∈Top x

0



x

∈U

}

⇒ ∃c∈ x

0

, x

 : f  x=

∑

k

=0

n

−1

f

k

 x

0



k

!

 x−x

0



k

R

n

c ,

gdzie R

n

c=

f

n

c

n

!

 x−x

0

.

Jeżeli przy n

∞ reszta ze wzoru Taylora dąży do zera

R

n

c=

f

n

c

n

!

 x−x

0

 

n

∞

0,

to

lim

n

∞

S

n

 x= f  x ,

gdzie S

n

 x=

∑

k

=0

n

−1

f

k

 x

0



k

!

 x−x

0



k

czyli funkcja f jest wtedy sumą szeregu potęgowego.

Twierdzenie (o rozwijaniu funkcji w szereg Taylora)

f :

ℝ ℝ

f

∈C

∞

U  , U ∈Top x

0



lim

n

∞

R

n

c=0

}

⇒ ∀ x∈U : f  x=

∑

n

=0

∞

f

n

 x

0



n

!

 x−x

0



n



szereg Taylora T

x

0

f funkcji f w punkcie x

0

Uwaga

Założenie lim

n

∞

R

n

 x=0 jest istotne .

Przykład

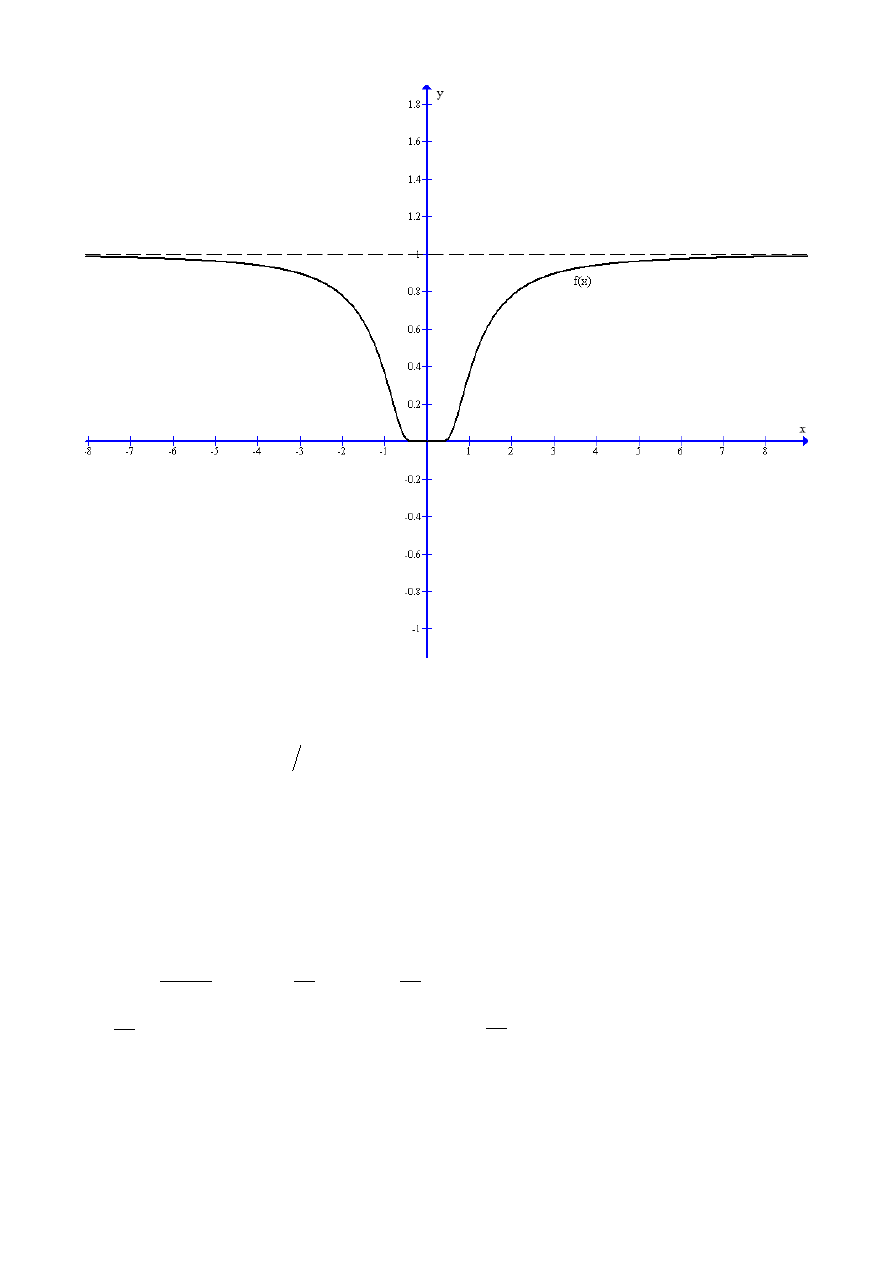
f

 x=

{

e

−

1

x

2

, gdy x

≠0 ,

0

, gdy x

=0 .

Można udowodnić, że f ∈ℂ

∞

- 7 -

Ponieważ

f

n

0=0

∀ n∈ℕ

0

więc
T

0

f

=

∑

0

=0 ≡ f

Lemat o reszcie we wzorze Taylora.

Z:

∀ 0 ∃M 0

∀ x∈ x

0

− , x

0

 ∀ n∈ℕ : ∣ f

n

 x∣M

T: lim

n

∞

R

n

 x=0

dla x

∈ x

0

− , x

0

.

Dowód

∣R

n

c∣=∣

f

n

c

n

!

 x−x

0



n

∣

M

n

!

∣ x−x

0



n

∣

M

n

!



n

∑

n

=0

∞

M

n

!



n

-zbieżny z kryterium D'Alemberta

⇒

WK

lim

n

∞

M

n

!



n

=0 ⇒

⇒ lim

n

∞

∣R

n

c∣=0 ⇒ lim

n

∞

R

n

c=0

□

- 8 -

Przykład

Rozwinąć w szereg Maclaurina (wyznaczyć T

0

f ) funkcję

f

 x=e

x

dla x

∈ℝ

.

Z tw. Taylora:

f

 x=e

x

=

∑

k

=0

n

−1

x

k

k

!

R

n

c.

Ponadto

f

n

 x=e

x

∀ n∈ℕ ⇒ f ∈ℂ

∞

Niech x

0

=0 , x∈ , dla 0 .

Wtedy

∣ f

n

 x∣=∣e

x

∣=e

x

e



⇒ (spełnione są założenia lematu) ⇒

⇒ lim

n

∞

R

n

 x=0 ⇒ e

x

=

∑

n

=0

∞

x

n

n

!

dla

∣x∣.

Ponieważ

0 jest dowolne , więc e

x

=

∑

n

=0

∞

x

n

n

!

dla x

∈ℝ.

Uwaga (do twierdzenia o reszcie szeregu potęgowego)

Jeżeli funkcja f jest sumą szeregu potęgowego

f

 x=

∑

n

=0

∞

a

n

 x−x

0



n

dla x

∈K  x

0

, R

 ⇒ a

n

=

f

n

 x

0



n

!

na podstawie twierdzenia o różniczkowalności szeregu potęgowego.

Uwaga

Rozwinięcie funkcji w szereg Taylora jest jednoznaczne. Zatem rozwinięcie funkcji w
szereg wyznaczone jakąkolwiek metodą jest rozwinięciem w szereg Taylora.

- 9 -

Szeregi

Maclaurina podstawowych

funkcji

sin x

=

∑

n

=0

∞

−1

n

x

2 n

1

2 n1!

dla x

∈ℝ ,

cos x

=

∑

n

=0

∞

−1

n

x

2 n

2 n!

dla x

∈ℝ ,

ln

1x=

∑

n

=1

∞

−1

n

−1

x

n

n

dla x

∈(−1,1 ] ,

1x



=

∑

n

=0

∞




n



x

n

, dla

∣x∣1 oraz ∈ℝ

 jeśli ∈ℕ

0

, to rozwinięcie jest prawdziwe

∀ x∈ℝ

gdzie





n



:

=

−1−2⋅⋅−n1

n

!

dla

∈ℝ , n∈ℕ.

Przykład

Rozwiń w szereg Maclaurina funkcję f

 x=



1

x dla x∈−1,1.

=

1
2

:



1

x=

∑

n

=0

∞



1
2
n



x

n

=1

1
2

x



1
2



−

1
2



2

!

x

2



1
2



−

1
2



−

3
2



3

!

x

3

=

=1

1
2

x

−

1
8

x

2



1

16

x

3

−

5

27

x

4



dla x

∈−1,1.

Definicja

Niech

Y ,∥⋅∥

-przestrzeń Banacha nad K ,

U

∈TopK

f :U Y , f ∈C

∞

Funkcja f jest analityczna w punkcie x

0

∈U wtedy i tylko wtedy, gdy

∃r0 ∀ x∈K  x

0

, r

 : f  x=

∑

n

=0

∞

a

n

 x−x

0



n

.

Np. funkcje : sin x , cos x , ln1x ,1x



są analityczne w punkcie 0.

- 10 -

Funkcja wykładnicza i funkcje trygonometryczne zmiennej zespolonej

Rozszerzmy funkcje e

x

,sin

 x , cos x na zbiór liczb zespolonych korzystając z

otrzymanych rozwinięć w szeregi Taylora.

e

z

:

=

∑

n

=0

∞

z

n

n

!

, z

∈ℂ

sin z :

=

∑

n

=0

∞

−1

n

z

2 n

1

2 n1!

, z

∈ℂ

cos z :

=

∑

n

=0

∞

−1

n

z

2 n

2 n!

, z

∈ℂ

Twierdzenie

∀ z

1

, z

2

∈ℂ

e

z

1

⋅e

z

2

=e

z

1

z

2

Dowód

Na podstawie definicji

e

z

1

:

=

∑

n

=0

∞

z

1

n

n

!

, e

z

2

:

=

∑

n

=0

∞

z

2

n

n

!

.

Ponieważ powyższe szeregi są zbieżne bezwzględnie zatem na podstawie twierdzenia
Cauchy'ego o iloczynie szeregów otrzymujemy

e

z

1

e

z

2

:

=



∑

z

1

n

n

!



∑

z

2

n

n

!



=

∑

n

=0

∞

c

n

,

gdzie

c

n

=

∑

k

=0

n

z

1

k

k

!

⋅

z

2

n

−k

n−k !

=

∑

k

=0

n

1

n

!



k
n



⋅z

1

k

⋅z

2

n

−k

=

1

n

!

⋅

∑

k

=0

n



k
n



z

1

k

⋅z

2

n

−k

=

1

n

!

⋅ z

1

z

2



n

.

Stąd

e

z

1

⋅e

z

2

=

∑

n

=0

∞

1

n

!

⋅ z

1

z

2



n

=e

z

1

z

2

□

Twierdzenie

∀ z∈ℂ : 1 e

iz

=cos zi⋅sin z

2 e

−iz

=cos z−i⋅sin z

Dowód

Ad.(1) e

iz

=

∑

n

=0

∞

i

n

z

n

n

!

Ponieważ powyższy szereg jest zbieżny zatem w szczególności lim

n

∞

S

2 n

1

=e

iz

,

gdzie S

2 n

1

=1

iz

1

!

−

z

2

2

!

−

iz

3

3

!



z

4

4

!



iz

2 n

1

2 n1!

.

- 11 -

Jednakże składniki sumy cząstkowej S

2 n

1

można pogrupować wybierając do pierwszej

grupy co drugi wyraz i wtedy

lim

n

∞

S

2 n

1

=lim

n

∞

[

1

−

z

2

2

!



z

4

4

!



−1

n

⋅z

2 n

2 n!

i



z

1

!

−

z

3

3

!



z

5

5

!

−1

n

 z

2 n

1

2 n1!



]

=

=lim

n

∞



1

−

z

2

2

!



z

4

4

!

−

1



n

⋅z

2 n

2 n!



i lim

n

∞



z

1

!

−

z

3

3

!



z

5

5

!

−1

n

 z

2 n

1

2 n1!



=cos zi sin z

Ad.(2)

cos

−z=cos z

sin

−z=−sin z

}

⇒ e

−iz

=

1

cos

−zi sin−z=cos z−i sin z .

Z powyższego twierdzenia wynikają następujące

□

WZORY EULERA

cos z

=

e

iz

e

−iz

2

∧

sin z

=

e

iz

−e

−iz

2

dla z

∈ℂ

- 12 -

Szeregi ortogonalne

Będziemy rozważać funkcje całkowalne w sensie Riemanna w przedziale

[a ,b].

Definicja

Niech f , g - całkowalne (w sensie Riemanna) w

[a , b] .

Liczbę

〈 f , g 〉

równą

〈 f , g 〉:=

∫

a

b

f

 x g  xdx

nazywamy iloczynem skalarnym funkcji f i g .
Jednakże

〈· ,·〉 nie spełnia warunków określających iloczyn skalarny . Co prawda

spełnione są warunki (IS1)-(IS3) , ale warunek

IS4: 〈 f , f 〉=

∫

a

b

f

2

 xdx=0 ⇒ f ≡0

nie zachodzi bo funkcja równa zero poza skończoną liczbą punktów nie spełnia powyższej
implikacji.

Przykład

f

 x=

{

1, x

=0

0, x

∈( 0 ;1 ] ⇒

∫

0

1

f

2

 xdx=0

Zatem

〈 f , f 〉=0 mimo, że f ≡0 .

Dygresja

Całkowalność w sensie Lebesgue’a (względem miary)

Rozważmy całkę Lebesgue’a (całkę względem miary).
Wtedy

f -całkowalna w sensie Riemanna

⇒ f - całkowalna w sensie Lebesgue’a

oraz

∫

R=

∫

 L

Wśród funkcji całkowalnych w sensie Lebesgue'a rozważa się rodzinę L

2

[a , b] , gdzie

L

2

[a , b]:={ f :[a , b] ℝ;

∫

[a , b]

f

2

 xdx∞}

L

2

[a , b] , - rodzina funkcji całkowalnych w sensie Lebesque’a wraz z kwadratem.

Definicja (równości funkcji)

Mówimy, że funkcje

f i g

są równe, f

=g , jeśli f  x=g  x poza zbiorem miary zero.

Uwaga

Przy tak sformułowanej definicji równości funkcji, rodzina L

2

[a , b] jest przestrzenią

wektorową.

- 13 -

Definicja

Niech f , g ∈L

2

[a , b].

Wtedy definiujemy

〈 f , g 〉:=

∫

[ a , b]

f

 x g  xdx

Uwaga

Funkcja

〈· ,·〉 spełnia własności iloczynu skalarnego w przestrzeni L

2

[a , b] .

Wniosek

L

2

[a , b] - przestrzeń unitarna

Zatem z twierdzenia o indukowaniu normy wynika , że

∥ f ∥=



〈 f , f 〉=



∫

[ a , b]

f

2

 xdx

jest normą w L

2

[a , b] . Normę tę nazywamy normą kwadratową.

Ponadto

d

 f , g =∥ f −g∥=



〈 f −g , f −g 〉=



∫

[ a , b]

 f  x−g  x

2

dx

jest metryką w L

2

[a , b] wyznaczoną przez normę kwadratową zadaną iloczynem

skalarnym.

Definicja

Niech

 f

n



n

∈ℕ

⊂L

2

[a , b] oraz f ∈L

2

[a , b].

Wtedy

f

n

 f :⇔d  f

0

, f

n

 

n

∞

0

⇔

⇔



∫

[a , b]

 f  x− f

n

 x

2

dx



n

∞

0

⇔

⇔

∫

[a , b]

 f  x− f

n

 x

2

dx



n

∞

0

Koniec dygresji

Powróćmy do funkcji całkowalnych w sensie Riemanna

Definicja

Liczbę ∥ f ∥=



∫

a

b

f

2

 xdx nazywamy normą kwadratową funkcji f w [a , b].

- 14 -

Przykład

Obliczyć normę kwadratową funkcji f

 x=sin x dla x∈[0,].

∥ f ∥=



∫

0



sin

2

xdx

=



∫

0



1

−cos 2 x

2

dx

=



[



x

2

−

1
4

sin2 x



]

0



=





2

Uwaga

1

˚ f ∈C [a , b] ⇒ ∥ f ∥=0 ⇔ f ≡0 

2

˚ f ∉C [a ,b]⇒∥ f ∥=0 ⇔ f ≡0 

Definicja

Funkcje f , g – całkowalne w sensie Riemanna nazywamy ortogonalnymi w

[a , b] ,

jeśli ich iloczyn skalarny jest równy 0, czyli

〈 f , g 〉=0 .

Przykład

Niech f  x=x , g  x=x

2

oraz x

∈[0,1] .

Wtedy

〈 f , g 〉=

∫

0

1

x

⋅x

2

dx

=

[

x

4

4

]

0

1

=

1
4

≠0 ⇒

funkcje f , g nie są ortogonalne w

[0,1].

Natomiast dla x

∈[−1,1]funkcje f , g są ortogonalne w [−1,1] , bo

〈 f , g 〉=

∫

−1

1

x

3

dx

=

[

1

4

x

4

]

−1

1

=0.

Definicja

Niech



n

:

[a , b] ℝ

dla

n

∈ℕ

0

oraz



n

- całkowalna

∀ n∈ℕ

0

.

Ciąg funkcyjny 

n



n

∈ℕ

0

nazywamy ciągiem ortogonalnym w

[a , b] ,

jeśli :

1

˚ ∀ n , m∈ℕ

0

, n

≠m: 〈

n

,



m

〉=0

oraz

2

˚ ∀ n∈ℕ

0

∥

n

∥0 .

- 15 -

Przykład

Ciąg sinn1 x

n

∈ℕ

0

jest ciągiem ortogonalnym w

[− ,] ,bo

1

˚ dla n≠m i n , m∈ℕ

0

〈sinn1 x ,sinm1 x〉=

∫

−



sin

n1 x⋅sinm1 x⋅dx=

=

1
2

∫

−



cos

n−m x⋅dx−

1
2

∫

−



cos

nm2 x⋅dx=0

2

˚ dla n∈ℕ

0

∥sinn1 x∥=



∫

−



sin

2

n1 x dx=



∫

−



1

−cos2n1 x

2

dx

=

=



[



1
2

x

−

sin2

n1 x

4

n1



]

−



=



0

z 1

˚ i 2 ˚ wynika, że ciąg funkcyjny

sinn1 x

n

∈ℕ

0

jest ortogonalny w

[− ,].

Definicja

Ciąg funkcyjny 

n



n

∈ℕ

0

nazywamy ciągiem unormowanym w

[a , b] ,

jeśli

∀ n∈ℕ

0

∥

n

∥=1.

Przykład

Ciąg



1





⋅sinn1 x



n

∈ℕ

0

jest unormowany w

[− ,].

Definicja

Ciąg funkcyjny 

n



n

∈ℕ

0

nazywamy ciągiem ortonormalnym w

[a , b] , jeśli jest

ortogonalny i unormowany w tym przedziale.

Przykład c.d.



1





⋅sinn1 x



n

∈ℕ

0

-ciąg ortonormalny w [−,].

Wniosek

Jeżeli 

n



n

∈ℕ

0

jest ciągiem ortogonalnym , to





n

∥

n

∥



n

∈N

0

jest ciągiem ortonormalnym.

- 16 -

Uwaga



n



n

∈ℕ

jest ortonormalnym

⇔ 〈

n

,



m

〉=

nm

dla n , m

∈ℕ

0

,

gdzie symbol



nm

oznacza deltę Kroneckera,



nm

:

=

{

1 , gdy n

=m ,

0 , gdy n

≠m.

Definicja

Niech 

n



n

∈ℕ

0

- ciąg ortogonalny w

[a , b] ,



n



n

∈ℕ

0

- ciąg liczbowy .

Wtedy szereg

∑

n

=0

∞



n

⋅

n

 x nazywamy szeregiem ortogonalnym w [a , b] .

Lemat (o szeregu ortogonalnym)

Niech

∑

n

=0

∞



n

⋅

n

 x - szereg ortogonalny w [a , b] i zbieżny jednostajnie w [a , b]

oraz

niech jego suma f

 x=

∑

n

=0

∞



n

⋅

n

 x jest funkcją całkowalną w [a , b].

Wtedy



n

=

〈 f ,

n

〉

∥

n

∥

2

∀ n∈ℕ

0

.

Dowód

Niech n

∈ℕ

0

, x

∈[a , b].

〈 f ,

n

〉=

∫

a

b

f

 x⋅

n

 xdx=

∫

a

b



∑

k

=0

∞



k



k

 x

n

 xdx=

∫

a

b

[

∑

k

=0

∞



k



k

 x⋅

n

 x]dx=

=

∑

k

=0

∞

∫

a

b



k



k

 x

n

 xdx=

∑

k

=0

∞



k

∫

a

b



k

 x

n

 xdx=

∑

k

=0

∞



k

〈

k

,



n

〉=

n

〈

n

,



n

〉=

=

n

∥

n

∥

2

stąd



n

=

〈 f ,

n

〉

∥

n

∥

2

.

□

Wniosek

f - całkowalna w

[a , b] ⇒ ∃ co najwyżej jeden szereg ortogonalny zbieżny

jednostajnie do funkcji f , mianowicie jest to szereg postaci

- 17 -

∑

n

=0

∞

c

n



n

 x

o współczynnikach

c

n

=

〈 f ,

n

〉

∥

n

∥

2

dla n

∈ℕ

0

.

Powyższe wzory określające współczynniki c

n

nazywamy wzorami Eulera-Fouriera ,

c

n

nazywamy współczynnikami Fouriera funkcji f względem ciągu ortogonalnego



n



n

∈ℕ

0

w

[a , b] ,

a szereg

∑

n

=0

∞

c

n



n

 x nazywamy szeregiem Fouriera funkcji f względem ciągu



n



n

∈ℕ

0

w

[a , b] i piszemy

f

 x~

∑

k

=0

∞

c

n



n

 x dla x∈[a , b]

Zatem jeśli f jest całkowalna w

[a , b]

, to odpowiada jej szereg Fouriera utworzony

względem dowolnego ciągu 

n



n

∈ℕ

0

ortogonalnego w tym przedziale . Jednakże nic nie

wiemy o zbieżności utworzonego szeregu , a w szczególności nie wiemy , czy sumą tego
szeregu jest funkcja f .

Jeśli f

 x=

∑

k

=0

∞

c

n



n

 x , to o funkcji f mówimy , że jest rozwijalna w szereg Fouriera.

Definicja

Liczbę d

 f , g =∥ f −g∥=



∫

a

b

[ f  x−g  x]

2

dx nazywamy

odległością kwadratową funkcji f i g w przedziale

[a , b].

Uwaga

1

˚ f ∈C [a , b] ⇒ d  f , g =0 ⇒ f =g 

2

˚ f ∉C [a , b] ⇒ d  f , g =0 ⇒ f =g 

Definicja

Niech 

n



n

∈ℕ

0

- ciąg ortogonalny,



n



n

∈ℕ

0

- ciąg liczbowy.

funkcję



N

 x:=

∑

n

=0

N



n



n

 x nazywamy wielomianem ortogonalnym rzędu N

utworzonym z wyrazów ciągu 

n



n

∈ℕ

0

.

- 18 -

Zagadnienie

najlepszej

aproksymacji kwadratowej.

Niech f - całkowalna w

[a , b] ,



n



n

∈ℕ

0

- ciąg ortogonalny w

[a , b] ,

N

∈ℕ

0

.

Zagadnienie polega na dobraniu

dla n

=0,1 ,, N

współczynników



n

wielomianu

ortogonalnego



N

 x=

∑

n

=0

N



n



n

 x tak, aby odległość kwadratowa d  f ,

N

 była

minimalna. Wtedy



N

będzie wielomianem aproksymujacym funkcję f w

[a , b]

najlepiej w sensie odległości kwadratowej .

Twierdzenie (o aproksymacji kwadratowej)

Spośród wszystkich wielomianów



N

 x=

∑

n

=0

N



n



n

 x najlepszą aproksymację

kwadratową funkcji f w przedziale

[a , b] stanowi wielomian o współczynnikach

Fouriera.

Dowód

d

2

〈 f ,

N

〉=〈 f −

N

, f

−

N

〉=〈 f , f 〉−2 〈 f ,

N

〉〈

N

,



N

〉=

=∥ f ∥

2

−2 〈 f ,

∑

n

=0

N



n



n

〉〈

∑

n

=0

N



n



n

,

∑

m

=0

N



m



m

〉=

=∥ f ∥

2

−2

∑

n

=0

N



n

〈 f ,

n

〉

∑

n , m

=0

N



n



m

〈

n

,



m

〉=

=∥ f ∥

2

−2

∑

n

=0

N



n

〈 f ,

n

〉

∑

n

=0

N



n

2

〈

n

,



n

〉=

=∥ f ∥

2

−2

∑

n

=0

N

〈 f ,

n

〉

∥

n

∥

2



n

∥

n

∥

2



∑

n

=0

N



n

2

∥

n

∥

2

=

=∥ f ∥

2

−2

∑

n

=0

N

c

n

⋅

n

∥

n

∥

2



∑

n

=0

N



n

2

∥

n

∥

2

=

=∥ f ∥

2



∑

n

=0

N

c

n

−

n



2

∥

n

∥

2

−

∑

n

=0

N

c

n

2

∥

n

∥

2

.

Powyższe wyrażenie ma najmniejszą wartość, gdy suma

∑

n

=0

N

c

n

−

n



2

∥

n

∥

2

jest

najmniejsza czyli, gdy



n

=c

n

∀ n∈{0,1,2 ,, N }.

□

Uwaga

Jeśli



n

=c

n

dla n

=0,1 ,, N , to d

2

 f ,

n

=∥ f ∥

2

−

∑

n

=0

N

c

n

2

∥

n

∥

2

0 dla N ∈ℕ

0

.

Zatem

∀ N ∈ℕ

0

∑

n

=0

N

c

n

2

∥

n

∥

2

∥ f ∥

2

.

- 19 -

Wprowadźmy oznaczenie S

n

1

:

=

∑

n

=0

N

c

n

2

∥

n

∥

2

. Na podstawie powyższej nierówności ciąg

S

n

1



N

∈ℕ

0

jest ograniczony. Ponadto jest to ciąg rosnący. Zatem

S

n

1



N

∈ℕ

0

jest

ciągiem zbieżnym.

Stąd

∑

n

=0

∞

c

n

2

∥

n

∥

2

-zbieżny oraz

∑

n

=0

∞

c

n

2

∥

n

∥

2

≤∥ f ∥

2

.

Powyższą nierówność nazywamy nierówność Bessela.

Nierówność ta jest prawdziwa dla dowolnego ciągu 

n



n

∈ℕ

ortogonalnego w przedziale

[a , b]

oraz dla dowolnej funkcji f całkowalnej w tym przedziale.

Definicja

Ciąg 

n



n

∈ℕ

0

ortogonalny w

[a , b] nazywamy układem zupełnym w klasie funkcji

całkowalnych w

[a , b] , jeśli dla każdej funkcji f z tej klasy zachodzi

∑

n

=0

∞

c

n

2

∥

n

∥

2

=∥ f ∥

2

Powyższą równość nazywamy równością Parsevala lub warunkiem zupełności.

Uwaga

Układ zupełny w klasie funkcji całkowalnych jest również układem zupełnym w klasie
funkcji ciągłych.

Uwaga.



n



n

∈ℕ

0

-ciąg ortogonalny

⇒

∑

n

=0

∞

c

n

2

=∥ f ∥

2

- 20 -

Analogie między teorią wektorów a teorią ciągów i szeregów ortogonalnych

wektory w

ℝ

3

szeregi ortogonalne

⋅ wersory i , j , k ⋅ ortogonalny układ zupełny 

n



n

∈ℕ

0

⋅ współrzędne x , y , z wektora ⋅ współczynniki Fouriera c

n

funkcji f



V

=[ x , y , z] względem 

n



n

∈ℕ

0

⋅ x=〈 V , i〉 ⋅ c

n

=〈 f ,

n

〉 , gdy



n



n

∈ℕ

0

-układ

y=〈 V , j 〉 ortonormalny
z=〈 V , k 〉

⋅ kwadrat długości wektora



V

⋅ równość Parsevala

∣V∣

2

=x

2

 y

2

z

2

∥ f ∥

2

=

∑

n

=0

∞

c

n

2

⋅ rozkład wektora na składowe ⋅ f  x=

?

∑

n

=0

∞

c

n



n

 x



V

=x i y jz k szereg może nie być zbieżnym lub

być zbieżnym, ale nie do funkcji f

Aby odpowiedność w ostatnim wierszu tabelki zachodziła, określamy odpowiednio pojęcie
zbieżności. Wykorzystamy definicję zbieżności ciągu w przestrzeni L

2

[a , b] według

metryki.

Definicja

Ciąg funkcyjny  f

n



n

∈ℕ

funkcji

f

n

:

[a , b] R ,

n

∈ℕ , nazywamy

zbieżnym przecietnie z kwadratem w przedziale

[a , b] , jeśli

lim

n

∞

∫

[ a , b]

 f  x− f

n

 x

2

dx

=0.

Uwaga

Ciąg  f

n



n

∈ℕ

może być zbieżnym przecietnie z kwadratem w

[a , b]

, ale nie zbieżnym

punktowo w

[a , b].

Przykład

Niech

f

n

 x=

{



n , dla 0

≤x≤

1
n

2

0 , dla

1

n

2

≤x≤1

oraz niech

f

≡0

w

[0,1].

Wtedy

lim

n

∞

∫

0

1

 f  x− f

n

 x

2

dx

=lim

n

∞

∫

0

1
n

2

 f

n

 x

2

dx

=lim

n

∞

∫

0

1
n

2

ndx

=lim

n

∞

1

n

=0

Zatem  f

n



n

∈ℕ

jest zbieżny przeciętnie z kwadratem do funkcji f

w

[a , b].

- 21 -

Jednak dla x

=0 mamy f

n

0=



n



n

∞

∞ ⇒  f

n



n

∈ℕ

nie jest zbieżny punktowo w

[0,1].

Uwaga

Ciąg  f

n



n

∈ℕ

może być zbieżnym punktowo ale nie zbieżnym przecietnie z kwadratem.

Przykład

Niech

f

n

 x=

{

0

dla x

=0,

n

dla 0

x

1

n

,

0

dla

1
n

x1.

Ciąg  f

n



n

∈ℕ

jest zbieżny punktowo do funkcji

f

≡0 w [0,1].

Jednak

lim

n

∞

∫

0

1

 f

n

 x− f  x

2

dx

=lim

n

∞

∫

0

1

n

n

2

dx

=lim

n

 ∞

n

=∞

Zatem

 f

n



n

∈ℕ

nie jest

zbieżny przeciętnie z kwadratem.

Niech 

n



n

∈ℕ

0

-układ zupełny.

Wtedy

∀ f całkowalna w[a , b]:

∑

n

=0

∞

c

n

2

∥

n

∥

2

=∥ f ∥

2

.

Stąd

lim

N

∞

d

2

 f ,

N

= lim

N

∞

∥ f ∥

2

−

∑

n

=0

N

c

n

2

∥

n

∥

2

=∥ f ∥

2

−

∑

n

=0

∞

c

n

2

∥

n

∥

2

=0

i otrzymujemy następujący wniosek

Wniosek

Szereg Fouriera

∑

n

=0

∞

c

n



n

 x dowolnej funkcji f całkowalnej w przedziale [a , b] ,

względem układu zupełnego 

n



n

∈ℕ

0

jest zbieżny przecietnie z kwadratem w tym

przedziale do funkcji f .

Uwaga

Oczywiście szereg Fouriera nie musi być zbieżny w zwykły sposób. Jeśli spełniona jest

równość f

 x=

∑

n

=0

∞

c

n



n

 x to mówimy, że funkcja f jest rozwijalna w szereg

Fouriera.

- 22 -

SZEREG TRYGONOMETRYCZNY FOURIERA

Definiujemy ciąg funkcyjny



n



n

∈ℕ

0

:



0

 x=1



2 n

−1

 x=cos

n

 x

l

, n

∈ℕ



2 n

 x=sin

n

 x

l

czyli ciąg :

1, cos

 x

l

, sin

 x

l

, cos

2

 x

l

, sin

2

 x

l

,



Stwierdzenie

Ciąg



n



n

∈ℕ

0

jest ortogonalny w

[−l , l ].

Dowód

Dla n

∈ℕ mamy

〈

0

,



2 n

−1

〉=

∫

−l

l

cos

n

 x

l

dx

=

[

l

n



sin

n

 x

l

]

−l

l

=0

〈

0

,



2 n

〉=

∫

−l

l

sin

n

 x

l

dx

=

[

−

l

n



cos

n

 x

l

]

−l

l

=0

dla n , m

∈ℕ otrzymujemy

〈

2 n

−1

,



2 m

〉=

∫

−l

l

cos

n

 x

l

sin

m

 x

l

dx

=

=

1
2

∫

−l

l



sin

m−n x

l

sin

mn x

l



dx

=0

Ponadto dla n

≠m

〈

2 n

−1

,



2 m

−1

〉=

∫

−l

l

cos

n

 x

l

cos

m

 x

l

dx

=

=

1
2

∫

−l

l



cos

m−n x

l

cos

mn x

l



dx

=0

oraz

〈

2 n

,



2 m

〉=

∫

−l

l

sin

n

 x

l

sin

m

 x

l

dx

=

=

1
2

∫

−l

l



cos

m−n x

l

−cos

mn x

l



dx

=0

- 23 -

Nadto kwadraty norm kwadratowych wynoszą

∥

0

∥

2

=

∫

−l

l

dx

=2l0

oraz dla n

∈ℕ

∥

2 n

−1

∥

2

=

∫

−l

l

cos

2

n

 x

l

dx

=

[

x

2



l

4 n



sin

2 n

 x

l

]

−l

l

=l0 ,

∥

2 n

∥

2

=

∫

−l

l

sin

2

n

 x

l

dx

=

[

x

2

−

l

4 n



sin

2 n

 x

l

]

−l

l

=l0 .

□

Uwaga

Jeśli

∀ n∈ℕ:



2 n

−1

,



2 n

- funkcje okresowe o okresie 2 l

⇒ ciąg 

n



n

∈ℕ

0

jest

ortogonalny w każdym przedziale o długości 2 l .

Twierdzenie

Ciąg



n



n

∈ℕ

0

:



0

 x=1



2 n

−1

 x=cos

n

 x

l



2 n

 x=sin

n

 x

l

dla n

∈ℕ

stanowi układ zupełny w klasie funkcji całkowalnych w

[−l , l ].

Niech f -całkowalna w

[−l , l ].

Wtedy współczynniki Fouriera względem układu zupełnego wynoszą

c

n

=

〈 f ,

n

〉

∥

n

∥

2

Stąd

c

0

=

1

2 l

∫

−l

l

f

 xdx

c

2 n

−1

=

1

l

∫

−l

l

f

 xcos

n

 x

l

dx

c

2 n

=

1

l

∫

−l

l

f

 xsin

n

 x

l

dx

i funkcji f odpowiada szereg Fouriera f

 x~

∑

i

=0

∞

c

n



n

 x.

- 24 -

Uwaga

Powyższy szereg zapiszemy w postaci tradycyjnej, podstawiając

a

0

:

=2 c

0

a

n

:

=c

2 n

−1

b

n

:

=c

2 n

dla n

∈ℕ.

Wtedy

f

 x~

a

0

2



∑

n

=1

∞



a

n

cos

n

 x

l

b

n

sin

n

 x

l



-szereg trygonometryczny Fouriera

funkcji f w

[−1,1] , gdzie

a

0

=

1

l

∫

−l

l

f

 xdx

a

n

=

1

l

∫

−l

l

f

 xcos

n

 x

l

dx

b

n

=

1

l

∫

−l

l

f

 xsin

n

 x

l

dx

Wniosek

Szereg trygonometryczny Fouriera jest zbieżny przeciętnie z kwadratem do funkcji f.

Wniosek

Dla szeregu trygonometrycznego Fouriera spełniona jest równość Parsevala, czyli

2 lc

0

2

l

∑

n

=1

∞

c

n

2

=∥ f ∥

2

la

0

2

2

l

∑

n

=1

∞

a

n

2

b

n

2

=∥ f ∥

2

stąd

a

0

2

2



∑

n

=1

∞

a

n

2

b

n

2

=

1

l

∥ f ∥

2



równość Parsevala dla szeregu trygonometrycznego
Fouriera

Definicja

Niech funkcja f jest ograniczona w

a , b.

Mówimy, że f jest przedziałami monotoniczna w

a , b ,

jeśli przedział ten można

podzielić na skończoną liczbę przedziałów, wewnątrz których funkcja jest monotoniczna.

- 25 -

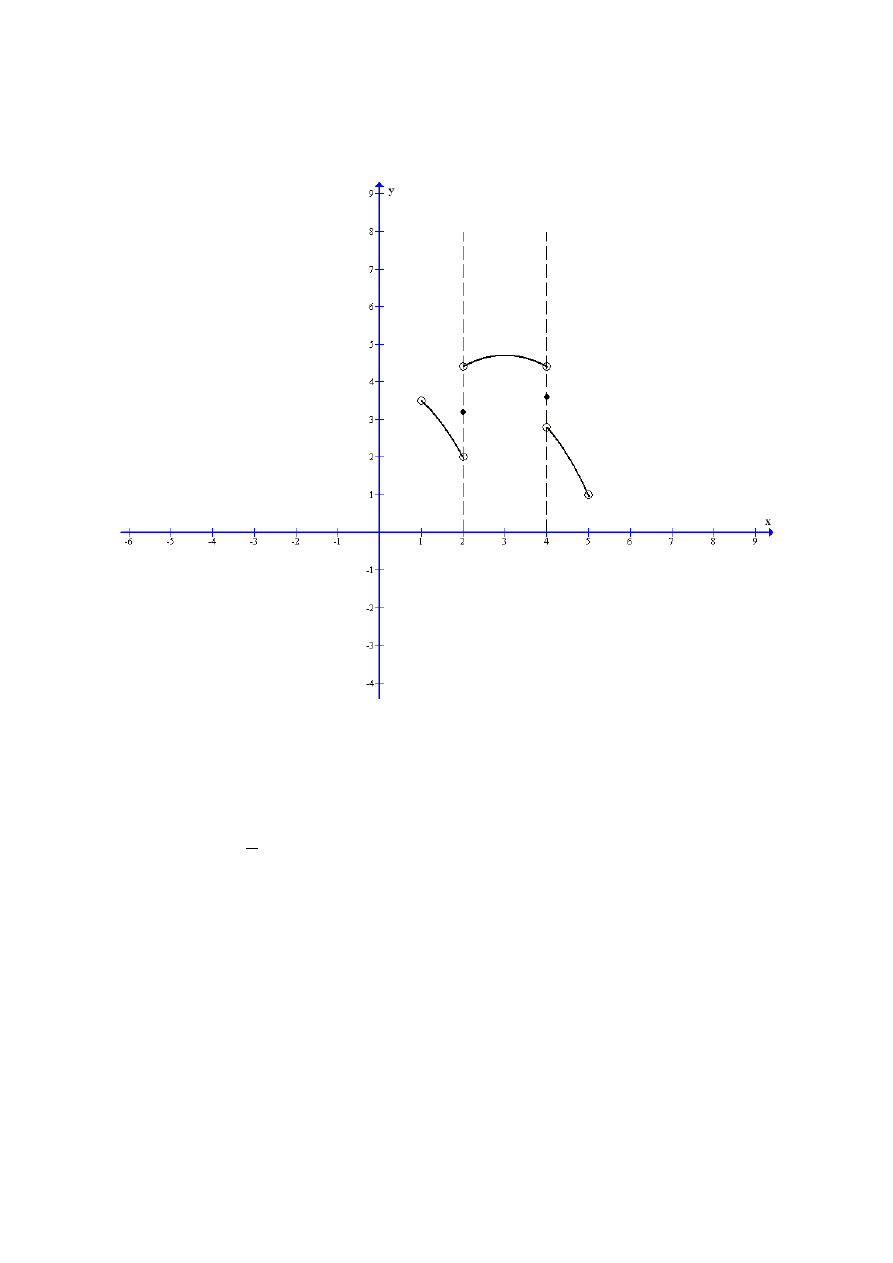
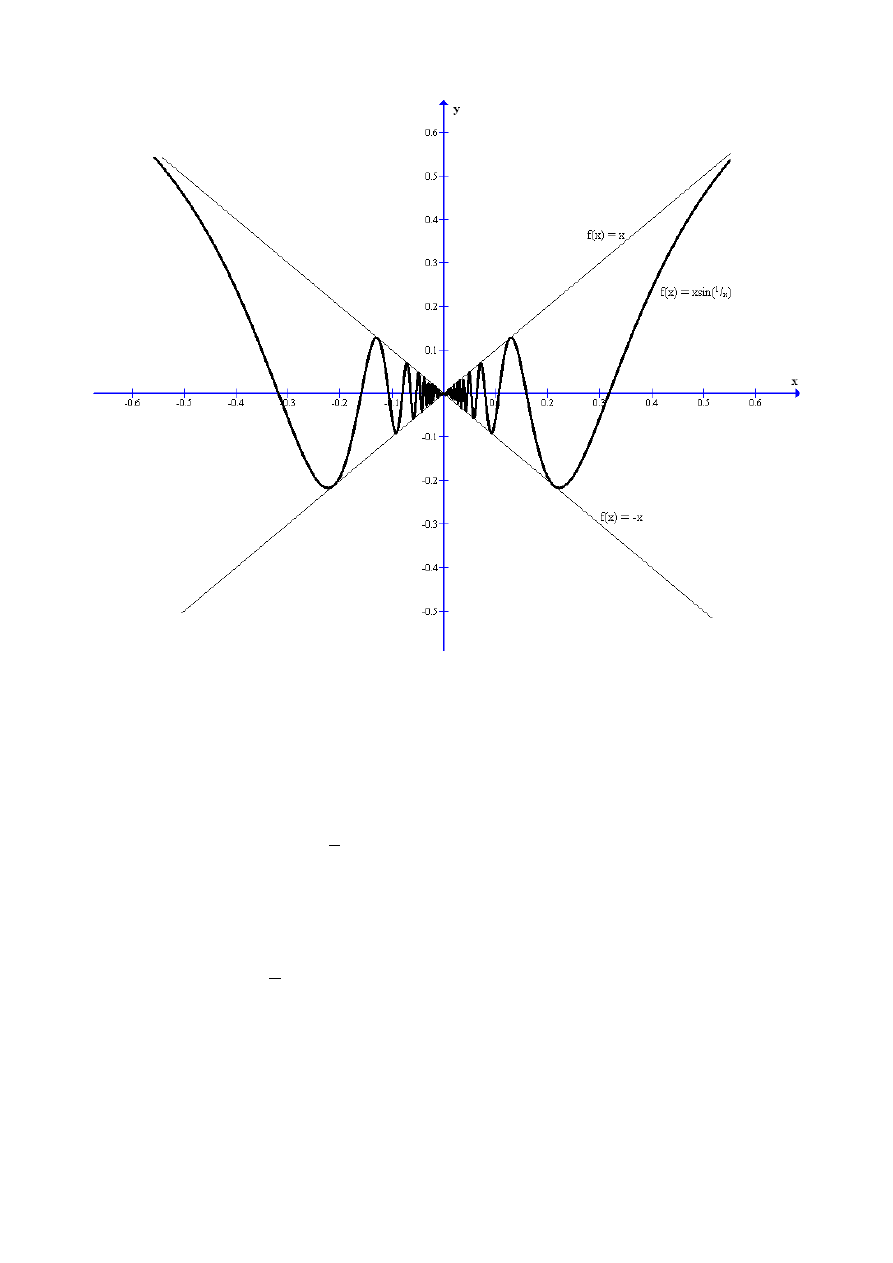
Przykład

Przykład

Funkcja f

 x=x sin

1

x

nie jest przedziałami monotoniczna w

[−l , l ].

- 26 -

Definicja

Funkcja f spełnia w przedziale

[a , b] warunki Dirichleta, jeśli:

1

˚ jest przedziałami monotoniczna w

a , b

(jest więc ograniczona)

2

˚ f ∈C a , b∖{x

1

, x

2

,

, x

n

}

oraz w każdym punkcie nieciągłości x

i

zachodzi

f

 x

i

=

1
2

[ f  x

i

-

 f  x

i

+

] ,

gdzie f

 x

i

-

 f  x

i

+

oznaczają granice odpowiednio lewo i prawostronne funkcji f

w punkcie x

i

,

f

 x

i

-

:=lim

x

 x

i

-

f

 x , f  x

i

+

:= lim

x

 x

i

+

f

 x

3

˚

f

a= f b=

1
2

[ f a

+

 f b

-

].

gdzie f b

-

=lim

x

b

-

f

 x , f a

+

= lim

x

 a

+

f

 x

- 27 -

Twierdzenie (Dirichleta)

Jeśli f spełnia w

[−l , l ] warunki Dirchleta, to jest rozwijalna w szereg trygonometryczny

Fouriera w

[−l , l ] , czyli zachodzi równość

f

 x=

a

0

2



∑

n

=1

∞



a

n

cos

n

 x

l

b

n

sin

n

 x

l



dla x

∈[−l , l ].

Jeśli dodatkowo f jest okresowa o okresie 2 l , to f jest rozwijalna w szereg
trygonometryczny Fouriera w całej swojej dziedzinie.

Uwaga

Niech f spełnia warunki Dirchleta w

[−l , l ].

Jeśli
1

˚

f - parzysta, tzn.

f

−x= f  x

to

a

0

=

2

l

∫

0

l

f

 xdx

a

n

=

2

l

∫

0

l

f

 xcos

n

 x

l

dx

b

n

=0

}

⇒ f  x=

a

0

2



∑

n

=1

∞

a

n

cos

n

 x

l

czyli f jest rozwijalna w szereg kosinusów
Natomiast, jeśli
2

˚ f - nieparzysta, tzn. f −x=− f  x to

a

0

=a

n

=0

b

n

=

2

l

∫

0

l

f

 xsin

n

 x

l

dx

}

⇒ f  x=

∑

n

=1

∞

b

n

sin

n

 x

l

czyli f jest rozwijalna w szereg sinusów.

Przykład

Rozwinąć w szereg trygonometryczny Fouriera funkcję

f

 x=

{

sgn x dla x

∈−l , l  ,

0

dla x

=−l∨x=l .

- 28 -

Funkcja f spełnia warunki Dirchleta oraz jest nieparzysta.
Zatem

∀ n∈ℕ

0

a

n

=0 oraz

f

 x=

∑

n

=1

∞

b

n

sin

n

 x

l

, gdzie

b

n

=

2

l

∫

0

l

sin

n

 x

l

dx

=

[

2

l



−

l

n

⋅



cos

n

 x

l

]

0

1

=−

2

n



cos n−cos0=−

2

n



−1

n

−1=

=

{

0 ,

gdy n - parzyste,

4

n



, gdy n - nieparzyste.

Stąd b

2 k

=0 i b

2 k

−1

=

4

2 k−1

dla k

∈ℕ i w konsekwencji

f

 x=

∑

n

=1

∞

b

2 n

−1

sin

2 n−1 x

l

=

∑

n

=1

∞

4

2 n−1

sin

2 n−1 x

l

dla x

∈[−l , l ].

Zatem

- 29 -

f

 x=

4



∑

n

=1

∞

1

2 n

−1

sin

2 n−1 x

l

dla x

∈[−l ,l ]

Powyższe rozwinięcie funkcji f można wykorzystać do obliczania sumy szeregów liczbowych

np. dla x

=

l

2

otrzymujemy

f



l

2



=

4


⋅

∑

n

=1

∞

1

2 n

−1

sin



−



2

n



⇒

1

=

4



∑

n

=1

∞

−1

n

1

2 n

−1

a stąd

∑

n

=1

∞

−1

n

1

2 n

−1

=



4

wzór Leibniza.

Do obliczenia sum szeregów liczbowych można wykorzystać też równośc Parsevala.

Przykład c.d.

Zapiszmy równość Parsevala dla funkcji f zdefiniowanej wcześniej.

∑

n

=1

∞

b

n

2

=

1

l

∥ f ∥

2

,

gdzie b

2 n

−1

=

4

2 n−1

, b

2 n

=0,

stąd

∑

n

=1

∞



4

2 n−1



2

=

1

l

∫

−l

l

f

2

 xdx

16



2

∑

n

=1

∞

1

2 n−1

2

=

2

l

∫

−l

l

f

2

 xdx=

[

2

l

x

]

0

l

=2

i ostatecznie

∑

n

=1

∞

1

2 n−1

2

=



2

8

.

Rozwijanie w szereg sinusów lub kosinusów.

Niech f spełnia 1

˚ i 2 ˚ warunek Dirchleta w przedziale 0, l . Wtedy funkcję f

można rozwinąć albo w szereg samych sinusów albo w szereg samych kosinusów
odpowiednio ją przedłużając na przedział

[−l , l ].

a) szereg sinusów

f przedłużamy nieparzyście

f *

 x=

{

0

, gdy x

=−l

− f −x

, gdy x

=−l ,0

0

, gdy x

=0

f

 x

, gdy x

∈0, l 

0

, gdy x

=l

b)szereg kosinusów

f przedłużamy parzyście

- 30 -

f *

 x=

{

f

l

-



, gdy x

=−l

f

−x

, gdy x

=−l ,0

f

0

, gdy x

=0

f

 x

, gdy x

∈0, l 

f

l

-



, gdy x

=l

Ponieważ f * spełnia wszystkie warunki Dirichleta, zatem rozwinięcie f * w szereg
trygonometryczny Fouriera w

[−l , l ]. jest rozwinięciem f w szereg trygonometryczny

Fouriera w

0, l .

Przykłady

1. Rozwinąć funkcję

f

 x=x

w przedziale

0, w szereg sinusów.

Mamy l

= i f przedłużamy nieparzyście.

Wtedy

f *

 x=

{

x

, x

∈− ,

0

, x

= , x=−

b

n

=

2



∫

0



f

 xsin

n

 x


dx

=

2



∫

0



x sin

nxdx=

2



[

−

x

n

cos

nx

1

n

2

sin

nx

]

0



=

=

2





−



n



−1

n

=

2
n

−1

n

1

Zatem

f *

 x=

∑

n

=1

∞

2
n

−1

n

1

sin

nxdla x∈[− ,]

a stąd

f

 x=

∑

n

=1

∞

2
n

−1

n

1

sin

nx

dla x

∈0,.

2. Funkcję f

 x=x rozwinąć w przedziale 0, w szereg kosinusów.

Mamy l

= i f przedłużamy parzyście.

Wtedy
f *

 x=∣x∣ , x∈[− ,]

a

0

=

2



∫

0



f

 xdx=

2



∫

0



x dx

=

2



[

1
2

x

2

]

0



=

a

n

=

2



∫

0



f

 xcos

n

 x


dx

=

2



∫

0



x cos

nxdx=

2



[

x

n

sin

nx

1

n

2

cos

nx

]

0



=

=

2

 n

2



−1

n

−1



=

{

0

,

gdy n

−parzyste

−

4

 n

2

,

gdy n

−nieparzyste

- 31 -

zatem

f *

 x=



2

−

4



∑

n

=1

∞

1

2 n−1

2

cos

[2 n−1 x] dla x∈[− ,]

a stąd

f

 x=



2

−

4



∑

n

=1

∞

1

2 n−1

2

cos

[2 n−1 x] dla x∈[0,].

- 32 -

Postać zespolona szeregu trygonometrycznego Fouriera.

Wzory Eulera

cos z

=

e

iz

e

−iz

2

sin z

=

e

iz

−e

−iz

2i

zachodzą

∀ z∈ℂ , zatem w szczególności dla z=

n

 x

l

, gdzie x

∈ℝ.

Stąd

cos

n

 x

l

=

1
2



e

i

n

 x

l

e

−i

n

 x

l



sin

n

 x

l

=

1

2i



e

i

n

 x

l

−e

−i

n

 x

l



=

i

2



−e

i

n

 x

l

e

−i

n

 x

l



i szereg trygonometryczny Fouriera

a

0

2



∑

n

=1

∞



a

n

cos

n

 x

l

b

n

sin

n

 x

l



można zapisać w postaci

a

0

2



∑

n

=1

∞



a

n

−i b

n

2

e

i

n

 x

l



a

n

i b

n

2

e

−i

n

 x

l



  

c

0

c

n

c

−n

to znaczy

c

0



∑

n

=1

∞



c

n

e

i

n

 x

l

c

−n

e

−i

n

 x

l



, gdzie

{

c

0

=

a

0

2

c

n

=

a

n

−i b

n

2

, n

∈ℕ

c

−n

=

a

n

i b

n

2

lub krótko

∑

n

=−∞

n

=∞

c

n

e

i

n

 x

l

,

gdzie powyższy szereg jest ciągiem sum cząstkowych S

N

 x=

∑

n

=−N

N

c

n

e

i

n

 x

l

.

Jest to postać zespolona szeregu trygonometrycznego Fouriera(krótko zespolony

szereg Fouriera).

Jeśli f spełnia warunki Dirichleta w

[−l , l ] , to jest rozwijalna w szereg zespolony

Fouriera i, podobnie jak wyżej, można wyprowadzić wzory na współczynniki Fouriera.

c

n

=

1

2 l

∫

−l

l

f

 xe

−i

n

 x

l

dx , dla n

∈ℤ

- 33 -

Uwaga

Jesli dodatkowo f jest funkcją okresową o okresie 2 l , to

c

n

=

1

2 l

∫

0

2 l

f

 xe

−i

n

 x

l

dx dla n

∈ℤ.

- 34 -