Katedra Genetyki i Podstaw Hodowli Zwierząt

Wydział Hodowli i Biologii Zwierząt, UTP w Bydgoszczy

Ćwiczenie:
Badanie normalności rozkładu. Wyznaczanie przedziałów ufności

Badanie normalności rozkładu

Shapiro-Wilka: jest on najbardziej zalecanym testem normalności rozkładu. Jednak wskazane jest,
aby liczebność próby była poniżej 2000, gdyż w przeciwnym wypadku daje mylne wyniki. Test ten
wymaga, aby cecha miała rozkład ciągły.
Kołmogorowa-Smirnowa (K-S): Wymaga znajomości średniej i odchylenie standardowego dla
populacji. W sytuacji, gdy nie znamy wyżej wymienionych parametrów stosujemy test K-S z
poprawką Lilieforsa. Test K-S wymaga, aby cecha była ciągła. Jest to test mocniejszy, aniżeli test

Χ

2

.

Przykład 1: Sprawdź czy zmienne: imisja SO

2

i pyłu posiadają rozkład zgodny z normalnym.

1.

W menu wybieramy polecenie STATYSTYKA  STATYSTYKI PODSTAWOWE
I TABELE.

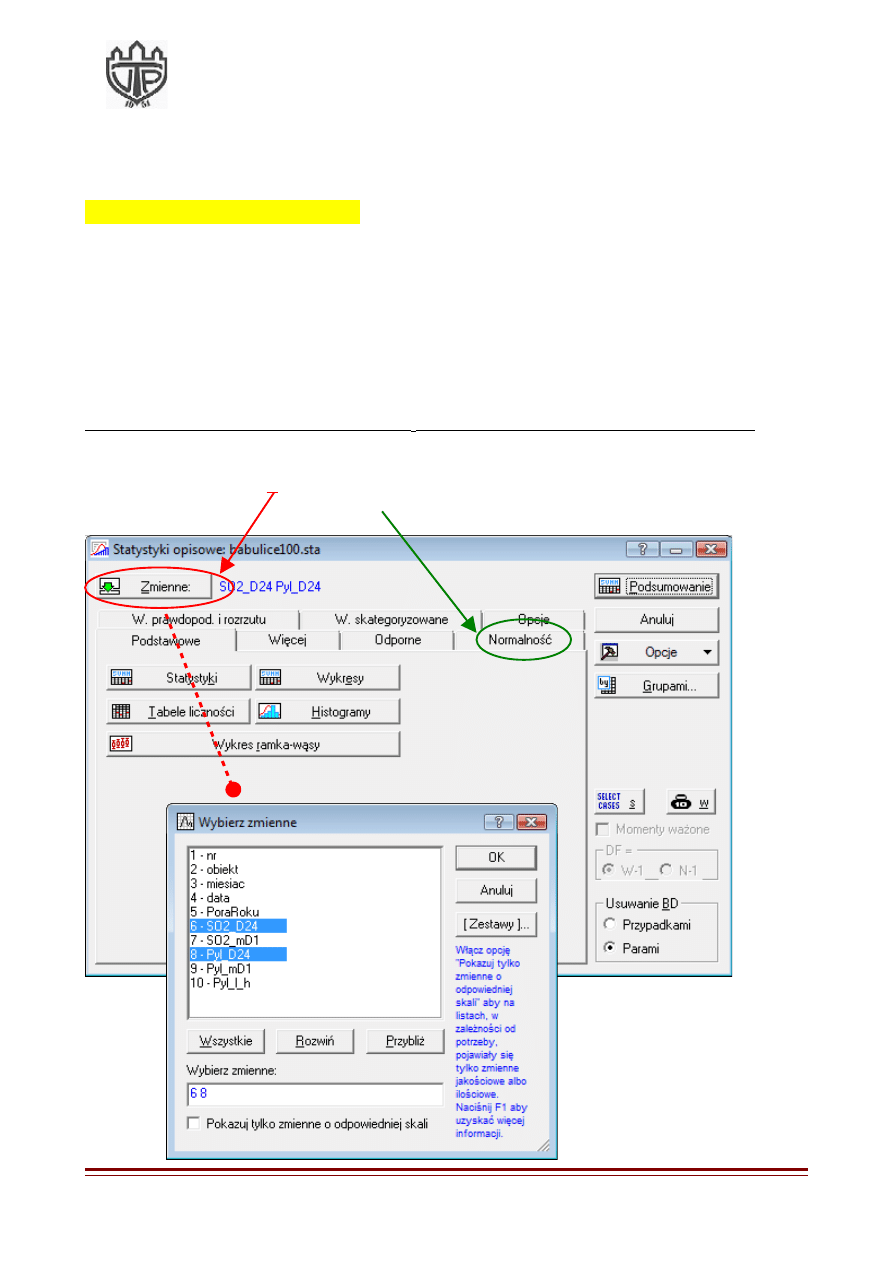
2.

Klikamy na przycisk

Zmienne

i wskazujemy na SO2_D24 i Pyl_D24.

3.

Następnie klikamy na przycisk

Normalność

.

Statystyka i modelowanie w ochronie środowiska

Strona 1

2009-04-15 21:29:00

Katedra Genetyki i Podstaw Hodowli Zwierząt

Wydział Hodowli i Biologii Zwierząt, UTP w Bydgoszczy

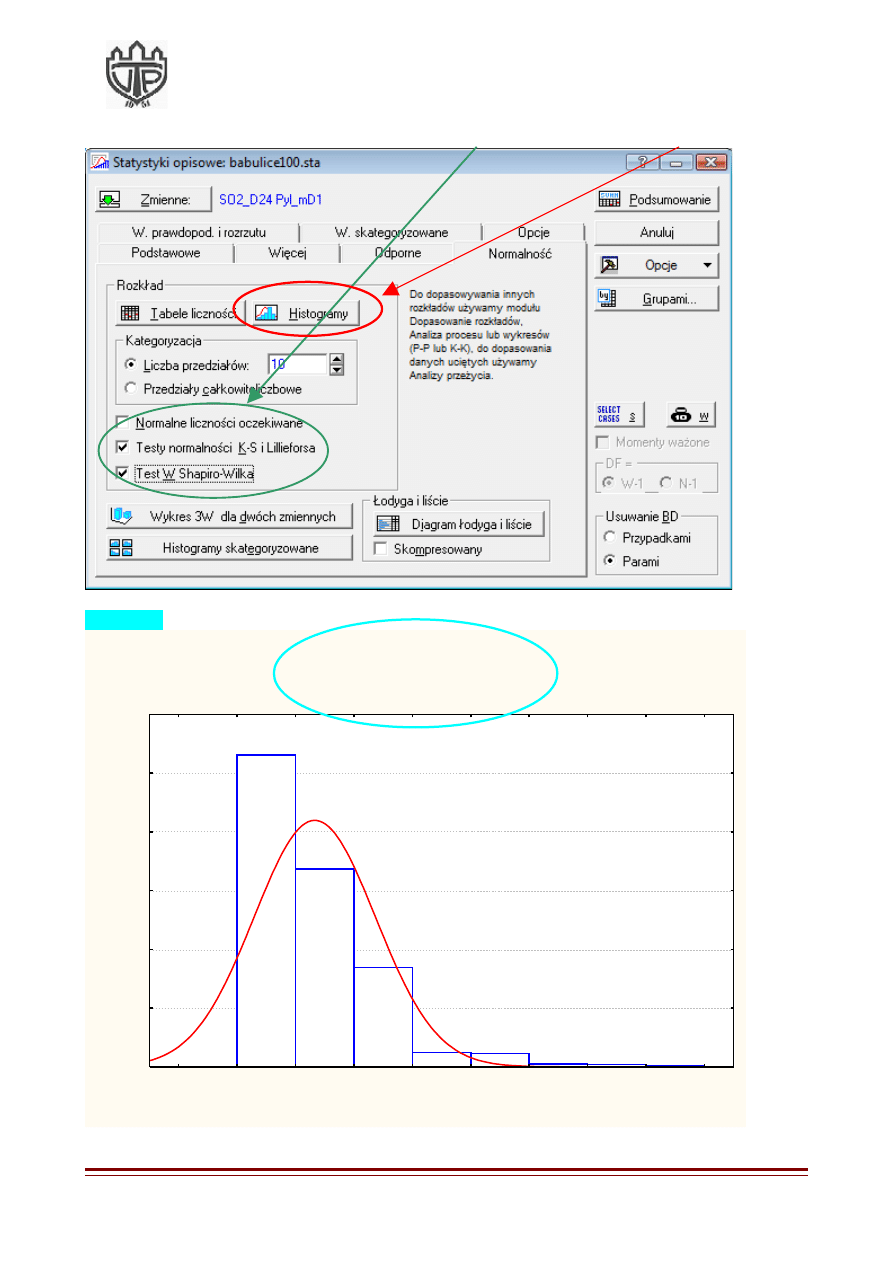
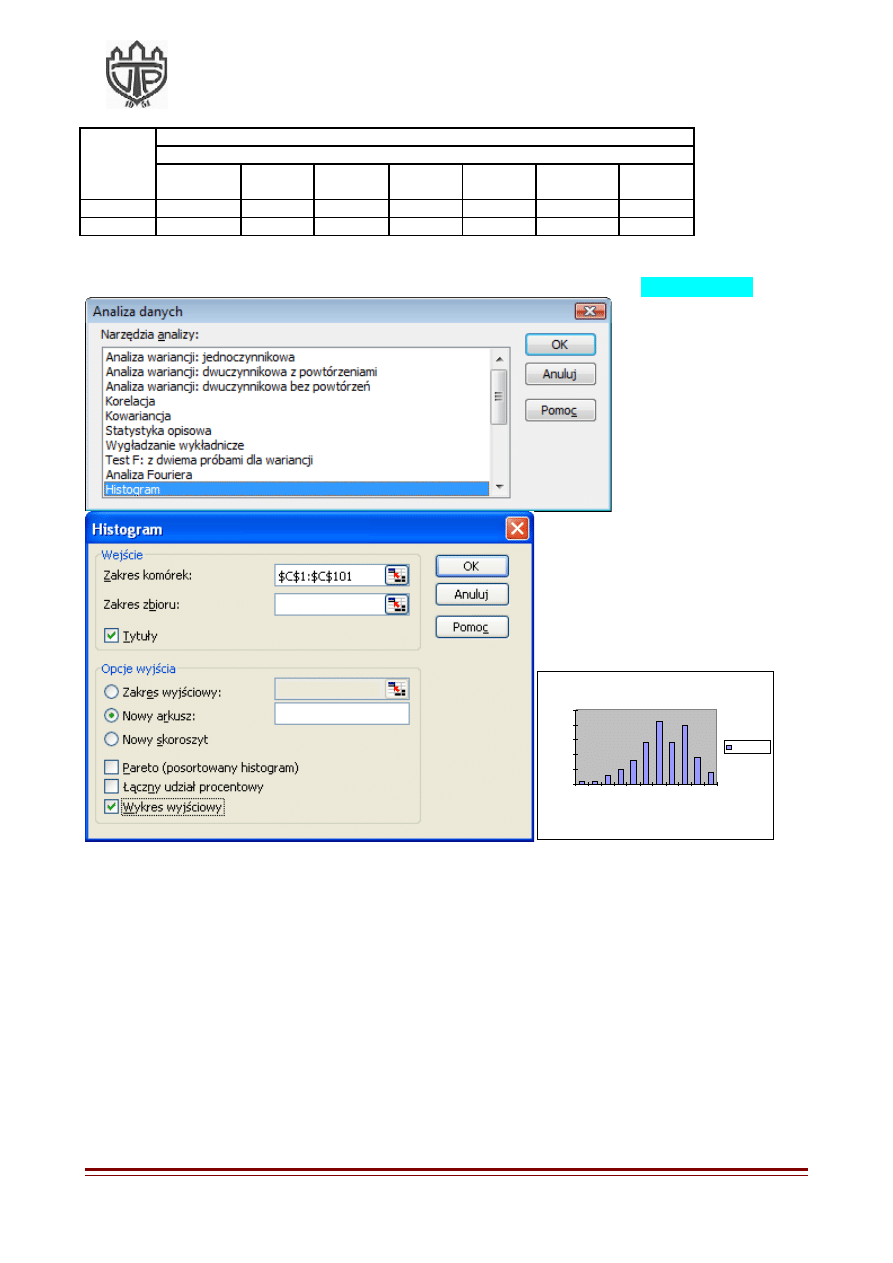
4. W kolejnym kroku zaznaczamy wskazane pola wyboru, a następnie klikamy

na Histogramy:

WYNIKI:

Histogram: SO2_D24

K-S d=.13113, p<.01 ; Lillief ors p<.01

Shapiro-Wilk W=.84723, p=0.0000

-5

0

5

10

15

20

25

30

35

40

X <= Granica klasy

0

100

200

300

400

500

600

Li

cz

ba

o

bs

.

Statystyka i modelowanie w ochronie środowiska

Strona 2

2009-04-15 21:29:00

Katedra Genetyki i Podstaw Hodowli Zwierząt

Wydział Hodowli i Biologii Zwierząt, UTP w Bydgoszczy

Zmienna

Statystyki opisowe (babulice100.sta)

N ważnych

Średnia

Mediana

Moda

Liczność

Mody

Minimum

Maksimum

Odch.std

SO2_D24

1095

6.64559

5.26560 8.800000

11

0.60000

36.7000

5.20404

Pyl_mD1

1095 54.06121 51.48000 Wielokr.

10

12.60000

146.2384 25.77776

Zmienna

Statystyki opisowe
(babulice100.sta)

Skośność

Kurtoza

SO2_D24

1.788387 4.905109

Pyl_mD1

0.842483 0.510501

W celu

stwierdzenia czy badana cecha posiada rozkład zgodny z normalnym patrzymy na wartość „p”. Jeśli
ta wartość jest równa lub mniejsza aniżeli 0,05, to mamy podstawę do odrzucenia hipotezy zerowej
i stwierdzenia, iż badana cecha nie posiada rozkładu zgodnego z normalnego.

W powyższym przykładzie wszystkie testy normalności rozkładu dowodzą, iż istnieją podstawy do
odrzucenia hipotezy zerowej. Oznacza to, że rozkład SO

2

i Pyłu jest niezgodny zgodny z rozkładem

normalnym. Obydwie cechy posiadają rozkłady asymetryczne – dodatnie (prawostronne).

Statystyka i modelowanie w ochronie środowiska

Strona 3

2009-04-15 21:29:00

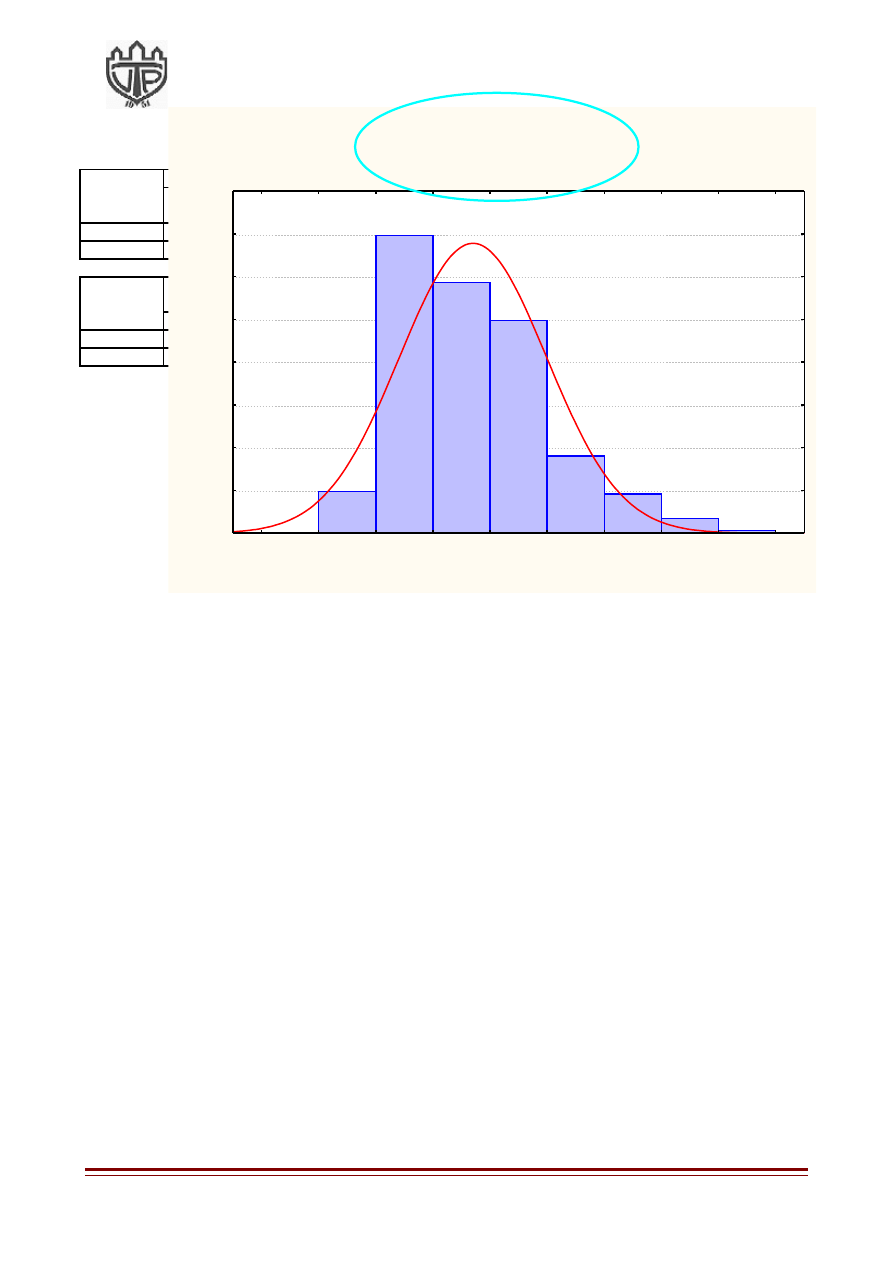
Histogram: Pyl_mD1

K-S d=.07521, p<.01 ; Lilliefors p<.01

Shapiro-Wilk W=.94728, p=0.0000

-20

0

20

40

60

80

100

120

140

160

X <= Granica klasy

0

50

100

150

200

250

300

350

400

Li

cz

ba

o

bs

.

Katedra Genetyki i Podstaw Hodowli Zwierząt

Wydział Hodowli i Biologii Zwierząt, UTP w Bydgoszczy

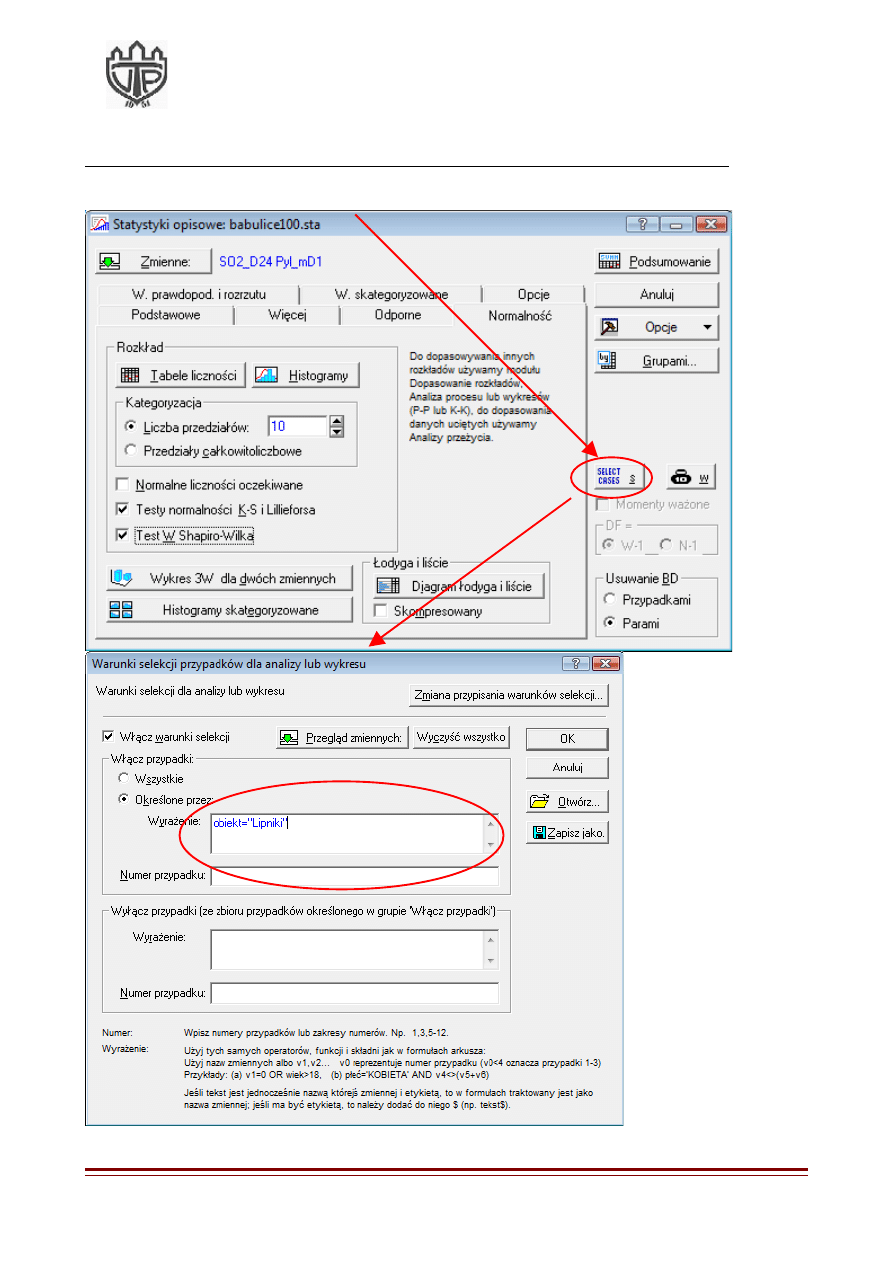
Przykład 2: Oblicz podstawowe miary położenia i zmienności w odniesieniu do LIPNIK!

1. Kliknij na przycisk SELECT CASES, a następnie wprowadź warunek selekcji!

Statystyka i modelowanie w ochronie środowiska

Strona 4

2009-04-15 21:29:00

Katedra Genetyki i Podstaw Hodowli Zwierząt

Wydział Hodowli i Biologii Zwierząt, UTP w Bydgoszczy

Zmienna

Statystyki opisowe (babulice100.sta)Warunek uwzględniania: obiekt="Lipniki"

N ważnych Średnia

Ufność

-95.000%

Ufność

95.000

Minimum Maksimum Odch.std

SO2_D24

365

5.17849

4.83351

5.52348

0.60000

13.9700

3.35162

Pyl_mD1

365 52.70718 50.17044 55.24391 12.60000

130.5700 24.64488

Zadanie 1 (MS EXCEL). Wykonaj wykresy typu HISTOGRAM, na którym zaprezentujesz
rozkład masy i długości ciała noworodków. W tym celu posłuż się modułem Analiza danych.

Histogram

0

5

10

15

20

25

20

00

25

00

30

00

35

00

40

00

W

ięc

ej

Zbiór danych (koszyk)

C

zę

st

o

ść

Częstość

Zadanie 2 (Statistica PL). Sprawdź czy długość, szerokość i masa jaj srok posiadają rozkład
zgodny z normalnym (jajaSROK.xls).
Zadanie 3 (Statistica PL). Jaki rozkład posiadają liczebności drobnoustrojów (bakterie100.xls)?
Czy rozkład uległ zmianie po wykonaniu transformacji logarytmicznych?
Zadanie 4 (Statistica PL). Czy grubość rogówki posiada rozkład zgodny z normalnym?

Statystyka i modelowanie w ochronie środowiska

Strona 5

2009-04-15 21:29:00

Katedra Genetyki i Podstaw Hodowli Zwierząt

Wydział Hodowli i Biologii Zwierząt, UTP w Bydgoszczy

Wyznaczanie przedziałów ufności

Estymacja to postępowanie statystyczne zmierzające do oszacowania parametrów populacji
generalnej (

µ

,

σ

) na podstawie statystyk uzyskanych z populacji próbnej.

Estymator – statystyka z próby służąca do oszacowania parametru (

θ

). Może nim być średnia

arytmetyczna, odchylenie standardowe, mediana, współczynniki zmienności. Estymator, podobnie jak sama
zmienna losowa, posiada własny rozkład. Nie zawsze jednak wymienione wcześniej statystyki będą
uznawane za najlepsze estymatory. Powinny spełniać one określone własności.
Estymacja przedziałowa - polega na wyznaczeniu przedziału liczbowego, który z określonym
prawdopodobieństwem zawiera szacowany parametr. Końce przedziału zależą od wartości estymatora.
Przedział ufności - losowy przedział, który z określonym prawdopodobieństwem określa wartość parametru.
To inaczej przedział liczbowy, w którym znajduje się prawdziwa, lecz nieznana wartość parametru

θ

.

Przedział (g1,g2) jest przedziałem ufności parametru

θ

, określonym na poziomie ufności 1-

α

, jeżeli

prawdopodobieństwo, że

θ

leży w tym przedziale jest równe 1-

α

.

Poziom ufności 1-

α

jest prawdopodobieństwem, że

θ

leży w przedziale (g1,g2). Przedział (g1,g2), którym g1

i g2 przyjmują skończone wartości nazywa się dwustronnym przedziałem ufności.
Jeżeli

α

=0,05, to 1-

α

=0,95 oznacza to, że średnio na każde 100 przedziałów ustalonych na 100 prób

losowych, w 95 przypadkach prawdziwa wartość parametru

θ

znajduje się wewnątrz przedziału, natomiast

w 5 przypadkach znajduje się poza przedziałem.

Im niższy przyjmiemy poziom ufności, tym mniejsze będzie prawdopodobieństwo błędnego określenia
przedziału, jednak jednocześnie wydłużony będzie przedział ufności.

Statystyka i modelowanie w ochronie środowiska

Strona 6

2009-04-15 21:29:00

Katedra Genetyki i Podstaw Hodowli Zwierząt

Wydział Hodowli i Biologii Zwierząt, UTP w Bydgoszczy

Przykład: Wyznacz 95% przedział ufności w odniesieniu do imisji SO

2

i pyłu.

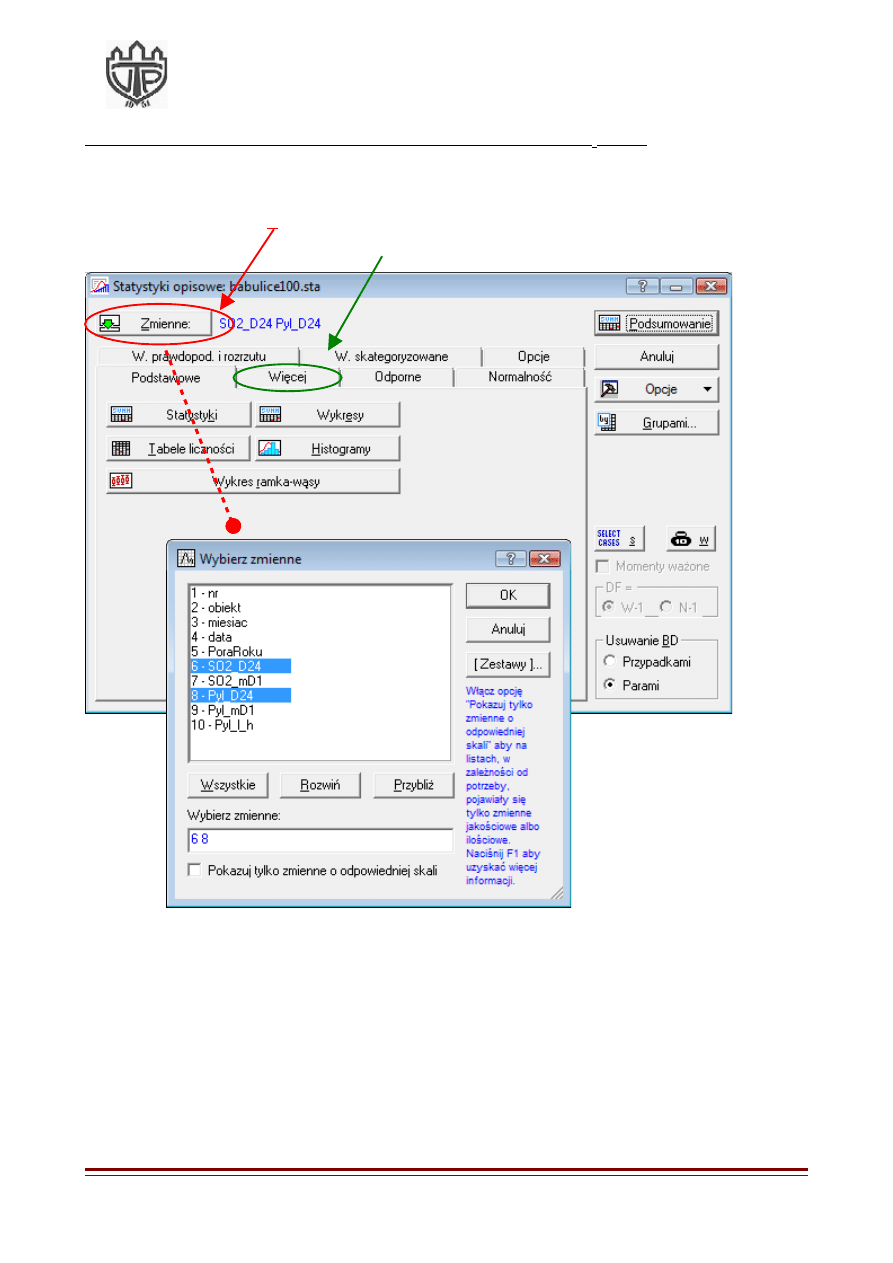
1.

W menu wybieramy polecenie STATYSTYKA  STATYSTYKI PODSTAWOWE
I TABELE.

2.

Klikamy na przycisk

Zmienne

i wskazujemy na SO2_D24 i Pyl_D24.

3.

Następnie klikamy na przycisk

Więcej

.

Statystyka i modelowanie w ochronie środowiska

Strona 7

2009-04-15 21:29:00

Katedra Genetyki i Podstaw Hodowli Zwierząt

Wydział Hodowli i Biologii Zwierząt, UTP w Bydgoszczy

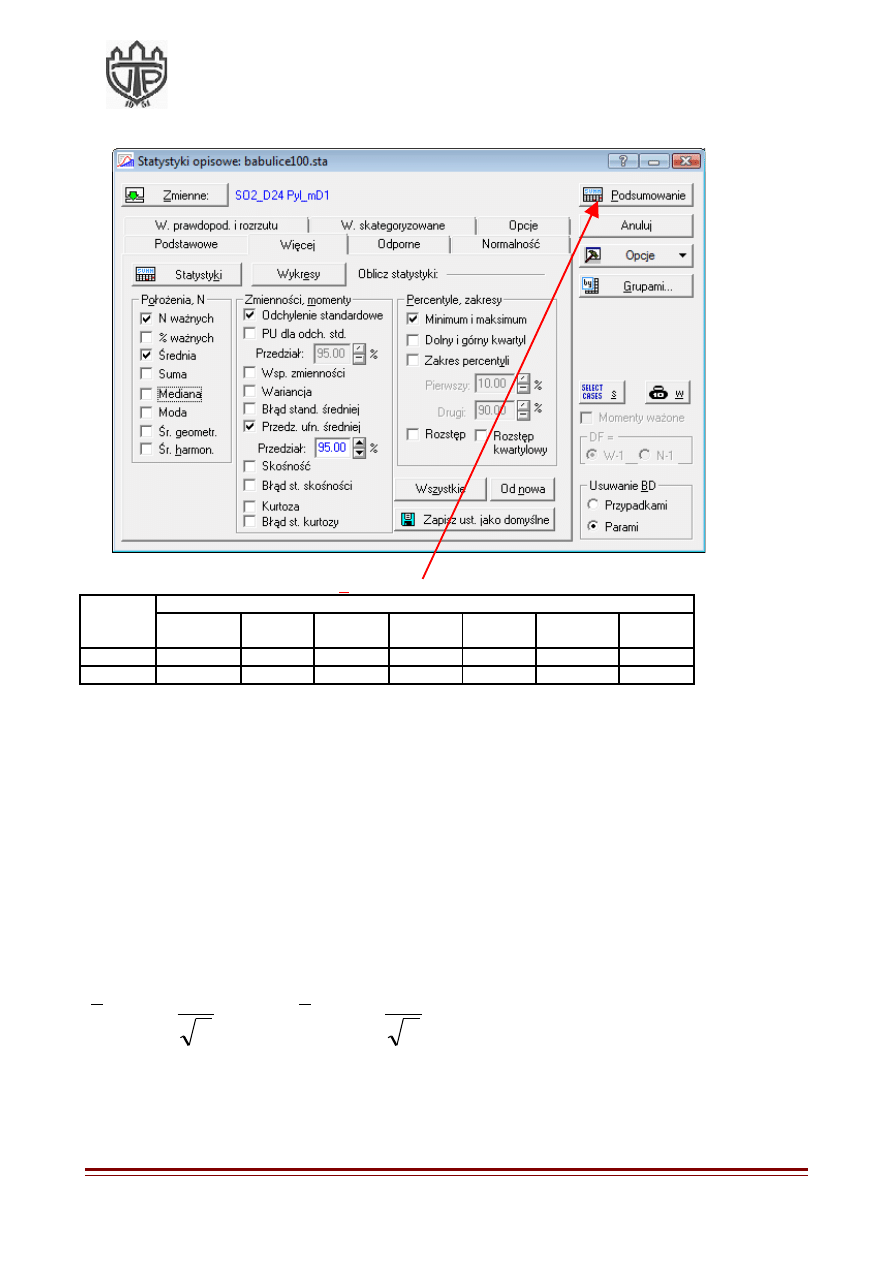
4. W kolejnym kroku zaznaczamy wskazane pola wyboru:

5.

Następnie klikamy na przycisk

Podsumowanie

.

Zmienna

Statystyki opisowe (babulice100.sta)
N ważnych Średnia

Ufność

-95.000%

Ufność

95.000

Minimum Maksimum Odch.std

SO2_D24

1095

6.64559

6.33701

6.95416

0.60000

36.7000

5.20404

Pyl_mD1

1095 54.06121

52.53270 55.58971

12.60000

146.2384 25.77776

Odp.: Wyznaczony przedział ufności pozwala wnioskować z prawdopodobieństwem 95%, że
średnia imisja dwutlenku siarki w otoczeniu zakładów przemysłowych o profilu zbliżonym do
badanego powinna zawierać się w przedziale 6,33-6,96

µ

g / m

3

.

Należy oczekiwać, że średni poziom pyłu winien zawierać się w przedziale 52,53-55,59

µ

g / m

3

.

Zadanie 1 (MS EXCEL).

1.

Otwórz plik roztocze.xls (wcześnie przekopiuj plik do własnego folderu) zawierający dane
dotyczące liczebności roztoczy w pobliżu zakładów produkcyjnych.

2.

Skopiuj do kolejnego wolnego arkusza wiersz zawierający nazwy cech.

3.

Zmień nazwę tegoż arkusza roboczego na „ufnosc”.

4.

Sporządź tabelę zawierającą wybrane miary położenia i zmienności w odniesieniu do liczby
roztoczy w próbach z okolic Białowieży (średnia arytmetyczna, odchylenie standardowe).

5.

Oblicz lewą i prawą stronę ufności (95%) dla wszystkich rodzajów mechowców i roztoczy.

)

*

(

)

(

n

S

t

x

n

S

t

x

x

x

α

α

+

<

Θ

<

∗

−

6.

Sporządź szereg rozdzielczy prezentujący liczebność „roztocze” na m

2

. W oparciu

o sporządzony szereg rozdzielczy wykonaj wykres typu histogram. Jaki jest to typ rozkładu
(roztocze.xls)?

Statystyka i modelowanie w ochronie środowiska

Strona 8

2009-04-15 21:29:00

Katedra Genetyki i Podstaw Hodowli Zwierząt

Wydział Hodowli i Biologii Zwierząt, UTP w Bydgoszczy

Zadanie 2 (STATISTICA PL).

1.

Otwórz plik jajaSROK.xls, który znajduje się w S:\OS_STAT\BAZY_XLS.

Skonstruuj przedziały ufności (95 i 99%) dla długości, szerokości i masy jaj srok.

Statystyka i modelowanie w ochronie środowiska

Strona 9

2009-04-15 21:29:00