WEAIiE
Imię i Nazwisko:
1. Michał Idzik
2. Bartosz Niemczura
Imię i Nazwisko:
1. Michał Idzik
2. Bartosz Niemczura
ROK I
GRUPA 1
ZESPÓŁ 9
Pracownia
fizyczna I i II
TEMAT:
Współczynnik załamania światła
TEMAT:
Współczynnik załamania światła
TEMAT:
Współczynnik załamania światła
TEMAT:
Współczynnik załamania światła
Nr ćwiczenia
51
Data wykonania:
21.05.10
Data oddania:
28.05.10
Zwrot do
poprawy:
Data oddania:
Data
zaliczenia:
OCENA
I. Cel ćwiczenia
Wyznaczenie współczynnika załamania światła dla szkła i pleksiglasu metodą pomiaru
grubości pozornej za pomocą mikroskopu
II. Wstęp teoretyczny
Wiązka światła przechodząca przez dwa ośrodki o różnych współczynnikach załamania częściowo
odbija się, a częściowo przechodzi do drugiego ośrodka ulegając załamaniu. Współczynnik załamania
ośrodka drugiego względem pierwszego definiowany jest następująco: n
=
sin
α
sin
β
, gdzie
α,β - kąty
jakie tworzą promienie z prostą prostopadłą do powierzchni. Jest to również postać prawa załamania,
z którego wynika, że współczynnik n nie zależy od długości fali światła padającego. Wynika stąd, że
zjawisko załamania światła można wykorzystać do rozłożenia wiązki światła na składowe o różnych
długościach fali. Jeżeli umieścimy przedmiot w środowisku optycznie większym, to ten sam przedmiot
obserwowany np. z powietrza wydje się mniejszy. Doskonałym przykładem jest łyżeczka w herbacie,
która wydaje się być bliższa powierzchni niż jest w rzeczywistości. Zaznaczając flamastrem znak na
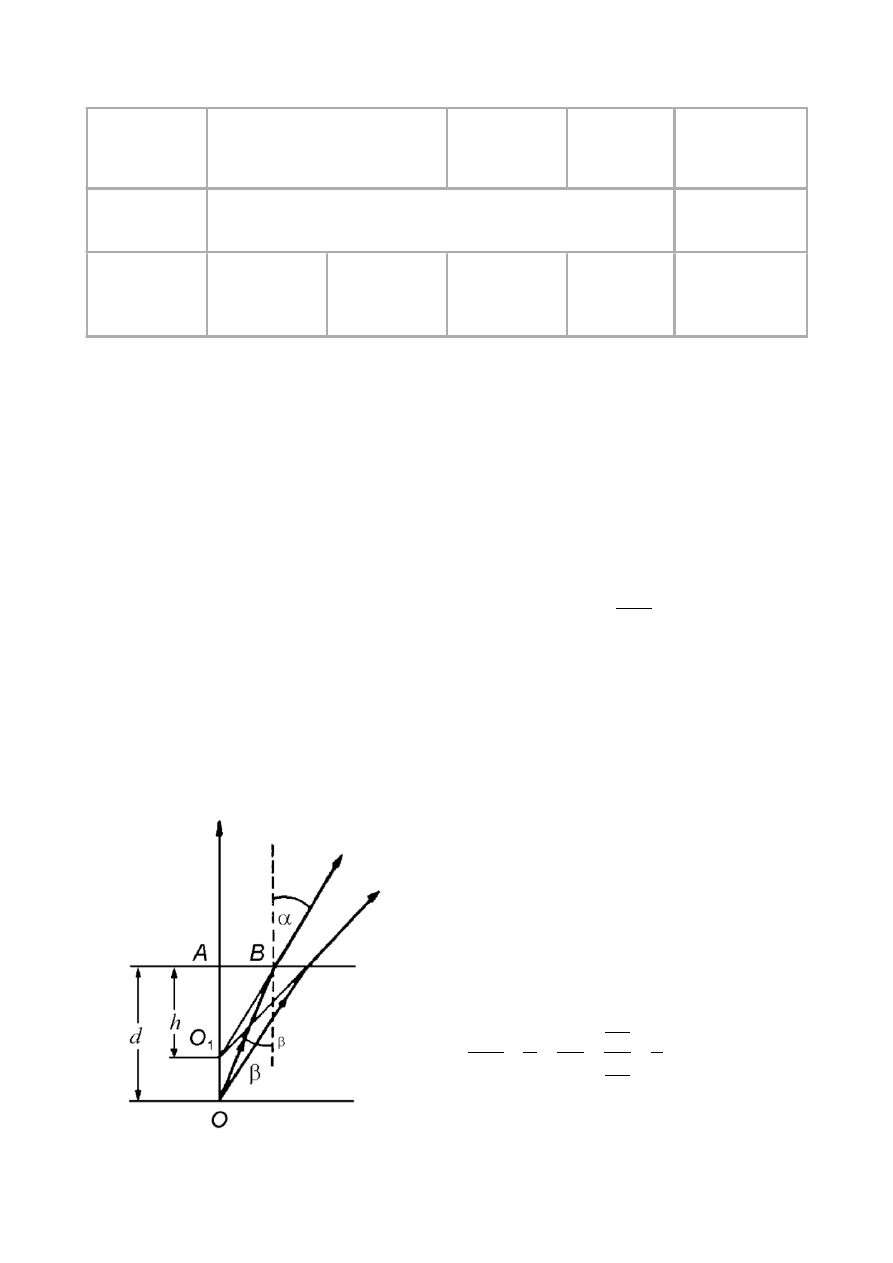
jednej stronie płytki płasko równoległej można prześledzić jak będzie powstawał jego pozorny obraz:
Z punktu O wychodzą promienie OA i OB. Pierwszy
z nich jest prostopadły i nie ulega załamaniu, natomiast
drugi pada na powierzchnię szkła pod kątem
β i
załamuje się tworząc w powietrzu kąt załamania
α .
Ponadto kąt alfa jest większy od beta właśnie w skutek
załamania. Przedłużenia załamań wszystkich promieni
(nie prostopadłych do płytki) będą się przecinać w
punkcie O1 tworzac tym samym obraz pozorny.
Stosując prawo załamania dla małych kątów
otrzymujemy wzór:
n
=
sin
α
sin
β
≈
α
β
≈
tg
α
tg
β
=
AB
h
AB
d
=
d
h
z którego doświadczalnie będziemy wyznaczali
współczynnik załamania światła.
I
Michał Idzik, Bartosz Niemczura - Współczynnik załamania światła
III. Wyniki pomiarów
Doświadczenie rozpoczęliśmy od zapoznania się z budową mikroskopu. Wyregulowaliśmy połozenie
lampy mikroskopowej tak, aby światło padało na obiektyw. W doświadczeniu wykorzystaliśmy płytkę
szklaną oraz plexiglasową, które zostały wcześniej oznaczone flamastrem po obu stronach kreskami
pionowymi i poziomymi. Każdą z nich zmierzyliśmy dziesięciokrotnie śrubą mikrometryczną o
dokładności 0,01mm w trzech miejscach.
Dla obu płytek wykonaliśmy następujące czynności:
ustawiliśmy płytkę na stoliku mikroskopu w uchwycie, wyregulowaliśmy wysokość stolika tak, aby
uzyskać ostre obrazy kresek: pionowej
a
d
i pionowej
a
g
(każdej z osobna) oraz dziesięciokrotnie
odczytaliśmy wskazania czujnika mikrometrycznego.
Kolejnym etapem doświadczenia było zbadanie współczynnika załamania w zależności od długości fali
dla płytki plexiglasowej. Na lampę nakładaliśmy kolejno filtry: zielony (
λ = 0,5µm ), czerwony
(
λ = 0,63µm ), żółty (λ = 0,59µm ). W każdym z przypadków wykonywaliśmy pomiar trzykrotnie w
sposób analogiczny jak poprzednio.
IV.Opracowanie wyników pomiarów
Opracowanie wyników pomiaru rozpoczęliśmy od obliczenia wyliczenia grubości pozornych
h
= a
d
− a
g
oraz współczynnika załamania n
=
d
h
dla wszystkich przeprowadzonych pomiarów
(przykładowe obliczenie 4.1). Następnie obliczyliśmy wartość średnią współczynnika załamania dla obu
płytek (4.2): n
szklo
=
n
i
i
=1
10
∑
10
= 1,514 , n
plexi
=
n
i
i
=1
10
∑
10
= 1,502 . W przypadku badania zależności n(
λ)
przyjęliśmy, że grubość rzeczywista jest stała i równa średniej arytmetycznej grubości rzeczywistych
zmierzonych na początku doświadczenia(4.3): d
plexi
=
d
i
i
=1
10
∑
10
= 3,89mm .
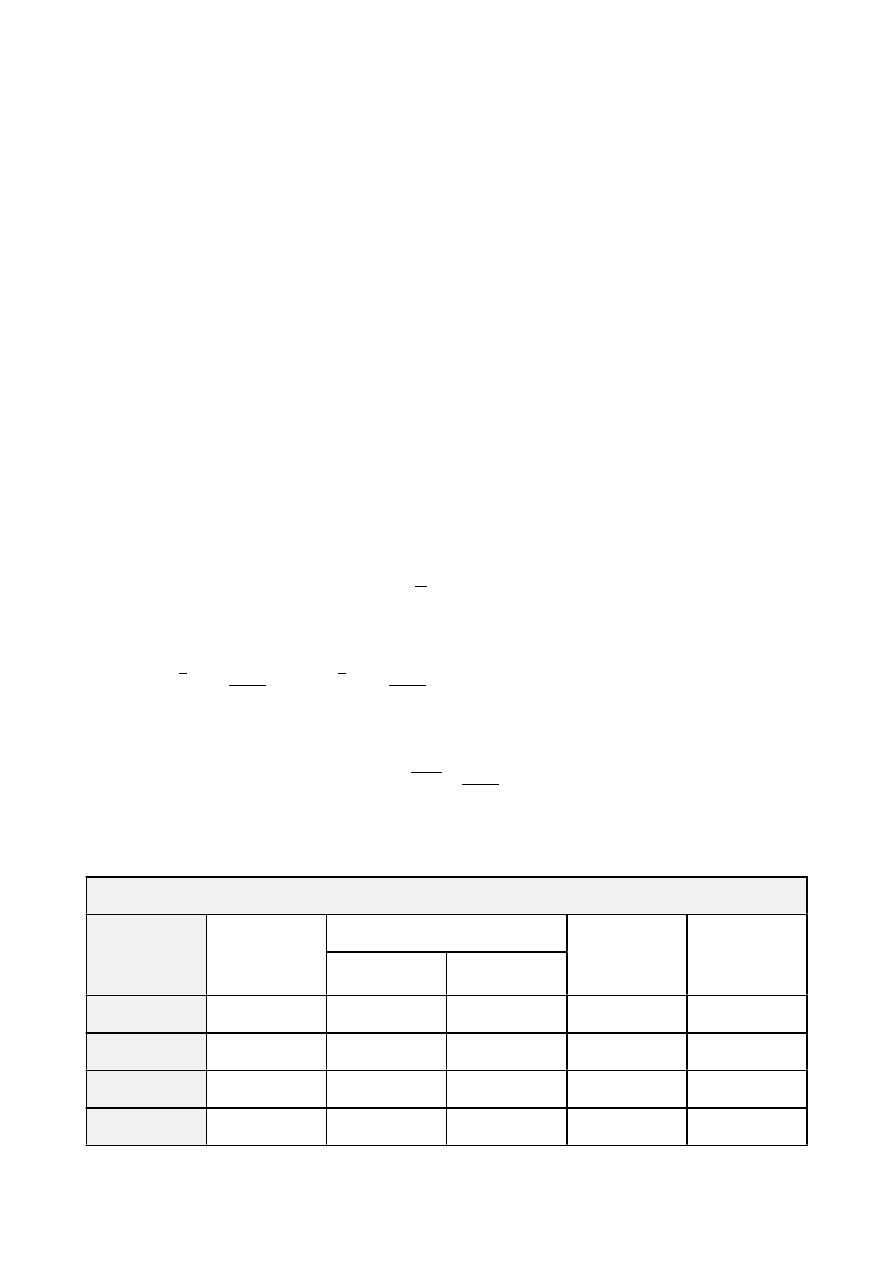
Otrzymane wyniki umieściliśmy w poniższych tabelach:
Materiał: szkło
Materiał: szkło
Materiał: szkło
Materiał: szkło
Materiał: szkło
Materiał: szkło
L.p.
grubość
rzeczywista
d[mm]
wskazanie czujnika
wskazanie czujnika
grubość
pozorna
h[mm]
współczynnik
załamania
n
L.p.
grubość
rzeczywista
d[mm]
a
d
[mm]
a
g
[mm]
grubość
pozorna
h[mm]
współczynnik
załamania
n
1
2,34
9,21
7,66
1,55
1,51
2
2,34
9,2
7,63
1,57
1,49
3
2,32
9,14
7,66
1,48
1,568
4
2,31
9,23
7,64
1,59
1,453
II
Michał Idzik, Bartosz Niemczura - Współczynnik załamania światła
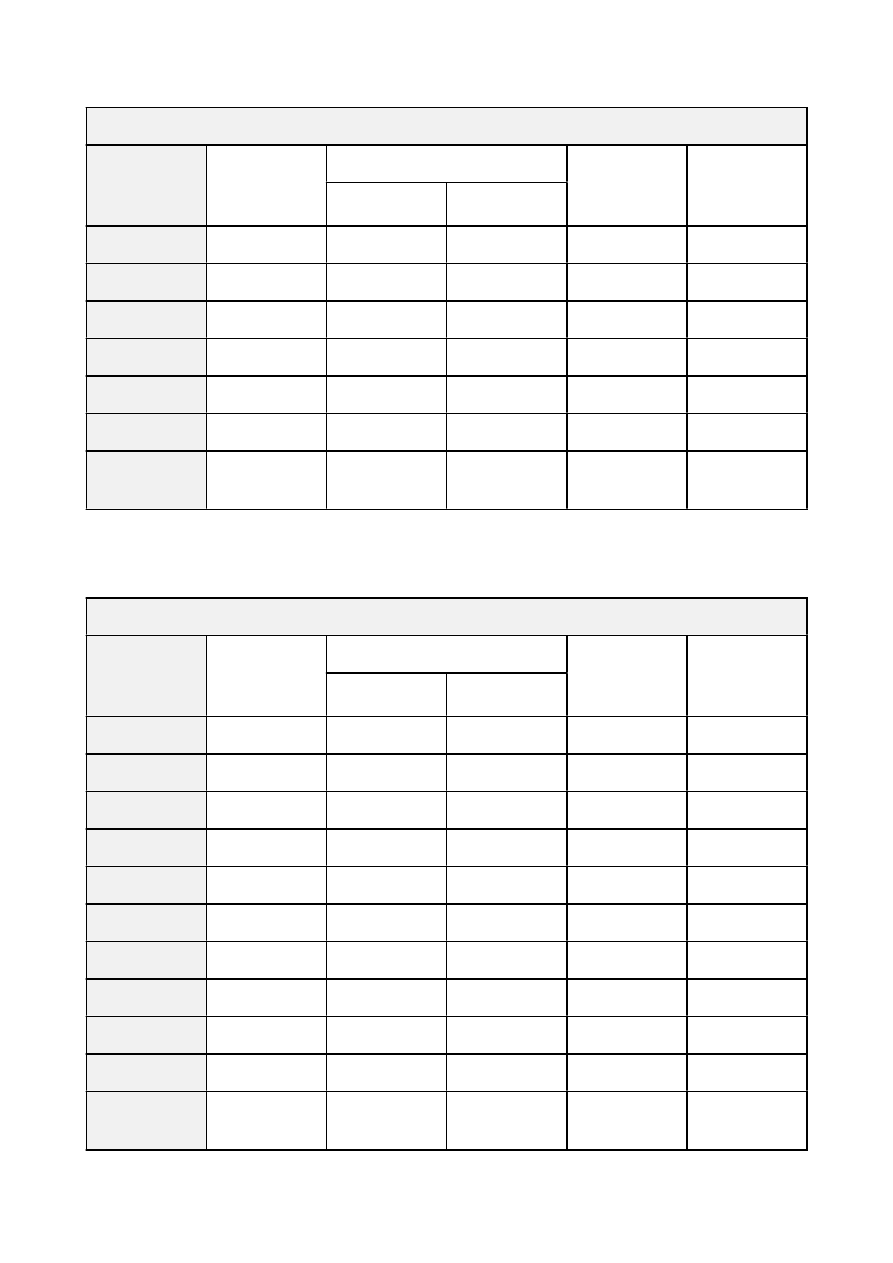
Materiał: szkło
Materiał: szkło
Materiał: szkło
Materiał: szkło
Materiał: szkło
Materiał: szkło
L.p.
grubość
rzeczywista
d[mm]
wskazanie czujnika
wskazanie czujnika
grubość
pozorna
h[mm]
współczynnik
załamania
n
L.p.
grubość
rzeczywista
d[mm]
a
d
[mm]
a
g
[mm]
grubość
pozorna
h[mm]
współczynnik
załamania
n
5
2,3
9,15
7,69
1,46
1,575
6
2,31
9,18
7,66
1,52
1,52
7
2,29
9,19
7,71
1,48
1,547
8
2,29
9,22
7,68
1,54
1,487
9
2,34
9,2
7,65
1,55
1,51
10
2,32
9,22
7,65
1,57
1,478
wartość
średnia n
1,514
Materiał: plexiglas
Materiał: plexiglas
Materiał: plexiglas
Materiał: plexiglas
Materiał: plexiglas
Materiał: plexiglas
L.p.
grubość
rzeczywista
d[mm]
wskazanie czujnika
wskazanie czujnika
grubość
pozorna
h[mm]
współczynnik
załamania
n
L.p.
grubość
rzeczywista
d[mm]
a
d
[mm]
a
g
[mm]
grubość
pozorna
h[mm]
współczynnik
załamania
n
1
3,94
8,69
6,07
2,62
1,5038
2
3,92
8,69
6,13
2,56
1,5313
3
3,88
8,63
6,04
2,59
1,4981
4
3,88
8,63
6,07
2,56
1,5156
5
3,88
8,56
5,97
2,59
1,4981
6
3,88
8,62
6,04
2,58
1,5039
7
3,88
8,56
5,94
2,62
1,4809
8
3,88
8,55
5,99
2,56
1,5156
9
3,88
8,7
6,09
2,61
1,4866
10
3,88
8,65
6,04
2,61
1,4866
wartość
średnia n
1,502
III
Michał Idzik, Bartosz Niemczura - Współczynnik załamania światła
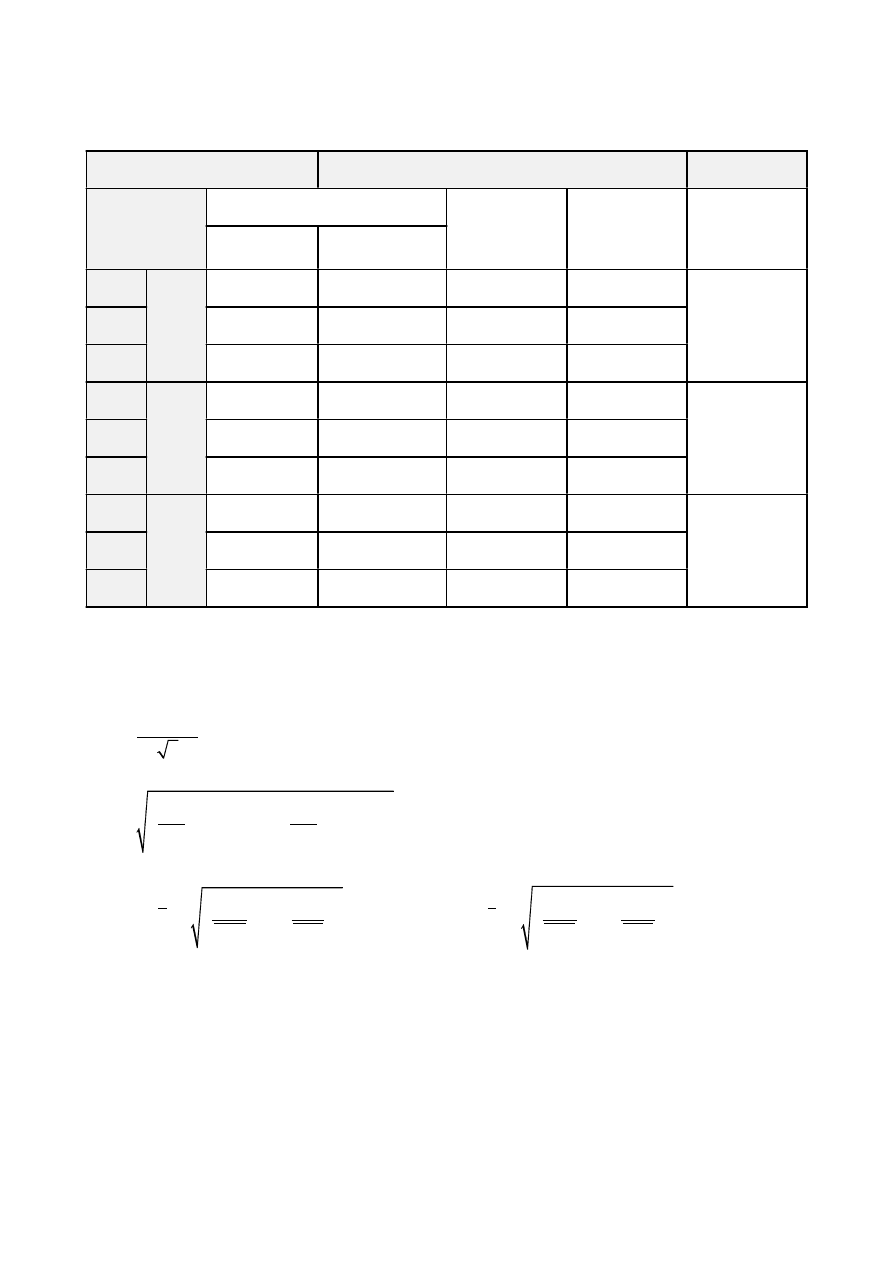
Materiał: plexiglas
Materiał: plexiglas
Materiał: plexiglas
Grubość rzeczywista d = 3,89mm
Grubość rzeczywista d = 3,89mm
Grubość rzeczywista d = 3,89mm
Długość fali
Długość fali
wskazanie czujnika
wskazanie czujnika
grubość
pozorna
h[mm]
współczynnik
załamania
n
wartość średnia
Długość fali
Długość fali
a
d
[mm]
a
g
[mm]
grubość
pozorna
h[mm]
współczynnik
załamania
n
wartość średnia
1
0,5
8,68
6,1
2,58
1,5078
1,5117
2
0,5
8,68
6,1
2,58
1,5078
1,5117
3
0,5
8,64
6,08
2,56
1,5195
1,5117
4
0,63
8,68
6,06
2,62
1,4847
1,4791
5
0,63
8,63
6
2,63
1,4791
1,4791
6
0,63
8,72
6,08
2,64
1,4735
1,4791
7
0,59
8,65
6,05
2,6
1,4962
1,4849
8
0,59
8,7
6,1
2,6
1,4962
1,4849
9
0,59
8,69
6,03
2,66
1,4624
1,4849
Policzyliśmy także niepewność standardową typu B dla pomiaru grubości rzeczywistej (4.4):
u(d)
=
0, 01mm
3
= 0,0058mm . Ponadto u(a
d
)
= u(a
g
)
= 0,0058mm . W konsekwencji niepewność
złożona wartości grubości pozornej wyniosła (4.5):
u(h)
=
∂h
∂a
d
⎛
⎝⎜
⎞
⎠⎟
2
[u(a
d
)]
2
+
∂h
∂a
g
⎛
⎝⎜
⎞
⎠⎟
2
[u(a
g
)]
2
= 0,01mm . Wyniki obliczeń posłużyły nam do
wyznaczenia niepewności współczynnika załamania światła (4.6):
u(n
szklo
)
= n
szklo
u(d)
d
szklo
⎛
⎝⎜
⎞
⎠⎟
2
+
u(h)
h
szklo
⎛
⎝⎜
⎞
⎠⎟
2
= 0,011 , u(n
plexi
)
= n
plexi
u(d)
d
plexi
⎛
⎝
⎜
⎞
⎠
⎟
2
+
u(h)
h
plexi
⎛
⎝
⎜
⎞
⎠
⎟
2
= 0,0062 .
Dla każdej długości fali policzyliśmy średnią wartość współczynnika załamania na podstawie
trzykrotnego pomiaru (4.7).
IV
Michał Idzik, Bartosz Niemczura - Współczynnik załamania światła
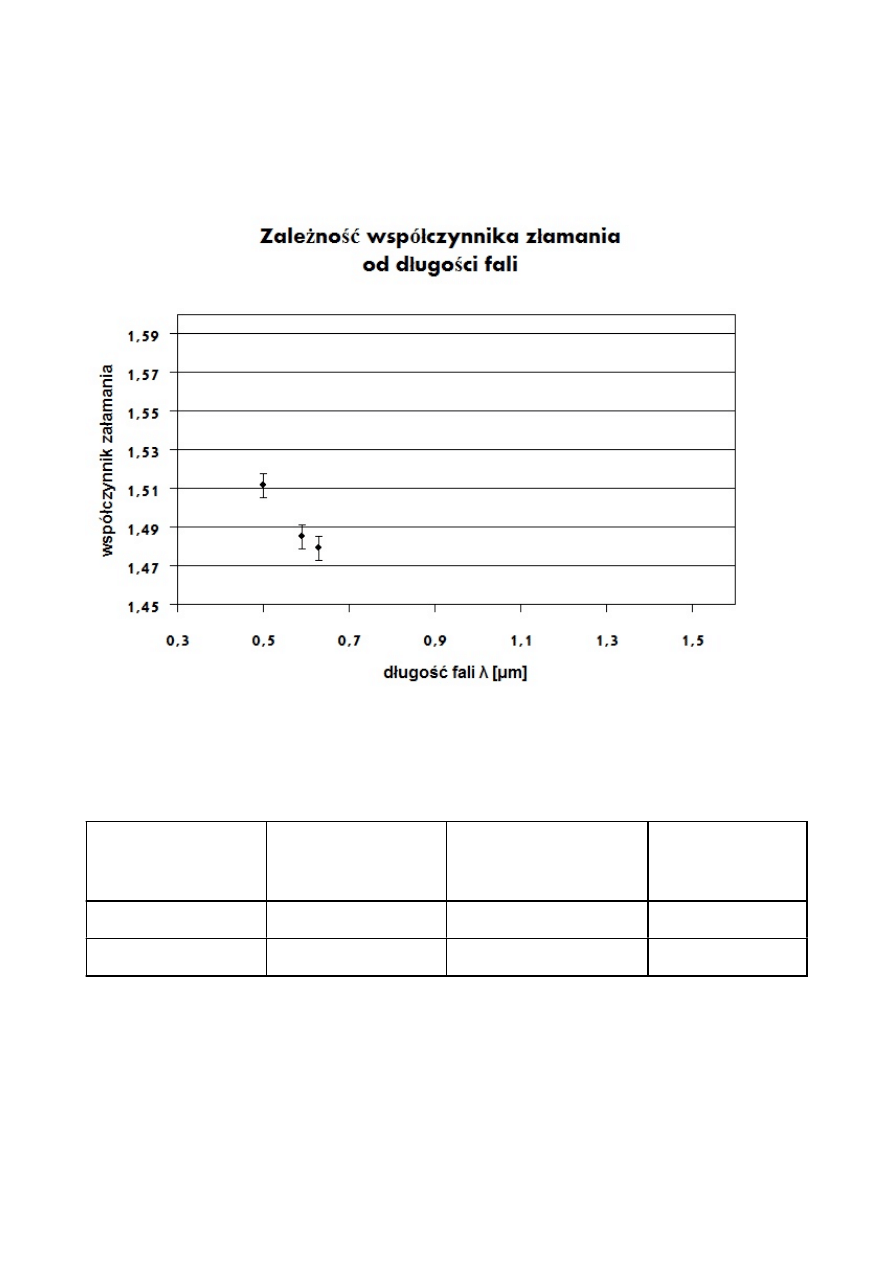
Wykonaliśmy wykres zależności współczynnika załamania od długości fali dla płytki z plexiglasu:
V. Wnioski
• Poniżej zamieszczamy zestawienie wyników doświadczenia z wartościami tablicowymi:
Rodzaj materiału
Współczynnik
załamania światła
n
Niepewność pomiaru
u(n)
Wartość tablicowa
Szkło
1,514
0,011
1,50-1,54
Plexiglas
1,502
0,0062
1,489
Wyznaczony przez nas współczynnik załamania światła dla szkła mieści się w granicach
niepewności względem wartości tablicowej, natomiast współczynnik załamania dla plexiglasu
nieznacznie różni się od swojej wartości tablicowej.
• Na dokładność wyników pomiaru mogła wpłynąć niepewność oceny ostrości obrazu przez oko
ludzkie.
V
Michał Idzik, Bartosz Niemczura - Współczynnik załamania światła
• Ze względu na małą liczbę punktów pomiarowych trudno jednoznacznie określić kształt
wykresu zależności współczynnika załamania światła od długości fali. Jednakże można przyjąć, że w
pewnym przybliżeniu jest hiperbolą.
• Wartość współczynnika załamania światła maleje logarytmicznie wraz ze wzrostem długości fali.
V.Uwagi
Obliczenia zostały wykonane przy pomocy programów komputerowych Numbers oraz Pages.
Zgodnie z zaleceniem prowadzących, przykładowe obliczenia zostały spisane ręcznie i umieszczone w
załączniku (przykładowy odnośnik do danego obliczenia wygląda następująco:
(4.3)
). W załączniku
umieszczamy również wyniki pomiarów przeprowadzonych w trakcie zajęć oraz pisemnie
opracowanie zagadnień związanych ze współczynnikiem załamania światła.
VII. Bibliografia
D. Halliday, R. Resnick, Fizyka, PWN, Warszawa 1996.
Wikipedia -
Encyklopedia powszechna, pisana i redagowana przez internautów.
VI
Michał Idzik, Bartosz Niemczura - Współczynnik załamania światła