Pole magnetyczne prądu elektrycznego

= q

- siła działająca na ładunek q, zarówno nieruchomy

jak i poruszający się.

Jeśli ładunek porusza się, działa dodatkowa siła, propocjonalna do jego
prędkości i ładunku q, dana wyrażeniem :

mag.

= q x

siła Lorentza

Wyrażenie to definiuje pole magnetyczne B:

B

≡

#

Jednostką B jest tesla : 1T =

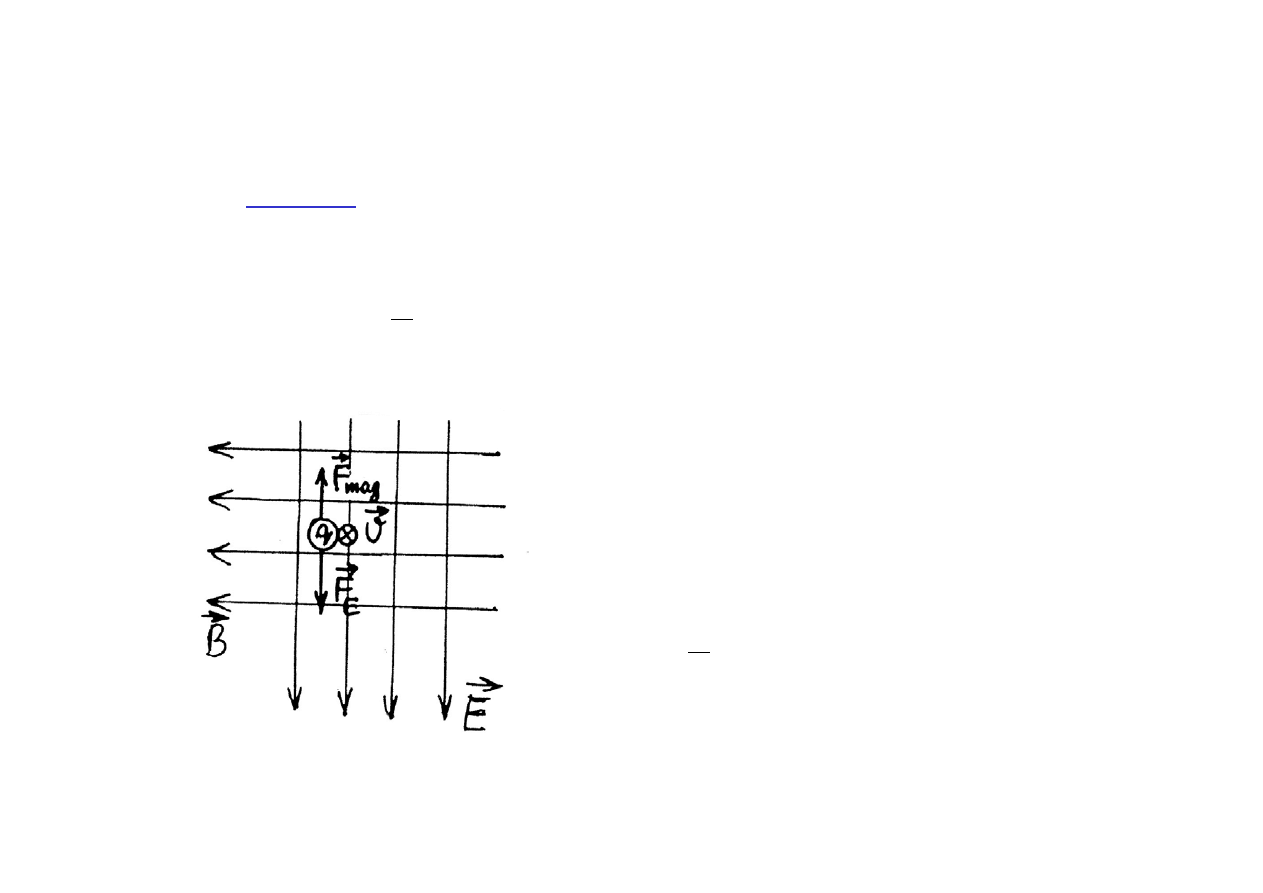
Siła całkowita działająca na poruszający się ładunek :

Siła elektomagnetyczna

=

E

+

mag.

= q + q x

Siła

mag.

może działać również gdy siła elektrostatyczna

E

= 0, np. pomiędzy przewodami z płynącym prądem

→

E

F

→

E

→

V

→

F

→

V

→

B

mag

F

qV

N

Am

→

F

→

F

→

F

→

E

→

V

→

B

→

F

→

F

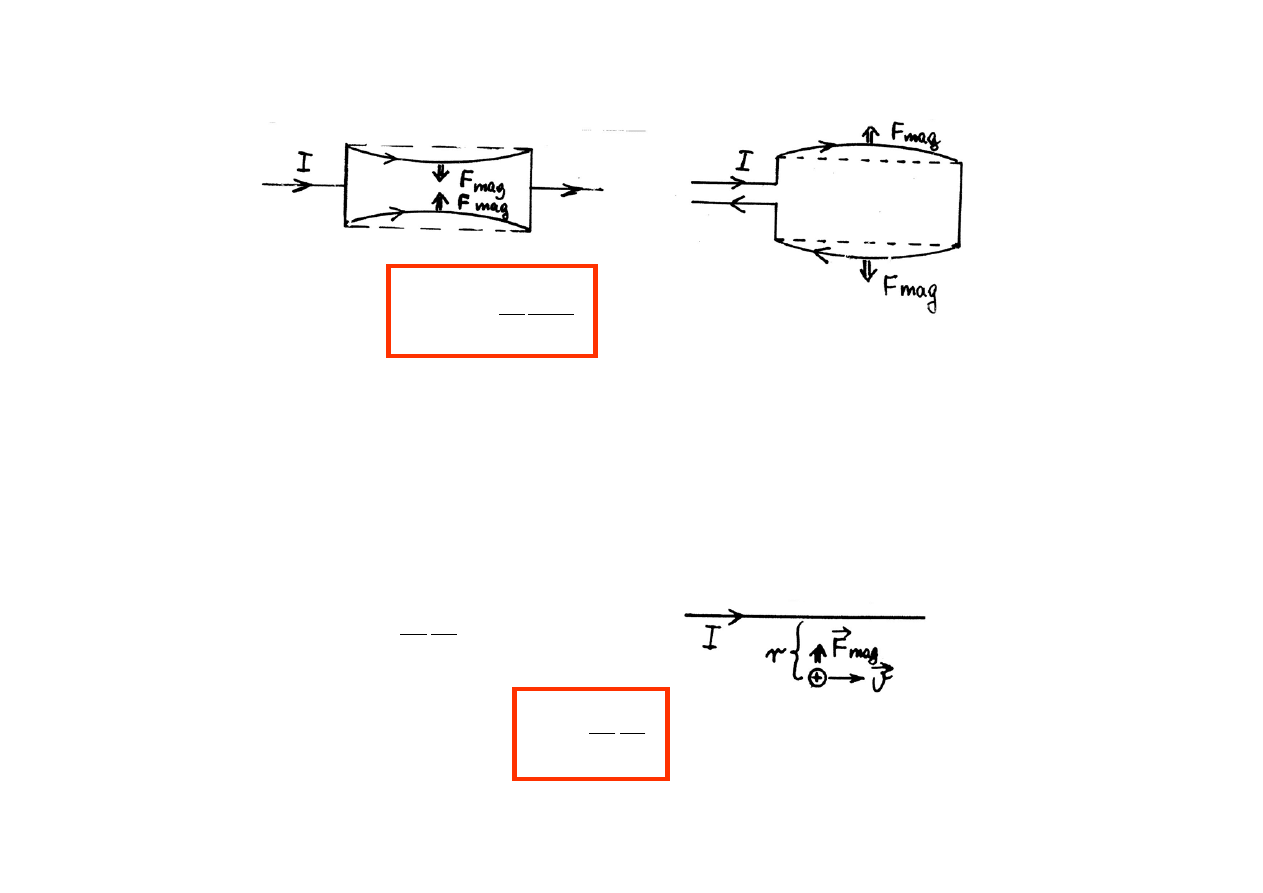
Wykazano, że

mag.

=

r - odległość, w jakiej element przewodu l znajduje się od drugiego
przewodu.

Dla pojedynczego ładunku q poruszającego się w pobliżu przewodnika
z prądem, równolegle do tego przewodnika:

Z równania # : B =

→

F

k

c

2I I

r

2

⋅ l

F

mag.

=

k

c

I

r

qV

2

2

k

c

I

r

2

2

Pole magnetyczne w odległości r od
nieskończenie długiego, prostego
przewodu z prądem.

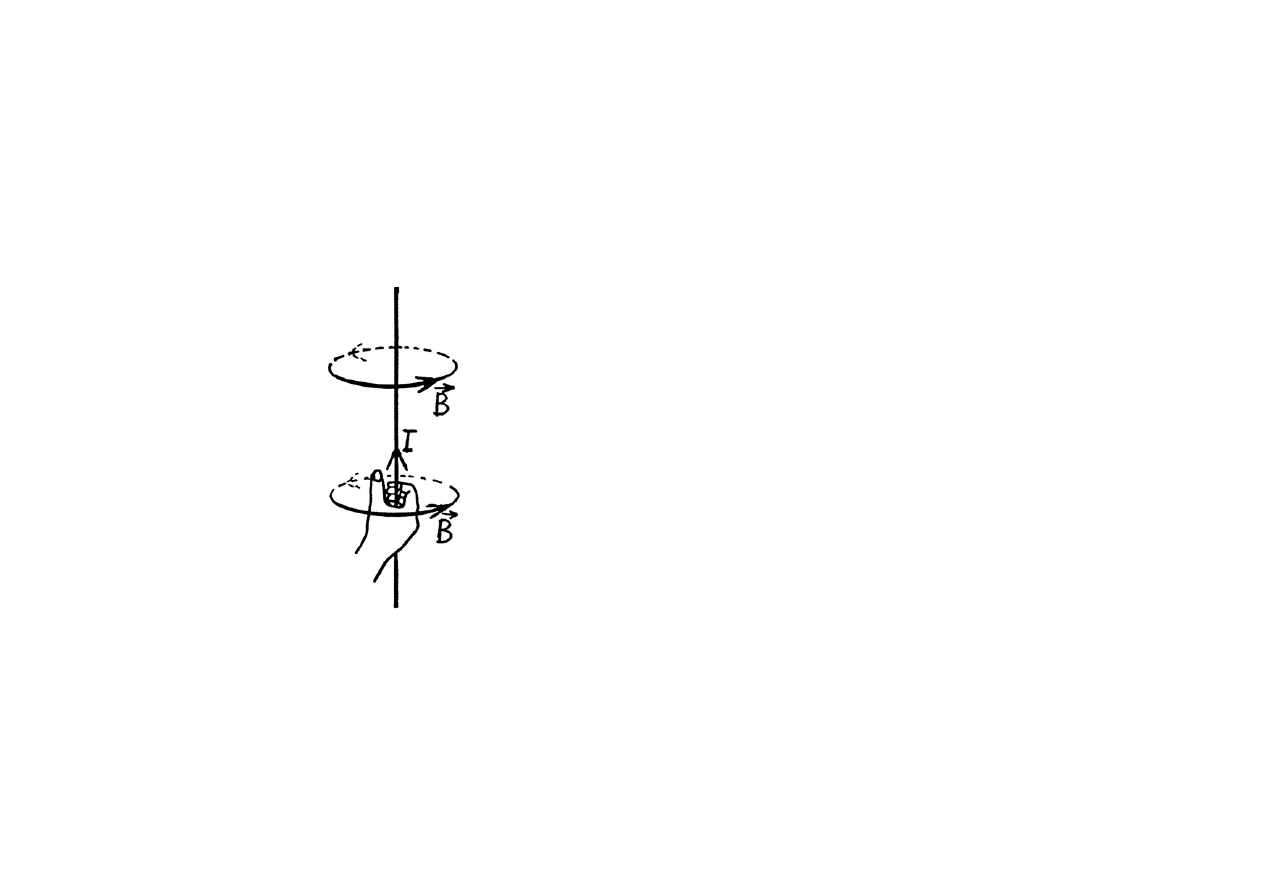
Kierunek i zwrot wektora pola
magnetycznego określa się z
reguły prawej ręki : jeśli
ujmiemy przewód z prądem
tak, że kciuk jest skierowany
zgodnie z I, to pozostałe palce
wskażą zwrot

Z tej reguły, i z równania wektorowego

mag.

= q x

można

wyznaczyć kierunek i zwrot

mag

dla różnych .

→

B

→

F

→

V

→

B

→

F

→

V

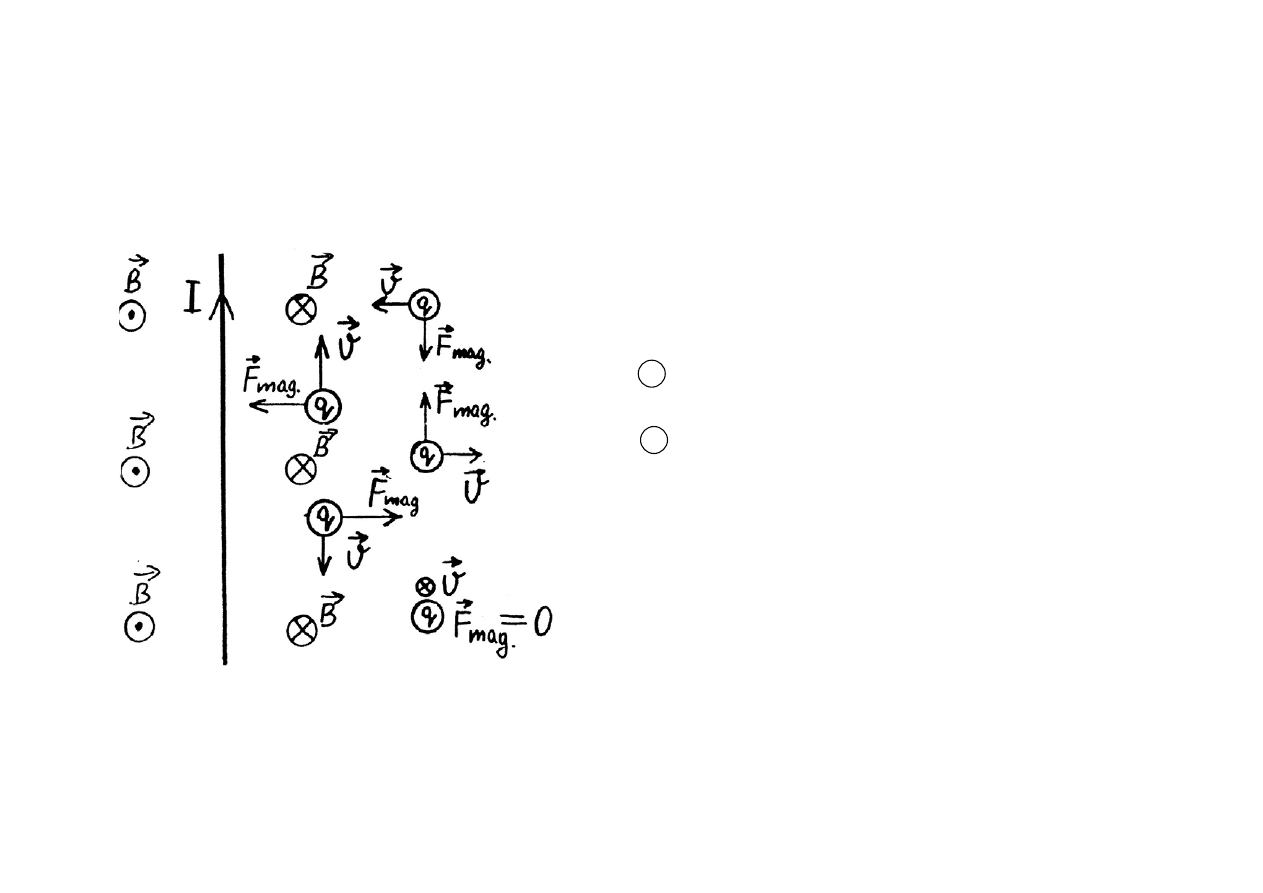
Konwencja oznaczania wektorów
prostopadłych do płaszczyzny rysunku:

X

zwrot do płaszczyzny

•

zwrot od płaszczyzny

(

mag.

zawsze prostopadłe do !)

→

F

→

V

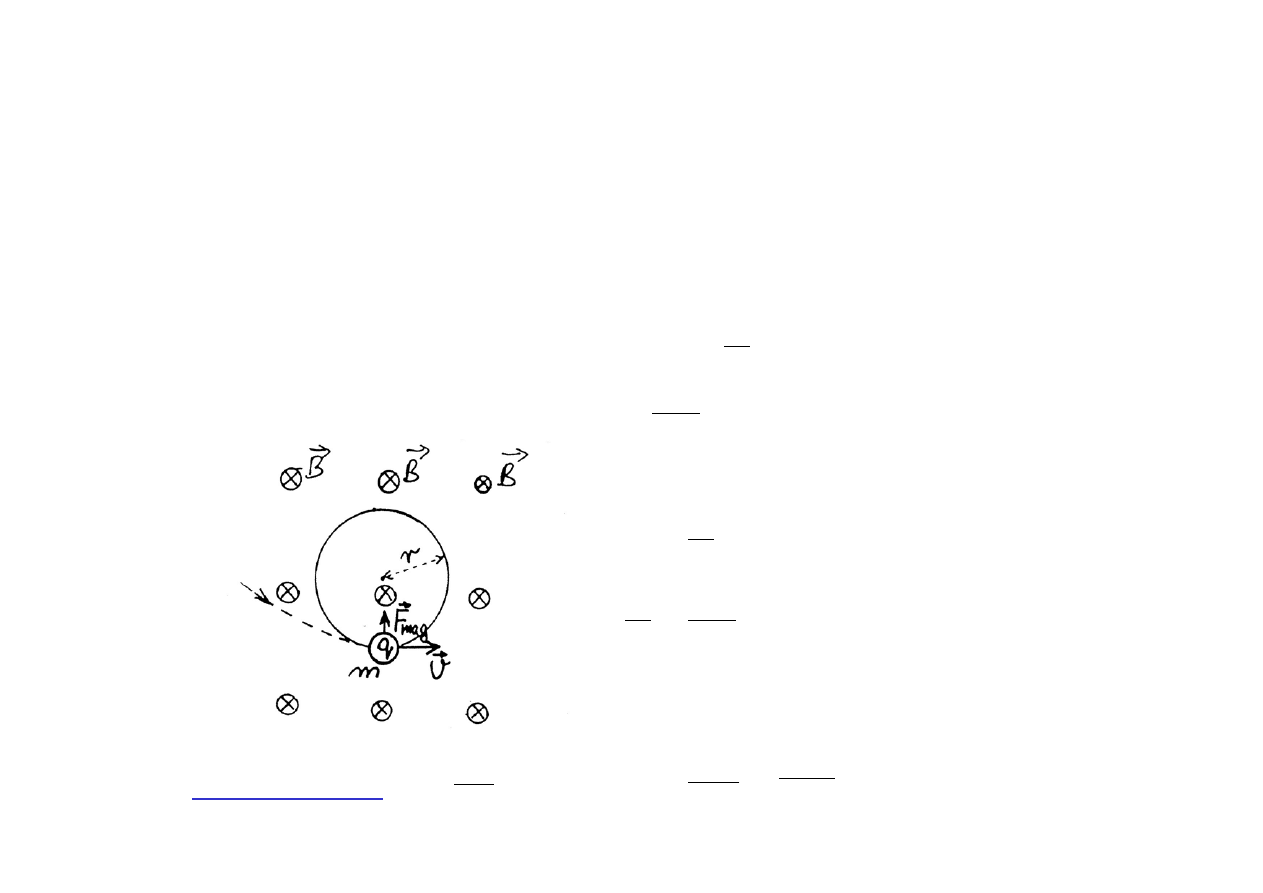
Ładunek, który wpadnie do jednorodnego pola magnetycznego z

prędkością

⊥

będzie poruszał się po okręgu.

Siła F = q V B wywoła przyspieszenie a

n

=

, normalne (prostopadłe)

do v.

a

n

=

Z kinematyki ruchu po okręgu

a

n

=

=

Promień okręgu

: r =

; Okres: T =

=

→

V

→

B

F

m

qvB

m

2

v

r

2

v

r

qvB

m

mv

qB

2 r

v

π

2

πm

qB

Przykład:

Do skrzyżowanych prostopadle pól i . wpada wiązka

protonów z v = 0,1c i

⊥

oraz

⊥ .

Dla jakiego siła elektromagnetyczna działająca na protony równa

się zero ?

=

E

+

mag.

= q

+ q x

= 0 ; q = e

⇒ e

+ e x =0

= - x

⊥ więc skalarnie E = v B

czyli =

v (cząstki o innym v

będą odchylone)

→

E

→

B

→

V

→

E

→

V

→

B

E

B

→

F

→

F

→

F

→

E

→

V

→

B

→

F

→

E

→

V

→

B

→

E

→

V

→

B

→

V

→

B

E

B

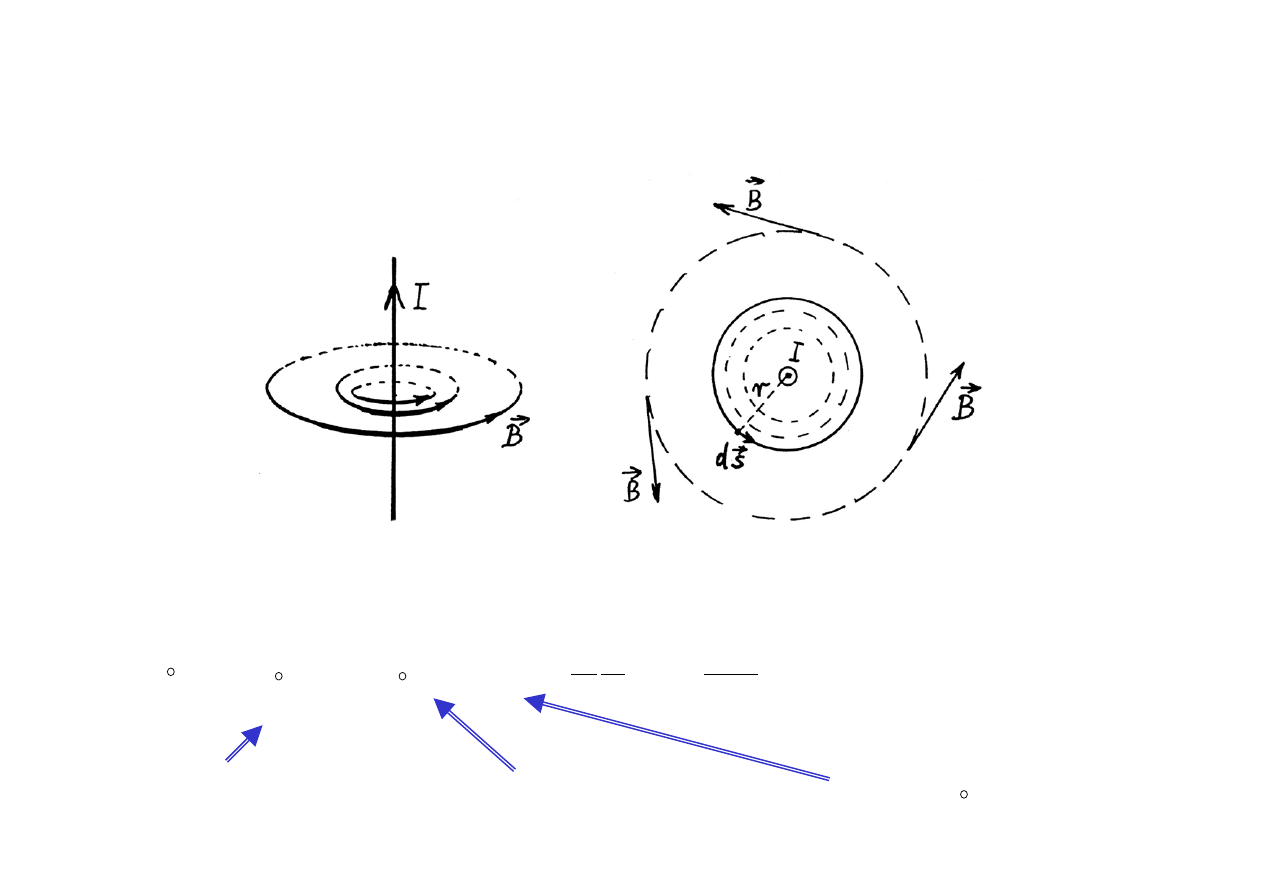
Obliczmy całkę z po okręgu o promieniu r przez środek którego przechodzi
przewód z prądem I.

d

= =

B

= B 2

πr =

okrąg okrąg okrąg

(wartość całki nie zależy od r !)

(

; dla danego r wartość B = const.; całka krzywoliniowa:

)

Jakie jest pole magnetyczne wytwarzane przez dowolny układ
przewodników z prądem?

(inaczej: czy istnieje odpowiednik prawa Gaussa

dla pola magnetycznego?)

→

B

→

∫ B

→

s

Bds

∫

ds

∫

k

c

2I

r

2 r 4 k

c

I

2

2

π

π

=

ds

r

=

∫

2

π

→

→



B

d s

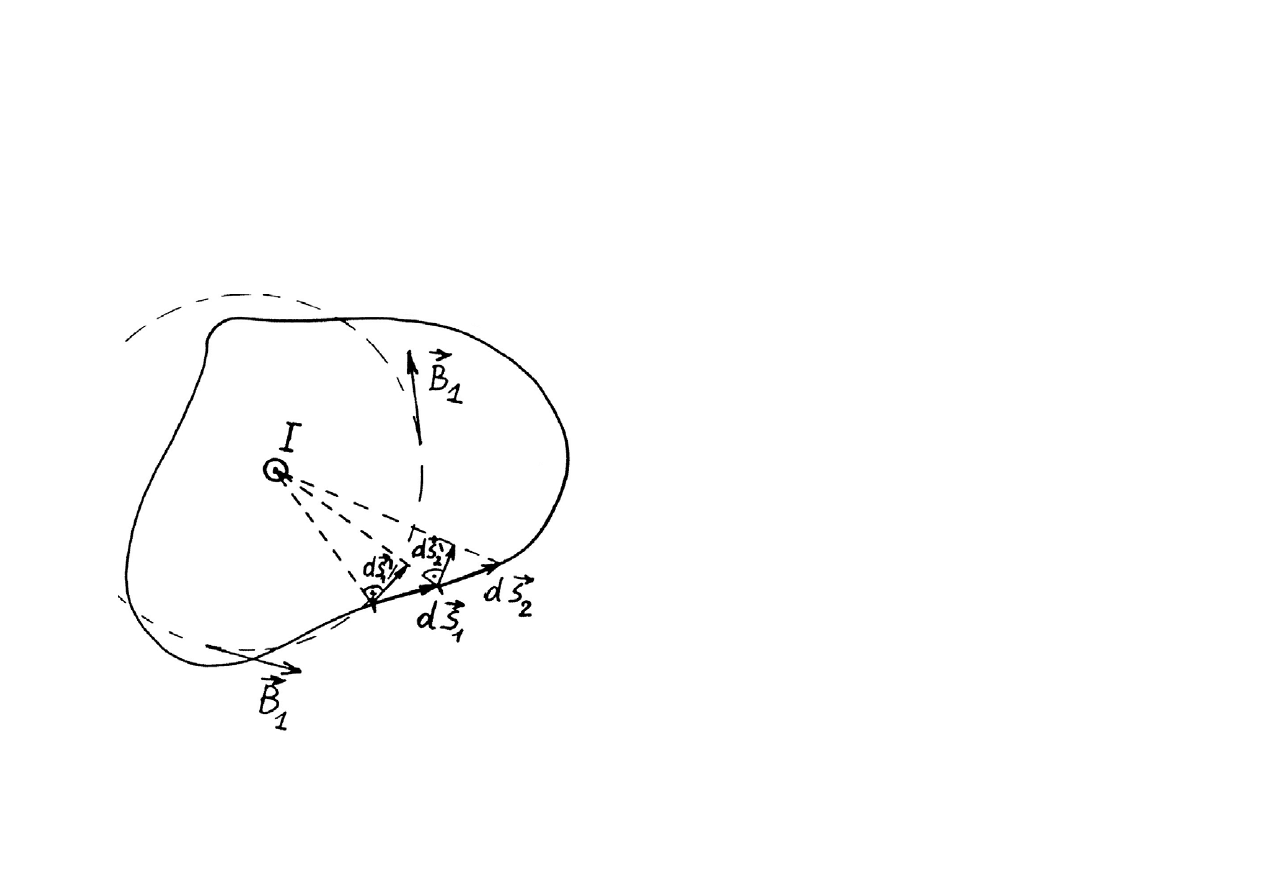
Dla elementu konturu d

d

= d

(bo składowa wektora d
prostopadła do nie daje
wkładu do iloczynu skala-
rnego)

również

d = d

d

i d

są elementami okręgów

współśrodkowych ze środkiem w
przewodniku I.

Obliczmy całkę z pola

dla dowolnego konturu zamkniętego otaczającego

przewód z prądem.

→

B

→

1

s

→

1

B

→

1

s

→

1

B

→

1

'

s

→

1

s

→

B

→

2

B

→

2

s

→

2

B

→

2

'

s

→

1

'

s

→

2

'

s

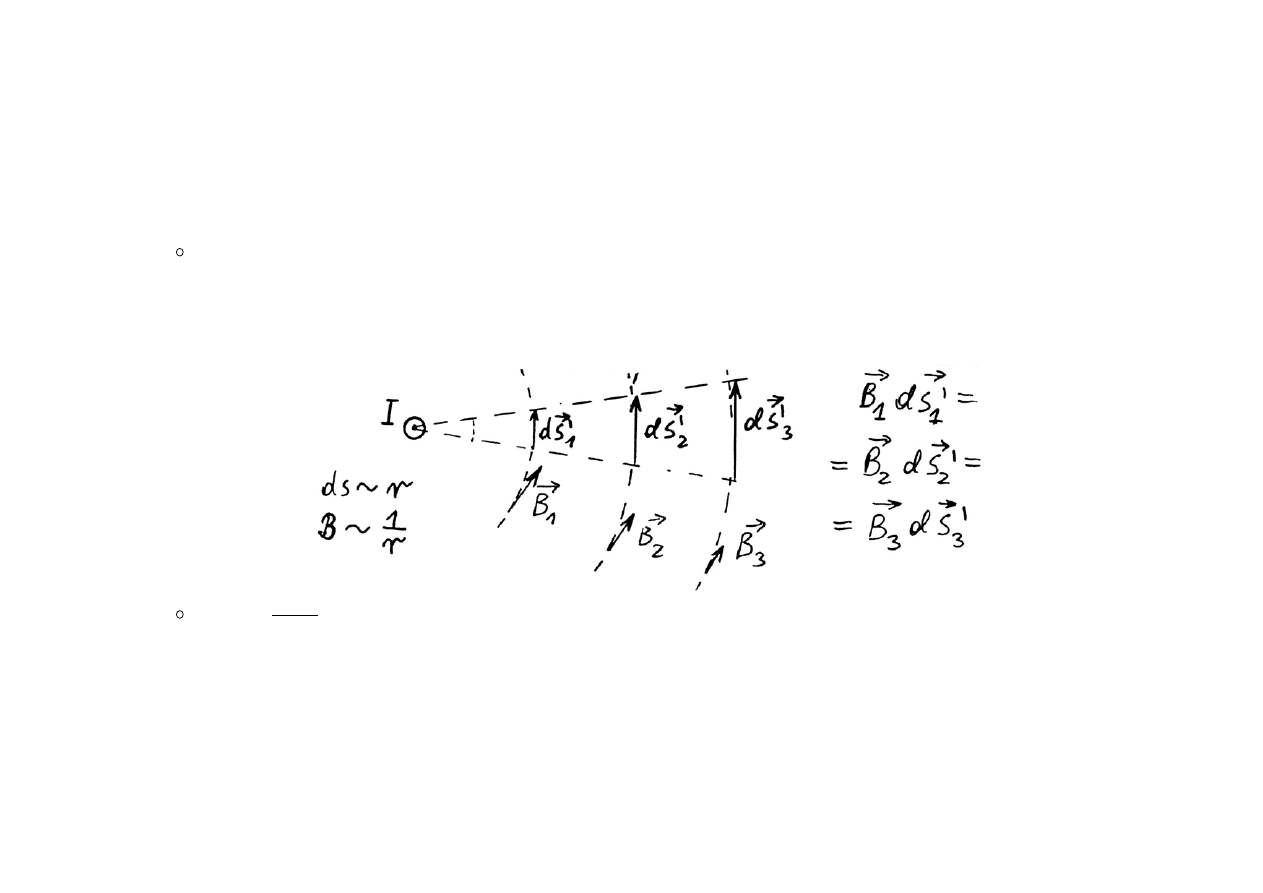
d = d + d +

.......

+

= d

’

+ d

’

+ ...=

d '

kontur dowolny

całka nie zależy od promienia okręgu którego elementem jest

d

’

d =

dowolny okrąg

→

∫ B

→

s

→

1

B

→

1

s

→

2

B

→

2

s

→

1

B

→

1

s

→

2

B

→

2

s

B

→

→

s

→

s

→

∫ B

→

s

4

2

πk

c

I

Jeśli kontur zamknięty otacza n przewodów z prądami
I

1

, I

2

,......I

n

, możemy zastosować zasadę superpozycji pól.

1

d

=

1

; .....

n

d

=

n

(całki

n

d

są całkami krzywoliniowymi po konturach zamkniętych)

1

d

+ ....... +

n

d

=

1

+ ..... +

n

+ + .... + ) d

=

I

1

+ I

2

+ ..... I

n

)

Prawo
Ampere

’

a

d

=

K

I

K

jest sumarycznym prądem objętym konturem K

I

K

= d

gdzie A jest dowolną powierzchnią

ograniczoną konturem K

(całka powierzchniowa)

→

∫ B

→

s

4

2

πk

c

I

→

∫ B

→

s

4

2

πk

c

I

→

∫ B

→

s

→

∫ B

→

s

→

∫ B

→

s

4

2

πk

c

I

4

2

πk

c

I

(

→

∫

1

B

→

2

B

→

n

B

→

s

4

2

πk

c

(

→

B

k

∫

→

s

4

c

I

k

2

π

→

∫ j

A

→

A

Prawo Ampere

’

a jest słuszne nie tylko dla prostych przewodów z prądem

I

1

, I

2

, .... I

n

, ale dla przewodów o dowolnym kształcie.

Prawo Ampere

’

a jest słuszne nie tylko dla prostych przewodników z

prądem I

1

, I

2

, .... I

n

, ale dla przewodników o dowolnym kształcie.

Przez analogię do strumienia elektrycznego

φ

E

można określić

strumień magnetyczny przez pewną powierzchnię s jako liczbę linii
pola B przechodzących przez s.

d

φ

B

= d ;

φ

B

=

d

→

B

→

s

→

∫ B

s

→

s

Linie pola B są ciągłe wokół przewodnika, zatem strumień przez

dowolną powierzchnię zamkniętą s jest

równy zeru (bo wszystkie linie które
wchodzą do s muszą także wyjść):

d = 0

Dla n przewodników z prądami I

1

, I

2

, .... I

n

φ

B

=

d =

1

d

+ .....+

n

d

=

φ

1

+

φ

2

+ ... +

φ

n

Dla powierzchni zamkniętej :

d

= 0

Jest to słuszne dla n przewodników z prądami I

1

..... I

n

o dowolnym

kształcie.

→

∫ B

s

→

s

→

∫ B

s

→

s

→

∫ B

s

→

s

→

∫ B

s

→

s

→

∫ B

s

→

s

Pochodzenie siły magnetycznej

Obojętny elektrycznie przewód w którym płynie prąd I dla obserwatora
poruszającego się z prędkością v wzdłuż przewodu (w kierunku zgodnym
z I) wykazuje gęstość ładunku

λ

‘

= -

( )I

#

Efekt ten wynika ze szczególnej teorii względności, z tzw.

skrócenia

Lorentza

: długość przedmiotu który porusza się względem nas z

prędkością v będzie miał dla nas długość:

l

'

=

l (skrócenie wymiaru l wystąpi w kierunku ruchu);

l - długość przedmiotu w spoczynku

2

v

c

2

1

c

2

−

1

1 v

c

2

−

v

2

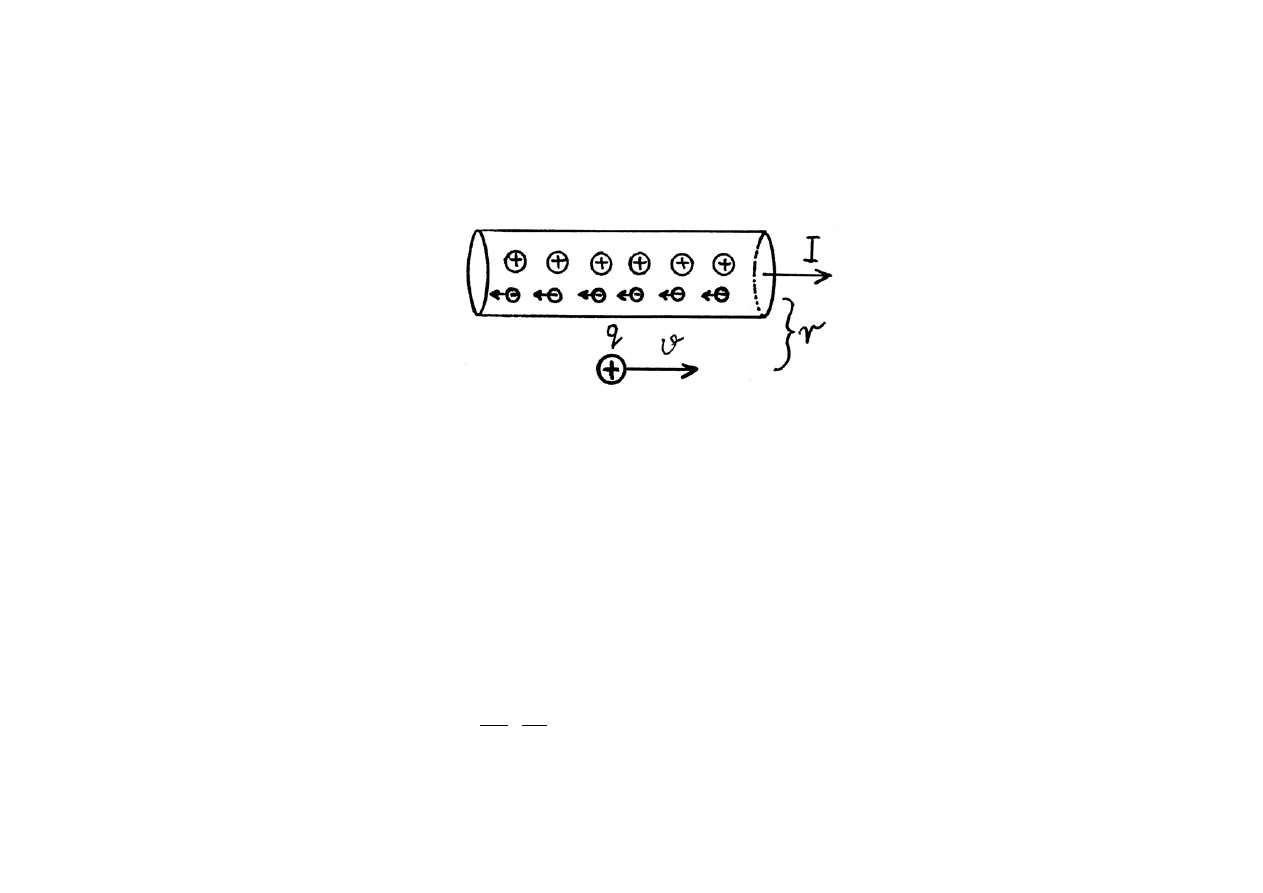
Dla "obserwatora" na ładunku q odległości między ładunkami + w
przewodniku ulegną skróceniu, więc gęstość liniowa

λ

+

wzrośnie.

Ten efekt jest jeszcze silniejszy dla poruszających się ładunków
ujemnych w przewodniku (większa prędkość względna), czyli

λ

-

>

λ

+

.

A więc przewód nie jest obojętny elektrycznie dla poruszającego się
ładunku q, lecz wykazuje wypadkowy ładunek ujemny. Dla
zewnętrznego obserwatora, ten wypadkowy ładunek działa na
ładunek q siłą :

F =

o

k
c

I

r

qV

2

2

( )

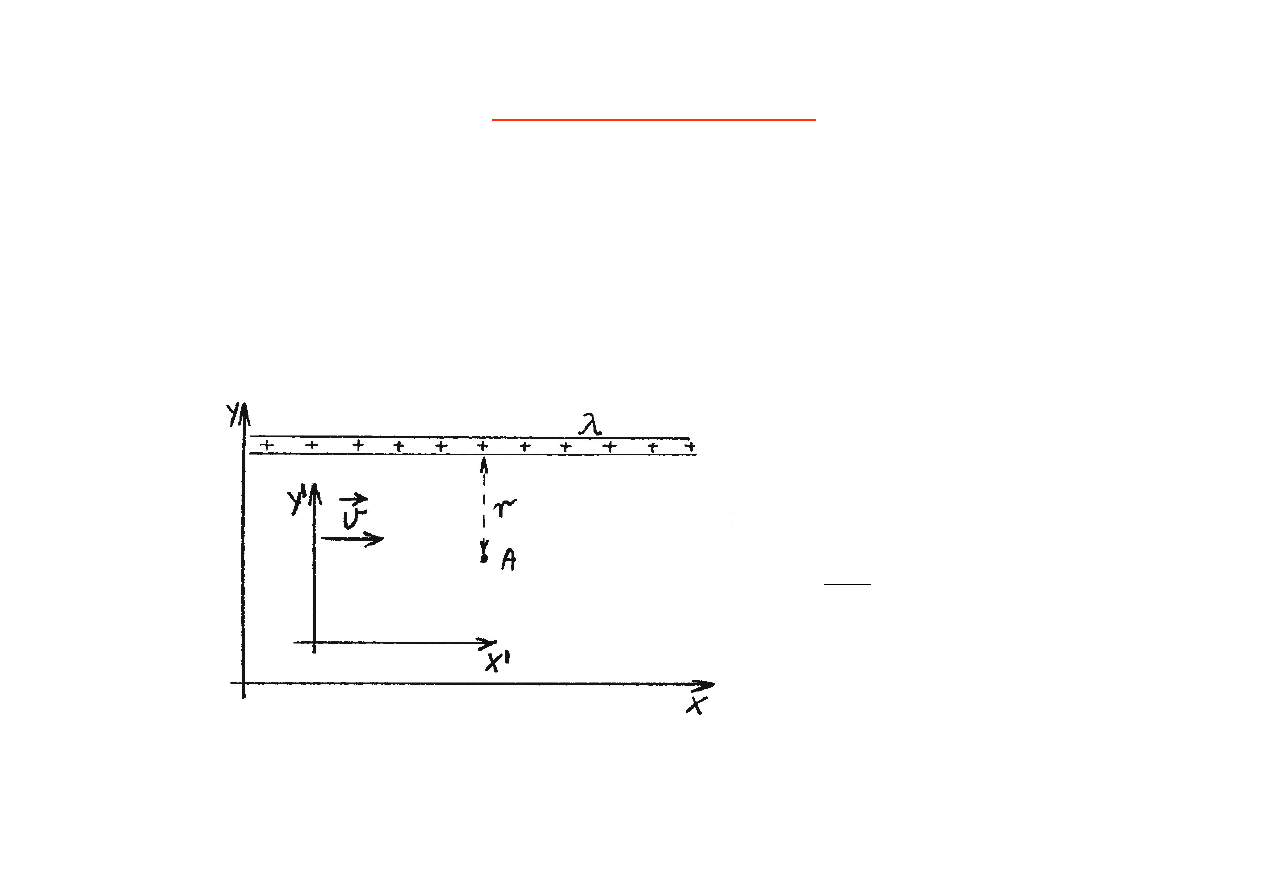
Pole elektromagnetyczne

Wykażemy, że i są

składowymi tego samego pola

elektromagnetycznego. Dla poruszających się obserwatorów zachodzi
transformacja relatywistyczna i (oba pola przechodzą wzajemnie
jedno w drugie).
Załóżmy, że w układzie laboratoryjnym xy znajduje się nieruchomy
przewodnik zawierający ładunek dodatni o gęstości liniowej

λ

- prąd

nie płynie.

W układzie xy
B = 0

E =

(np. w punkcie A)

Obserwator związany z układem x

’

y

’

poruszającym się z prędkością

zaobserwuje przepływ prądu (w lewo) o natężeniu: I

’

= v

λ

‘

(

λ

‘

- gęstość

liniowa ładunku obserwowana w układzie x

’

y

’

).

→

E

→

B

→

E

→

B

2k

r

λ

→

v

Stwierdzi więc pole magnetyczne:

B

’

=

i elektryczne: E

’

=

czyli: B

’

= E ; wektorowo: = x

To znaczy, że poruszający się układ ładunków elektrycznych z
prędkością v wytworzy pole magnetyczne:

= x

Podobnie, rozpatrując przewodnik nienaładowany w którym płynie prąd
i który porusza się z prędkością

, można wykazać, że będzie on

wytwarzał pole elektryczne

= - x

Jest to ogólny związek między polem elektrycznym i polem
magnetycznym wytwarzanym przez źródło prądu poruszające się z
prędkością .

Tak wytworzone pole elektryczne nazywamy indukcją

elektromagnetyczną

⇒

prawo Faradaya

k

c

I

r

2

2

'

=

k

c

v '

r

2

2

λ

2k '

r

λ

v

c

2

→

B

v

c

2

→

E

→

B

v

c

2

→

E

→

v

→

E

→

v

→

B

→

v

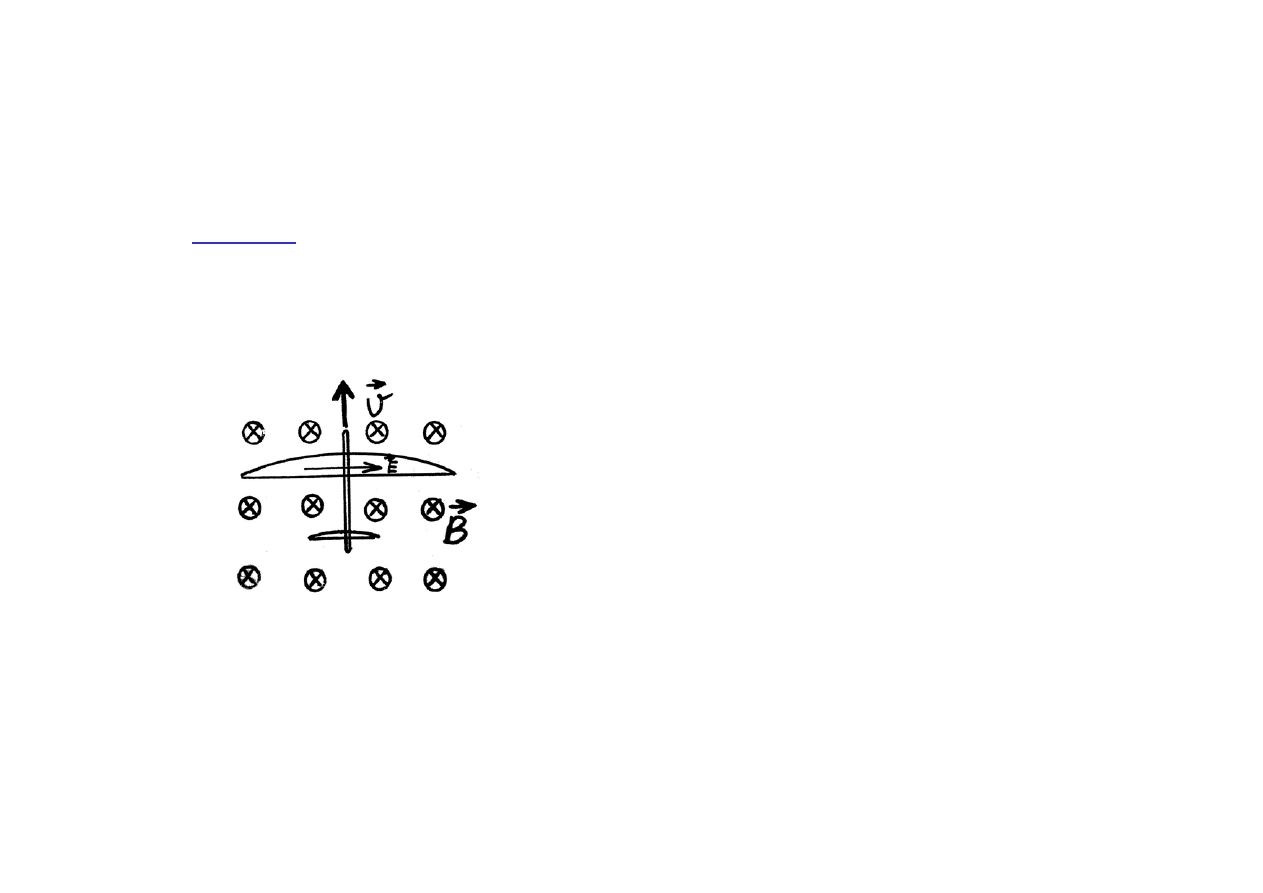
Przykład

: Jakie napięcie powstanie na końcach skrzydeł samolotu

lecącego wzdłuż południka z prędkością 1000 km/godz.? Długość
skrzydeł l = 25m ; składowa pionowa pola magnetycznego Ziemi B

⊥

=

0,6 10

-4

T

= - x

E

→

v

B

→

→

(bo porusza się względem Ziemi,

czyli źródła pola magnetycznego)

.

⊥

⊥

, czyli E = v B

⊥

→

v

→

B

E = 1000 (km/godz) • 0,6 •10

-4

(T)

≅

278 (m/s) • 0,6 •10

-4

(Vs/m

2

)

≅ 0,017 V/m

dV = -

d

= - E l = 0,017 V/m • 25 m

≅ 0,4 V

→

E

→

s

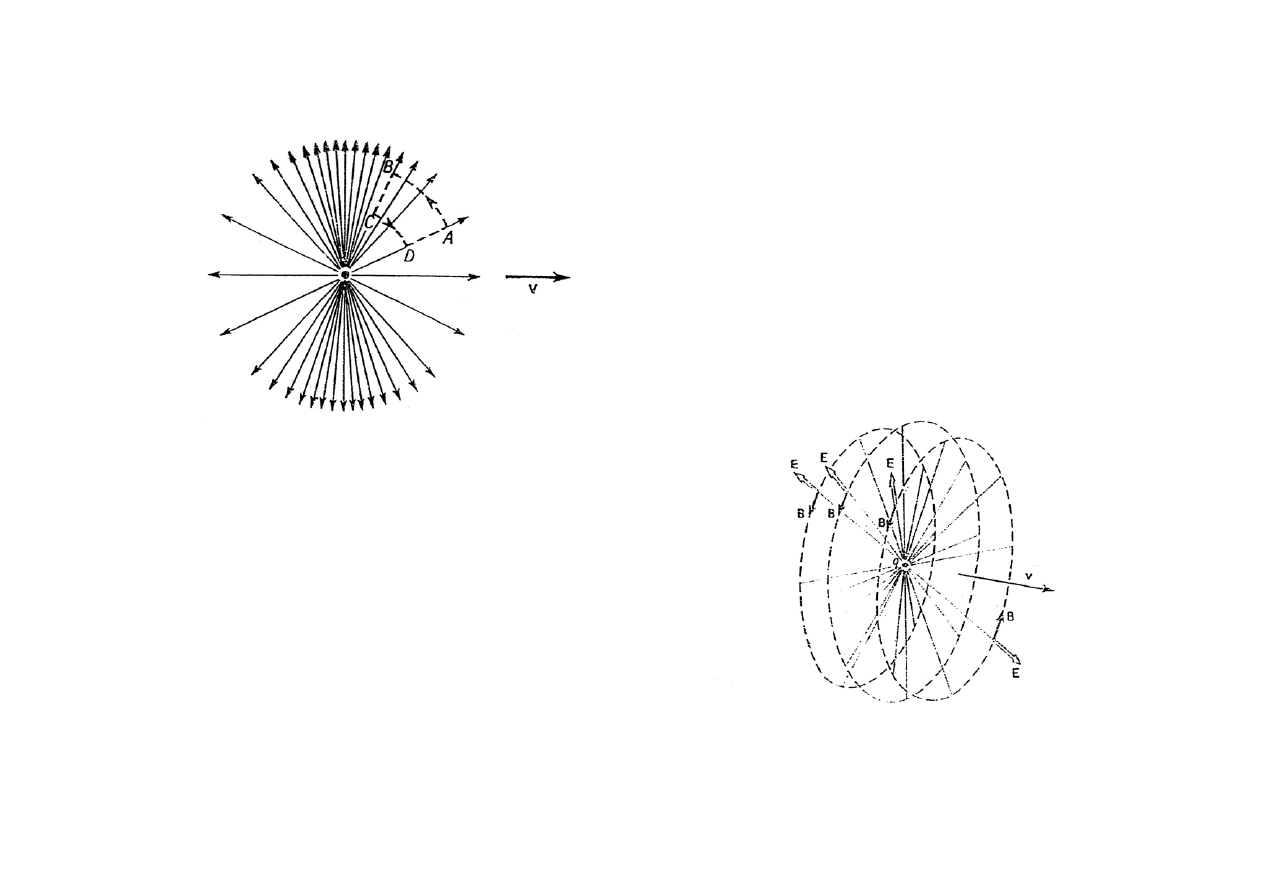
Inny sposób przedstawienia
rozkładu pola ładunku będącego w
ruchu jednostajnym

Pola elektryczne i magnetyczne wytworzone
w pewnej chwili przez ładunek poruszający
się ruchem jednostajnym.

Prawo Biota - Savarta

Rozważmy ładunek q poruszający się z prędkością v

<<

c.

Wytwarza on pole elektryczne w odległości r:

= k

- wektor jednostkowy skierowany od q do punktu

w którym wyznaczamy pole E

ponieważ : = x

=

x (k

) =

x

Zastosujmy to równanie do ładunku dq płynącego w elemencie dl

obwodu z prądem :

d =

x =

(d jest wektorem długości elementu dl z prądem; )

d =

Prawo Biota-Savarta jest równoważne prawu Ampera. Całkowite

pole w danym punkcie oblicza się całkując powyższe równanie po
całym, zamkniętym obwodzie z prądem (tzn. sumując pola d
wytworzone przez wszystkie elementy dl obwodu z prądem)

→

E

q

r

r

2

∧

∧

r

→

B

c

v

2

→

→

E

→

B

c

v

2

→

q

r

r

2

∧

k

c

q

r

2

2

∧

r

→

B

dt

d

r

dq

c

k

2

2

l

→

∧

r

r

r

x

d

dt

dq

c

k

2

2

∧

→

l

→

l

d

dt

v;

→

→

=

l

dq

dt

I

=

B

→

r

r

d

I

c

k

2

2

ˆ

x

l

r

→

B

→

B

v

→

Prawo Biota - Savarta

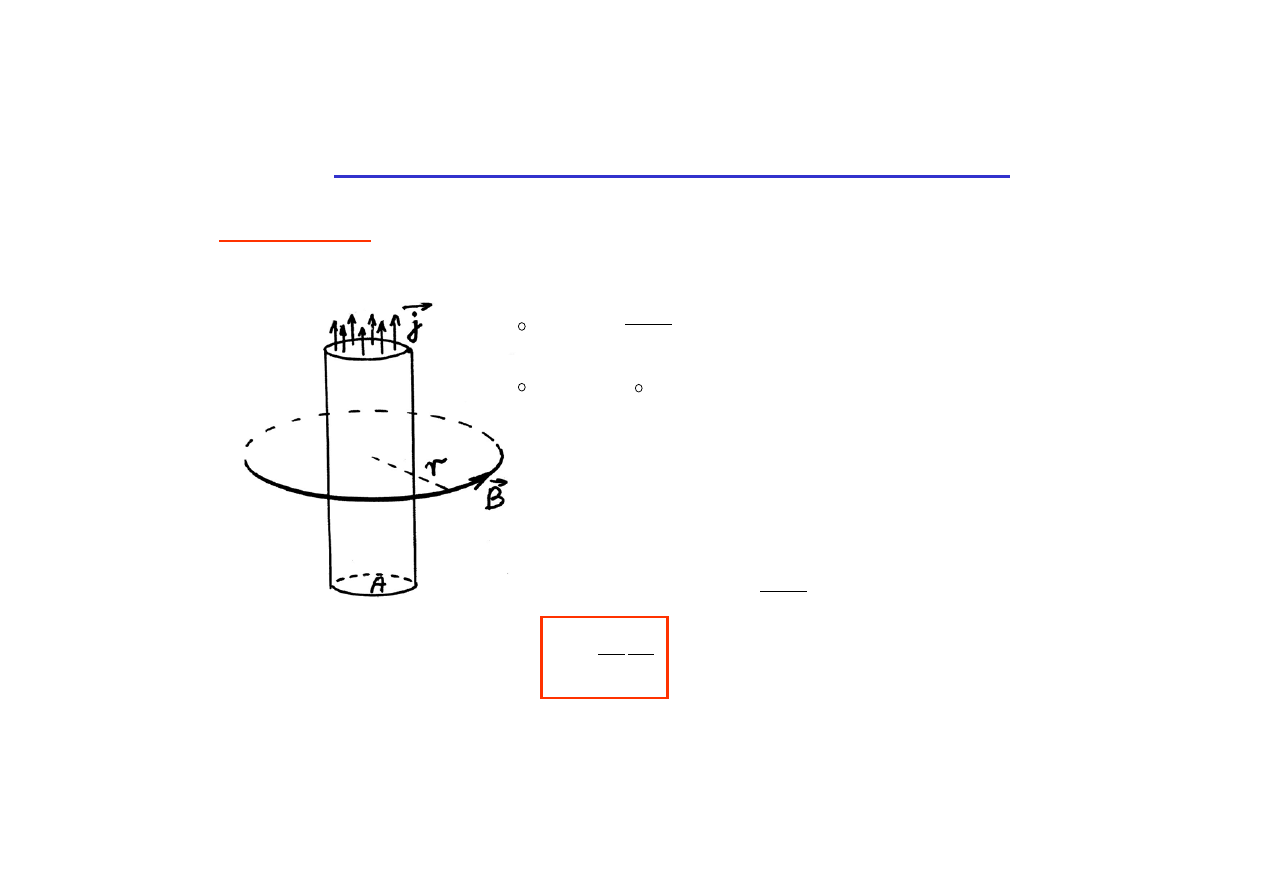
Zastosowania prawa Ampere’a i prawa Biota-Savarta

Pręt lub drut

: wyznaczyć pole B na zewnątrz pręta w którym płynie prąd o

jednorodnej gęstości j

=

I (prawo Ampere’a)

= B

= B 2

π

r

okrąg

(B jest stałe na okręgu ze środkiem w środku

pręta, oraz



)

B 2

π r = I

B = gdzie I = d

(

por. równanie ze str. 11.2

)

Pole magnetyczne na zewnątrz pręta jest takie same jak dla cienkiego
drutu umieszczonego w środku pręta, w którym płynąłby prąd o takim
samym natężeniu I.

→

∫ B

4 k

c

2

π

→

∫ B

d s

→

d s

→

ds

∫

→

B

d s

→

4 k

c

2

π

k

c

2I

r

2

→

∫ j

→

A

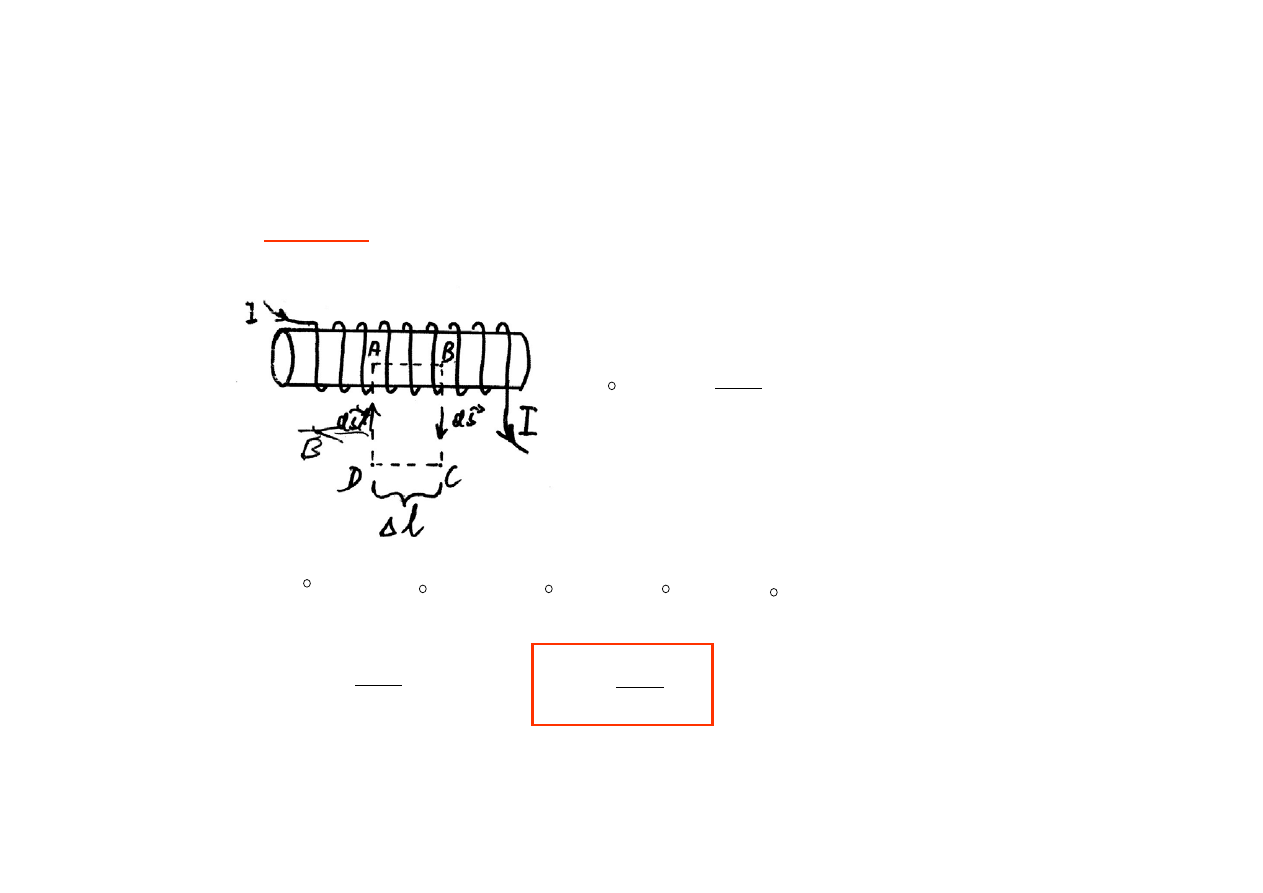
Solenoid

: wyznaczyć pole B

w

wewnątrz długiego solenoidu

posiadającego n zwojów na jednostkę długości.

=

I

k

(prawo Ampere

’

a)

I

k

=

∆

l n I

=

w

+

+

+

ABCD

AB BC CD DA

B

w

∆

l =

∆

ln I

⇒ B

w

=

n I

→

∫ B

d s

→

4 k

c

2

π

→

∫ B

d s

→

→

∫ B

d s

→

→

∫ B

d s

→

→

∫ B

d s

→

→

∫ B

d s

→

4 k

c

2

π

4

2

πk

C

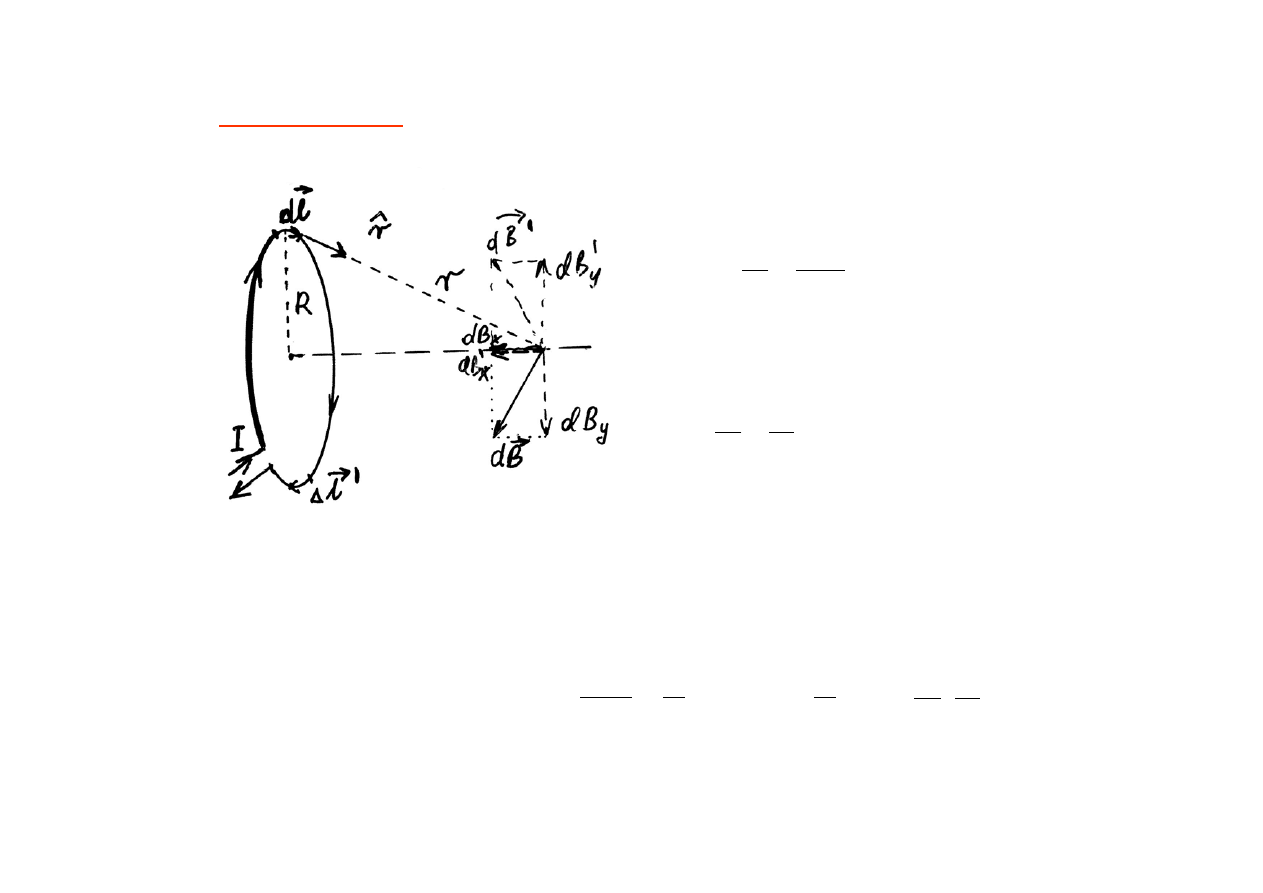
Obwód kołowy

: Wyznaczyć pole B wzdłuż osi obwodu kołowego o

promieniu R

d

=

I

(Prawo Biota-Savarta)

d

⊥

dB = I

Interesuje nas tylko składowa dB

x

(bo składowa dB

y

dla każdego

elementu

∆ będzie skompensowana przez taką samą co do wartości,

ale przeciwnie skierowaną składową dB

y

’

wytworzoną przez element d

’

przeciwległy do d )

z podobieństwa trójkątów:

dB

x

=

=

→

B

k

c

2

d xr

r

2

l

→

l

∧

r

k

c

2

d

r

2

l

→

l

→

l

→

l

d B

dB

R

r

x

=

R

r

dB

k

c

I R

r

d

2

3

l

Sumując składowe dB

x

pochodzące od wszystkich elementów dl obwodu

kołowego (czyli całkując):

B

x

=

okrąg okrąg

A =

π

- powierzchnia otoczona przez obwód kołowy.

Podobnie jak dla dipola elektrycznego (E

∼

), pole magnetyczne obwodu

kołowego B

∼

(wzdłuż osi).

k

c

I R

r

d

k

c

I R

r

d

k

c

I R

r

2 R

2

3

2

3

2

3

l

l

=

=

=

∫

∫

π

k

c

2I

r

R

2 3

2

π

= k

c

2I

r

A

2 3

2

R

1

3

r

1

3

r

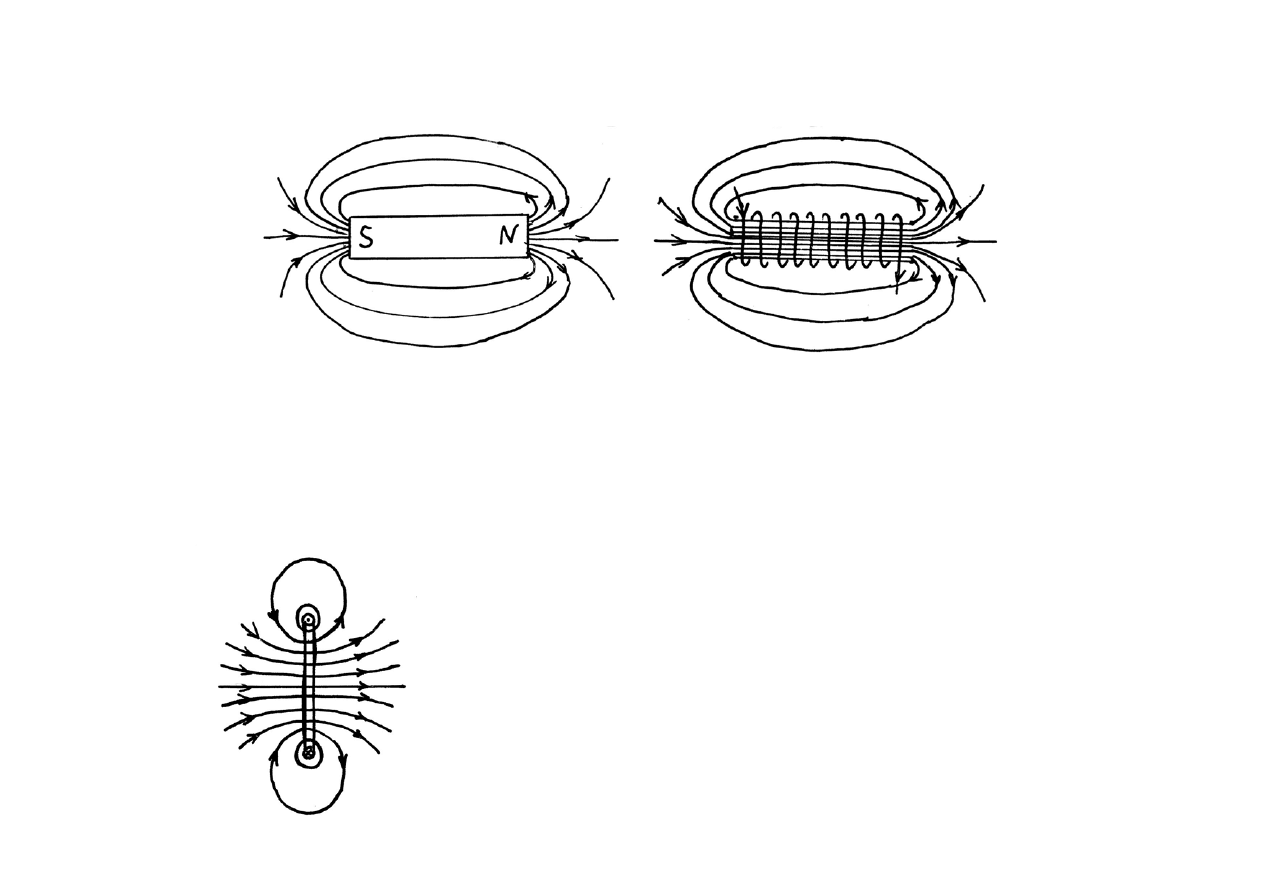
Linie pola magnetycznego B magnesu sztabkowego i solenoidu o
skończonej długości.

Linie pola B

obwodu kołowego (w

płaszczyźnie prostopadłej do płaszczyzny
obwodu i przechodzącej przez średnicę
obwodu).

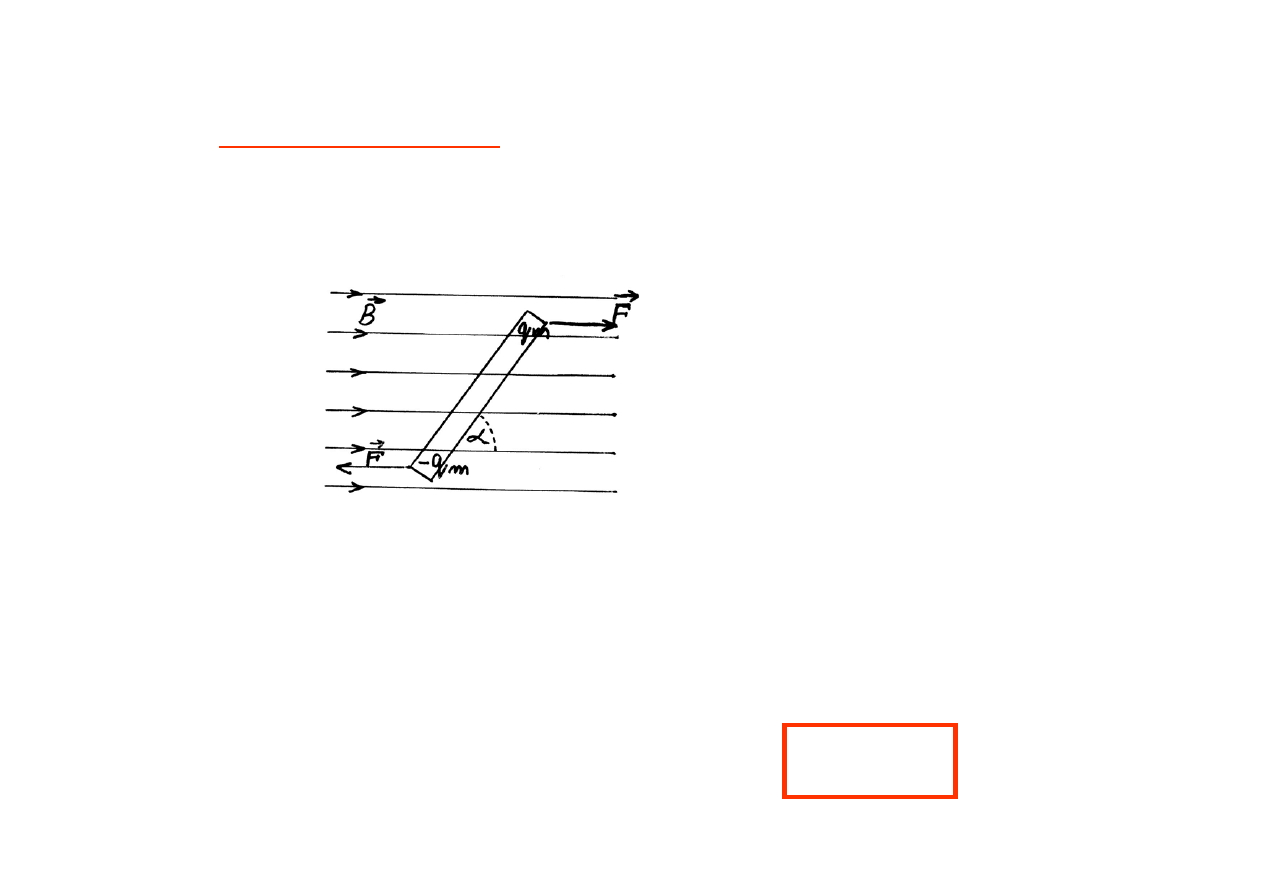
Moment magnetyczny

: na magnes sztabkowy umieszczony w

jednorodnym polu magnetycznym B działają siły (orientujące magnes
zgodnie z polem) takie, jakby na biegunach magnesu były „ładunki”
magnetyczne q

m

i -q

m

(nie istnieją, ale pojęcie wygodne do opisu !)

= q

m

Moment sił F:

T = F l sin

α

= q

m

B l sin

α

(l - długość magnesu)

µ

= q

m

l - moment magnetyczny

T =

µ

B sin

α

lub = x

→

F

→

B

→

T

→

µ

→

B

Z jaką siłą pole magnetyczne działa na element obwodu z prądem?

Siła Lorentza : = q

x

dla elementu dl w którym płynie ładunek dq:

d

= dq

x = dq

x =

d x

d

= I d x

→

F

→

v

→

B

→

F

→

v

→

B

d

dt

→

l

→

B

dq

dt

→

l

→

B

→

F

→

l

→

B

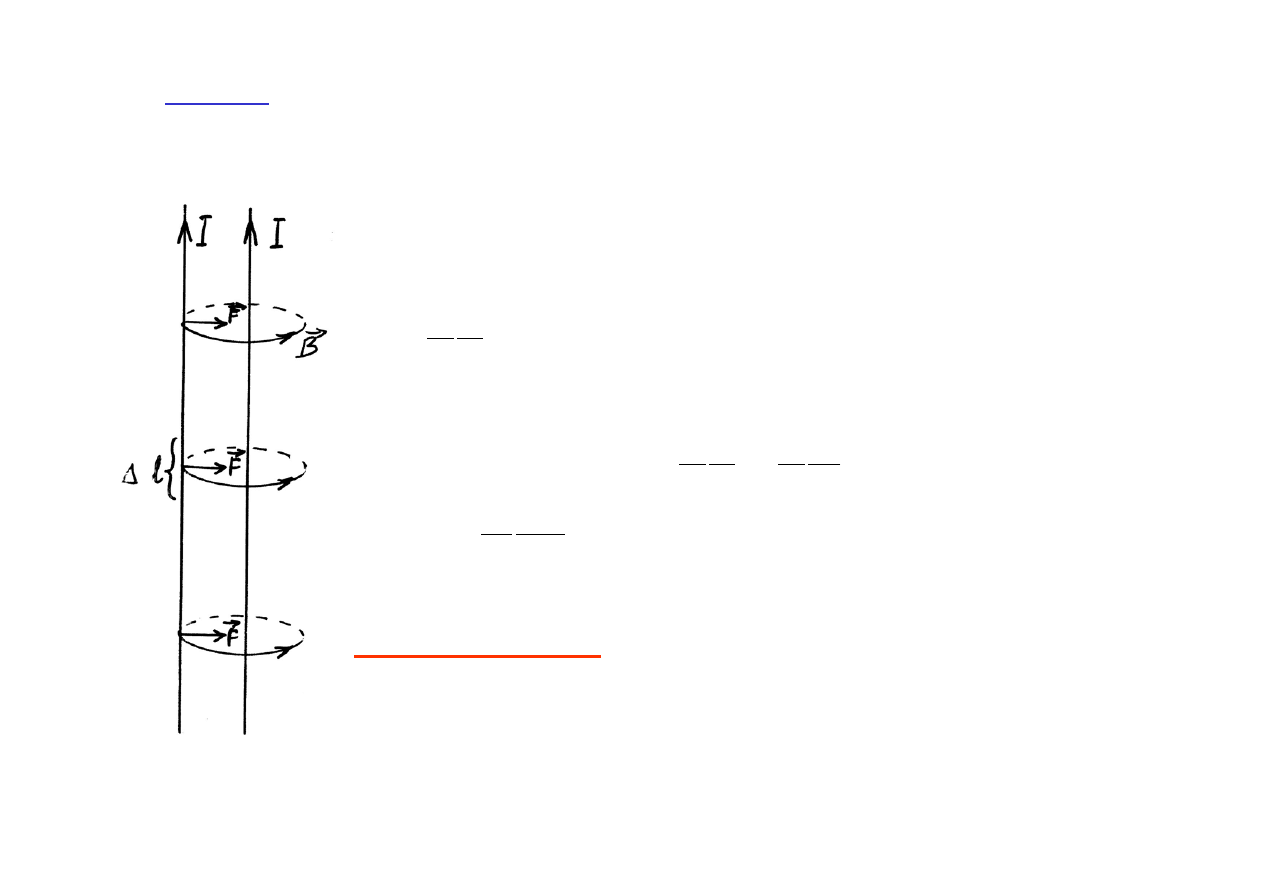
Przykład

: Z jaką siłą oddziałują na siebie elementy

∆l = 1m nieskończenie

długich, równoległych przewodów oddalonych od siebie o r = 1m, w których
płynie prąd o natężeniu 1A?

Jeden z przewodników wytwarza w odległości r pole B:

B =

ponieważ d

= I d x ;

d

⊥

dla elementu

∆

l :

∆

F = I

∆

l

=

∆

l

∆

F = 10

-7

1m = 2 10

-7

N

k

c

2I

r

2

→

F

→

l

→

B

→

l

→

B

k

c

2I

r

2

k

c

2II

r

2

N

A

A

m

2

2

2

1

Definicja Ampere’a

: prąd stały o natężeniu 1A płynący w

dwu prostoliniowych, równoległych, nieskończonych i
cienkich przewodach oddalonych o 1 m, wywołuje w próżni
siłę wzajemnego oddziaływania równą 2x10

-7

N na 1m.

Jaki moment sił działa na ramkę z prądem umieszczoną w

jednorodnym polu magnetycznym?

d = I d x

Siły działające na boki l

2

znoszą się (nie są

zaznaczone na rysunku, są skierowane do
środka ramki, w jej płaszczyźnie).
Na boki l

1

działają siły

= I

x

⊥

więc F = I l

1

B

Moment sił: T = F l

2

sin

α

= I l

1

B l

2

sin

α

= I l

1

l

2

B sin

α

= I A B sin

α

A = l

1

l

2

- powierzchnia otoczona przez obwód

Przez analogię do magnesu sztabkowego : T =

µ

B sin

α

µ

= I A

moment magnetyczny pętli z prądem

→

F

→

l

→

B

→

F

→

1

l

→

B

→

1

l

→

B

Dla solenoidu o n zwojach

: T = n I A B sin

α

,

przy długości l solenoidu, po jego powierzchni płynie wypadkowy prąd

powierzchniowy J =

czyli T = J l A B sin

α

(dla magnesu sztabkowego T = q

m

B l sin

α

)

przez analogię : q

m

= J A „ładunek” magnetyczny solenoidu

µ

= J A l

Magnesy sztabkowe można traktować jako solenoidy o prądzie
powierzchniowym będącym prądem wypadkowym prądów atomowych; na
całkowity moment magnetyczny magnesu składają się momenty
magnetyczne atomowe wywołane prądami elektronowymi.

nI

nI J

l

l

⇒

=

Przykład

: Obliczyć moment magnetyczny atomu żelaza.

Prąd elektronu o ładunku e na orbicie o promieniu r przy

prędkości v wynosi : I = (T - okres obiegu orbity)

T =

⇒ I =

Moment magnetyczny pętli z prądem :

µ

= I A

A =

π r

2

⇒ µ

e

= I

π r

2

=

π r

2

=

e

T

2 r

v

π

ev

2 r

π

ev

2 r

π

ev r

2

Mnożąc licznik i mianownik przez masę elektronu m :

µ

e

= (mVr) =

L (L = mVr - moment pędu)

Z mechaniki kwantowej: L jest wielkością skwantowaną, o minimalnej

wartości (kwancie); L = =

h

,

gdzie h jest stałą Plancka: h = 6,63 10

-34

J s

więc :

µ

e

=

= 9,3

⋅ 10

-24

Am

2

Magneton Bohra

Wartość

µ

e

nie zależy od r - wszystkie elektrony na orbitach mają taki

sam minimalny moment magnetyczny. W atomie żelaza, momenty
magnetyczne 24 elektronów się znoszą; tylko dla 2 elektronów są
zgodne, więc:

µ

Fe

= 2

µ

e

= 1,86 10

-23

A m

2

e

m

2

e

m

2

π

2

h

e

m

2

h

2

π

Równania Maxwella dla prądu stałego

1) Prawo Gaussa

d =

4

πkQ

wew.

(całka powierzchniowa)

________________________________________________________________________________________

2) W elektrostatyce różnica

d

= 0

potencjałów nie zależy od

(całka krzywoliniowa)

drogi (praca siły zachowa-
czej na drodze zamkniętej = 0)

_______________________________________________________________________________________

3) Strumień magnetyczny
przez dowolną powierzchnię

d =

0

zamkniętą jest zero

(całka powierzchniowa)

(linie pola B są ciągłe,
bo nie istnieją ładunki magnetyczne).

________________________________________________________________________________________

4) Prawo Ampere

’

a

d

=

I

wew.

(całka krzywoliniowa)

________________________________________________________________________________________

→

∫ E

→

s

→

∫ E

→

s

→

∫ B

→

s

→

∫ B

→

s

4 k

2

c

π

Powyższe równania można wyprowadzić z równania Coulomba i ze szczególnej teorii
względności (przy założeniu, że ładunki w ruchu wnoszą do prawa Gaussa wkład
niezależny od swojej prędkości). Siła magnetyczna nie jest nowym rodzajem oddziaływań.