mgr inż. Anna Jabłonka

Zadanie 2

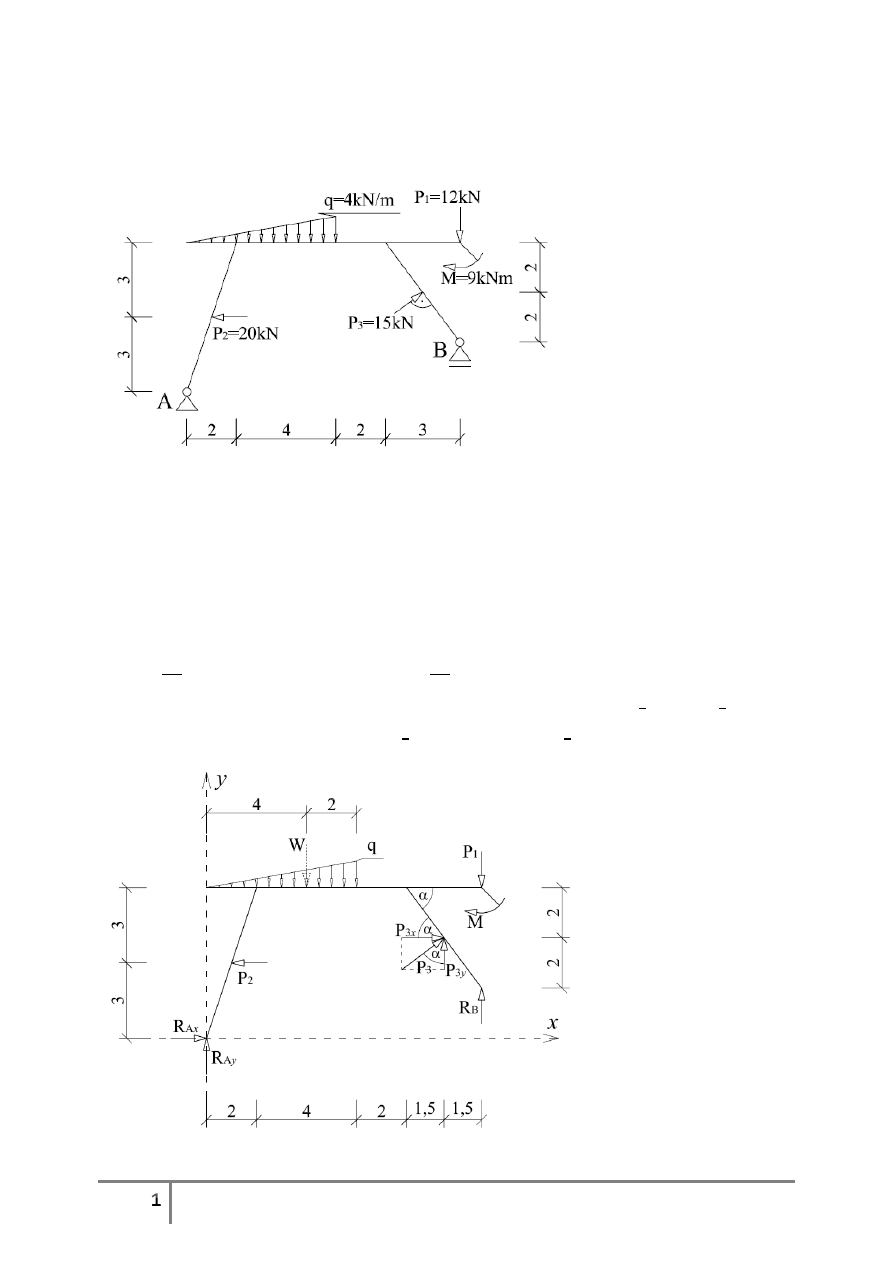
Obliczyć reakcje w podporach ramy.

Rozwiązanie:

Ramę umieszczamy w układzie współrzędnych {x,y} i w miejscu podpór zakładamy reakcje.
Podpora A jest nieprzesuwna, zatem zakładamy w niej dwie składowe reakcji R

A

, zaś w podporze

przesuwnej B reakcja R

B

jest pionowa.

Siłę P

3

, która jest prostopadła do pręta, rozkładamy na składowe: poziomą P

3x

i pionową P

3y

.

Zależności pomiędzy składowymi a wypadkową P

3

zapisujemy w postaci funkcji trygonometrycznych

dla pomocniczo oznaczonego kąta α:

⇒

,

⇒

Funkcje trygonometryczne dla kąta α wyznaczamy z geometrii układu:

,

Stąd składowe siły P

3

są równe:

kN,

kN

mgr inż. Anna Jabłonka

Wyznaczamy wypadkową obciążenia trójkątnego

kN

którą umieszczamy w środku ciężkości trójkąta.

Reakcje w podporach wyznaczamy z równań równowagi, którymi mogą być:



Sumy rzutów sił na oś x (lub y) – dodajemy do siebie wszystkie siły działające równolegle do

osi x (lub y) oraz składowe sił ukośnych równoległe do osi x (lub y); znak siły przyjmujemy
dodatni, kiedy jej zwrot jest taki sam jak zwrot osi x (lub y). UWAGA: Momentów skupionych
nie rzutujemy na o oś x (lub y).



Sumy momentów sił względem punktu – dodajemy do siebie momenty wszystkich sił

działających względem danego punktu oraz momenty skupione. Zakładamy, że momenty sił,
działające przeciwnie do ruchu wskazówek zegara są dodatnie, a momenty działające zgodnie
z ruchem wskazówek zegara są ujemne.

Aby układ był w równowadze, sumy rzutów sił / momentów muszą być równe zero.

Równania możemy zapisywać w dowolnej kolejności. Pisząc sumę rzutów sił na oś x mamy

∑

⇒

kN

Z równania sumy momentów względem punktu A otrzymujemy

∑

⇒

(

)

( )

kN

Aby obliczyć wartość reakcji R

Ay

możemy zapisać równanie sumy rzutów sił na oś y

∑

⇒

kN

W celu sprawdzenia poprawności wykonanych obliczeń, układamy sumę momentów względem
innego niż wcześniej punktu, np. względem punktu B

∑

Otrzymaliśmy ∑

, zatem równanie sprawdzające zostało spełnione.

mgr inż. Anna Jabłonka

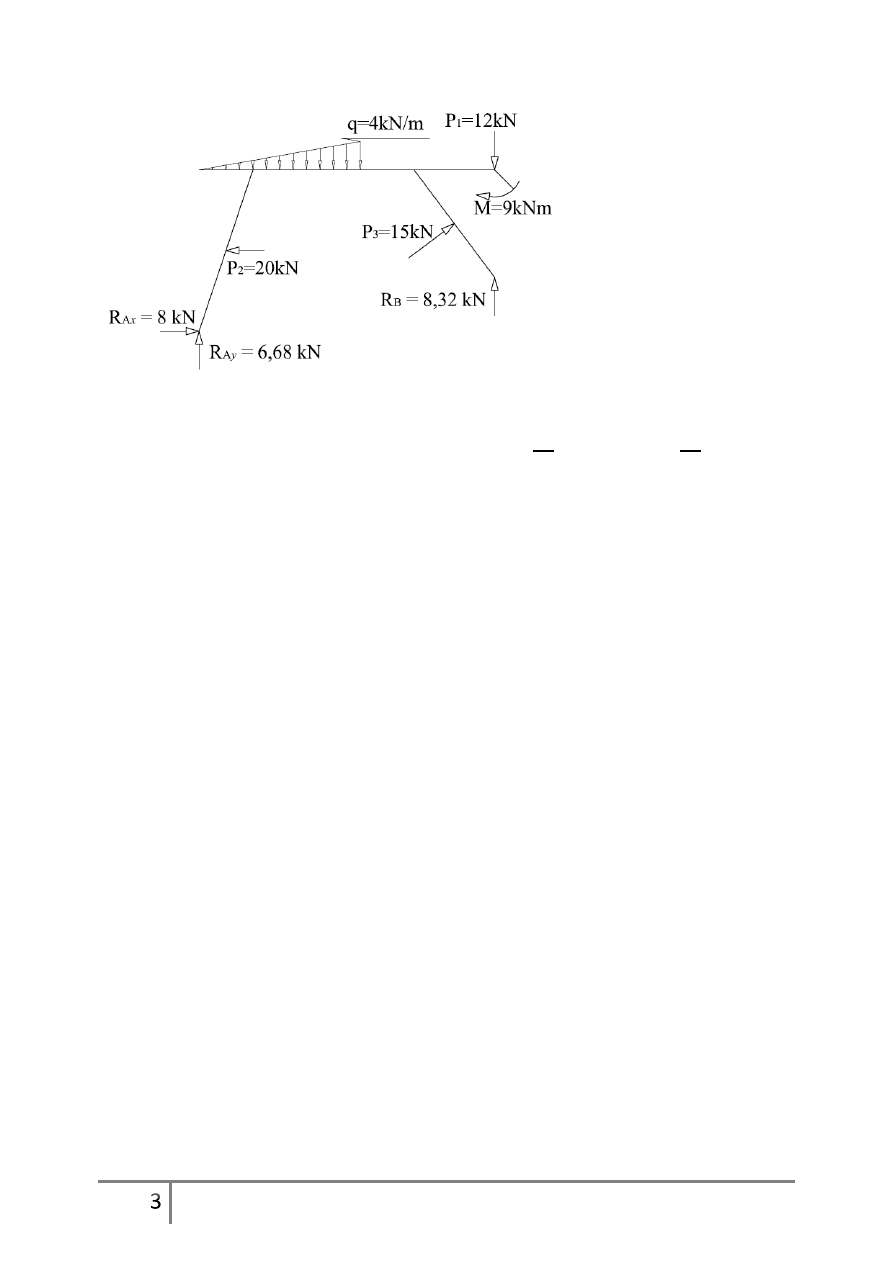
Ostatecznie otrzymaliśmy układ, w którym wszystkie obciążenia i reakcje podporowe się równoważą.

Odp. Reakcje w podporach ramy wynoszą:

kN,

kN,

kN.