1
KINEMATYKA I DYNAMIKA RELATYWISTYCZNA
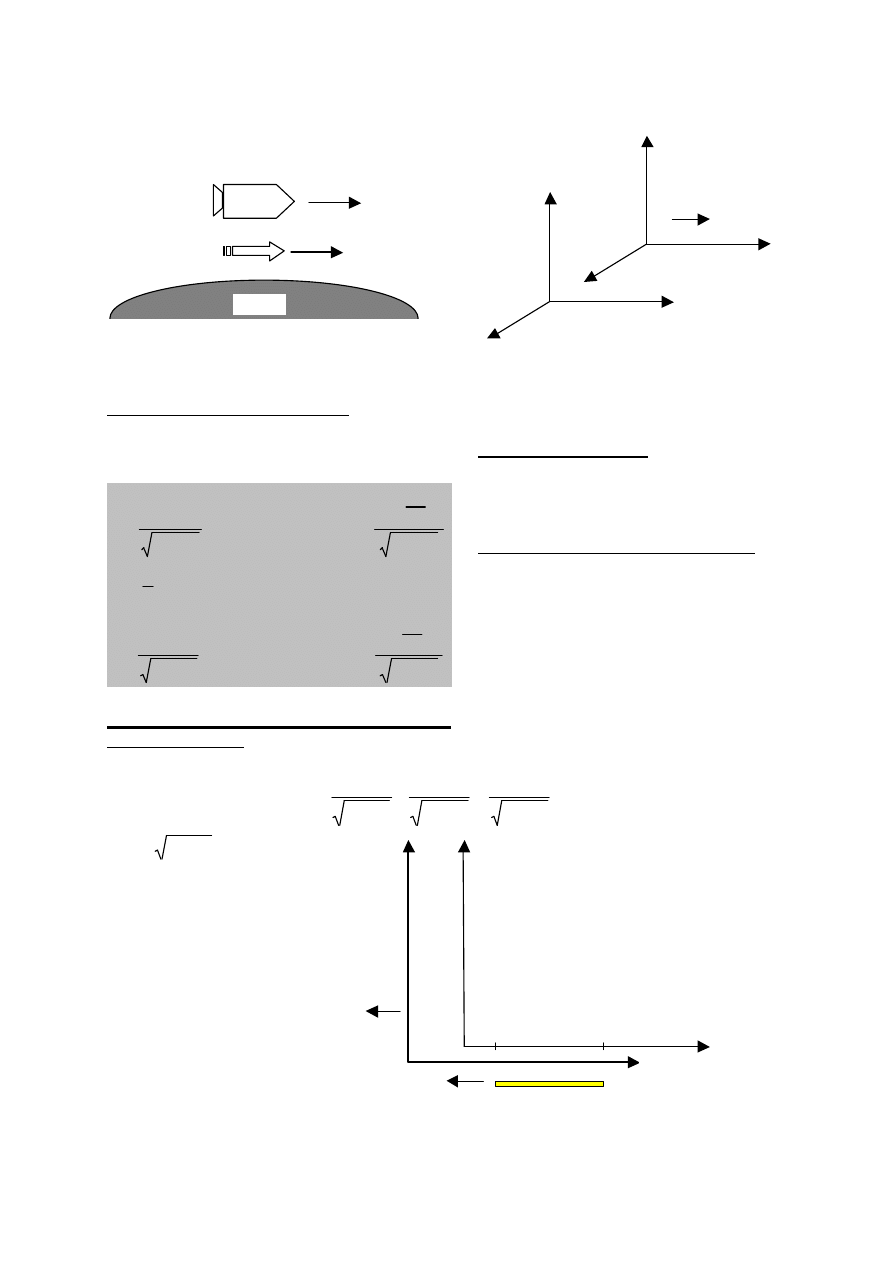
Transformacja Galileusza i Lorentza
t
t
z
z
y
y
vt
x
x
=
=
=
+
=
'
,
'
,
'
,
'
Transformacja Galileusza
1
,
1
)
(
'
,
'
,
'
,
1
'
2
2
2
<
=
−
+
=
=
=
−
+
=
c
v
x
c
v
t
t
z
z
y
y
vt
x
x
β
β
β
Transformacja Lorentza czasoprzestrzeni
,
1
'
)
(
'
,
'
,
'
,
1
'
2
2
2
β
β
−
−
=
=
=
−
−
=
x
c
v
t
t
z
z
y
y
vt
x
x
Konsekwencje transformacji czasoprzestrzeni:
Kontrakcja dlugosci (skrócenie Lorentza)
2
0
'
0
2
'
0
2
'
1
2
'
2
1
2
0
1
2
0
1
1
1
1
,
β
β
β
β
−
=
−
=
−
+
−
−
+
=
−
=
−
=
l
l
l
vt
x
vt
x
x
x
l
x
x
l
l
0
’
– dlugosc poruszajacego sie preta,
l
0
– dlugosc preta w spoczynku
Pan Prim
Pan X
z’
y
z
x
x’
v
y’
pan X widziany przez pana Prima
x
1
’
x
2
’
y’
y
v
x
2
x
1
Pan X
x
x’
A
Ziemia
v
imp
v
B
Pojazd kosmiczny
B
Impuls swiatla
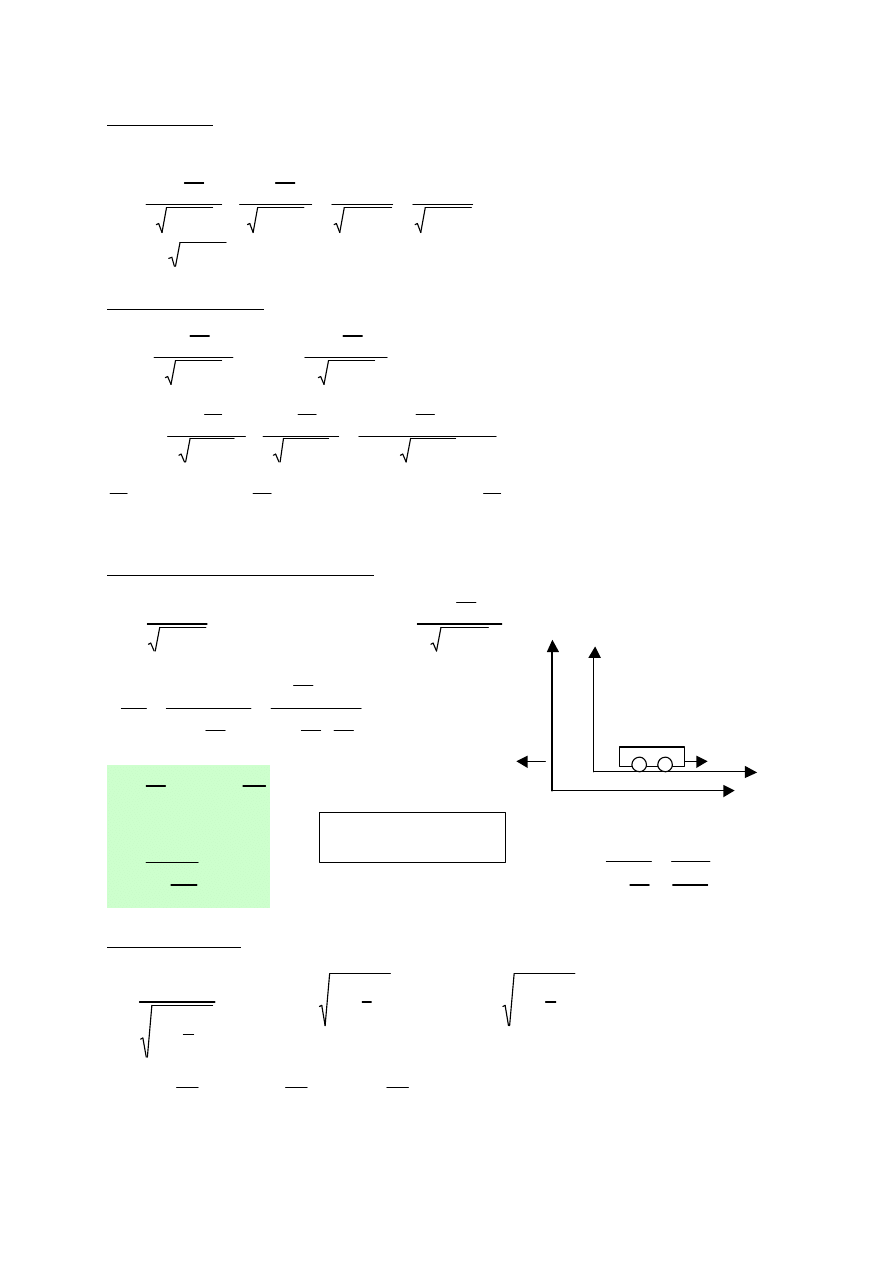
2
Dylatacja czasu (wydluzenie)
2
'
2
2
1
2
2
2
1
2
2
2
'
1
'
2
1
2
1
1
1
1
)
(
1
)
(
'
'
,
β
β
β
β
β
−
∆
=
∆
−
∆
=
−
−
=
−
+
−
−
+
=
∆
−
=
∆
−
=
∆
t
t
t
t
t
x
c
v
t
x
c
v
t
t
t
t
t
t
t
t
Jednoczesnosc zdarzen
2
2
2
2
'
2
2
1
2
1
1
1
)
(
1
)
(
'
β
β
−
+
=
−
+
=
∆
x
c
v
t
t
i
x
c
v
t
t
0
)
(
0
0
)
(
0
1
)
(
1
)
(
1
)
(
'
'
2
1
2
2
1
2
1
2
2
2
1
2
2
1
2
2
1
2
1
2
2
2
2
1
2
≠
−
≠
>
=
−
=
−
−
+
−
=
−
+
−
−
+
=
−
x
x
c
v
czyli
x
x
oraz
c
v
x
x
c
v
czyli
x
x
c
v
t
t
x
c
v
t
x
c
v
t
t
t
β
β
β
czyli t
1
=t
2
, ale t
1
’
≠
t
2
’
Dodawanie predkosci wedlug Einsteina
,
1
)
(
'
,
'
,
'
,
1
'
2
2
2
β
β
−
+
=
=
=
−
+
=
dx
c
v
dt
dt
dz
dz
dy
dy
vdt
dx
dx
2
'
'
'
'
1
c
vu
v
u
u
dt
dx
u
i
dt
dx
u
x
x
x
x
x
+
+
=
=
=
Ped relatywistyczny
Czas wlasny:
τ
τ
τ
τ
τ
τ
d
dz
m
p
d
dy
m
p
d
dx
m
p
c
v
dt
d
c
v
t
c
v
t
z
y
x
0
0
0
2
2
2
,
1
1
1
=
=
=
−
=
⇒
−
=
⇒
−
=
y
u
x
x
v
x’
y‘
Wzór Einsteina na
dodawanie predkosci
,
)
)(
(
1
)
(
2
2
'
'
dt
dx
c
v
v
dt
dx
dx
c
v
dt
vdt
dx
dt
dx
+
+
=
+
+
=
Dla u
x
= c
c
c
v
c
v
c
c
vc
v
c
u
x
=
+
+
=
+
+
=
2
'
1
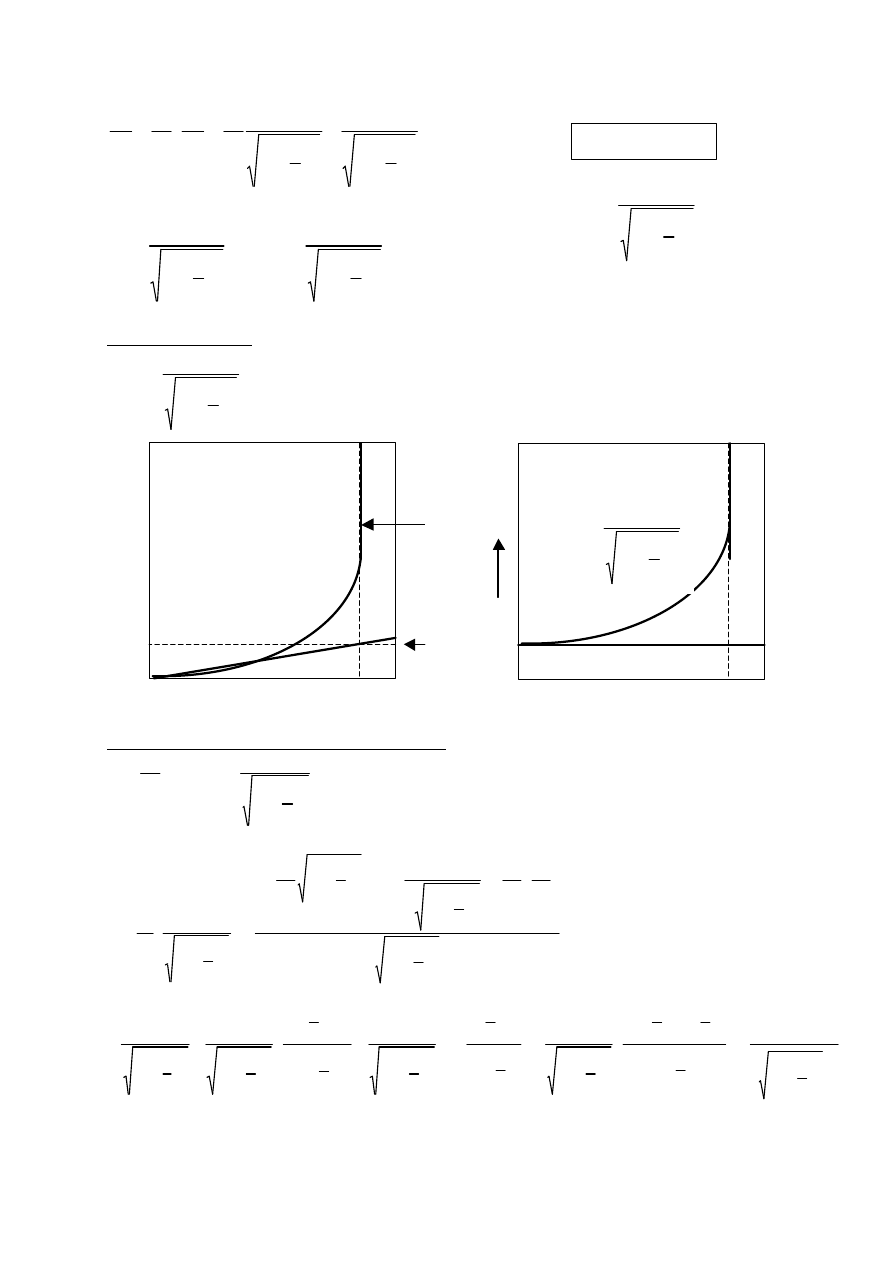
3
,....
1
,
1
1
1
1
2
0
2
0
2
2
−
=
−
=
−
=
−
=
⋅
=
c
v
v
m
p
c
v
v
m
p
zatem
c
v
v
c
v
dt
dx
d
dt
dt
dx
d
dx
y
y
x
x
x
τ
τ
2
0
1
−
=
c
v
v
m
p
r
v
Masa relatywistyczna
2
0
1
)
(
−
=
c
v
m
v
m
gdzie m
0
– masa spoczynkowa
Druga zasada dynamiki w postaci relatywistycznej
2
0
1
−
=
=
c
v
v
m
p
dt
p
d
F
r
r
r
r
3
2
0
2
2
2
2
0
2
2
2
0
2
2
2
0
2
0
2
2
2
0
2
0
2
0
1
1
1
1
1
1
1
1
1
1
1
2
1
2
1
1
1
−
=
−
+
−
−
=
−
+
−
=
−
⋅
−
+
−
=
=
−
⋅
−
−
−
−
=
−
=
c
v
a
m
c
v
c
v
c
v
c
v
a
m
c
v
c
v
c
v
a
m
c
v
c
v
c
v
a
m
c
v
a
m
c
v
dt
v
d
c
v
c
v
v
m
c
v
dt
v
d
m
c
v
v
m
dt
d
F
r
r
r
r
r
r
r
r
r
r
r
Dla v<<c ? v/c ? 0
F = ma
m(v)
v/c
1,0
mc
p
R
p
NR
v/c
1,0
m
0
2
0
1
−
=
c
v
m
m
dla v? c ped ? 8 ,
dla v<<c, v/c? 0 i p
R
= p
NR
Ogólnie ped
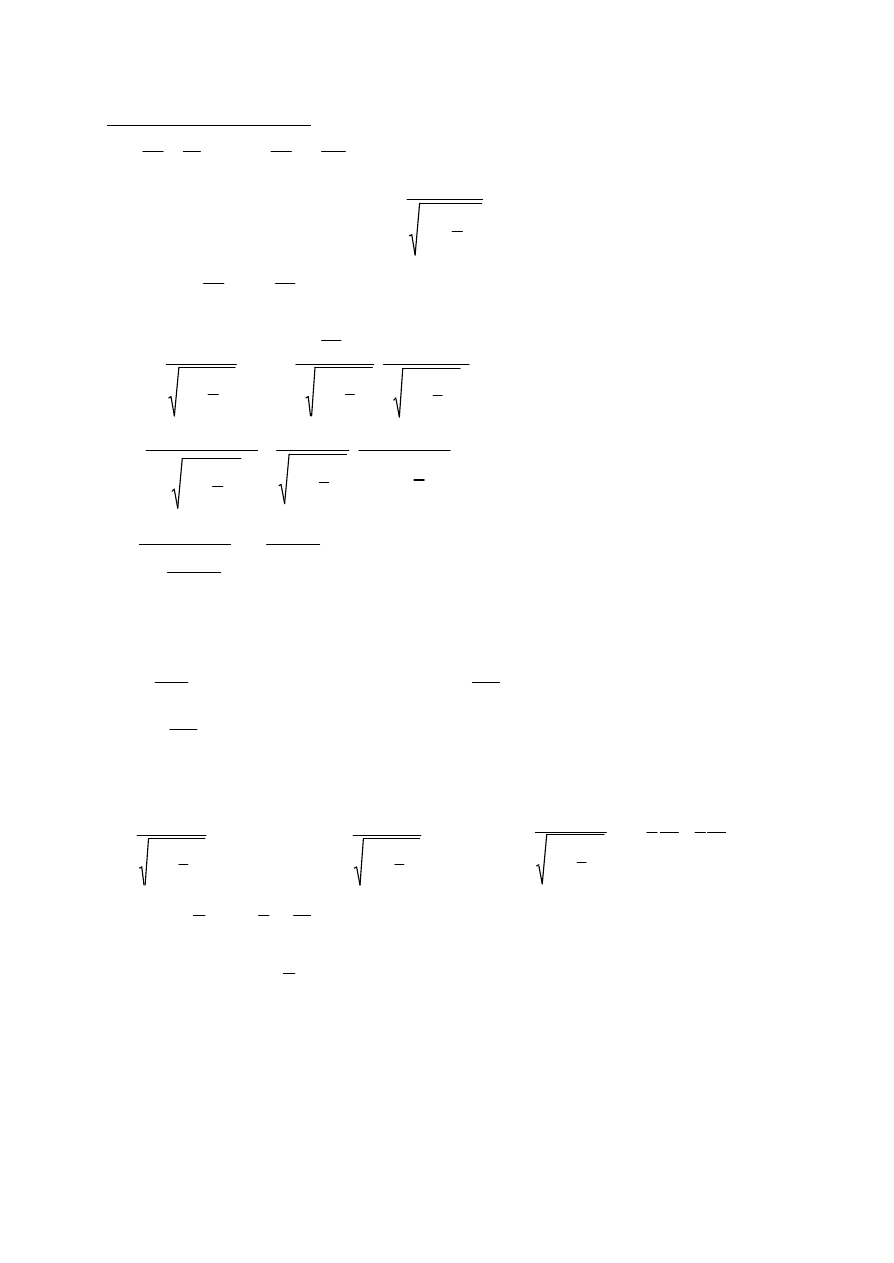
4
Równowaznosc masy i energii
( )
dt
dm
v
dt
v
d
m
v
m
dt
d
dt
p
d
F
r
r
r
r
r
+
=
=
=
m = m(t),
m = m(v)
i
2
0
1
−
=
c
v
m
m
dm
v
v
d
v
m
v
dm
v
v
v
d
m
dt
s
d
dm
v
dt
s
d
v
md
s
d
F
⋅
+
⋅
=
⋅
⋅
+
⋅
⋅
=
+
=
⋅
2
r
r
r
r
r
r
r
r
r
r
r
r
=
−
⋅
−
−
−
=
−
=
2
2
2
0
2
0
1
1
1
2
2
1
c
v
c
v
v
d
c
v
m
c
v
m
d
dm
r
r
=
−
⋅
⋅
−
=
−
⋅
=
2
2
2
0
3
2
2
0
1
1
1
c
v
c
v
d
v
c
v
m
c
v
c
v
d
v
m
r
r
r
r
2
2
2
2
2
2
v
c
v
d
v
m
c
v
c
c
v
d
v
m
−
⋅
=
−
⋅
=
r
r
r
r
(
)
dm
v
c
v
d
v
m
2
2
−
=
⋅
r
r
( )
2
2
2
2
2
)
(
mc
d
dm
c
dm
v
dm
v
c
s
d
F
=
=
+
−
=
r
r
ds
dE
F
p
−
=
E
p
= U,
ds
dU
F
−
=
0
)
(
)
(
)
(
2
2
2
=
+
=
−
=
−
=
dU
mc
d
i
mc
d
dU
mc
d
ds
ds
dU
Fds
const
U
mc
E
=
+
=
2
v
≠
0
R
E
c
v
c
m
gdzie
const
U
c
v
c
m
E
=
−
=
+
−
=
2
2
0
2
2
0
1
1
....
8
3
2
1
1
1
1
4
4
2
2
2
+
+
+
=
−
c
v
c
v
c
v
const
U
c
v
m
v
m
c
m
E
=
+
+
+
+
=
..
8
3
2
1
2
4
0
2
0
2
0
E = mc
2
gdy v?0 oraz U=0
U
c
m
E
+
=
2
0
gdy
v=0
gdy v<<c
U
v
m
c
m
E
+
+
=
2
0
2
0
2
1
5
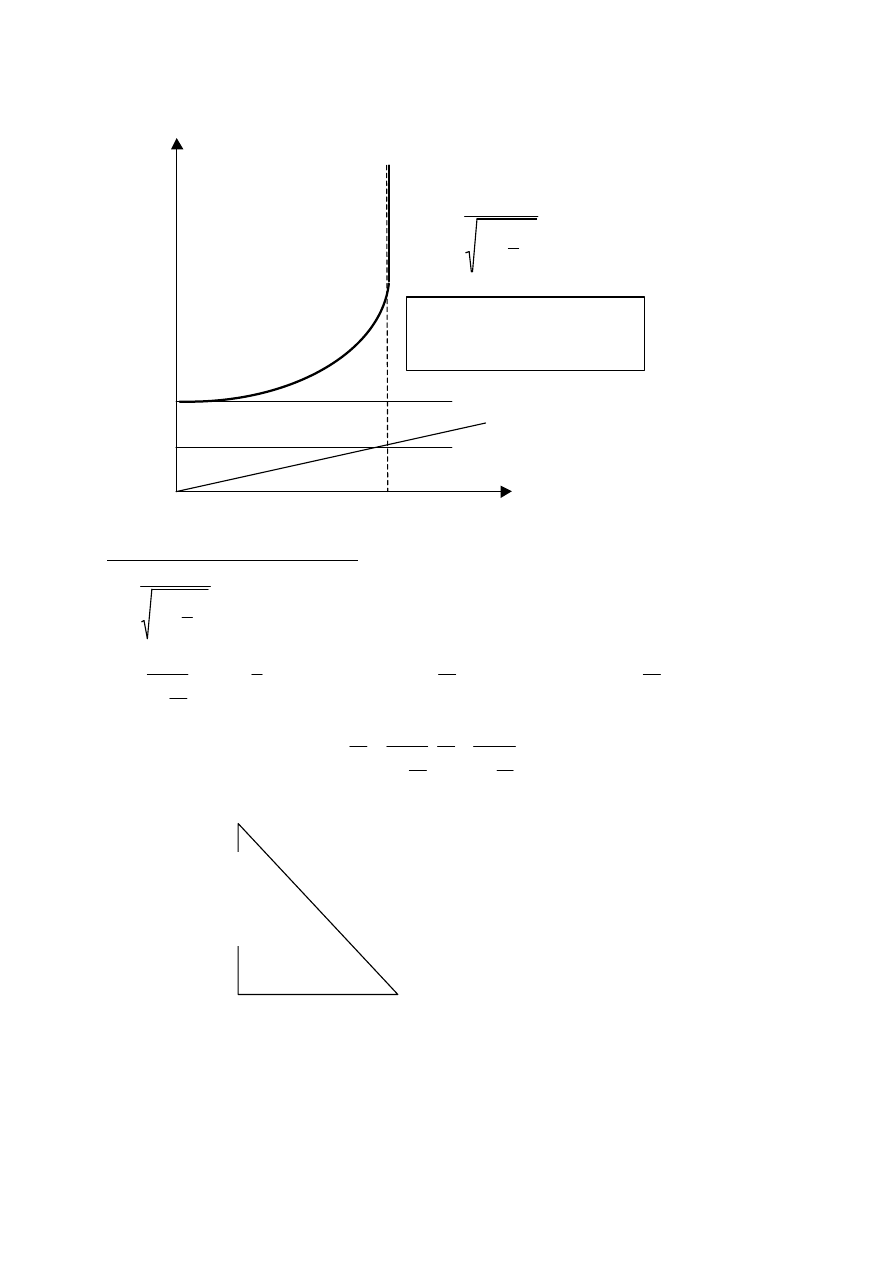
Energia i ped czastki relatywistycznej
2
2
2
2
2
2
2
0
2
2
2
2
4
2
0
2
2
2
2
2
4
2
0
2
2
2
2
4
2
0
2
4
2
0
2
2
2
2
4
2
0
2
2
2
2
4
2
0
2
2
2
0
1
1
1
1
1
c
p
c
c
v
v
m
c
v
c
v
c
m
c
v
E
bo
c
p
c
m
E
c
v
E
c
m
E
c
m
c
v
E
E
c
m
E
c
v
c
v
c
m
E
c
v
c
m
E
=
⋅
−
=
⋅
−
=
+
=
+
=
⇒
=
−
⇒
=
−
⇒
−
=
−
=
E
(energia
calkowita)
m
0
c
2
(energia
spoczynkowa)
m
0
c
2
½ m
0
c
2
E
k
= ½mv
2
v/c
1,0
E
2
2
0
1
−
=
c
v
c
m
E
R
E
R
– opisuje relatywistyczna
postac energii calkowitej bez
pola sil potencjalnych (U=0).
pc (energia kinetyczna)
Wyszukiwarka
Podobne podstrony:
04 kin dyn relatywistyczna w
DYN cz 2 aktualizacja 04 X
DYN cz 2 aktualizacja 04 X(1)
W4 Kin chemI 5 04 16
W5 Kin chemII 12 04 16
Wykład 04
04 22 PAROTITE EPIDEMICA
04 Zabezpieczenia silnikówid 5252 ppt
Wyklad 04
Wyklad 04 2014 2015
04 WdK
od relatywizmu do prawdy
MECHANIKA II DYN
04) Kod genetyczny i białka (wykład 4)
2009 04 08 POZ 06id 26791 ppt
2Ca 29 04 2015 WYCENA GARAŻU W KOSZTOWEJ
04 LOG M Informatyzacja log
więcej podobnych podstron