Metody statystyczne

w

pomocy społecznej

Dr Alicja Maksimowicz-Ajchel

MIARY POŁOŻENIA

(przeciętnego poziomu)

Klasyczne

Pozycyjne

- Średnia

- Dominanta D(x)

arytmetyczna

x

- Mediana M(x)

- pozostałe kwantyle Q

b/v

(x)

MIARY DYSPERSJI

(ZRÓŻNICOWANIA)

Klasyczne

Pozycyjne

- Wariancja S

2

(x)

- Odchylenie ćwiartkowe Q(x)

- Odchylenie

- Pozycyjny współczynnik

standardowe S(x)

zmienności V

p

(x)

- Klasyczny współczynnik

zmienności V(x)

MIARY ASYMETRII

Klasyczne

Pozycyjne

- Klasyczny

- Współczynnik skośności A

s

(x)

współczynnik

-Pozycyjny współczynnik

asymetrii A(x)

asymetrii A

p

(x)

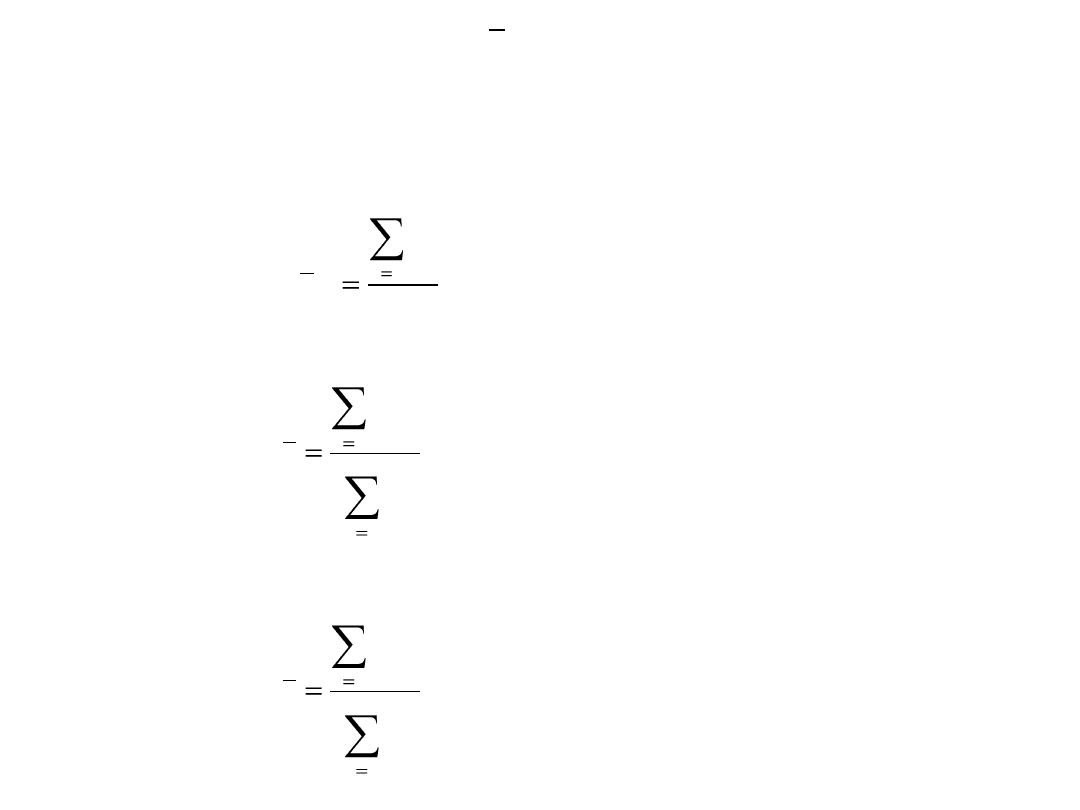
n

x

x

n

i

i

N

1

k

i

i

k

i

i

i

v

v

x

x

1

1

k

i

i

k

i

i

i

v

v

x

x

1

1



Średnia arytmetyczna –

-

ogólna suma wartości

podzielona przez liczbę wartości (liczebność zbiorowości)

a/ szereg szczegółowy

b/ szereg rozdzielczy punktowy

c/ szereg rozdzielczy przedziałowy

x

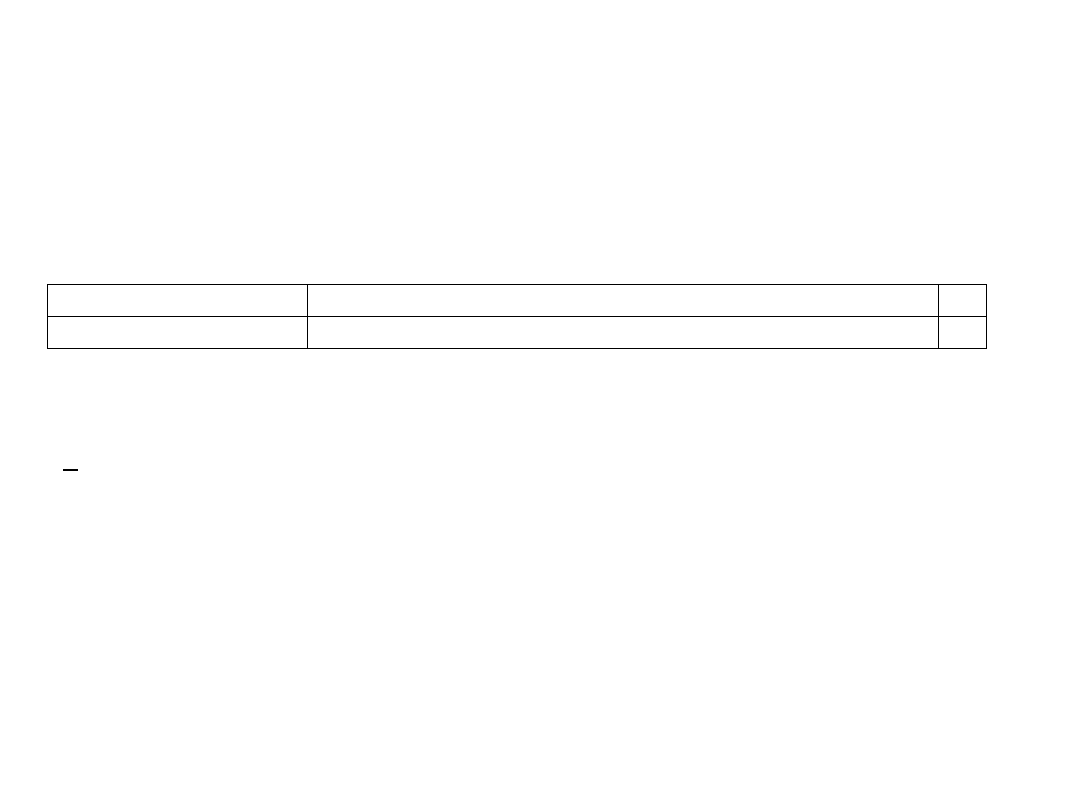
a/ szereg szczegółowy (średnia nieważona)

20 rodzin zbadano ze względu na liczbę posiadanych dzieci.
Rozkład cechy przedstawia szereg szczegółowy:

Numer jednostki (i)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

Σ

Liczba dzieci (x

i

)

1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 3 3 4 5

40

n=20 - liczba jednostek w zbiorowości
Σ x

i

=40 - ogólna suma wartości; jest to łączna liczba dzieci w 20 rodzinach.

N

x

= 40/20=2- średnia wartość cechy

Średnia liczba dzieci w badanej zbiorowości rodzin wynosi 2 (przeciętnie na 1
rodzinę przypada 2 dzieci).

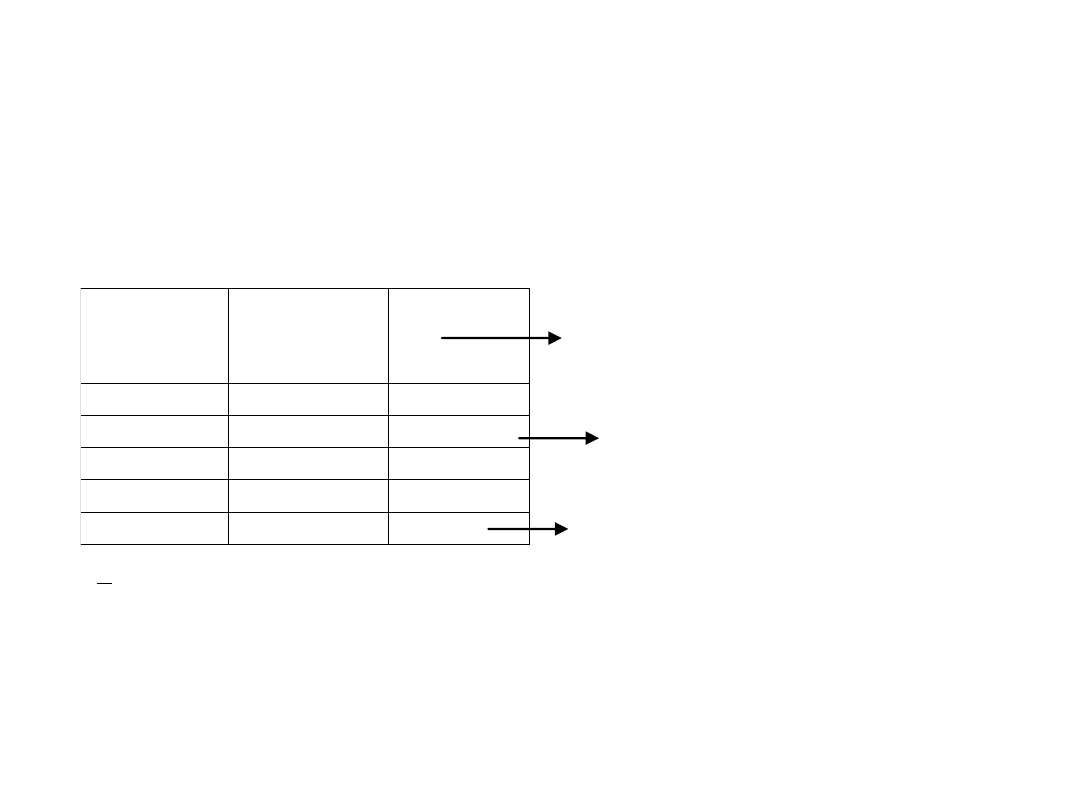
b/ szereg rozdzielczy punktowy (średnia ważona)

n= 20 rodzin.
x- liczba dzieci w rodzinie

Liczba

dzieci

x

i

Liczba

rodzin.

n

i

x

i

n

i

cząstkowe sumy wartości

1

5

1 · 5= 5

2

11

2 · 11= 22 łączna liczba dzieci w rodzinach z

3

3

3 · 3=9

dwojgiem dzieci (cząstkowa suma wartości)

4

1

4 · 1=4

Suma

20

40

łączna liczba dzieci w 20 rodzinach

x

=40/20=2

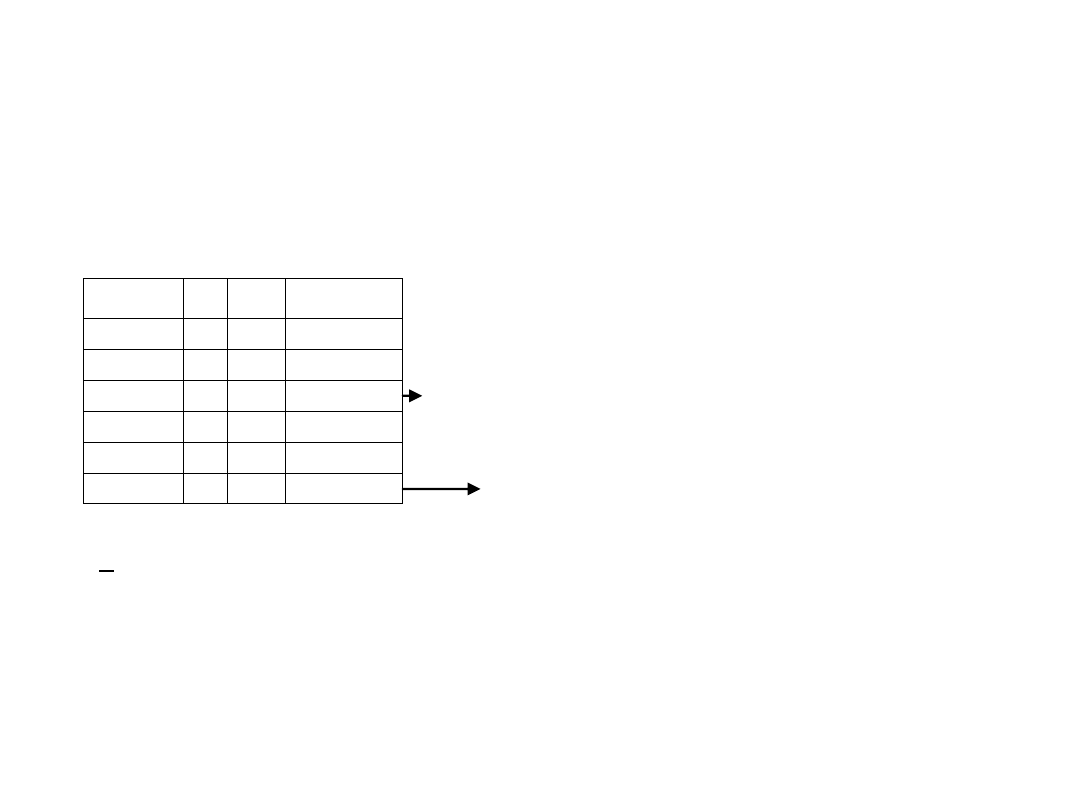
c/ szereg rozdzielczy przedziałowy

(średnia ważona)

n=25 gospodarstw 2-osobowych
x- miesięczny dochód gospodarstwa (tys.zł)

X

0i

-x

1i

n

i

i

x

i

i

n

x

0,5- 1,5

2 1

1 · 2= 2

1,5- 2,5

5 2

2 · 5= 10 łączny dochód 10 gospodarstw o miesięcznych

2,5-3,5 10 3

3 · 10=30 dochodach z przedziału od 2,5 do 3,5 tys.zł

3,5-4,5

6 4

4 · 6=24 (oszacowana cząstkowa suma wartości)

4,5-5,5

2 5

5 · 2= 10

Suma

25 X

76

łączny dochód 25 gospodarstw

(oszacowana ogólna suma wartości)

x

=

76/25=3,04 Średni dochód gospodarstwa 2-osobowego 3,04 tys. zł

Dominanta (moda, wartość najczęściej występująca)

Warunki stosowania dominanty:

- cecha mierzalna i niemierzalna

- szereg rozdzielczy (nie wyznaczamy dla danych

nie pogrupowanych)

- rozkład typowy

- równe rozpiętości przedziału dominanty i
dwóch sąsiadujących

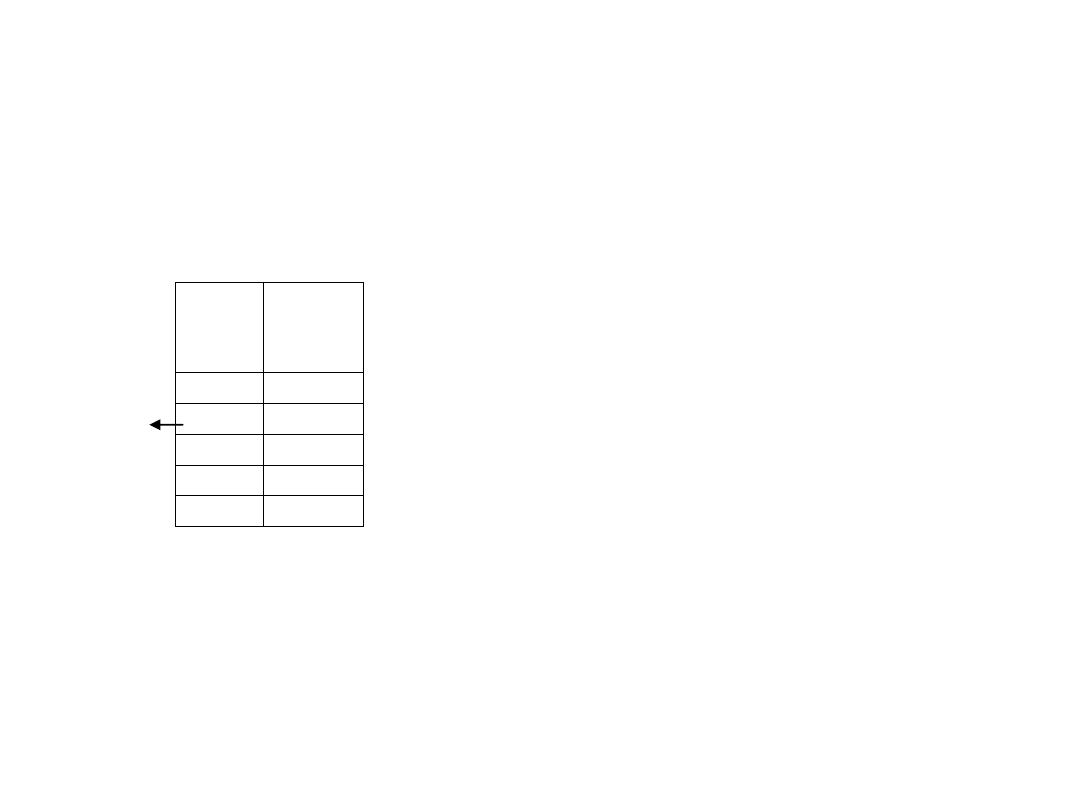
Sposoby wyznaczania dominanty:

a/ szereg rozdzielczy punktowy

D(x)= x

i (ni=max)

Liczba

dzieci

x

i

Liczba

rodzin

n

i

1

5

D(x)

2

11

największa liczebność

3

3

4

1

Suma

20

D(x)=2 dominanta, wartość najczęściej występująca

Najwięcej rodzin miało 2 dzieci

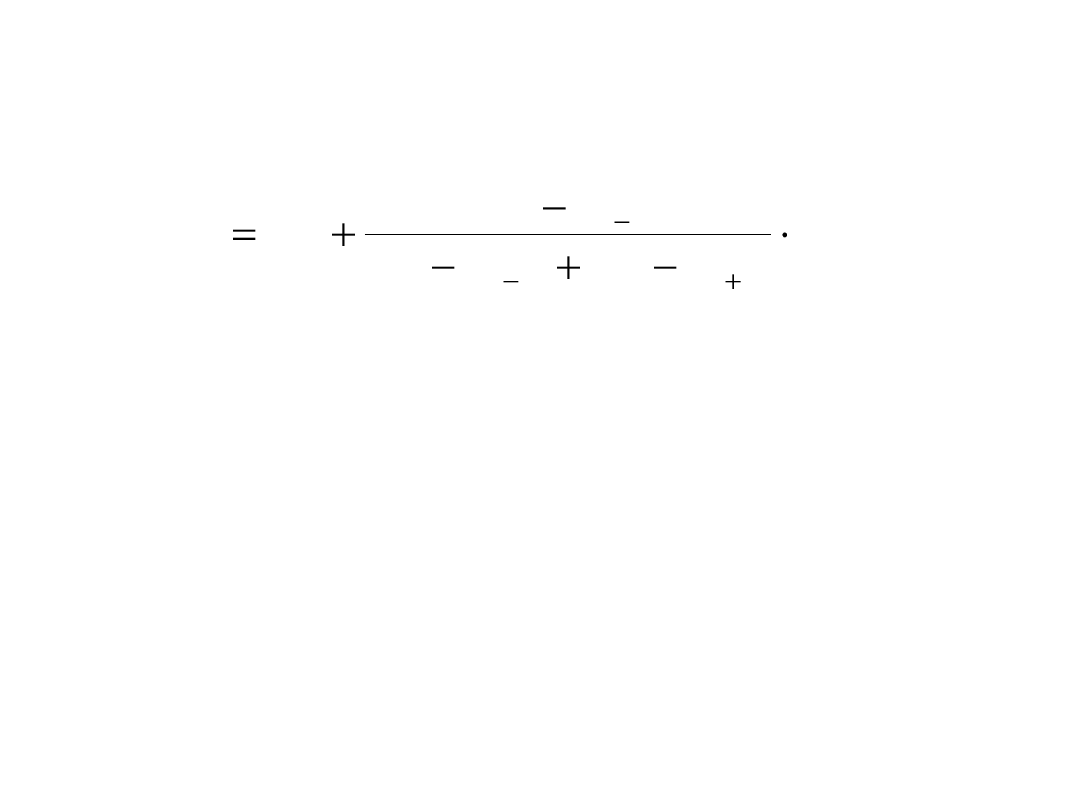
b/ szereg rozdzielczy przedziałowy

d

d

d

d

d

d

d

d

h

n

n

n

n

n

n

x

x

D

)

(

)

(

)

(

1

1

1

0

gdzie:
x

0d

- dolna granica przedziału dominanty

n

d

- liczebność przedziału dominanty

n

d-1

- liczebność przedziału poprzedzającego

dominantę
n

d+1

- liczebność przedziału następnego po przedziale

dominanty
h

d

- rozpiętość przedziału dominanty

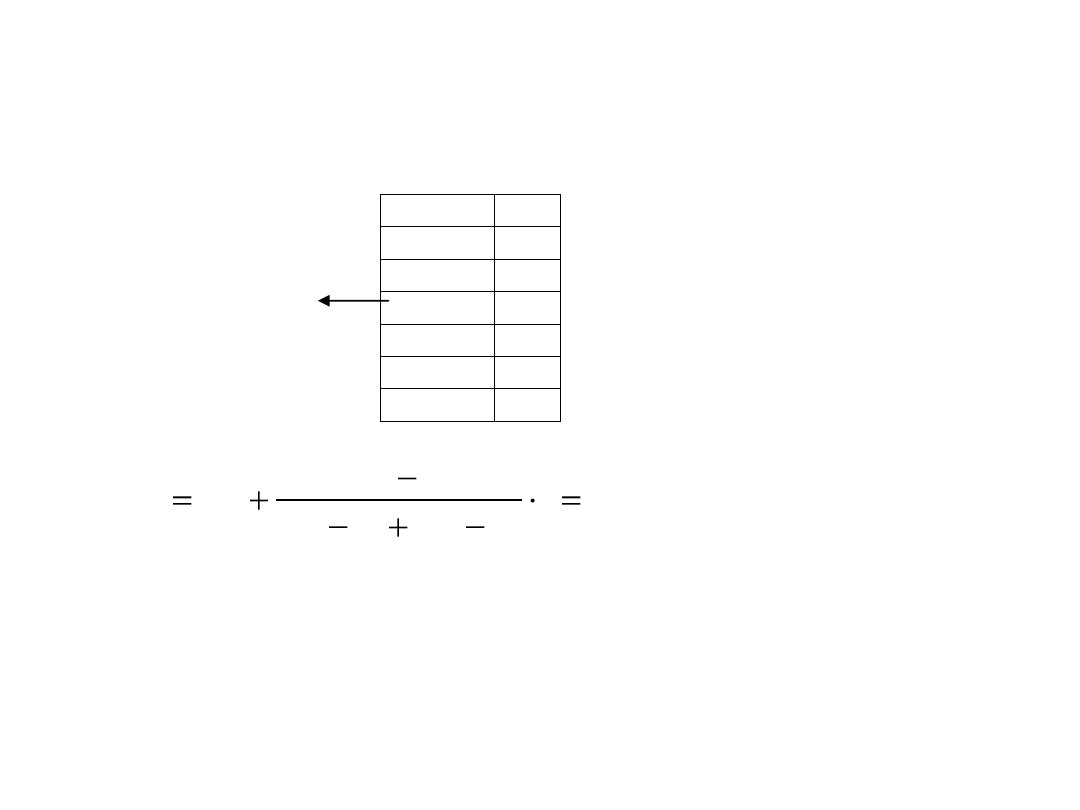
n=25 gospodarstw 2-osobowych
x- miesięczny dochód gospodarstwa (tys.zł)

x

0i

-x

1i

n

i

0,5- 1,5

2

1,5- 2,5

5

przedział dominanty

2,5-3,5

10 największa liczebność

3,5-4,5

6

4,5-5,5

2

Suma

25

056

,

3

1

)

6

10

(

)

5

10

(

5

10

5

,

2

)

(x

D

Najwięcej badanych gospodarstw 2-osobowych miało miesięczny dochód
około 3,056 tys.zł.

Mediana – wartość środkowa

Sposoby wyznaczania:

a/ szereg szczegółowy

* Jeśli liczebność zbiorowości statystycznej jest
nieparzysta
- określamy numer jednostki środkowej (inaczej
pozycję mediany) - (n+1)/2
- wskazujemy wartość mediany - jest to wartość cechy
dla jednostki środkowej

2

1

)

(

n

x

x

M

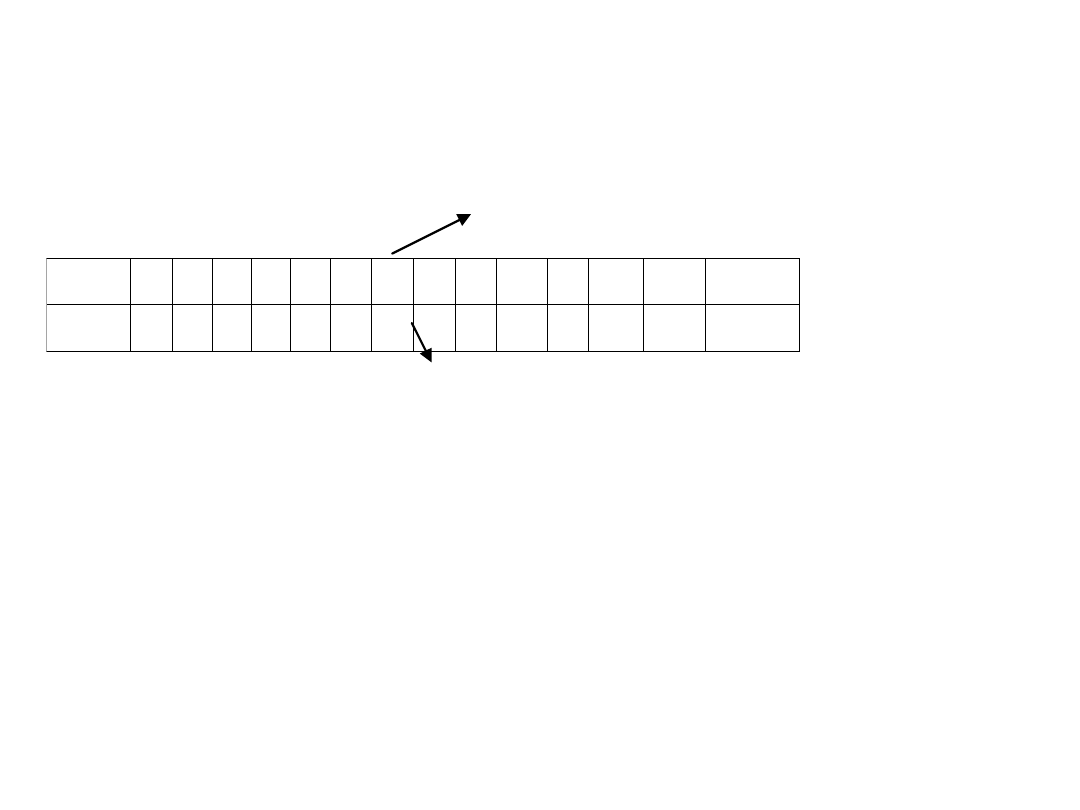
n=13 ośrodków pomocy społecznej x- miesięczne wydatki (tys.zł)

numer jednostki środkowej (13+1)/2=7

lp.(i)

1 2 3 4 5 6 7 8 9 10 11 12 13

Suma

x

i

5 7 8 8 9 10 12 16 16 17 20 24 25

177

mediana (wartość wydatków środkowej jednostki)

M(x)=12

Połowa badanych ośrodków ma wydatki nie większe niż 12 tys. zł, a połowa 12 tys. zł i więcej.

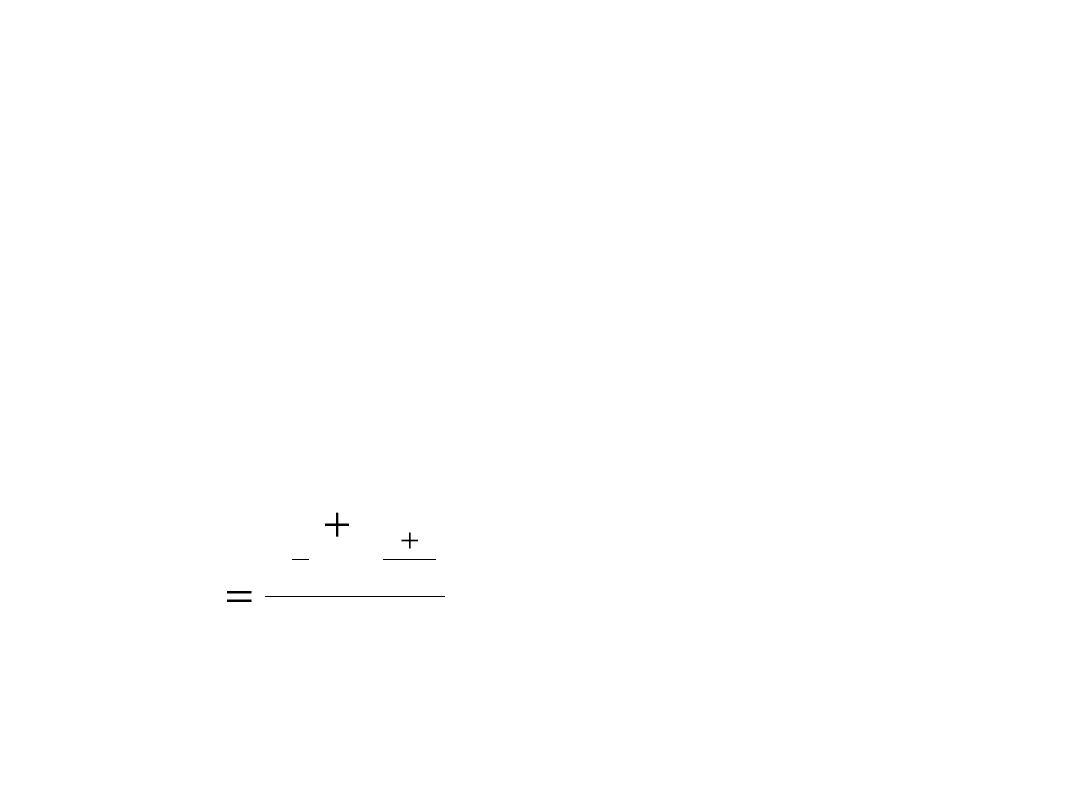
* Jeśli liczebność zbiorowości statystycznej jest
parzysta
- określamy numery dwóch jednostek środkowych:
n/2 oraz (n+2)/2

- dla cech skokowych wskazujemy dwie
wartości

- dla cech ciągłych wyznaczamy wartość

mediany jako średnią z wartości
przyjmowanych przez jednostki środkowe.

2

)

(

2

2

2

n

n

x

x

x

M

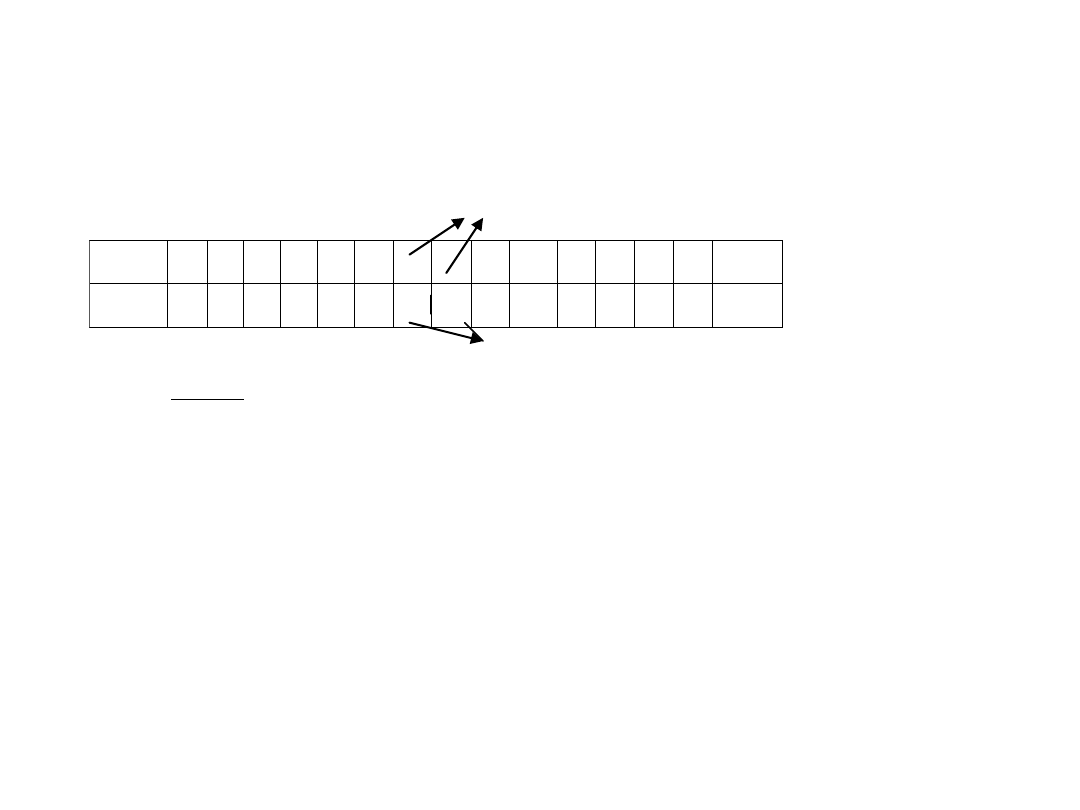
n=14 firm handlowych

x- miesięczna sprzedaż (mln.zł)

numery jednostek środkowych 14/2=7oraz (14+2)/2=8

lp.(i)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 Suma

x

i

5 7 8 8 9 10 12 16 16 17 20 24 25 26 203

wartości sprzedaży dla środkowych firm

M(x)=12+16 =14

2

Połowa badanych firm ma sprzedaż nie większą niż 14 mln. zł, a połowa 14

mln. zł i więcej.

b/ szereg rozdzielczy punktowy

- określamy pozycję mediany i wyznaczamy jej wartość tak
jak w szeregu szczegółowym.
Jednostek środkowych szukamy wykorzystując liczebności
skumulowane.

n=40 firm usługowych x– dzienna liczba zleceń

x

i

n

i

n

i

sk

n/2=40/2=20

1

4

4

(n+2)/2 = 42/2=21 numery jednostek środkowych

2

10

14

Mediana M(x)=3

3

20

34

liczebność skumulowana po raz pierwszy

4

4

38

przekroczyła 20 i 21 - numery jednostek środkowych

5

2

40

Σ

30

X

Mediana rozkładu dziennej liczby zleceń jest równa 3 co oznacza, że

przynajmniej połowa firm miała co najwyżej 3 zlecenia w ciągu dnia i

przynajmniej połowa miała 3 zlecenia lub więcej.

c/ szereg przedziałowy

- określamy numer jednostki środkowej - n/2 (pozycję
mediany)
- wskazujemy przedział mediany - jest to przedział, dla
którego liczebność skumulowana osiąga lub po raz
pierwszy lub przekracza numer jednostki środkowej
(pozycję mediany)
- wyznaczamy wartość mediany z następującego wzoru
interpolacyjnego

:

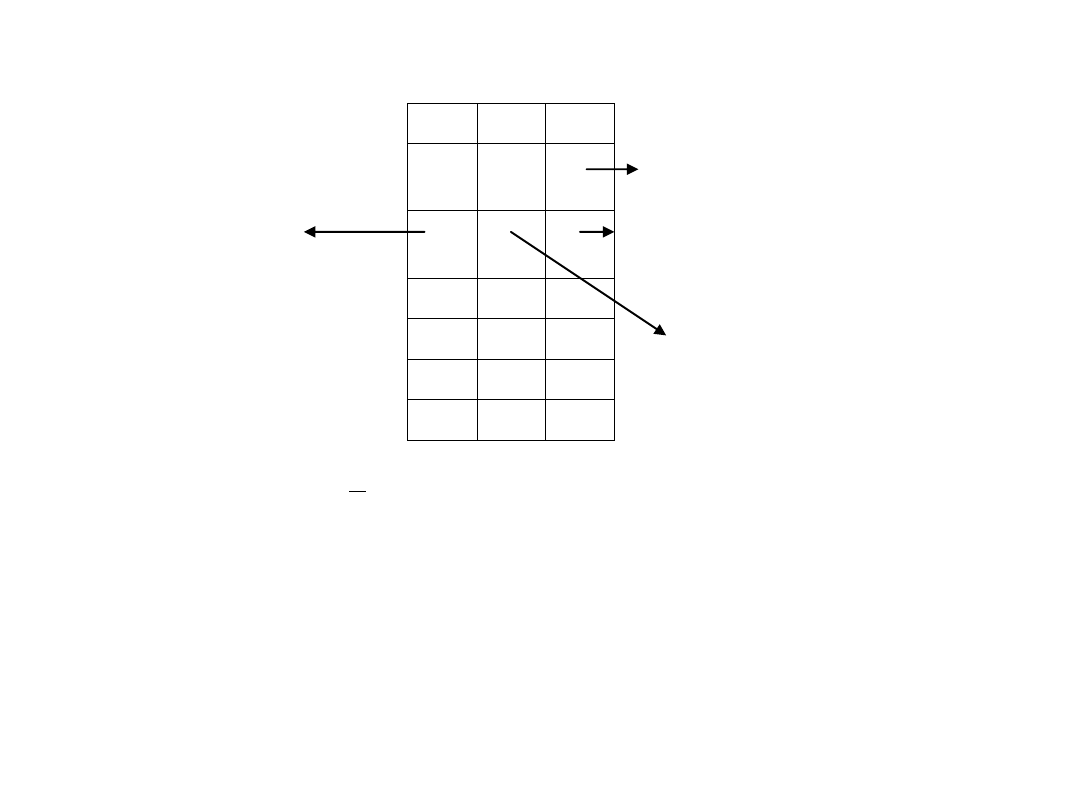
m

m

sk

m

m

n

h

n

n

x

x

M

1

0

2

1

)

(

gdzie:

m

x

0

- dolna granica przedziału mediany

sk

m

n

1

- liczebność skumulowana dla przedziału

poprzedzającego przedział mediany

m

h

- rozpiętość przedziału mediany

n=104 gospodarstwa domowe x- miesięczny dochód (tys.zł)

x

0i

-x

1i

ni

ni

sk

0- 2

45

45

suma liczebności przedziałów

poprzedzających przedział mediany

przedział mediany

x

0m

=2 dolna granica przedziału

2- 4

34

79

liczebności skum. po raz pierwszy przekroczyły

104/2=52

h

m

=2 rozpiętość przedziału

4- 6

15

94

6- 8

9

103

liczebność przedziału mediany n

m

=34

8-10

1

104

Suma

104

M(x)= 2+(1/2∙104 -45) 2 = 2,41

34

Mediana rozkładu dochodów wynosi 2,41, co oznacz, że połowa gospodarstw

(50%) ma dochody nie przekraczające 2,41 tys.zł, a połowa (50%) ma dochody

2,41 tys.zł i więcej.

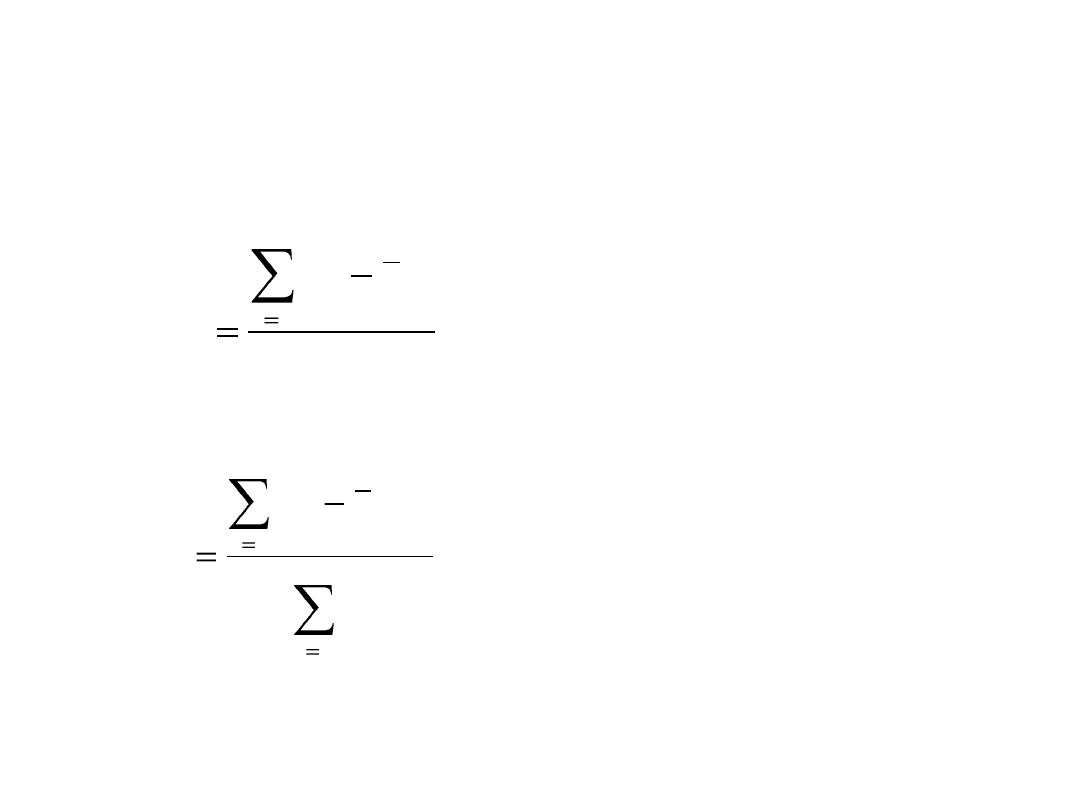
MIARY DYSPERSJI

Wariancja
a/ szereg szczegółowy - wariancja nieważona

n

x

x

x

S

n

i

i

N

1

2

2

)

(

)

(

b/ szereg rozdzielczy- wariancja ważona

k

i

i

k

i

i

i

v

v

x

x

x

S

1

1

2

2

)

(

)

(

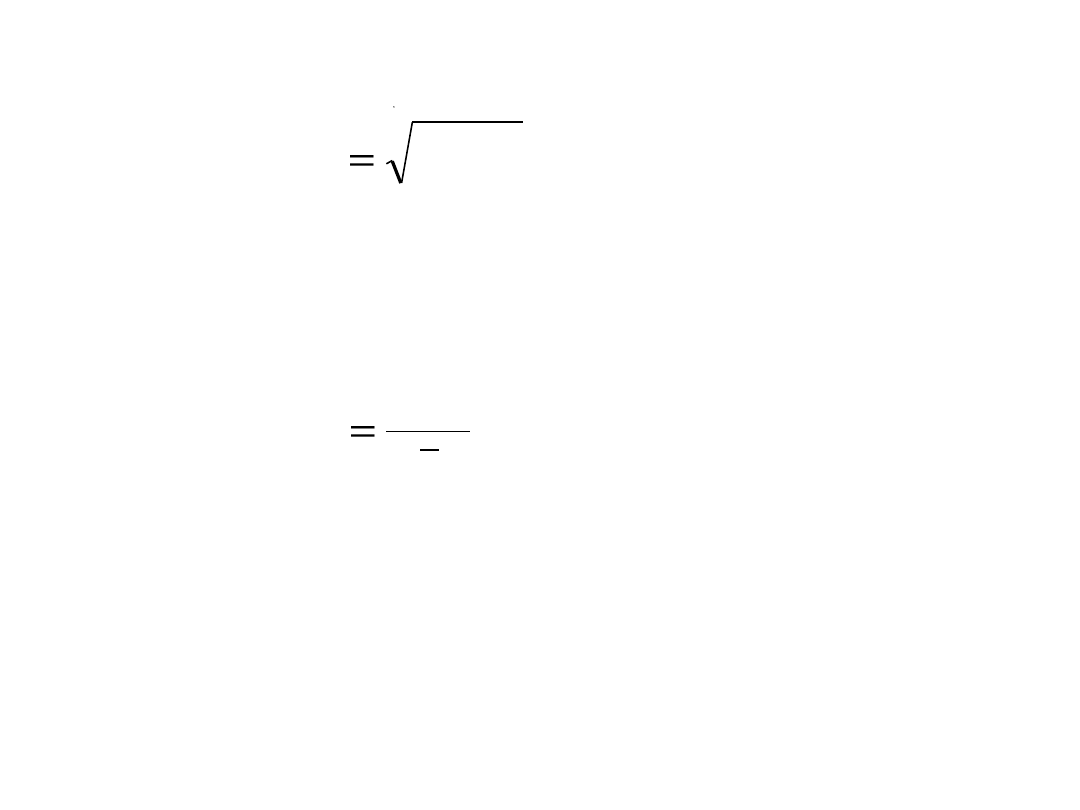
Odchylenie standardowe (miara absolutna)

)

(

)

(

2

x

S

x

S

Interpretacja: przeciętne odchylenie wartości cechy od średniej
arytmetycznej

Klasyczny współczynnik zmienności (miara
stosunkowa)

x

x

S

x

V

)

(

)

(

Ocena siły dyspersji (skala trójstopniowa):
0,0-0,30 słaba dyspersja
0,31-0,60 umiarkowana
powyżej 0,60 silna

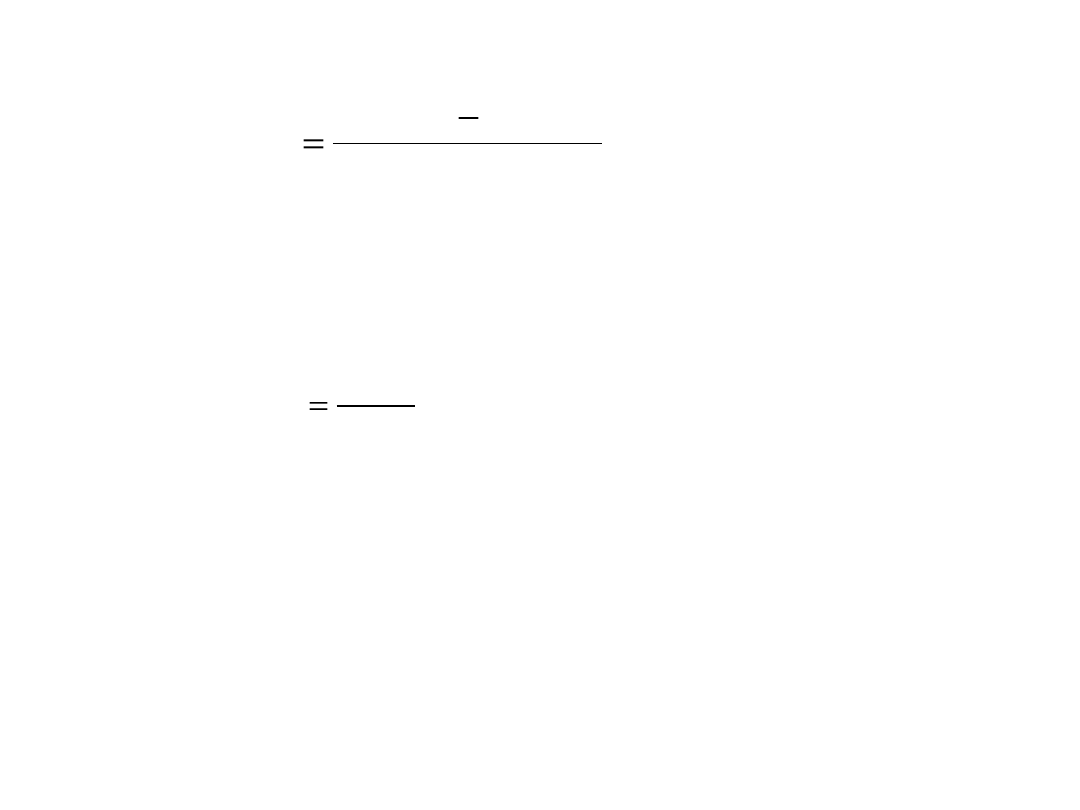
Odchylenie ćwiartkowe (miara absolutna)

2

)

(

)

(

)

(

4

/

1

4

/

3

x

Q

x

Q

x

Q

Interpretacja: średnia rozpiętość cechy w dwóch
środkowych ćwiartkach rozkładu.

Pozycyjny współczynnik zmienności (miara
stosunkowa)

)

(

)

(

)

(

x

M

x

Q

x

V

p

Ocena siły dyspersji w dwóch środkowych
ćwiartkach rozkładu (skala trójstopniowa):
0,0-0,30 słaba dyspersja
0,31-0,60 umiarkowana
powyżej 0,60 silna

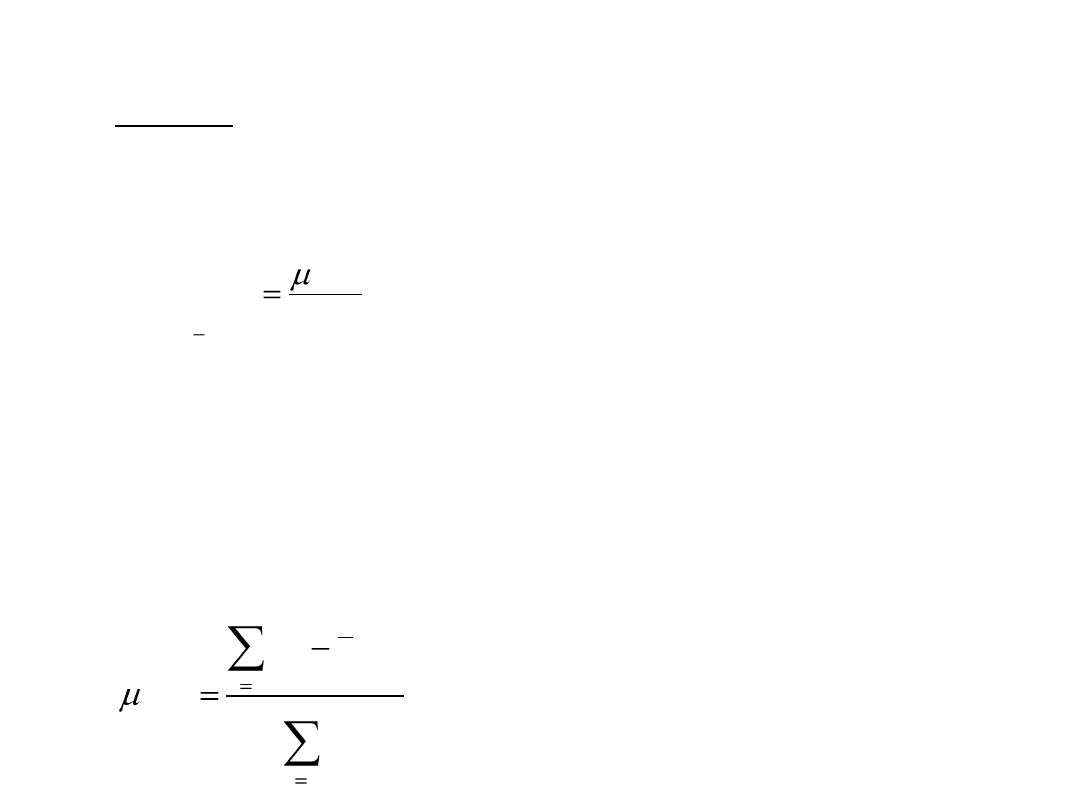
III. MIARY ASYMETRII

klasyczne

1. Klasyczny współczynnik asymetrii (miara

stosunkowa)

)

(

)

(

3

3

)

2

,

2

(

)

(

x

S

x

x

A

Ocena siły asymetrii (skala trójstopniowa):
0,0-0,7 słaba asymetria
0,71-1,4 umiarkowana asymetria
1,41-2,0 silna asymetria

gdzie: μ

3

(x) – trzeci moment centralny

k

i

i

k

i

i

i

v

v

x

x

x

1

1

3

3

)

(

)

(

pozycyjne

2. Współczynnik skośności (miara stosunkowa)

)

(

)

(

)

(

1

,

1

x

S

x

D

x

s

x

A

Ocena siły asymetrii (skala trójstopniowa):

0,0-0,3 słaba asymetria
0,3-0,6 umiarkowana
0,6-1,0 silna

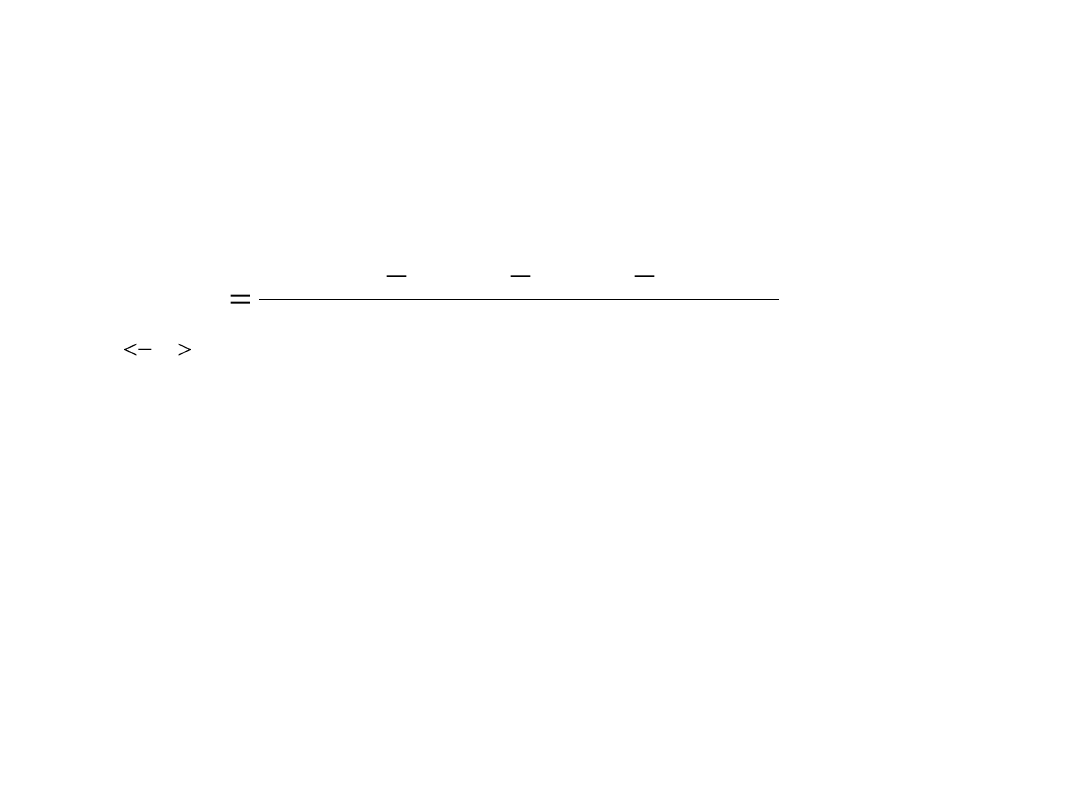
3. Pozycyjny współczynnik asymetrii (miara

stosunkowa)

)

(

2

)]

(

)

(

[

)]

(

)

(

[

4

/

1

4

/

3

1

,

1

)

(

x

Q

x

Q

x

M

x

M

x

Q

p

x

A

Ocena siły asymetrii (skala trójstopniowa):

0,0-0,3 słaba asymetria
0,3-0,6 umiarkowana
0,6-1,0 silna

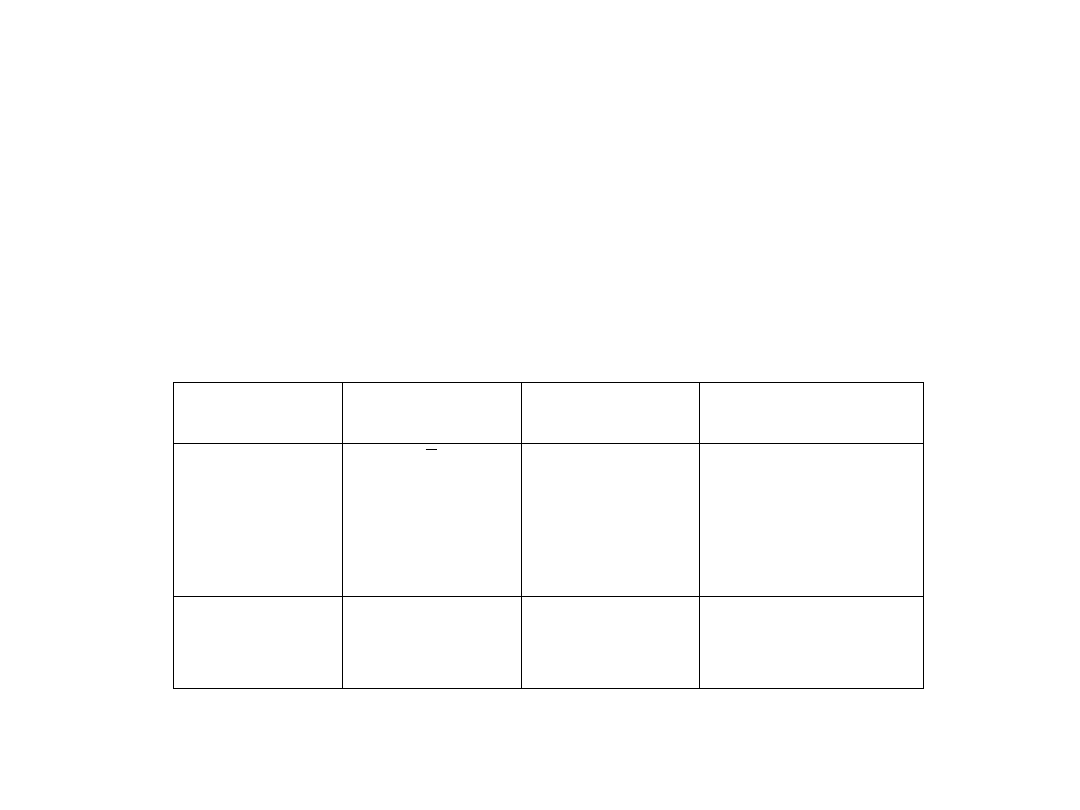
Miary stosowane do opisu rozkładów jednowymiarowych:

Typ rozkładu

Położenie

Dyspersja

Asymetria

Typowy

x

D(x)

M(x)

i inne kwantyle

S

2

(x)

S(x)

V(x)

A(x)

albo

A

s

(x)

Nietypowy

M(x)

i inne kwantyle

V

p

(x)

A

p

(x)

PORÓWNANIA ROZKŁADÓW
JEDNOWYMIAROWYCH

a/ Porównania liczbowe
Zasady porównań:
1/ można porównywać wyłącznie te same miary
2/ dyspersję, asymetrię i koncentrację należy porównywać za pomocą
miar względnych
3/ położenie można porównywać wtedy, gdy rozkłady dotyczą tej
samej cechy

Miary stosowane do porównań rozkładów:
Typ
rozkładów

Położenie

Dyspersja

Asymetria

Wszystkie
typowe

x

D(x)

M(x)

i inne kwantyle

V(x)

A(x)

albo

A

s

(x)

Jeden lub
więcej
nietypowy

M(x)

i inne kwantyle

V

p

(x)

A

p

(x)

Porównania graficzne –

wykres pudełkowy (ramkowy, skrzynkowy,
"pudełko z wąsami")

x

min

Q

1/4

M(x)

Q

3/4

x

max

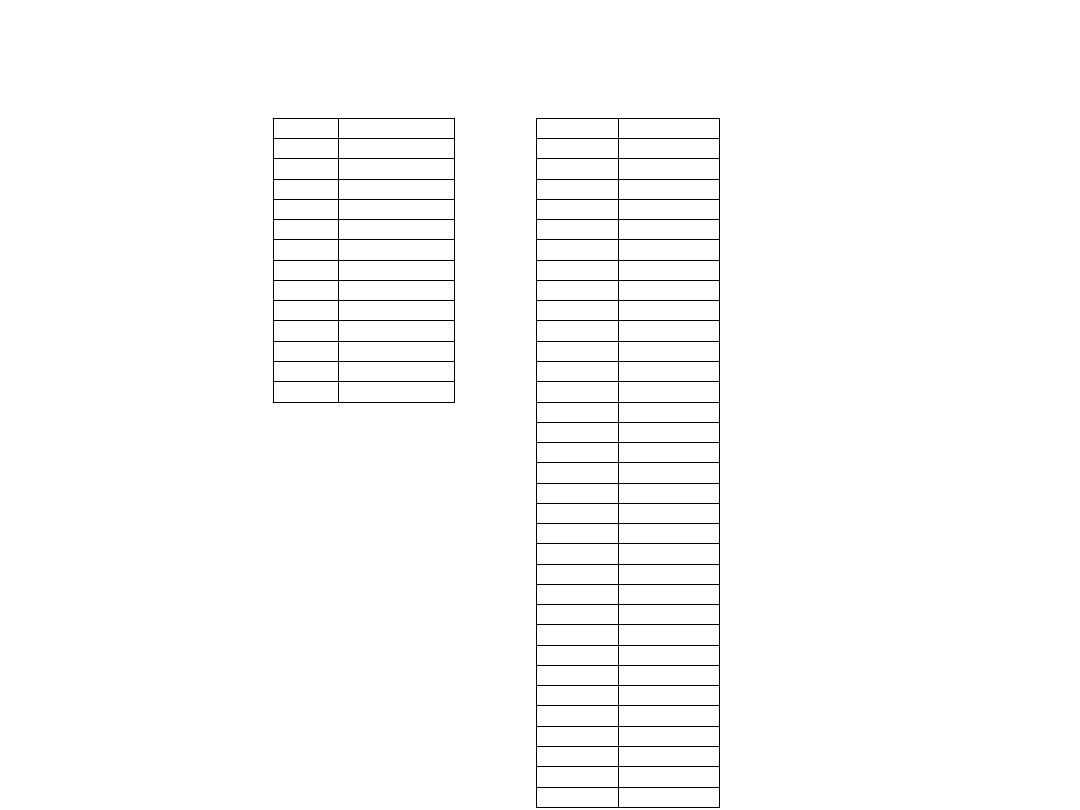
Przykład

Szeregi szczegółowe prezentują rozkład stażu pracy wśród studentów MBA

pewnej uczelni, zatrudnionych na stanowiskach kierowniczych i niekierowniczych

Stanowiska

Stanowiska

niekierownicze

kierownicze

lp. Staż (lata)

lp. Staż (lata)

1

0

1

0

2

3

2

4

3

3

3

4

4

3

4

4

5

4

5

6

6

4

6

7

7

6

7

7

8

6

8

7

9

9

9

7

10

9

10

8

11

18

11

8

12

20

12

8

Suma

85

13

8

14

8

15

8

16

9

17

9

18

9

19

10

20

10

21

10

22

10

23

10

24

11

25

11

26

13

27

14

28

14

29

15

30

17

31

18

32

18

suma

302

Porównanie rozkładów stażu pracy studentów MBA ztrudnionych na stanowiskach
kierowniczych i niekierowniczych

a/ porównanie liczbowe

(wydruk z Excela -

Narzędzia - analiza danych - statystyka opisowa)

stanowisko kierownicze

stanowisko niekierownicze

Średnia

9,4375

Średnia

7,083333

Błąd standardowy

0,725316

Błąd standardowy

1,772938

Mediana

9

Mediana

5

Tryb

8

Tryb

3

Odchylenie standardowe

4,103

Odchylenie
standardowe

6,142

Wariancja próbki

16,835

Wariancja próbki

37,720

Kurtoza

0,400

Kurtoza

1,017

Skośność

0,331

Skośność

1,342

Zakres

18

Zakres

20

Minimum

0

Minimum

0

Maksimum

18

Maksimum

20

Suma

302

Suma

85

Licznik

32

Licznik

12

Poziom ufności(95,0%)

1,479293

Poziom ufności(95,0%) 3,902212

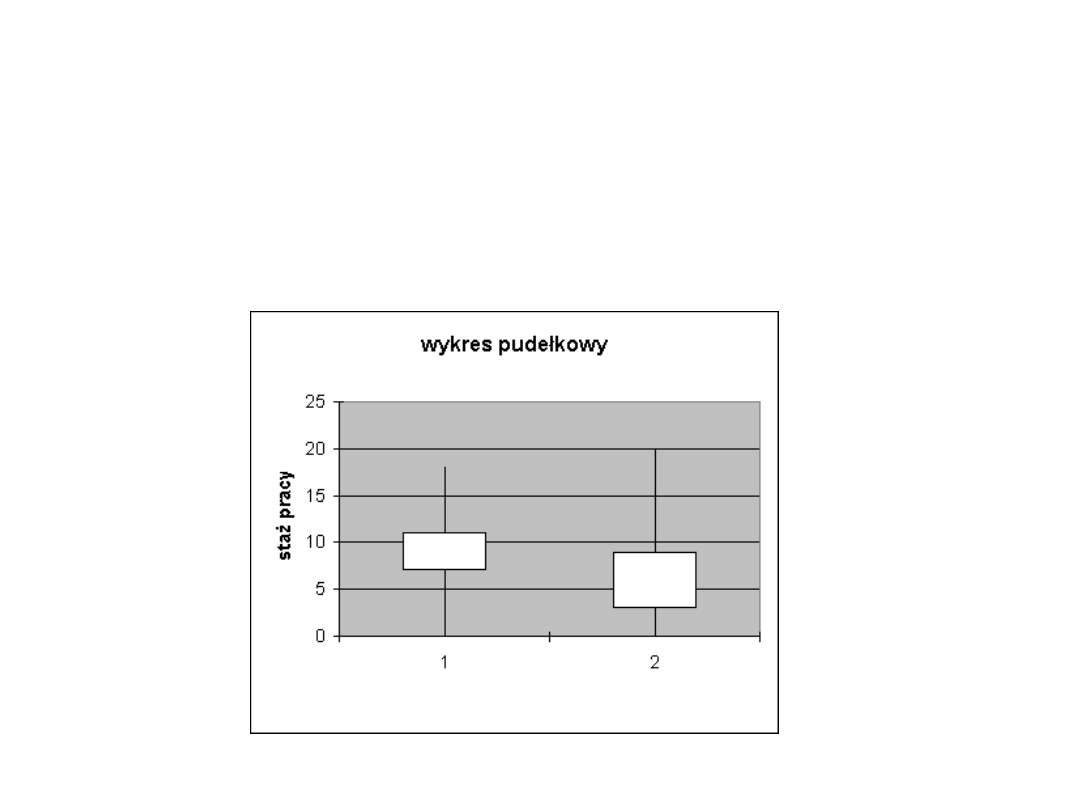
b/ porównanie graficzne
(wykresy pudełkowe - wydruk z Excela - kreator wykresów - wykres giełdowy)

kierownicze-1 niekierownicze-2

kwartyl pierwszy

7

3

minimum

0

0

maksimum

18

20

kwartyl trzeci

11

9