dr Agnieszka Bobrowska

1

Ekonomia matematyczna II

Wykład 2

2. Modele równowagi krótkookresowej

Modele opisuj

ą

warunki, mo

ż

liwo

ś

ci i zwi

ą

zki mi

ę

dzy kategoriami makroekonomicznymi

charakteryzuj

ą

ce gospodark

ę

pozostaj

ą

c

ą

w równowadze w krótkim okresie.

Produkcja oraz wynikaj

ą

cy z jej skali dochód narodowy zmieniaj

ą

si

ę

na skutek oddziaływania

wielu czynników:

- w długim okresie wielko

ść

i struktura produkcji zdeterminowane s

ą

przez zmiany mo

ż

liwo

ś

ci

wytwórczych gospodarki wynikaj

ą

cych ze zmian w zasobach kapitału i siły roboczej.

- w krótkim czasie czynniki te stanowi

ą

swego rodzaju barier

ę

, a ich zmiana wymaga

niejednokrotnie wielu lat.

Rozbudowa b

ą

d

ź

zmiana struktury zdolno

ś

ci produkcyjnych wymaga inwestycji, trwaj

ą

cych

czasami kilkana

ś

cie lub kilkadziesi

ą

t lat. We współczesnej gospodarce rynkowej na ogół nie wyst

ę

puje

globalny deficyt siły roboczej, jednak zdarzaj

ą

si

ę

sytuacje niedoboru siły roboczej o okre

ś

lonych

kwalifikacjach lub niedopasowania struktury popytu do struktury poda

ż

y na lokalnych rynkach pracy.

Likwidacja takich dysproporcji wymaga równie

ż

czasu.

Analiza krótkookresowa dotyczy tak krótkiego odcinka czasu,

ż

e mimo przeprowadzonych

inwestycji mo

ż

na pomin

ąć

wynikaj

ą

ce z nich zmiany zasobu kapitału. Zagadnienie akumulacji kapitału

(jego wzrostu lub spadku) rozpatrywane jest wył

ą

cznie jako problem długoterminowy w ramach

równowagi długookresowej. W modelach równowagi krótkookresowej uwzgl

ę

dnia si

ę

głównie zmiany

dochodów, zatrudnienia oraz zmiany wielko

ś

ci inwestycji i oszcz

ę

dno

ś

ci, dotycz

ą

ce ustalonego

okresu.

W krótkim okresie produkcja, a zatem i dochód narodowy, nie mo

ż

e przekroczy

ć

pułapu

wyznaczonego przez istniej

ą

ce w danym momencie zasoby czynników produkcji. Natomiast stopie

ń

wykorzystania zasobów zale

ż

y od rozmiarów zgłoszonego popytu. Oznacza to,

ż

e w planie

krótkookresowym zmiany poziomu produkcji okre

ś

lane s

ą

przez wahania popytu.

W obr

ę

bie teorii makroekonomii problem równowagi krótkookresowej rozwa

ż

a si

ę

w trzech ró

ż

nych

aspektach:

- równowagi rynku pracy,

- równowagi rynku pieni

ęż

nego,

- równowagi rynku produkcji i warunku przepływu (inwestycje = oszcz

ę

dno

ś

ci).

2.1. Dwusektorowy model równowagi krótkookresowej

1

Najprostszym modelem gospodarki rynkowej jest model dwusektorowy, w którym wyst

ę

puj

ą

dwie

grupy podmiotów gospodarczych: gospodarstwa domowe oraz przedsi

ę

biorstwa. Pomija si

ę

w nim

rol

ę

pa

ń

stwa jako podmiotu gospodarczego. Ponadto w modelu tym wyklucza si

ę

jak

ą

kolwiek

wymian

ę

z zagranic

ą

(model gospodarki zamkni

ę

tej).

1

Charakterystyk

ę

modelu przygotowano na podstawie M.Garbicz, E.Golachowski: Elementarne modele

makroekonomiczne, Szkoła Główna Handlowa, Warszawa 1996, rozdział 1.

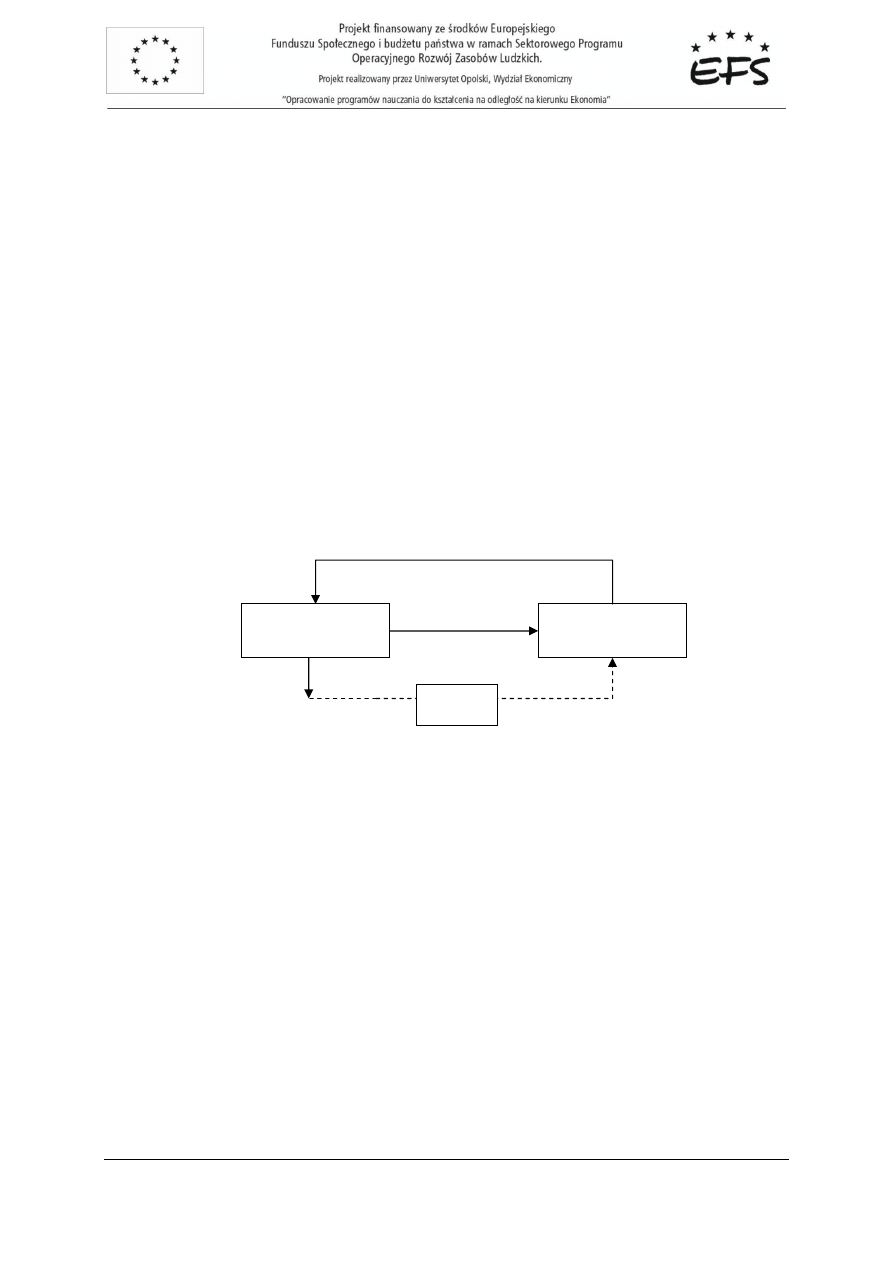
dr Agnieszka Bobrowska

2

Ekonomia matematyczna II

W dwusektorowym modelu równowagi krótkookresowej przyjmujemy,

ż

e wła

ś

cicielami wszystkich

czynników wytwórczych s

ą

gospodarstwa domowe. Przedsi

ę

biorstwa wytwarzaj

ą

towary lub

ś

wiadcz

ą

ró

ż

nego rodzaju usługi. Aby móc produkowa

ć

musz

ą

one naby

ć

od sektora gospodarstw domowych

czynniki produkcji, za które płac

ą

okre

ś

lon

ą

cen

ę

. Dochód uzyskany ze sprzeda

ż

y czynników

wytwórczych słu

ż

y gospodarstwom domowym do zaspokojenia potrzeb i jest przeznaczany na zakup

wytworzonych przez przedsi

ę

biorstwa towarów.

Zakładamy,

ż

e gospodarstwa domowe zamiast wyda

ć

całe swoje dochody na konsumpcj

ę

, pewn

ą

ich cz

ęść

przeznaczaj

ą

na oszcz

ę

dno

ś

ci. Oszcz

ę

dno

ś

ci gospodarstw domowych, traktowane jako

chwilowo wolne

ś

rodki pieni

ęż

ne, mog

ą

za po

ś

rednictwem banków zosta

ć

po

ż

yczone

przedsi

ę

biorstwom, które ich potrzebuj

ą

na cele inwestycyjne. Inwestycje przedsi

ę

biorstw s

ą

warunkiem ich dalszego rozwoju. Przedsi

ę

biorstwa musz

ą

po

ż

ycza

ć

pieni

ą

dze, poniewa

ż

jak

zało

ż

yli

ś

my wcze

ś

niej jedynymi wła

ś

cicielami czynników wytwórczych s

ą

gospodarstwa domowe, co

jest równoznaczne z pozbawieniem przedsi

ę

biorstw własnych

ś

rodków pieni

ęż

nych.

Zale

ż

no

ś

ci mi

ę

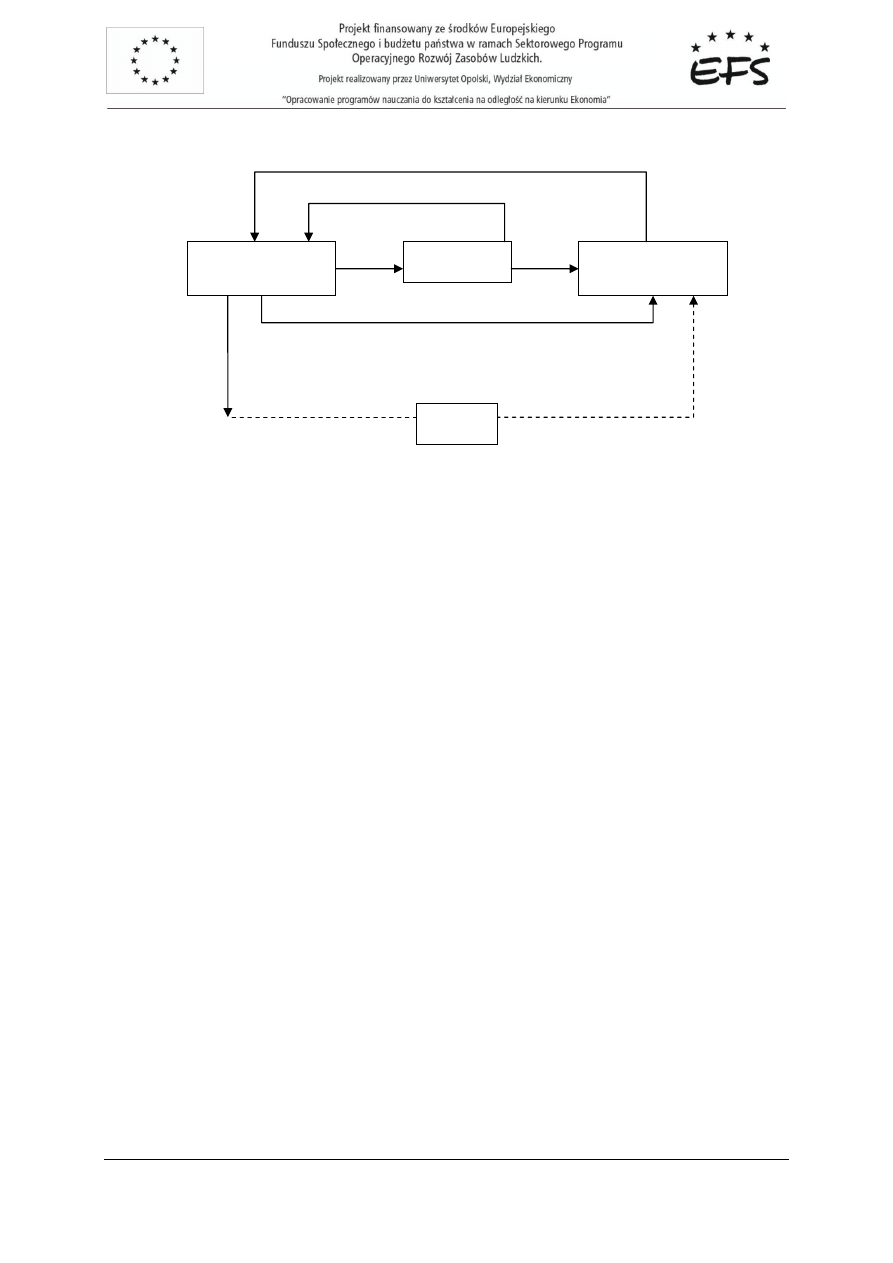
dzy uczestnikami rynku w modelu dwusektorowym ilustruje rysunek 2.1.

Rys. 2.1. Zale

ż

no

ś

ci mi

ę

dzy podmiotami gospodarczymi w dwusektorowym modelu rynku.

Wprowad

ź

my nast

ę

puj

ą

ce oznaczenia:

AD

- wielko

ść

zgłaszanego w gospodarce globalnego popytu,

C

- wielko

ść

popytu na towary i usługi konsumpcyjne zgłaszanego przez gospodarstwa domowe,

I

- wielko

ść

popytu na dobra inwestycyjne zgłaszanego przez przedsi

ę

biorstwa prywatne,

G

- wielko

ść

popytu zarówno na dobra konsumpcyjne, jak i inwestycyjne zgłaszanego przez

władze pa

ń

stwowe (centralne i lokalne),

X

- wielko

ść

popytu na krajowe dobra i usługi konsumpcyjne i inwestycyjne zgłaszanego przez

zagranicznego nabywc

ę

,

Y

- wynagrodzenie, dochód gospodarstw domowych uzyskany ze sprzeda

ż

y b

ę

d

ą

cych w ich

posiadaniu czynników wytwórczych,

S

- nie wydatkowana na konsumpcj

ę

cz

ęść

dochodów gospodarstw domowych (oszcz

ę

dno

ś

ci).

gospodarstwa

domowe

przedsi

ę

biorstwa

C

Y

S

bank

I

dr Agnieszka Bobrowska

3

Ekonomia matematyczna II

W dwusektorowym modelu równowagi krótkookresowej zakładamy brak udziału pa

ń

stwa

w procesach rynkowych oraz brak wymiany z zagranic

ą

, co zapisujemy:

0

=

=

X

G

.

Mówimy,

ż

e gospodarka znajduje si

ę

w poło

ż

eniu równowagi, gdy spełniony jest nast

ę

puj

ą

cy

warunek:

Y

AD

=

,

czyli gdy globalny popyt równa si

ę

wielko

ś

ci produkcji (dochodowi narodowemu).

W modelu dwusektorowym, je

ż

eli przedsi

ę

biorstwa sprzedaj

ą

towary o warto

ś

ci

Y

, to

Y

oznacza

równocze

ś

nie ich przychód, który przeznaczaj

ą

na zakup czynników produkcji od gospodarstw

domowych – jedynych ich wła

ś

cicieli. Wówczas Y oznacza tak

ż

e dochód gospodarstw domowych. Na

tej podstawie, w ramach przyj

ę

tych zało

ż

e

ń

, poj

ę

cia dochód i produkcja mog

ą

by

ć

stosowane

zamiennie.

W dwusektorowym modelu równowagi krótkookresowej popyt globalny

AD

zgłaszany na rynku

jest sum

ą

popytu konsumpcyjnego

C

i popytu inwestycyjnego

I

:

I

C

AD

+

=

.

Natomiast dochód gospodarstw domowych

Y

(produkcja

Y

), jako,

ż

e jest w cało

ś

ci przeznaczany na

konsumpcj

ę

i oszcz

ę

dno

ś

ci, mo

ż

e by

ć

przedstawiony w modelu w postaci sumy wydatków

konsumpcyjnych i oszcz

ę

dno

ś

ci:

S

C

Y

+

=

.

Je

ż

eli w jakim

ś

momencie gospodarka nie znajduje si

ę

w poło

ż

eniu równowagi, czyli

Y

AD

≠

, to

mechanizm rynkowy przywraca równowag

ę

rynkow

ą

. Wówczas

Y

AD

=

, ale poniewa

ż

I

C

AD

+

=

oraz

S

C

Y

+

=

, to mo

ż

emy napisa

ć

,

ż

e zachodzi równo

ść

:

S

C

I

C

+

=

+

.

St

ą

d otrzymujemy warunek równowagi w omawianym modelu gospodarki:

S

I

=

.

dr Agnieszka Bobrowska

4

Ekonomia matematyczna II

Wniosek:

W dwusektorowym modelu równowagi krótkookresowej, równowaga zachodzi wtedy i tylko wtedy,

gdy inwestycje

I

równaj

ą

si

ę

oszcz

ę

dno

ś

ciom

S

.

Załó

ż

my,

ż

e wydatki konsumpcyjne w omawianym modelu s

ą

liniowo zale

ż

ne od dochodów

gospodarstw domowych. Wówczas funkcja konsumpcji okre

ś

laj

ą

ca t

ą

zale

ż

no

ść

przyjmuje posta

ć

:

Y

C

β

α

+

=

(

)

1

;

0

(

,

0

∈

>

β

α

)

,

gdzie:

α

- stała oznaczaj

ą

ca popyt autonomiczny niezale

ż

ny od

Y

,

β

- stała okre

ś

laj

ą

ca kra

ń

cow

ą

skłonno

ść

do konsumpcji,

Y

- dochody gospodarstw domowych.

Parametr

α

, wyst

ę

puj

ą

cy w funkcji konsumpcji, jest interpretowany jako niezmienny w krótkim

okresie, niezb

ę

dny w danej gospodarce poziom konsumpcji (konsumpcja autonomiczna). Przyjmuje

si

ę

,

ż

e nawet, gdy chwilowe dochody kształtuj

ą

si

ę

na bardzo niskim poziomie (s

ą

bliskie zeru),

konsumpcja i tak wyst

ę

puje. W takiej sytuacji b

ę

dzie ona finansowana z wcze

ś

niej nagromadzonych

ś

rodków pieni

ęż

nych (oszcz

ę

dno

ś

ci).

Współczynnik kierunkowy

β

interpretowany jako kra

ń

cowa skłonno

ść

do konsumpcji, okre

ś

la

stosunek przyrostu konsumpcji do przyrostu dochodu. Warto

ść

współczynnika

β

informuje nas zatem

o ile jednostek pieni

ęż

nych wzro

ś

nie warto

ść

konsumpcji, je

ż

eli dochód wzro

ś

nie o jednostk

ę

.

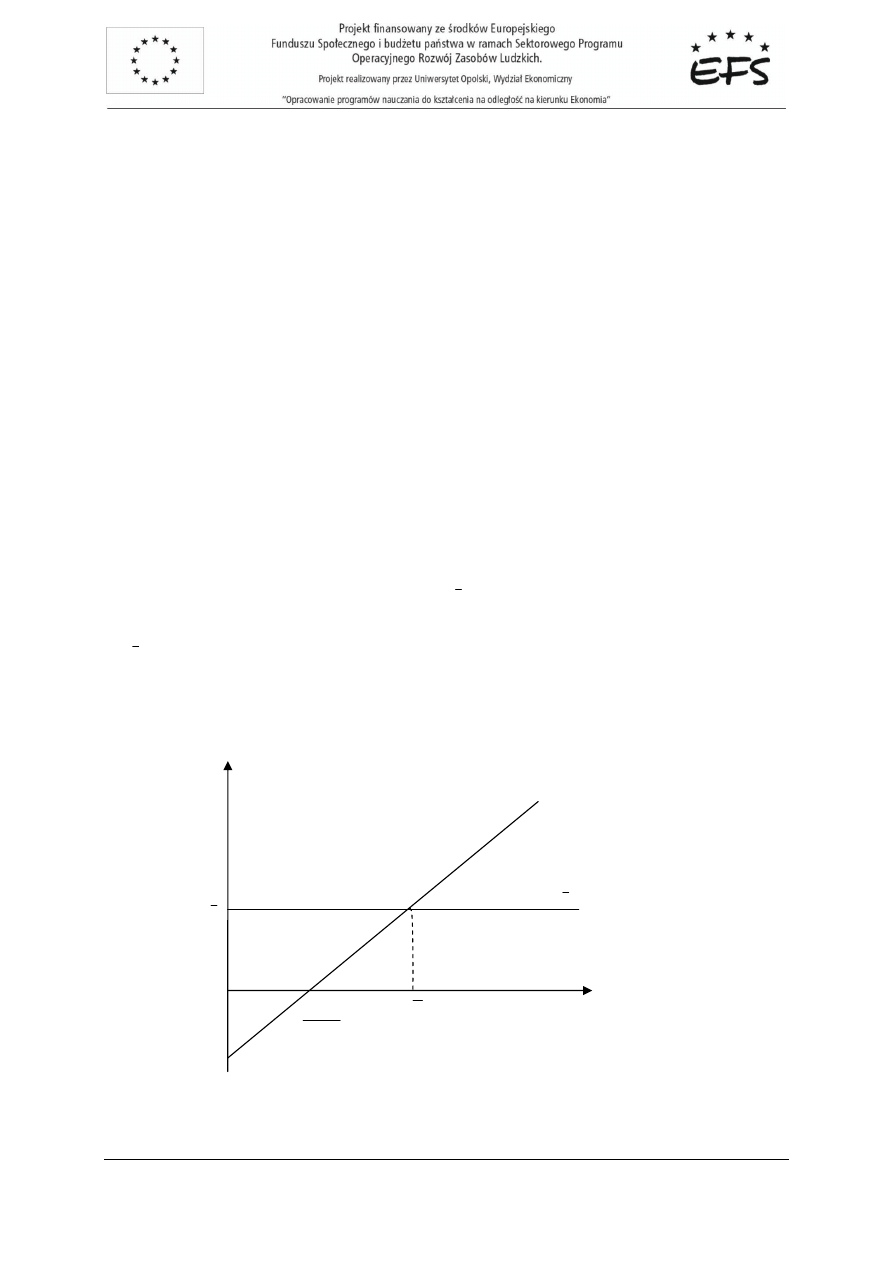
Wykres liniowej funkcji konsumpcji przedstawia rysunek 2.2.

Rys.2.2. Wykres liniowej funkcji konsumpcji

C

.

Y

C

α

Y

C

β

α

+

=

dr Agnieszka Bobrowska

5

Ekonomia matematyczna II

W omawianym modelu ze wzoru na funkcj

ę

konsumpcji, mo

ż

na wyznaczy

ć

oszcz

ę

dno

ś

ci S jako

funkcj

ę

dochodu. Poniewa

ż

S

C

Y

+

=

, to

C

Y

S

−

=

. Podstawiaj

ą

c do wzoru na

S

funkcj

ę

konsumpcji

Y

C

β

α

+

=

, otrzymujemy nast

ę

puj

ą

c

ą

posta

ć

funkcji oszcz

ę

dno

ś

ci:

Y

S

)

1

(

β

α

−

+

−

=

, (

)

1

;

0

(

,

0

∈

>

β

α

)

,

Współczynnik kierunkowy w przypadku funkcji oszcz

ę

dno

ś

ci wynosi (

β

−

1

) i oznacza kra

ń

cow

ą

skłonno

ść

do oszcz

ę

dzania, tj. stosunek przyrostu oszcz

ę

dno

ś

ci do przyrostu dochodu. Kra

ń

cowa

skłonno

ść

do oszcz

ę

dzania okre

ś

la o ile jednostek pieni

ęż

nych wzrosn

ą

oszcz

ę

dno

ś

ci, je

ż

eli dochód

wzro

ś

nie o jednostk

ę

.

W rzeczywisto

ś

ci obserwujemy,

ż

e wraz ze wzrostem dochodów udział wydatków na konsumpcj

ę

w dochodzie zmniejsza si

ę

, ro

ś

nie natomiast udział oszcz

ę

dno

ś

ci. Nie nale

ż

y jednak przez to

rozumie

ć

,

ż

e wydatki na konsumpcj

ę

malej

ą

w stosunku do poprzedniego okresu, wr

ę

cz przeciwnie

wydatki te rosn

ą

, ale tempo ich wzrostu jest mniejsze ni

ż

tempo wzrostu dochodów.

Co si

ę

tyczy inwestycji, w rozwa

ż

anym modelu przyjmujemy,

ż

e nie zale

żą

one ani od dochodów

ani od kosztów kredytu (oprocentowania po

ż

yczonego kapitału). Przy tych zało

ż

eniach funkcja

inwestycji ma uproszczon

ą

posta

ć

:

I

I

=

,

gdzie:

I

- inwestycje autonomiczne.

Wykres funkcji oszcz

ę

dno

ś

ci wraz z funkcj

ą

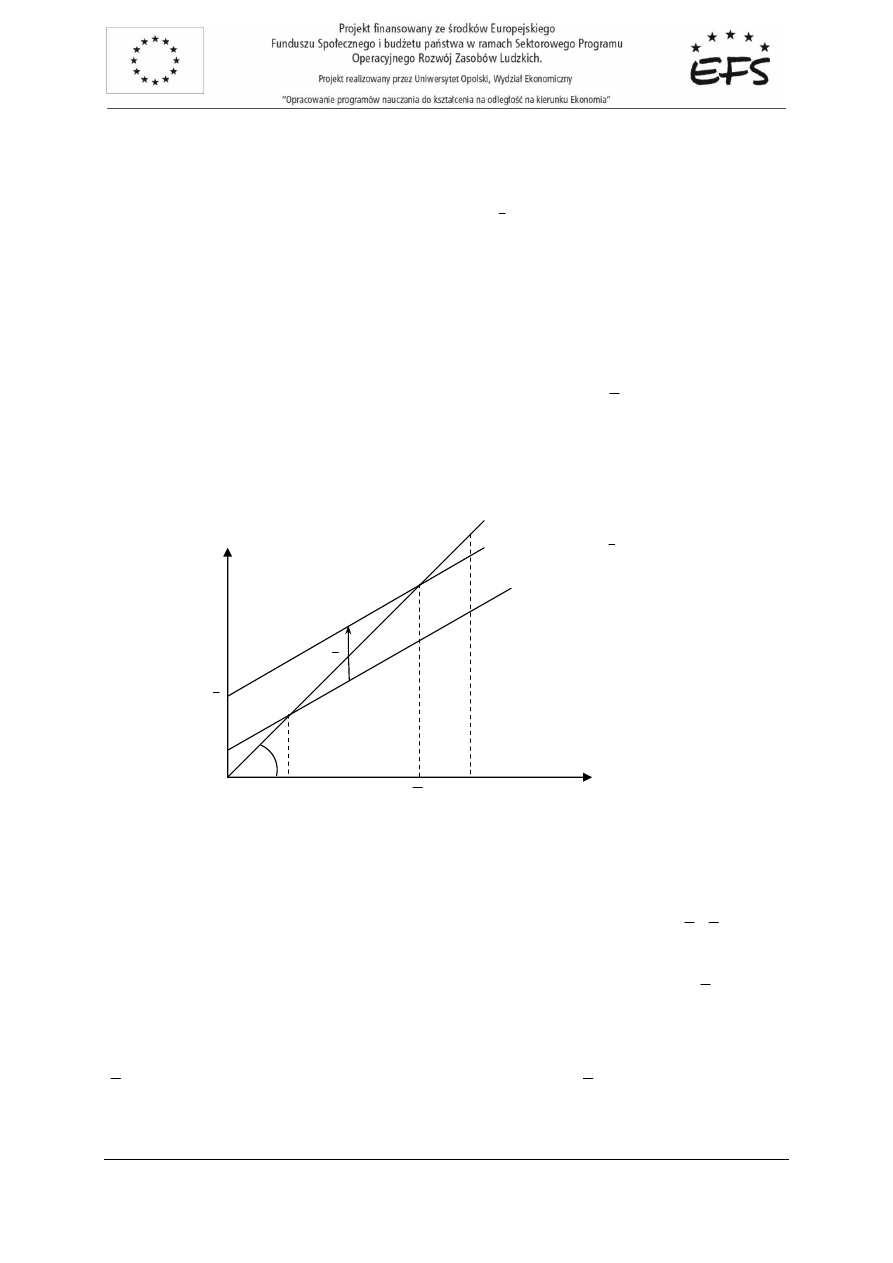
inwestycji przedstawia rysunek 2.3.

Rys.2.3. Wykresy funkcji oszcz

ę

dno

ś

ci

S

i funkcji inwestycji

I

.

Y

C

-

α

)Y

-

(1

-

S

β

α

+

=

β

α

−

1

I

I

I

=

Y

dr Agnieszka Bobrowska

6

Ekonomia matematyczna II

Je

ż

eli zało

ż

ymy,

ż

e wielko

ść

popytu konsumpcyjnego

C

, przy danym poziomie dochodów,

wyznacza omówiona przed chwil

ą

funkcja konsumpcji, to poprzez dodanie do niej warto

ś

ci popytu

inwestycyjnego

I

otrzymamy wzór na popyt globalny

AD

:

I

Y

AD

+

+

=

β

α

.

Wykres funkcji popytu konsumpcyjnego i odpowiadaj

ą

cy mu wykres funkcji popytu globalnego ilustruje

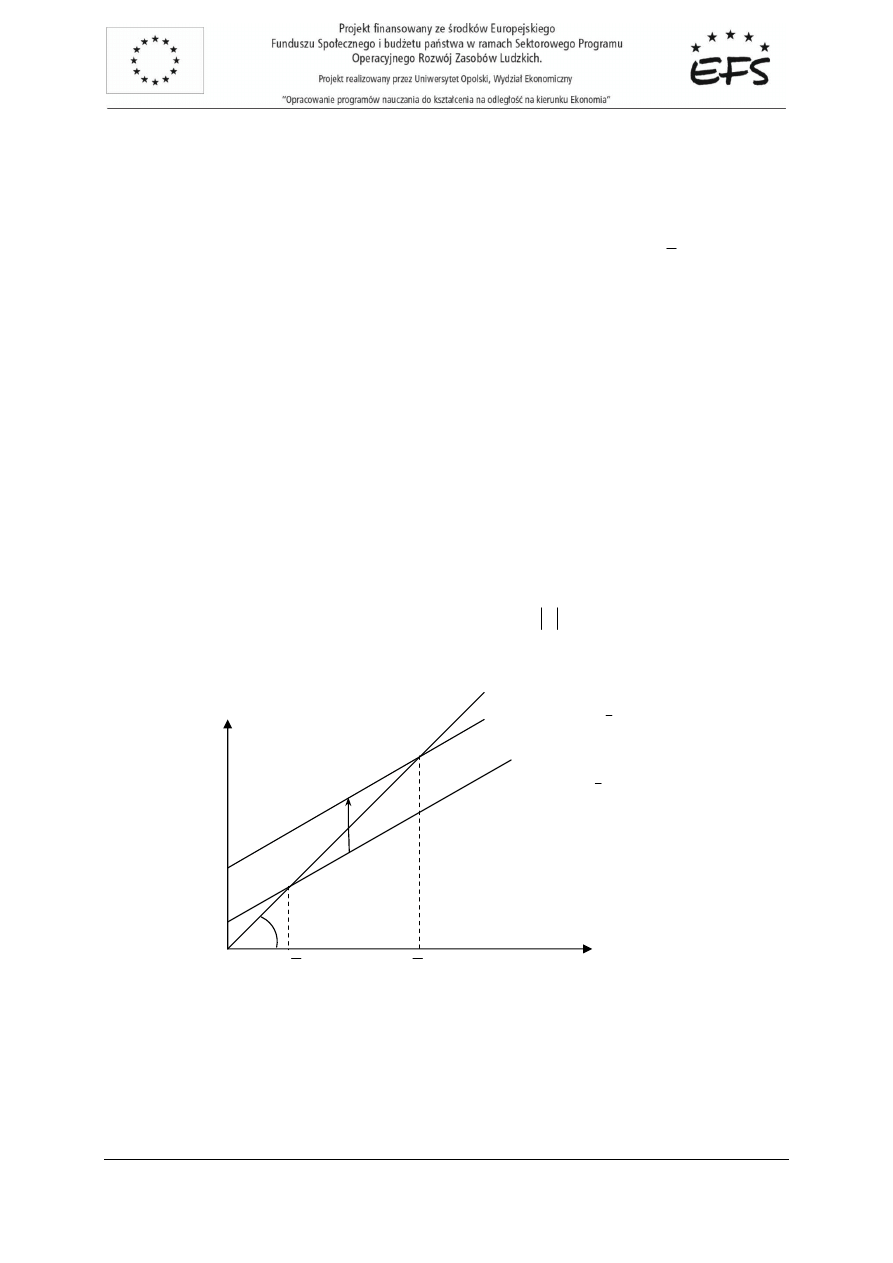
rysunek 2.4.

Na rysunku tym przedstawiono konstrukcj

ę

wykresu funkcji globalnego popytu wyprowadzon

ą

z funkcji popytu konsumpcyjnego oraz zale

ż

no

ś

ci mi

ę

dzy popytem a produkcj

ą

w modelu

dwusektorowym. Linia

Ο

45

to zbiór wszystkich punktów, dla których

Y

AD

=

, czyli zbiór punktów,

dla których globalny popyt równa si

ę

produkcji (dochodom). W punkcie

Y

, le

żą

cym na przeci

ę

ciu

prostej globalnego popytu z lini

ą

Ο

45

, globalny popyt równa si

ę

produkcji. Punkt ten wyznacza zatem

stan równowagi rynkowej dla gospodarki dwusektorowej z funkcj

ą

popytu globalnego

AD

.

Rys. 2.4. Konstrukcja funkcji globalnego popytu.

Poka

ż

emy,

ż

e gdy poziom produkcji kształtuje si

ę

na innym poziomie ni

ż

Y

)

(

Y

Y

≠

, to

w gospodarce uruchomiony zostaje mechanizm zapewniaj

ą

cy zrównowa

ż

enie si

ę

produkcji

z wielko

ś

ci

ą

zgłaszanego popytu. Załó

ż

my,

ż

e produkcja kształtuje si

ę

na poziome

Y

Y

<

1

. Wówczas

popyt globalny

AD

przewy

ż

sza produkcj

ę

Y

)

(

Y

AD

>

. W takiej sytuacji, na skutek zmniejszaj

ą

cych

si

ę

zapasów, producenci b

ę

d

ą

zwi

ę

ksza

ć

swoj

ą

produkcj

ę

dopóki nie osi

ą

gn

ą

poło

ż

enia równowagi

Y

. Je

ż

eli natomiast produkcja ukształtowałaby si

ę

na poziomie

Y

Y

>

2

, to odpowiadaj

ą

cy jej popyt

Y

C

α

Y

C

β

α

+

=

I

Y

AD

+

+

=

β

α

I

+

α

1

Y

Y

Ο

45

I

2

Y

dr Agnieszka Bobrowska

7

Ekonomia matematyczna II

globalny byłby od niej mniejszy

)

(

Y

AD

<

i producenci, aby móc sprzeda

ć

rosn

ą

ce zapasy obni

ż

yliby

produkcj

ę

do poziomu

Y

, przy którym poziom produkcji zrównałby si

ę

z popytem.

Pierwszy z rozwa

ż

anych przypadków, tj. gdy popyt przewy

ż

sza poda

ż

)

(

Y

AD

>

implikuje

sytuacj

ę

, w której wydatki inwestycyjne s

ą

wy

ż

sze ni

ż

oszcz

ę

dno

ś

ci

)

(

S

I

>

. Mamy wówczas do

czynienia z ekspansj

ą

gospodarki.

Je

ż

eli natomiast w gospodarce wyst

ę

puje nadwy

ż

ka poda

ż

y nad popytem

)

(

Y

AD

<

, to mamy

wtedy do czynienia z sytuacj

ą

, w której planowane wydatki inwestycyjne s

ą

mniejsze od planowanych

oszcz

ę

dno

ś

ci

)

(

S

I

<

i nast

ę

puje wówczas regres produkcji.

Wnioski:

1. W punkcie

Y

inwestycje równaj

ą

si

ę

oszcz

ę

dno

ś

ciom a gospodarka znajduje si

ę

w stanie

równowagi (popyt równa si

ę

poda

ż

y).

2. Gdy poziom produkcji kształtuje si

ę

na dowolnym poziomie

Y

Y

<

, wówczas inwestycje s

ą

wi

ę

ksze od oszcz

ę

dno

ś

ci i gospodarka znajduje si

ę

w fazie wzrostu.

3. W sytuacji, gdy poziom produkcji ustala si

ę

na poziomie

Y

Y

>

, lub inaczej, gdy inwestycje s

ą

mniejsze od oszcz

ę

dno

ś

ci, mamy wówczas do czynienia z ograniczeniem dotychczasowej

produkcji, czyli gospodarka znajduje si

ę

w fazie regresji.

4. O tym czy gospodarka znajduje si

ę

w fazie wzrostu, w fazie regresji lub mo

ż

e w stanie

równowagi, decyduje zale

ż

no

ść

pomi

ę

dzy planowanymi inwestycjami a oszcz

ę

dno

ś

ciami.

Załó

ż

my,

ż

e gospodarka znajduje si

ę

w stanie równowagi. Mo

ż

emy wówczas wyznaczy

ć

poziom

produkcji zapewniaj

ą

cy stan równowagi w gospodarce. Z warunku na stan równowagi, mamy:

Y

Y

AD

=

=

.

Jednak poniewa

ż

I

Y

AD

+

+

=

β

α

, to otrzymujemy:

Y

I

Y

=

+

+

β

α

.

Przekształcaj

ą

c powy

ż

sz

ą

równo

ść

otrzymujemy punkt równowagi

Y

w zale

ż

no

ś

ci od popytu

autonomicznego

α

, wielko

ś

ci inwestycji

I

oraz kra

ń

cowej skłonno

ś

ci do oszcz

ę

dzania

)

1

(

β

−

.:

β

α

−

+

=

1

I

Y

.

Wynika st

ą

d,

ż

e poziom produkcji zapewniaj

ą

cy w gospodarce stan równowagi jest tym wy

ż

szy, im

wy

ż

sza jest skłonno

ść

gospodarstw domowych do konsumpcji, a zatem im wi

ę

kszy jest popyt.

Dotychczas rozwa

ż

ali

ś

my sytuacje, w której wielko

ść

autonomicznego popytu była ustalona i nie

podlegała zmianom. Rozwa

ż

ymy teraz mo

ż

liwo

ść

zmiany tego popytu i poka

ż

emy jej skutki. Wzrost

dr Agnieszka Bobrowska

8

Ekonomia matematyczna II

popytu autonomicznego z dotychczasowego poziomu

α

do poziomu

α

α

α

∆

+

=

'

spowoduje

przesuni

ę

cie prostej popytu globalnego w gór

ę

o wielko

ść

zmiany, czyli o

α

∆

. Sytuacj

ę

t

ą

zilustrowano na rysunku 2.5.

Zakładamy,

ż

e gospodarka znajduje si

ę

w stanie równowagi. W momencie wzrostu popytu

autonomicznego, dotychczasowy poziom produkcji okazuje si

ę

niewystarczaj

ą

cy, w zwi

ą

zku z czym

nast

ę

puje wzrost produkcji. Nowy poziom równowagi ustala si

ę

na poziomie

'

Y

. Ze wzrostem

produkcji wi

ąż

e si

ę

wzrost dochodów gospodarstw domowych, z których pewn

ą

cz

ęść

przeznacz

ą

one

na konsumpcj

ę

a pozostał

ą

cz

ęść

przekształc

ą

w oszcz

ę

dno

ś

ci. Zakładamy przy tym,

ż

e

w gospodarce istniej

ą

rezerwy zdolno

ś

ci wytwórczych. Je

ż

eli

β

oznacza kra

ń

cow

ą

skłonno

ść

do

konsumpcji, to wzrost wydatków na konsumpcj

ę

jest równowa

ż

ny z dodatkowym popytem

konsumpcyjnym i wynosi

α

β

∆

, natomiast przeznaczenie cz

ęś

ci dodatkowego dochodu na

oszcz

ę

dno

ś

ci oznacza przyrost oszcz

ę

dno

ś

ci w wysoko

ś

ci

α

β

∆

−

)

1

(

. Wzrost popytu

konsumpcyjnego o

α

β

∆

poci

ą

ga za sob

ą

wzrost produkcji o t

ę

sam

ą

wielko

ść

, który z kolei

powoduje wzrost popytu konsumpcyjnego o

)

(

α

β

β

∆

. Wida

ć

,

ż

e wzrost popytu autonomicznego

powoduje ci

ą

g zmian (wzrostów) produkcji i popytu konsumpcyjnego, przy czym ka

ż

dy kolejny

przyrost produkcji i dochodów jest coraz mniejszy. I tak np. w k-tym kroku przyrost produkcji (dochodu)

b

ę

dzie wynosi

ć

α

β

∆

k

. Łatwo zauwa

ż

y

ć

,

ż

e cz

ą

stkowe przyrosty produkcji tworz

ą

zbie

ż

ny ci

ą

g

geometryczny, którego pierwszy wyraz wynosi

α

∆

, a iloraz

)

1

(

<

β

β

.

Rys. 2.5. Wpływ zmian autonomicznego popytu na poziom produkcji

Y

C

α

I

Y

AD

+

+

=

β

α

I

Y

AD

+

+

=

β

α

'

'

α

α

α

∆

+

=

'

Y

'

Y

Ο

45

α

∆

dr Agnieszka Bobrowska

9

Ekonomia matematyczna II

Licz

ą

c niesko

ń

czon

ą

sum

ę

wszystkich przyrostów produkcji wywołanych wzrostem popytu

autonomicznego o

α

∆

, otrzymamy całkowity przyrost wielko

ś

ci produkcji

Y

∆

:

β

α

−

∆

=

∆

1

Y

.

Wniosek:

Wzrost popytu autonomicznego o

α

∆

wywołuje

β

−

1

1

razy wi

ę

kszy przyrost produkcji (dochodu).

Wielko

ść

β

−

1

1

, gdzie

β

−

1

oznacza kra

ń

cow

ą

skłonno

ść

do oszcz

ę

dzania nazywamy

mno

ż

nikiem

i oznaczamy przez

ω

.

Mno

ż

nik

β

ω

−

=

1

1

okre

ś

la sił

ę

wpływu zmian (wzrostu lub spadku) popytu autonomicznego na

przyrost produkcji.

2.2. Wielosektorowe modele równowagi krótkookresowe

2

Omówiony powy

ż

ej dwusektorowy model równowagi krótkookresowej jest uproszczonym modelem

gospodarki i nie wyst

ę

puje w rzeczywisto

ś

ci. Mo

ż

na go jednak urealni

ć

wprowadzaj

ą

c pa

ń

stwo jako

podmiot gospodarczy oraz wymian

ę

z zagranic

ą

.

Je

ż

eli do modelu dwusektorowego dodamy wyst

ę

puj

ą

ce w aktywnej roli pa

ń

stwo, otrzymamy now

ą

trójsektorow

ą

posta

ć

modelu gospodarki. Model uwzgl

ę

dniaj

ą

cy sektor rz

ą

dowy przedstawia rysunek

2.6.

Wprowad

ź

my oznaczenia:

T

- podatki płacone przez gospodarstwa domowe na rzecz pa

ń

stwa,

TR

- płatno

ś

ci transferowe,

G

- wydatki pa

ń

stwa na zakup towarów i usług.

W modelu trójsektorowym oprócz omówionych, przy okazji modelu dwusektorowego, zale

ż

no

ś

ci

mi

ę

dzy gospodarstwami domowymi a przedsi

ę

biorstwami wyst

ę

puj

ą

dodatkowo zale

ż

no

ś

ci mi

ę

dzy

pa

ń

stwem a gospodarstwami domowymi oraz zale

ż

no

ś

ci mi

ę

dzy pa

ń

stwem a przedsi

ę

biorstwami.

Dochodami pa

ń

stwa s

ą

podatki od dochodów płacone przez gospodarstwa domowe. W ten sposób

uzyskane dochody pa

ń

stwo przeznacza na zakup towarów i usług oraz na płatno

ś

ci transferowe,

obejmuj

ą

ce m.in. zasiłki dla bezrobotnych, ró

ż

nego rodzaju

ś

wiadczenia socjalne, a tak

ż

e odsetki od

zaci

ą

gni

ę

tego przez pa

ń

stwo długu publicznego.

2

Charakterystyk

ę

modelu przygotowano na podstawie M.Garbicz, E.Golachowski: Elementarne modele

makroekonomiczne, Szkoła Główna Handlowa, Warszawa 1996, rozdział 2.

dr Agnieszka Bobrowska

10

Ekonomia matematyczna II

Rys.2.6. Zale

ż

no

ś

ci mi

ę

dzy podmiotami gospodarczymi w trójsektorowym modelu rynku.

Poniewa

ż

gospodarstwa domowe musz

ą

płaci

ć

podatki i otrzymuj

ą

dodatkowe

ś

wiadczenia, wi

ę

c

ich dochody osobiste do dyspozycji (dochody rozporz

ą

dzalne) ró

ż

ni

ą

si

ę

od tych w modelu

dwusektorowym i wynosz

ą

d

Y

:

TR

T

Y

Y

d

+

−

=

.

Cz

ęść

tych dochodów gospodarstwa domowe przeznaczaj

ą

na konsumpcj

ę

C

, a reszt

ę

na

oszcz

ę

dno

ś

ci

S

. Funkcja konsumpcji z modelu dwusektorowego przyjmuje w przypadku omawianego

modelu nast

ę

puj

ą

c

ą

posta

ć

:

d

Y

C

β

α

+

=

i ró

ż

ni si

ę

tym od funkcji konsumpcji opisanej w poprzednim podrozdziale,

ż

e w miejsce dochodu

Y

wstawiamy dochód rozporz

ą

dzalny

d

Y

. Poniewa

ż

TR

T

Y

Y

d

+

−

=

, to funkcj

ę

konsumpcji mo

ż

emy

równowa

ż

nie zapisa

ć

w postaci:

(

)

TR

T

Y

C

+

−

+

=

β

α

.

W modelu trójsektorowym na popyt globalny

AD

składa si

ę

wielko

ść

konsumpcji

C

, inwestycji

I

oraz wydatki rz

ą

dowe na zakup towarów i usług

G

:

G

I

C

AD

+

+

=

.

gospodarstwa

domowe

przedsi

ę

biorstwa

C

Y

S

bank

I

rz

ą

d

TR

T

G

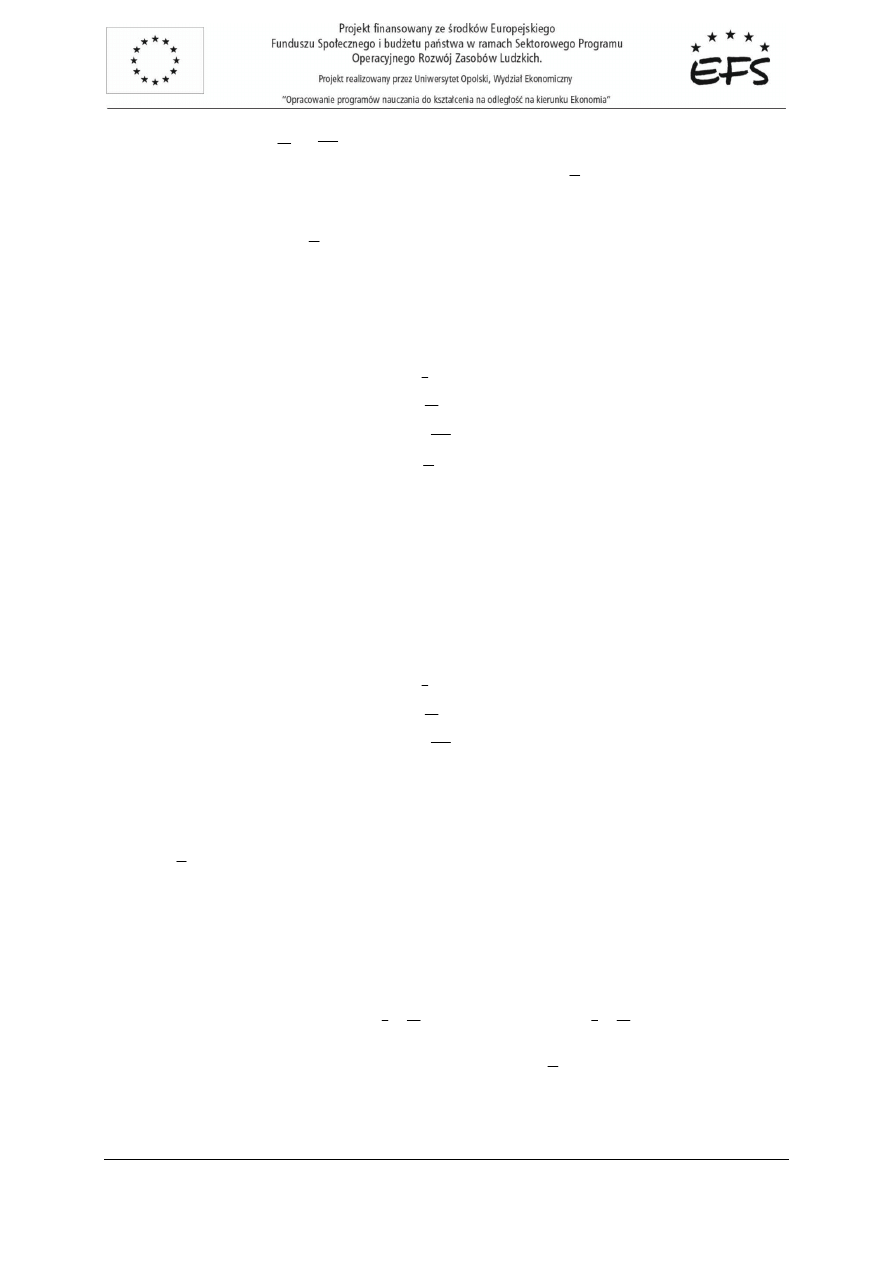
dr Agnieszka Bobrowska

11

Ekonomia matematyczna II

Zakładamy,

ż

e wielko

ść

wydatków rz

ą

dowych

G

i wielko

ść

transferów

TR

s

ą

z góry zadane

i wynosz

ą

odpowiednio

G

i

TR

(wielko

ś

ci autonomiczne). O podatku

T

mo

ż

emy zało

ż

y

ć

,

ż

e

gospodarstwa domowe płac

ą

pa

ń

stwu okre

ś

lon

ą

kwot

ę

podatku

T

(podatek kwotowy) albo,

ż

e

podatki s

ą

funkcj

ą

osi

ą

ganego dochodu, czyli

Y

T

γ

=

. Parametr

( )

1

;

0

∈

γ

i oznacza stop

ę

podatku.

Je

ż

eli przyjmiemy,

ż

e

T

T

=

, wówczas trójsektorowy model gospodarki opisuje układ równa

ń

:

























=

=

=

=

+

−

=

+

=

+

+

=

T

T

TR

TR

G

G

I

I

TR

T

Y

Y

Y

C

G

I

C

AD

d

d

β

α

.

W przypadku, gdy podatek

T

jest liniow

ą

funkcj

ą

dochodu, model gospodarki trójsektorowej ma

posta

ć

:

























=

=

=

=

+

−

=

+

=

+

+

=

Y

T

TR

TR

G

G

I

I

TR

T

Y

Y

Y

C

G

I

C

AD

d

d

γ

β

α

.

Dla rozwa

ż

anego modelu, podobnie jak w przypadku modelu dwusektorowego, punkt równowagi

rynkowej

Y

le

ż

y na przeci

ę

ciu wykresu funkcji popytu globalnego

AD

z lini

ą

Ο

45

i mo

ż

emy go

wyznaczy

ć

z warunku równowagi rynkowej:

Y

AD

=

.

Z tego,

ż

e

G

I

C

AD

+

+

=

, podstawiaj

ą

c za

C

,

I

oraz

G

odpowiednie wielko

ś

ci, otrzymujemy:

.

)

(

G

I

TR

T

Y

G

I

Y

AD

d

+

+

+

−

+

=

+

+

+

=

β

α

β

α

Poniewa

ż

jednak

Y

AD

=

, to dla dwóch przypadków

T

T

=

i

tY

T

=

mamy odpowiednio

nast

ę

puj

ą

ce równania:

dr Agnieszka Bobrowska

12

Ekonomia matematyczna II

G

I

T

TR

Y

G

I

TR

T

Y

Y

+

+

−

+

+

=

+

+

+

−

+

=

)

(

)

(

β

β

α

β

α

, dla

T

T

=

i

TR

TR

=

oraz i

G

I

TR

Y

G

I

TR

Y

Y

Y

+

+

+

−

+

=

+

+

+

−

+

=

β

γ

β

α

γ

β

α

)

1

(

)

(

, dla

Y

T

γ

=

i

TR

TR

=

.

Po odpowiednich przekształceniach obu równa

ń

uzyskujemy wielko

ść

produkcji w stanie równowagi:

)

)

(

(

1

1

G

I

T

TR

Y

+

+

−

+

−

=

β

α

β

, dla

T

T

=

oraz

)

(

1

1

G

I

TR

Y

+

+

+

+

−

=

β

α

βγ

β

, dla

Y

T

γ

=

.

Jak wida

ć

, w obu przypadkach na wielko

ść

produkcji

Y

wpływa zarówno wielko

ść

popytu

autonomicznego

α

, inwestycje autonomiczne

I

oraz transfery

TR

, a tak

ż

e wielko

ść

autonomicznych wydatków rz

ą

dowych

G

.

W przypadku pierwszym na wielko

ść

Y

wpływa dodatkowo stała wielko

ść

podatków

T

, a tak

ż

e

warto

ść

mno

ż

nika

β

ω

−

=

1

1

, natomiast w przypadku drugim na wielko

ść

Y

wpływa dodatkowo

stopa podatku

γ

.

Rozwa

ż

my teraz przypadek, gdy

T

T

=

. Je

ż

eli zmianie ulega dokładnie jeden ze składników

popytu globalnego, tj.

C

,

I

lub

G

, przy zało

ż

eniu,

ż

e pozostałe składniki si

ę

nie zmieniaj

ą

, to

wówczas produkcja zmienia si

ę

proporcjonalnie, ze współczynnikiem proporcjonalno

ś

ci

ϖ

. Na

przykład je

ż

eli inwestycje wzrastaj

ą

o jedn

ą

jednostk

ę

pieni

ęż

n

ą

, to produkcja wzrasta o

ω

jednostek

pieni

ęż

nych. Zatem mno

ż

nik dla zmiennych

C

,

I

i

G

wynosi

β

ω

−

=

1

1

.

W przypadku, gdy

Y

T

γ

=

wielko

ść

produkcji ustabilizuje si

ę

na tym wy

ż

szym poziomie, im ni

ż

sza

b

ę

dzie stopa podatkowa

γ

i im wy

ż

sza b

ę

dzie skłonno

ść

gospodarstw domowych do konsumpcji

β

.

Pa

ń

stwo chc

ą

c wpływa

ć

na wielko

ść

produkcji mo

ż

e manipulowa

ć

wielko

ś

ci

ą

wydatków rz

ą

dowych

G

, wielko

ś

ci

ą

transferów

TR

albo stop

ą

podatkow

ą

γ

.Je

ż

eli zało

ż

ymy,

ż

e zmianie ulegaj

ą

jedynie

wydatki rz

ą

dowe

G

(warto

ść

pozostałych zmiennych pozostaje na dotychczasowym poziomie), to

zmiana ta poci

ą

ga za sob

ą

zmian

ę

wielko

ś

ci produkcji

Y

o krotno

ść

βγ

β

γ

ω

+

−

=

1

1

)

(

G

, gdzie

)

(

γ

ω

G

- współczynnik wzrostu produkcji wzgl

ę

dem wydatków rz

ą

dowych.

Wprowad

ź

my teraz do omawianego modelu trójsektorowego sektor wymiany z zagranic

ą

.

Otrzymujemy w ten sposób czterosektorowy model gospodarki otwartej, w której na poziom produkcji

oprócz pa

ń

stwa istotny wpływ ma równie

ż

skala obrotów z zagranic

ą

.

dr Agnieszka Bobrowska

13

Ekonomia matematyczna II

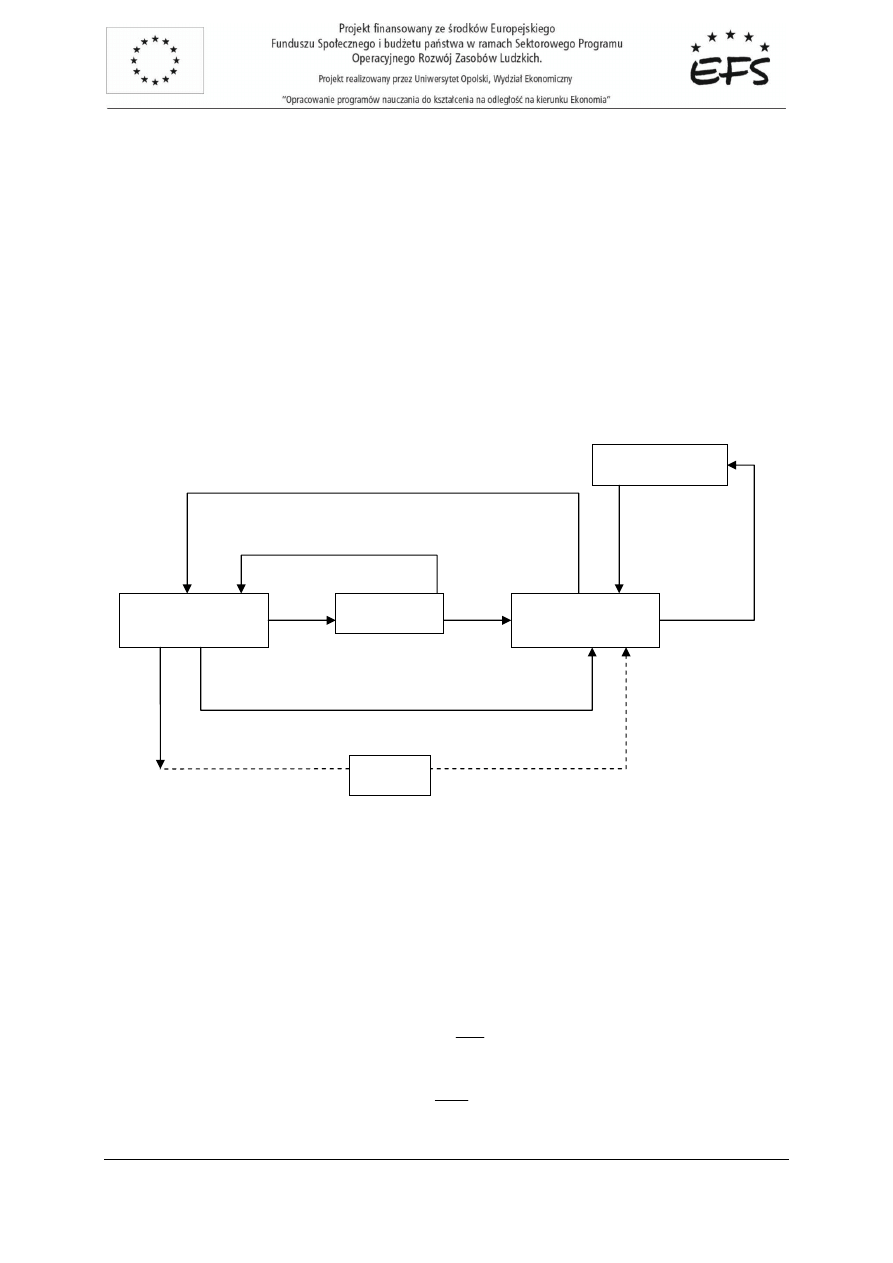
Model czterosektorowy przedstawia rysunek 2.7. W modelu tym oprócz gospodarstw domowych,

przedsi

ę

biorstw i pa

ń

stwa wyst

ę

puje otoczenie zewn

ę

trzne (zagranica). Mi

ę

dzy otoczeniem

zewn

ę

trznym a przedsi

ę

biorstwami zachodzi wymiana dóbr i usług. Przedsi

ę

biorstwa importuj

ą

obce

wyroby i usługi z zagranicy i jednocze

ś

nie eksportuj

ą

krajowe dobra i usługi za granic

ę

.

Przez Imp b

ę

dziemy oznacza

ć

wielko

ść

importowanych towarów i usług, a przez Exp wielko

ść

eksportu. Ró

ż

nica mi

ę

dzy eksportem i importem zwana nadwy

ż

k

ą

eksportow

ą

wyznacza dodatkowy

zewn

ę

trzny popyt X=Exp-Imp, przy czym eksport jest miar

ą

popytu zagranicznego na dobra krajowe,

natomiast import oznacza popyt wewn

ę

trzny na wyroby zagraniczne i sprzyja rozwojowi produkcji za

granic

ą

. X mo

ż

e przyjmowa

ć

zarówno warto

ś

ci dodatnie, gdy Exp>Imp (eksport przewy

ż

sza import),

co oznacza dodatkowy zewn

ę

trzny popyt na produkty krajowe (efektywny przyrost popytu), jak

i warto

ś

ci ujemne, gdy Exp<Imp (import przewy

ż

sza eksport), co oznacza,

ż

e masowy import towarów

zagranicznych nie równowa

ż

y spadku popytu na produkty krajowe.

Rys. 2.7. Zale

ż

no

ś

ci mi

ę

dzy poszczególnymi sektorami w czterosektorowym modelu gospodarki.

Warto

ść

zerowa X oznacza zrównowa

ż

enie popytu na wyroby obce z popytem na wyroby krajowe.

W modelu uwzgl

ę

dniaj

ą

cym wymian

ę

z zagranic

ą

wielko

ść

popytu globalnego definiujemy

w sposób nast

ę

puj

ą

cy:

X

G

I

C

AD

+

+

+

=

, gdzie X=Exp-Imp.

W omawianym modelu zakładamy nast

ę

puj

ą

ce postaci funkcji eksportu i importu:

Exp

Exp

=

oraz

Y

p

p

η

+

=

Im

Im

,

gospodarstwa

domowe

przedsi

ę

biorstwa

C

Y

S

bank

I

rz

ą

d

TR

T

G

zagranica

Exp

Imp

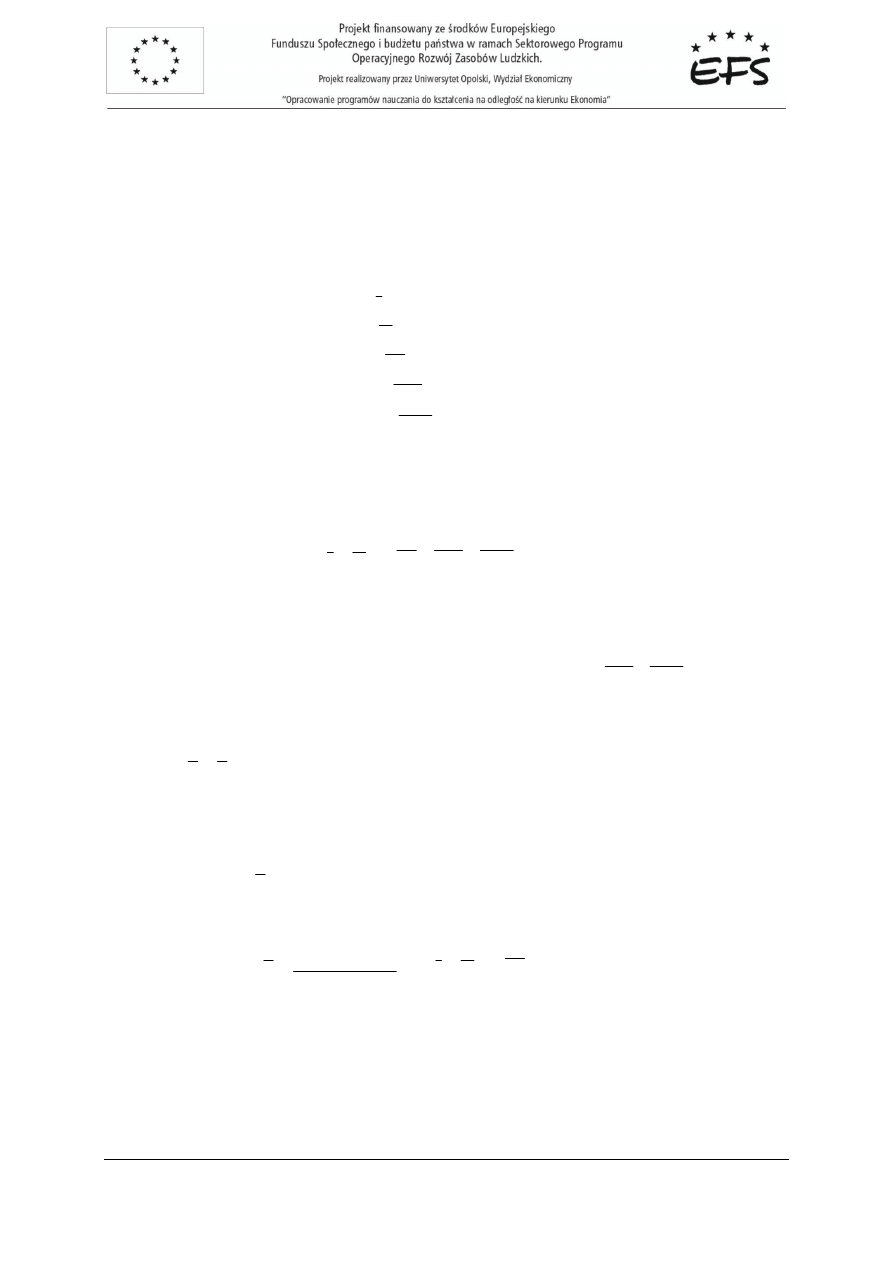
dr Agnieszka Bobrowska

14

Ekonomia matematyczna II

przy czym

( )

1

;

0

∈

η

oznacza kra

ń

cow

ą

skłonno

ść

do importu.

Przy danych zało

ż

eniach czterosektorowy model gospodarki mo

ż

emy zapisa

ć

w postaci układu

równa

ń

:



























=

+

=

=

=

=

=

+

=

−

+

+

+

=

Y

T

Y

p

p

Exp

Exp

TR

TR

G

G

I

I

Y

C

p

Exp

G

I

C

AD

d

γ

η

β

α

Im

Im

Im

Z powy

ż

szego układu równa

ń

, gdzie

TR

T

Y

Y

d

+

−

=

, otrzymujemy nast

ę

puj

ą

c

ą

posta

ć

AD

:

Y

p

Exp

TR

G

I

AD

]

)

1

(

[

Im

η

γ

β

β

α

−

−

+

−

+

+

+

+

=

.

Nie ró

ż

ni si

ę

ona zbyt wiele od postaci

AD

w modelu trójsektorowym, bo jedynie współczynnikiem

przy

Y

, który jest mniejszy o

η

(funkcja popytu

AD

dla omawianego modelu ma mniejszy k

ą

t

nachylenia ni

ż

dla modelu trójsektorowego) oraz dodatkowym składnikiem

p

Exp

Im

−

.

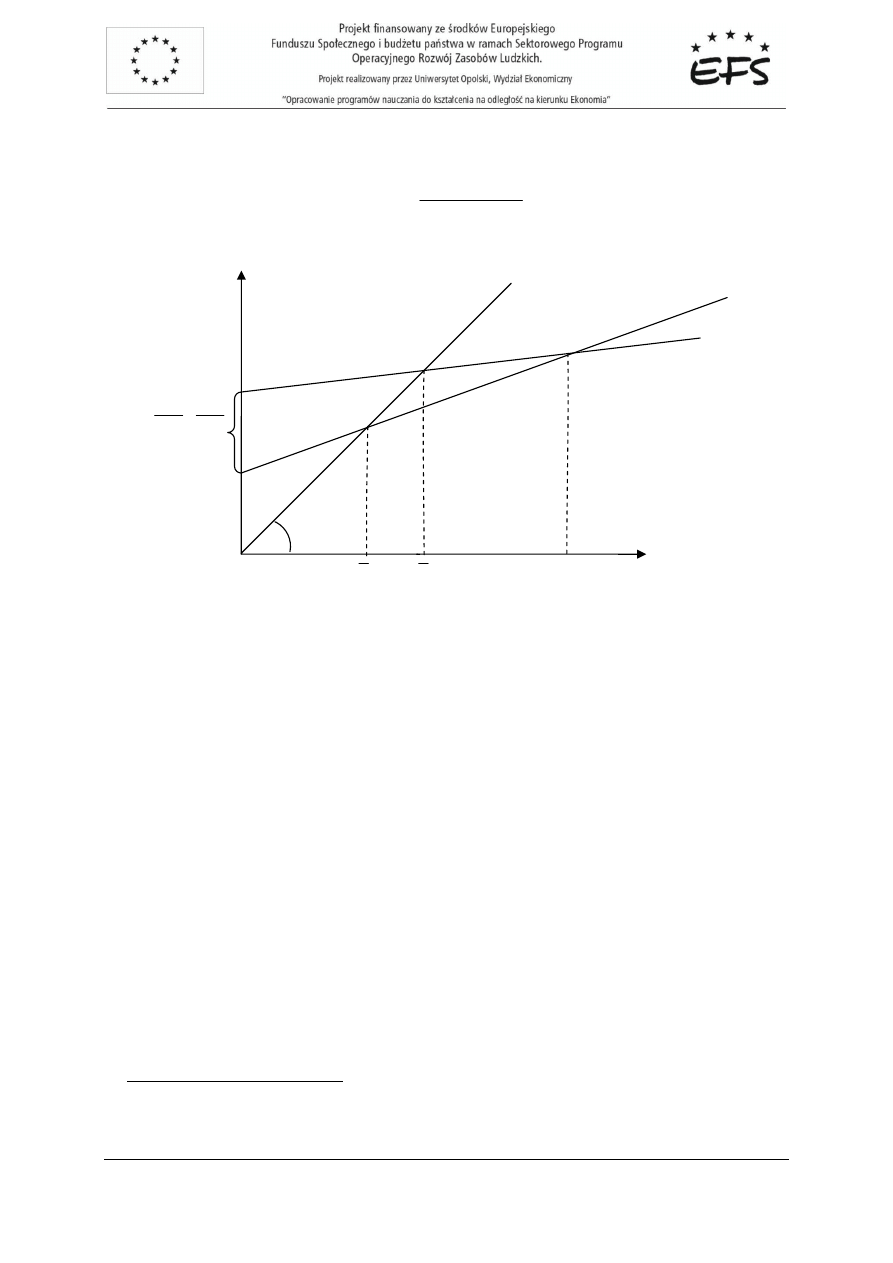
Na rysunku 2.8. przedstawiono przebieg funkcji popytu globalnego

AD

dla omawianego modelu

gospodarki otwartej wzgl

ę

dem funkcji popytu globalnego

'

AD

zwi

ą

zanej z modelem trójsektorowym.

Punkty

'

,

Y

Y

zaznaczone na rysunku wyra

ż

aj

ą

stan równowagi odpowiednio dla modelu

czterosektorowego i modelu trójsektorowego. Punkt przeci

ę

cia prostej

AD

z prost

ą

'

AD

, czyli punkt

a

Y

odpowiada poziomowi produkcji, przy którym zanika nadwy

ż

ka eksportowa X=Exp-Imp=0.

Punkt równowagi

Y

dla modelu gospodarki otwartej wyznaczamy analogicznie jak w przypadku

gospodarki zamkni

ę

tej z równo

ś

ci

Y

AD

=

, sk

ą

d otrzymujemy:

(

)

p

Exp

TR

G

I

Y

Im

1

1

−

+

+

+

+

+

+

−

=

β

α

η

βγ

β

.

dr Agnieszka Bobrowska

15

Ekonomia matematyczna II

Ze wzoru na poziom produkcji w stanie równowagi wynika,

ż

e mno

ż

nik dla gospodarki z sektorem

wymiany z zagranic

ą

jest mniejszy ni

ż

dla gospodarki zamkni

ę

tej i wynosi:

η

βγ

β

η

ω

+

+

−

=

1

1

)

(

.

Rys.2.8. Zale

ż

no

ś

ci mi

ę

dzy wielko

ś

ci

ą

produkcji

Y

a wielko

ś

ciami popytu globalnego w modelu trój- i

czterosektorowym.

2.3. Prosty i kompletny model keynesowski

3

Wprowad

ź

my dodatkowe oznaczenia:

Y

- dochody pieni

ęż

ne sektora gospodarstw domowych (dochód narodowy w cenach bie

żą

cych).

y

- dochody realne (dochód narodowy w cenach porównywalnych),

n

- wielko

ść

zatrudnienia w gospodarce,

M

- poda

ż

pieni

ą

dza w gospodarce,

L

- popyt na pieni

ą

dz w gospodarce,

i

- stopa procentowa,

W

- wielko

ść

płacy nominalnej,

w

- wielko

ść

płacy realnej,

p

- wska

ź

nik poziomu cen.

3

Charakterystyki modeli opracowano w oparciu o R.G.D. Allen: Teoria makroekonomiczna, PWN, Warszawa

1975, rozdział 7 oraz M.Garbicz, E.Golachowski: Elementarne modele makroekonomiczne, Szkoła Główna
Handlowa, Warszawa 1996, rozdział 7

Y

AD

Ο

45

'

AD

AD

Imp

-

Exp

Y

'

Y

a

Y

dr Agnieszka Bobrowska

16

Ekonomia matematyczna II

Jak wspomnieli

ś

my na pocz

ą

tku tego paragrafu, w teorii makroekonomii problem równowagi

krótkookresowej dotyczy trzech ró

ż

nych rynków: rynku dóbr, rynku pieni

ą

dza i rynku pracy. Dla

ka

ż

dego z tych rynków wyznaczamy wielko

ś

ci popytu i poda

ż

y. Modelem obejmuj

ą

cym wszystkie trzy

rynki jest kompletny model keynesowski. W modelu tym wymienione rynki s

ą

wzajemnie powi

ą

zane,

a centraln

ą

rol

ę

odgrywa w nim mechanizm wyznaczania dochodu narodowego. Dominuj

ą

cy wpływ na

dochód narodowy ma w tym modelu relacja oszcz

ę

dno

ś

ci - inwestycje.

Zanim jednak przejdziemy do omówienia kompletnego modelu Keynesa, przedstawimy najpierw

prosty model Keynesa.

Prosty model Keynesa, to dwusektorowy model gospodarki zamkni

ę

tej nie uwzgl

ę

dniaj

ą

cy roli

pa

ń

stwa w systemie ekonomicznym i mo

ż

na go zapisa

ć

w postaci układu równa

ń

:











=

+

=

+

=

I

I

Y

C

I

C

AD

β

α

.

Z powy

ż

szego układu otrzymujemy dla

AD

:

I

Y

AD

+

+

=

β

α

.

Z warunku równowagi

Y

AD

=

otrzymujemy:

I

Y

Y

+

+

=

β

α

.

St

ą

d i z układu równa

ń

wyznaczamy poziom konsumpcji

C

oraz poziom produkcji (dochodu)

Y

w stanie równowagi, które jak si

ę

okazuje zale

żą

od parametrów

β

α

,

oraz od wielko

ś

ci

zaplanowanych inwestycji

I

:

(

)

I

C

β

α

β

+

−

=

1

1

i

(

)

I

Y

+

−

=

α

β

1

1

.

Licz

ą

c pochodne cz

ą

stkowe z

C

oraz z

Y

po parametrach

β

α

,

oraz po

I

mo

ż

emy okre

ś

li

ć

kierunek oraz skal

ę

zmian

C

oraz

Y

w wyniku nieznacznych zmian (przyrostów) poszczególnych

wielko

ś

ci, przy zało

ż

eniu,

ż

e pozostałe wielko

ś

ci si

ę

nie zmieniaj

ą

.

I tak dla

C

mamy:

dr Agnieszka Bobrowska

17

Ekonomia matematyczna II

0

1

1

>

−

=

∂

∂

β

α

C

,

0

)

1

(

)

1

(

2

>

−

+

+

=

∂

∂

β

β

α

β

I

C

,

0

1

>

−

=

∂

∂

β

β

I

C

Dla

Y

mamy z kolei:

0

1

1

>

−

=

∂

∂

=

∂

∂

β

α

I

Y

Y

,

0

)

1

(

2

>

−

+

=

∂

∂

β

α

β

I

Y

.

Wnioski:

1. Przyrost warto

ś

ci któregokolwiek z parametrów

α

lub

β

o bardzo mał

ą

wielko

ść

, przy

zało

ż

eniu,

ż

e pozostałe wielko

ś

ci nie ulegaj

ą

zmianie, implikuje wzrost poziomu konsumpcji

C

odpowiednio o:

β

−

1

1

i

2

)

1

(

)

1

(

β

β

α

−

+

+

I

.

2. Przyrost warto

ś

ci inwestycji

I

o bardzo mał

ą

wielko

ść

, przy zało

ż

eniu,

ż

e pozostałe wielko

ś

ci

nie ulegaj

ą

zmianie, implikuje wzrost poziomu konsumpcji

C

o:

β

β

−

1

.

3. Pochodne cz

ą

stkowe z

Y

interpretujemy analogicznie do pochodnych cz

ą

stkowych z

C

.

Uwaga:

Łatwo zauwa

ż

y

ć

,

ż

e omawiany prosty model Keynesa ma posta

ć

dwusektorowego modelu

gospodarki zamkni

ę

tej.

Przejdziemy teraz do omówienia kompletnego modelu keynesowskiego. Punktem wyj

ś

cia do

dalszych rozwa

ż

a

ń

jest zało

ż

enie o danym poziomie cen

p

.

W modelu Keynesa rynek dóbr scharakteryzowany jest przez funkcj

ę

inwestycji i funkcj

ę

oszcz

ę

dno

ś

ci.

dr Agnieszka Bobrowska

18

Ekonomia matematyczna II

Zakładamy,

ż

e w krótkim okresie oszcz

ę

dno

ś

ci

S

s

ą

rosn

ą

c

ą

funkcj

ą

Y

, natomiast inwestycje

I

s

ą

malej

ą

c

ą

funkcj

ą

stopy procentowej

i

, co zapisujemy w nast

ę

puj

ą

cy sposób:

)

(

Y

S

S

=

, przy czym

0

>

dY

dS

oraz

)

(

i

I

I

=

, przy czym

0

<

di

dI

.

Na rynku dóbr warunek równowagi ma posta

ć

:

)

(

)

(

Y

S

i

I

=

.

Warunek ten zakłada jednoznaczn

ą

zale

ż

no

ść

mi

ę

dzy

i

i

Y

. Wynika st

ą

d,

ż

e

Y

jest funkcj

ą

i

i odwrotnie. Z monotoniczno

ś

ci funkcji

S

i

I

otrzymujemy,

ż

e

Y

maleje wraz ze wzrostem

i

.

W przypadku rynku pieni

ęż

nego w stanie równowagi popyt na pieni

ą

dz

L

zrównuje si

ę

z jego

poda

żą

M

, co zapisujemy w postaci warunku:

M

L

=

.

Przyjmujemy,

ż

e poda

ż

pieni

ą

dza jest okre

ś

lana w ramach polityki monetarnej i przyjmuje pewn

ą

ustalon

ą

warto

ść

:

M

M

=

.

O popycie na pieni

ą

dz

L

zakładamy natomiast,

ż

e jest rosn

ą

c

ą

funkcj

ą

dochodu

Y

(popyt

transakcyjny) i malej

ą

c

ą

funkcj

ą

stopy procentowej

i

(popyt spekulacyjny), co zapisujemy:

)

,

(

i

Y

L

L

=

, przy czym

0

,

0

<

∂

∂

>

∂

∂

i

L

Y

L

.

Na rynku pracy w stanie równowagi popyt równa si

ę

poda

ż

y siły roboczej. Przypomnijmy,

ż

e przez

n

oznaczamy wielko

ść

zatrudnienia w sensie popytu na sił

ę

robocz

ą

i jej poda

ż

y. Zakładamy, przy

tym,

ż

e popyt na prac

ę

okre

ś

lony jest po

ś

rednio za pomoc

ą

funkcji produkcji:

)

(

n

y

y

=

, przy czym

0

,

0

2

2

<

>

dn

y

d

dn

dy

.

Tak zdefiniowana funkcja produkcji okre

ś

la zwi

ą

zek mi

ę

dzy realn

ą

produkcj

ą

y

a wielko

ś

ci

ą

zatrudnienia

n

. Ujemny znak drugiej pochodnej z funkcji produkcji oznacza malej

ą

cy produkt

kra

ń

cowy. Nale

ż

y podkre

ś

li

ć

,

ż

e w warunkach konkurencji doskonałej, gdy mamy do czynienia

z maksymalizacj

ą

zysku, kra

ń

cowa produkcja przypadaj

ą

ca na jednego zatrudnionego jest równa

stawce płac realnych

w

:

dr Agnieszka Bobrowska

19

Ekonomia matematyczna II

w

dn

dy

=

.

Co si

ę

tyczy poda

ż

y siły roboczej, to zakładamy,

ż

e nie zale

ż

y ona od stawki płac realnych

w

, ale

od płac nominalnych

W

. Funkcja poda

ż

y siły roboczej, to funkcja odwrotna do funkcji płac

nominalnych zadanej wzorem:

)

(

n

W

W

W

+

=

, gdzie

Pw

W

=

,

przy czym:

0

)

(

=

n

W

, dla

n

n

≤

<

0

oraz

0

>

dn

dW

, dla

n

n

>

.

Przy wielko

ś

ci zatrudnienia poni

ż

ej pewnego poziomu

n

, stawka płac nominalnych jest sztywna

i wynosi

W

. Nie da si

ę

jej dostosowa

ć

tak, aby na rynku miało miejsce pełne zatrudnienie. Przy

zatrudnieniu powy

ż

ej poziomu

n

wyst

ę

puje taka stawka płac nominalnych, przy której ma miejsce

pełne zatrudnienie.

Wielko

ść

zatrudnienia

n

, dla którego spełnione s

ą

równocze

ś

nie warunki nało

ż

one na funkcj

ę

produkcji

y

i funkcj

ę

płac nominalnych

W

jest zatrudnieniem w stanie równowagi.

Ł

ą

cznie wszystkie zało

ż

enia o rynku dóbr, rynku pieni

ęż

nym i rynku pracy stanowi

ą

kompletny

model keynesowski, przy zało

ż

eniu stałego poziomu cen

p

.

dr Agnieszka Bobrowska

20

Ekonomia matematyczna II

Podsumowanie:

1. Modele równowagi krótkookresowej stanowi

ą

du

ż

e uproszczenie rzeczywisto

ś

ci gospodarczej.

2. Zakłada si

ę

w nich natychmiastowe dostosowania rozwa

ż

anych makrokategorii (np. dochód

narodowy, inwestycje, konsumpcje) i cen.

3. Modele równowagi krótkookresowej pozwalaj

ą

wyznaczy

ć

relacje zapewniaj

ą

ce stan równowagi

w gospodarce.

4. Cech

ą

modeli równowagi krótkookresowej jest to,

ż

e przedstawiaj

ą

stan w danym momencie,

a nie pozwalaj

ą

na analiz

ę

rozwoju gospodarki.

Pytania kontrolne:

1. Zdefiniuj poj

ę

cie równowagi ogólnej w gospodarce.

2. Opisz zale

ż

no

ś

ci mi

ę

dzy podmiotami gospodarczymi w modelu dwusektorowym.

3. Jaki jest warunek równowagi rynkowej w dwusektorowym modelu gospodarki?

4. Podaj interpretacj

ę

ekonomiczn

ą

parametrów

β

α

,

wyst

ę

puj

ą

cych w funkcji konsumpcji.

5. Opisz funkcjonowanie efektu mno

ż

nikowego w przypadku modelu dwusektorowego.

6. Jakie dodatkowe zało

ż

enia w porównaniu z modelem dwusektorowym wprowadza si

ę

konstruuj

ą

c model trój- i czterosektorowej gospodarki?

7. Wyznacz punkt równowagi w modelu gospodarki otwartej.

8. Jak definiowane s

ą

funkcje oszcz

ę

dno

ś

ci i inwestycji w modelu keynesowskim?

9. Jakie zało

ż

enie dotycz

ą

ce ogranicze

ń

procesu dostosowania poziomu płac do poda

ż

y i popytu

na rynku pracy przyjmuje si

ę

w modelu Keynesa?