OPRACOWANIE WYNIKÓW

I. ZALEŻNOŚD CZĘSTOTLIWOŚCI DRGAO STRUNY OD LICZBY FALOWEJ, DYSPERSJA

Dla każdego numeru harmonicznej drgao struny policzono odpowiednią liczbę falową fali w

strunie. Skorzystano ze wzoru:

Gdzie: N – numer harmonicznej, L – długośd struny (0,85m) , a za π podstawiono

wartośd: 3,141592653589793.

Policzono również prędkośd fali dla każdej harmonicznej. Skorzystano ze wzoru:

Gdzie: N – numer harmonicznej, L – długośd struny (0,85m),

– zmierzona częstotliwośd

dla da każdej harmonicznej.

Wyniki dla poszczególnych obliczeo zostały przedstawione w tabeli nr 1.

Wartości zostały zaokrąglone do dwóch miejsc po przecinku.

Tabela nr 1. Częstotliwośd zmierzona, liczba falowa i prędkośd fali dla poszczególnych
harmonicznych

N

, Hz

k

N

,

V

N

,

1

67

3,70

113,90

2

135

7,34

114,75

3

203

11,09

115,04

4

271

14,78

115,18

5

339

18,48

115,26

6

407

22,18

115,32

7

475

25,87

115,36

8

542

29,57

115,18

9

609

33,26

115,04

10

684

36,96

116,28

11

750

40,66

115,91

12

819

44,35

116,06

13

890

48,05

116,38

14

958

51,74

116,33

15

1027

55,44

116,39

16

1099

59,14

116,77

17

1162

62,83

116,20

18

1239

66,53

117,02

19

1314

70,22

117,57

20

1383

73,92

117,56

N – numer harmonicznej

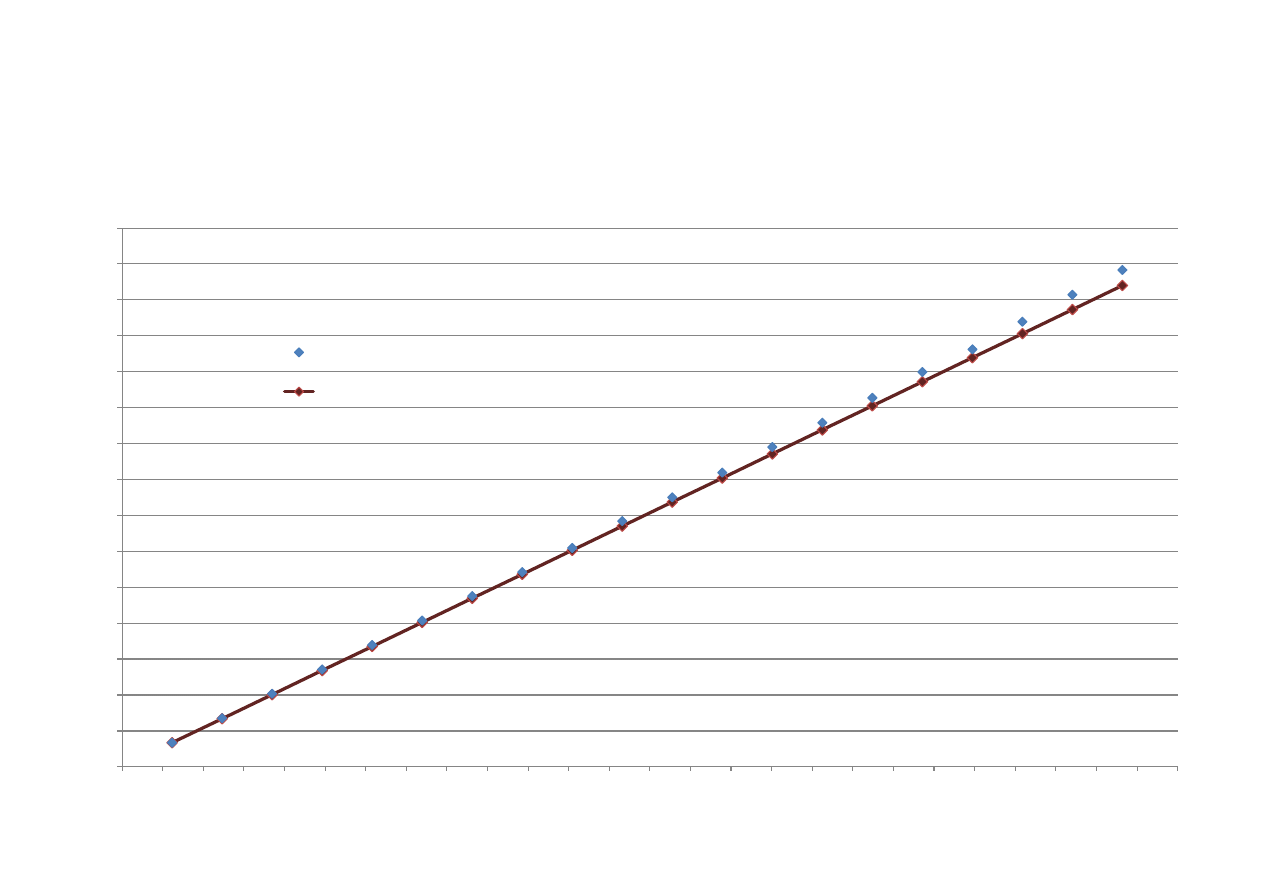
Sporządzono wykresy:

Wykres nr 1: Zależnośd rejestrowanych częstotliwości harmonicznych

od liczby falowej

(wartości rzeczywiste)

.

Zaznaczono również przebieg funkcji

, która zakłada liniową zależnośd między częstotliwością

wyższych harmonicznych a częstotliwością podstawową

(wartości teoretyczne).

0

100

200

300

400

500

600

700

800

900

1000

1100

1200

1300

1400

1500

0

3

6

9

12

15

18

21

24

27

30

33

36

39

42

45

48

51

54

57

60

63

66

69

72

75

78

k

N

, 1/m

f

N

, Hz

f

N

, Hz

f'

N

, Hz

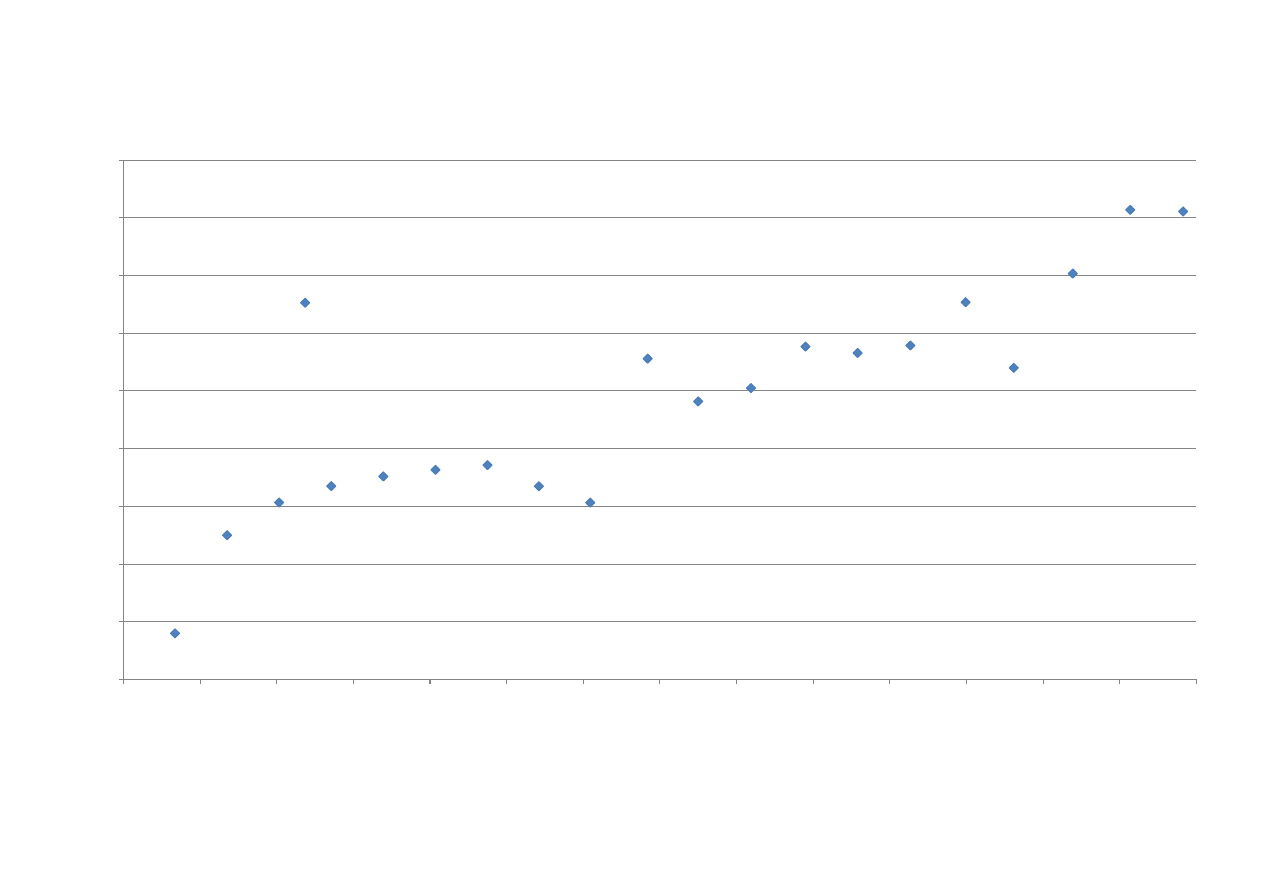
Wykres nr 2: Zależnośd prędkości fali od jej częstotliwości.

113,5

114,0

114,5

115,0

115,5

116,0

116,5

117,0

117,5

118,0

0

100

200

300

400

500

600

700

800

900

1000

1100

1200

1300

1400

f

N

, Hz

V

N

, m/s

V

N

, m/s

II. WYZNACZANIE PRĘDKOŚCI DŹWIĘKU W STRUNIE

Dla każdej długości struny począwszy od 85 cm, skracając ją o 2 cm aż do 59 cm obliczono

odwrotnośd długości struny. Dane przedstawiono w tabeli nr 2 i zaokrąglono je do dwóch

miejsc po przecinku.

Tabela nr 2. Odwrotnośd długości struny

L , m

L

-1

, m

-1

0,85

1,18

0,83

1,20

0,81

1,23

0,79

1,27

0,77

1,30

0,75

1,33

0,73

1,37

0,71

1,41

0,69

1,45

0,67

1,49

0,65

1,54

0,63

1,59

0,61

1,64

0,59

1,69

Na podstawie danych z tabeli nr 2 i karty pomiarowej sporządzono wykres nr 3, który

obrazuje zależnośd częstotliwości pierwszej harmonicznej drgao struny od odwrotności

długości struny.

Za pomocą MS Excel i gotowej funkcji REGLINP wyznaczono współczynniki a i b wraz z ich

niepewnościami prostej regresji y = ax + b:

a = 56, 27299533,

b = - 0,016623523,

u(a) = 0,694694425,

u(b) = 0, 983523622 ,

zatem: y = 56,273x – 0,017

Wzór prostej umieszczono na wykresie nr 3.

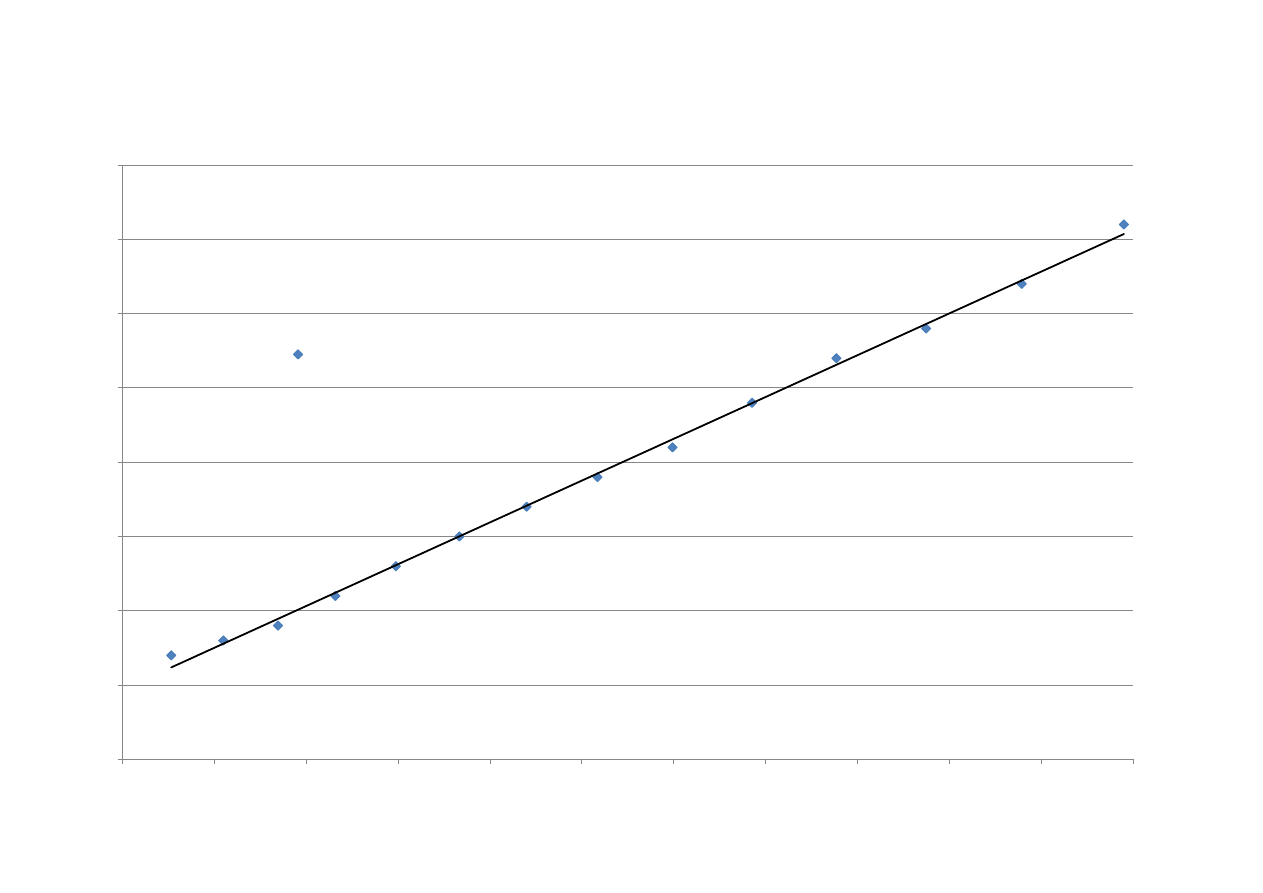
Wykres nr 3. Zależnośd częstotliwości pierwszej harmonicznej drgao struny od odwrotności długości struny.

y = 56,273x - 0,017

60

65

70

75

80

85

90

95

100

1,15

1,2

1,25

1,3

1,35

1,4

1,45

1,5

1,55

1,6

1,65

1,7

1/L , 1/m

f

1

, Hz

f

1

, Hz

Ostatnim zadaniem było policzenie prędkości fali w strunie, wraz z niepewnością.

Obliczając prędkośd korzystamy ze wzoru:

,

gdzie: N zawsze będzie równe 1, gdyż liczymy za każdym razem prędkośd dla częstotliwości

podstawowej (pierwszej harmonicznej) struny o danej długości.

Obliczając niepewnośd, korzystamy z prawa propagacji. Wykorzystujemy wzór:

,

gdzie: ,

Wyniki dla poszczególnych obliczeo zostały przedstawione w tabeli nr 3.

Tabela nr 3. Prędkośd fali w strunie wraz z niepewnością dla poszczególnych częstotliwości
podstawowych (dla różnych długości struny).

0,85

67

113,90

3,40

0,83

68

112,88

3,32

0,81

69

111,78

3,24

0,79

71

112,18

3,16

0,77

73

112,42

3,08

0,75

75

112,50

3,00

0,73

77

112,42

2,92

0,71

79

112,18

2,84

0,69

81

111,78

2,76

0,67

84

112,56

2,69

0,65

87

113,10

2,61

0,63

89

112,14

2,53

0,61

92

112,24

2,45

0,59

96

113,28

2,37

WNIOSKI

Na wykresie nr 1 widad, że istnieje rozbieżnośd pomiędzy wartościami rzeczywistymi
zmierzonymi podczas doświadczenia a wartościami teoretycznymi częstotliwości
harmonicznej. Odchylenie otrzymanej doświadczalnie zależności f

N

= f(k

N

) od prostej,

dowodzi istnienia zjawiska zwanego dyspersją fal poprzecznych w strunie.
Z wykresu 2 wnioskujemy, że prędkośd fali w strunie rośnie wraz z jej częstotliwością.
W dodatku im bardziej skrócimy strunę tym częstotliwośd podstawowa jest większa.
Wszystkie odstępstwa od teoretycznych obliczeo mogą wynikad z tego, że elektromagnes nie
został dokładnie ustawiony w strzałce fali, z niedokładności pomiaru długości struny czy
trudności w zaobserwowaniu maksymalnych drgao na oscyloskopie dla coraz wyższych
harmonicznych.