Z6/1. Mimośrodowe działanie siły – zadanie 1
1
Z6/1.Mimośrodowe działanie siły – zadanie 1
Z6/1.1 Zadanie 1
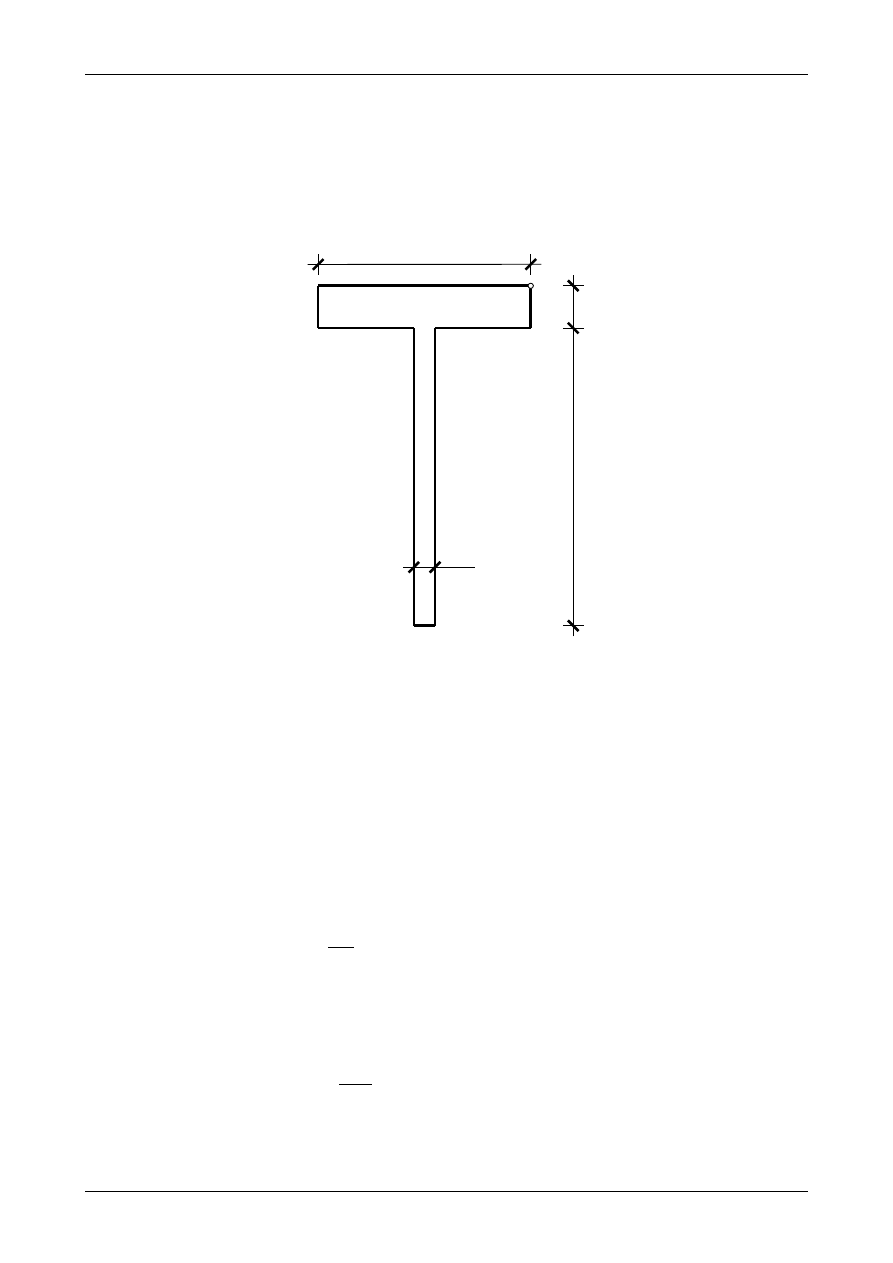
W przekroju teowym przedstawionym na rysunku Z6/1.1 działa siła normalna o wartości +220,0 kN.
Siła ta jest przyłożona w punkcie A. Narysować wykres naprężeń normalnych w przekroju.
4
,0
20,0
28
,0
2,0
[cm]
A
Rys. Z6/1.1. Przekrój teowy obciążony mimośrodowo.
Z6/1.2 Środek ciężkości i główne momenty bezwładności przekroju teowego
Ponieważ przekrój teowy posiada jedną oś symetrii środek ciężkości znajduje się na tej osi.
Współrzędna z
C
środka ciężkości przekroju teowego wynosi zero. W celu wyznaczenia położenia środka
ciężkości teownika obieramy początkowy układ współrzędnych Y
P
Z
P
. Oś Y
P
jest osią symetrii przekroju
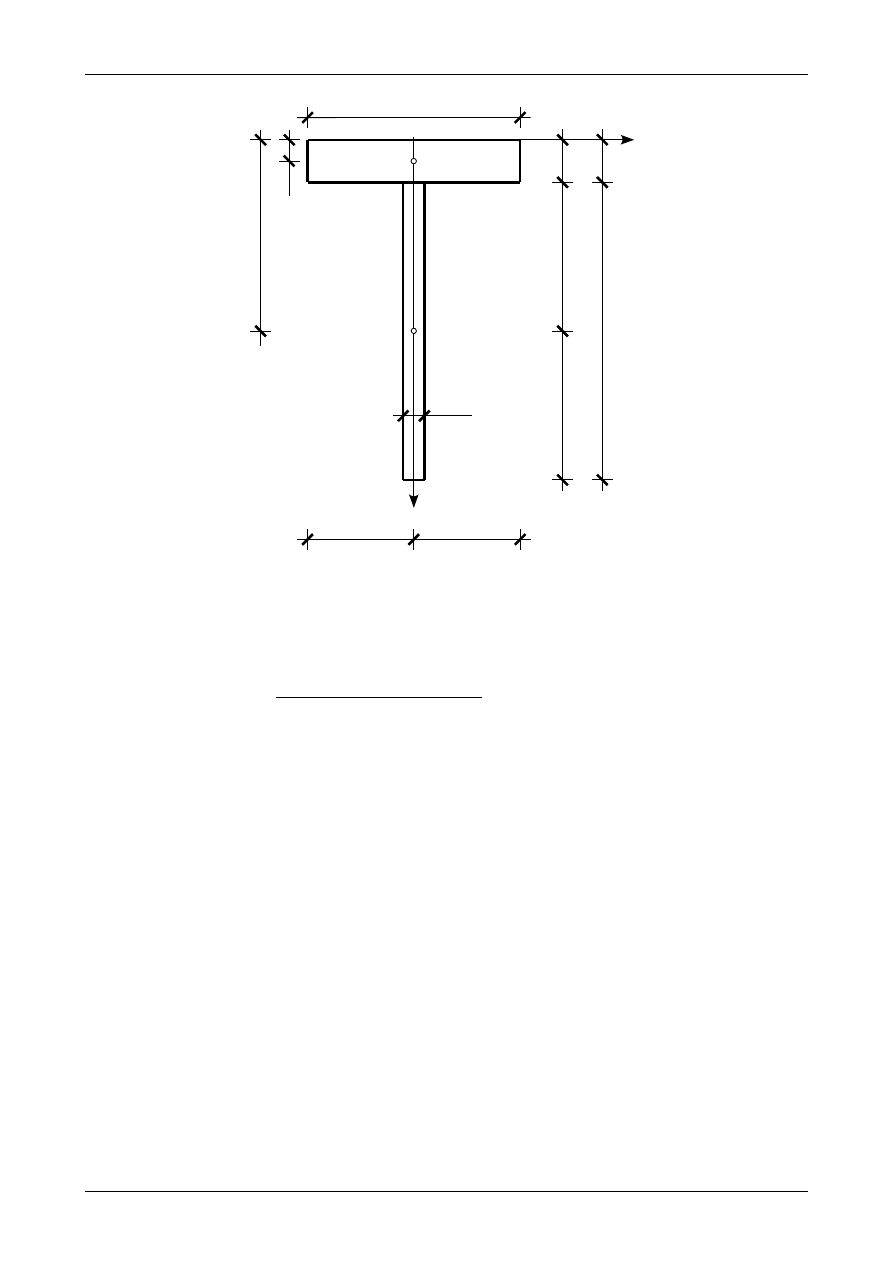
teowego. Przekrój teowy dzielimy na dwa prostokąty: półkę o wymiarach 20,0 cm na 4,0 cm oraz środnik o
wymiarach 28,0 cm na 2,0 cm. Rysunek Z6/1.2 przedstawia położenie środków ciężkości poszczególnych
figur składowych w układzie Y
P
Z
P
.
Środek ciężkości figury numer 1 posiada współrzędne
y
P1
=
4,0
2
=2,0 cm z
P1
=0,0 cm
.
(Z6/1.1)
Środek ciężkości figury numer 2 posiada współrzędne
y
P2
=4,0
28,0
2
=18,0cm z
P2
=0,0 cm
.
(Z6/1.2)
Dr inż. Janusz Dębiński
BZZ
Z6/1. Mimośrodowe działanie siły – zadanie 1
2
10,0
10,0
20,0
4,
0
14
,0
1
4,
0
1
8,
0
Z
P
Y
0
=Y
P
sc
1
sc
2
[cm]
4,
0
28
,0
2,0
2
,0
Rys. Z6/1.2. Podział przekroju teowego na figury składowe.
Zgodnie ze wzorem (3.18) współrzędna y
C
środka ciężkości wynosi
y
C
=
20,0
⋅4,0⋅2,028,0⋅2,0⋅18,0
20,0
⋅4,028,0⋅2,0
=8,588 cm
.
(Z6/1.3)
Pole powierzchni przekroju teowego wynosi
A
=20,0⋅4,028,0⋅2,0=136,0 cm
2
.
(Z6/1.4)
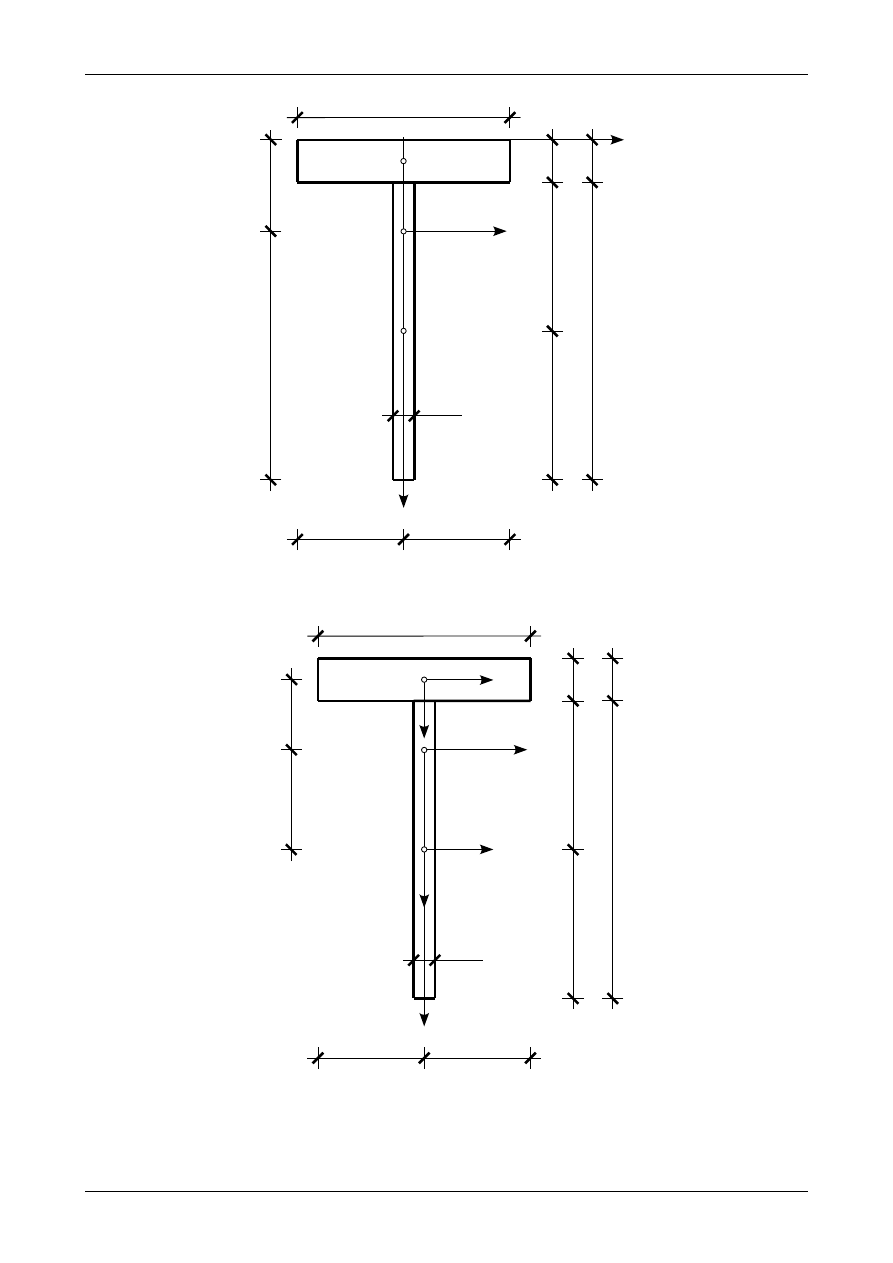
Rysunek Z6/1.3 przedstawia położenie środka ciężkości przekroju teowego. Zgodnie z wzorami
transformacyjnymi (3.11) i (3.12) współrzędne środka ciężkości figury numer 1 w układzie osi środkowych
wynoszą
y
01
=2,0−8,588=−6,588cm z
01
=0,0 cm
.
(Z6/1.5)
Współrzędne środka ciężkości figury numer 2 w układzie osi środkowych wynoszą
y
02
=18,0−8,588=9,412 cm z
02
=0,0cm
.
(Z6/1.6)
Dr inż. Janusz Dębiński
BZZ
Z6/1. Mimośrodowe działanie siły – zadanie 1
3
10,0
10,0
20,0
4,
0
14
,0
1
4,
0
8,
5
88
Z
P
Y
0
=Y
P
sc
1
sc
2
[cm]
4,
0
28
,0
2,0
Z
0
23
,4
1
sc
Rys. Z6/1.3. Położenie środka ciężkości przekroju teowego.
10,0
10,0
20,0
4,
0
14
,0
1
4,
0
6,
58
8
Y
0
=Y
gl
sc
1
sc
2
[cm]
4,
0
28
,0
2,0
9,
41
2
sc
Z
0
=Z
gl
Z
01
Y
01
Z
02
Y
02
Rys. Z6/1.4. Współrzędne środków ciężkości figur składowych w układzie osi głównych.
Dr inż. Janusz Dębiński
BZZ
Z6/1. Mimośrodowe działanie siły – zadanie 1
4
Współrzędne (Z6/1.5) i (Z6/1.6) zostały pokazane na rysunku Z6/1.4. Na rysunku tym zaznaczono także fakt,
że osi środkowe Y
0
i Z
0
są także osiami głównymi, ponieważ oś Y
0
jest osią symetrii przekroju teowego, a jak
wiadomo dewiacyjny moment bezwładności w układzie, w którym jedna z osi jest osią symetrii wynosi zero.
Dewiacyjny moment bezwładności wynosi zero także w układzie osi głównych.
Zgodnie ze wzorem (3.48) moment bezwładności względem osi Y
0
=Y
gl
wynosi
I
Y0
=I
Ygl
=
4,0
⋅20,0
3
12
0,0
2
⋅20,0⋅4,0
28,0
⋅2,0
3
12
0,0
2
⋅28,0⋅2,0=2685,0 cm
4
.
(Z6/1.7)
Zgodnie ze wzorem (3.49) moment bezwładności względem osi Z
0
=Z
gl
wynosi
I
Z0
=I
Zgl
=
20,0
⋅4,0
3
12
−6,588
2
⋅20,0⋅4,0
2,0
⋅28,0
3
12
9,412
2
⋅28,0⋅2,0=12200,0 cm
4
.
(Z6/1.8)
Z6/1.3 Wykres naprężeń normalnych
σ
X
w przekroju teowym
W przypadku przekroju teowego wykres naprężeń normalnych
σ
X
najprościej jest wyznaczyć w osiach
głównych. Współrzędne punktu przyłożenia siły normalnej wynoszą
y
N
=−8,588 cm z
N
=10,0 cm
.
(Z6/1.9)
Zgodnie z wzorem (6.3) moment zginający względem osi Y=Y
gl
wynosi
M
Y
=M
Ygl
=220,0⋅10,0=2200,0 kNcm
.
(Z6/1.10)
Zgodnie z wzorem (6.4) moment zginający względem osi Z=Z
gl
wynosi
M
Z
=M
Zgl
=220,0⋅
−8,588
=−1889,0 kNcm
.
(Z6/1.11)
Naprężenia normalne
σ
X
zgodnie ze wzorem (6.54) będą wynosiły
X
=
220,0
136,0
−1889,0
12200,0
⋅y
2200,0
2685,0
⋅z
.
(Z6/1.12)
Wzór (Z6/1.12) możemy zapisać w postaci
Dr inż. Janusz Dębiński
BZZ
Z6/1. Mimośrodowe działanie siły – zadanie 1
5
X
=1,618−0,1548⋅y0,8194⋅z
.
(Z6/1.13)
Równanie osi obojętnej będzie miało postać
1,618
−0,1548⋅y0,8194⋅z=0
,
(Z6/1.14)
które można przedstawić w postaci
−0,1548⋅y0,8194⋅z=−1,618
.
(Z6/1.15)
Dzieląc obustronnie równanie (Z6/1.15) przez -1,618 otrzymamy
0,09567
⋅y−0,5064⋅z=1
.
(Z6/1.16)
Postać odcinkowa osi obojętnej wynosi
y
10,45
z
−1,975
=1
(Z6/1.17)
Współrzędne odcinkowe osi obojętnej wynoszą
y
0
=10,45 cm z
0
=−1,975 cm
.
(Z6/1.18)
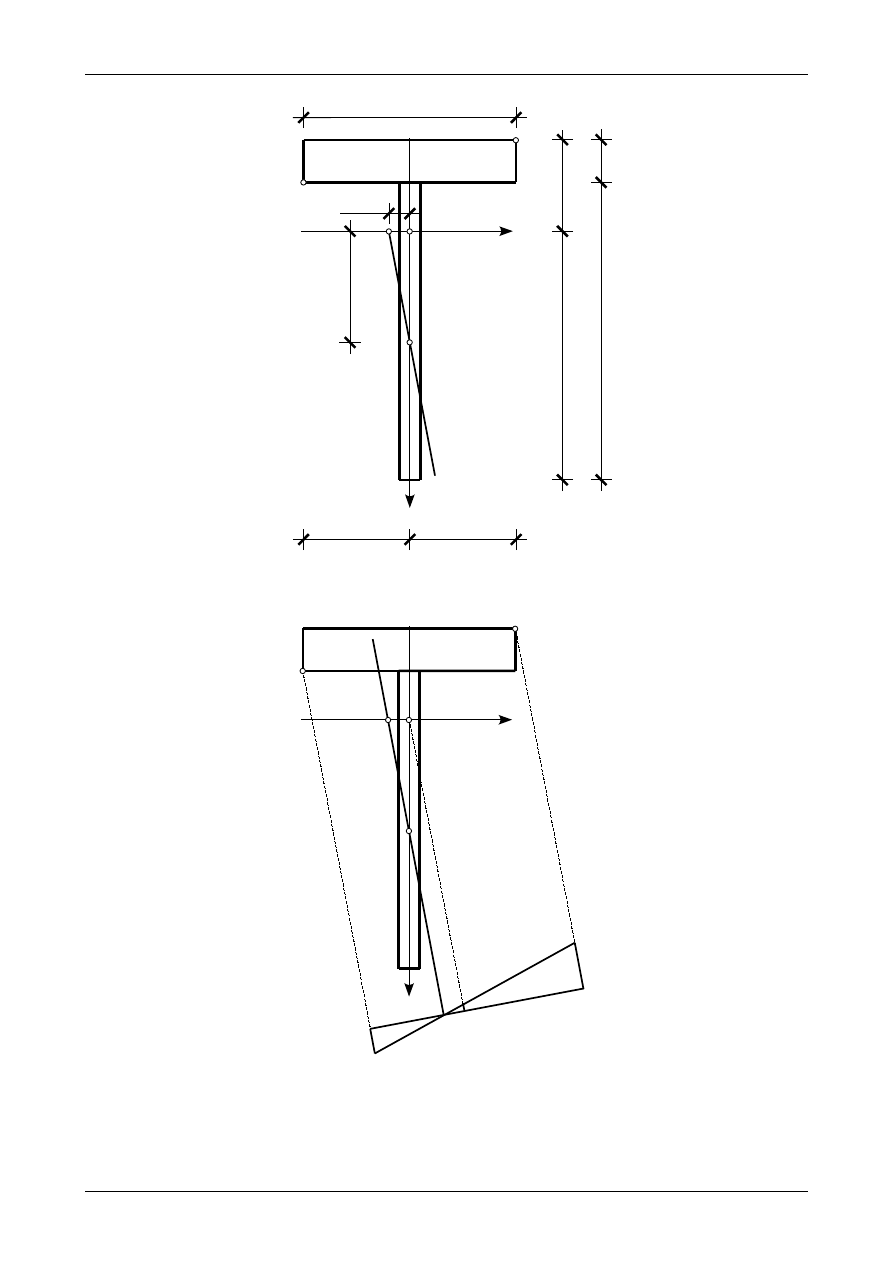
Położenie osi obojętnej przedstawia rysunek Z6/1.5. Jak widać oś obojętna przechodzi przez te ćwiartki
układu osi głównych Y
gl
Z
gl
, w których nie leży siła normalna +220,0 kN. Widać na nim także, że najdalej
oddalonymi punktami od osi obojętnej są punkty A i B. Współrzędne punktu A wynoszą
y
A
=−8,588 cm z
A
=10,0 cm
.
(Z6/1.19)
Naprężenie normalne
σ
X
w punkcie A wynosi
X
A
=1,618−0,1548⋅
−8,588
0,8194⋅10,0=11,14
kN
cm
2
=111,4 MPa
.
(Z6/1.20)
Współrzędne punktu B wynoszą
y
B
=−
8,588
−4,0
=−4,588 cm z
B
=−10,0 cm
.
(Z6/1.21)
Dr inż. Janusz Dębiński
BZZ
Z6/1. Mimośrodowe działanie siły – zadanie 1
6
10,0
10,0
20,0
8,
5
88
[cm]
4,
0
28
,0
23
,4
1
sc
Y
0
=Y
gl
Z
0
=Z
gl
1,975
10
,4
5
A
B
Rys. Z6/1.5. Położenie osi obojętnej w przekroju teowym mimośrodowo zginanym.
sc
Y
0
=Y
gl
Z
0
=Z
gl
A
B
X
+
11
1,4
M
P
a
-5
8,6
6 M
P
a
+
16
,1
8 M
P
a
0,0
M
P
a
Rys. Z6/1.6. Wykres naprężeń normalnych
σ
X
w przekroju teowym obciążonym mimośrodowo.
Dr inż. Janusz Dębiński
BZZ
Z6/1. Mimośrodowe działanie siły – zadanie 1
7
Naprężenie normalne
σ
X
w punkcie B wynosi
X
B
=1,618−0,1548⋅
−4,588
0,8194⋅
−10,0
=−5,866
kN
cm
2
=−58,66 MPa
.
(Z6/1.22)
Naprężenia normalne
σ
X
w środku ciężkości wynoszą
X
sc
=
220,0
136,0
=1,618
kN
cm
2
=16,18 MPa
.
(Z6/1.23)
Wykres naprężeń normalnych
σ
X
przedstawia rysunek Z6/1.6.
Dr inż. Janusz Dębiński
BZZ
Document Outline