www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´N Z

M

ATEMATYKI

P

RÓBNY

E

GZAMIN

M

ATURALNY

Z

M

ATEMATYKI

Z

ESTAW PRZYGOTOWANY PRZEZ SERWIS

WWW

.

ZADANIA

.

INFO

POZIOM PODSTAWOWY

26

KWIETNIA

2008

C

ZAS PRACY

: 120

MINUT

1

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´N Z

M

ATEMATYKI

Z

ADANIE

1

(5

PKT

.)

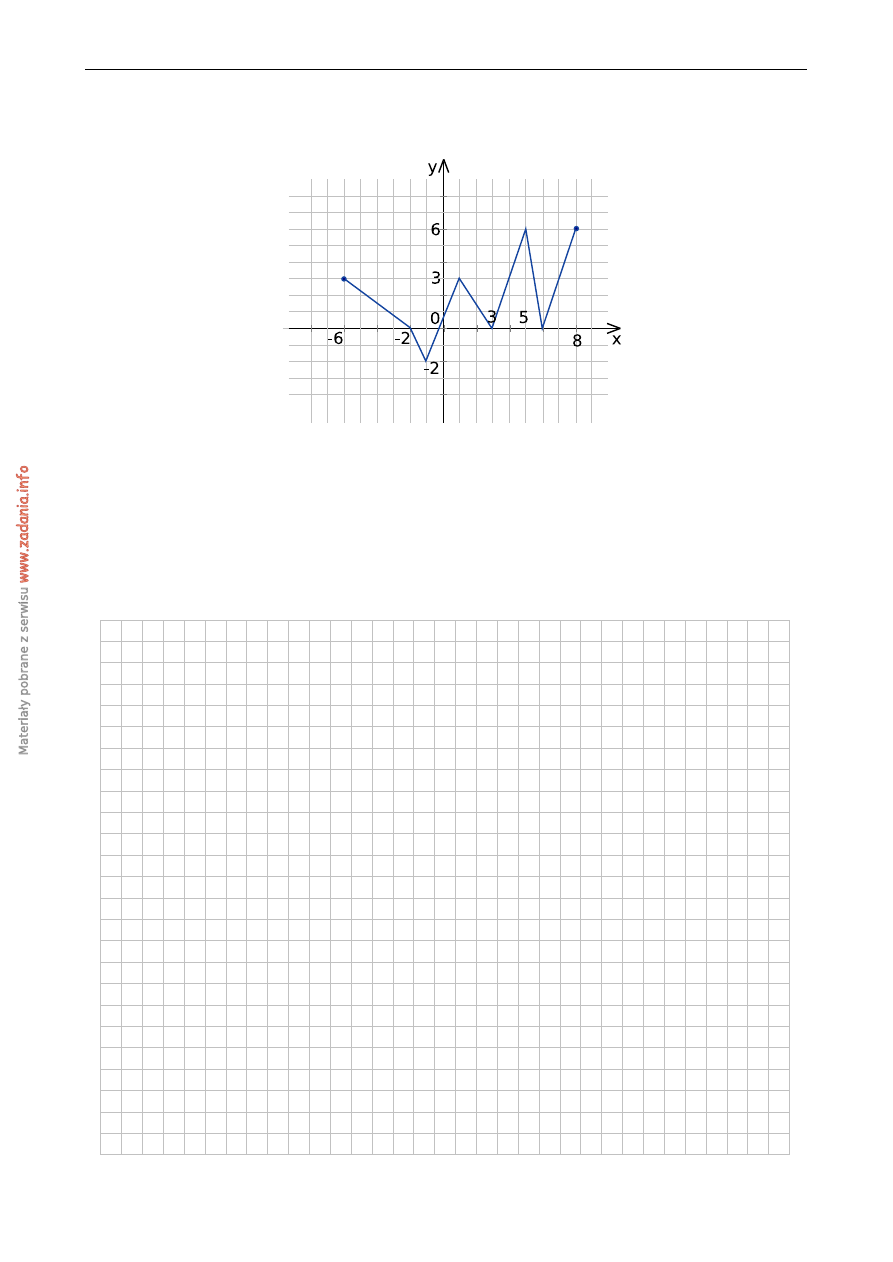
Na podstawie podanego wykresu funkcji f

a) wyznacz najwi˛eksz ˛a i najmniejsz ˛a warto´s´c funkcji;

b) podaj najdłu ˙zszy przedział na którym funkcja jest malej ˛aca;

c) zapisz w postaci sumy przedziałów zbiór rozwi ˛aza ´n nierówno´sci f

(

x

) <

3;

d) oblicz w ilu punktach wykres funkcji g

(

x

) = [

f

(

x

)]

2

przecina prost ˛a y

=

4.

2

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´N Z

M

ATEMATYKI

Z

ADANIE

2

(4

PKT

.)

W sze´scianie o kraw˛edzi długo´sci 2 poł ˛aczono ze sob ˛a ´srodki trzech ´scian maj ˛acych wspólny
wierzchołek. Sporz ˛ad´z odpowiedni rysunek i oblicz pole otrzymanego trójk ˛ata.

3

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´N Z

M

ATEMATYKI

Z

ADANIE

3

(5

PKT

.)

Sprzedawca kwiatów notował w tabeli ilo´s´c otrzymanych banknotów z podziałem według
ich nominałów.

1 dzie ´

n

2 dzie ´

n

3 dzie ´

n

4 dzie ´

n

5 dzie ´

n

10 zł

2

7

4

6

1

20 zł

5

5

2

4

3

50 zł

2

3

0

3

5

100 zł

1

3

1

1

2

a) Podaj, w których dniach jego przychody były wy ˙zsze ni ˙z ´sredni dzienny przychód w

ci ˛agu tych pi˛eciu dni.

b) Oblicz odchylenie standardowe liczby otrzymanych banknotów w ci ˛agu tych pi˛eciu

dni. Wynik podaj z dokładno´sci ˛a do 0,1.

4

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´N Z

M

ATEMATYKI

Z

ADANIE

4

(5

PKT

.)

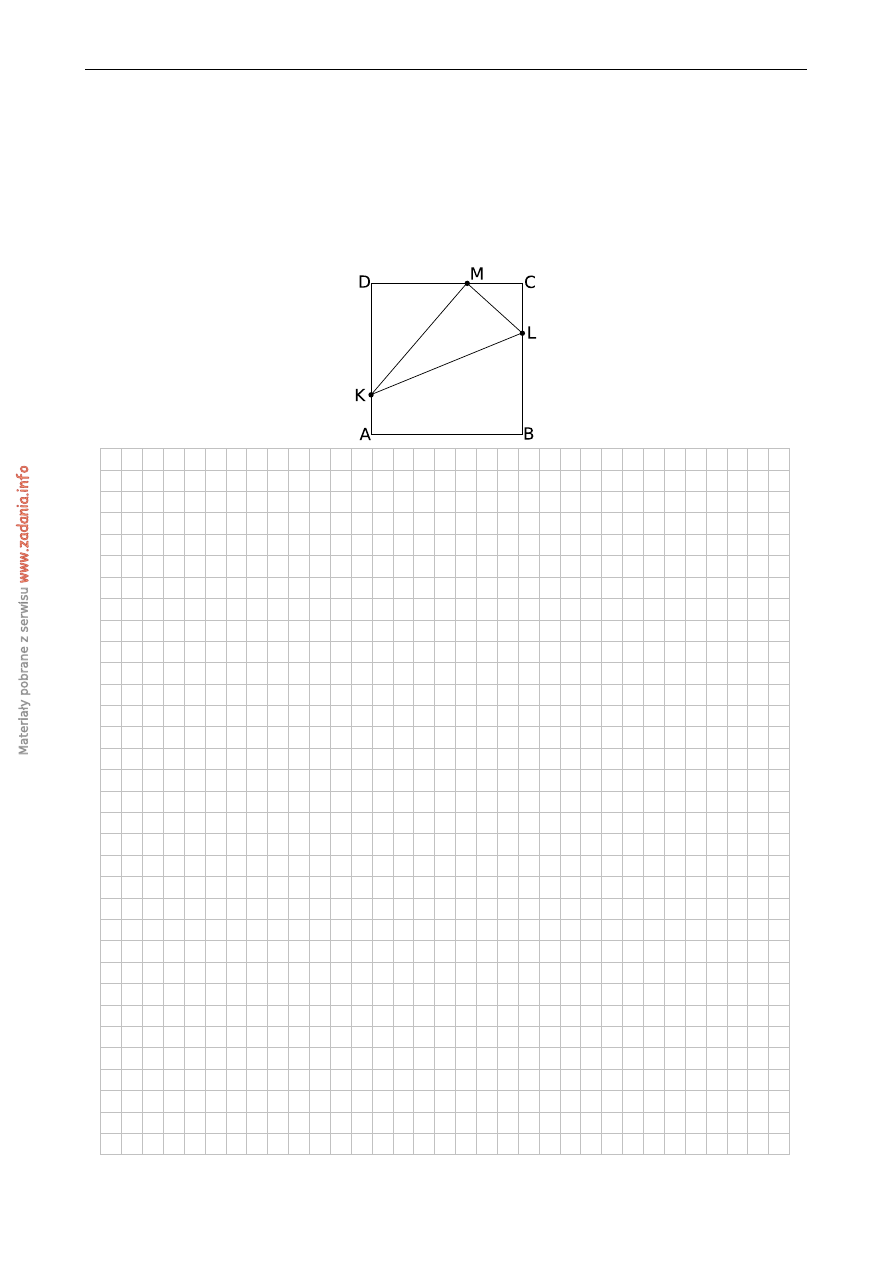
Na bokach AD, DC i CB kwadratu ABCD wybrano punkty K, M i L ten sposób, ˙ze

|

DK

| =

2

|

KA

|

,

|

DM

| =

2

|

MC

|

, oraz

|

BL

| =

2

|

LC

|

.

a) Uzasadnij, ˙ze trójk ˛at KLM jest prostok ˛atny.

b) Oblicz tangensy k ˛atów ostrych trójk ˛ata KLM.

5

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´N Z

M

ATEMATYKI

Z

ADANIE

5

(6

PKT

.)

Wykres funkcji kwadratowej f jest styczny do prostej y

= −

4, przechodzi przez punkt

(

3, 14

)

oraz jest symetryczny wzgl˛edem osi Oy.

a) Wyznacz wzór funkcji f i narysuj jej wykres.

b) Rozwi ˛a˙z nierówno´s´c

−

1

2

f

(

x

) >

x

6

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´N Z

M

ATEMATYKI

Z

ADANIE

6

(3

PKT

.)

Janek, Tomek i Łukasz zbierali pieni ˛adze na zakup piłki. Janek dał 60% potrzebnej kwoty,
Tomek dał 40% pozostałej cz˛e´sci. Łukasz doło ˙zył brakuj ˛ace 48 zł. Ile kosztowała piłka?

7

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´N Z

M

ATEMATYKI

Z

ADANIE

7

(5

PKT

.)

Dany jest okr ˛ag o ´srodku w punkcie

(

15,

−

35

)

i promieniu 16. Sprawd´z czy okr ˛ag ten jest

styczny do

a) prostej 6x

+

8y

+

30,

b) okr˛egu o ´srodku w punkcie

(

23,

−

20

)

i promieniu 2?

Uzasadnij swoj ˛a odpowied´z.

8

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´N Z

M

ATEMATYKI

Z

ADANIE

8

(5

PKT

.)

Wszystkie liczby parzyste z przedziału

h

1, 100

i

, które nie s ˛a podzielne przez 4 ustawiamy w

ci ˛ag

(

a

n

)

.

a) Wyznacz wzór ci ˛agu a

n

i uzasadnij, ˙ze jest on arytmetyczny.

b) Oblicz sum˛e wszystkich wyrazów tego ci ˛agu.

9

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´N Z

M

ATEMATYKI

Z

ADANIE

9

(5

PKT

.)

Wiedz ˛ac, ˙ze wielomian

(

x

2

−

bx

)

2

− (

ax

2

+

x

)

2

+

5b

+

5 jest wielomianem stopnia 3 oraz 1

jest jego pierwiastkiem wyznacz a i b.

10

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´N Z

M

ATEMATYKI

Z

ADANIE

10

(4

PKT

.)

Spo´sród 5 monet jednozłotowych, 7 dwuzłotowych i 6 pi˛eciozłotowych wybieramy 3 mone-
ty. Oblicz prawdopodobie ´nstwo, ˙ze wszystkie trzy monety b˛ed ˛a miały ten sam nominał.

11

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´N Z

M

ATEMATYKI

Z

ADANIE

11

(3

PKT

.)

Suma pól dwóch kół stycznych zewn˛etrznie jest równa 234π cm

2

. Oblicz promienie tych kół,

je ˙zeli wiadomo, ˙ze obwód wi˛ekszego koła jest o 400% wi˛ekszy od obwodu mniejszego koła.

12