Relativistic

Relativistic

Universe

Universe

Quantitative

Quantitative

theory

theory

of

of

star

star

structure

structure

and

and

star

star

evolution

evolution

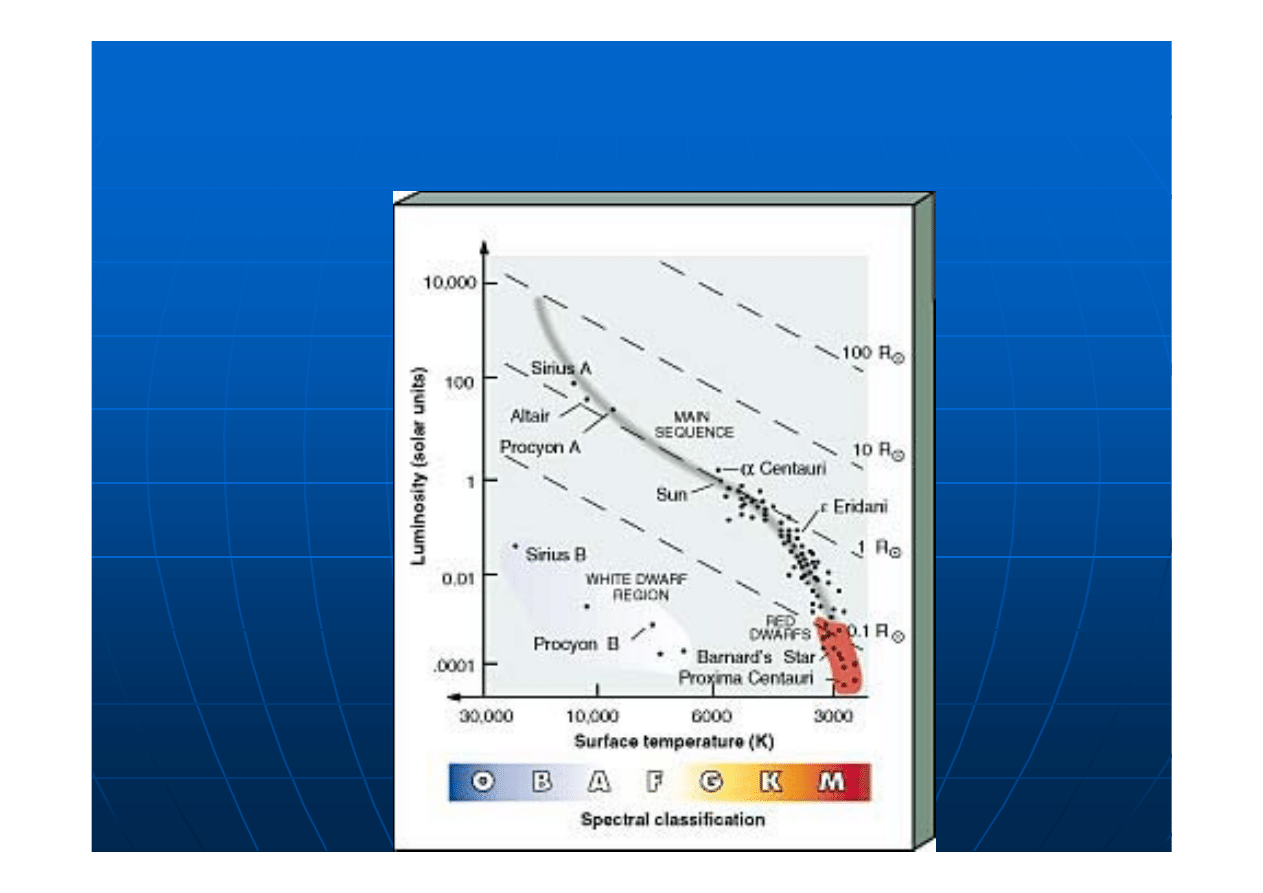
The

The

Hertzprung

Hertzprung

-

-

Russel

Russel

diagram

diagram

Three

Three

main

main

stages

stages

„

„

There are three main stages of star

There are three main stages of star

evolution:

evolution:

1.

1.

From molecular cloud to main

From molecular cloud to main

sequrence

sequrence

star;

star;

2.

2.

Main sequence;

Main sequence;

3.

3.

From main sequence, through red giant

From main sequence, through red giant

to white dwarf (neutron star, black hole).

to white dwarf (neutron star, black hole).

Both evolution and internal

Both evolution and internal

structure of stars are now well

structure of stars are now well

understood!

understood!

The

The

interior

interior

of

of

a star

a star

…

…

„

„

Can

Can

be

be

described

described

by Euler

by Euler

equation

equation

of

of

fluid

fluid

dynamics

dynamics

1

(

)

u

u

u

P

t

ρ

∂

+ ⋅∇ = −∇Φ − ∇

∂

Euler

Euler

equation

equation

1

(

)

u

u

u

P

t

ρ

∂

+ ⋅∇ = −∇Φ − ∇

∂

u is vector of velocity of small element of the fluid;

ρ

is density;

P

is pressure;

Φ

is Newtonian potential.

In

In

equilibrium

equilibrium

„

„

Equation of hydrostatic equilibrium

Equation of hydrostatic equilibrium

P

ρ

∇ = − ∇Φ

Stars in equilibrium

Stars in equilibrium

„

„

The equilibrium equation implies

The equilibrium equation implies

relation among pressure, mass, and

relation among pressure, mass, and

radius.

radius.

P

ρ

∇ = − ∇Φ ⇒

(

)

3

2

2

/

( )

M M R

dP

M r

dr

r

R

ρ

∼

∼

„

„

On

On

the

the

other

other

hand

hand

2

4

dP

P

M

P

dr

R

R

⇒

∼

∼

For

For

white

white

dwarf

dwarf

„

„

The star is composed of degenerate

The star is composed of degenerate

gas of electrons, for which

gas of electrons, for which

5 / 3

5 / 3

5

M

P

R

ρ

∼

∼

2

4

dP

P

M

P

dr

R

R

⇒

∼

∼

It

It

follows

follows

that

that

„

„

As the mass of configuration

As the mass of configuration

increases the radius decreases. More

increases the radius decreases. More

massive the white dwarf, the smaller

massive the white dwarf, the smaller

its radius. Adding matter to white

its radius. Adding matter to white

dwarf (by accretion, for example)

dwarf (by accretion, for example)

causes its radius to decrease.

causes its radius to decrease.

3

~

M

R

−

„

„

Sooner or later the equation of state

Sooner or later the equation of state

must change over to the fully

must change over to the fully

relativistic one. Here

relativistic one. Here

4 / 3

4 / 3

4

~

~

~

M

P

M

const

R

ρ

⇒

„

„

Thus for fully relativistic degenerate

Thus for fully relativistic degenerate

gas, there is a unique mass for which

gas, there is a unique mass for which

the configuration is stable. If this

the configuration is stable. If this

mass is exceeded, the star would

mass is exceeded, the star would

collapse. Thus white dwarfs cannot

collapse. Thus white dwarfs cannot

be more massive than this limiting

be more massive than this limiting

mass, called the Chandrasekhar limit

mass, called the Chandrasekhar limit

and equal 1.4 M

and equal 1.4 M





Let

Let

us

us

derive

derive

a

a

time

time

averaged

averaged

form

form

of

of

Euler

Euler

equation

equation

„

„

By standard calculation we can convince

By standard calculation we can convince

ourselves that

ourselves that

(

)

u

du

u

u

t

dt

∂

+ ⋅∇ =

∂

„

„

So that we can write

So that we can write

0

du

P

dt

ρ

ρ

+ ∇Φ + ∇ =

„

„

We

We

multiply

multiply

by

by

and

and

then

then

integrate

integrate

over

over

volume

volume

of

of

the

the

star

star

0

du

P

dt

ρ

ρ

+ ∇Φ + ∇ =

0

V

V

V

du

r

dV

r

dV

r

P dV

dt

ρ

ρ

⋅

+

⋅∇Φ

+

⋅∇

=

∫

∫

∫

r

Consider

Consider

this

this

equation

equation

term by term

term by term

V

du

r

dV

dt

ρ

⋅

=

∫

2

2

V

d r

r

dV

dt

ρ

⋅

=

∫

2

2

2

2

2

2

1

1

2

2

2

V

V

d

d I

r dV

u dV

T

dt

dt

ρ

ρ

−

=

−

∫

∫

I is the total moment of inertia about the origin,
T is total kinetic energy

V

r

P dV

ρ

⋅∇

=

∫

3

3

(

)

s

S

V

r n P dA

P

r

dV

⋅

−

=

∇ ≡

∫

∫

3

2

V

P dV

U

−

= −

∫

The pressure P vanishes on the surface;
We assume that gas inside the star is ideal.

V

r

dV

ρ

⋅∇Φ

= Ω

∫

For 1/r

2

force this is just the total potential energy.

Non

Non

-

-

averaged

averaged

virial

virial

theorem

theorem

„

„

Finally

Finally

we

we

get

get

2

2

1

2(

)

2

d I

T

U

dt

=

+

+ Ω

Virial

Virial

theorem

theorem

„

„

If we consider a system in

If we consider a system in

equilibrium, or at least long

equilibrium, or at least long

-

-

term

term

steady state, then the time average

steady state, then the time average

of moment of inertia vanishes and

of moment of inertia vanishes and

we have

we have

2

2

0

T

U

+

+ Ω =

Consequences

Consequences

„

„

Let us estimate the parameters of

Let us estimate the parameters of

the cloud from which star can

the cloud from which star can

eventually form. The internal kinetic

eventually form. The internal kinetic

energy of the gas in the cloud must

energy of the gas in the cloud must

be less than one half the

be less than one half the

gravitational energy, in order for

gravitational energy, in order for

moment of inertia to show any

moment of inertia to show any

accelerative contraction.

accelerative contraction.

„

„

For uniform gas confined to a sphere

For uniform gas confined to a sphere

with radius

with radius

R

R

c

c

and of temperature T

and of temperature T

2

2

4

3

2

2

3

c

h

c

R

kT

GM

m

R

π

ρ

μ

⎛

⎞⎛

⎞

≤

⎜

⎟⎜

⎟

⎝

⎠

⎝

⎠

μ

m

h

is an effective mass of a particle in the gas.

„

„

This distance is called Jeans length, it is

This distance is called Jeans length, it is

the distance below which a gas cloud

the distance below which a gas cloud

becomes gravitationally unstable.

becomes gravitationally unstable.

„

„

For a solar mass of material at the typical

For a solar mass of material at the typical

temperature of 50K, the cloud would be

temperature of 50K, the cloud would be

smaller than about 5

smaller than about 5

×

×

10

10

-

-

3

3

pc, with mean

pc, with mean

density greater than about 10

density greater than about 10

8

8

particles

particles

per cubic cm.

per cubic cm.

„

„

These are

These are

not

not

typical conditions in the

typical conditions in the

interstellar cloud!

interstellar cloud!

0.25(

/

)

3

h

c

M M

GM m

R

pc

kT

T

μ

≤

≈

The

The

parameter

parameter

μ

μ

„

„

It

It

is

is

convenient

convenient

to

to

devide

devide

the

the

composition

composition

of

of

the

the

stellar

stellar

matter

matter

into

into

three

three

categories

categories

:

:

„

„

X

X

–

–

mass

mass

fraction

fraction

of

of

gas

gas

which

which

is

is

hydrogen

hydrogen

„

„

Y

Y

–

–

mass

mass

fraction

fraction

of

of

gas

gas

which

which

is

is

helium

helium

„

„

Z

Z

–

–

mass

mass

fraction

fraction

of

of

gas

gas

which

which

is

is

everything

everything

else

else

(

(

metals

metals

)

)

„

„

Now we want to calculate the

Now we want to calculate the

number of particles in the unit

number of particles in the unit

volume of ionized gas.

volume of ionized gas.

„

„

Hydrogens

Hydrogens

contributes

contributes

2

2

X

X

: (

: (

electron

electron

+ proton)

+ proton)

„

„

Helium

Helium

contributes

contributes

¾

¾

Y

Y

: (2

: (2

electrons

electrons

+

+

α

α

particle

particle

but

but

the

the

mass

mass

is

is

4

4

times

times

that

that

of

of

hydrogen

hydrogen

)

)

„

„

Metals

Metals

contribute

contribute

½

½

Z

Z

: (z

: (z

electrons

electrons

+ 1

+ 1

nuclei

nuclei

, but

, but

the

the

mass

mass

is

is

2z

2z

that

that

of

of

hydrogen

hydrogen

)

)

„

„

All

All

together

together

we

we

have

have

„

„

But

But

X

X

+

+

Y

Y

+

+

Z

Z

=1

=1

(

)

3

1

2

4

2

h

N

m

ρ

=

+

+

X

Y

Z

(

)

1

1

3

1

2

2

h

N

m

ρ

=

+

+

X

Y

„

„

For

For

ideal

ideal

gas

gas

„

„

where

where

h

kT

P

NkT

m

ρ

μ

=

=

2

1

1 3

2

μ

=

+

+

X

Y

Interior

Interior

of

of

a star

a star

„

„

It

It

is

is

assumed

assumed

that

that

the

the

density

density

is

is

a

a

monotonically

monotonically

decreasing

decreasing

function

function

of

of

radius

radius

( )

( )

for

0

r

r

r

ρ

ρ

≤

>

2

3

0

( )

( )

,

( )

4

( )

4

/ 3

r

M r

r

M r

r r dr

r

ρ

π ρ

π

=

=

∫

Poisson

Poisson

’

’

s

s

equation

equation

„

„

In

In

spherical

spherical

coordinates

coordinates

2

4 G

π ρ

∇ Ω =

2

2

4

d

d

r

G r

dr

dr

π ρ

Ω

⎛

⎞ =

⎜

⎟

⎝

⎠

„

„

Integrating

Integrating

2

2

2

0

( )

4

r

d

G

GM r

r

dr

dr

r

r

π ρ

Ω

=

=

∫

But

2

( ) ( )

dP

GM r

r

P

dr

r

ρ

ρ

∇ = − ∇Ω ⇒

= −

This is the equation of hydrostatic equilibrium

for spherical stars

„

„

We

We

introduced

introduced

total

total

mass

mass

in

in

the

the

interior to r by

interior to r by

using

using

mass

mass

conservation

conservation

2

0

2

( )

4

( )

( )

4

( ),

(0)

0

r

M r

r

r dr

dM r

r

r M

dr

π ρ

π ρ

=

⇔

=

=

∫

Chandrasekhar

Chandrasekhar

variables

variables

„

„

For

For

example

example

,

,

total

total

gravitational

gravitational

energy

energy

[

]

,

0

( )

( )

( )

4

r

M r

G

I

r

dM r

r

σ

σ ν

ν

π

≡

∫

2

1,1

0

4

( )

( ) 4

R

dr

I

R

G M r

r

r

π

ρ π

=

∫

„

„

Chandrasekhar

Chandrasekhar

variables

variables

can

can

be

be

used

used

to

to

express

express

some

some

useful

useful

quantieties

quantieties

:

:

2,4

0

1,1

0

1,2

0

( )

( )

( )

;

( )

4

( )

( )

;

3

( )

( )

( )

M

M

h

M

I

R

dM r

P

P r

M

M

I

R

m

dM r

T

T r

M

k

M

I

R

dM r

g

g r

M

M

πμ

≡

=

≡

=

≡

=

∫

∫

∫

It

It

can

can

be

be

checked

checked

that

that

/ 3

1

/ 3

/ 3

,

/ 3

1

/ 3

/ 3

2

( )

4

3

1

/ 3

( )

2

( )

4

3

1

/ 3

c

G

M

r

I

r

G

M

r

ν

σ

ν

ν

σ ν

ν

σ

ν

ν

π

ρ

π

σ

ν

π

ρ

π

σ

ν

+ −

+ −

⎡

⎤

≥

⎢

⎥

+ −

⎣

⎦

≥

⎡

⎤

⎢

⎥

+ −

⎣

⎦

It

It

follows

follows

that

that

2

4

2

8

4

6

2

2

2

2

3

5.4 10

;

20

4.61 10

;

5

3

2.05 10

/

4

h

R

GM

M

P

atm

R

M

R

R

G m M

M

T

K

kR

M

R

R

GM

M

g

m s

R

M

R

π

μ

μ

⎛

⎞ ⎛

⎞

≥

=

×

⎜

⎟ ⎜

⎟

⎝

⎠

⎝

⎠

⎛

⎞⎛

⎞

≥

=

×

⎜

⎟⎜

⎟

⎝

⎠

⎝

⎠

⎛

⎞⎛

⎞

≡

=

×

⎜

⎟⎜

⎟

⎝

⎠

⎝

⎠

Polytropes

Polytropes

„

„

To complete the theory of processes

To complete the theory of processes

taking place in stars we still need

taking place in stars we still need

equation of state. It turned out that

equation of state. It turned out that

significant insight into the structure

significant insight into the structure

and evolution of stars is provided by

and evolution of stars is provided by

assuming the

assuming the

polytropic

polytropic

equation of

equation of

state.

state.

(

1) /

( )

( )

n

n

P r

K

r

ρ

+

=

„

„

Using equation of state we can

Using equation of state we can

eliminate pressure from the equation

eliminate pressure from the equation

of hydrostatic equilibrium for

spherical stars

2

( ) ( )

dP

GM r

r

dr

r

ρ

= −

„

„

We

We

differentiate

differentiate

this

this

equation

equation

and

and

use

use

2

( )

4

( )

dM r

r

r

dr

π ρ

=

2

2

( )

4

( )

( )

d

r

dP

d

GM r

Gr

r

dr

r dr

dr

π

ρ

ρ

⎛

⎞

= −

= −

⎜

⎟

⎝

⎠

1/

1

n

dP

n

d

K

dr

n

dr

ρ

ρ

+

=

Polytropic

Polytropic

star (

star (

Lame

Lame

-

-

Emden

Emden

)

)

equation

equation

2

2

(

1) /

(

1)

4

;

n

n

d

Kr n

d

Gr

dr

n

dr

ρ

π

ρ

ρ

−

⎛

⎞

+

= −

⎜

⎟

⎝

⎠

Initial

Initial

conditions

conditions

„

„

We want to use natural initial

We want to use natural initial

conditions

conditions

ρ(0) =

ρ(0) =

ρ

ρ

c

c

;

;

ρ(

ρ(

R

R

) = 0.

) = 0.

But this

But this

naive choice does not work because it

naive choice does not work because it

follows from the equilibrium condition that

follows from the equilibrium condition that

0 = P (0)

0 = P (0)

∼

∼

ρ

ρ

’

’

(0).

(0).

Thus the initial conditions

Thus the initial conditions

are

are

ρ(0) =

ρ(0) =

ρ

ρ

c

c

,

,

ρ

ρ

’

’

(0) = 0

(0) = 0

, while radius of the

, while radius of the

star R is to be computed from

star R is to be computed from

ρ(

ρ(

R

R

) = 0.

) = 0.

Solutions

Solutions

„

„

Polytropic

Polytropic

equation

equation

can

can

be

be

solved

solved

analytically

analytically

only

only

for

for

few

few

(not

(not

particularly

particularly

interesting

interesting

)

)

values

values

of

of

n.

n.

It

It

can

can

be,

be,

however

however

,

,

easily

easily

solved

solved

numerically

numerically

for

for

any

any

n.

n.

„

„

For

For

all

all

polytropes

polytropes

(

1) /

(3

) /

const( )

n

n

n

n

M

R

n

−

−

=

„

„

For

For

example

example

, for

, for

isothermal

isothermal

star

star

(n=4) we

(n=4) we

have

have

1/ 3

M

R

≈

Realistic

Realistic

stars

stars

„

„

Real stars are composed of several

Real stars are composed of several

polytropic

polytropic

layers. For example red

layers. For example red

giant has isothermal (n=4) helium

giant has isothermal (n=4) helium

core surrounded by convective

core surrounded by convective

(n=1.5) hydrogen envelope. One can

(n=1.5) hydrogen envelope. One can

model such a star by appropriate

model such a star by appropriate

matching these two phases at some

matching these two phases at some

radius

radius

.

.

Nuclear

Nuclear

reactions

reactions

in

in

stars

stars

„

„

There

There

are

are

two

two

major

major

processes

processes

that

that

are

are

sources

sources

of

of

energy

energy

in

in

stars

stars

:

:

p

p

-

-

p

p

cycle

cycle

and

and

CNO

CNO

cycle

cycle

.

.

„

„

The effectiveness of a process can be

The effectiveness of a process can be

measured by amount of energy

measured by amount of energy

produced by one gram of stellar

produced by one gram of stellar

material in unit time

material in unit time

0

T

ν

ε ε ρ

=

p

p

-

-

p

p

cycle

cycle

1

H

P

2

H

β

+

γ

P

3

He

3

He

4

He

ν

2p

Other

Other

p

p

-

-

p

p

cycles

cycles

4

He

7

Be

γ

3

He

β

−

ν

3

H

4

He

Triple

Triple

α

α

process

process

0

T

ν

ε ε ρ

=

„

It is a general property of these types of reaction

rates that the temperature dependence

"weakens" as the temperature increases. At the

same time the efficiency ε

0

increases. In general,

the efficiency of the nuclear cycles rate is

governed by the slowest process taking place. In

the case of p-p cycles, this is always the

production of deuterium given in step 1. For the

CNO cycle, the limiting reaction rate depends on

the temperature. At moderate temperatures, the

production of

15

O (step 4) limits the rate at which

the cycle can proceed. However, as the

temperature increases, the reaction rates of all

the capture processes increase, but the steps

involving inverse β decay (particularly step 5),

which do not depend on the state variables, do

not and therefore limit the reaction rate. So there

is an upper limit to the rate at which the CNO

cycle can produce energy independent of the

conditions which prevail in the star.

Collapse

Collapse

of

of

protostar

protostar

„

If the cloud is gravitationally confined

within a sphere of the Jeans' length, the

cloud will experience rapid core collapse

until it becomes optically thick. If the

outer regions contain dust, they will

absorb the radiation produced by the core

contraction and reradiate it in the infrared

part of the spectrum. After the initial free-

fall collapse of a 1M

⊙

cloud, the inner core

will be about 5 AU surrounded by an outer

envelope about 20000 AU.

Jeans length

Jeans length

2

2

4

3

2

2

3

c

h

c

R

kT

GM

m

R

π

ρ

μ

⎛

⎞⎛

⎞

≤

⎜

⎟⎜

⎟

⎝

⎠

⎝

⎠

3

h

J

GM m

R

kT

μ

=

„

When the core temperature reaches

about 2000 K, the

2

H molecules

dissociate, thereby absorbing a

significant amount of the internal

energy. The loss of this energy

initiates a second core collapse of

about 10 percent of the mass with

the remainder following as a "heavy

rain".

„

After a time, sufficient matter has

rained out of the cloud, and the

cloud becomes relatively transparent

to radiation and falls freely to the

surface, producing a fully convective

star. While this scenario seems

relatively secure for low mass stars

(i.e., around 1M

⊙

), difficulties are

encountered with the more massive

stars.

Contraction onto Main Sequence

„

Once the protostar has become opaque to

radiation, the energy liberated by the

gravitational collapse of the cloud cannot

escape to interstellar space. The collapse

slows down dramatically and the future

contraction is limited by the star's ability

to transport and radiate the energy away

into space. Hayashi showed that there

would be a period after the central regions

became opaque to radiation during which

the star would be in convective

equilibrium.

Convection

Convection

by

by

buoyance

buoyance

δ

T>0

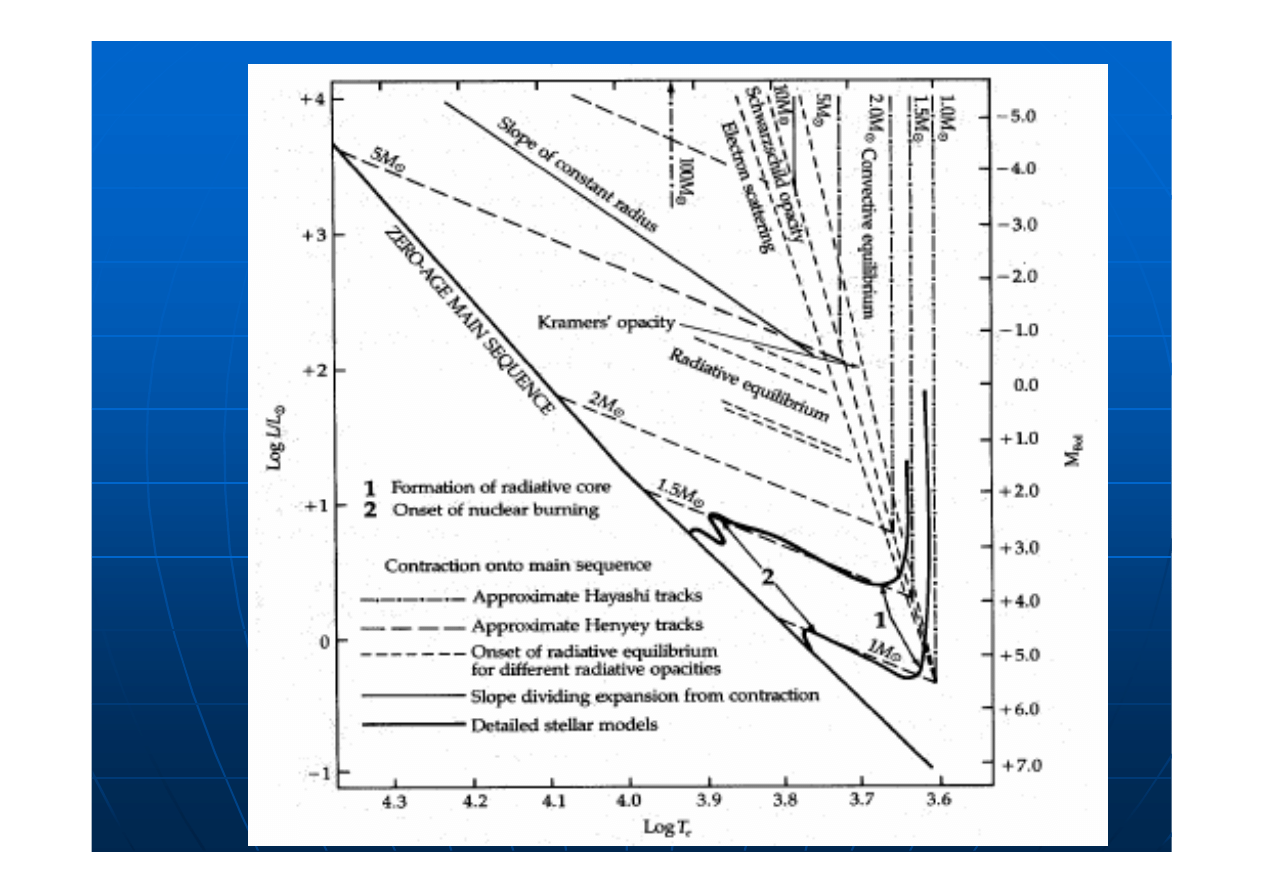
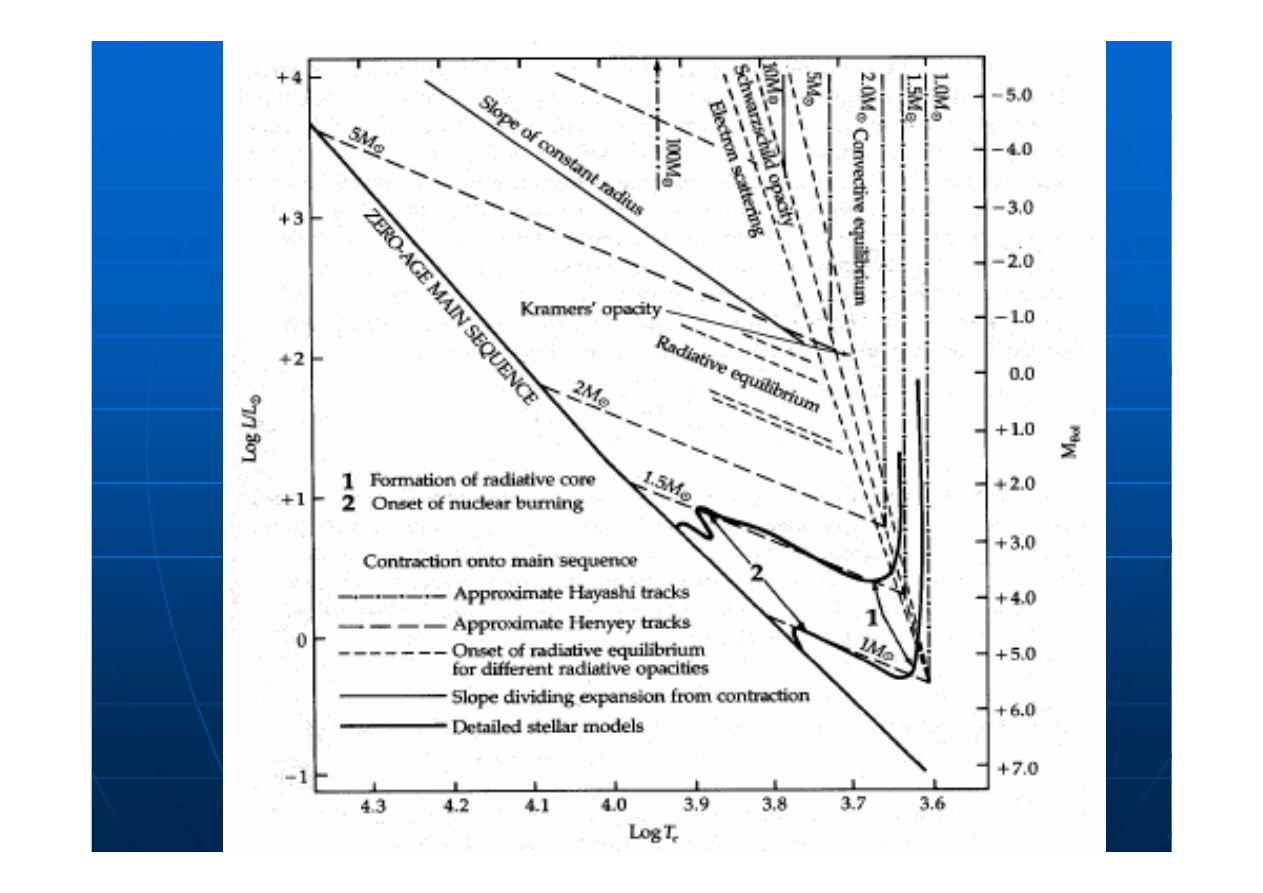
Hayashi Evolutionary Tracks

„

Once convection is established, it is

incredibly efficient at transporting energy.

Thus, as long as there are no sources of

energy other than gravitation, the future

contraction is limited by the star's ability

to radiate energy into space rather than

by its ability to transport energy to the

surface. The structure of a fully convective

star is that of a polytrope of index n =

1.5. We may combine these two

properties of the star to approximately

trace the path it must take on the

Hertzsprung-Russell diagram.

„

Some of the energy generated by

contraction will be released from the

stellar surface in the form of

photons. As long as the process is

slow, the virial theorem will hold and

<T> ≈ 0. Thus

½ <Ω> = - <U>

„

This implies that one-half of the

change in the gravitational energy

will go into raising the internal

kinetic energy of the gas. The other

half is available to be radiated away.

„

„

Therefore

Therefore

„

Since the

luminosity is

related to the

surface

parameters by

(def. of effective

temperature)

„

the change in the

luminosity with

respect to the

radius will be

2

2

2

1

1

2

2

d

GM

GM dR

L

dt

R

R

dt

⎛

⎞

=

= −

⎜

⎟

⎝

⎠

2

4

4

e

L

R

T

π σ

∗

=

4

2

e

e

dT

dL

L

L

dR

T dR

R

∗

∗

∗

=

+

„

As long as there are no sources of

energy other than gravitation, the

contraction is limited by the star's

ability to radiate energy into space

rather than by its ability to transport

energy to the surface.

„

So as long as the stellar luminosity is

determined solely by the change in

gravity, and the energy loss is

dictated by the atmosphere, we

might expect that T

e

remains

unchanged.

„

Thus dT

e

/dR

*

is approximately zero,

and we expect the star to move

vertically down the Hertzsprung-

Russell (H-R) diagram with the

luminosity changing roughly as R

*

2

until the internal conditions within

the star change. For the Hayashi

tracks

ln

0,

2

ln

e

e

dT

dT

d

L

dR

dL

d

R

∗

∗

=

=

=

log L

log T

e

„

While the location of a specific track

depends on the atomic physics of the

photosphere, the relative location of

these tracks for stars of differing

mass is determined by the fact that

the star is a polytrope of index n =

3/2. From the polytropic mass-radius

relation

1/ 3

log

1

log

3

d

R

M

R

const

d

M

∗

∗

=

⇒

= −

„

If we inquire as to the spacing of the vertical

Hayashi tracks in the H-R diagram, then we

can look for the effective temperatures for

stars of different mass but at the same

luminosity.

2

4

4

e

L

R

T

π σ

∗

=

4

2

e

e

dT

dL

L

L

dR

T dR

R

∗

∗

∗

=

+

2

4

4

e

L

R

T

π σ

∗

=

4

2

e

e

dT

dL

L

L

dR

T dR

R

∗

∗

∗

=

+

2

4

e

e

dT

dR

dL

L

L

dM

R dM

T dM

∗

∗

+

⇒

=

log

1

log

6

e

d

T

d

M

=

„

This extremely weak dependence of the

effective temperature on mass means that

we should expect all the Hayashi tracks

for the majority of main sequence stars to

be bunched on the right side of the H-R

diagram. Since the star is assumed to be

radiating as a blackbody of a given T

e

and

is in convective equilibrium, no other

stellar configuration could lose its energy

more efficiently. Thus no stars should lie

to the right of the Hayashi track of the

appropriate mass on the H-R diagram;

this is known as the Hayashi zone of

avoidance.

„

We may use arguments like these to

describe the path of the star on the

H-R diagram followed by a

gravitationally contracting fully

convective star. This contraction will

continue until conditions in the

interior change as a result of

continued contraction.

„

As the star moves down the Hayashi

track, the internal temperature

increases so that T = µM/R.

„

At some point, depending on the

dominant source of opacity, and

convection will cease.

„

At that point the mode of collapse

will change because the primary

barrier to energy loss will move from

the photosphere to the interior and

the diffusion of radiant energy.

„

As the star continues to shine, the gravitational

energy continues to become more negative,

and to balance it, in accord with the virial

theorem, the internal energy continues to rise.

This results in a slow but steady increase in the

temperature gradient which results in a steady

increase in the luminosity as the radiative flux

increases. This increased luminosity combined

with the ever-declining radius produces a

sharply rising surface temperature as the

photosphere attempts to accommodate the

increased luminosity. This will yield tracks on

the H-R diagram which move sharply to the left

while rising slightly.

„

We may quantify this by asking how

the luminosity changes in time.

„

If we further invoke the virial

theorem and require that the

contraction proceed so as to keep

the second derivative of the moment

of inertia equal to zero, then

2

2

2

2

2

2

2

1

1

2

2

2

dR

d R

dL

d

GM

dt

dt

R

R

dt

dt

∗

∗

∗

∗

⎛

⎞

Ω

⎛

⎞

= −

= −

−

+

⎜

⎟

⎜

⎟

⎜

⎟

⎝

⎠

⎝

⎠

(

)

2

2

2

2

2

2

2

2

0

0

dR

d R

d I

d

MR

R

dt

dt

dt

dt

α

∗

∗

∗

∗

⎛

⎞

=

=

⇒

+

=

⎜

⎟

⎝

⎠

Thus

Thus

(

(

Henyey

Henyey

evolution

evolution

)

)

„

„

Moreover

Moreover

log

3

log

d

L

d

R

∗

= −

2

4

e

e

dT

dR

dL

L

L

dM

R dM

T d

R dM

M dR

M

∗

∗

∗

∗

⎛

⎞

⎜

⎟

⎝

=

⎠

+

⇒

log

5

log

12

,

log

4

log

5

e

e

d

T

d

L

d

R

d

T

∗

= −

=