
110
ARKUSZ V
ZADANIA ZAMKNIĘTE
Zadanie 1 (1 pkt)
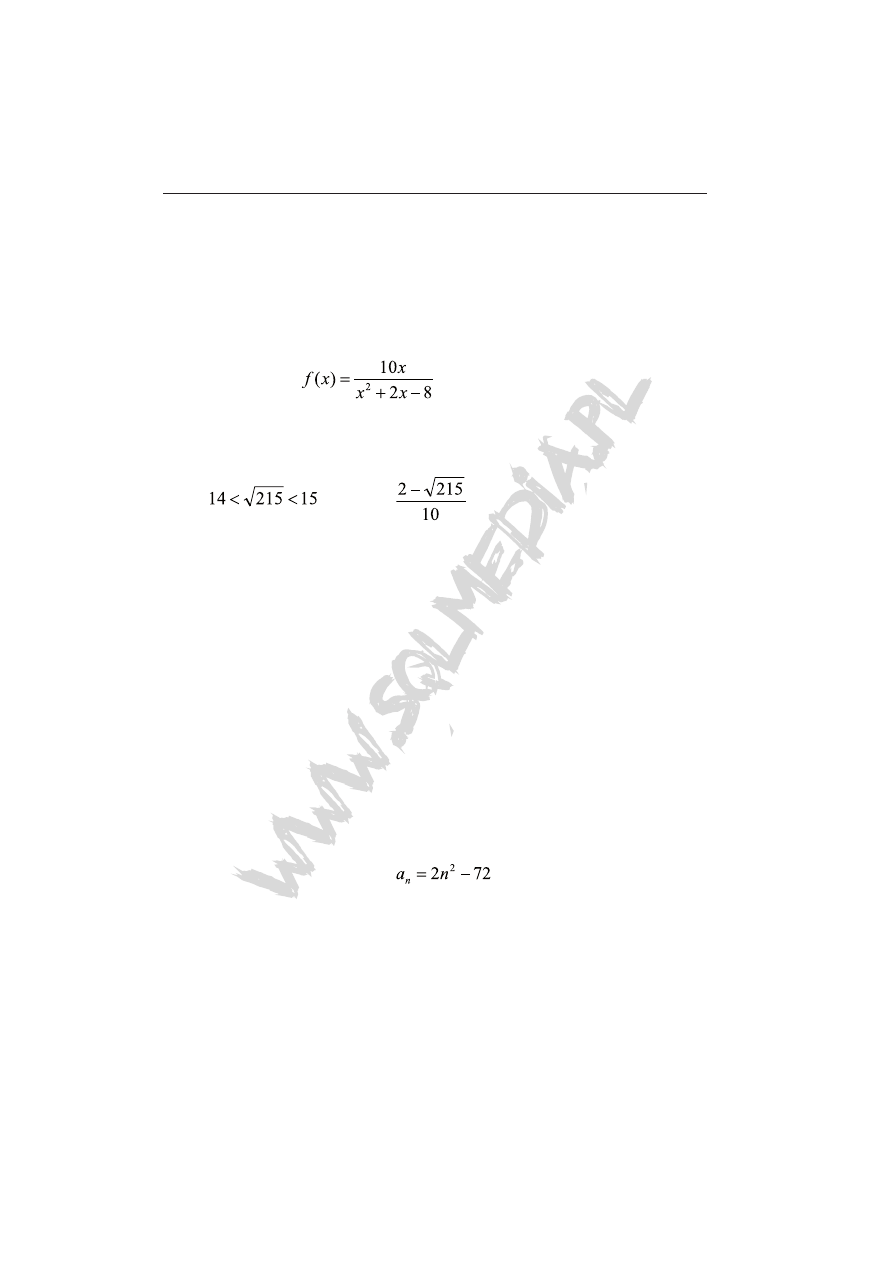
Dziedziną funkcji
jest
A) R \ {2} B) R C) R \ {2, −4} D) R \ {−4}
Zadanie 2 (1 pkt)
Jeżeli
, to liczba
należy do przedziału
A) (1,1; 1,2) B) (−1,2; −1,1) C) (−1,3; −1,2) D) (1,2; 1,3)
Zadanie 3 (1 pkt)
Ciąg (log
3
90, k, log
3
0,1) jest arytmetyczny. Zatem
A) k = 9 B) k = 2 C) k = 1 D) k = 5
Zadanie 4 (1 pkt)
Postać ogólna funkcji wyrażona jest wzorem y = x
2
+ 10x + 16.
Przedstaw tę funkcję w postaci kanonicznej.
A) y = (x + 5)
2
− 9 B) y = (x − 5)
2
+ 9
C) y = (x + 2)
2
− 8 D) y = (x − 2)
2
+ 8
Zadanie 5 (1 pkt)
Ciąg
)
(
n
a
określony jest wzorem
. Liczba ujemnych wyrazów
tego ciągu jest równa
A) 4 B) 5 C) 6 D) 7
Zadanie 6 (1 pkt)
Dany jest trapez prostokątny ABCD. Jego ramiona pozostają w stosunku
2:1 więc miara kąta ostrego wynosi
A) 15º
B) 30º
C) 45º
D) 60º
Próbny arkusz maturalny V
Poziom podstawowy
111
Zadanie 7 (1 pkt)
Wiadomo, że W
(3) =
126, gdy W
(
x
) =
x
5
– 2x
4
+ 5x
3
− 10x
2
− 2ax + 18.
Wobec tego wartość współczynnika a wynosi
A) 14 B) −3 C) 3 D) −1
Zadanie 8 (1 pkt)
Wysokość trójkąta prostokątnego poprowadzona z wierzchołka kąta prostego
ma długość 10 i dzieli przeciwprostokątną na dwa odcinki, z których
krótszy ma długość 4. Przeciwprostokątna tego trójkąta ma długość
A) 14 B) 29 C) 10 D) 18
Zadanie 9 (1 pkt)
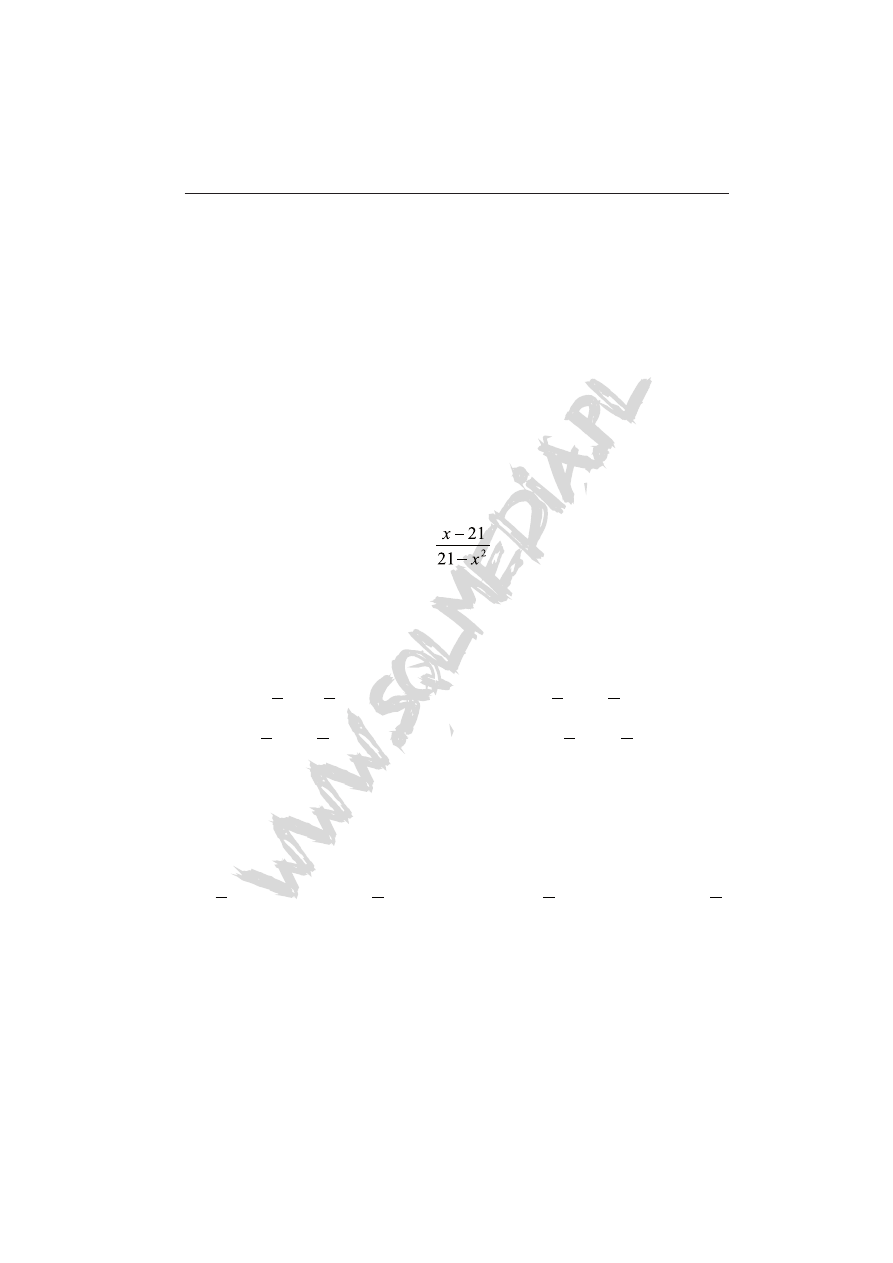
Wskaż liczbę rozwiązań równania
= 0
A) 0 B) 1 C) 2 D) 3
Zadanie 10 (1 pkt)
Wskaż postać iloczynową trójmianu y = −12x
2
+ 5x + 3.
A) −12(x +
3
1
)(x −
4
3
) B) 12(x +
3
1
)(x −
4
3
)
C) 12(x −
3
1
)(x +
4
3
) D) −12
(
x
−
3
1
)(
x
+
4
3
)
Zadanie 11 (1 pkt)
W pudełku znajdują się kule koloru białego i czerwonego. Stosunek liczby
kul białych do czerwonych wynosi 6:9. Z pudełka losujemy jedną kulę.
Prawdopodobieństwo wylosowania kuli czerwonej jest równe
A)
5
3
B)
5
2
C)
3
2
D)
2
3
Zadanie 12 (1 pkt)
Zbiór A jest zbiorem wszystkich argumentów, dla których funkcja
f
(
x
) = −
2
(
x
+
4
)(
x
− 7)
przyjmuje wartości nieujemne. Zatem
A) A
= <−
4, 7
>
B) A
= (−
∞
,
−
4
>
∪
<
7,
+
∞
)
C) A
= (−
∞
, −4
>
D) A
= <7
,
+∞)
Próbny arkusz maturalny V
Poziom podstawowy

112
Zadanie 13 (1 pkt)
Wybieramy jedną liczbę ze zbioru
{
6, 7, 8, 9
}
i jedną liczbę ze zbioru
{4
, 5
}
. Na ile sposobów można wybrać te liczby tak, aby ich iloczyn był
liczbą nieparzystą?
A) 6 B) 4 C) 5 D) 2
Zadanie 14 (1 pkt)
Liczba dodatnich pierwiastków równania
(x + 12)(x
2
− 5)(2x
3
+ 1)(3x + 1) = 0 jest równa
A) 1 B) 2 C) 5 D) 4
Zadanie 15 (1 pkt)
Osią symetrii wykresu funkcji f(x) = −6x
2
− 24x − 7 jest prosta
o równaniu
A) y
= 2
B) x
= −
2 C) x
=
2 D) y
=
−2
Zadanie 16 (1 pkt)
Pole kwadratu wpisanego w okrąg wynosi 16 j
2
. Oblicz promień okręgu.
A) 4
2
B) 4 C) 2 D) 2
2
Zadanie 17 (1 pkt)
Punkt A
= (
4,
2)
jest początkiem odcinka AB, gdzie S
= (5
, −7
)
jest jego
środkiem. Punkt B, który jest końcem tego odcinka posiada współrzędne
A) (6, −16) B) (1, −9) C) (
2
1
, −
2
9
) D) (3, −8)
Zadanie 18 (1 pkt)
Liczba
jest liczbą
A) niewymierną B) ujemną
C) należącą do przedziału (0, 1) D) większą od 1
Próbny arkusz maturalny V
Poziom podstawowy

113
Zadanie 19 (1 pkt)
Uczeń otrzymał z matematyki następujące oceny: 1, 1, 1, 2, 3, 3, 5. Średnia
tych ocen wynosi
A) 2,49 B) 2,79 C) 2,29 D) 2
Zadanie 20 (1 pkt)
Środek S okręgu o równaniu x
2
+ y
2
− 2x + 8y + 12 = 0 ma współrzędne
A) S = (1, −4) B) S = (−1, 4) C) S = (2, −8) D) S = (−2, 8)
Zadanie 21 (1 pkt)
Dany jest trójkąt o bokach a = 8 cm i b = 14 cm oraz kącie zawartym
między nimi α = 30º. Oblicz pole tego trójkąta.
A) 28 cm
2
B) 14 cm
2
C) 28
3
cm
2
D) 14
3
cm
2
Zadanie 22 (1 pkt)
Liczbą odwrotną do 2
−
6
jest
A)
2
6
2 −
B)
6
− 2 C)
6
+ 2 D)
2
2
6 −
−
Zadanie 23 (1 pkt)
Równanie x
2
+ 16 = (x − 4)
2
+ 8x
A) jest sprzeczne
B) ma tylko jedno rozwiązanie
C) jest nieoznaczone
D) ma dokładnie dwa rozwiązania
Zadanie 24 (1 pkt)
W głosowaniu dotyczącym zorganizowania studniówki wzięło udział
200 maturzystów. Za zorganizowaniem było 85% uczniów. Ile osób było
przeciwnych zorganizowaniu studniówki?
A) 36 B) 30 C) 28 D) 31
Próbny arkusz maturalny V
Poziom podstawowy

114
Zadanie 25 (1 pkt)
Kąt rozwarcia stożka wynosi 60º, natomiast wysokość 12 cm. Oblicz pole
podstawy stożka.
A) 48π cm
2
B) 24π cm
2
C) 12π cm
2
D) 96π cm
2
ZADANIA OTWARTE
Zadanie 26 (2 pkt)
Przedstaw
w postaci nieskracalnego ułamka zwykłego.
Zadanie 27 (2 pkt)
Znajdź miejsce zerowe funkcji f(x) =
Zadanie 28 (2 pkt)
Udowodnij, że skoro k, n N oraz n ≥ k ≥ 2, to k(n – k + 2) ≥ 2n.
Zadanie 29 (2 pkt)
Rozwiąż równanie −x
3
+ 5x
2
+ 3x − 15 = 0.
Zadanie 30 (2 pkt)
Dany jest ostrosłup trójkątny prawidłowy, jego wysokość ma taką samą
długość jak bok podstawy. Jaką miarę ma kąt nachylenia krawędzi bocznej
do podstawy?
Próbny arkusz maturalny V
Poziom podstawowy

115
Zadanie 31 (6 pkt)
Ze zbioru liczb {1, 2, 3, 4, … , 999, 1000} losujesz jedną liczbę. Oblicz
prawdopodobieństwo, że otrzymasz liczbę podzielną przez 3 lub przez 5.
Zadanie 32 (4 pkt)
Dany jest prostopadłościan o przekątnej długości 12. Tworzy ona
z podstawą kąt α = 60º. Jeden z boków podstawy jest równy
.
Oblicz pole powierzchni całkowitej prostopadłościanu.
Zadanie 33 (5 pkt)
Dany jest ciąg geometryczny (a
n
). Iloczyn pięciu kolejnych początkowych
wyrazów to 32. Jaki jest trzeci wyraz tego ciągu?
Próbny arkusz maturalny V
Poziom podstawowy

Wyszukiwarka
Podobne podstrony:
mat 2013 k5
mat 2013 k11
mat 2013 k3
Nauka o Mat 2013
mat 2013 k4
mat 2013 k10
mat 2013 k9
ŚWINIE MAT. 2013, weterynaria, Choroby zakaźne zwierząt gospodarskich
mat 2013 k8
mat 2013 k2
mat 2013 k11
mat 2013 k3
mat 2013 k10
mat 2013 k2
mat 2013 k11
mat 2013 k3
K Pedagogika mi-dzykulturowa, Pedagogika ogólna APS 2013 - 2016, I ROK 2013 - 2014, II semestr, 2) K
Mat Fin egz 2013
więcej podobnych podstron