Analiza języka

Wstęp

3

1. Język

4

1.1. Systemy znakowe

4

1.2. Alfabet

4

1.3. Składnia

5

1.4. Kategorie syntaktyczne

5

1.5. Funktory

5

1.6. Analiza syntaktyczna

6

1.7. Spójność syntaktyczna a sensowność

7

1.8. Elipsa

7

2. Znaczenie

9

2.1. Funkcje języka

9

2.2. Obraz świata

9

2.3. Semantyka Fregego

10

2.4. Wieloznaczność

10

2.5. Supozycje

11

2.6. Metajęzyk

11

2.7. Znaczenie potencjalne i aktualne

12

2.8. Błędy logiczne

12

3. Nazwy

13

3.1. Funkcje nazw

13

3.2. Pojęcie

13

3.3. Nieostrość nazw

14

3.4. Klasyfikacje nazw

14

3.5. Nazwy indywidualne

15

3.6. Nazwy puste

15

3.7. Nazwy jednostkowe

15

3.8. Relacje między zakresami nazw

16

4. Zdania

18

4.1. Znaczenie zdania

18

4.2. Prawda i fałsz

18

4.3. Zasada dwuwartościowości

18

4.4. Zasada niesprzeczności

19

4.5. Okazjonalność

19

4.6. Zdania analityczne i syntetyczne

20

4.7. Funktory zdaniotwórcze

20

4.8. Funktory ekstensjonalne

21

4.9. Funktory intensjonalne

21

5. Relacje logiczne

22

5.1. Równoważność

22

5.2. Sprzeczność

22

5.3. Sprzeczność jawna i utajona

23

5.4. Sprzeczność mocna

24

5.5. Dopełnianie

24

5.6. Analityczność a relacje logiczne

24

5.7. Języki naturalne a języki sztuczne

25

Bibliografia

26

Słownik

28

Spis symboli

33

3

Wstęp

Rozważania poprzedniego rozdziału pokazują, że analiza języka ma dla logiki i teorii
argumentacji pierwszorzędne znaczenie. Rozumowania są przecież prezentowane
w języku, ich poprawność zależna jest od struktury zdań, a siła oddziaływania od
użytych wyrażeń i ich kompozycji. Jednak punkt widzenia logików jest inny niż
językoznawców. Mniej interesuje ich całościowy opis języka, bardziej skupieni są na
analizie tych mechanizmów językowych, które mogą zakłócać proces komunikacji.
Zatem logików interesuje język w aspekcie j a s n e g o i p r e c y z y j n e g o
p r z e k a z u i p r z e t w a r z a n i a i n f o r m a c j i .

Zaprezentujemy teraz wybrane elementy l o g i c z n e j t e o r i i j ę z y k a , czyli takiej,
która daje ogólny opis budowy dowolnego języka naturalnego lub sztucznego.
Skupimy się przede wszystkim na problemie opisu struktury języka (temat 1)
i wyjaśnieniu pewnej teorii znaczenia (temat 2). W kolejnych dwóch tematach
omówimy szczególne kwestie, związane z kategorią nazw i zdań w języku naturalnym.
Na koniec omówimy ważniejsze relacje logiczne, zachodzące między zdaniami.

4

1. Język

1.1. Systemy znakowe

Język naturalny (etniczny) pełni niezwykle ważne funkcje kulturowe i społeczne. Jest
też fenomenem trudnym do precyzyjnego i pełnego scharakteryzowania. W

semiotyce

logicznej

rozważa się języki naturalne jako szczególny przypadek

systemów znakowych

.

W ten sposób włącza się języki naturalne do szerokiej klasy zjawisk, która zawiera
bardzo różne elementy.

Przykładem prostego systemu znakowego jest sygnalizacja świetlna — mimo
ewidentnych różnic, można jednak odnaleźć pewne cechy wspólne dla takiego
systemu i dla języka naturalnego, np. takiego, jak język polski. W obu wypadkach
mamy do czynienia z pewną liczbą znaków, których zachowaniem rządzą pewne
reguły, a inne reguły precyzują, jakie znaczenia przypisane są poszczególnym znakom
i ich kombinacjom. Generalnie można więc wyróżnić trzy s k ł a d n i k i s y s t e m u
z n a k o w e g o :
—

alfabet

albo słownik tego systemu,

—

reguły składniowe

, czyli zasady budowy poprawnych wyrażeń złożonych,

—

reguły semantyczne

, czyli zasady interpretacji komunikatów sformułowanych

w tym systemie.

W tym temacie skupimy się na pierwszych dwóch składnikach.

1.2. Alfabet

Przez

znaki

rozumiemy tutaj dowolne, trwałe (np. słowo pisane) lub nietrwałe (np.

słowo mówione, impulsy elektryczne) zjawiska, wytworzone w celu przekazywania
pewnej informacji. Czasem wyrażenie „znak” używane jest szerzej — na określenie
tego, co my nazywamy znakiem oraz związanego z nim znaczenia. W takim ujęciu
to, co tutaj nazywa się znakiem, jest określane jako substrat znaku. Nasze rozumienie
znaku wydaje się lepiej dostosowane do analizy języków sztucznych i ich użycia przez
komputery.

Znaki należy odróżnić od

oznak

(symptomów), które przekazują znaczenie w sposób

naturalny, np. dym jest oznaką ognia. Znaki powstają jako świadomy wytwór
zorganizowanej działalności człowieka, a sposób przypisywania im znaczeń ma
charakter konwencjonalny. Zespół wszystkich znaków elementarnych (słów,
wyrazów) danego języka naturalnego to jego

alfabet

lub

słownik

.

5

1.3. Składnia

Komunikaty formułowane w językach naturalnych mają zazwyczaj charakter
złożony, tzn. wymagają użycia pewnej liczby słów. To, jakie kombinacje są na gruncie
danego języka dozwolone, jest wyznaczone przez reguły składni, a opis ich działania
to

gramatyka

danego języka. Współcześnie w logice i w lingwistyce matematycznej

używa się różnych rodzajów gramatyk. Można je podzielić na dwie grupy:
—

analityczne

, które pozwalają odróżniać dozwolone (na gruncie danego języka)

kombinacje znaków od niedozwolonych,

—

syntetyczne

, które pozwalają konstruować tylko poprawne kombinacje znaków.

Gramatyki, o których tu mówimy, bardzo różnią się od tradycyjnej gramatyki
opisowej, która jest dość nieprecyzyjnym środkiem opisu języka. Dla naszych celów
wygodniejsze będzie posłużenie się jakimś rodzajem gramatyki analitycznej. Jedna
z popularniejszych gramatyk analitycznych to

gramatyka kategorialna

. Autorem tego

podejścia — posiadającego obecnie wiele odmian — jest Kazimierz Ajdukiewicz.

1.4. Kategorie syntaktyczne

W gramatyce tego rodzaju podstawowe pojęcie to

kategoria syntaktyczna

rozumiana

jako klasa wyrażeń, które mogą być wzajemnie z a s t ę p o w a l n e w dowolnym
wyrażeniu złożonym bez utraty s k ł a d n i o w e j s p ó j n o ś c i . Kategorie syntaktyczne
dzielimy na s a m o d z i e l n e i n i e s a m o d z i e l n e . Do tych pierwszych zaliczymy

zdania

i

nazwy

, na drugą grupę składają się

funktory

różnych kategorii.

Podstawowe założenie tej gramatyki sprowadza się do następującej zasady: każde
poprawne syntaktycznie wyrażenie złożone składa się z wyrażenia głównego
(f u n k t o r a ), które organizuje jego strukturę, oraz z wyrażeń podporządkowanych
(a r g u m e n t ó w tego funktora). Argumenty oczywiście same mogą być wyrażeniami
złożonymi — wtedy znów można w nich wyróżnić funktor główny i jego
argumenty.

Jedyne argumenty będące wyrażeniami prostymi to nazwy. Zdania zawsze muszą
zawierać przynajmniej jeden funktor. Jako zdania będziemy dalej traktować tylko
te wyrażenia języka naturalnego, które w gramatyce tradycyjnej określa się jako
z d a n i a o z n a j m u j ą c e . Innych rodzajów zdań nie będziemy omawiać. Co do nazw,
uznajemy za nie te wyrażenia, które w tradycyjnej gramatyce są zaliczane do takich
części mowy, jak: r z e c z o w n i k i , p r z y m i o t n i k i czy z a i m k i o s o b o w e .

W naszym omówieniu sposobu, w jaki gramatyka kategorialna dokonuje podziału
wyrażeń języka, abstrahujemy od problemów fleksji, dlatego — choć w przykładach
zdań nazwy będą występować w odpowiednim przypadku — to w izolacji podawać
będziemy je zwyczajowo w mianowniku.

1.5. Funktory

Kategorie niesamodzielne to różne typy

funktorów

, czyli takich wyrażeń, które

w połączeniu z innymi wyrażeniami (swoimi argumentami) tworzą nowe wyrażenia.

6

Funktory można podzielić — ze względu na rodzaj tworzonych wyrażeń — na trzy
grupy:

zdaniotwórcze

,

nazwotwórcze

i

funktorotwórcze

.

Dla pełnej charakterystyki funktora musimy podać nie tylko, jakiego rodzaju
wyrażenia wytwarza, ale również jakich argumentów potrzebuje i w jakiej ilości.
Dlatego charakterystykę funktora wygodnie jest podawać w postaci ułamka,
gdzie literą z oznaczamy zdanie, a literą n — nazwę. Symbole z, n oraz ułamkowe
charakterystyki funktorów to

indeksy kategorii

danego wyrażenia (dalej krótko zwane

indeksami). Oto kilka przykładów funktorów języka polskiego i ich indeksów, wraz
z przykładami zastosowań:
„...biegnie” jest kategorii z/n (funktor zdaniotwórczy od jednego argumentu
nazwowego, np. „Ro m e k biegnie”);
„...kocha...” jest kategorii z/n, n (funktor zdaniotwórczy od dwóch argumentów
nazwowych, np. „Ro m e k kocha M a ł g o s i ę ”);
„nieprawda, że...” jest kategorii z/z (funktor zdaniotwórczy od jednego argumentu
zdaniowego, np. „Nieprawda, że Ro m e k b i e g n i e ”);
„...albo...” jest kategorii z/z, z (funktor zdaniotwórczy od dwóch argumentów
zdaniowych, np. „Ro m e k b i e g n i e albo Ro m e k k o c h a M a ł g o s i ę ”);
„brat...” jest kategorii n/n (funktor nazwotwórczy od jednego argumentu nazwowego,
np. „brat A d a m a ”);
„...w sumie z...” jest kategorii n/n, n (funktor nazwotwórczy od dwóch argumentów
zdaniowych, np. „2 w sumie z 3”);
„głośno...” jest kategorii (z/n)/(z/n) (funktor funktorotwórczy (tworzy funktor
o kategorii z/n) od jednego argumentu funktorowego kategorii z/n, np. „...głośno
śpiewa” jest kategorii z/n, gdyż po dołączeniu nazwy (np. „Kowalski”) utworzy zdanie:
„K o w a l s k i głośno śpiewa”. Natomiast „...śpiewa” jest funktorem kategorii z/n,
które w wyrażeniu „...głośno śpiewa” stało się argumentem funktora „głośno...”).

Ostatni przykład wydaje się już dość skomplikowany, gdyż mamy do czynienia
z ułamkiem piętrowym. Wyrażenia języka naturalnego mogą mieć jednak jeszcze
bardziej złożony charakter, np. w zdaniu „Kowalski bardzo głośno śpiewa” wyrażenie
„bardzo...” ma kategorię ((z/n)/(z/n))/((z/n)/(z/n)), gdyż jako argument bierze funktor
„głośno...” o kategorii (z/n)/(z/n) i wytwarza funktor „bardzo głośno...”, który też
ma kategorię (z/n)/(z/n).

Złożoność syntaktyczną klasy funktorów potęguje fakt, że funktory mogą mieć także
argumenty różnych kategorii, np. „...uważa, że...” ma kategorię z/n, z, jak w zdaniu:
„Kowalski uważa, że tegoroczna zima będzie ostra”.

1.6. Analiza syntaktyczna

Gramatyka tego typu pozwala nam sprawdzać poprawność składniową danego
wyrażenia, o ile wcześniej ustalimy, do jakich kategorii należą jego części. My
ograniczymy się tylko do zilustrowania tej metody dla zdań. Najpierw wypisujemy
ciąg indeksów wszystkich wyrażeń składowych występujących w zdaniu. Jest to
syntaktyczna charakterystyka tego zdania. Dla ostatniego przykładu (tj. zdania
„Kowalski uważa, że tegoroczna zima będzie ostra”) ma ona następującą postać:

n; z/n, z; n/n; n; z/n, n; n

Podany wyżej ciąg dowodzi, że analizowane wyrażenie jest zdaniem i pokazuje, jaką ma

7

strukturę. Można to wykazać przez systematyczne skracanie ułamków wchodzących
w skład ciągu w ten sposób, że dla każdego funktora znajdujemy potrzebne mu
argumenty. Każdemu skróceniu ułamka odpowiada połączenie funktora (którego
jest on indeksem) z jednym z argumentów, co daje nowy funktor o innym indeksie.
Jeżeli w wyniku tej procedury otrzymujemy indeks z, to sprawdzane wyrażenie jest
zdaniem.

W badanym wyrażeniu indeks funktora nazwotwórczego „tegoroczna” skraca się
przez nazwę „zima” i otrzymujemy nazwę złożoną „tegoroczna zima” (n/n i n dają
indeks n). Ta nazwa i nazwa prosta „ostra” są argumentami funktora „będzie”. Po
dwukrotnym skróceniu otrzymujemy więc zdanie „tegoroczna zima będzie ostra”
(z/n, n oraz n i n dają z). Głównym funktorem całego wyrażenia jest „uważa, że”
(z/n, z), którego pierwszym argumentem jest nazwa „Kowalski”, a drugim wyrażenie
złożone „tegoroczna zima będzie ostra”. Po skróceniu przez nazwę „Kowalski”
powstaje wyrażenie złożone „Kowalski uważa, że”, które ma indeks z/z, zatem
potrzebujemy zdania jako argumentu. Ponieważ już wiemy, że wyrażenie „tegoroczna
zima będzie ostra” istotnie jest zdaniem, możemy dokonać kolejnego skrócenia,
co daje zdanie w mowie zależnej. Jak widać, każdy funktor w tym wyrażeniu ma
przyporządkowaną odpowiednią liczbę argumentów właściwej kategorii, co pozwala
je uznać za poprawne zdanie w języku polskim.

1.7. Spójność syntaktyczna a sensowność

Zwróćmy jeszcze uwagę na to, że

spójność syntaktyczna

to coś innego niż sensowność.

Zilustrujemy to na prostym przykładzie: „Kowalski kocha żonę” jest zdaniem,
w którym „kocha” to funktor kategorii z/n, n. Do tej samej kategorii należą też
wyrażenia: „bije”, „pije”, „liczy”, „miesza”, „dokręca” itd., co oznacza, że każde
z nich może poprawnie zastąpić w powyższym zdaniu wyrażenie „kocha”.

Wynik takiej operacji daje nowe zdanie w języku polskim, jednak trudno oprzeć się
wrażeniu, że — o ile zastąpienie „kocha” przez „bije” wydaje się zupełnie poprawne
— to pozostałe przykłady z trudnością dają się potraktować jako sensowne zdania
w języku polskim. Zdanie „Kowalski dokręca żonę” nie jest jednak niespójne
syntaktycznie — brak jest tutaj spójności znaczenia. Zdanie „Kowalski dokręca
zaworek” nie budzi już żadnych kontrowersji, choć jeżeli zamienimy np. nazwy
w orzeczeniu, to zdanie „Kowalski kocha zaworek” znów może wydać się dziwaczne.
Pamiętajmy, że gramatyka kategorialna daje tylko syntaktyczny opis języka, a jej
reguły wykluczają tylko „nonsensy” syntaktyczne.

1.8. Elipsa

Warto również podkreślić, że reguły omawianej gramatyki mogą też wykluczyć
z grona dopuszczalnych wyrażeń składnych szereg kombinacji, które wydają
się dopuszczalne. Wydaje się, że wyrażenie złożone „Bolek pije” jest w pełni
akceptowalnym zdaniem języka polskiego. Jednak „pije” jest funktorem kategorii
z/n, n, zatem dla utworzenia zdania potrzebuje jeszcze jednej nazwy, np. „kawa”
(oczywiście w odpowiedniej formie gramatycznej). Akceptujemy takie wyrażenia jako

8

zdania, gdyż język naturalny dopuszcza szereg mechanizmów służących zwiększeniu
ekonomii komunikacji.

Ogólnie można tu mówić o różnych rodzajach e l i p s y, która polega na pomijaniu
pewnych składników wyrażenia złożonego.

Retoryka

wyróżnia tutaj rozmaite zabiegi

służące zwiększeniu siły wyrazu poprzez maksymalną skrótowość, np. a s y n d e t o n ,
polegający na eliminacji spójników (jak w znanej reklamie „Palisz, płacisz, zdrowie
tracisz”).

Jeden z częstych przypadków elipsy to używanie funktorów nazwotwórczych
bez argumentów — jako skrótów pełnych nazw. Przykład tego rodzaju mieliśmy
w zdaniu „Kowalski kocha żonę”, gdzie „żona” występowała jako nazwa, podczas
gdy generalnie jest to funktor kategorii z/n, tworzący nazwę dopiero w złożeniach
typu „żona Kowalskiego”. W powyższym przykładzie, dla zwięzłości, pominęliśmy
domyślny argument tego funktora. Pełna rozwinięta postać mogłaby wyglądać
następująco: „Kowalski kocha swoją żonę” (gdzie zaimek „swój” zastępuje nazwę
„Kowalski”) lub „Kowalski kocha żonę sąsiada” (uwaga! znów skrót — „sąsiad”
to też funktor). Równie często mamy do czynienia z pomijaniem podmiotu, części
orzeczenia lub spójników.

Powyższe uwagi mają jedynie wyczulić Czytelnika na pewne subtelności składni
języka naturalnego. Szersza prezentacja gramatyki kategorialnej czy jakiejś innej teorii
gramatycznej, jak np. popularna w językoznawstwie g r a m a t y k a g e n e r a t y w n o -
t r a n s f o r m a c y j n a , będąca przykładem gramatyki syntetycznej, nie jest tutaj
możliwa.

9

2. Znaczenie

2.1. Funkcje języka

Język naturalny może pełnić rozmaite funkcje komunikacyjne, m.in.:
1)

e k s p r e s y w n ą (wyrażanie stanów wewnętrznych użytkownika języka),

2)

p e r s w a z y j n ą (oddziaływanie na słuchacza),

3)

f a t y c z n ą (utrzymywanie kontaktu między użytkownikami),

4)

o p i s o w ą (informowanie).

Znaczenie i oznaczanie

Najważniejsza z punktu widzenia logiki jest

funkcja opisowa

, umożliwia bowiem

przenoszenie informacji. Pełnienie tej funkcji zakłada, że znaki językowe posiadają
z n a c z e n i e i że odnoszą się w jakiś sposób do świata — że coś

znaczą

i

oznaczają

.

Relacja znaczenia

zachodzi między wyrażeniami a pewną sferą pozajęzykową

— uniwersum znaczeń.

Relacja oznaczania

(odnoszenia, referencji) łączy wyrażenia

ze światem. Obie relacje są badane na gruncie semantyki.

Trzeba podkreślić, że istnieje wiele konkretnych teorii semantycznych, proponujących
różne teorie znaczenia i oznaczania lub redukujących np. znaczenie do oznaczania.
Różnice w definiowaniu znaczenia zależą przede wszystkim od tego, w jaki sposób
pojmuje się uniwersum znaczeń — w szczególności, czy znaczenia pojmuje się jako byty
umysłowe (subiektywne lub nie), czy jakiegoś rodzaju byty idealne, nieredukowalne
do umysłu. Analizując relację oznaczania, uzależnieni jesteśmy z kolei od pewnych
z a ł o ż e ń o n t o l o g i c z n y c h , czyli naszych wyobrażeń dotyczących struktury
świata.

2.2. Obraz świata

Używanie języka w celu przekazywania informacji o świecie zakłada, że ten świat
nie jest chaosem, ale pewną s t r u k t u r ą . Zakłada też, że struktura języka w jakiś
sposób odwzorowuje strukturę świata. Filozofia wytworzyła wiele interesujących
teorii na ten temat, nas jednak interesuje taki obraz świata, który stanowi najbardziej
naturalne odniesienie struktury gramatycznej języków indoeuropejskich.

Na fundamencie takich wyobrażeń została bowiem zbudowana tradycyjna logika
arystotelesowska, a logika nowoczesna również — w pewien sposób — na nim
bazuje. Obraz ten można określić jako zdroworozsądkowy, lub — bardziej uczenie
— jako arystotelesowski.

Zasadnicze elementy tej teorii to przekonanie, że świat składa się z mnogości
p r z e d m i o t ó w (rzeczy, indywiduów, substancji) posiadających (stale lub czasowo)
rozmaite c e c h y (własności).

10

Przedmiotem jest zarówno Kowalski, jak i noszony przez niego płaszcz, ale
przedmiotem jest też dowolna liczba naturalna, choć jej status istnienia jest z pewnością
różny od sposobu istnienia płaszcza czy człowieka. Cechą Kowalskiego jest np. jego
ciężar, cechą płaszcza jego kolor, a cechą liczby np. parzystość. Jak widać, różne
typy przedmiotów mogą mieć różne rodzaje cech. Ze względu na posiadane cechy
przedmioty dzielą się na rozmaite k l a s y (gatunki i rodzaje naturalne).

Klasy te tworzą naturalną hierarchię, w ramach której zasadne jest używanie
określeń „gatunek” i „rodzaj” w sensie względnym, np. „ssak” będzie rodzajem dla
gatunku „człowiek”, ale gatunkiem dla rodzaju „zwierzę”. Indywidualne przedmioty
(ale również ich klasy) wchodzą między sobą w różnorodne r e l a c j e (stosunki).
Konfiguracje różnych przedmiotów, ich cech i zachodzących między nimi relacji to
s t a n y r z e c z y, a zmiany w tych konfiguracjach to p r o c e s y (zdarzenia).

Taki sposób widzenia otaczającego świata jest niezwykle rozpowszechniony w naszym
kręgu kulturowym i stanowi naturalne podłoże wielu teorii semantycznych oraz
wielu metod porządkowania wiedzy, np. d e fi n i o w a n i a czy k l a s y fi k a c j i .

2.3. Semantyka Fregego

Wspomnieliśmy już, że istnieje wiele konkretnych teorii semantycznych. W dalszym
ciągu, omawiając kolejno problematykę nazw i zdań, odwoływać się będziemy do
teorii, którą zasadniczo można przypisać Gottlobowi Fregemu. W ujęciu Fregego
każde wyrażenie językowe posiada swoją

ekstensję

(odniesienie) i

intensję

(sens,

znaczenie, treść). Zanim scharakteryzujemy specyficzne problemy semantyczne
takich kategorii, jak nazwy i zdania, omówimy krótko kilka ogólnych problemów
dotyczących semantyki języków naturalnych.

2.4. Wieloznaczność

Charakterystyczną cechą języków naturalnych, jeżeli chodzi o ich charakterystykę
semantyczną, jest brak jednoznaczności przyporządkowania pomiędzy wyrażeniami
a sferą znaczeń.

Z jednej strony wyrażenia języka naturalnego są

polisemiczne

, czyli jedno wyrażenie

posiada wiele znaczeń (np. „głowa” jako część ciała i „głowa” jako osoba stojąca
na czele — np. rodziny czy państwa). W języku naturalnym zachodzi też zjawisko

homonimii

. Różne znaczenia przysługują wyrażeniom o takim samym brzmieniu

i identycznej pisowni (np. „rola” jako grunt uprawny i jako postać utworu
scenicznego). Występuje też zjawisko

homofonii

, polegające na tym, że istnieją

wyrażenia o różnej pisowni, ale identycznej wymowie, między którymi nie ma
żadnych związków znaczeniowych (np. „morze” i „może”). Z drugiej strony zachodzi
zjawisko

synonimii

— te same znaczenia są reprezentowane przez różne wyrażenia

(np. „auto” i „samochód”).

Są to zjawiska powszechne w języku i niezależne od kategorii syntaktycznych wyrażeń,
aczkolwiek najczęściej używa się nazw jako przykładów. Wyrażenia typu „zamek”,
„laska”, „osioł” są ewidentnymi przykładami wieloznaczności, niewymagającymi

11

komentarza. Wiele wyrażeń może wydawać się na pozór jednoznacznych, ale bliższa
analiza kontekstów użycia pokazuje, że tak nie jest. Porównajmy, tytułem przykładu,
znaczenie wyrazu „gość” w zdaniach:

Gość w dom, Bóg w dom.
Ten gość pod latarnią jest wyraźnie zawiany.

W pierwszym zdaniu wyraz „gość” został użyty w znaczeniu „osoba przybyła
do kogoś w gościnę, w odwiedziny” i ma zdecydowanie dodatnie zabarwienie
uczuciowe. W drugim zdaniu ten sam wyraz oznacza kogoś bliżej nieznanego, użyty
jest ze zdecydowanie ujemnym zabarwieniem uczuciowym i wyraża lekceważenie.

2.5. Supozycje

W pewnym specjalnym znaczeniu wieloznaczność przysługuje każdemu wyrażeniu
językowemu. Chodzi tu o

supozycję

, czyli funkcję, w jakiej użyto danego wyrażenia.

Porównajmy znaczenie słowa „zając” w zdaniach:

Zając przebiegł mi drogę.
Zając jest popularnym gryzoniem.
Zając zaczyna się od Z.

W pierwszym wypadku „zając” użyty jest w odniesieniu do konkretnego egzemplarza,
w drugim — w odniesieniu do całego gatunku, w trzecim — chodzi o samo słowo.
W logice tradycyjnej mówi się — kolejno — o s u p o z y c j i p r o s t e j , f o r m a l n e j
i m a t e r i a l n e j . Rozróżnienie supozycji materialnej i formalnej dotyczy zasadniczo
nazw i ma dziś znaczenie drugorzędne. Nie zawsze też łatwo odróżnić, w jakiej
supozycji dana nazwa jest użyta, np. w zdaniu „Zając w potrawce jest bardzo
smaczny” — w grę mogą wchodzić obie supozycje.

2.6. Metajęzyk

Wyróżnienie supozycji materialnej ma duże znaczenie i stosuje się do wyrażeń
dowolnych kategorii. Współcześnie częściej mówi się o

metajęzykowym

użyciu

wyrażenia — kiedy wyraz staje się znakiem dla samego siebie, zamiast odnosić się
do czegoś spoza języka. W piśmie użycia metajęzykowe zaznacza się zazwyczaj przez
operowanie cudzysłowem, kursywą lub innymi środkami tego typu, jednak w mowie
tego rodzaju rozróżnienie łatwo może przejść niezauważone.

W potocznej komunikacji rzadko prowadzi to do problemów, ale tam, gdzie
chodzi o precyzyjne rozważania nad językiem (jak w logice czy w językoznawstwie)
rozróżnianie języka i metajęzyka jest niezwykle istotne. Zaniedbania tego typu mogą
bowiem prowadzić do powstawania rozmaitych

paradoksów

i

antynomii

.

Antynomiami nazywamy rozumowania, które od powszechnie akceptowalnych
przesłanek prowadzą do sprzeczności. Określenie „paradoks” jest używane szerzej
na określenie dowolnego tekstu, który — nawet jeżeli nie jest sprzeczny w sensie
logicznym — to wydaje się niemożliwy do zaakceptowania. Sprzeczność przejawia
się w wystąpieniu zdań, które sobie wzajemnie zaprzeczają. Trudności tego rodzaju
często mają swoje źródło właśnie w pomieszaniu języka z metajęzykiem.

12

Jeden z najsłynniejszych przykładów, o starożytnym rodowodzie, to tzw.

paradoks

kłamcy

, który można wyrazić następująco. Ktoś twierdzi: „Zdanie, które teraz

wygłaszam, jest fałszywe”. Jeżeli to zdanie jest prawdziwe, to jest tak, jak to zdanie
głosi — zatem jest ono fałszywe. Jeżeli jest fałszywe, to nie jest prawdą to, o czym
się w nim mówi — zatem jest ono prawdziwe. W obu wypadkach popadamy
w sprzeczność, a przyczyną problemu jest to, że zdanie to mówi coś o samym sobie.

2.7. Znaczenie potencjalne i aktualne

Najczęściej odwoływaliśmy się do nazw w celu ilustracji różnych form wieloznaczności,
jednak niektóre rodzaje wyrażeń stwarzają dodatkowe problemy. Przeanalizujemy
— dla przykładu — specyficzną formę wieloznaczności związaną z czasownikami.

W zdaniu „Kowalski pięknie śpiewa” nie wiemy, czy chodzi o to, że Kowalski
generalnie ma taki dar, czy raczej o to, że w tym momencie udało mu się pięknie
zaśpiewać. W pierwszym przypadku powiemy, że czasownik użyty jest w z n a c z e n i u
p o t e n c j a l n y m , w drugim — że w a k t u a l n y m . Warto zauważyć, że np. język
angielski nie stwarza problemów tego rodzaju, gdyż to, czy używamy czasownika
w takim, czy w innym znaczeniu musi być już zdeterminowane przez odpowiednią
formę gramatyczną. Nie oznacza to oczywiście, że język angielski jest „lepszy” od
polskiego — jest po prostu pod tym względem inny.

2.8. Błędy logiczne

Obu zjawisk (homonimii i synonimii) nie należy oceniać w kategorii wad języka
naturalnego. Bywają one bardzo przydatne — zwłaszcza wtedy, gdy chodzi
o użycia języka w funkcji ekspresywnej. Jednak tam, gdzie w grę wchodzi jasność
i precyzja wypowiedzi, mogą być przyczyną nieporozumień, tradycyjnie określanych
jako

błędy logiczne

. Pojęcie błędu logicznego nie ma jasno określonego zakresu.

Błędy ortograficzne raczej do tej kategorii nie należą, ale granica między błędem
stylistycznym a logicznym jest płynna.

13

3. Nazwy

3.1. Funkcje nazw

Jedną z wyróżnionych przez nas samodzielnych kategorii syntaktycznych są nazwy.
Jest to grupa wyrażeń niezwykle zróżnicowana — zarówno co do kształtu, jak
i pełnionych funkcji. Tak jak zdania odnoszą do stanów rzeczy, tak nazwy odnoszą
się do szeroko rozumianych przedmiotów. Stosują się zarówno do rzeczy fizycznych,
jak i idealnych, ale również do ich klas, do cech czy relacji. „Adam Małysz” jest
nazwą pewnego indywiduum, „ssak” nazwą klasy indywiduów, „biały” nazwą cechy,
natomiast „równość” nazwą relacji.

Ogólnie — przedmiot, do którego dana nazwa się odnosi, nazywamy jej

desygnatem

,

a zbiór wszystkich desygnatów danej nazwy to jej

ekstensja

(zakres, denotacja).

Intensją

nazwy jest

pojęcie logiczne

, które tradycyjnie rozumiane jest jako zbiór cech

posiadanych przez desygnaty danej nazwy. Używamy przydawki „logiczne” dla
odróżnienia od pojęcia w sensie psychologicznym, czyli pewnego wyobrażenia (idei)
wiązanej z daną nazwą przez konkretnego użytkownika języka. Pojęcie logiczne jest
tu rozumiane jako pewna t r e ś ć obiektywna związana z daną nazwą, niezależna od
stanu czyjejś świadomości językowej.

3.2. Pojęcie

Przy omawianiu pojęć pojawia się szereg problemów związanych z rozumieniem
słów „treść” i „cecha”, a także z wyróżnianiem rozmaitych klas cech. Desygnat danej
nazwy może mieć ogromną ilość cech, z których jedne są ważne (z pewnego punktu
widzenia), a inne nie. Jan Kowalski może być np. rudy, ale ta cecha nie jest istotna ze
względu na to, że jest desygnatem nazwy „człowiek”. Jest wielu ludzi (desygnatów
tej samej nazwy), którzy tej cechy nie posiadają, zatem cecha ta nie należy do
pojęcia człowieka. Jest — z tego punktu widzenia — c e c h ą a k c y d e n t a l n ą
(przypadkową) Jana Kowalskiego. Z drugiej strony, jeżeli ten sam Kowalski jest
przez nas rozpatrywany jako desygnat nazwy „rudy mężczyzna”, to ta sama cecha
jest tutaj istotna, gdyż należy do pojęcia rudego mężczyzny.

Nawet wśród cech składających się na dane pojęcie można starać się wyróżnić te,
które przysługują wszystkim desygnatom w sposób

istotny

(konstytutywny) lub

pochodny

(konsekutywny). Przykładowo, wszystkie kwadraty mają cztery równe

boki i wszystkie kąty proste, zatem te cechy możemy uznać za konstytutywne, ale
np. równość przekątnych można już uznać za cechę konsekutywną. Generalnie,
zbiór cech, które przysługują wszystkim desygnatom danej nazwy i tylko im, to zbiór
c e c h s w o i s t y c h albo charakterystyczny zbiór cech.

14

3.3. Nieostrość nazw

Powyższe rozważania w miarę dobrze ilustruje się przykładami nazw typu „trójkąt”,
dlatego że zarówno intensja, jak i ekstensja takiej nazwy jest dobrze określona. Należy
jednak pamiętać, że w przypadku większości nazw sytuacja wygląda odmiennie.
Nazwy typu: „gruby”, „chudy”, „mądry”, „ładny” to

nazwy nieostre

, dlatego że nie

dysponujemy precyzyjnym kryterium, pozwalającym w każdym wypadku określić,
czy jakiś obiekt jest, czy nie jest desygnatem danej nazwy.

Nieostrość zazwyczaj idzie w parze z n i e j a s n o ś c i ą z n a c z e n i a (chwiejność
znaczeniowa). Nazwa jest dla nas niejasna albo niewyraźna, gdy nie umiemy wskazać,
jakie cechy składają się na jej pojęcie. Nazwy nieostre są zarazem niewyraźne, ale
odwrotna zależność nie zachodzi. Dla wielu nazw nie mamy problemu z określeniem
zakresu, ale ich pojęcie jest dla nas uchwytne tylko intuicyjnie. Staje się to oczywiste
wtedy, gdy zmuszeni jesteśmy komuś wyjaśnić znaczenie danej nazwy. „Czym jest
czas? Wiem, póki mnie nie zapytasz” — twierdził już św. Augustyn w Wyznaniach.

Takich zjawisk nie należy uważać zdecydowanie za wadę języka naturalnego. W wielu
sytuacjach operowanie wyrażeniami tego typu sprzyja zwiększeniu efektywności
komunikacji bądź osiąganiu interesujących efektów estetycznych. Jednak tam, gdzie
wskazane jest użycie języka precyzyjnego i jednoznacznego, takie wyrażenia mogą
prowadzić do nieporozumień. Jednym ze środków zapobiegawczych jest umiejętność
budowania definicji wyrażeń nazwowych.

3.4. Klasyfikacje nazw

W logice tradycyjnej poświęcano dużo uwagi analizie problematyki nazw i wyróżniano
sporo rodzajów wyrażeń nazwowych. Omówimy tu krótko najważniejsze:
1.

Ze względu na stopień złożoności, można wyróżnić

nazwy proste

, jednowyrazowe,

i

nazwy złożone

, w których występuje co najmniej jeden funktor nazwotwórczy, np.

„wuj Mariana”, „kobieta w chustce na głowie”, „2 + 3”.

2.

Nazwy można dzielić na

indywidualne

i

generalne

— w zależności od tego, czy

podstawa oznaczania jest arbitralna (umowna), czy nie. Nazwy generalne, jak
„człowiek” czy „góra”, są przypisywane swoim desygnatom ze względu na posiadane
przez nie cechy. Natomiast i m i o n a w ł a s n e , będące typowym przykładem nazw
indywidualnych, przysługują swoim desygnatom na mocy umowy.

3.

Ze względu na ilość desygnatów, można rozróżnić

nazwy ogólne

(więcej niż jeden

desygnat),

jednostkowe

(dokładnie jeden) i

puste

(brak desygnatu, ale nie ekstensji

— jest nią zbiór pusty!). Przykładowo: „człowiek”, „Jan Kowalski”, „dziecko
bezdzietnej matki”.

Nie są to jedyne podziały wyrażeń nazwowych, które omawia się w literaturze, ale
dla naszych celów powyższe omówienie jest wystarczające.

Chociaż podane wyżej kryteria odróżniania typów nazw wydają się dość czytelne,
to jednak kwestia, czy jakąś nazwę uznamy za przedstawiciela danej klasy może być
— i często jest — sporne. Przeanalizujemy bliżej kilka przykładów.

15

3.5. Nazwy indywidualne

Nie należy utożsamiać nazw indywidualnych z nazwami jednostkowymi. Zarówno
„Mount Everest”, jak i „najwyższa góra świata” są nazwami jednostkowymi, ale tylko
pierwsza z nich jest nazwą indywidualną. Druga jest przykładem tzw. d e s k r y p c j i
o k r e ś l o n e j , czyli nazwy opisowej o jednym desygnacie, i jest ewidentnym
przykładem nazwy generalnej.

W użyciu jest również syntaktyczne kryterium rozróżnienia nazw indywidualnych
i generalnych: pierwsze występują tylko w podmiocie z d a ń p o d m i o t o w o
o r z e c z n i k o w y c h , drugie mogą występować zarówno w podmiocie, jak
i w orzeczniku.

Mamy tutaj na myśli zdania typu „Kowalski jest człowiekiem”, czyli takie, w których
orzeka się jakąś cechę o pewnym indywiduum. Funktor „jest” występuje w takich
zdaniach w znaczeniu: „jest elementem zbioru”, dlatego należy odróżnić je od z d a ń
t o ż s a m o ś c i o w y c h , które pozornie mogą przybierać taką samą formę (np. „Wenus
jest gwiazdą poranną”), jednak funktor „jest” oznacza w nich relację identyczności.

3.6. Nazwy puste

Podany przez nas przykład nazwy pustej (dziecko bezdzietnej matki) nie budzi
wątpliwości, gdyż jest również przykładem nazwy wewnętrznie sprzecznej (tradycyjne
określenie contradictio in adiecto), ale to, czy nazwa „krasnoludek” jest pusta, czy
nie — może już budzić wątpliwości.

Tak naprawdę wiele sporów natury filozoficznej można zinterpretować jako spory
o to, czy pewna nazwa jest pusta, czy nie, a jeżeli nie jest pusta, to czy ogólna, czy
jednostkowa? Przykładem może być spór o istnienie Boga, a wśród wierzących spór
między mono- a politeistami.

Nazwy puste można również dzielić na nazwy o i n t e n c j i j e d n o s t k o w e j (np.
„smok wawelski”) i o g ó l n e j (np. „centaur”), zależnie od domniemanej liczby
nieistniejących desygnatów. Należy pamiętać, że pustość czy niepustość nazwy nie
zależy od obecnego stanu rzeczy. Nazwa „brontozaur” jest niepustą nazwą ogólną,
choć jej desygnaty nie żyją od milionów lat.

3.7. Nazwy jednostkowe

Użycie wyrażenia „Jan Kowalski” jako przykładu nazwy jednostkowej również
może budzić pewne wątpliwości — z pewnością jest w Polsce wielu różnych Janów
Kowalskich. Nam jednak chodzi o to, że każde konkretne i standardowe użycie tego
wyrażenia odnosi do konkretnego desygnatu, zatem jest ona nazwą jednostkową ze
względu na pełnioną w komunikacji funkcję.

16

3.8. Relacje między zakresami nazw

Zastanówmy się, jakie relacje mogą zachodzić pomiędzy zakresami dowolnych
dwóch nazw. W przypadku nazw pustych i jednostkowych jest to zagadnienie
trywialne. Dwie różne nazwy puste mają zawsze ten sam zakres — zbiór pusty
— i z tego punktu widzenia nie ma między nimi różnicy, choć mogą diametralnie
różnić się co do swego sensu (intensji). Dwie różne nazwy jednostkowe mogą mieć
ten sam zakres („zwycięzca spod Grunwaldu” a „Władysław Jagiełło”) lub różny („Jan
Paweł II” a „Leszek Miller”) i żadne inne relacje nie wchodzą w grę. W przypadku
nazw ogólnych można wyróżnić pięć rodzajów relacji zachodzących między ich
zakresami. Ekstensje dwóch nazw mogą:
— być

równoważne

(tożsame), gdy jest to ten sam zbiór, np. „kobieta” i „niewiasta”,

— być w relacji

podrzędności

(ostrego zawierania się), gdy każdy desygnat jednej

nazwy jest desygnatem drugiej, ale nie odwrotnie (ta druga nazwa jest wtedy
w relacji

nadrzędności

względem pierwszej), np. „ssak”, „kręgowiec”,

—

wykluczać się

(być rozłączne), gdy nie mają wspólnych desygnatów, np. „piernik”

i „wiatrak”,

—

krzyżować się

, gdy mają jakieś desygnaty wspólne i każda z nich ma desygnaty,

które nie należą do zakresu drugiej, np. „ssak”, „drapieżnik”.

Pożytecznym ćwiczeniem rozwijającym umiejętność analizy logicznej (i wyobraźnię
przestrzenną) jest rysowanie

diagramów Eulera

ilustrujących relacje między zakresami

nazw. Na diagramach tego typu zaznacza się zakresy nazw za pomocą okręgów.
Oczywiście, muszą to być nazwy ostre, a w przypadku wieloznaczności wybieramy
zawsze jedno znaczenie. Zbiory desygnatów danej nazwy dalej będziemy oznaczać
dużymi literami z początku alfabetu. Zilustrujemy tę technikę na kilku przykładach.

Niech A reprezentuje zakres nazwy „kręgowiec”, B — „krokodyl”, C — „ssak”,
D — „drapieżnik”. Diagram wygląda następująco:

D

B

C

A

A otacza na diagramie pozostałe okręgi, gdyż jest nadrzędne dla pozostałych
zakresów. Podobnie jak D względem B. Natomiast C krzyżuje się z D, gdyż nie każdy
ssak to drapieżnik i odwrotnie. B i C są rozłączne.

A — „część głowy”, B — „głowa”, C — „szczęka”, D — „ząb”, E — „siekacz”

Rysunek 1

Rysunek 2

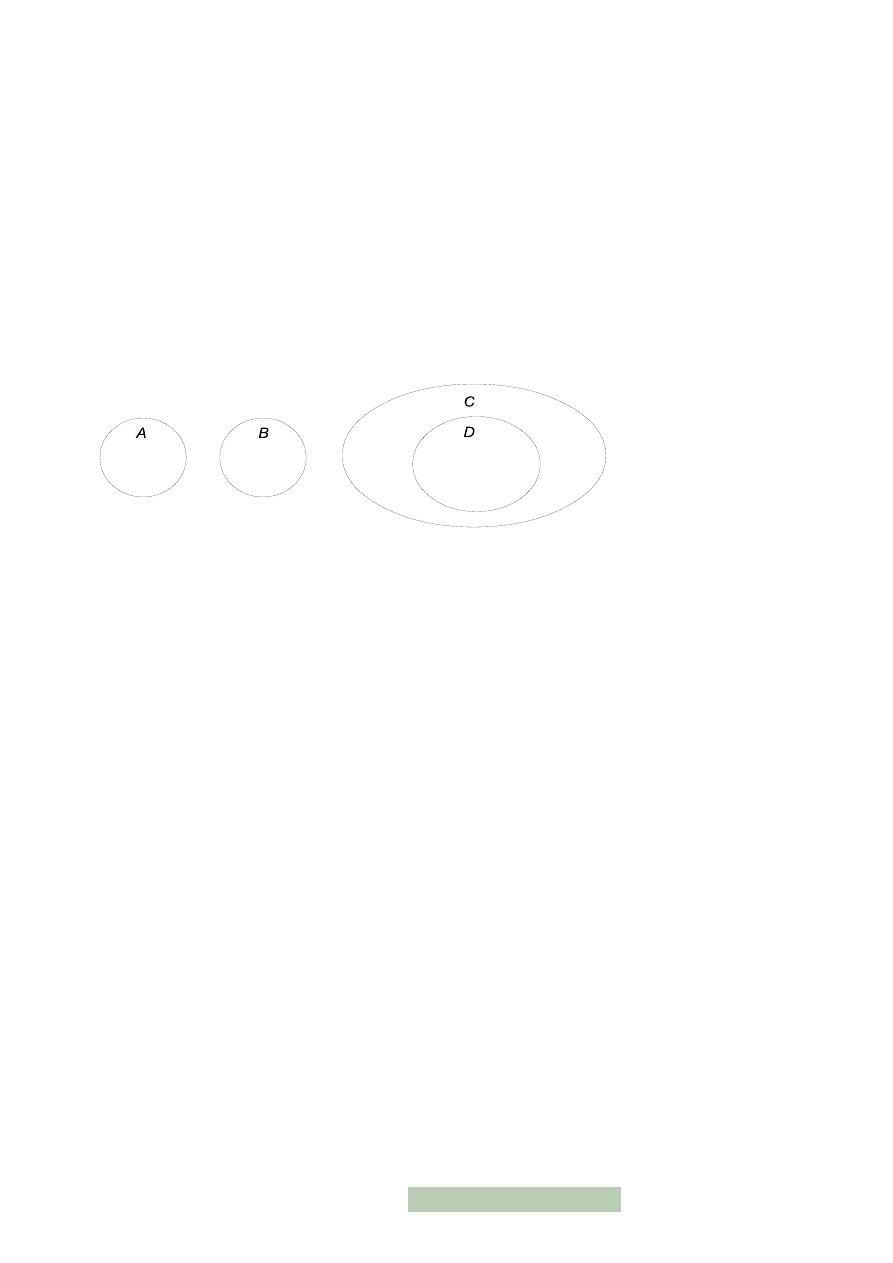
17

Powyższy przykład pokazuje, że przy rozważaniu relacji zachodzących między
zakresami nazw ważne jest, aby nie mylić np. relacji podrzędności z r e l a c j ą
b y c i a c z ę ś c i ą . Przykładowo, między zakresami nazw „głowa” i „szczęka” (B
i C) zachodzi relacja wykluczania, gdyż żadna konkretna szczęka nie jest głową
i odwrotnie. Podobnie wygląda sytuacja dla C i D, gdyż żaden ząb nie jest szczęką
i odwrotnie (chociaż ząb może być częścią szczęki). Analogicznie jest z siekaczami,
chociaż każdy z nich jest zębem, co wyjaśnia relację między E i D. Wreszcie wszystkie
desygnaty nazw: „szczęka”, „ząb” i „siekacz” są częściami głowy — stąd nadrzędność
A względem C, D i E — ale żadna głowa nie jest częścią głowy, zatem A i B też się
wykluczają.

A — „mąż”, B — „żona”, C — „rodzina”, D — „małżeństwo”

Te Czytelniczki, które poczuły się zaniepokojone powyższym diagramem, ponieważ
uważają, że miejsce męża jest w małżeństwie, śpieszymy uspokoić, że nie narusza
on tak ważnej zasady! Wystarczy chwila refleksji nad charakterem desygnatów
podanych wyżej nazw. Zarówno elementy A, jak i B to pojedyncze osoby, a ponieważ
reprezentują odmienne płci, to rozłączność jest tutaj jak najbardziej na miejscu.
Natomiast dowolny desygnat nazwy „małżeństwo” lub „rodzina” to przecież co
najmniej para osób! Żaden mąż czy żona w pojedynkę nie są małżeństwem ani
rodziną — są ich częściami w sensie prawnym czy społecznym. Ponieważ każde
małżeństwo jest rodziną, więc D jest podrzędne w stosunku do C.

Rysunek 3

18

4. Zdania

4.1. Znaczenie zdania

Poświęcimy teraz nieco uwagi zdaniom. Przypomnijmy, że ograniczamy się tutaj do
analizy zdań oznajmujących.

Intensją

takich zdań jest tzw. s ą d l o g i c z n y, czyli

informacja przekazywana przez to zdanie o jakimś stanie rzeczy. Przykładowo
informacja, że pewien przedmiot posiada daną cechę (jak w zdaniu „Kowalski
jest wysoki”) lub że między nim a innym przedmiotem zachodzi pewna relacja
(np. „Kowalski czyta gazetę”).

Określenie „sąd” bywa też często używane w sensie psychologicznym — jako nazwa
czyichś przekonań, żywionych w umyśle w związku z jakimś zdaniem. My jednak
mamy tu na myśli pewien byt pozaumysłowy — stąd określenie „sąd logiczny”.
Różne zdania sformułowane z użyciem odmiennych form gramatycznych lub
w innych językach mogą wyrażać ten sam sąd, np. „Adam kocha Kasię”, „Kasia
jest kochana przez Adama”, „Adam loves Kathy”. Ponieważ operowanie stanami
rzeczy stwarza pewne trudności w semantyce, więc za

ekstensję

zdania uznamy

jego w a r t o ś ć l o g i c z n ą , czyli prawdziwość bądź fałszywość. W dalszym ciągu
skupimy się głównie na problematyce tak rozumianej ekstensji zdań.

4.2. Prawda i fałsz

Problematyka filozoficzna, dotycząca prawdy i fałszu jest bardzo obszerna i nie
będziemy jej tu dokładnie referować. Najstarsza definicja prawdy (tzw.

klasyczna

albo

korespondencyjna

) pochodzi od Arystotelesa i głosi, że p r a w d z i w o ś ć z d a n i a

p o l e g a n a j e g o z g o d n o ś c i z r z e c z y w i s t o ś c i ą .

Charakterystyka taka może budzić wiele wątpliwości, gdyż nie jest jasne ani to,
czym jest rzeczywistość, ani na czym ma polegać ta postulowana zgodność. Później
wprowadzimy bardziej techniczny sposób rozumienia prawdziwości zdań (w językach
sztucznych), na razie ograniczymy się do spostrzeżenia, że chociaż możemy nie
wiedzieć, na czym polega istota prawdziwości, to — przynajmniej czasami — jesteśmy
w stanie odróżnić od siebie zdania prawdziwe i fałszywe.

4.3. Zasada dwuwartościowości

Intuicyjne rozumienie prawdziwości i fałszywości w zupełności wystarczy, ponieważ
logicy traktują prawdę i fałsz raczej utylitarnie, jako

wartości logiczne zdań

.

W logice klasycznej przyjmuje się ponadto, jako podstawowe założenie, tzw.

zasadę

dwuwartościowości

, która głosi, że każde zdanie jest prawdziwe lub fałszywe.

19

Zasada ta wydaje się cokolwiek odbiegać od potocznych intuicji — często zdania
wydają się nie mieć żadnej wartości logicznej, tzn. nie być ani prawdziwe, ani fałszywe.
Wątpliwości tego rodzaju miał już Arystoteles — ojciec logiki klasycznej — kiedy
rozważał zdania dotyczące przyszłości. Logik klasyczny będzie się upierał, że bez
względu na naszą wiedzę dane zdanie jednak jest prawdziwe bądź fałszywe — my po
prostu jego wartości logicznej nie znamy! Można jednak potraktować takie względy
epistemiczne (poznawcze) poważnie i przyjąć, że w analizie rozumowań ważniejszy
niż jakiś absolutny punkt widzenia jest nasz aktualny stan wiedzy. Takie podejście
było głównym motywem stworzenia przez Jana Łukasiewicza

logiki trójwartościowej

,

a potem jej uogólnienia do postaci

logik wielowartościowych

.

4.4. Zasada niesprzeczności

Innym ważnym założeniem logiki klasycznej jest tzw.

zasada niesprzeczności

,

która głosi, że żadne zdanie stwierdzające jakiś stan rzeczy nie może być zarazem
prawdziwe i fałszywe. Innymi słowy, nie jest możliwe, aby jakiś stan rzeczy zachodził
i nie zachodził zarazem. Razem z zasadą dwuwartościowości sprowadza się to do
wymogu, żeby każde zdanie posiadało dokładnie jedną z dwóch wartości logicznych
— prawdę albo fałsz.

Jak się wydaje, tutaj też mamy pewien problem. Wiele zdań zmienia swą wartość
logiczną — zdanie „Dzisiaj pada śnieg” jednego dnia jest prawdziwe, a drugiego nie.
To jednak problem pozorny. Zasada niesprzeczności stwierdza tylko, że dane zdanie
nie może być r ó w n o c z e ś n i e prawdziwe i fałszywe.

Oczywiście znów należy rozumieć to w sensie absolutnym — jasne jest, że to samo
zdanie może mieć przypisywane różne wartości logiczne w tym samym czasie przez
różnych ludzi — na tym polegają spory. Jednak zdanie, które jedni oceniają jako
prawdziwe, zaś drudzy jako fałszywe, ma tylko jedną z tych wartości logicznych.
Ludzie, którzy tego nie rozumieją, mają skłonność do mówienia o relatywności
(względności) prawdy.

4.5. Okazjonalność

W przytoczonym wyżej przykładzie przyczyną tej zmienności wartości logicznej jest
okolicznik czasu „dzisiaj”, który jest

wyrażeniem okazjonalnym

, czyli zmieniającym

znaczenie w zależności od kontekstu wypowiedzi. Typowe wyrażenia okazjonalne to
o k o l i c z n i k i c z a s u (np. „jutro”), m i e j s c a (np. „za rogiem”), a także z a i m k i
(np. „on”, „ten”, „tam”). Niezbędnym kontekstem do określenia wartości logicznej
takiego zdania mogą być okoliczności zewnętrzne towarzyszące wypowiedzi bądź
inne zdania występujące w tym samym tekście. Używanie wyrażeń okazjonalnych
jest powszechnym zabiegiem, służącym skracaniu komunikacji. Trzeba jednak
pamiętać, że takie zdania wyrwane z kontekstu mogą prowadzić do poważnych
nieporozumień.

Jeżeli odróżnimy od siebie z d a n i a o z n a j m u j ą c e (kryterium gramatyczne)
i z d a n i a w s e n s i e l o g i c z n y m (kryterium semantyczne — wyrażenia, których
ekstensją jest wartość logiczna), to wyrażenia zawierające np. zaimki należy uznać

20

za tzw. f u n k c j e z d a n i o w e , czyli rodzaj schematów, które dopiero mogą stać się
zdaniami w sensie logicznym.

Przykładem takiego quasi-zdania jest wyrażenie złożone „Kowalski jest od niego
wyższy”. Ma ono określoną wartość logiczną w kontekście pewnego tekstu, gdzie
inne zdania precyzują odniesienie wyrażenia „niego”. Po wyrwaniu z kontekstu
można zamienić je w zdanie bądź przez s p e c j a l i z a c j ę , czyli podstawienie
nazwy własnej („Kowalski jest od Nowaka wyższy”), bądź przez k w a n t y fi k a c j ę
(„Kowalski jest wyższy od każdego członka swej rodziny”).

4.6. Zdania analityczne i syntetyczne

Niezależnie od tego, że z ustaleniem wartości logicznej zdań mogą pojawiać się
rozliczne kłopoty, warto zwrócić uwagę na fakt, że prawda (lub fałsz) wydają się
przysługiwać zdaniom w różny sposób. Porównajmy zdania:

a) Kwadrat ma cztery boki.
b) Polska jest krajem demokratycznym.

Oba wyrażenia są bez wątpienia zdaniami prawdziwymi. Jednak zdanie a) nie tylko
jest, ale m u s i być prawdziwe, natomiast prawdziwość b) jest czymś przypadkowym,
gdyż łatwo można sobie wyobrazić sytuację, że w Polsce panuje inny ustrój.

Zdania, których wartość logiczna zależy tylko od ich struktury i znaczenia
występujących w nich wyrażeń, to

zdania analityczne

. Zdania, których wartość logiczna

zależy również od okoliczności zewnętrznych, to

zdania syntetyczne

. W szczególności

każde zdanie analitycznie fałszywe to zdanie wewnętrznie sprzeczne, zwane też
zdaniem

kontradyktorycznym

, np. „Jurek jest żonatym kawalerem”.

W wielu pracach można znaleźć nieco inne określenia zdań analitycznych
i syntetycznych, a nawet spotkać się z kwestionowaniem zasadności takiego podziału,
jednak wydaje się on ważny. W szczególności, w systemach logicznych, które pojawią
się w kolejnych częściach tego kursu nabierze on bardziej technicznego sensu.

4.7. Funktory zdaniotwórcze

Omawiając zdania, należy poświęcić trochę uwagi kwestii budowania zdań złożonych,
czyli różnym rodzajom f u n k t o r ó w z d a n i o t w ó r c z y c h o d a r g u m e n t ó w
z d a n i o w y c h . Te funktory, których argumentami są jedynie zdania, określa się
w logice jako s p ó j n i k i . Jest to użycie słowa „spójnik” szersze niż w gramatyce
tradycyjnej, gdyż np. wyrażenia takie, jak: „nieprawda, że...”, „z konieczności...”,
„jest możliwe, że...”, są w logice traktowane jako spójniki (funktory kategorii z/z).

W języku naturalnym występuje imponująca mnogość spójników, jednak tylko
niektóre z nich pozwalają na stosunkowo prostą analizę swojego znaczenia.
Podzielmy spójniki na

ekstensjonalne

i

intensjonalne

. Pierwsze są tego rodzaju,

że ekstensja zdania, którego są głównym funktorem, zależy tylko i wyłącznie od
ekstensji argumentów. W przypadku drugich zależy także od ich intensji.

21

4.8. Funktory ekstensjonalne

Zastanówmy się nad znaczeniem funktora „nieprawda, że”. Jeżeli dołączymy to
wyrażenie do zdania prawdziwego (zanegujemy to zdanie), to w efekcie otrzymamy
zdanie fałszywe, np. „Nieprawda, że woda jest mokra”. Odwrotnie, jeżeli dokonamy
zaprzeczenia zdania fałszywego, to w efekcie otrzymamy zdanie prawdziwe. Efekt
nigdy nie zależy od treści zaprzeczanego zdania, tylko zawsze od jego wartości,
zatem „nieprawda, że” jest spójnikiem ekstensjonalnym.

Do spójników, które przynajmniej w jednym ze swoich znaczeń są ekstensjonalne,
zaliczyć można np. wyrażenia: „i”, „lub”, „albo”, „jeżeli..., to”, „wtedy i tylko wtedy”,
„ani..., ani” i parę innych. Przykładowo, zdanie złożone: „Jurek jest studentem i nie
zaliczył sesji” można uznać za prawdziwe tylko wtedy, gdy za prawdziwe uznamy
oba zdania składowe, tj. „Jurek jest studentem” i „Jurek nie zaliczył sesji”.

4.9. Funktory intensjonalne

Zastanówmy się dla odmiany nad znaczeniem funktora „z konieczności”. Na pewno
— jeżeli dołączymy to wyrażenie do zdania fałszywego — to otrzymamy również
zdanie fałszywe, ale jeżeli jego argumentem stanie się zdanie prawdziwe, to sytuacja
może wyglądać rozmaicie. Zdanie „Z konieczności 2 + 2 = 4” jest prawdziwe, ale
zdanie „Z konieczności Polska jest krajem demokratycznym” wydaje się fałszywe
— bez względu na to, w jaki sposób rozumiemy konieczność.

Dokładniejsza analiza pokazuje, że funktor „z konieczności” dołączony do zdania
prawdziwego daje zawsze zdanie prawdziwe tylko wtedy, gdy jego argument jest
zdaniem analitycznie prawdziwym. W przypadku zdań syntetycznie prawdziwych
wynik może być różny.

Powyższe przykłady pokazują, że zwroty modalne, takie jak „z konieczności” czy
„jest możliwe, że” są funktorami intensjonalnymi. Są to wyrażenia niezwykle ważne.
Do funktorów modalnych można też zaliczyć wyrażenia takie, jak: „...wierzy, że...”,
„jest zabronione...”, „...jest zobowiązany do...” i wiele innych. Dlatego logika
zajmuje się również analizą takich funktorów (l o g i k i m o d a l n e , e p i s t e m i c z n e ,
d e o n t y c z n e ), ale jest to zadanie bardziej skomplikowane. Logika klasyczna
ogranicza się do użycia funktorów ekstensjonalnych.

22

5. Relacje logiczne

Rozumowania nie są jedynym rodzajem tekstów, a wynikanie nie jest jedynym
ważnym pojęciem analizowanym na gruncie logiki. Poniżej scharakteryzujemy kilka
ważnych relacji logicznych zachodzących pomiędzy zdaniami. Warto porównać je
z omawianymi w temacie 3 relacjami zachodzącymi pomiędzy zakresami nazw.

5.1. Równoważność

Używaliśmy już kilka razy skrótu „wtw” dla zwrotu „wtedy i tylko wtedy, gdy”
dla zaznaczenia, że między dwoma zdaniami zachodzi

relacja równoważności

. Jest

to relacja logiczna mocniejsza od wynikania, którą scharakteryzować możemy
następująco:

Dwa zdania są sobie równoważne wtw, m u s z ą mieć tę samą wartość logiczną
(muszą być albo oba prawdziwe, albo oba fałszywe).

Równoważność jest mocniejsza od wynikania w tym sensie, że zachodzi między
dwoma zdaniami wtedy, gdy pierwsze wynika z drugiego, a drugie z pierwszego.
Jest po prostu obustronnym wynikaniem dwóch zdań. W sposób negatywny, chociaż
równoważny, równoważność można scharakteryzować następująco:

Dwa zdania są sobie równoważne wtw, jest n i e m o ż l i w e , żeby miały różną wartość
logiczną (jedno z nich nie może być prawdziwe, a drugie fałszywe).

5.2. Sprzeczność

Logika pomaga badać dowolne teksty pod kątem ich spójności. Najgorszym
objawem chaosu myślowego jest sytuacja, kiedy ktoś sam sobie przeczy i nawet tego
nie zauważa. Dlatego dla logiki, jako dyscypliny dbającej o porządek i konsekwencję
myślenia, niemniej ważna jest analiza s p r z e c z n o ś c i /n i e s p r z e c z n o ś c i ludzkich
przekonań. Powiemy, że:

Zbiór zdań jest sprzeczny wtw, jest n i e m o ż l i w e , aby wszystkie zdania w tym
zbiorze były prawdziwe.

W powyższym określeniu, podobnie jak przy charakteryzacji wynikania czy
równoważności, znów nacisk kładziemy na modalny zwrot „niemożliwe”. Nie należy
sprzeczności w powyższym sensie mylić z innymi przejawami niekonsekwencji.
Człowiek, który twierdzi, że kłamstwo jest niemoralne, a sam okłamuje swoich
bliźnich, jest z pewnością niekonsekwentny, ale w sensie interesującym raczej
etyka niż logika. Ponieważ sprzeczność łatwo jest pomylić z innymi fenomenami,
takimi jak dwulicowość, niesprawiedliwość czy nielojalność, więc rozważymy kilka
przykładów. Wyobraźmy sobie ludzi wypowiadających poniższe zdania.

23

1. Byłoby niestosowne poddawać cenzurze programy TV, w których pokazuje się

przemoc, gdyż to, co widać na ekranie, nie ma wpływu na ludzkie zachowania.
Natomiast dobrą ideą jest pokazywanie większej ilości programów, które ukazują
nasze osiągnięcia gospodarcze, gdyż to mogłoby osłabić argumentację, a nawet
zmienić poglądy malkontentów.

2. W ciągu ostatnich pięciu lat miałem trzy duże i kilka mniejszych wypadków

samochodowych. W dwóch przypadkach sąd orzekł moją odpowiedzialność, ale
naprawdę jestem bardzo dobrym kierowcą, tylko nie mam szczęścia.

3. Powierzchnia Ziemi jest płaska (wyjąwszy góry, morza i inne względnie małe

wypukłości i wgłębienia). Kiedy ludzie myślą, że opłynęli Ziemię dookoła, to
tak naprawdę tylko przemieścili się z jednego miejsca do drugiego, które jest
identyczne, jak to z którego wystartowali, ale oddalone od tamtego o tysiące mil
(Hodges, 1991).

Czy każdy z powyższych tekstów jest sprzeczny? Pierwszy jest sprzeczny bez
wątpienia. Nie można równocześnie utrzymywać, że to, co oglądamy w telewizji, nie
ma wpływu i zarazem może mieć wpływ na nasze zachowanie. Autor wypowiedzi 1.
mógłby starać się ją poprawić, na przykład zaznaczając, że według niego pokazywanie
zjawisk negatywnych nie ma wpływu na ludzi, a pokazywanie zjawisk pozytywnych
ma. Poglądy takie nie byłyby już sprzeczne (choć wydają się dziwaczne).

Tekst 2. nie jest sprzeczny, choć wydaje się głupi i nierozsądny. Jednak jest możliwe,
że autor istotnie jest dobrym kierowcą, tylko ma niezwykłego pecha. W końcu — jak
wiadomo — nawet sądy często się mylą.

Tekst 3. jest po prostu fałszywy (w świetle powszechnie uznawanych poglądów), ale
pogląd w nim reprezentowany nie jest niemożliwy w sensie logicznym. Co więcej,
należy podkreślić, że jego autor usilnie stara się o konsekwencję swojego wywodu,
np. tłumaczy, na czym polega zjawisko opłynięcia świata dookoła. Zatem, chociaż
reprezentowane stanowisko samo w sobie nie jest sprzeczne, to jest sprzeczne
z naszymi poglądami.

5.3. Sprzeczność jawna i utajona

W krótkich i prostych tekstach sprzeczność jest zazwyczaj dosyć łatwa do
wykrycia, a to, że mamy skłonność uznać za sprzeczność mniej niebezpieczne
fenomeny, jak zwykły fałsz lub niskie prawdopodobieństwo, nie wydaje się groźne.
Bardziej niebezpieczne jest to, że możemy sprzeczność przeoczyć w sytuacji,
kiedy ona faktycznie występuje. Jest tak zwłaszcza w przypadku długich tekstów
o skomplikowanej strukturze.

Ważność systemów formalnych polega m.in. na tym, że pozwalają nam na
wykazywanie sprzeczności nawet w dużych zbiorach złożonych ze skomplikowanych
zdań. Odpowiednie reguły pozwalają nam bowiem wyprowadzić z takich zbiorów
j a w n ą s p r z e c z n o ś ć albo znaleźć dla nich interpretację, co jest równoznaczne
z wykazaniem ich niesprzeczności.

Co w takim razie należy uznać za jawną sprzeczność? Zasadniczo tylko w jednym
przypadku nie możemy mieć wątpliwości. Sprzeczność jest ewidentna, kiedy mamy
dwa zdania, z których jedno jest po prostu zaprzeczeniem drugiego.

24

5.4. Sprzeczność mocna

W takim przypadku zachodzi między dwoma zdaniami mocniejsza relacja logiczna,
gdyż nie tylko nie mogą być razem prawdziwe, ale również nie mogą być razem
fałszywe. Krótko mówiąc, nie mogą mieć równocześnie tej samej wartości
logicznej.

Warto zauważyć, że w tradycyjnej terminologii logicznej, nadal często używanej,
właśnie ta mocna relacja określana jest jako sprzeczność, podczas gdy w przypadku
dwóch zdań, które tylko nie mogą być razem prawdziwe (choć mogą być oba
fałszywe), mówi się, że wzajemnie się

wykluczają

lub że są zdaniami przeciwnymi.

Przykładem może być para zdań: „Każdy Polak to pijak” i „Żaden Polak nie jest
pijakiem”. Nie mogą być one oba prawdziwe, chociaż mogą być (i są) oba fałszywe.
Są zatem sprzeczne w sensie definicji podanej na początku tematu, chociaż nie są
sprzeczne w sensie mocnym.

5.5. Dopełnianie

Dwa zdania, które dla odmiany nie mogą być razem fałszywe (choć mogą być oba
prawdziwe) to zdania, które się

dopełniają

(są zdaniami podprzeciwnymi). Jako

przykład niech posłuży para zdań: „Niektórzy Polacy to pijacy” i „Niektórzy Polacy
nie są pijakami”.

Łatwo zauważyć, że dwa zdania są sprzeczne w sensie mocnym wtw, zarazem
dopełniają się i wykluczają. W dalszych rozważaniach terminu „sprzeczność”
będziemy używać zasadniczo zgodnie z definicją podaną na początku tego tematu.
Taka charakterystyka sprzeczności ma pewną przewagę nad pojęciem sprzeczności
mocnej, gdyż stosuje się nie tylko do par zdań, ale do ich zbiorów o dowolnej
wielkości, nawet nieskończonych.

5.6. Analityczność a relacje logiczne

Odwołanie się do pojęcia zdania analitycznego pozwala w odmienny, ale równoważny
sposób scharakteryzować relacje logiczne zachodzące między zdaniami. Dla
dowolnych zdań Z

1

i Z

2

powiemy, że:

a)

Z

2

w y n i k a z Z

1

wtw, „Jeżeli Z

1

, to Z

2

” jest zdaniem analitycznie prawdziwym,

b)

Z

1

i Z

2

są r ó w n o w a ż n e wtw, „Z

1

wtw, Z

2

” jest zdaniem analitycznie

prawdziwym,

c)

Z

1

i Z

2

w y k l u c z a j ą s i ę wtw, „Z

1

i Z

2

” jest zdaniem kontradyktorycznym,

d)

Z

1

i Z

2

d o p e ł n i a j ą s i ę wtw, „Z

1

lub Z

2

” jest zdaniem analitycznie

prawdziwym,

e)

Z

1

i Z

2

są s p r z e c z n e wtw, „Z

1

wtw, Z

2

” jest zdaniem kontradyktorycznym.

W punkcie e) mówimy oczywiście o sprzeczności mocnej, natomiast wykluczanie to
szczególny przypadek (dwa zdania) zwykłej sprzeczności. Przypadki a) i c) (a także
d)) możemy uogólnić na dowolne skończone zbiory zdań, w zgodzie z przyjętymi
przez nas wcześniej definicjami wynikania i sprzeczności.

25

Otrzymamy wtedy następujące charakterystyki:
a)

Z wynika ze zbioru zdań {Z

1

, ..., Z

n

} wtw, „Jeżeli Z

1

i .... i Z

n

, to Z” jest zdaniem

analitycznie prawdziwym,

b)

zbiór {Z

1

, ..., Z

n

} jest sprzeczny wtw, „Z

1

i .... i Z

n

” jest zdaniem

kontradyktorycznym.

5.7. Języki naturalne a języki sztuczne

Dotychczasowe rozważania pokazują, że dla potrzeb logiki nieodzowna jest
konstrukcja języków sztucznych. Chodzi przecież o analizę formalnych relacji
logicznych, takich jak wynikania czy sprzeczność, a zbytnia złożoność języka
naturalnego może być tu jedynie przeszkodą.

Zasadnicze różnice między językami naturalnymi a sztucznymi biorą swój początek
w genezie tych systemów znakowych. Każdy język naturalny powstawał spontanicznie,
kształtował się na przestrzeni wielu wieków i dostosowywał do aktualnych potrzeb
komunikacyjnych posługującej się nim społeczności. Efektem takich procesów
jest m.in.:
a)

bogactwo środków leksykalnych, a z punktu widzenia przenoszenia informacji

— redundancja (nadmiarowość) środków, występująca np. jako synonimia
wyrażeń,

b)

płynność kategorii syntaktycznych, czyli wielość funkcji składniowych pełnionych

przez takie same wyrażenia,

c)

wieloznaczność (homonimia i homofonia) wyrażeń,

d)

uniwersalność języka powodująca pomieszanie poziomów językowych (język
i metajęzyk).

Języki sztuczne są tworzone w sposób przemyślany, dla konkretnych celów, co
powoduje, że w przeciwieństwie do języków naturalnych są one ekonomiczne
i konsekwentne (syntaktycznie i semantycznie), a język jest precyzyjnie odróżniany
od metajęzyka, co pozwala uniknąć rozmaitych paradoksów.

Należy też podkreślić, że języki naturalne są systemami zinterpretowanymi,
w tym sensie, że użytkownik takiego języka używa jego wyrażeń w odpowiednich
(dopuszczalnych) znaczeniach. Język sztuczny zawsze może być używany tylko
syntaktycznie (np. w użyciach maszynowych), a nawet istnieją języki tylko
syntaktyczne, tzn. takie, dla których nie skonstruowano semantyki, czyli teorii
znaczenia.

Z tego powodu większość wyrażeń języka sztucznego to

zmienne

określonych

kategorii, dla których określa się jedynie zakres możliwych podstawień (zbiór
d o p u s z c z a l n y c h w a r t o ś c i d a n e j z m i e n n e j ). Cel danego języka decyduje
o tym, jakie wprowadzamy do niego

wyrażenia stałe

, czyli o ustalonym znaczeniu.

Dla ekonomiczności wyrażania niebanalną sprawą jest też stosowanie w językach
tego typu prostych symboli. Kto tego nie rozumie, niech spróbuje za pomocą języka
polskiego zapisać kilka wybranych przypadkowo wzorów z dowolnego podręcznika
algebry lub innego działu matematyki. Nie jest też kwestią przypadku, że gwałtowny
rozwój matematyki w Europie zaczął się dopiero pod koniec średniowiecza, kiedy
pozycyjny zapis dziesiętny z użyciem cyfr arabskich wyparł nieporęczną notację
łacińską.

26

Bibliografia

1.

Ajdukiewicz K., 1965: Logika pragmatyczna, PWN, Warszawa.

2.

Arystoteles, 1990: Dzieła wszystkie, t. 1, PWN, Warszawa.

3.

Bremer J. W., 2004: Wprowadzenie do logiki, Wydawnictwo WAM, Kraków.

4.

Gumański L., 1990: Wprowadzenie w logikę współczesną, PWN, Warszawa.

5.

Hodges W., 1991: Logic, Penguin Books, London.

6.

Marciszewski W., 1977: Metody analizy tekstu naukowego, PWN, Warszawa.

7.

Mill J., S., 1962: System logiki dedukcyjnej i indukcyjnej, t. I–II, PWN,
Warszawa.

8.

Pawłowski T., 1977: Pojęcia i metody współczesnej humanistyki, Ossolineum,
Warszawa.

9.

Pawłowski T., 1986: Tworzenie pojęć w naukach humanistycznych, PWN,
Warszawa.

10.

Pelc J., 1984: Wstęp do semiotyki, Wiedza Powszechna, Warszawa.

11.

Przybyłowski J., 2001: Logika z ogólną metodologią nauk, Wydawnictwo
Uniwersytetu Gdańskiego, Gdańsk.

12.

Skarbek W., 2004: Logika dla humanistów, NWP, Piotrków Trybunalski.

13.

Stanosz B., 1984: Wprowadzenie do logiki formalnej, PWN, Warszawa.

14.

Stonert H., 1964: Język i nauka, Wiedza Powszechna, Warszawa.

15.

Szymanek K., 2001: Sztuka argumentacji. Słownik terminologiczny, PWN,
Warszawa.

16.

Tokarz M., 1994: Elementy formalnej teorii składni, Biblioteka myśli semiotycznej,
Warszawa.

17.

Tokarz M., 1984: Wprowadzenie do logiki, Uniwersytet Śląski, Katowice.

18.

Trzęsicki K., Logika, nauka i sztuka, Temida 1996, Białystok.

19.

Ziembiński Z., 1993: Logika praktyczna, PWN, Warszawa.

27

Słownik

Argumenty

— typowe sposoby uzasadniania poglądów stosowane w dyskusji. Ich

ocena dotyczy raczej skuteczności, nie zaś logicznej poprawności. Niektóre można
jednak zdecydowanie uznać za nieuczciwe sposoby przekonywania, toteż określa
się je często jako fortele (sztuczki) erystyczne i traktuje jako rodzaj błędnych
rozumowań. Do najbardziej znanych należą argumentum ad autoritatem (odwołanie
się do autorytetu, odwoływanie się do litości dyskutanta lub audytorium),
argumentum ad verecundiam (odwoływanie się do nieśmiałości dyskutanta),
argumentum ad vanitatem (odwoływanie się do próżności naszego rozmówcy),
argumentum ad hominem (odwołanie się do poglądów oponenta, aby wykorzystać
je dla własnych celów), argumentum ad personam (argumenty, w których poglądy
oponenta podważa się w sposób pośredni, wskazując, że jest to osoba nieuczciwa,
niemoralna, niekompetentna itp.), argumentum ad baculum (odwołanie się „do kija”,
do gróźb), argumentum ad misericordiam (odwoływanie się do litości dyskutanta
lub audytorium), argumentum ad populum (używanie rozmaitych chwytów
demagogicznych „pod publiczkę”, aby zyskać jej poparcie).

Błędy definicji

— błędy popełniane podczas definiowania. Wyróżnić można m.in. błąd

ignotum per ignotum (niezrozumiałe przez niezrozumiałe) oraz błąd idem per idem,
zwany też błędnym kołem (circulus vitiosus) w definicji. Tutaj dodatkowo występują
dwa typy — błędne koło bezpośrednie (ten sam termin w definiendum i definiensie
tej samej definicji) oraz błędne koło pośrednie, gdzie mamy do czynienia z ciągiem
definicji takim, że każda następna wyjaśnia pewien termin występujący w definiensie
poprzedniej, a w definiensie ostatniej pojawia się ponownie termin z definiendum
pierwszej definicji. Inne rodzaje błędów dotyczą niezgodności zakresów definiensa
i definiendum. Definicja jest za szeroka, gdy zakres definiendum jest podrzędny
względem zakresu definiensa, natomiast za wąska, gdy zakres definiendum jest
nadrzędny względem zakresu definiensa.Może też zachodzić krzyżowanie się zakresów
lub tzw. błąd kategorialny, gdy zakresy obu członów definicji są rozłączne.

Błędy logiczne

— różne rodzaje wykroczeń przeciwko regułom użycia języka,

powodujące zakłócenia w komunikacji, wynikające m.in. z wieloznaczności,
nieostrości, niedookreśloności, używania wyrażeń okazjonalnych, niezrozumiałych.
Typowym przykładem takiego błędu jest amfibologia, czyli wadliwa składnia
umożliwiająca różną interpretację tekstu.

Błędy rozumowań

— tradycyjnie dzieli się je na materialne (fałszywość przynajmniej

jednej przesłanki) i formalne (niepoprawny schemat rozumowania). Dodatkowo
wyróżnia się wiele szczególnych przypadków. Do najważniejszych należą ekwiwokacja
(użycie pewnego terminu w różnych znaczeniach w obrębie jednego rozumowania)
oraz logomachia (użycie pewnego terminu w różnych znaczeniach w dyskusji).

Błąd formalny

— brak wynikania w rozumowaniu, które przedstawia się jako

poprawne (niezawodne).

Błąd materialny

— fałszywość co najmniej jednej przesłanki w rozumowaniu.

Definicja

— językowy sposób wyjaśnienia znaczenia jakiegoś wyrażenia (definicja

nominalna) lub podanie charakterystyki przedmiotu (definicja realna). Definicja
składa się z trzech części: definiendum (część zawierająca termin definiowany),
łącznika definicyjnego (zwanego często spójką definicyjną) i definiensa (część
wyjaśniająca znaczenie). Ze względu na spełniane zadania wyróżnia się trzy

28

rodzaje definicji: definicje sprawozdawcze — inaczej słownikowe — które służą
do wyjaśniania, w jakim znaczeniu dane wyrażenie jest obecnie w pewnym języku
używane; definicje regulujące — które służą precyzacji znaczenia danego wyrażenia,
np. w przypadku nazw nieostrych podają propozycję uściślenia ich zakresu; definicje
projektujące — powstające wówczas, gdy pojawia się potrzeba nazwania nowego
zjawiska w danym języku.

Funkcje komunikacyjne

— ogół celów realizowanych przez użycie języka. Do funkcji

komunikacyjnych należą: funkcja ekspresywna (wyrażanie stanów wewnętrznych
użytkownika języka), funkcja perswazyjna (oddziaływanie na słuchacza), funkcja
fatyczna (utrzymywanie kontaktu między użytkownikami), funkcja opisowa
(przekazywanie informacji).

Indukcja

— ogólna nazwa klasy schematów rozumowania, z których większość jest

zawodna, ale często wykorzystywana w praktyce. Można tu wyróżnić: indukcję
eliminacyjną, indukcję enumeracyjną oraz indukcję matematyczną. Najpopularniejsza
(często zwana po prostu indukcją) jest indukcja enumeracyjna, czyli przez wyliczenie.
Na podstawie skończonej liczby przesłanek, które są zdaniami szczegółowymi,
dochodzi się do wniosku ogólnego. W indukcji eliminacyjnej stosuje się tzw. kanony,
czyli pewne dodatkowe schematy rozumowania. Należą do nich m.in. kanony:
jedynej zgodności i jedynej różnicy.

Języki sztuczne

— języki konstruowane do specjalnych celów, np. w logice do analizy

znaczenia wybranych wyrażeń. Charakteryzują się prostą i konsekwentną gramatyką,
a w semantyce brakiem wieloznaczności.

Kategoria syntaktyczna

— zbiór wyrażeń, które mogą być wzajemnie wymienialne bez

utraty składniowej spójności kontekstu, w którym ta wymiana się odbywa. Kategorie
syntaktyczne dzielimy na samodzielne (zdania i nazwy) oraz niesamodzielne
(funktory).

Klasyczny rachunek kwantyfikatorów (KRK)

— podstawowy rachunek logiczny, zwany

często po prostu logiką klasyczną (również rachunek predykatów, rachunek 1-go
rzędu, rachunek funkcyjny).

Klasyczny rachunek zdań (KRZ)

— elementarna część logiki klasycznej, w której jedyne

wyróżnione stałe logiczne to pewne spójniki ekstensjonalne.

Klasyfikacja odpowiedzi

— wśród wielu rodzajów możliwych odpowiedzi na różne

rodzaje pytań można wyróżnić odpowiedź właściwą — uzupełnienia pewnego
schematu, który sugeruje pytanie; odpowiedź częściową — zdanie, z którego nie
wynika żadna odpowiedź właściwa, ale które wyklucza niektóre spośród nich;
odpowiedź wyczerpującą — zdanie prawdziwe, z którego wynikają wszystkie
odpowiedzi właściwe i prawdziwe.

Kwadrat logiczny

— graficzny sposób prezentacji relacji logicznych zachodzących

między zdaniami kategorycznymi o tym samym podmiocie i orzeczniku.

Kwantyfikatory

— wyrażenia określające, czy chodzi o wszystkie elementy danego

zbioru (kwantyfikator ogólny), czy o ich część (kwantyfikator szczegółowy).
Kwantyfikator zawsze występuje wraz z symbolem zmiennej nazwowej, która jest
przez niego związana.

Operacja formalizacji tekstu

— przekład z języka naturalnego na język KRK lub inny

język sztuczny w celu wyeliminowania wieloznaczności. Poprawna formalizacja musi
zachować co najmniej warunki prawdziwości zdań tłumaczonych.

Podział logiczny

— jest to podstawowy zabieg porządkujący określoną dziedzinę

badań. Podział — aby był logiczny — musi spełniać warunek adekwatności (suma
zbiorów będących członami podziału musi dawać w rezultacie zbiór dzielony),

29

warunek rozłączności (zbiory będące członami podziału muszą być parami rozłączne),
warunek niepustości (każdy człon podziału musi coś zawierać). Skrzyżowanie różnych
podziałów to klasyfikacja, zaś uporządkowanie członów podziału to systematyzacja.

Pytania

— wypowiedzi, których zasadniczym celem jest zdobycie informacji. Składają

się zazwyczaj z partykuły pytajnej i tzw. datum questionis (danej pytania). Wyróżnić
można pytania otwarte i pytania zamknięte (pytania zamknięte dopełnienia, pytania
zamknięte rozstrzygnięcia).

Rachunek nazw (tradycyjny)

— system logiki stworzony przez Arystotelesa,

w którym analizuje się pewne formy rozumowań zachodzących pomiędzy zdaniami
kategorycznymi.

Reguły niezawodne

— schematy rozumowań, w których wniosek wynika z przesłanek,

np. modus ponendo ponens, sylogizm hipotetyczny, dylemat konstrukcyjny prosty.

Relacje logiczne

— zachodzą między zdaniami w sensie logicznym. Do najważniejszych

należy pięć niżej wymienionych:
— Z

2

w y n i k a z Z

1

wtw, „Jeżeli Z

1

, to Z

2

” jest zdaniem analitycznie prawdziwym.

— Z

1

i Z

2

są r ó w n o w a ż n e wtw, „Z

1

wtw, Z

2

” jest zdaniem analitycznie

prawdziwym.

— Z

1

i Z

2

w y k l u c z a j ą s i ę wtw, „Z

1

i Z

2

” jest zdaniem kontradyktorycznym.

— Z

1

i Z

2

d o p e ł n i a j ą s i ę wtw, „Z

1

lub Z

2

” jest zdaniem analitycznie

prawdziwym.

— Z

1

i Z

2

są s p r z e c z n e wtw, „Z

1

wtw, Z

2

” jest zdaniem kontradyktorycznym.

Relacje między zakresami nazw

— w przypadku nazw ogólnych można wyróżnić pięć

rodzajów relacji zachodzących między ich zakresami. Ekstensje dwóch nazw mogą:
— być r ó w n o w a ż n e (tożsame), gdy jest to ten sam zbiór, np. „kobieta”

i „niewiasta”,

— być w relacji p o d r z ę d n o ś c i (ostrego zawierania się), gdy każdy desygnat jednej

nazwy jest desygnatem drugiej, ale nie odwrotnie (ta druga nazwa jest wtedy
w relacji n a d r z ę d n o ś c i względem pierwszej), np. „ssak”, „kręgowiec”,

— w y k l u c z a ć s i ę (być rozłączne), gdy nie mają wspólnych desygnatów, np.

„piernik” i „wiatrak”,

— k r z y ż o w a ć s i ę , gdy mają jakieś desygnaty wspólne i każda z nich ma

desygnaty, które nie należą do zakresu drugiej, np. „ssak”, „drapieżnik”.

Rozumowanie

— jako czynność: proces psychiczny zmierzający do uznania pewnych

zdań (wniosków) na podstawie innych zdań (przesłanek); jako rezultat: tekst
językowy, w którym pewne zdania występują w funkcji przesłanek, a inne w funkcji
wniosków.

Rozumowanie entymematyczne

— rozumowanie, w którym pominięto przesłanki lub

uznano za oczywiste, lub zdania w oczywisty sposób z nich wynikające a prowadzące
do wniosku końcowego.

Rozumowanie poprawne (dedukcyjne, niezawodne)

— takie rozumowanie, w którym

pomiędzy przesłankami a wnioskiem zachodzi relacja wynikania.

Rozumowanie uprawdopodobniające

— rozumowanie, w którym nie zachodzi

wynikanie między przesłankami a wnioskiem, ale w którym prawdziwość przesłanek
zwiększa prawdopodobieństwo zachodzenia wniosku, np. różne formy indukcji czy
rozumowania przez analogię.

Semiotyka logiczna

— dział logiki zajmujący się badaniem systemów znakowych.

Dzieli się na syntaktykę, badającą reguły składni, semantykę, badającą relacje między
znakami i ich znaczeniem oraz pragmatykę, badającą relacje między znakami a ich
użytkownikami.

30

Semantyka KRZ

— (czyli teoria znaczenia języka) jest ekstensjonalna — oznacza to,

że nie uwzględnia się w niej formalnie sądów logicznych, a tylko wartości logiczne
zdań. Podstawowe jest tutaj pojęcie wartościowania zmiennych. Wartościowaniem
nazywamy dowolne odwzorowanie V ze zbioru zmiennych zdaniowych w zbiór
{1,0}. Definicje znaczenia spójników pokazują, w jaki sposób dane wartościowanie
należy poszerzyć na dowolną formułę złożoną.

Sprzeczność w KRZ

— zbiór formuł X jest sprzeczny wtw, nie istnieje wartościowanie,

przy którym wszystkie formuły z tego zbioru są prawdziwe.

Stałe logiczne

— są to wyróżnione wyrażenia, których znaczenie jest precyzyjnie

ustalone na gruncie semantyki danej logiki. W KRZ są to spójniki, czyli funktory
zdaniotwórcze: funktor negacji oraz dwuargumentowe funktory koniunkcji,
alternatywy, implikacji, równoważności.

Tautologia KRZ

— formuła, która jest prawdziwa przy każdym wartościowaniu

(prawda logiczna). Formuła, która przy każdym wartościowaniu jest fałszywa, to
kontrtautologia albo fałsz logiczny. Formuły, których wartość logiczna nie jest stała,
lecz zmienia się — w zależności od wartościowania — to formuły kontyngentne.
Przykłady tautologii KRZ:
— prawo wyłączonego środka p∨¬p,
— prawo (nie)sprzeczności ¬(p∧¬p),
— prawo tożsamości p → p (lub, w mocniejszej postaci p ↔ p),
— sylogizm hipotetyczny [(p → q) ∧ (q → r)] → (p → r),
— modus ponendo ponens [(p → q) ∧ p] → q.

Wynikanie w KRZ: ze zbioru X wynika p wtw, dla dowolnego wartościowania V,
przy którym V(X) = 1, to V(p) = 1.

Wnioskowania bezpośrednie

— reguły niezawodne, w których wniosek wyprowadza

się z jednej przesłanki (np. obwersja, konwersja, kontrapozycja).

Wnioskowania pośrednie (sylogizmy)

— reguły niezawodne, w których wniosek

wyprowadza się z dwóch przesłanek. W sylogizmie występują trzy różne terminy,
każdy po dwa razy w całym rozumowaniu ale tylko raz w danym zdaniu. Termin
występujący w obu przesłankach to termin średni, orzecznik wniosku to termin
większy a podmiot wniosku to termin mniejszy.

Wynikanie

— wniosek wynika z przesłanek wtw, jeżeli jest n i e m o ż l i w e , żeby

wszystkie przesłanki były prawdziwe, a wniosek fałszywy.

Zasada brzytwy Ockhama

— zasada nawołująca do tego, by nie mnożyć bytów bez

potrzeby.

Zasada dwuwartościowości

— każde zdanie (w sensie logicznym) posiada jedną

z dwóch wartości logicznych: jest prawdziwe lub fałszywe.

Zasada niesprzeczności

— żadne zdanie stwierdzające jakiś stan rzeczy nie może być

zarazem prawdziwe i fałszywe. Innymi słowy, nie jest możliwe, aby jakiś stan rzeczy
zachodził i nie zachodził zarazem.

Zasada racji dostatecznej

— zasada mówiąca, że dla każdego twierdzenia należy podać

wystarczające uzasadnienie, czyli dostateczną rację dla jego uznania.

Zasada życzliwej interpretacji

— taki sposób interpretowania tekstu w procesie

formalizacji, który stara się zachować logiczne relacje i własności (np. wynikanie
i niesprzeczność).

Zbiór uporządkowany

— zbiór, na którego elementy nałożono pewną relację

porządkującą. Dwa ważne rodzaje takich relacji to relacja częściowego porządku
i relacja liniowego porządku.

31

Zdania kategoryczne (asertoryczne)

— zdania podmiotowo-orzecznikowe, których

analizą zajmował się już Arystoteles, tworząc pierwszy system logiki. Wyróżniamy:
zdania ogólno-twierdzące (Każde S jest P — SaP), zdania ogólno-przeczące (Żadne
S nie jest P — SeP), zdania szczegółowo-twierdzące (Niektóre S są P — SiP), zdania
szczegółowo-przeczące (Niektóre S nie są P — SoP).

Znaczenie wyrażeń

— informacja przekazywana przez wyrażenie. Wyróżnia się dwa

rodzaje znaczenia:

ekstensję

(zakres, odniesienie, denotację),

intensję

(sens, treść).

W przypadku nazw ekstensją jest zbiór desygnatów nazwy (obiektów, do których
odnosi), a intensją zbiór cech desygnatów. W przypadku zdań ekstensją jest ich
wartość logiczna, a intensją sąd logiczny (komunikowany w zdaniu stan rzeczy).

32

Spis symboli

n — nazwa

z — zdanie

z/z — funktor zdaniotwórczy od jednego argumentu zdaniowego

z/z,z — funktor zdaniotwórczy od dwóch argumentów zdaniowych

z/n — funktor zdaniotwórczy od jednego argumentu nazwowego

z/n,n — funktor zdaniotwórczy od dwóch argumentów nazwowych

n/n — funktor nazwotwórczy od jednego argumentu nazwowego

n/n, n — funktor nazwotwórczy od dwóch argumentów zdaniowych

(z/n)/(z/n) — funktor funktorotwórczy (tworzy funktor o kategorii z/n) od jednego
argumentu funktorowego kategorii z/n

Z

1

, Z

2

— zdania oznajmujące

p, q, r, s, t — zmienne zdaniowe (dowolne zdania oznajmujące)

X — zbiór zdań

X / p — schemat rozumowania o przesłankach X i wniosku p ( X, zatem p)

¬p — negacja p (nieprawda, że p)

(p ∧ q) — koniunkcja p i q (p i q)

(p ∨ q) — alternatywa p i q (p lub q)

(p → q) — implikacja o poprzedniku p i następniku q (jeżeli p, to q)

(p ↔ q) — równoważność p i q (p wtedy i tylko wtedy, gdy q)

1 — symbol prawdy

0 — symbol fałszu

S — podmiot (subiectum) zdania kategorycznego

P — orzecznik (predicatum) zdania kategorycznego

T — termin średni

S’ — nazwa zaprzeczona (nie-S)

SaP — zdanie ogólno-twierdzące (Każde S jest P)

SeP — zdanie ogólno-przeczące (Żadne S nie jest P)

SiP — zdanie szczegółowo-twierdzące (Niektóre S są P)

SoP — zdanie szczegółowo-przeczące (Niektóre S nie są P)
∅ — zbiór pusty

S∪P — suma zbiorów S i P

S∩P — iloczyn (przekrój) zbiorów S i P

33

S−P — różnica zbiorów S i P

−S — dopełnienie zbioru S

S ⊆ P — relacja zawierania (S jest podzbiorem P)

a, b, c — stałe nazwowe

x, y, z — zmienne nazwowe

A – Z — predykaty
∀x — kwantyfikacja ogólna (duża, uniwersalna) zmiennej x (dla każdego x)
∃x — kwantyfikacja szczegółowa (mała, egzystencjalna) x (dla pewnego x)