1.

PRĄD STAŁY

1.1. Prąd elektryczny – podstawowe pojęcia i określenia

Prądem elektrycznym nazywa się zjawisko przepływu elementarnych ładunków

elektrycznych. W metalach i węglu ładunkami tymi są elektrony (ujemne ładunki
elementarne). W innych rodzajach przewodników (gazy, roztwory soli nieorganicznych)
ładunkami elementarnymi są jony.

Ź

ródłami energii elektrycznej są urządzenia pobierające z zewnątrz energię

mechaniczną, chemiczną, cieplną itp., i przetwarzające ją na energię elektryczną (generatory
elektromaszynowe, akumulatory, ogniwa galwaniczne itp.).

Obwód elektryczny w najprostszym przypadku składa się ze źródła energii elektrycznej,

przewodów łączeniowych i odbiornika (rys.1.1). Bardziej złożone obwody elektryczne
składają się z większej liczby źródeł, przewodów i odbiorników.

Rys.1.1. Najprostszy obwód elektryczny

Przewody łączeniowe służą do przenoszenia energii elektrycznej od źródła do

odbiornika. Jako materiały na przewody używane są prawie wyłącznie materiały o
przewodnictwie elektronowym, czyli metale.

Odbiornikami nazywane są urządzenia, które pobierają energię elektryczną i

przetwarzają ją na inne rodzaje energii, takie jak energia cieplna (grzejniki), mechaniczna
(silniki elektryczne), świetlną (źródła światła), chemiczną itp. Przetworzona energia jest
wydzielana poza obwodem elektrycznym.

Kierunek prądu, zgodnie z konwencją Maxwella, przyjmuje się jako zgodny z

kierunkiem przepływu elektryczności dodatniej, tj. przeciwny do kierunku ruchu ładunków
ujemnych (elektronów) tak, jak to przedstawiono na rysunku 1.2.

Rys.1.2. Kierunek prądu i kierunek ruchu elektronów w obwodzie elektrycznym

Ź

ródło prądu stałego (P) posiada dwa zaciski zewnętrzne. Zacisk, z którego prąd wypływa,

nazywa się biegunem dodatnim i jest oznaczony symbolem „+”, a zacisk, do którego prąd
dopływa, nazywa się biegunem ujemnym i jest oznaczony symbolem „-”. Wewnątrz źródła
prąd płynie od bieguna „-” do bieguna „+”. Każde źródło wprowadza do obwodu swoją
rezystancję, zwaną rezystancją wewnętrzną źródła.

Natężeniem prądu nazywa się stosunek ładunku elektrycznego Q, który przepływa

przez przekrój przewodu w czasie t, do tego czasu, tj.

t

Q

I

=

(1.1)

przy czym: I - natężenie prądu w [A],

Q - ładunek elektryczny w kulombach [C],

T - czas w sekundach [t].

Jednostką natężenia, zgodnie z uchwałą Międzynarodowego Komitetu Miar, prądu jest

jeden amper [A].

Najczęściej stosowaną jednostką podwielokrotną ampera jest 1 miliamper [mA] = 0,001

[A], a wielokrotną 1 kiloamper [kA] = 1000 [A].

Jednostką ładunku elektrycznego jest kulomb [C], równy amperosekundzie [As].

Kulomb jest więc ładunkiem elektrycznym, przenoszonym w ciągu jednej sekundy, przez
prąd o natężeniu jednego ampera.

Prądem stałym

nazywa się prąd, którego kierunek przepływu i natężenie są niezmienne

w czasie (rys.1.3a).

Rys.1.3. Przebiegi czasowe prądów: a) - stałego, b) - przemiennego

Prądem zmiennym

nazywa się prąd, którego kierunek przepływu lub natężenie

zmieniają się w czasie. Jeżeli cykl zmian powtarza się w jednakowych okresach czasu, to taki
prąd nazywa się prądem zmiennym okresowym.

Prądem przemiennym

nazywa się prąd, którego kierunek i natężenie zmieniają się w

czasie. Jeżeli cykl zmian kierunku przepływu i natężenia powtarza się w jednakowych
okresach czasu, to taki prąd nazywa się prądem przemiennym okresowym. Przykład prądu
przemiennego, którego natężenie zmienia się w czasie sinusoidalnie, przedstawiono na
rysunku 1.3.b.

Rozdział pierwszy będzie poświęcony wyłącznie zagadnieniom, związanym z prądem

stałym.

1.2. Siła elektromotoryczna źródła energii elektrycznej

W zamkniętym obwodzie elektrycznym prąd elektryczny płynie wówczas, gdy w tym

obwodzie występuje źródło energii elektrycznej, w którym ma miejsce wzrost potencjału
elektrycznego. Jeżeli źródłem tym jest prądnica prądu stałego (P), to zaciski tego źródła
oznacza się symbolami A1 i B2, będącymi oznaczeniami końcówek uzwojeń prądnicy, przy
czym biegun dodatni stanowi zacisk A1, a biegun ujemny zacisk B2 (rys.1.4).

Siłą elektromotoryczną ź

ródła (SEM) nazwano wzrost potencjału elektrycznego, mający

miejsce wewnątrz źródła. Siłę elektromotoryczną oznacza się symbolem E, a jej kierunek
przyjmuje się jako zgodny ze wzrostem potencjału elektrycznego. Siła elektromotoryczna
stanowi w zamkniętym obwodzie elektrycznym wymuszenie, powodujące przepływ prądu
elektrycznego. Kierunek prądu przyjmuje się więc jako zgodny z kierunkiem SEM (rys.1.4).

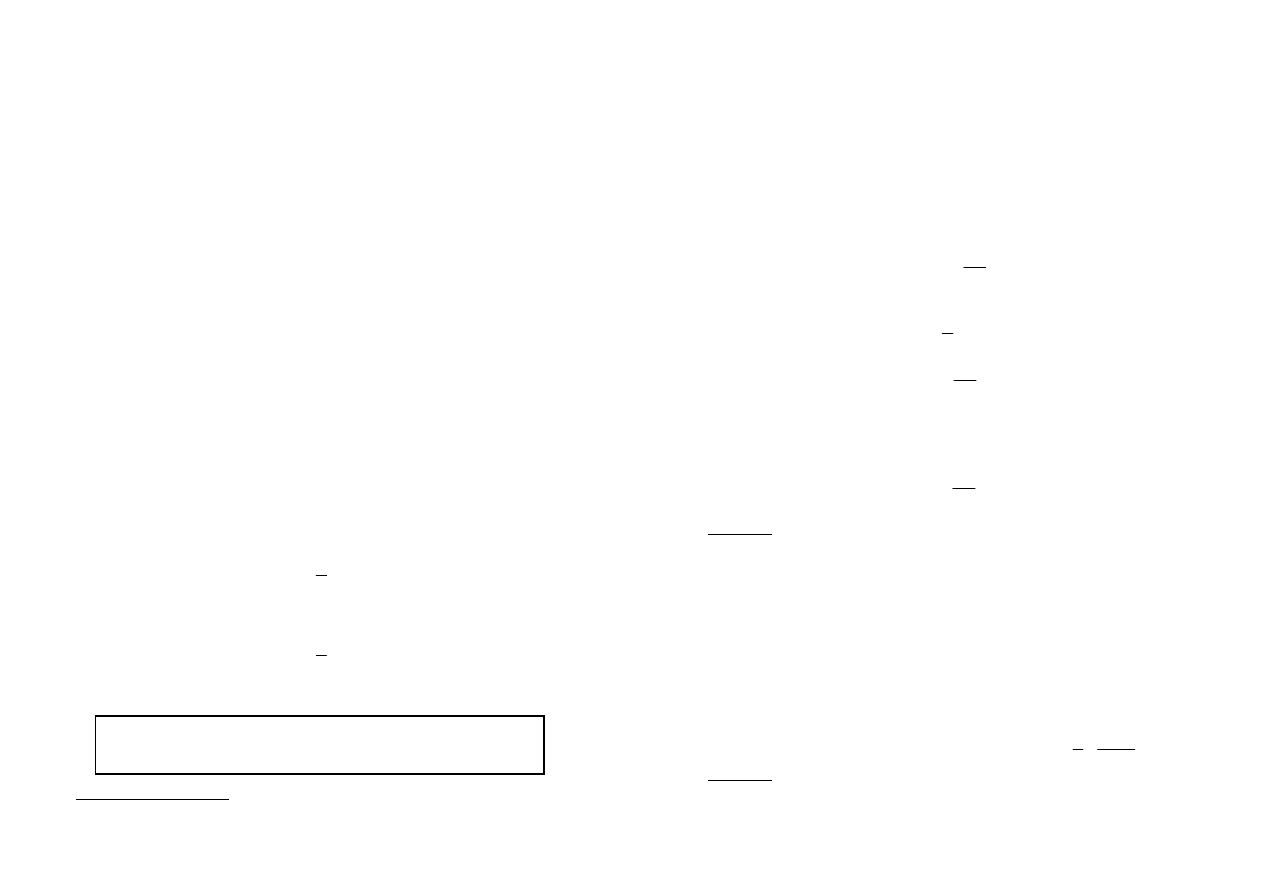
Rys.1.4. Zamknięty obwód elektryczny

Napięciem elektrycznym nazywa się różnicę potencjałów między dwoma punktami

obwodu elektrycznego i oznacza symbolem U. Jeżeli obwód elektryczny nie jest zamknięty,
to prąd w takim obwodzie nie płynie (I = 0), a napięcie na zaciskach źródła jest równe sile
elektromotorycznej. Jeżeli obwód elektryczny jest zamknięty, to w takim obwodzie płynie
prąd elektryczny, a napięcie na zaciskach źródła jest mniejsze od siły elektromotorycznej.

Jednostką siły elektromotorycznej i napięcia elektrycznego jest jeden wolt [V].
Najczęściej stosowaną jednostką podwielokrotną wolta jest 1 miliwolt [mV] = 0,001

[V], a wielokrotną 1 kilowolt [kV] = 1000 [V].

1.3.

Prawo Ohma

W zamkniętym obwodzie elektrycznym, zawierającym źródło energii elektrycznej i

odbiornik, pod wpływem siły elektromotorycznej E źródła, płynie prąd elektryczny I

1)

1)

(rys.1.5). Ustalono, że natężenie tego prądu jest proporcjonalne do siły elektromotoryczne,

tj.

GE

I

=

(1.2)

przy czym G jest współczynnikiem proporcjonalności i nazywa się przewodnością
elektryczną obwodu. Wielkość ta, w ogólnym przypadku, zależy od rodzaju elementów
obwodu (źródła, przewodów, odbiornika), ale też może posiadać wartość stałą. Obwody, w
których przewodność elektryczna jest wartością stałą, są nazywane obwodami liniowymi, a w
przeciwnym przypadku – obwodami nieliniowymi. Proporcjonalność natężenia prądu do siły
elektromotorycznej jest więc cechą obwodów liniowych. W obwodach nieliniowych taka
proporcjonalność nie występuje.

W praktyce używana jest wielkość będąca odwrotnością przewodności, tj.

G

R

1

=

(1.3)

Wielkość ta nazywa się opornością elektryczną lub rezystancją (nazwa obowiązująca) i
charakteryzuje ona własności obwodu elektrycznego.

Po podstawieniu wyrażenia (1.3) do równania (1.2) otrzymuje się zależność

R

E

I

=

(1.4)

stanowiącej ogólną postać prawa Ohma, które słownie można sformułować w następujący
sposób:

W zamkniętym obwodzie elektrycznym natężenie prądu jest wprost proporcjonalne

do siły elektromotorycznej źródła energii elektrycznej i odwrotnie proporcjonalne

do rezystancji.

1)

Słowa „prąd” i „natężenie prądu” są w elektrotechnice używane jako pojęcia równoznaczne.

Prawo Ohma dotyczy także części zamkniętego obwodu elektrycznego, np. jeżeli

napięcie między dowolnymi punktami A i B obwodu (rys.1.5) wynosi U

AB

,

Rys.1.5. Część zamkniętego obwodu elektrycznego

a rezystancja między tymi punktami jest równa R

AB

, to natężenie prądu

AB

AB

R

U

I

=

(1.5)

Jednostką rezystancji jest jeden om, a jej symbolem jest grecka litera omega (Ω). Z

prawa Ohma (wzór 1.4) wynika, że

I

U

R

=

(1.6)

zatem

]

A

[

1

]

V

[

1

]

[

1

=

Ω

Można więc powiedzieć, że jeden om jest rezystancją odcinka obwodu elektrycznego, w

którym napięcie panujące na tym odcinku, powoduje przepływ prądu o natężeniu jednego
ampera.

Jednostką przewodności elektrycznej jest jeden simens, a jej symbolem jest litera S. Z

równania (1.3) wynika, że

V]

[

1

]

A

[

1

]

[

1

=

S

Przykład 1.1

W obwodzie jak na rys.1.6 napięcie zasilania E=220 V, rezystancja całkowita obwodu

R=40 Ω. Obliczyć natężenie prądu w obwodzie.

Rys.1.6. Obwód elektryczny do przykładu 1.1

Rozwiązanie

Zgodnie z wzorem (1.4) natężenie prądu w obwodzie wynosi

A]

[

5

,

5

]

[

40

]

V

[

220

=

Ω

=

=

R

E

I

.

Przykład 1.2

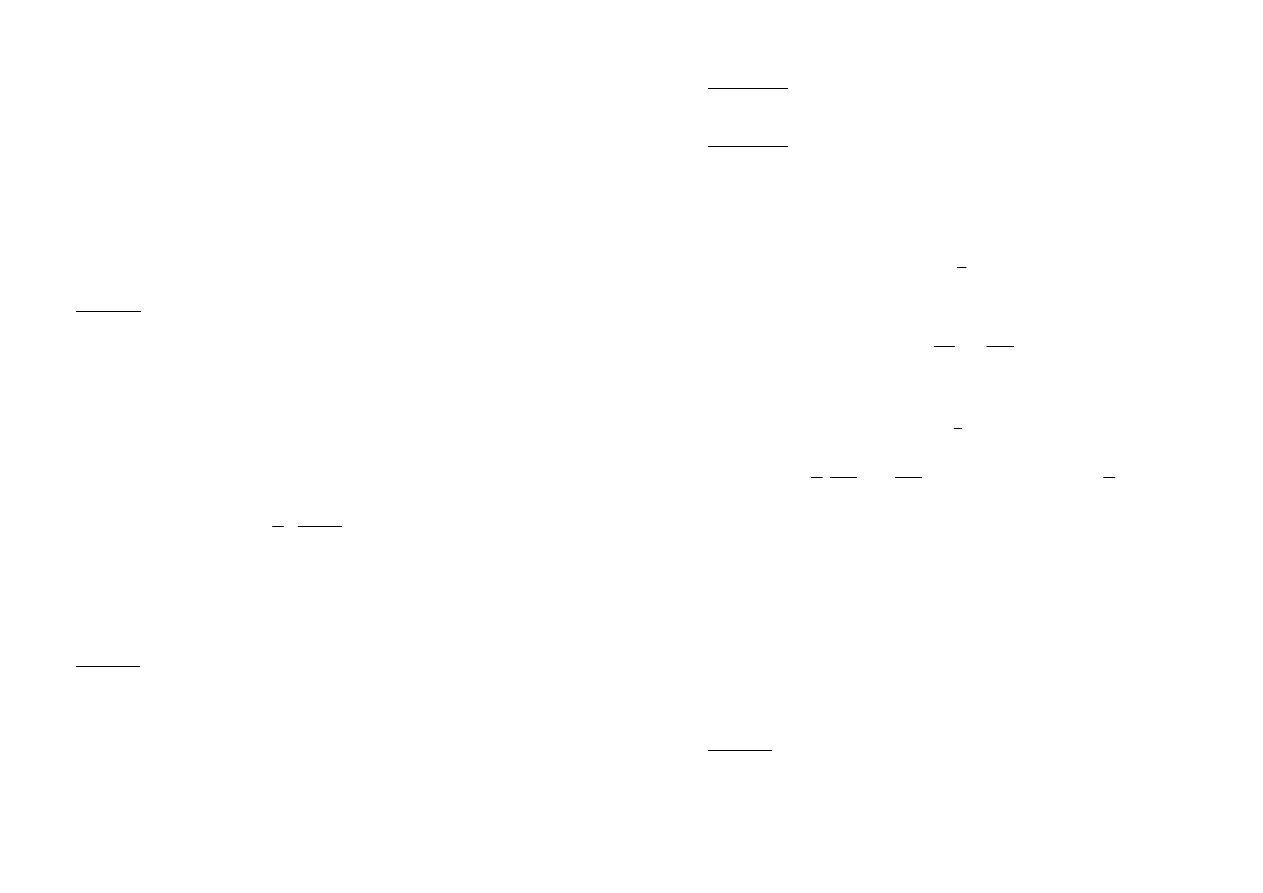
Natężenie prądu płynącego między punktami A i B odcinka obwodu elektrycznego o

rezystancji R

AB

=5 Ω (rys.1.7) wynosi I=20 A. Obliczyć napięcie U

AB

występujące między

tymi punktami.

Rys.1.7. Odcinek obwodu elektrycznego do przykładu 1.2

Rozwiązanie

Z wzoru (1.5) otrzymuje się, że

]

V

[

100

]

[

5

]

A

[

20

AB

AB

=

Ω

⋅

=

⋅

=

R

I

U

.

Przykład 1.3

Obliczyć natężenie prądu I, jaki popłynie przez ciało człowieka, który dotknął szyny, na

której występuje napięcie względem ziemi U=150 V (rys.1.8), jeżeli rezystancja jego ciała
wynosi R=2500 Ω.

Rys.1.8. Rysunek do przykładu 1.3

Rozwiązanie

Z wzoru (1.5) otrzymuje się

A]

[

06

,

0

]

[

2500

]

V

[

150

=

Ω

=

=

R

U

I

.

Uwaga!
Prąd o takim natężeniu może skutkować śmiertelnym porażeniem człowieka.

1.4. Rezystancja

Ze względu na łatwość przewodzenia prądu elektrycznego, wszystkie ciała występujące

w przyrodzie, można podzielić na trzy grupy: przewodniki, nieprzewodniki i półprzewodniki.
Przewodniki są to materiały, posiadające małą rezystancję i stosunkowo łatwo przewodzące
prąd elektryczny pod wpływem napięcia. Ze względu na charakter przewodzenia prądu
elektrycznego, można je podzielić na dwie klasy:

- Klasa I, do której należą przewodniki nie zmieniając swojej struktury i nie ulegające

zmianom chemicznym podczas przewodzenia prądu (wszystkie metale i węgiel).
Istota przewodzenia prądu w przewodnikach tej klasy polega na ruchu swobodnych
elektronów, a taki rodzaj przewodnictwa nazywa się przewodnictwem elektronowym;

- Klasa II, do której należą przewodniki, podlegające zmianom chemicznym podczas

przewodzenia prądu (wodne roztwory kwasów, zasad i soli). Istota przewodzenia
prądu w tej klasie przewodników polega na ruchu jonów, a taki rodzaj przewodnictwa
nazywa się przewodnictwem jonowym.

Nieprzewodniki są to materiały, posiadające bardzo dużą rezystancję, która powoduje, że
materiały te praktycznie nie przewodzą prądu elektrycznego (gazy, oleje i prawie wszystkie
ciała stałe, z wyjątkiem metali i węgla). W elektrotechnice są one często stosowane jako
materiały izolacyjne (mika, szkło, porcelana, azbest, bawełna itp.).
Półprzewodniki są materiałami o właściwościach pośrednich, których przewodnictwo
elektryczne zależy od różnych czynników, takich jak pole elektryczne, oświetlenie,
temperatura itp. Do materiałów tego typu należą krzem, selen, tlenki metali alkalicznych i
wapniowców, a także niektóre węgliki i siarczki. Materiały te znalazły olbrzymie
zastosowanie w współczesnej technice, szczególnie elektronice.

Rezystancja przewodników zależy od rodzaju materiału i jego wymiarów. Dla

przewodu o długości l i powierzchni o przekroju S jest ona wprost proporcjonalna do jego
długości i odwrotnie proporcjonalna do powierzchni przekroju, tj.

S

l

R

ρ

=

(1.7)

przy czym ρ jest współczynnikiem proporcjonalności, który dla każdego materiału ma
określoną wartość. Współczynnik ten nazywa się rezystywnością lub rezystancją właściwą.
Jednostkę rezystywności można określić z zależności (1.7)

]

m

mm

[

1

]

[

1

]

[

1

]

[

1

]

[

1

2

Ω

=

⋅

=

ρ

S

l

R

Jednostką rezystywności w układzie jednostek SI jest

]

m

[

1

⋅

Ω

.

Istnieje również pojęcie konduktywności (przewodności właściwej), zdefiniowanej jako

odwrotność rezystywności, czyli

ρ

=

γ

1

(1.8)

Jednostką konduktywności jest

]

mm

m

S

[

1

]

mm

m

1

[

1

]

[

1

2

2

⋅

=

⋅

Ω

=

γ

lub (układzie jednostek SI)

]

m

S

[

1

.

Rezystancja materiałów przewodzących nie jest wielkością stałą. Zależy ona od

temperatury i, na ogół (nie zawsze), zwiększa się wraz z jej wzrostem. W pewnych zakresach
temperatury (od około -100

0

C do +200

0

C) zależność rezystancji od temperatury jest liniowa i

określona zależnością

)]

(

1

[

)

(

1

1

t

t

R

t

R

−

α

+

=

(1.9)

przy czym: R

1

- rezystancja przewodnika w temperaturze t

1

0

C,

R - rezystancja przewodnika w temperaturze t

0

C,

α

- współczynnik temperaturowy rezystancji, zdefiniowany jako względny

przyrost rezystancji przy wzroście temperatury o 1

0

C.

Wartość rezystancji R przewodnika w temperaturze t wyższej lub niższej od 20

0

C

oblicza się z zależności

)]

20

(

1

[

20

20

−

α

+

=

t

R

R

(1.10)

Współczynnik α

20

dla większości czystych metali wynosi około +0,004. Dla niektórych

stopów, węgla i elektrolitów współczynnik posiada wartość ujemną, tzn. rezystancja tych
materiałów zmniejsza się z wzrostem temperatury.

Przykład 1.4

Rezystancja przewodu miedzianego w temperaturze 20

0

C wynosi R

20

= 50 Ω. Ile wynosi

rezystancja tego przewodu w temperaturze 70

0

C, jeżeli współczynnik temperaturowy

rezystancji dla miedzi α

20

=0,00393 [1/1

0

C]?

Rozwiązanie

Z wzoru (1.10) otrzymuje się

Ω

=

−

⋅

+

=

−

α

+

=

825

,

59

)]

20

70

(

00393

,

0

1

[

50

)]

20

(

1

[

20

20

t

R

R

.

Przykład 1.5

Rezystancja miedzianego uzwojenia wzbudzenia prądnicy prądu stałego w temperaturze

20

0

C wynosi R

20

= 200 Ω, a po nagrzaniu R= 240 Ω. Obliczyć do jakiej temperatury nagrzało

się uzwojenie.

Rozwiązanie

Po przekształceniu zależności (1.10), otrzymuje się

.

9

,

70

200

00393

,

0

200

240

20

0

20

20

20

C

R

R

R

t

t

=

⋅

−

+

=

α

−

+

=

1.4. Spadki napięć w obwodzie zamkniętym

Zamknięty obwód elektryczny składa się z dwóch części: wewnętrznej - składającej się

ze źródła energii o sile elektromotorycznej E z jego rezystancją wewnętrzną R

w

oraz części

zewnętrznej, którą stanowi rezystancja R

z

, dołączona do zacisków źródła energii (rys.1.9).

Rys.1.9. Zamknięty obwód elektryczny

Pod wpływem siły elektromotorycznej E w obwodzie płynie prąd I. Ponieważ

rezystancje R

w

i R

z

są połączone szeregowo, to przez nie przepływa ten sam prąd. Całkowita

rezystancja obwodu R równa się więc sumie obydwu rezystancji, czyli

z

w

R

R

R

+

=

(1.11)

Natężenie prądu w obwodzie, zgodnie z prawem Ohma, wynosi

z

w

R

R

E

R

E

I

+

=

=

(1.12)

co, po przekształceniu, daje równanie

z

w

IR

IR

E

+

=

(1.13)

Iloczyn

w

IR nazywa się spadkiem napięcia na rezystancji R

w

spowodowanym

przepływem prądu I, a iloczyn

z

IR spadkiem napięcia na rezystancji zewnętrznej R

z

. Spadki

napięć na poszczególnych rezystancjach są skierowane przeciwnie do kierunku prądu, który
te spadki wywołuje. Na zaciskach źródła energii występuje więc napięcie U=

z

IR , określone

równaniem

z

IR

E

U

−

=

(1.14)

Można więc sformułować następujący wniosek.

W obwodzie zamkniętym, przy przepływie prądu I, napięcie na zaciskach źródła

jest równe sile elektromotorycznej E, pomniejszonej o spadek napięcia na

rezystancji wewnętrznej źródła IR

w

, spowodowany tym prądem.

Zależność napięcia na zaciskach źródła od prądu obciążenia można przedstawić

graficznie tak, jak to zrobiono na rys.1.10.

Rys.1.10. Zależność napięcia na zaciskach źródła energii od prądu obciążenia

Znaczy to, że napięcie na zaciskach źródła energii zależy od natężenia płynącego w obwodzie
prądu. Jeżeli prąd w obwodzie nie płynie (R

z

=

∞

, I = 0), to taki stan nazywa się stanem

jałowym obwodu. W stanie jałowym napięcia na zaciskach źródła energii jest równe sile
elektromotorycznej, tj. U = E.

Przykład 1.6

Do zacisków prądnicy prądu stałego o sile elektromotorycznej E=230 V i rezystancji

wewnętrznej R

w

= 0,5 Ω dołączono obciążenie o rezystancji R

z

=12 Ω. Obliczyć napięcie U na

zaciskach prądnicy.

Rozwiązanie

Napięcie na zaciskach prądnicy można obliczyć z równania (1.14)

z

IR

E

U

−

=

.

Natężenie prądu płynącego w obwodzie, niezbędne do obliczenia spadku napięcia na
rezystancji wewnętrznej, oblicza się z prawa Ohma, które w tym przypadku ma postać

]

A

[

4

,

18

]

12)[

(0,5

]

V

[

230

z

w

=

Ω

+

=

+

=

R

R

E

I

Po podstawieniu do równania (1.14) wartości liczbowych, otrzymuje się

]

V

[

8

,

220

2

,

9

230

5

,

0

4

,

18

230

w

=

−

=

⋅

−

=

−

=

IR

E

U

Przykład 1.7

Obliczyć siłę elektromotoryczną źródła energii, jeżeli napięcie na jego zaciskach

wynosi U=1[V], rezystancja wewnętrzna R

w

=0,15Ω, a rezystancja obwodu zewnętrznego

R

z

=0,5Ω.

Rozwiązanie

Z prawa Ohma (1.5) wynika, że natężenie prądu w obwodzie

]

A

[

2

]

0,5[

]

V

[

1

z

=

Ω

=

=

R

U

I

a z równania (1.14), że siła elektromotoryczna źródła

]

V

[

3

,

1

]

V

[

15

,

0

2

]

V

[

1

w

=

⋅

+

=

⋅

+

=

R

I

U

E

1.5.

Sposoby łączenia rezystancji

W rzeczywistych obwodach elektrycznych często występuje kilka rezystancji

połączonych szeregowo lub równolegle. Zachodzi wtedy potrzeba obliczenia tak zwanej
rezystancji zastępczej, tzn. takiej, której podłączenie do sieci, powoduje ten sam skutek co
podłączenie wszystkich rezystancji składowych.

1.5.1. Szeregowe łączenie rezystancji

Przykład obwodu z szeregowo połączonymi rezystancjami przedstawiono na rys.1.11.

Na drodze prądu znajdują kolejno rezystancje

3

2

1

,

,

R

R

R

, a natężenie prądu jest jednakowe we

wszystkich punktach obwodu.

Rys.1.11. Obwód elektryczny z szeregowo połączonymi rezystancjami

Ogólnie można powiedzieć, że rezystancja zastępcza jest to taka rezystancja, która po
zastąpieniu nią wszystkich rezystancji, powoduje przepływ takiego samego prądu w
obwodzie. Tak więc,

w obwodzie z szeregowo połączonymi rezystancjami, rezystancja zastępcza R

z

jest równa

sumie wszystkich rezystancji wchodzących w skład tego obwodu, tj.

3

2

1

R

R

R

R

z

+

+

=

(1.15)

Dla danego obwodu

3

2

1

R

R

R

R

E

R

E

I

w

z

+

+

+

=

=

(1.16)

oraz

3

2

1

IR

IR

IR

IR

E

w

+

+

+

=

(1.17)

Zgodnie z prawem Ohma, napięcia na poszczególnych rezystancjach wyniosą:

1

1

IR

U

=

2

2

IR

U

=

3

3

IR

U

=

(1.18)

Ponieważ napięcie na zaciskach źródła wynosi

w

IR

E

U

−

=

, to można stwierdzić, że

W obwodzie z szeregowo połączonymi rezystancjami, napięcie na zaciskach źródła

jest równe sumie napięć na wszystkich rezystancjach zewnętrznej części obwodu.

W rozpatrywanym przypadku

)

(

3

2

1

3

2

1

R

R

R

I

U

U

U

U

+

+

=

+

+

=

(1.19)

Stosując prawo Ohma do poszczególnych odcinków obwodu, w których płynie ten sam

prąd, można także napisać, że

3

3

2

2

1

1

R

U

R

U

R

U

I

+

+

=

(1.20)

lub po przekształceniu

3

2

1

3

2

1

:

:

:

:

R

R

R

U

U

U

=

(1.21)

Z równania (1.21) wynika więc wniosek, że

W obwodzie z szeregowo połączonymi rezystancjami stosunek napięć na

poszczególnych odcinkach obwodu jest równy stosunkowi rezystancji.

Ponieważ przez wszystkie rezystancje przepływa ten sam prąd, to na większej rezystancji
wystąpi większe napięcie, a na mniejszej mniejsze.

Przykład 1.8

Do sieci elektrycznej o napięciu 230V dołączono dwa szeregowo połączone odbiorniki

o rezystancjach

Ω

=

10

1

R

oraz

Ω

=

90

2

R

(rys.1.12). Obliczyć napięcia na poszczególnych

rezystancjach.

Rozwiązanie

Rys.1.12. Schemat obwodu do przykładu 1.8

Prąd płynący w obwodzie oblicza się z prawa Ohma

A

R

R

U

R

U

I

z

3

,

2

90

10

230

2

1

=

+

=

+

=

=

Napięcia na poszczególnych rezystancjach są równe:

V

IR

U

23

10

3

,

2

1

1

=

⋅

=

=

V

IR

U

207

90

3

,

2

2

2

=

⋅

=

=

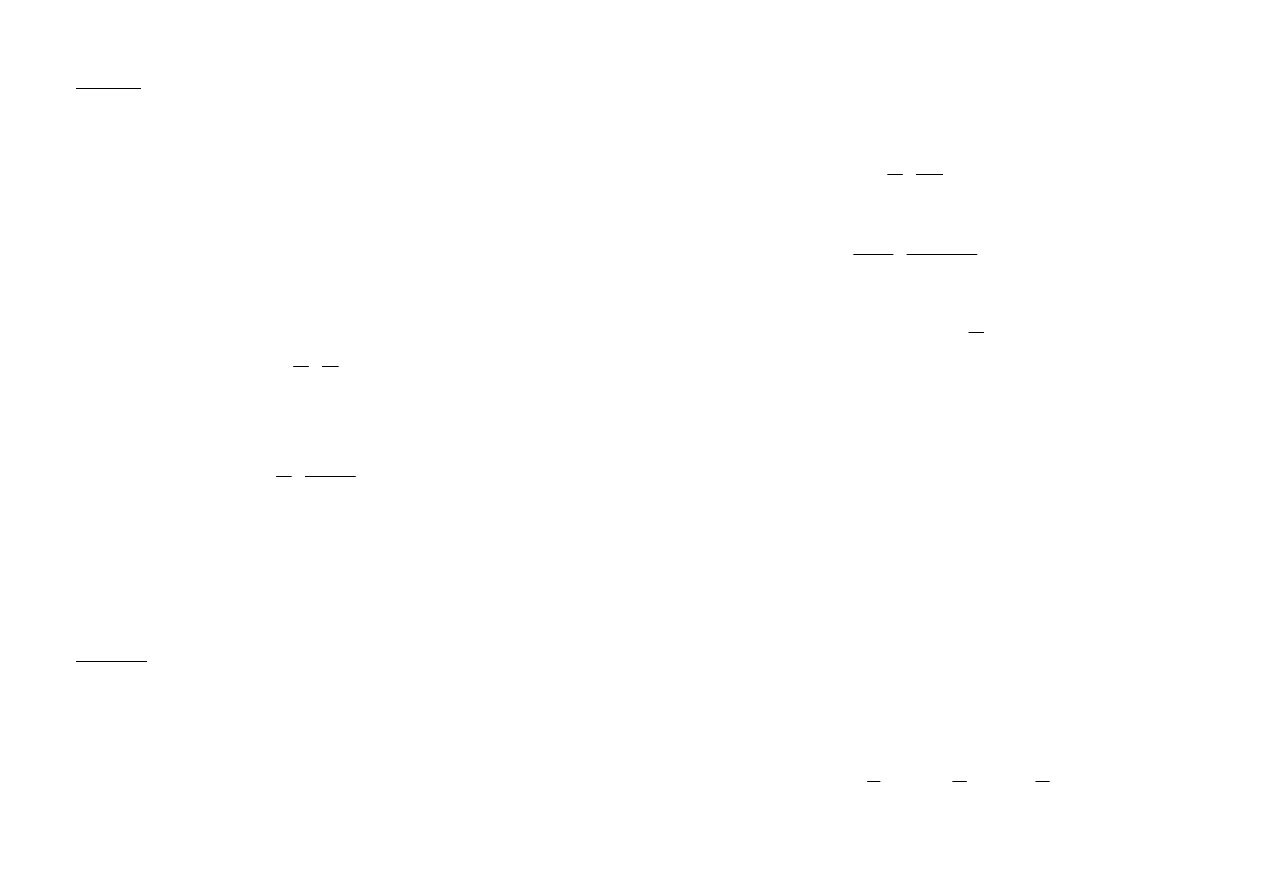
Przykład 1.9

Obliczyć jaką dodatkową rezystancję należy dołączyć szeregowo do woltomierza

(przyrząd do pomiaru napięcia) o napięciu znamionowym U

v

i rezystancji wewnętrznej R

v

,

aby można nim zmierzyć napięcie N razy większe od znamionowego, tj. U = N·U

v

(rys.1.13).

Rozwiązanie

Rys.1.13. Schemat obwodu do przykładu 1.9

Do rozwiązania problemu można posłużyć się zależnością (1.21). Dla obwodu jak na

rys.1.13 można napisać proporcję

v

d

v

d

U

U

R

R

=

Spadek napięcia na dodatkowej rezystancji powinien wynieść

v

v

v

v

d

U

N

U

U

N

U

U

U

)

1

(

−

=

−

⋅

=

−

=

Po podstawieniu ostatniego wyrażenia do pierwszego równania otrzymuje się proporcję

v

v

v

d

U

U

N

R

R

)

1

(

−

=

z której oblicza się poszukiwaną wartość rezystancji

)

1

(

−

=

N

R

R

v

d

Przy takiej wartości dołączonej szeregowo rezystancji przez woltomierz popłynie prąd I

v

, na

który został zaprojektowany przyrząd. Przedstawioną metodę stosuje się do rozszerzania
zakresów woltomierzy. Dołączony szeregowo do woltomierza rezystor, rozszerzający zakres
woltomierza, nazywa się posobnikiem. Wskazania woltomierza z dołączonym posobnikiem
należy mnożyć przez N = U/U

v

.

Przykład 1.10

Woltomierz o napięciu znamionowym U

v

=50V ma być użyty do pomiaru napięcia w

sieci U=500V. Rezystancja wewnętrzna woltomierza wynosi R

v

=5000Ω. Obliczyć jaką

dodatkową rezystancję R

d

należy włączyć w szereg z woltomierzem, aby przy tym napięciu

płynął przez niego prąd znamionowy I

v

.

Rozwiązanie

W poprzednim przykładzie wykazano, że dodatkowa rezystancja włączona szeregowo z

woltomierzem powinna wynosić

)

1

(

−

=

N

R

R

v

d

Ponieważ w tym przypadku R

v

=5000Ω, N=U/U

v

=500/50=10, to wartość dodatkowej

rezystancji wyniesie

Ω

=

−

⋅

=

45000

)

1

10

(

5000

d

R

Prąd znamionowy I

v

woltomierza jest równy

mA

10

A

01

,

0

5000

50

=

=

=

=

v

v

v

R

U

I

Po szeregowym dołączeniu rezystancji R

d

i napięciu sieci U=500V przez woltomierz popłynie

prąd o natężeniu

mA

10

A

01

,

0

45000

5000

500

=

=

+

=

+

=

d

v

v

R

R

U

I

a więc również prąd znamionowy.

W ten sposób zakres pomiarowy woltomierza został powiększony z 50V do 500V. Wskazania

woltomierza należy przy tym mnożyć przez

10

N

=

=

v

U

U

.

1.5.2. Równoległe łączenie rezystancji

Przykład obwodu z równolegle połączonymi rezystancjami przedstawiono na rys.1.14.

W przeciwieństwie do obwodów z szeregowo połączonymi rezystancjami, w których
natężenie prądu we wszystkich częściach obwodu jest takie samo, w obwodach z
rezystancjami połączonymi równolegle prąd I, płynący ze źródła, rozgałęzia się w punkcie
węzłowym (punkt A na rys.1.14) na prądy I

1

, I

2

, I

3

, płynące w gałęziach równoległych o

rezystancjach odpowiednio R

1

, R

2

i R

3

. W punkcie węzłowym B prądy te łączą się i jako prąd

I wpływają do źródła.

W przypadku obwodów z równolegle połączonymi rezystancjami, rezystancją zastępczą

nazywa się taką rezystancję, przez którą, po włączeniu na miejsce połączonych równolegle
rezystancji, płynie prąd o natężeniu równym sumie natężeń prądów, płynących w
poszczególnych gałęziach, przy tym samym napięciu między punktami węzłowymi.

Rys.1.14. Obwody elektryczne: a) - z równolegle połączonymi rezystancjami, b) - z

rezystancją zastępczą

Zgodnie z prawem Ohma prądy w gałęziach wynoszą

1

1

R

U

I

=

2

2

R

U

I

=

3

3

R

U

I

=

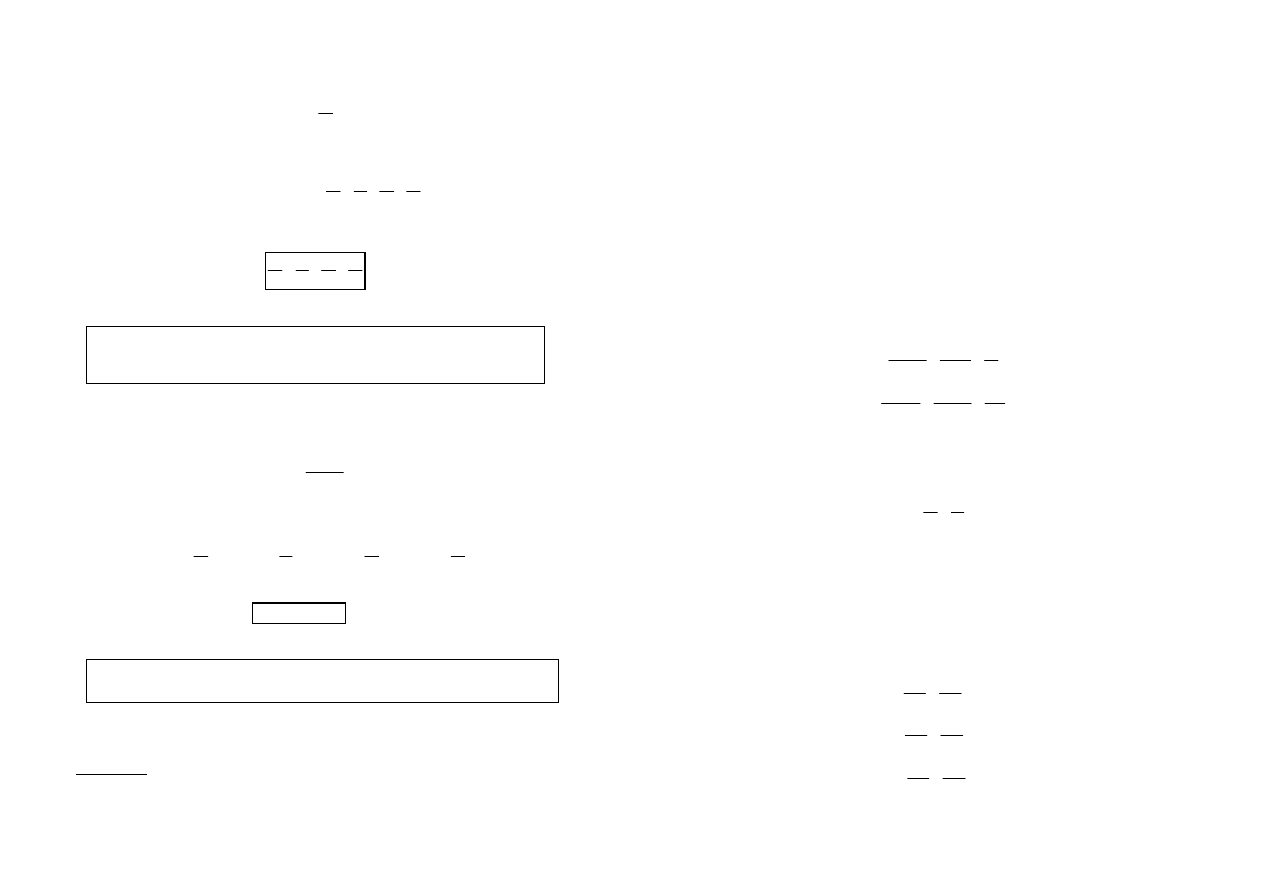
a w gałęzi z rezystancją zastępczą R

z

z

R

U

I

=

Ponieważ prąd pobierany ze źródła jest równy sumie prądów gałęzi (ładunek nie może się
gromadzić w węźle), to

3

2

1

3

2

1

R

U

R

U

R

U

R

U

I

I

I

I

z

+

+

=

=

+

+

=

Stąd otrzymuje się zależność, określającą rezystancję zastępczą rezystancji połączonych
równolegle

3

2

1

1

1

1

1

R

R

R

R

z

+

+

=

(1.22)

Uogólniając, można powiedzieć, że

W obwodzie z równolegle połączonymi rezystancjami, odwrotność rezystancji

zastępczej jest równa sumie odwrotności rezystancji poszczególnych rezystancji gałęzi

połączonych równolegle.

W szczególnym przypadku, kiedy obwód elektryczny składa się tylko z dwóch gałęzi z

rezystancjami R

1

i R

2

, rezystancja zastępcza R

z

jest równa iloczynowi tych rezystancji,

podzielonemu przez ich sumę, tj.

2

1

2

1

R

R

R

R

R

z

+

=

(1.23)

Powyższe wynika bezpośrednio z równania (1.22).

Zastępując w zależności (1.22) rezystancje przewodnościami

z

z

R

G

1

=

1

1

1

R

G

=

2

2

1

R

G

=

3

3

1

R

G

=

otrzymuje się

3

2

1

G

G

G

G

z

+

+

=

(1.24)

Uogólniając, można powiedzieć, że

W obwodzie z równolegle połączonymi rezystancjami, przewodność zastępcza jest równa

sumie przewodności poszczególnych gałęzi połączonych równolegle.

Obliczenia z zastosowaniem przewodności wygodnie jest przeprowadzać w przypadku

obwodów elektrycznych z większą liczbą gałęzi równoległych.

Przykład 1.11

Na rys.1.15 przedstawiono obwód elektryczny z czterema połączonymi równolegle

rezystorami. Obliczyć natężenia prądów I

1

, I

2

, I

3

, I

4

w poszczególnych gałęziach, napięcie U

na zaciskach źródła oraz napięcia między punktami AB i BC obwodu. Parametry obwodu są
równe: E = 12V, R

w

= 0,1Ω, R

1

= 5 Ω, R

2

= 10 Ω, R

3

= 15 Ω, R

4

= 20 Ω.

Rys.1.15. Schemat obwodu do przykładu 1.11

Rozwiązanie

Najpierw należy obliczyć rezystancje zastępcze R

zAB

oraz R

zBC

dla gałęzi z równolegle

połączonymi rezystancjami.

A

33

,

3

15

50

10

5

10

5

2

1

2

1

zAB

=

=

+

⋅

=

+

=

R

R

R

R

R

A

57

,

8

35

300

20

15

20

15

4

3

4

3

zBC

=

=

+

⋅

=

+

=

R

R

R

R

R

Całkowita rezystancja obwodu wynosi

Ω

=

+

+

=

+

+

=

0

,

12

57

,

8

33

,

3

1

,

0

zBC

zAB

R

R

R

R

w

z

Natężenie prądu pobieranego ze źródła wynosi

A

1

12

12

=

=

=

z

R

E

I

Napięcie na zaciskach źródła

V

9

,

11

1

,

0

1

12

=

⋅

−

=

−

=

w

R

E

U

Napięcie między punktami A i B oraz B i C obwodu

V

33

,

3

33

,

3

1

zAB

AB

=

⋅

=

=

IR

U

V

57

,

8

57

,

8

1

zBC

BC

=

⋅

=

=

IR

U

Prądy płynące w poszczególnych gałęziach równoległych wynoszą

A

666

,

0

5

33

,

3

1

AB

1

=

=

=

R

U

I

A

333

,

0

10

33

,

3

2

AB

2

=

=

=

R

U

I

A

57

,

0

15

57

,

8

3

BC

3

=

=

=

R

U

I

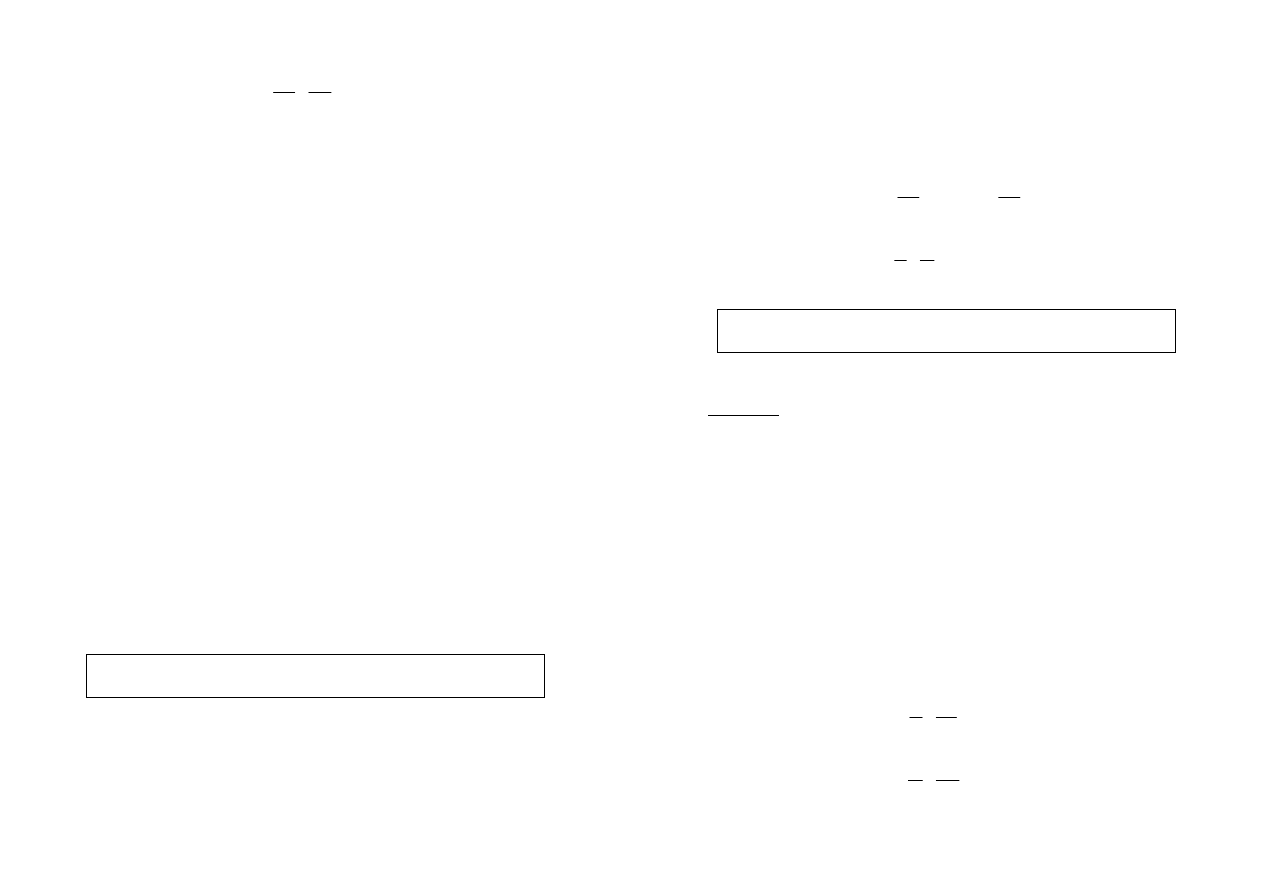
A

429

,

0

20

57

,

8

4

BC

4

=

=

=

R

U

I

Prądy, dopływające z gałęzi równoległych do węzłów, powinny być równe prądowi
pobieranemu ze źródła, a mianowicie:

A

1

999

,

0

333

,

0

666

,

0

2

1

≈

=

=

+

=

+

I

I

I

A

1

999

,

0

429

,

0

57

,

0

4

3

≈

=

=

+

=

+

I

I

I

Niedokładność wynika z zaokrągleń wyników obliczeń.

1.6.

Prawa Kirchhoffa

1.6.1. Pierwsze prawo Kirchhoffa

Jak już wcześniej wspomniano, ładunek elektryczny nie może gromadzić się w żadnym

punkcie obwodu elektrycznego, co może mieć miejsce tylko w przypadku, gdy przepływ
prądu jest ciągły. Wynika z tego, że w obwodach rozgałęzionych suma prądów
dopływających do węzłów, musi się równać sumie prądów odpływających.

Rys.1.16. Wyjaśnienie pierwszego prawa Kirchhoffa

Rozpatrując ogólny przypadek, przedstawiony na rys.1.16a, powyższe słowne

sformułowanie można zapisać w postaci

''

''

3

''

2

''

1

'

'

3

'

2

'

1

...

...

n

n

I

I

I

I

I

I

I

I

+

+

+

+

=

+

+

+

+

(1.25)

przy czym wyrażenie po lewej stronie znaku równości jest sumą prądów dopływających do
węzła W, a wyrażenie po prawej stronie - sumą prądów odpływających.

Równanie (1.25) jest matematycznym zapisem I prawa Kirchhoffa, które można

sformułować w następujący sposób:

W rozgałęzionych obwodach elektrycznych suma prądów dopływających do

każdego węzła jest równa sumie prądów odpływających.

Przyjmując prądy dopływające do węzła jako dodatnie, a odpływające jako ujemne,

I prawo Kirchhoffa można sformułować nieco inaczej, a mianowicie:

W rozgałęzionych obwodach elektrycznych algebraiczna suma prądów w każdym

węźle jest równa zeru.

Matematycznie zapisuje się to w postaci

∑

=

0

I

(1.26)

Prądy płynące w gałęziach równoległych zależą od wartości rezystancji. Dla obwodu

jak na rys.1.16b prądy w gałęziach równoległych, zgodnie z prawem Ohma, wyniosą:

1

1

R

U

I

AB

=

2

2

R

U

I

AB

=

(1.27)

Po podzieleniu pierwszego z równań (1.27) przez drugie, otrzymuje się zależność

1

2

2

1

R

R

I

I

=

(1.28)

którą uogólniając na dowolną liczbę gałęzi, można sformułować następująco:

W obwodach rozgałęzionych natężenia prądów płynących w gałęziach równoległych

są odwrotnie proporcjonalne do rezystancji tych gałęzi.

Powyższe oznacza, że przez większe rezystancje płyną mniejsze prądy i odwrotnie.

Przykład 1.12

Do sieci prądu stałego o napięciu

V

230

=

U

dołączono żarówkę o mocy 100W i

rezystancji

Ω

=

530

1

R

, żelazko o rezystancji

Ω

=

5

,

26

2

R

oraz grzejnik o rezystancji

Ω

=

35

3

R

(patrz rys.1.17). Obliczyć prądy pobierane z sieci przez poszczególne odbiorniki

oraz prąd pobierany z sieci.

Rys.1.17. Schemat obwodu do przykładu 1.12

Rozwiązanie

Prądy w gałęziach równoległych obwodu oblicza się z prawa Ohma.

- prąd płynący przez żarówkę

=

=

=

530

230

1

1

R

U

I

0,434 A

- prąd płynący przez żelazko

=

=

=

5

,

26

230

2

2

R

U

I

8,679 A

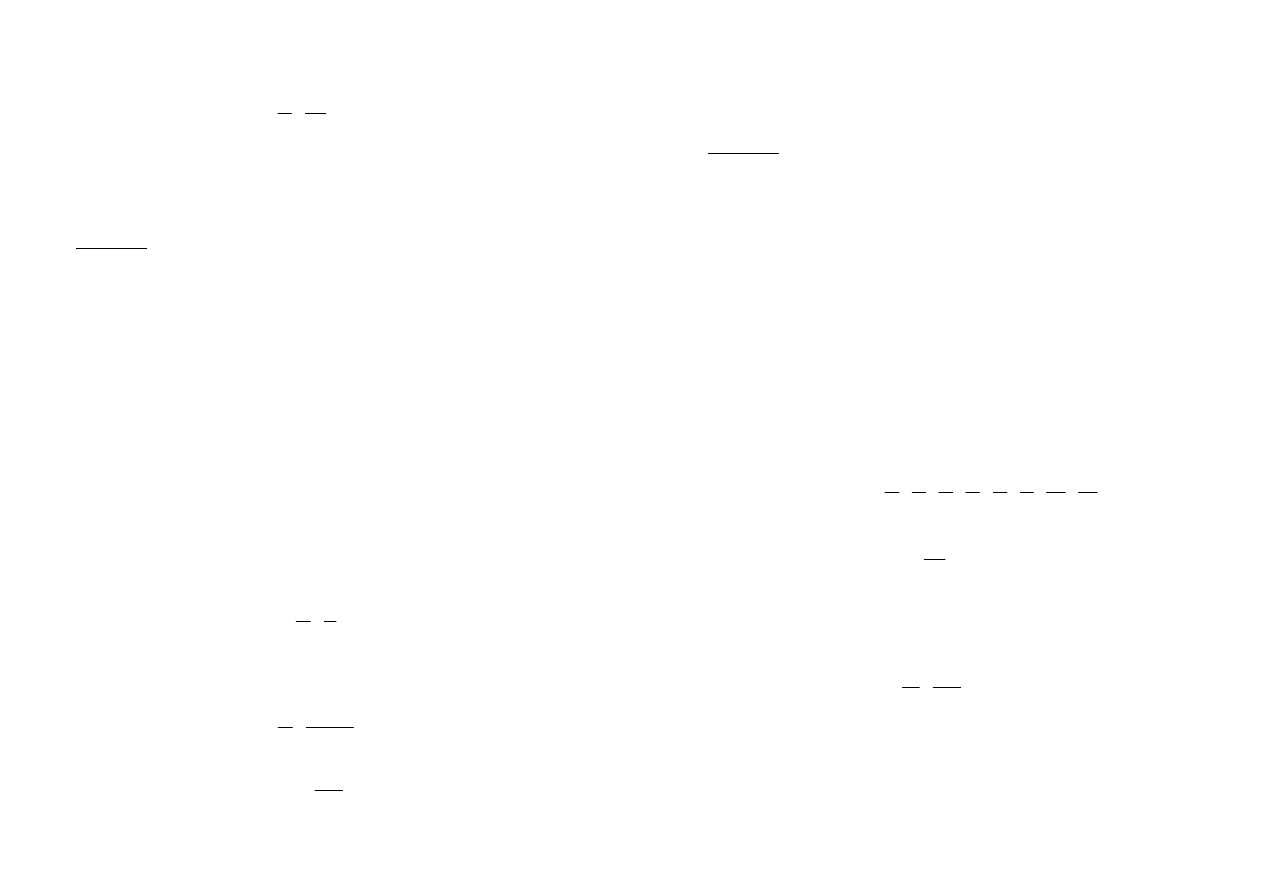
- prąd płynący przez grzejnik

=

=

=

35

230

3

3

R

U

I

6,571 A

Prąd pobierany przez wszystkie odbiorniki z sieci jest prądem dopływającym do węzła A i,
zgodnie z I prawem Kirchhoffa, równa się sumie prądów odpływających od tego węzła, tj
sumie prądów poszczególnych gałęzi (odbiorników)

=

+

+

=

3

2

1

I

I

I

I

0,434 + 8,679 + 6,571 = 15,684 A

Przykład 1.13

Jaką rezystancję

R

b

należy dołączyć równolegle do amperomierza (przyrząd do pomiaru

natężenia prądu) o prądzie znamionowym

I

a

, aby można nim zmierzyć prąd N razy większy,

tj,

a

I

I

⋅

=

N

(patrz rys.1.18). Rezystancja wewnętrzna amperomierza wynosi

a

R .

Rys.1.18. Schemat obwodu do przykładu 1.13

Rozwiązanie

Aby rozwiązać problem, do amperomierza należy dołączyć równolegle rezystor

(bocznik) o tak dobranej rezystancji, aby popłynął przez niego prąd o natężeniu

a

a

a

a

b

I

N

I

I

N

I

I

I

)

1

(

−

=

−

⋅

=

−

=

Ponieważ prąd w gałęziach równoległych jest odwrotnie proporcjonalny do rezystancji, to na
podstawie równania (1.28) można napisać zależność

b

a

a

b

I

I

R

R

=

w której:

I

a

- prąd płynący przez amperomierz,

I

b

- prąd płynący przez bocznik.

Podstawiając do tej zależności wyrażenie na prąd płynący w boczniku, otrzymuje się

)

1

(

−

=

N

I

I

R

R

a

a

a

b

Stąd

1

−

=

N

R

R

a

b

Przedstawiony przykład prezentuje metodę rozszerzania zakresów pomiarowych

amperomierzy. Po zastosowaniu tej metody, wskazania amperomierza należy mnożyć przez
N = I/I

a

.

Przykład 1.13

Prądnica prądu stałego o sile elektromotorycznej

V

230

=

E

i rezystancji wewnętrznej

Ω

=

1

w

R

zasila układ odbiorników, połączony tak, jak to przedstawiono na rys.1.19a.

Rezystancje poszczególnych odbiorników wynoszą:

Ω

=

10

1

R

,

Ω

=

60

2

R

,

Ω

=

80

3

R

,

Ω

=

100

4

R

,

Ω

=

120

5

R

. Obliczyć napięcie U na zaciskach prądnicy i natężenia prądów

płynących w poszczególnych odbiornikach.

Rys.1.19. Schemat obwodu do przykładu 1.13: a) - schemat pełny, b) - schemat zastępczy

Rozwiązanie

Ponieważ w obwodzie występuje znaczna liczba gałęzi równoległych, wygodnie jest

obliczyć przewodność zastępczą

AB

G

między węzłami A i B

=

+

+

+

=

+

+

+

=

+

+

+

=

120

1

100

1

80

1

60

1

1

1

1

1

5

4

3

2

5

4

3

2

R

R

R

R

G

G

G

G

G

AB

0,048 S

Rezystancja zastępcza

z

R czterech gałęzi równoległych wynosi

=

=

AB

z

G

R

1

20,83 Ω

a rezystancja zastępcza R

zc

całego obwodu

=

+

+

=

w

z

zc

R

R

R

R

1

10 + 20,83 + 1 = 31,83 Ω

Natężenie prądu pobieranego z prądnicy, równe natężeniu prądu w odbiorniku o rezystancji

1

R , wynosi

A

226

,

7

83

,

31

230

=

=

=

zc

R

E

I

Napięcie U na zaciskach prądnicy jest równe

V

774

,

222

226

,

7

1

230

=

⋅

−

=

−

=

I

R

E

U

w

W celu obliczenia prądów w gałęziach równoległych należy najpierw obliczyć napięcie

AB

U

między węzłami A i B. Napięcie to jest równe

V

52

,

150

83

,

20

226

,

7

=

⋅

=

=

z

AB

IR

U

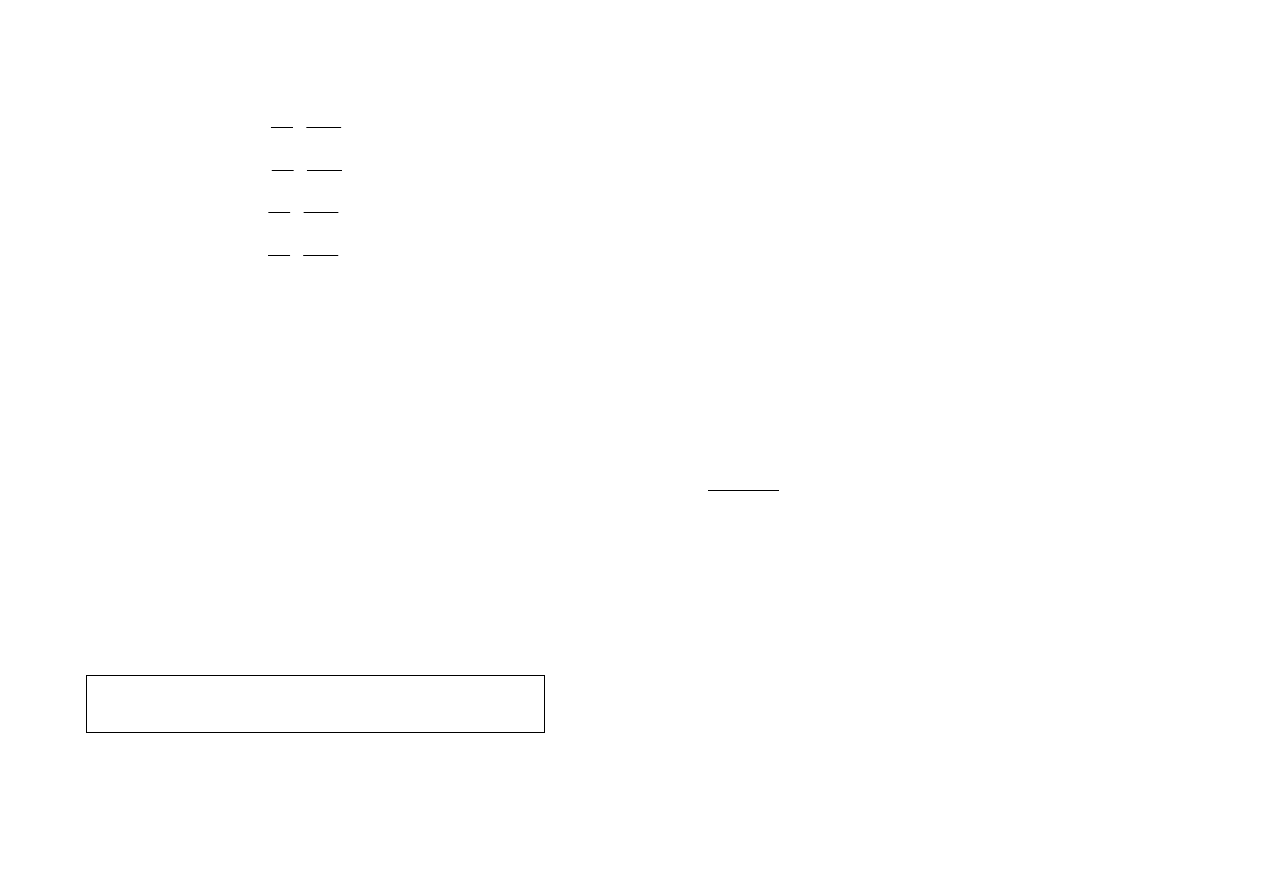
Znając to napięcie, z prawa Ohma można obliczyć natężenie prądów w odbiornikach
połączonych równolegle, a mianowicie:

A

51

,

2

60

52

,

150

2

2

=

=

=

R

U

I

AB

A

88

,

1

80

52

,

150

3

3

=

=

=

R

U

I

AB

A

505

,

1

100

52

,

150

4

4

=

=

=

R

U

I

AB

A

254

,

1

120

52

,

150

5

5

=

=

=

R

U

I

AB

1.6.2. Drugie prawo Kirchhoffa

Jeżeli

w

obwodzie

elektrycznym

występuje

nie

jedna

lecz

kilka

sił

elektromotorycznych, to w celu obliczenia prądów płynących w obwodzie, trzeba uwzględnić
kierunki działania tych sił, tj. uwzględnić, czy są one skierowane w jedną stronę (połączenie
na współdziałanie), czy w przeciwne strony (połączenie na przeciwdziałanie).

Rys.1.20. Obwód elektryczny z kilkoma siłami elektromotorycznymi

W obwodzie przedstawionym na rys.1.20, siły elektromotoryczne

1

E i

2

E są

skierowane w jedną stronę, a

3

E w przeciwną. Wypadkowa siła elektromotoryczna

E jest

równa sumie algebraicznej wszystkich sił elektromotorycznych, działających w obwodzie, tj.

3

2

1

E

E

E

E

−

+

=

Drugie prawo Kirchhoffa można sformułować w następujący sposób:

W każdym zamkniętym obwodzie elektrycznym suma algebraiczna wszystkich sił

elektromotorycznych działających w obwodzie jest równa sumie spadków napięć na

elementach tego obwodu.

Matematyczny zapis tego prawa ma postać

∑

∑

=

IR

E

(1.29)

Drugie prawo Kirchhoffa stanowi rozszerzenie prawa Ohma i może być stosowane nie

tylko do pojedynczego obwodu, ale również do każdego zamkniętego obwodu elektrycznego,
stanowiącego część dowolnej sieci elektrycznej np. takiej, jak przedstawiona na rys.1.21.

Rys.1.21. Wydzielona część sieci elektrycznej

W celu obliczenia prądów w wybranych gałęziach, należy wybrać zamknięte obwody,

zawierające te gałęzie, np. ABCA, ACDA itd., i do tych obwodów zastosować II prawo
Kirchhoffa wzór (1.29). Następnie do każdego punktu węzłowego zastosować I prawo
Kirchhoffa wzór (1.26). Otrzymuje się w ten sposób układ równań, z którego, po jego
rozwiązaniu, otrzymuje się wartości natężenia prądów w poszczególnych gałęziach.
Praktycznie, jeżeli w obwodzie rozgałęzionym istnieje n węzłów, to wystarczy zastosować I
prawo Kirchhoffa do (n-1) węzłów, natomiast II prawo Kirchhoffa do takiej liczby obwodów
zamkniętych aby otrzymać układ równań, w którym liczba równań jest równa liczbie
niewiadomych prądów.

Opisany sposób obliczania prądów stosuje się do stosunkowo prostych obwodów

elektrycznych. Do obliczania prądów w złożonych obwodach, stosuje się inne metody,
wchodzące w zakres przedmiotu

Teoria obwodów.

Przykład 1.14

Prądnica prądu stałego o sile elektromotorycznej

V

230

1

=

E

i rezystancji wewnętrznej

Ω

=

5

,

0

1

w

R

jest

połączona

równolegle

z

baterią

akumulatorów

o

sile

elektromotorycznej

V

220

2

=

E

i rezystancji wewnętrznej

Ω

=

2

,

0

2

w

R

oraz rezystorem o

rezystancji

Ω

=

20

R

(rys.1.22). Obliczyć prąd

1

I płynący przez prądnicę, prąd

2

I płynący

przez baterię akumulatorów, oraz prąd

3

I płynący przez rezystor

R .

Rys.1.22. Schemat do przykładu 1.14

Rozwiązanie

Aby obliczyć trzy niewiadome prądy gałęziowe

,

1

I

2

I i

,

3

I należy napisać trzy

niezależne równania, tworzące układ z trzema niewiadomymi. Sposób postępowania jest
następujący:

a)

ponieważ układ posiada n = 2 węzły (C i D), to I prawo Kirchhoffa należy napisać
tylko dla (n - 1) = 1 węzła, np. węzła C

2

1

3

I

I

I

+

=

b)

drugie równanie można napisać stosując II prawo Kirchhoffa dla wybranego obwodu
zamkniętego, np. ACEFDB. W tym celu należy założyć dowolny kierunek
obchodzenia obwodu, np. zgodny z kierunkiem ruchu wskazówek zegara
(odpowiadający kolejności liter ACEFDB na rys.1.22). Poruszając się w wybranym
kierunku, wyznacza się sumę sił elektromotorycznych

∑

E w tym obwodzie i sumę

spadków napięć

IR

∑

. Siłę elektromotoryczną uważa się za dodatnią, jeżeli jej

kierunek jest zgodny z przyjętym kierunkiem obchodzenia obwodu i odwrotnie.
Spadek napięcia

IR uważa się za dodatni, jeżeli założony kierunek prądu w gałęzi jest

zgodny z przyjętym kierunkiem obchodzenia. I odwrotnie. Uwzględniając powyższe
otrzymuje się drugie równanie, zapisane z wykorzystaniem II prawa Kirchhoffa w
postaci

R

I

R

I

E

w

3

1

1

1

+

=

c)

trzecie równanie można napisać stosując II prawo Kirchhoffa np. do obwodu CEFD,
przyjmując analogiczny kierunek obchodzenia obwodu, tj. zgodnie z kolejnością liter
CEFD. Postępując tak jak w punkcie b), otrzymuje się trzecie równanie w postaci

R

I

R

I

E

w

3

2

2

2

+

=

Rozwiązując otrzymany układ trzech równań, uzyskuje się wyrażenia, z których można

obliczyć poszukiwane wartości natężenia prądów w gałęziach. I tak:

1

3

1

1

w

R

R

I

E

I

−

=

2

3

2

2

w

R

R

I

E

I

−

=

3

2

3

1

2

1

1

2

2

1

3

w

w

w

w

w

w

w

w

R

R

R

R

R

R

R

E

R

E

I

+

+

+

=

Po podstawieniu danych liczbowych otrzymuje się:

11,06A

20

2

,

0

20

5

,

0

2

,

0

5

,

0

5

,

0

220

2

,

0

230

2

1

2

1

1

2

2

1

3

=

⋅

+

⋅

+

⋅

⋅

+

⋅

=

+

+

−

=

R

R

R

R

R

R

R

E

R

E

I

w

w

w

w

w

w

A

4

,

6

2

,

0

20

06

,

11

220

2

3

2

2

−

=

⋅

−

=

−

=

w

R

R

I

E

I

A

44

,

17

5

,

0

20

06

,

11

230

1

3

1

1

=

⋅

−

=

−

=

w

R

R

I

E

I

Jak widać, prąd I

2

posiada wartość ujemną, co znaczy, że rzeczywisty kierunek tego

prądu jest przeciwny do kierunku, przyjętego do obliczeń. Zatem w układzie o schemacie jak
na tym rysunku 1.22 prądnica ładuje baterię akumulatorów.

Poprawność obliczeń można sprawdzić, stosując I prawo Kirchhoffa, np. do węzła C.

Zgodnie z tym prawem, suma prądów dopływających do tego węzła, powinna się równać
sumie prądów odpływających, tj.

2

1

I

I

+

powinno się równać I

3

. Podstawiając wyniki

obliczeń, otrzymuje się, że suma prądów dopływających równa się

A

04

,

11

)

4

,

6

(

44

,

17

=

−

+

, a

prąd odpływający równa się 11,06 A. Niedokładność wynika z zaokrągleń wyników obliczeń.

1.7.

Sposoby łączenia źródeł energii elektrycznej

Ź

ródła energii elektrycznej, analogicznie jak rezystory, można łączyć zarówno

szeregowo, równolegle jak i szeregowo-równolegle. Kilka źródeł połączonych szeregowo,
równolegle lub szeregowo i równolegle nazywa się baterią (np. bateria akumulatorów, bateria
ogniw galwanicznych).

Łączenie szeregowe źródeł energii elektrycznej polega na tym, że łączy się biegun dodatni
jednego źródła, z biegunem ujemnym kolejnego źródła, a odbiornik dołącza się do
końcowych zacisków, tj tak, jak to pokazano na rys.1.23.

Rys.1.23. Schemat obwodu z szeregowo połączonymi źródłami energii elektrycznej

Wypadkowa siła elektromotoryczna

E baterii jest równa sumie algebraicznej SEM

wszystkich źródeł połączonych szeregowo, przy czym SEM źródeł mogą mieć różne
wartości. W przypadku przedstawionym na rys.1.23

∑

=

=

+

+

+

=

4

1

4

3

2

1

i

i

E

E

E

E

E

E

(1.30)

przy czym i – kolejne numery źródeł połączonych szeregowo,
W przypadku, jeżeli SEM któregoś ze źródeł jest skierowana przeciwnie, to SEM tego źródła
należy brać z przeciwnym znakiem. W przypadku ogólnym wypadkowa SEM baterii złożonej
z „n” źródeł połączonych szeregowo, jest równa

∑

=

=

±

±

±

±

=

n

i

i

n

E

E

E

E

E

E

1

3

2

1

...

(1.31)

przy czym n – liczba źródeł w baterii.

Ponieważ rezystancje wewnętrzne poszczególnych źródeł są także połączone

szeregowo, to zastępcza rezystancja wewnętrzna

R

wzb

całej baterii, złożonej z „n” szeregowo

połączonych źródeł, jest równa sumie rezystancji wewnętrznych tych źródeł, tj.

∑

=

=

+

+

+

+

=

n

i

wi

n

wzb

R

R

R

R

R

R

1

3

2

1

...

(1.32)

Rezystancje wewnętrzne źródeł energii elektrycznej są na ogół małe. Prądnice prądu stałego
mają rezystancję wewnętrzną rzędu dziesiątych (a nawet setnych) części oma, natomiast
ź

ródła typu akumulatorów posiadają rezystancję wewnętrzną rzędu tysięcznych części oma.

Łączenie równoległe źródeł energii elektrycznej polega na połączeniu wszystkich dodatnich
biegunów w jeden punkt, a wszystkich ujemnych w drugi punkt. Do otrzymanych dwóch
punktów dołącza się odbiornik energii (patrz rys.1.24). Przy łączeniu równoległym SEM
poszczególnych źródeł muszą być równe, a więc w ogólnym przypadku wypadkowa siłą
elektromotoryczna E baterii jest równa SEM pojedynczego źródła, tj.

m

E

E

E

E

E

...

3

2

1

=

=

=

=

(1.33)

przy czym „m” – liczba źródeł połączonych równolegle.

Rys.1.24. Schemat obwodu z równolegle połączonymi źródłami energii elektrycznej

W przypadku jeżeli SEM poszczególnych źródeł są sobie równe, to, ponieważ są one

skierowane przeciwko sobie, ich wypadkowa SEM jest równa zeru

0

1

=

∑

=

m

i

i

E

(1.34)

i prąd między poszczególnymi źródłami nie płynie (

0

3

2

1

=

=

=

I

I

I

).

Jeżeli warunek (1.33) nie jest spełniony, między źródłami popłyną prądy wyrównawcze,

które można obliczyć stosując II prawo Kirchhoffa. Przykładowo, jeżeli np. E

1

>E

2

oraz E

1

>E

3

to w obwodzie ABDCA (patrz rys.1.24) popłynie prąd wyrównawczy o natężeniu

2

1

2

1

1

w

w

w

R

R

E

E

I

+

−

=

a w obwodzie ABFEA prąd wyrównawczy o natężeniu

3

1

3

1

2

w

w

w

R

R

E

E

I

+

−

=

Ponieważ rezystancje wewnętrzne źródeł są bardzo małe, to nawet przy niewielkiej różnicy
SEM natężenia tych prądów mogą być duże. Prądy wyrównawcze są przyczyną strat energii
na rezystancjach wewnętrznych źródeł, przy czy straty te mają miejsce nawet przy
nieobciążonej baterii.

Jeżeli bateria, złożona z połączonych równolegle źródeł o równych wartościach SEM,

zostanie obciążona rezystancją R, to w obwodzie zewnętrznym popłynie prąd I, na który
składają się prądy równoległych gałęzi. Zgodnie z I prawem Kirchhoffa prąd w gałęzi
zewnętrznej (obciążeniu) jest równy sumie prądów poszczególnych gałęzi, tj.

I

I

I

I

=

+

+

3

2

1

(1.35)

Uogólniając można powiedzieć, że:

Prąd oddawany przez baterię złożoną z równolegle połączonych jednakowych źródeł,

jest równy sumie prądów poszczególnych źródeł.

Ponieważ rezystancje wewnętrzne źródeł są połączone równolegle, to zastępczą

rezystancję wewnętrzną baterii można obliczyć z zależności (1.22)

3

2

1

1

1

1

1

w

w

w

wzb

R

R

R

R

+

+

=

W praktyce baterie zawsze składają się z takich samych ogniw, więc ich zastępczą
rezystancję wewnętrzną można obliczyć z zależności

m

1

w

wzb

R

R

=

Łączenie szeregowo-równoległe źródeł energii elektrycznej odbywa się według schematu,
przedstawionego na rys.1.25. Baterie o takim połączeniu źródeł są często nazywane bateriami
grupowymi.

Rys.1.25. Schemat baterii z szeregowo-równoległym połączeniem źródeł

Niech bateria składa się z „m” gałęzi równoległych po „n” szeregowo połączonych źródeł
(ogniw) w każdej. Wtedy SEM każdej gałęzi

1

*

nE

E

w

=

, a jej rezystancja wewnętrzna jest

równa

1

*

n

w

w

R

R

=

, przy czym E

1

– SEM jednego źródła, R

w1

– rezystancja wewnętrzna

jednego źródła. Siłą elektromotoryczna baterii E jest równa SEM każdej gałęzi

1

*

nE

E

E

=

=

(1.36)

a wypadkowa rezystancja wewnętrzna

wzb

R

całej baterii

m

n

m

1

*

w

w

wzb

R

R

R

=

=

(1.37)

Jeżeli do zacisków baterii zostanie dołączona rezystancja zewnętrzna R, to prąd I, który

przez nią popłynie, wyniesie

n

m

m

n

n

1

1

1

1

R

R

E

R

R

E

R

R

E

I

w

w

wzb

+

=

+

=

+

=

(1.38)

Przykład 1.15

Obliczyć jaki prąd popłynie w obwodzie przedstawionym na rys.1.26, jeżeli parametry

obwodu wynoszą:

V

2

,

2

3

1

=

=

E

E

,

Ω

=

=

1

,

0

3

1

w

w

R

R

,

V

5

,

1

2

=

E

,

Ω

=

05

,

0

2

w

R

,

Ω

=

5

,

1

R

.

Rys.1.26. Schemat do przykładu 1.15

Rozwiązanie

Wypadkowa SEM baterii, zgodnie z (1.31), równa się algebraicznej sumie SEM

szeregowo połączonych ogniw, tj.

V

9

,

2

2

,

2

5

,

1

2

,

2

3

2

1

=

+

−

=

+

−

=

E

E

E

E

(ponieważ SEM

2

E jest skierowana przeciwnie do SEM pozostałych ogniw, dlatego brana

jest z przeciwnym znakiem).

Zastępcza rezystancja wewnętrzna baterii

wzb

R

, zgodnie z (1.32), wynosi

Ω

=

+

+

=

+

+

=

25

,

0

1

,

0

05

,

0

1

,

0

3

2

1

w

w

w

wzb

R

R

R

R

Zgodnie z prawem Ohma, natężenie prądu w obwodzie wyniesie

A

657

,

1

75

,

1

9

,

2

5

,

1

25

,

0

9

,

2

=

=

+

=

+

=

R

R

E

I

wzb

Przykład 1.16

W obwodzie jak na rys.1.27, źródło zasilające odbiornik składa się z dwóch gałęzi

równoległych, zawierających po n = 5 ogniw połączonych szeregowo. Obliczyć natężenie
prądu płynącego przez odbiornik oraz prądów w gałęziach równoległych źródła, jeżeli SEM
pojedynczego ogniwa wynosi

V

2

,

1

1

=

E

, rezystancja wewnętrzna każdego ogniwa

Ω

=

05

,

0

1

w

R

, a rezystancja odbiornika

Ω

=

2

R

.

Rys.1.27. Schemat do przykładu 1.16

Rozwiązanie

Napięcie E na zaciskach źródła, do którego dołączony jest odbiornik, jest równe

wypadkowej SEM każdej gałęzi równoległej, złożonej z pięciu szeregowo połączonych
ogniw. Wypadkowa SEM każdej z gałęzi, zgodnie z (1.31), wynosi

1

*

nE

E

=

, czyli

1

*

nE

E

E

=

=

Zastępcza rezystancja wewnętrzna baterii

wzb

R

składa się z dwóch równolegle

połączonych zastępczych rezystancji wewnętrznych

*

w

R gałęzi równoległych. Zastępcza

rezystancja wewnętrzna gałęzi

*
w

R

jest sumą „n” szeregowo połączonych rezystancji

wewnętrznych pojedynczych ogniw, tj.

1

*

n

w

w

R

R

=

. Zastępcza rezystancja wewnętrzna

baterii, zgodnie z (1.23), wynosi

2

n

2

2

1

*

*

*

*

*

*

*

*

w

w

w

w

w

w

w

w

w

wzb

R

R

R

R

R

R

R

R

R

R

=

=

=

+

=

Natężenie prądu płynącego przez odbiornik, obliczone się z prawa Ohma, wynosi

R

R

E

R

R

E

R

R

E

R

R

E

I

w

w

w

wzb

2

n

n

2

2

n

2

2

n

1

1

1

1

+

=

+

=

+

=

+

=

Po podstawieniu danych liczbowych otrzymuje się

A

824

,

2

25

,

4

12

2

2

05

,

0

5

2

,

1

5

2

2

n

n

2

1

1

=

=

⋅

+

⋅

⋅

⋅

=

+

=

R

R

E

I

w

Przykład 1.17

W obwodzie jak na rys.1.28, źródło zasilające odbiornik składa się z dwóch gałęzi

równoległych, zawierających po n = 3 połączone szeregowo ogniwa o sile
elektromotorycznej

V

2

,

1

1

=

E

i rezystancji wewnętrznej

Ω

=

1

,

0

1

w

R

każde, oraz p = 2

szeregowo z nimi połączonych ogniw o takiej samej sile elektromotorycznej i rezystancji
wewnętrznej. Obliczyć natężenie prądu płynącego przez odbiornik oraz prądów w gałęziach
równoległych źródła. Rezystancja odbiornika

Ω

=

2

R

.

Rys.1.28. Schemat do przykładu 1.17

Rozwiązanie

Wypadkowa SEM

*

1

E każdej z dwóch gałęzi połączonych równolegle (między

punktami AB) jest równa sumie SEM połączonych szeregowo, tj.

1

*

1

nE

E

=

. Wypadkowa

SEM

*

2

E dwóch ogniw połączonych szeregowo (między punktami BC) wynosi

1

*

2

pE

E

=

.

Całkowita SEM E, działająca w obwodzie (między punktami AC), składa się z dwóch
szeregowo połączonych SEM:

*

1

E i

*

2

E . Ponieważ te SEM są jednakowo skierowane, to

1

1

1

*

2

*

1

)

p

n

(

p

n

E

E

E

E

E

E

+

=

+

=

+

=

Zastępcza rezystancja wewnętrzna baterii jest sumą rezystancji zastępczych źródeł

między punktami AB – rezystancja zastępcza

*

wzAB

R

oraz między punktami BC - rezystancja

zastępcza

*
wzBC

R

. Rezystancja zastępcza

*

wzAB

R

jest równoległym połączeniem wewnętrznych

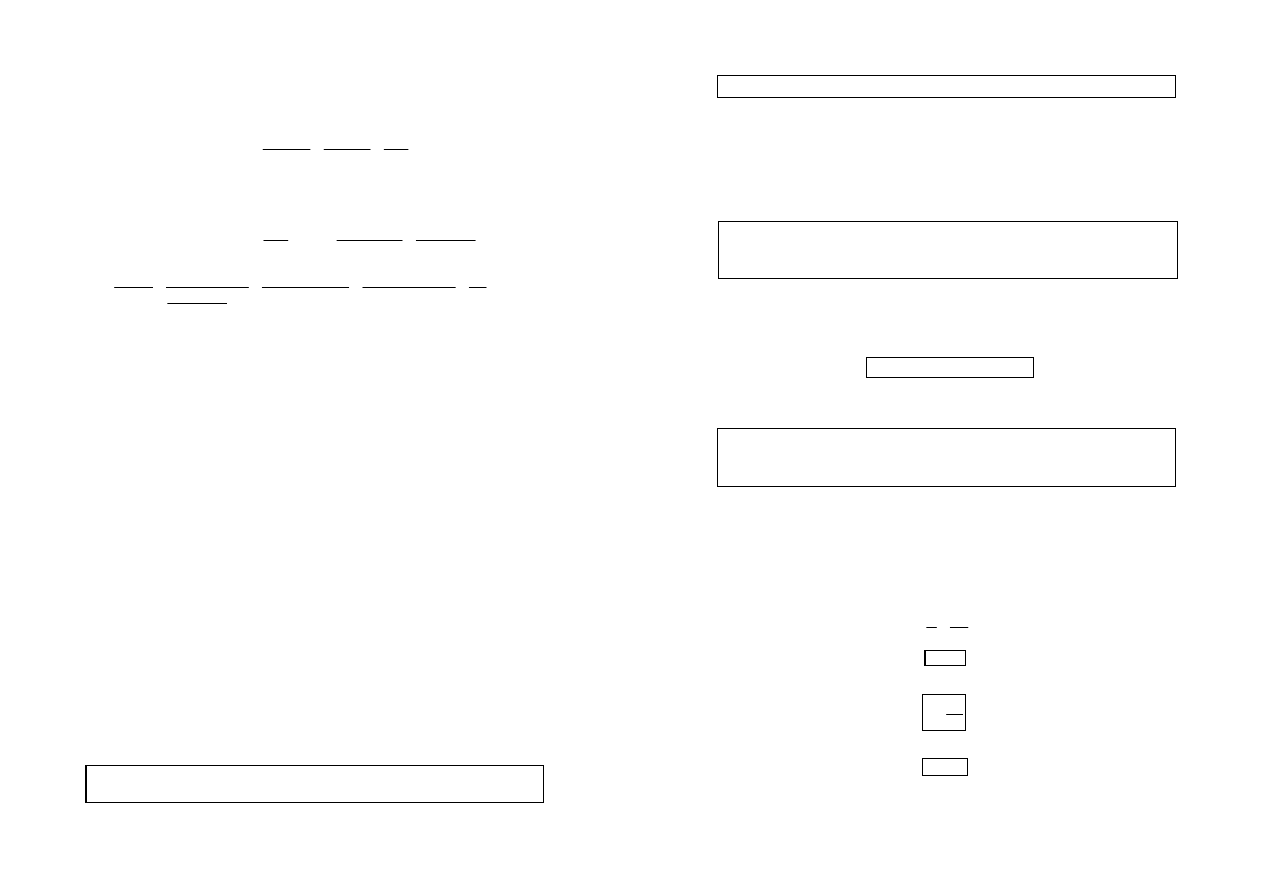
rezystancji zastępczych

*

1

w

R dwóch gałęzi. Ponieważ zastępcza rezystancja wewnętrzna każdej

z gałęzi jest sumą „n” szeregowo połączonych rezystancji wewnętrznych pojedynczych
ogniw, to

1

*

1

n

w

w

R

R

=

, a rezystancja

2

n

n

2

n

n

1

1

1

1

*

1

*

1

*

1

*

1

*

w

w

w

w

w

w

w

w

wzAB

R

R

R

R

R

R

R

R

R

=

=

+

=

Zastępcza rezystancja wewnętrzna

*

wzBC

R

jest szeregowym połączeniem rezystancji

wewnętrznych p = 2 ogniw i jest równa sumie tych rezystancji, tj.

1

*

p

w

wzBC

R

R

=

. Zastępcza

rezystancja wewnętrzna baterii

2

)

p

2

n

(

2

p

2

n

p

2

n

1

1

1

1

1

*

*

w

w

w

w

w

wzBC

wzAB

zb

R

R

R

R

R

R

R

R

+

=

+

=

+

=

+

=

Natężenie prądu w odbiorniku oblicza się z prawa Ohma

A

553

,

2

7

,

4

12

2

2

1

,

0

)

2

2

3

(

2

,

1

)

2

3

(

2

2

)

p

2

n

(

)

p

n

(

2

2

)

p

2

n

(

)

p

n

(

1

1

1

1

=

=

⋅

+

⋅

+

⋅

+

=

+

+

+

=

+

+

+

=

+

=

R

R

E

R

R

E

R

R

E

I

w

w

zb

Natężenie prądu w gałęziach równoległych oblicza się stosując I prawo Kirchhoffa np.

dla węzła A. Otrzymuje się wtedy, że

*

1

*

1

*

1

2I

I

I

I

=

+

=

Stąd

A

277

,

1

553

,

2

5

,

0

5

,

0

*

1

=

⋅

=

=

I

I

1.8.

Praca i moc elektryczna. Prawo Joule’a

Jeżeli spowodować przepływ prądu I przez rezystor R, na którym odkłada się napięcie

U (rys.1.29), to rezystor ten będzie się nagrzewał, tj. w nim będzie następowała przemiana
energii elektrycznej na energię cieplną. W wyniku badań ustalono, że ilość energii cieplnej A,
która wydzieli się na rezystorze R w czasie t, jest wprost proporcjonalna do napięcia U ,
natężenia prądu I, oraz czasu t, czyli

UIt

A

=

[Ws] lub [J] (1.39)

Rys.1.29.Schemat do wyjaśnienia prawa Joule’a

Ponieważ It = Q, gdzie Q jest ładunkiem elektrycznym, wyrażonym w kulombach [C] lub
amperosekundach [As], wzór (1.39) można zapisać w postaci

UQ

A

=

[J] (1.40)

Ostatnią zależność można sformułować słownie w następujący sposób:

Praca elektryczna A (równa energii elektrycznej wydzielonej na rezystorze R) jest

równa iloczynowi napięcia U przyłożonego do tego rezystora i ładunku Q, który

przepłynął przez ten rezystor.

Uwzględniając w (1.39), że

IR

U

=

, otrzymuję się inną zależność na energię elektryczną

wydzieloną na rezystorze

R, a mianowicie:

Rt

I

A

2

=

(1.41)

czyli że:

Praca elektryczna A (równa energii elektrycznej wydzielonej na rezystorze R) jest

wprost proporcjonalna do kwadratu prądu, płynącego przez ten rezystor oraz do

czasu przepływu prądu.

Energia elektryczna wydziela się na rezystorze w postaci ciepła. Z fizyki wiadomo, że

pracy jednego dżula [J] odpowiada 0,239 kalorii [cal] energii cieplnej. Zatem ilość ciepła Θ
wydzielonego na rezystorze

R podczas przepływu prądu o natężeniu I, wynosi

t

I

A

Θ

2

239

,

0

239

,

0

=

=

[cal] (1.42)

Wyrażenie (1.42) jest matematyczną postacią

prawa Joule’a, które słownie formułuje

się w następujący sposób:

Ilość ciepła Θ, wydzielonego przez prąd elektryczny I, przepływający przez rezystor

R, jest wprost proporcjonalna do kwadratu prądu, rezystancji rezystora i czasu

przepływu prądu

Ciepło Joule’a, wydzielane przez prąd przepływający przez rezystor, ma liczne

zastosowania w praktyce (grzejniki, piece, bezpieczniki topikowe itp.), ale jest również
przyczyną niepożądanych skutków (straty mocy w przewodach przesyłowych i nagrzewnie
przewodów, powodujące szybsze starzenie się izolacji).

Z fizyki wiadomo również, że w ogólnym przypadku, moc jest to stosunek pracy do

czasu, w którym ta praca zostałam wykonana. W odniesieniu do energii elektrycznej, moc

P

jest to stosunek pracy (energii) elektrycznej

A, w którym ta praca została wykonana (pobrana

energia), do czasu wykonania (pobrania)

t, tj.

UI

t

UIt

t

A

P

=

=

=

(1.43a)

UI

P

=

(1.43b)

Uwzględniając że

I = U/R, wyrażenie na moc można zapisać w postaci

R

U

P

2

=

(1.43c)

a uwzględniając że

U=IR, w postaci

R

I

P

2

=

(1.43d)

Jednostkę mocy można określić z równania (1.43)

]

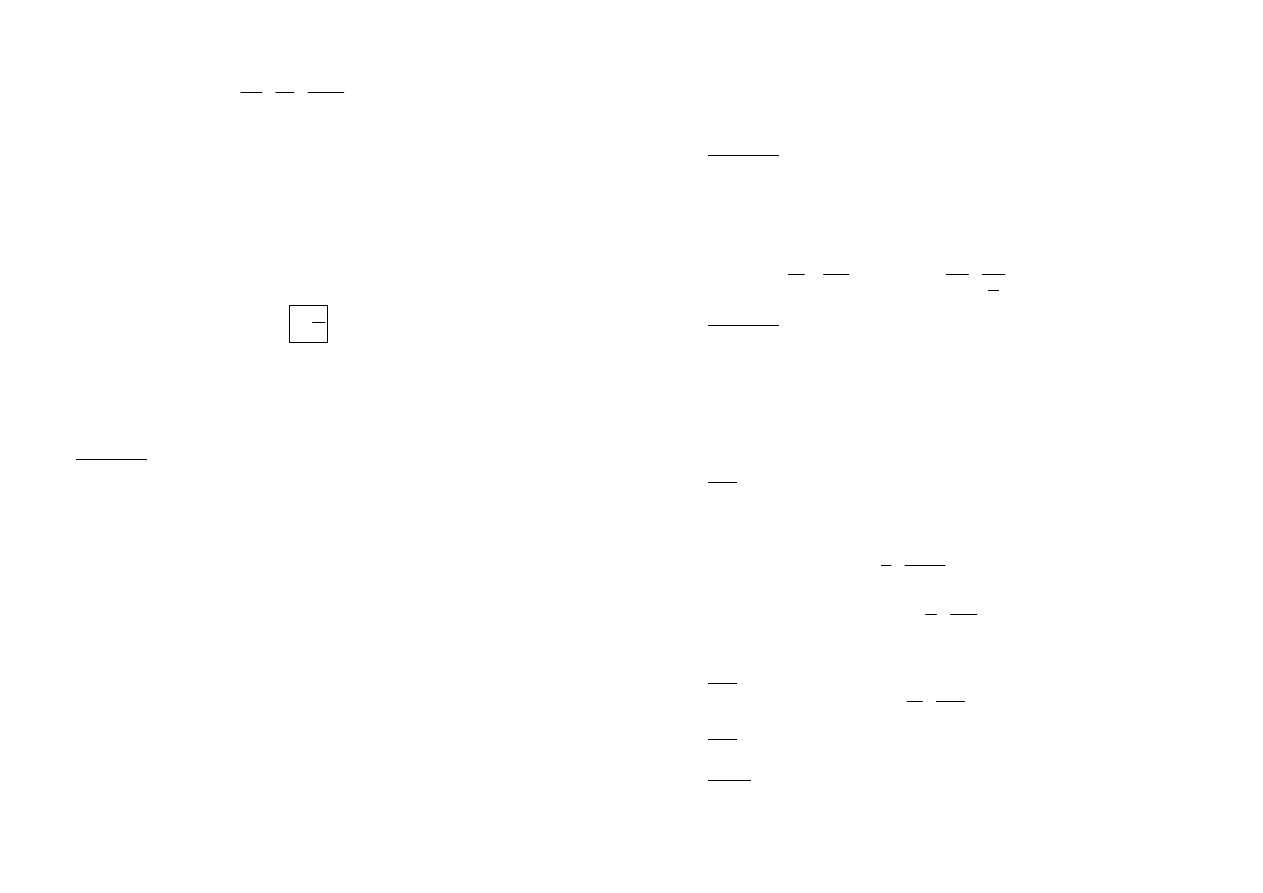
W

[

1

]

VA

[

1

]

s

[

1

]

VAs

[

1

]

s

[

1

]

J

[

1

]

[

1

]

[

1

]

[

1

=

=

=

=

=

t

A

P

Można powiedzieć, że wat [W] jest mocą, dla której praca wykonana w ciągu jednej sekundy
[s] jest równa jednemu dżulowi [J]. W praktyce są również stosowane jednostki wielokrotne

1 kilowat [kW] = 1000 W
1 megawat [MW] = 1000 kW = 1000000 W

lub podwielokrotne

1 miliwat [mW] = 0,001 W

We wszystkich urządzeniach, przetwarzających jeden rodzaj energii na inny, ilość

energii przetworzonej jest mniejsza od ilości przetwarzanej. Wynika to ze strat energii, które
towarzyszą praktycznie wszystkim przemianom. Dlatego wprowadza się pojęcie sprawności,
charakteryzujące urządzenie, w którym ta przemiana się odbywa. Sprawność urządzenia
oznacza się najczęściej przez η i definiuje się jako stosunek mocy użytecznej P

2

do mocy

doprowadzonej P

1

, tj.

1

2

P

P

=

η

(1.44)

Przy obliczaniu sprawności moce w liczniku i mianowniku muszą być wyrażone w tych
samych jednostkach. Sprawność wyraża się na ogół w procentach.

Uwaga:
Grzejniki przeznaczone do nagrzewania powietrza, jako jedyne urządzenia przetwarzające energię elektryczną
na ciepło, mają sprawność η = 1, bowiem straty mocy, towarzysząca tej przemianie, spowodowane
promieniowaniem i unoszeniem, również nagrzewają powietrze i są wliczane do mocy użytecznej.

Przykład 1.18

Grzejnik jest zasilany ze źródła o napięciu

V

230

=

U

i pobiera prąd

A

8

=

I

(rys.1.30).

Obliczyć moc P grzejnika i moc P

p

traconą w przewodach, jeżeli rezystancja przewodów

łączących grzejnik ze źródłem wynosi

Ω

=

2

p

R

.

Rys.1.30. Schemat do przykładu 1.18

Rozwiązanie

Moc grzejnika, zgodnie z zależnością (1.43b), można obliczyć jako

I

U

P

2

=

. Najpierw

jednak trzeba obliczyć napięcie

2

U na zaciskach grzejnika, bowiem napięcie to jest w

stosunku do napięcia sieci obniżone o spadki napięć na przewodach łączących. Zgodnie z II
prawem Kirchhoffa napięcie na zaciskach grzejnika jest równe

V

214

2

8

230

2

=

⋅

−

=

−

=

p

IR

U

U

Moc grzejnika wyniesie więc

kW

712

,

1

W

1712

8

214

2

=

=

⋅

=

=

I

U

P

natomiast moc tracona w przewodach, zgodnie z (1.43d),

W

128

2

8

2

2

=

⋅

=

=

R

I

P

p

Przykład 1.19

Obliczyć energię elektryczną pobraną przez grzałkę bojlera elektrycznego o rezystancji

Ω

=

25

R

, zasilanego z sieci o napięciu

V

230

=

U

, pracującą 8 godzin dziennie przez 30 dni

w miesiącu.

Rozwiązanie

Z zależności (1.43a) i (1.43c) otrzymuje się, że

507840

)

8

30

(

25

230

2

2

=

⋅

=

=

=

t

R

U

Pt

A

Wh]

VAh

A

V

h

V

h

V

[

2

2

=

=

=

Ω

= 507,84 kWh

Przykład 1.20

Grzejnik jest dołączony do sieci o napięciu

V

230

=

U

przewodami o rezystancji

Ω

=

5

,

0

p

R

(oba przewody). Licznik energii, zainstalowany na początku linii przesyłowej

wykazał zużycie energii

kWh

20

=

A

w ciągu 5 godzin. Obliczyć:

a)

- napięcie

U

2

na zaciskach grzejnika,

b)

- rezystancję

R grzejnika,

c)

- moc

P

g

pobieraną przez grzejnik,

d)

- ilość ciepła Θ

wydzielonego przez grzejnik.

Rozwiązanie

Ad.a) Napięcie na zaciskach grzejnika jest mniejsze od napięcia sieci o spadek napięcia na

rezystancji przewodów zasilających

5

,

0

230

2

⋅

−

=

−

=

I

IR

U

U

p

Aby określić nieznane natężenie prądu, najpierw trzeba określić moc pobieraną z linii.

Moc tę można określić z (1.43a) jako

4000W

kW

4

]

h

[

5

]

kW

[

20

=

=

=

=

t

A

P

Z tej samej zależności wynika, że

A

39

,

17

230

4000

=

=

=

U

P

I

Po podstawieniu tej wartości do pierwszego równania, otrzymuje się

V

3

,

221

5

,

0

39

,

17

230

2

≈

⋅

−

=

U

Ad.b) Rezystancja grzejnika

Ω

≈

=

=

73

,

12

39

,

17

3

,

221

2

I

U

R

g

Ad.c) Moc pobierana przez grzejnik

kW

848

,

3

W

3848

39

,

17

3

,

221

2

=

=

⋅

=

=

I

U

P

g

Ad.d) Aby określić ilość ciepła wydzieloną w grzejniku, najpierw trzeba obliczyć energię

A

g

, doprowadzoną do grzejnika. Energia ta jest równa

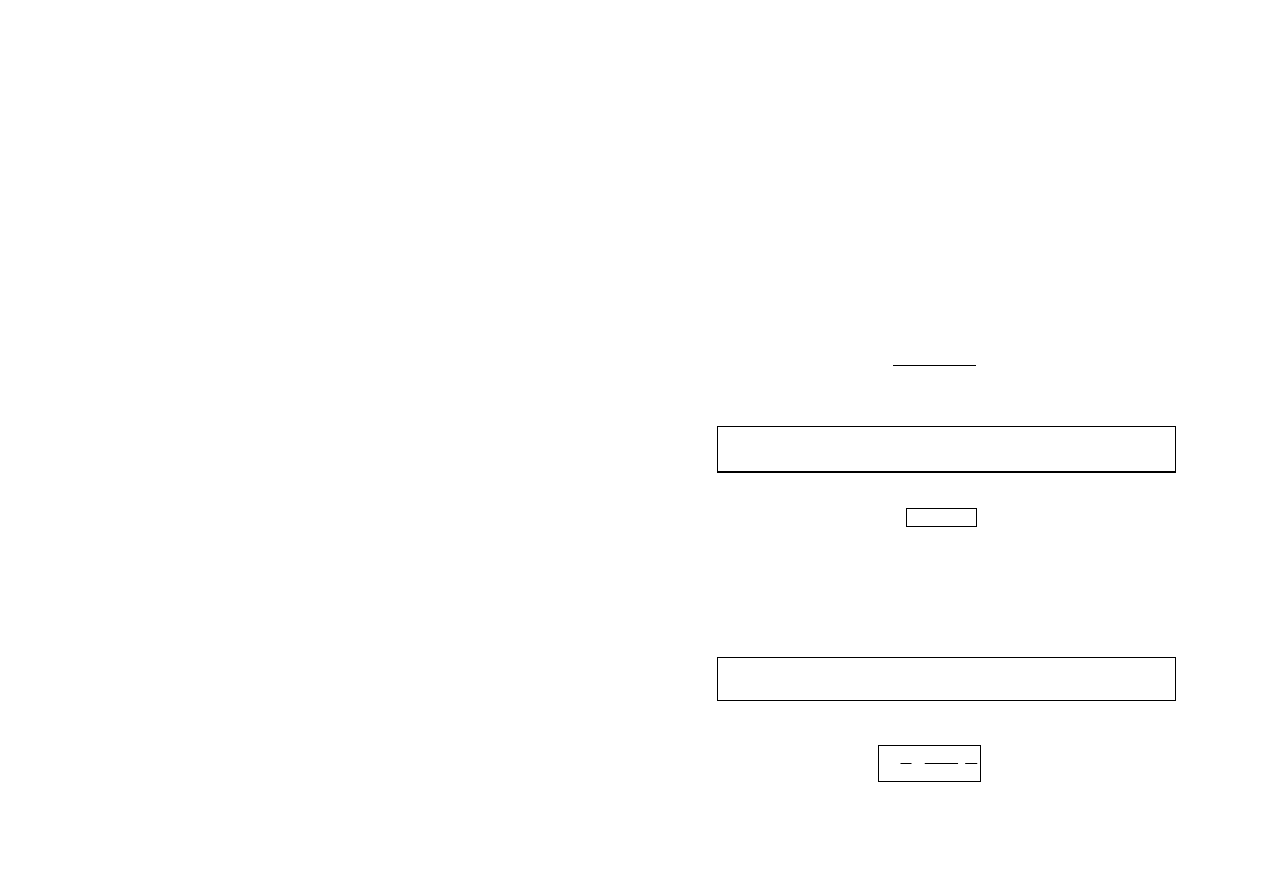
kWh

24

,

19

5

848

,

3

]

h

[

]

kW

[

=

⋅

=

=

t

P

A

g

g

Ponieważ pracy jednego dżula (watosekundy) odpowiada 0,239 kalorii energii cieplnej, to
ilość ciepła wydzielona w grzejniku wyniesie

]

Ws

[

10

264

,

69

239

,

0

]

s

[

3600

5

]

W

[

3848

239

,

0

]

h

[

5

]

kW

[

848

,

3

239

,

0

6

⋅

⋅

=

⋅

⋅

⋅

=

⋅

⋅

=

g

Θ

kcal

16554

cal

10

554

,

16

6

=

⋅

=

g

Θ

1.9.

Chemiczne działanie prądu elektrycznego

Należące do przewodników II klasy (patrz rozdz. 1.4) wodne roztwory soli, kwasów i

zasad oraz niektóre stopione sole nazywają się elektrolitami. W elektrolitach przepływ prądu
elektrycznego odbywa się za pośrednictwem jonów, a same elektrolity podczas przepływu
prądu podlegają pewnym zmianom chemicznym. Ponieważ nośnikami ładunku są w tym
przypadku jony, to takie przewodnictwo nazwano jonowym lub elektrolitycznym.

Jonem

nazywa się atom lub cząsteczkę materii z ładunkiem elektrycznym. Jeżeli atom

lub cząsteczka traci elektrony, to jon posiada ładunek dodatni, jeżeli zyskuje – ładunek
ujemny.

Dysocjacja

. Jest to zjawisko zachodzące w roztworach wodnych soli, zasad i kwasów,

polegające na rozpadzie części cząsteczek tych substancji na jony. Ilość zdysocjowanych
cząsteczek w roztworze określa tzw. stopień dysocjacji, który zdefiniowano jako stosunek
zdysocjowanych cząsteczek, do całkowitej ilości cząsteczek rozpuszczonych w wodzie.
Zgodnie z tą definicją, elektrolit ma tym większy stopień dysocjacji, im mniejsze jest stężenie
elektrolitu (im mniejsza jest masa zawarta w jednym centymetrze sześciennym roztworu).
Ponieważ woda jest dielektrykiem, to w roztworze cząsteczki wody izolują jony dodatnie od
jonów ujemnych, co powoduje wytworzenie się ustalonego stanu równowagi, w którym jony
są swobodnie zawieszone obok siebie w roztworze. W procesie dysocjacji jonami dodatnimi
są zawsze cząsteczki metali lub wodoru, a jonami ujemnymi reszty kwasowe, grupy
wodorotlenowe (OH) lub cząsteczki tlenu

W celu dokładniejszego poznania tego zjawiska, niżej zostaną opisane procesy,

zachodzące w naczyniu napełnionym wodnym roztworem siarczanu miedzi (CuSO

4

) z

zanurzonymi dwiema metalowymi lub węglowymi płytkami (patrz rys.1.31). Płytki nazywają
się elektrodami i są przyłączone do zacisków źródła energii elektrycznej.

Rys.1.31. Rysunek wyjaśniający zjawisko elektrolizy

Elektroda połączona z zaciskiem dodatnim nazywa się anodą, a z zaciskiem ujemnym
katodą

. Do elektrolitu prąd elektryczny jest doprowadzany przez anodę, dalej płynie przez

elektrolit od anody do katody, powodując jego rozkład chemiczny, po czym przez katodę
wraca do źródła. Zjawisko rozkładu elektrolitu pod działaniem prądu elektrycznego nazywa

się elektrolizą. W przypadku wodnego roztworu siarczanu miedzi przebieg elektrolizy jest
następujący:

•

dwuwartościowe dodatnie jony miedzi Cu

++

są przyciągane przez katodę (stąd ich

nazwa kationy), przyjmują od niej brakujące elektrony, i w postaci elektrycznie
obojętnych atomów wydzielają się na niej jako miedź elektrolityczna (czerwony osad),

•

dwuwartościowe ujemne jony reszty kwasowej

−

−

4

SO

są przyciągane przez anodę (stąd

ich nazwa aniony), oddają jej nadmiar elektronów i osadzają się na niej w postaci
elektrycznie obojętnych cząsteczek. Jeżeli anoda jest miedziana, to reszta kwasowa

−

−

4

SO

wchodzi w reakcję chemiczną z miedzią anody. W wyniku reakcji powstają

cząsteczki siarczanu miedzi (CuSO

4

), które w wyniku dysocjacji znowu rozkładają się

na jony Cu

++

oraz

−

−

4

SO

. Skutek jest taki, że w procesie elektrolizy miedź anody

stopniowo „rozpuszcza” się w elektrolicie.
Ogólnie można powiedzieć, że każda elektroliza przebiega w ten sposób, że jony oddają

lub przyjmują ładunki elektryczne i jako obojętne atomy lub cząsteczki bądź wydzielają się
na elektrodach, bądź wchodzą w reakcje chemiczne z elektrolitem lub materiałem elektrody.
Ponieważ ładunki pobierane lub oddawane na elektrodach są uzupełniane przez źródło energii
elektrycznej, to przepływ jonów odbywa się w sposób ciągły, a więc i prąd w elektrolicie ma
charakter ciągły. Ponadto, ponieważ przewodnictwo w elektrolicie odbywa się za
pośrednictwem jonów, które niosą ściśle określony ładunek elektryczny, to można określić
ś

cisły związek między masą ciała wydzielonego na elektrodzie i ładunkiem, który przepłynął

przez elektrolit. Zależność ta nosi nazwę I prawa Faradaya, które można sformułować w
następujący sposób:

Masa m ciała wydzielonego na elektrodzie podczas przepływu prądu elektrycznego

jest proporcjonalna do ładunku

It

Q

=

który przepłynął przez elektrolit

Matematyczny zapis I prawa Faradaya ma postać

kIt

kQ

m

=

=

(1.45)

przy czym: m - masa wydzielonego ciała w gramach,
Q - ładunek elektryczny w kulombach lub amperosekundach,
t - czas przepływu prądu w sekundach,
k - współczynnik proporcjonalności zwany równoważnikiem elektrochemicznym.

Równoważnik elektrochemiczny jest wielkością zależną tylko od rodzaju ciała i określa

on masę ciała wydzielonego na elektrodzie w g/C (w gramach przy przepływie i kulomba
ładunku elektrycznego). Można go wyznaczyć na podstawie II prawa Faradaya

, które brzmi:

Masy różnych ciał, wydzielone w wyniku elektrolizy przez ten sam prąd, są

proporcjonalne do chemicznych równoważników tych ciał.

W zapisie matematycznym prawo ma postać

w

A

96500

1

⋅

=

=

Q

m

k

(1.46)

przy czym: A - ciężar atomowy, w - wartościowość, Q – stała Faradaya.

Z zależności (1.46) wynika, że stała Faradaya wynosi Q = 96500kulombów, gdy

w

A

=

m

[g].

Oznacza to, że ilość elektryczności (ładunku) niezbędna do wydzielenia z elektrolitu liczby
gramów ciała równej chemicznemu równoważnikowi (A/w) tego ciała, jest jednakowa dla
różnych ciał i wynosi 96500 kulombów.

Na podstawie (1.45) i (1.46) otrzymuje się ostateczną zależność, na masę ciała

wydzielonego na elektrodach w procesie elektrolizy, w postaci

It

m

w

A

96500

1

⋅

=

(1.47)

przy czym: m - masa ciała wydzielonego z elektrolitu w gramach, A - ciężar atomowy

pierwiastka, w - wartościowość pierwiastka, t - czas przepływu prądu w
sekundach.

Przykład 1.21

Obliczyć masę miedzi, jaka wydzieli się na katodzie w wyniku elektrolizy wodnego

roztworu siarczanu miedzi w ciągu 10 godzin pod wpływem przepływu prądu o natężeniu 10
amperów. Równoważnik elektrochemiczny miedzi k = 329,4 10

-6

[g/C].

Rozwiązanie

Dysponując takimi danymi, należy skorzystać z wzoru (1.45), tj.

58

,

118

]

s

[

36000

]

A

[

10

]

[g/C

10

4

,

329

6

≈

⋅

⋅

⋅

=

=

−

kIt

m

g

s

A

s

A

g

s

A

C

g

[

=

⋅

⋅

⋅

=

⋅

⋅

]

Przykład 1.22

Obliczyć ile czasu potrzeba na wydzielenie się na katodzie 100 gramów srebra podczas

elektrolizy azotanu srebra (AgNO

3

), jeżeli natężenie prądu wynosi 10 amperów.

Równoważnik elektrochemiczny srebra k = 1118 10

-6

[g/C].

Rozwiązanie

Po przekształceniu wzoru (1.45) otrzymuje się

8945

]

A

[

10

]

C

g

[

10

1118

]

g

[

100

k

6

≈

⋅

⋅

=

=

−

I

m

t

s]

A

g

s

A

g

A

s

A

g

g

[

=

⋅

⋅

⋅

=

⋅

⋅

Przykład 1.23

Obliczyć jakie będzie zużycie energii elektrycznej, niezbędnej do otrzymania 100 kg

aluminium podczas elektrolizy tlenku glinu roztopionego w kriolicie. Napięcie zasilania
wanny elektrolitycznej wynosi 10 woltów, ciężar atomowy glinu A = 26,97, a jego
wartościowość w = 3.

Rozwiązanie

W tym przypadku należy najpierw obliczyć ładunek Q (ilość elektryczności), co można

zrobić korzystając z przekształconego wzoru (1.47)

9

3

10

073

,

1

97

,

26

3

]

[

96500

]

[

10

100

A

w

96500

⋅

≈

⋅

⋅

⋅

=

⋅

⋅

=

=

g

C

g

m

It

Q

s]

A

C

g

C

g

[

⋅

=

=

⋅

Ponieważ, zgodnie z (1.39), energia elektryczna (praca)

UQ

UIt

A

=

=

, to potrzebna do

wyprodukowania 100 kg aluminium energia elektryczna wyniesie

⋅

=

=

]

V

[

10

UQ

A

9

9

10

73

,

10

]

C

[

10

073

,

1

⋅

=

⋅

Ws]

s

A

V

C

[V

=

⋅

⋅

=

⋅

lub, biorąc pod uwagę, że 1 kWh = 3,6·10

6

Ws,

2980

10

3,6

10

73

,

10

6

9

=

⋅

⋅

=

A

[kWh]

Uwaga: W obliczeniach nie uwzględniono strat, występujących w samej wannie, w związku z czym rzeczywiste

zużycie energii elektrycznej będzie większe.

Zastosowania elektrolizy

Zjawisko elektrolizy jest dosyć powszechnie wykorzystywane w przemyśle

elektrochemicznym, a mianowicie w elektrometalurgii, galwanotechnice, galwanoplastyce i
wielu procesach chemicznych. Niżej podano krótką charakterystykę tych zastosowań.

1.

Elektrometalurgia , tj. wykorzystywanie elektrolizy do produkcji niektórych metali ze
związków oraz oczyszczania (rafinacji) metali z domieszek.

•

Produkcja aluminium. Aluminium otrzymuje się w wyniku elektrolizy tlenku
glinu (Al

2

O

3

) roztopionego w kriolicie (Na

2

AlF

6

), przeprowadzanej na gorąco

(punkt topliwości stopu wynosi około 900

0

). Wanna jest wykonana z cegły

szamotowej, której dno jest wyłożone płytami węglowymi, do których dołączony
jest ujemny biegun źródła (dno stanowi katodę). Anodę stanowią bezpopiołowe
płyty, wykonane z koksu. Do nich dołącza się dodatni biegun źródła. W procesie
elektrolizy dodatnie jony aluminium przemieszczają się do od anody do katody, a
czyste aluminium gromadzi się na dnie wanny. Jony ujemne tlenu wydzielają się
na anodzie, wchodząc w reakcję chemiczną z węglem anody, wytwarzając
głównie dwutlenek węgla (CO

2

) i pewną ilość tlenku węgla (CO). Wanny

elektrolityczne do produkcji aluminium są zasilane niskim napięciem (rzędu 7÷8V
i dużym prądem (rzędu kilkudziesięciu kiloamperów)

•

Produkcja miedzi elektrolitycznej. Miedź elektrolityczną otrzymuje się w wyniku
elektrolizy siarczanu miedzi (CuSO

4

). Anoda jest wykonana z surowca (miedzi

hutniczej), którą w ten sposób poddaje się oczyszczaniu (rafinacji). Katoda jest
wykonana z czystej miedzi. W procesie elektrolizy materiał anody rozpuszcza się
w elektrolicie a atomy czystej miedzi osadzają się na katodzie. Zanieczyszczenia
w postaci mułu gromadzą się na dnie wanny.

2.

Galwanizacja. Galwanizacja jest to proces pokrywania metalowych przedmiotów
warstwami innych metali w celu nadania im estetycznego wyglądu (srebrzenie,
złocenie), ochrony przed korozją (chromowanie, cynkowanie, niklowanie ) itp.
Pokrywany przedmiot stanowi katodę, a elektrolitem jest na ogół roztwór soli metalu,
jakim ma być pokryty dany przedmiot, np. przy niklowaniu – roztwór siarczanu
niklowoamonowego, przy srebrzeniu – roztwór azotanu srebra, złoceniu – roztwór
chlorku złota itp. Anodę stanowi płyta z metalu, którym ma być pokryty przedmiot.
Anoda stopniowo „rozpuszcza” się w elektrolicie, a dodatnie jony metalu są
przyciągane do katody, na której się wydzielają.

3.

Galwanoplastyka. Galwanoplastyka jest procesem umożliwiającym otrzymywanie
miedzianych odbitek różnych przedmiotów. W celu otrzymania takich odbitek
wykonuje się matryce z materiału plastycznego, których powierzchnię, w celu
zapewnienia przewodności, pokrywa się grafitem i dołącza do ujemnego bieguna
ź

ródła. Jest to katoda. Anodę wykonuje się z miedzi, a elektrolit stanowi wodny

roztwór siarczanu miedzi. Na powierzchni matrycy osadza się wtedy warstwa miedzi,
której grubość zależy od czasu trwania procesu elektrolizy. Po odłączeniu matrycy,
otrzymuje się dokładną kopię miedzianą przedmiotu.

4.

Przemysł chemiczny. Zastosowanie elektrolizy w przemyśle chemicznym jest bardzo
szerokie, w związku z czym, niesposób omówić je tutaj nawet w ograniczonym
zakresie. Główne zastosowania to otrzymywanie wodoru, tlenu, chloru, ługów soli
nieorganicznych, utleniaczy itp.

5.

Elektroosmoza i elektroforeza. Równolegle z elektrolizą zachodzą jeszcze dwa inne
procesy, które też mogą mieć pewne zastosowanie. Jeżeli między anodą i katodą
umieścić w elektrolicie porowatą przegrodę (przeponę), to niezależnie od ruchu
kationów ku katodzie i anionów ku anodzie, które przenikają przez przegrodę, na
skutek istnienia napięcia elektrycznego między elektrodami, przez przegrodę będzie
odbywał się także ruch cząsteczek wody. Zjawisko to nazywa się elektroosmozą.
Kierunek przenikania cieczy przez przegrodę podczas elektrolizy jest zależy od
rodzaju elektrolitu, materiału przegrody i wielu innych czynników. Jeżeli elektrolit
zawiera zawiesiny (stałe lub ciekłe cząstki koloidalne), to pod wpływem napięcia
elektrycznego między elektrodami, wystąpi ruch tych zawiesin względem cieczy w
kierunku jednej z elektrod. Kierunek ruchu zależy od rodzaju cieczy i rodzaju cząstek.
Zjawisko to nosi nazwę elektroforezy. Zjawiska elektroosmozy i elektroforezy są
wykorzystywane w procesach garbowania skór, oczyszczania wody, oczyszczania
kaolinu, oczyszczania kleju i żelatyny, produkcji gumowanych tkanin i wielu innych.

1.10. Ogniwa i akumulatory

Zanim zostaną omówione ogniwa i akumulatory, zostanie omówione zjawisko

występujące w jednych i drugich, a mianowicie zjawisko polaryzacji elektrod. Zjawisko to
polega na wytwarzaniu się w miejscach zetknięcia elektrod z elektrolitem sił
elektromotorycznych polaryzacji E

p

, będących skutkiem wydzielania się produktów

chemicznego rozkładu elektrolitu. Zjawisko polaryzacji elektrod powoduje, że po odłączeniu
ź

ródła energii elektrycznej, między elektrodami pozostaje pewne napięcie, równe sile

elektromotorycznej polaryzacji E

p

. Biegunem dodatnim jest anoda, ujemnym katoda. Jeżeli

do elektrod dołączy się zewnętrzny rezystor tak, jak to przedstawiono na rys.1.32, to w
otrzymanym w ten sposób obwodzie zamkniętym, popłynie prąd I o kierunku zgodnym z
kierunkiem E

p

.

Rys.1.32. Rysunek wyjaśniający powstawanie SEM polaryzacji elektrod

Tak więc wanna elektrolityczna o spolaryzowanych elektrodach zamieniła się w źródło

energii elektrycznej. Kierunek prądu, wydawanego przez takie źródło, jest przeciwny do
kierunku prądu powodującego elektrolizę. Zjawisko to znalazło praktyczne zastosowanie w
akumulatorach elektrycznych, natomiast w ogniwach elektrycznych występuje jako zjawisko
szkodliwe. Szczegóły zostaną omówione w podrozdziałach, poświęconych źródłom energii
elektrycznej, będących przedmiotem rozważań niniejszego rozdziału.

1.10.1. Ogniwa galwaniczne

Jeżeli w elektrolicie zanurzyć płytkę metalową, to między tą płytką i elektrolitem

powstanie tzw. elektrolityczna siła elektromotoryczna (ESEM), której wartość zależy od
rodzaju elektrolitu i rodzaju metalu. Proces powstawania ESEM polega na tym, że jony z
zanurzonego w elektrolicie metalu mają tendencję do przechodzenia do elektrolitu (ciśnienie
roztwórcze), pozostawiając na elektrodzie ładunek ujemny. Ładunek dodatni (jony metalu )
pozostaje w elektrolicie. W ten sposób między metalem elektrody i elektrolitem powstaje
elektrolityczna siła elektromotoryczna. Jeżeli w elektrolicie zanurzyć dwie płytki P

1

i P

2

,

wykonane z różnych metali, to w miejscach ich zetknięcia z elektrolitem powstaną dwie
różne ESEM E

1

i E

2

, a między płytkami wystąpi pewna wypadkowa ESEM. Urządzenie

takie, przedstawione schematycznie na rys. 1.33, nazywa się ogniwem galwanicznym.

Rys.1.33. Ogniwo galwaniczne

Siła elektromotoryczna E ogniwa galwanicznego jest równa różnicy ESEM E

1

i E

2

,

występujących na elektrodach

2

1

E

E

E

−

=

(1.48)

Historycznie najstarszym znanym ogniwem jest ogniwo Volty (rys.1.34). Ogniwo to

posiada dwie elektrody, miedzianą i cynkową, zanurzone w wodnym roztworze kwasu
siarkowego H

2

SO

4

. Elektroda miedziana stanowi biegun dodatni, a cynkowa ujemny. SEM

takiego ogniwa wynosi około 0,75 V.

Rys.1.34. Ogniwo Volty

Prąd płynący w elektrolicie i powodujący jego rozkład, płynie od elektrody cynkowej

do miedzianej. Dodatnie jony wodoru przemieszczają się zgodnie z kierunkiem prądu w
kierunku elektrody miedzianej, na której wydzielają się w postaci pęcherzyków jako obojętne
atomy. Wywołuje to SEM polaryzacji E

p

, skierowaną przeciwnie do kierunku prądu, a zatem

również przeciwnie do SEM ogniwa E. SEM polaryzacji E

p

zmniejsza SEM ogniwa do tego

stopnia, że nie nadaje się ono do praktycznych zastosowań. W celu likwidacji SEM
polaryzacji stosuje się tzw. depolaryzatory. Są to materiały bogate w tlen, którymi otacza się
elektrodę miedzianą. Wydzielany na elektrodzie dodatniej wodór, łączy się z tlenem, tworząc
cząsteczki wody.

Obecnie w użyciu są głównie ogniwa Leclanché, w których elektroda dodatnia jest

zbudowana z węgla, a elektroda ujemna z cynku. Elektrolitem jest roztwór chlorku amonu
N

4

HCl, zwany salmiakiem, a depolaryzatorem dwutlenek manganu MnO

2

, zwany

braunsztynem. Rozróżnia się trzy grupy ogniw Leclanche: suche, mokre i nalewane.
Największe zastosowanie praktyczne znalazły ogniwa suche. Dlatego też niżej ograniczono
się do omówienia tylko tego rodzaju ogniw. Na rys.1.35 przedstawiono przekrój suchego
ogniwa Leclanche.

Rys.1.35. Ogniwo Leclanche (przekrój)

Elektroda ujemna wykonana jest w postaci cynkowego naczyńka, zawierającego trociny
nasycone roztworem salmiaku. Elektroda dodatnia ma postać pręta, wykonanego z węgla,
otoczonego depolaryzatorem, którym jest dwutlenek manganu MnO

2

, sprasowany ze

sproszkowanym grafitem. Całość zalana jest masą asfaltową. Pojedyncze ogniwo posiada
SEM polaryzacji około 1,5 V. Baterie, zbudowane z takich ogniw, znajdują zastosowanie do
zasilania latarek kieszonkowych, radioodbiorników, przyrządów pomiarowych, pilotów
sprzętu RTV itp.

1.10.2. Akumulatory

Akumulatory są to urządzenia, w których zjawisko polaryzacji wykorzystane jest do

gromadzenia energii elektrycznej. Aby jednak akumulator stał się źródłem energii
elektrycznej, proces oddawania energii musi być poprzedzony procesem ładowania, podczas
którego doprowadzana energia elektryczna zamienia się w energię chemiczną, która się w
nim gromadzi. Podczas ładowania zachodzi proces elektrolizy, podczas którego
doprowadzana moc musi wynosić

I

E

R

I

P

p

e

+

=

2

(1.49

przy czym

R

e

- jest rezystancją elektrolitu,

I - natężeniem prądu elektrolizy, a E

p

- SEM

polaryzacji. Iloczyn

I

E

p

stanowi moc polaryzacji, która zamienia się na moc chemiczną.

Podczas ładowania akumulator jest odbiornikiem energii elektrycznej, a SEM

E

p

ma kierunek

przeciwny do kierunku prądu ładowania.

Naładowany akumulator stanowi źródło energii elektrycznej, którą oddaje w procesie

rozładowania. Podczas rozładowania energia chemiczna, zgromadzona w akumulatorze
zamienia się z powrotem na energię elektryczną. SEM polaryzacji

E

p

stanowi czynną SEM

ogniwa, a prąd rozładowania, płynący pod wpływem tej SEM, ma taki sam kierunek jak SEM
E

p

.

Zastosowanie praktycznie znalazły dwie grupy akumulatorów: akumulatory ołowiowe

(kwasowe) i akumulatory żelazo niklowe (zasadowe).

Akumulatory ołowiowe

Zasada działania akumulatora ołowiowego zostanie omówiona na przykładzie

akumulatora o budowie klasycznej. Prototyp takiego akumulatora zbudował w roku 1860
Plante. Akumulator ołowiowy składa się oczywiście z dwóch elektrod- dodatniej i ujemnej-
mających postać płyt zanurzonych w elektrolicie, którym jest 10% roztwór kwasu siarkowego
o ciężarze właściwym 1,17. W wyniku reakcji kwasu siarkowego z ołowiem płyt na ich
powierzchniach jest wytwarzany siarczan ołowiu PbSO

4

. Napięcia na zaciskach nie ma,

ponieważ obydwie elektrody są jednakowe. W celu naładowania akumulatora dołączamy go
do źródła energii elektrycznej tak, jak to przedstawiono na rys.1.36a. Dodatnie jony wodoru
H

+

przemieszczają się w elektrolicie ku katodzie, a ujemne jony

-

-
4

SO ku anodzie. Na

elektrodach zachodzą następujące reakcje chemiczne:

- na anodzie

4

2

2

2

4

4

SO

2H

PbO

O

2H

SO

PbSO

+

=

+

+

(1.50)

- na katodzie

4

2

2

4

SO

H

Pb

H

PbSO

+

=

+

(1.51)

Z powyższych równań wynika, że w procesie ładowania akumulatora w elektrolicie

zwiększa się ilość cząsteczek kwasu, i zmniejsza ilość cząsteczek wody. W wyniku tego
stężenie elektrolitu wzrasta i pod koniec ładowania wynosi 1,24÷1,25. Anoda pokrywa się
warstwą brunatnego dwutlenku ołowiu PbO

2

, a katoda warstwą ciemnoszarego czystego

ołowiu Pb.

Tak więc w wyniku ładowania w akumulatorze wytworzyły się dwie różne płytki

(elektrody): jedna z dwutlenku ołowiu, druga z czystego ołowiu. Ponieważ płytki te są
zanurzone w elektrolicie, to stanowią one ogniwo galwaniczne o SEM

E równej wypadkowej

SEM polaryzacji

E

p

, występującej w procesie ładowania i przeciwdziałającej prądowi

ładowania (rys.1.36a).

Rys.1.36.Wyjaśnienie zasady działania akumulatora ołowiowego: a) – ładowanie,

b) - rozładowanie

Jeżeli teraz zamiast źródła energii elektrycznej do elektrod dołączyć rezystor o

rezystancji R, to akumulator staje się źródłem energii, a w zamkniętym obwodzie popłynie
prąd elektryczny o kierunku zgodnym z kierunkiem SEM naładowanego akumulatora
(rys.1.36b), tj. przeciwnym do kierunku jaki miał podczas ładowania. Dodatnią elektrodą jest
płytka PbO

2

, a ujemną płytka Pb.

Równania, opisujące procesy zachodzące podczas rozładowania akumulatora mają

postać:

- na anodzie

O

2H

PbSO

SO

H

H

PbO

2

4

4

2

2

2

+

=

+

+

(1.52)

- na katodzie

4

4

PbSO

SO

Pb

=

+

(1.53)

Z równań tych wynika, że podczas procesu rozładowania akumulatora przybywa

cząsteczek wody, a ubywa cząsteczek kwasu. Stężenie elektrolitu zmniejsza się zdążając do
początkowej wartości 1,17. Jednocześnie powierzchnie elektrod też dążą do stanu przed
ładowaniem, tj. stają się jednakowe (PbSO

4

).

W praktyce nie należy dopuszczać się do całkowitego rozładowania akumulatora.

Warstwy czynne są wtedy jeszcze bardzo cienkie i zdolność akumulatora do magazynowania
energii elektrycznej (pojemność) jest niewielka. W celu zwiększenia pojemności, należałoby
przeprowadzić proces tzw. formowania, tj. wielokrotnego ładowania i rozładowania
akumulatora. Ponieważ w praktyce byłoby to kłopotliwe, omówione rozwiązanie
konstrukcyjne zostało zaniechane. Obecna technologia produkcji akumulatorów przewiduje
wykonanie elektrod ujemnych w postaci krat ołowiowych, wypełnionych gąbczastą masą
czynną z czystego ołowiu (Pb), a elektrod dodatnich w postaci przegródek z żeberkami,
wypełnionych masą czynną w postaci dwutlenku ołowiu (PbO

2

).

SEM

E akumulatora ołowiowego (równa SEM polaryzacji E

p

) wynosi około 2 V i

zależy od stopnia naładowania (rozładowania) akumulatora, którego miarą jest stężenie
kwasu siarkowego.

Przebiegi napięć podczas ładowania

U

ł

i rozładowania

U

r

przedstawiono na rys.1.37.

Rys.1.37. Przebiegi czasowe napięć ładowania i rozładowania akumulatora ołowiowego

Napięcie akumulatora podczas ładowania

U

ł

jest określone równaniem

w

ł

IR

E

U

+

=

(1.54)

przy czym:

E – SEM akumulatora, skierowana przeciwnie do napięcia U

ł

(patrz rys.1.36a),

I – natężenie prądu ładowania,
R

w

– rezystancja wewnętrzna akumulatora, zależna od powierzchni czynnej płyt i

ich odległości od siebie oraz od stopnia rozładowania i jest rzędu
tysięcznych części oma.

W początkowej fazie ładowania napięcie

U

ł

wnosi około 2,1 V, po czym w procesie

ładowania wzrasta do 2,2÷2,3 V i rośnie nadal. Proces ładowania przerywa się przy napięciu
rzędu 2,5÷2,7 V (mierzone podczas przepływu prądu ładowania). Obserwuje się wtedy
intensywne wydzielanie się tlenu i wodoru z elektrolitu (tzw. „gazowanie”), a stężenie
elektrolitu jest wtedy rzędu 1,24.

Uwaga! Mieszanina tlenu z wodorem jest wybuchowa, dlatego podczas ładowania akumulatora nie wolno

zbliżać się z otwartym ogniem.

Napięcie akumulatora podczas rozładowania jest określone równaniem

w

r

IR

E

U

−

=

(1.55)

Należy zauważyć, że kierunek SEM

E jest teraz zgodny z kierunkiem prądu (patrz rys.1.36b).

Napięcie

U

r

w procesie rozładowania zmniejsza się, poczynając od około 2 V. Rozładowanie

należy zakończyć, jeżeli napięcie to osiągnęło wartość 1,83 V. Dalsze rozładowanie grozi
zasiarczeniem płyt i kruszeniem. Z tych samych powodów akumulatorów kwasowych nie
należy przechowywać w stanie rozładowanym.

Stopień naładowania (rozładowania) akumulatorów określa się poprzez pomiar stężenia

elektrolitu. Do tego celu służy przyrząd zwany

aerometrem.

Pojemnością akumulatora nazywa się ilość elektryczności Q, wyrażoną w

amperogodzinach [Ah], jaką można uzyskać z naładowanego akumulatora podczas
rozładowania prądem znamionowym (zazwyczaj odpowiadającym trzygodzinnemu
rozładowaniu)

t

I

Q

N

=

[Ah] (1.56)

przy czym

t – czas rozładowania w godzinach, do chwili obniżenia się napięcia do wartości

U

r

=1,83 V.

Pojemność akumulatora zależy od powierzchni czynnych elektrod akumulatora i od

natężenia prądu rozładowania:

- pojemność akumulatora jest tym większa, im większa jest powierzchnia płyt (ilość

masy czynnej),

- pojemność akumulatora jest tym większa, im mniejszy jest prąd rozładowania w

stosunku do prądu znamionowego danego akumulatora.

Dla akumulatora, który w ciągu 3 godzin może być obciążony prądem znamionowym

I

N

=9A,

pojemność wyniesie

27Ah

3[h]

9[A]

=

⋅

=

=

It

Q

Jeżeli ten sam akumulator rozładowywać prądem 3,6A, to napięcie do poziomu 1,83V obniży
się po 10 godzinach [1]. Jego pojemność w tym przypadku wyniesie

36Ah

10[h]

3,6[A]

=

⋅

=

=

It

Q

tj. będzie o około 33% większa. Pojemność oraz prąd rozładowania określa producent
akumulatora.

Sprawność akumulatora. Ilość elektryczności Q

ł

dostarczona do akumulatora podczas

ładowania jest większa od ilości elektryczności Q

r

, jaką można otrzymać z naładowanego

akumulatora podczas rozładowania. Różnicę

r

Q

Q

−

ł

stanowią straty (na wytwarzanie gazów,

na rezystancji R

w

i inne). W przypadku akumulatorów można mówić o dwóch rodzajach

sprawności: elektrycznej i energetycznej.

- Sprawnością elektryczną akumulatora nazywa się stosunek pojemności użytecznej Q

r

(rozładowania) do pojemności ładowania Q

ł

]

Ah

[

]

Ah

[

Q

ład

rozł

ł

r

el

=

=

Q

η

(1.57)

Sprawność elektryczna akumulatorów ołowiowych jest rzędu 0,9.

-

Sprawnością energetyczną akumulatora nazywa się stosunek energii A

2

,

otrzymanej

podczas rozładowania, do energii

A

1

dostarczonej podczas ładowania

]

Wh

[

]

Wh

[

A

dostarcz

otrzym

1

2

en

=

=

A

η

(1.58)

Sprawność energetyczna akumulatorów ołowiowych wynosi 0,7 ÷ 0,8. Jak widać jest
ona mniejsza od sprawności elektrycznej. Spowodowane jest to tym, że napięcie
rozładowania jest mniejsze od napięcia ładowania.

Akumulatory ołowiowe wymagają umiejętnej obsługi. Pozostawienie w stanie

nienaładowanym powoduje powstawanie na płytach nierozpuszczalnych kryształków PbSO

4

(tzw. zasiarczanie płyt). Ze względu na zjawisko samoczynnego rozładowywania się
(orientacyjnie około 1% na dobę), nieeksploatowane akumulatory ołowiowe powinny być
okresowo (co 6 ÷ 8 tygodni) rozładowywane i ładowane. Akumulatory tego typu posiadają
bardzo małą rezystancję wewnętrzną (rzędu tysięcznych części ohma) i dlatego zwarcie
zacisków powoduje przepływ bardzo dużego prądu, który może uszkodzić płyty. Jeżeli nawet
podczas zwarcia płyty nie zostaną uszkodzone, to na pewno zostanie skrócona ich żywotność.

Akumulatory żelazo – niklowe

Akumulatory żelazo-niklowe, zwane również zasadowymi, mają elektrodę dodatnią

wykonaną z wodorotlenku niklu Ni(OH)

2

, a elektrodę ujemną z wodorotlenku żelaza

Fe(OH)

2

. Elektrolitem jest 20% roztwór wodorotlenku potasu KOH (ług potasowy). Na

elektrodach zachodzą w przybliżeniu następujące reakcje chemiczne:

- podczas ładowania

2

2

2Ni(OH)

2KOH

Fe

2Ni(OH)

KOH

2

Fe(OH)

+

+

=

+

+

(1.59)

(wodorotlenek niklu wydziela się na elektrodzie dodatniej, a żelazo na elektrodzie
ujemnej),

- podczas rozładowania

2

2

3

2Ni(OH)

KOH

2

)

Fe(OH

2Ni(OH)

KOH

2

Fe

+

+

=

+

+

(1.60)

tj. reakcja zachodzi w kierunku odwrotnym.

Jak wynika z równań (1.59) i (1.60), elektrody akumulatora przy ładowaniu i

rozładowaniu są utleniane lub odtleniane. Elektrolit nie tworzy nowych związków
chemicznych, na elektrodach nie wydzielają się żadne gazy, zatem gęstość i ilość elektrolitu
nie zmieniają się. Napięcie ładowania waha się w granicach (1,3÷1,8)V, a rozładowania w
granicach (1,25÷1,1)V.

Sprawność elektryczna akumulatorów zasadowych wynosi około

65

,

0

el

=

η

, a

sprawność energetyczna około

5

,

0

en

=

η

. Akumulatory te mogą długo pozostawać w stanie

nienaładowanym bez szkody dla ich stanu (nieeksploatowane nie wymagają okresowego
ładowania i rozładowania).

Zaletami, w porównaniu z akumulatorami kwasowymi, są niewrażliwość na

nieumiejętną obsługę oraz wstrząsy i udary.