3. PARAMETRY SYGNAŁÓW ELEKTRYCZNYCH
3.1. Parametry napięcia przemiennego
Napięcie jest jedną z podstawowych wielkości, charakteryzujących
obwody elektryczne i elektroniczne. Ze względu na zmienność w cza-
sie napięcia dzielimy na stałe i zmienne. Napięcie, którego przebieg w
funkcji czasu zmienia się zgodnie z zależnością:
u (t) = u( t + nT )
(3.1)
gdzie:
t – bieżący czas;
n – liczba całkowita;
T – okres rozpatrywanego napięcia;
nazywamy napięciem okresowo zmiennym. Napięcia okresowe dzielą
się na napięcia tętniące i przemienne. Szczególnym przypadkiem na-
pięcia przemiennego jest napięcie sinusoidalne.
Okres T – to czas, w ciągu którego, nastąpił jeden cykl zmian
przebiegu:
2
T
(3.2)
Okres napięcia sinusoidalnego to czas T (mierzony w jednostkach
czasu, tj. w sekundach i jednostkach pochodnych); okres funkcji sinus
to kąt pełny
2
(mierzony w jednostkach kątów, tj. w radianach albo
w stopniach), stąd konieczny jest współczynnik przeliczeniowy
(mierzony w radianach na sekundę).
Nosi on nazwę pulsacji. Jego wartość wynika z zależności:
2
T
(okres funkcji sinus musi odpowiadać okresowi przebiegu).
Stąd:
f
2
T
1
2
(3.3)
Wartość pulsacji przebiegu sinusoidalnego wynika z prędkości
kątowej (też oznaczanej
), z jaką kręci się wirnik prądnicy generują-
cej ten przebieg
1
.
Częstotliwość f – jest określana, jako odwrotność okresu:
T
1
f
.
1
Sprawa jest trochę bardziej skomplikowana, tak jest tylko wtedy, gdy pole
magnetyczne prądnicy ma jedną parę biegunów.
Charakterystycznymi parametrami przebiegu okresowego są:
- wartość chwilowa u = f (t) to wartość napięcia w danej, konkretnej
chwili czasowej; umożliwia ona określenie kształtu przebiegu na-
pięcia lub prądu.
W przypadku przebiegów wolnozmiennych (przy częstotliwościach
zmian nie większych niż ok. 0,1 Hz), jej wartość może być pomierzo-
na za pomocą przyrządów do pomiaru napięcia lub natężenia prądu
stałego.
Wartość chwilową napięcia przemiennego u(t) o kształcie sinuso-
idalnym określamy zależnością:
u(t) = U
m
sin (
t +
)
(3.4)
gdzie: U
m
– amplituda sygnału przemiennego;
- pulsacja;
- faza początkowa.
- wartość maksymalna U
m
- inaczej wartość szczytowa lub ampli-
tuda należy do zbioru wartości chwilowych i określa jej największą
chwilową wartość.
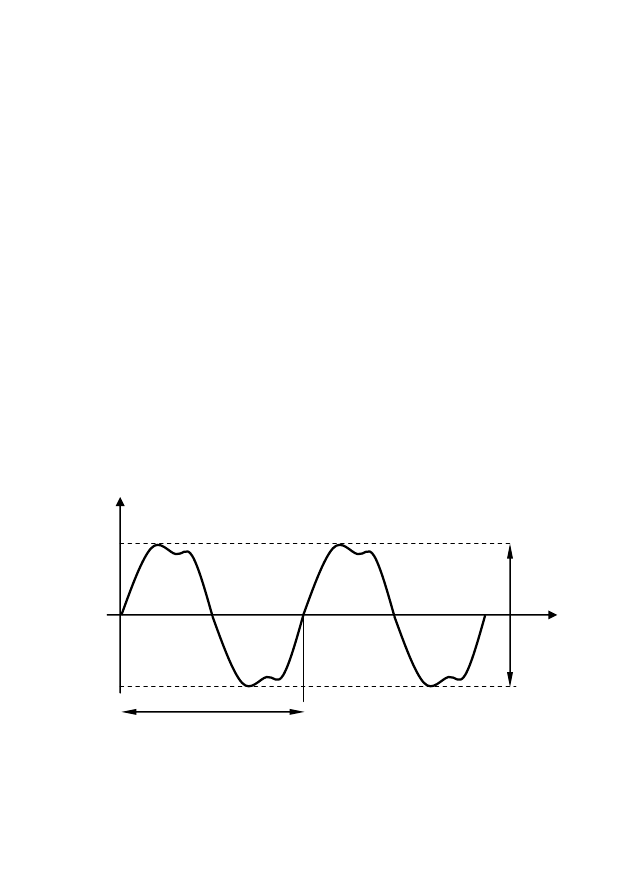
Rozważmy hipotetyczny przebieg napięcia przedstawiony na ry-
sunku 3.1.
Rys. 3.1. Parametry charakteryzujące napięcie przemienne.
Dla takiego przebiegu można zdefiniować następujące parametry na-
pięciowe:
t
U
m-
U
m+
U
U
p-p
T
- amplituda połówki dodatniej, czyli największa z wartości chwi-
lowych przebiegu. Można ją opisać wzorem:
U
m+
= max [u (t)]
- amplituda połówki ujemnej, czyli wartość bezwzględna naj-
mniejszej z wartości chwilowych przebiegu:
U
m-
= min [u (t)]
- wartość międzyszczytowa, definiowana jako suma amplitud po-
łówki dodatniej i ujemnej, co odpowiada podwojonej amplitudzie,
nazywanej napięciem „pik – pik” – U
p-p
lub „szczyt – szczyt”- U
s-s
.
U
p-p
= U
m+
+ U
m-
Warto w tym miejscu zaznaczyć, że dla przebiegów symetrycznych
zachodzi równość:
U
m
= U
m+
= U
m-
= U
p-p
/ 2
Jednocześnie dla przebiegów przemiennych o jednym rodzaju polary-
zacji (albo dodatnich albo ujemnych) nie definiuje się parametrów U
m+
i U
m
, zachodzi jednak równość:
U
m
= U
p-p
(3.5)
- Wartość średnia (average), którą generalnie definiuje się dla prą-
du przemiennego, jako taką jego wartość, która w tym samym cza-
sie równym okresowi napięcia przemiennego w tym samym obwo-
dzie przeniesie tę samą ilość ładunku elektrycznego, co prąd stały o
tej samej wartości.
Zakładając, że obwód jest zamknięty, definicję tę można uogólnić
także dla napięcia przemiennego. Definicję tę można zapisać w sposób
następujący:
T
dt
t
i
T
I
0
)
(
(3.6)
dt
T
R
t
u
T
R
U
0
)
(
(3.7)
T
śr
U
dt
t
u
T
U
0
)
(
1
(3.8)
Wartość średnia napięcia jest średnią arytmetyczną przebiegu.
Wartość średnia całookresowa przebiegu przemiennego (np. sinusoi-
dalnego) jest równa zeru, bowiem taki sam ładunek elektryczny prze-
płynie w kierunku dodatnim w ciągu jednej połowy okresu, jaki w
ciągu drugiej połowy w kierunku ujemnym. Dlatego uśrednienie prze-
biegów przemiennych ogranicza się do połowy okresu:
U
śr
=
T
2
2
0
T/
u(t)dt
Dla przebiegu sinusoidalnego:
u ( t ) = U
m
sin
t
wartość średnia wyniesie:
U
śr
=
2
U
m
= 0,637 U
m
Wartości średnie mają znaczenie przy rozpatrywaniu procesów
prostowania prądu przemiennego na prąd tętniący, m.in. w przetwor-
nikach pomiarowych. Mierniki magnetoelektryczne prostownikowe
najczęściej mierzą wartości średnie.
- wartość średnia jednopołówkowa U
śrI
dla sygnałów przemien-
nych:
2
0
)
(
1
T
dt
t
u
T
śrI
U
(3.9)
- wartość średnia dwupołówkowa U
śrII
dla sygnałów przemien-
nych:
2
0
)
(
2
T
dt
t
u
T
śrII
U
(3.10)
Wzór ten jest słuszny tylko w tych przypadkach, w których czas trwa-
nia połówki dodatniej jest równy czasowi połówki ujemnej oraz gdy
obydwie połówki mają ten sam kształt.
W innym przypadku należy korzystać ze wzoru:
T
dt
t
u
T
śrII
U
0
)
(
1
(3.11)
Łatwo zauważyć, że dla przebiegów symetrycznych przemiennych
spełniona jest zależność:
U
śrII
= 2 U
śrI
a wyrażenia 3.10 i 3.11 są równoważne.
Graficzną ilustrację wartości średniej wyprostowanej przedstawia
rysunek 3.2. Można ją zinterpretować jako wysokość prostokąta o
podstawie równej okresowi sygnału przemiennego i polu równym polu
pod krzywą opisującą przebieg wyprostowany.
Dla przebiegu sinusoidalnie zmiennego wartość średnia przebiegu
wyprostowanego (dwu- lub jednopołówkowo) jest różna od zera i
wynosi:
m
m
m
m
p
d
śr
U
U
t
U
t
d
t
U
U
2
)
1
(
)
1
(
)
cos(
(
)
sin(
2
2
1
0
0
.)
.
(
m
m
m
m
p
j
śr
U
U
t
U
t
d
t
U
U
1
)
1
(
)
1
(
2
)
cos(
(
2
)
sin(
2
1
0
0
.)
.
(
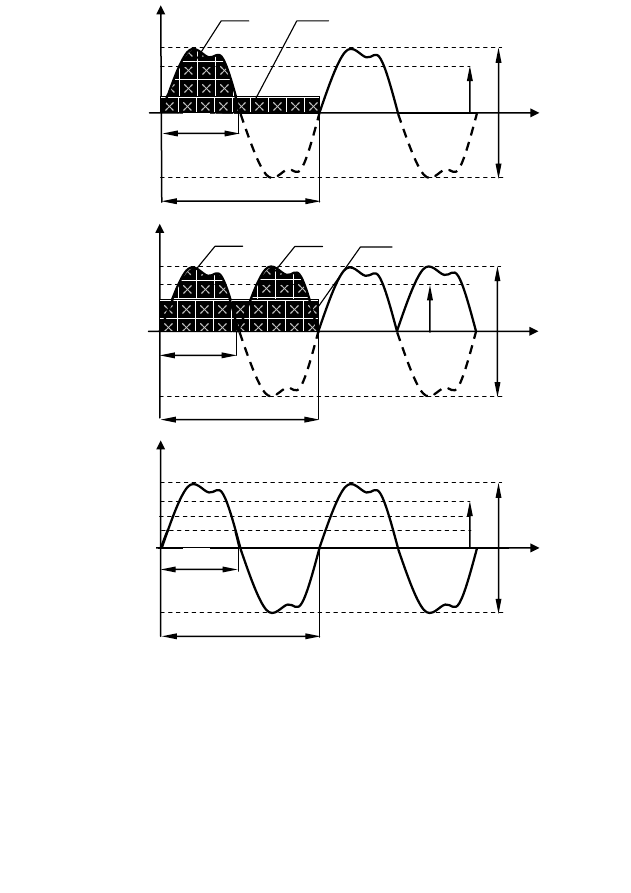
Rys. 3.2. Graficzna interpretacja wartości średniej wyprostowanej:
a) jednopołówkowo, b) dwupołówkowo,
c) wartości charakteryzujące sygnał przemienny we wspólnym ukła-
dzie współrzędnych.
- Wartość skuteczna (effective) sygnału okresowego o okresie T,
jest to wartość równoważnego napięcia stałego, które na rezystorze
R, w tym samym czasie, równym okresowi lub całkowitej krotności
t
U
m-
U
m
+
U
U
pp
T
u(t
)
U
śrI
U
sk
T/2
S
1
S’
S
1
= S’
t
U
m-
U
m
+
U
U
pp
T
u(t
)
U
śrII
U
sk
T/2
S
2
S
1
S”
S
1
+S
2
= S”
a)
t
U
m-
U
m
+
U
U
pp
T
u(t
)
U
śr
= 0
U
sk
U
śrII
=2U
śrI
U
śrI
T/2
c)
b)
okresu napięcia zmiennego spowoduje wydzielenie takiej samej
mocy, co napięcie zmienne.
Jest to więc wartość określająca parametry energetyczne przebie-
gu. Oznaczana jest ona jako U lub U
SK
.
Zakładając, że obwód jest zamknięty można zapisać:
T
dt
t
i
R
T
R
I
0
)
(
2
2
(3.12)
T
dt
R
t
u
T
R
U
0
)
(
2
2
(3.13)
T
dt
t
u
T
sk
U
U
0
)
(
2
1
(3.14)
Warto zauważyć, że podane definicje są prawdziwe tylko dla sygna-
łów okresowych, tzn. spełniających zależność:
)
(
)
(
T
t
u
t
u
t
gdzie:
- u(t) - wartość chwilowa napięcia zdeterminowanego (sygnał nie-
losowy).
Wartość skuteczna napięcia zawierającego składowe harmoniczne
wynosi:
2
2
1
2
0
.....
n
U
U
U
U
(3.15)
gdzie: U
o
- składowa stała;
U
1
... U
n
- wartości skuteczne kolejnych harmonicznych.
Dla napięcia sinusoidalnego wartość skuteczna jest równa:
m
m
U
,
U
U
707
0
2
(3.16)
Wartości skuteczne mierzą bezpośrednio m.in. przetworniki po-
miarowe elektromagnetyczne, elektrodynamiczne, RMS oraz termoe-
lektryczne.
- współczynnik kształtu k
k
- określony stosunkiem wartości sku-
tecznej do wartości średniej tego przebiegu. Dla przebiegu sinusoi-
dalnego posiada wartość:
2
2
2
2
Π
Π
U
U
U
U
k
m
m
śr
k
= 1,11
(3.17)
Współczynnik ten zawiera informację, w jakim stopniu rozpatry-
wany przebieg różni się od przebiegu prostokątnego. Dla przebiegu
prostokątnego k
k
= 1, ponieważ wartość skuteczna tego sygnału jest
równa jego wartości średniej, a dla przebiegu trójkątnego k
k
= 1,155.
Jeśli przetwornik mierzy napięcie średnie, to jego wartość prze-
mnożona przez współczynnik kształtu daje wartość skuteczną napię-
cia.
- współczynnik amplitudy (szczytu) k
a
- stosunek wartości maksy-
malnej do wartości skutecznej sygnału:
U
U
k
m
a
Przykładowe wartości współczynników amplitudy
wynoszą:
k
a
= 1
dla przebiegu prostokątnego;
k
a
=
2
dla przebiegu sinusoidalnego;
k
a
=
3
dla przebiegu trójkątnego.
- współczynnik uśredniania k
u
– to stosunek wartości maksymalnej
do wartości średniej dwupołówkowej i zapisujemy:
śrII
U
m
U
u
k
(3.18)
- współczynnik wypełnienia D:
D = t
i
/ T
(3.19)
gdzie:
t
i
- czas trwania impulsu.
Dla przebiegu prostokątnego D = 0,5.
W tabeli 3.1 przedstawione zostały niektóre wartości wyżej wy-
mienionych parametrów dla sygnałów o wybranych kształtach.
Tabela 3.1
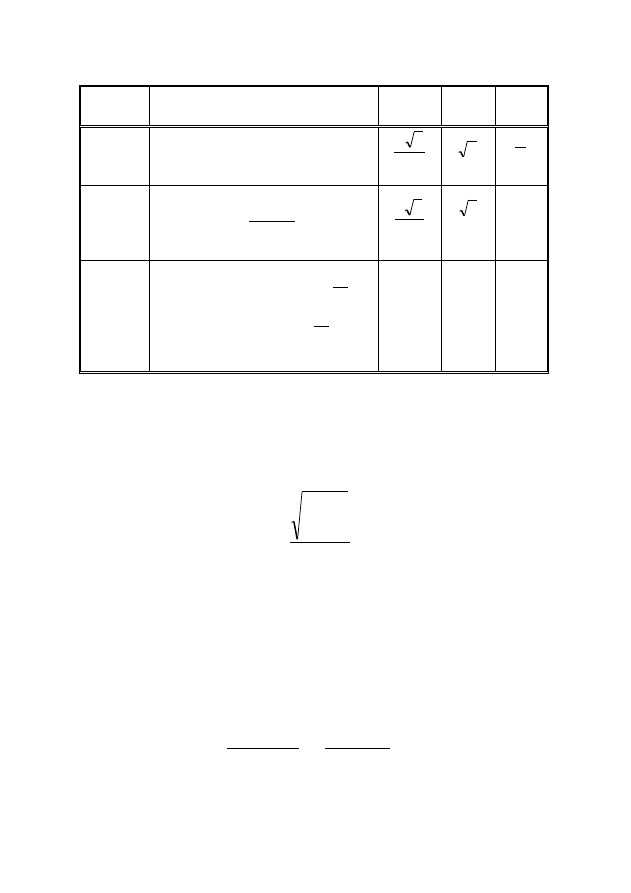
Kształt
napięcia
Zapis matematyczny
k
k
k
a
k
u
Sinus
t
m
U
t
u
sin
)
(
4
2
2
2
Trójkąt
m
U
T
m
U
t
t
u
2
)
(
3
3
2
3
2
Prostokąt
T
T
t
m
U
T
t
m
U
t
u
;
2
(
,
2
;
0
(
,
)
(
1
1
1
- współczynnik zawartości harmonicznych, inaczej zwany też
współczynnikiem zniekształceń h, jest określony stosunkiem su-
my wartości skutecznych wyższych harmonicznych (n = 2, 3 ...) do
wartości skutecznej pierwszej harmonicznej U
1
:
1
2
2
U
U
h
k
k
(3.20)
Najczęściej mierzoną wartością jest wartość skuteczna, natomiast
przebiegiem wzorcującym podziałki mierników jest przebieg sinusoi-
dalny.
Podczas pomiarów miernikami np. z prostownikami wartości
średniej, sygnałów o kształtach różniących się od sinusoidy, występują
dodatkowe błędy
k
pomiaru, zależne od kształtu krzywej mierzonego
przebiegu:
k
=
k x
k x
k
k
k
k
sin
=
k x
k x
k
k
11
,
1
(3.21)
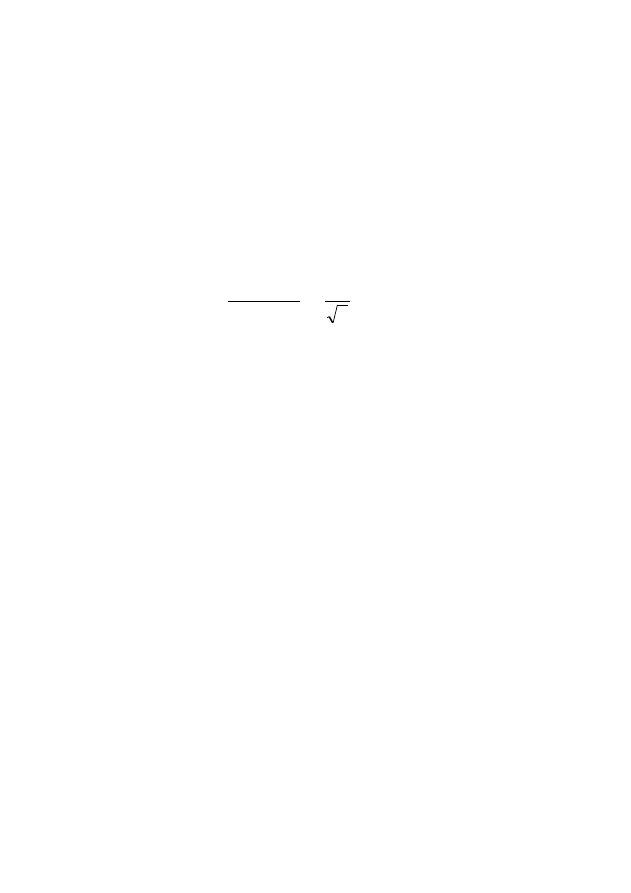
gdzie:
-
k
- względny błąd pomiaru napięć odkształconych, miernikiem
wzorcowanym przebiegiem sinusoidalnym;
- k
kx
- współczynnik kształtu mierzonego przebiegu odkształconego;
- k
ksin
- współczynnik kształtu przebiegu sinusoidalnego (k
ksin
=1,11).
W przypadku mierników z prostownikiem wartości szczytowej
istotnym staje się współczynnik amplitudy (szczytu) k
a
. Błąd pomiaru
takim miernikiem napięć niesinusoidalnych wynosi:
a
=
sin
sin
a
a
ax
k
k
k
=
2
ax
k
- 1
(3.22)
gdzie:
k
ax
- współczynnik amplitudy ( szczytu ) mierzonego napięcia,
k
asin
- współczynnik amplitudy przebiegu sinusoidalnego.
Wspomniane błędy są błędami systematycznymi i powinny być
wyeliminowane z wyniku pomiaru w postaci poprawek.
Natomiast wartość błędu względnego
d
U wynikającego z kształ-
tu sygnału określamy z zależności:
U
z
- U
p
d
U = ---------- 100 %
(3.23)
U
p
gdzie:
- U
p
- wartość napięcia zmierzona przyrządem cyfrowym (najbar-
dziej zbliżona do poprawnej);
- U
z
- wartość napięcia zmierzona innym miernikiem.