Przypadki szczególne przemiany politropowej
Opracowanie: Ewa Fudalej-Kostrzewa
1/6
5.4. Przemiana izobaryczna
Przemiana przy stałym ciśnieniu, czyli izobaryczna jest przemianą politropową
o wykładniku m = 0, gdyż
pv
m
=pv
0
=p= const.
Przemiana ta zachodzi, gdy ogrzewa się gaz zamknięty w cylindrze tłokiem, stale jednakowo
obciążonym, więc np. własnym ciężarem lub ciężarem dodatkowym. Przez ogrzewanie gaz
zwiększa swą objętość i tłok unosi się. Przy oziębianiu gaz będzie się kurczył, więc tłok będzie
opadać.
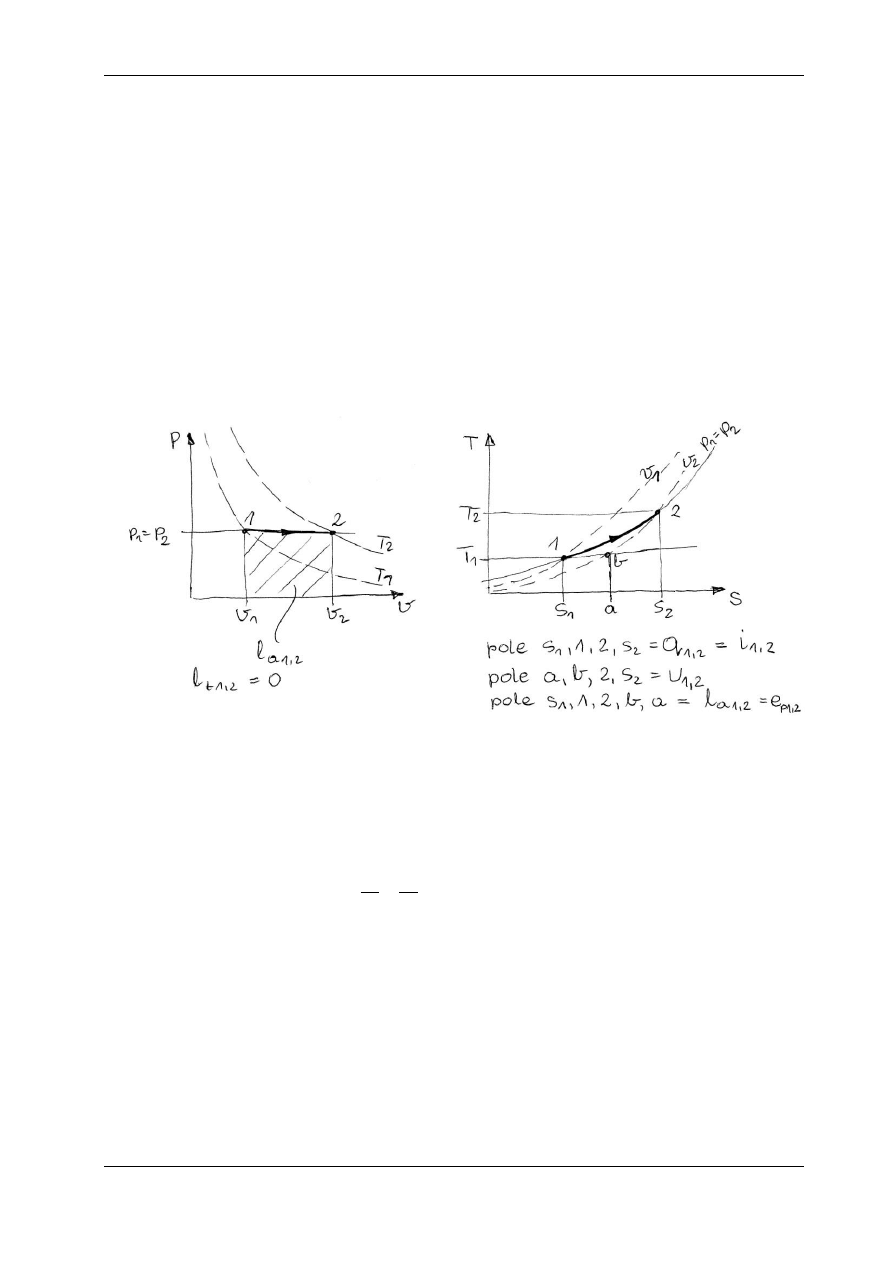
Krzywa przemiany izobarycznej nazywana izobarą jest przedstawiona na rys. 5.4.1
w układzie p – v i T – s.
Rys. 5.4.1. Przemiana izobaryczna na wykresie p – v i T – s
la
1,2
– praca absolutna, q
1,2
- ciepło, u
1,2
– przyrost energii wewnętrznej,
i
1,2
– przyrost entalpii, e
1,2
– energia przetłaczania
Parametry stanu w przemianie izobarycznej zmieniają się według zależności
Praca absolutna przemiany wynosi
2
1
1
2
2
,
1
)
(
v
v
p
dv
p
l
a
Praca techniczna wynosi
2
1
2
,
1
0
dp
v
l
t
Zgodnie z definicją, ciepło przemiany wynosi
2
1
2
1
T
T
v
v
Przypadki szczególne przemiany politropowej
Opracowanie: Ewa Fudalej-Kostrzewa
2/6
)
(
1
2
2
,
1
T
T
c
q
Wobec tego, że dla przemiany izobarycznej wykładnik politropy m = 0 ciepło właściwe c tej
przemiany wynosi
p
v
v
c
c
k
m
k
m
c
c
1
)
(
A zatem, ciepło dostarczone bądź odebrane w przemianie izobarycznej można przedstawić
zależnością
1
2
2
,
1
T
T
c
q
p
Wobec tego, że w przemianie izobarycznej l
t1,2
=0, z równania pierwszej zasady termodynamiki
w postaci
2
,
1
2
,
1
2
,
1
t
l
q
i
wynika, że dostarczone ciepło jest równe przyrostowi entalpii czynnika.
2
,
1
2
,
1
i
q
Przyrost entropii można wyznaczyć z definicji entropii:
T
dq
ds
Dla przemiany izobarycznej dq = c
p
·dT, a zatem
1
2
2
1
2
1
2
,
1
ln
T
T
c
T
dT
c
T
dq
s
p
p
Przyrost energii wewnętrznej, zgodnie z definicją wynosi
)
(
1
2
2
,
1
T
T
c
u
v
Przyrost entalpii, zgodnie z definicją wynosi
)
(
1
2
2
,
1
T
T
c
i
p
5.5. Przemiana izochoryczna
Przemiana przy stałej objętości czyli izochoryczna zachodzi wówczas, gdy mimo zmian
temperatury i ciśnienia oraz mimo doprowadzania i odprowadzania ciepła objętość gazu
zamkniętego w naczyniu nie ulega zmianie. Przemiana izochoryczna (v = const.) jest przemianą
politropową o wykładniku m = ± ∞ .
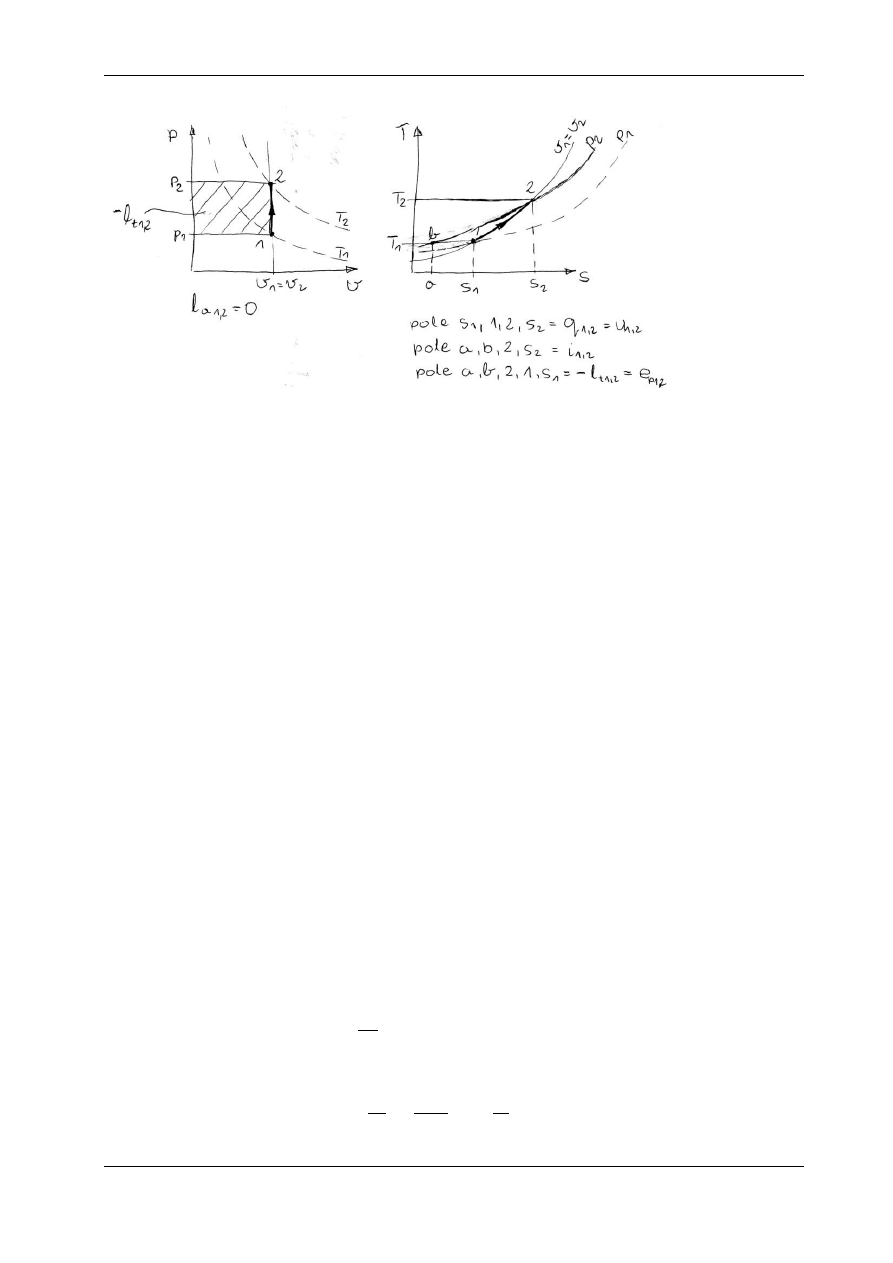
Krzywa przemiany izochorycznej nosi nazwę izochory i jest przedstawiona na rys. 5.5.1
w układzie p – v i T – s. Parametry stanu gazu w tej przemianie zmieniają się zgodnie z równaniem
2
1
2
1
T
T
p
p
Przypadki szczególne przemiany politropowej
Opracowanie: Ewa Fudalej-Kostrzewa
3/6
Rys. 5.5.1. Przemiana izochoryczna na wykresie p – v i T – s
lt
1,2
– praca techniczna, q
1,2
- ciepło, u
1,2
– przyrost energii wewnętrznej,
i
1,2
– przyrost entalpii, e
1,2
– energia przetłaczania
Praca absolutna przemiany wynosi
2
1
2
,
1
0
dv
p
l
a
Praca techniczna wynosi
2
1
1
2
2
,
1
p
p
v
dp
v
l
t
Zgodnie z definicją, ciepło przemiany wynosi
)
(
1
2
2
,
1
T
T
c
q
Wobec tego, że dla przemiany izochorycznej c =c
v
, otrzymuje się
1
2
2
,
1
T
T
c
q
v
Wobec tego, że w przemianie izobarycznej l
a1,2
=0, z równania pierwszej zasady termodynamiki
w postaci
2
,
1
2
,
1
2
,
1
a
l
q
u
wynika, że dostarczone ciepło jest równe przyrostowi energii wewnętrznej czynnika.
2
,
1
2
,
1
u
q
Przyrost entropii można wyznaczyć z definicji entropii:
T
dq
ds
Dla przemiany izochorycznej dq = c
v
·dT, a zatem
1
2
2
1
2
1
2
,
1
ln
T
T
c
T
dT
c
T
dq
s
v
v
Przypadki szczególne przemiany politropowej
Opracowanie: Ewa Fudalej-Kostrzewa
4/6
Przyrost energii wewnętrznej, zgodnie z definicją wynosi
)
(
1
2
2
,
1
T
T
c
u
v
Przyrost entalpii, zgodnie z definicją wynosi
)
(
1
2
2
,
1
T
T
c
i
p
5.6. Przemiana izotermiczna
Przemiana przy stałej temperaturze czyli izotermiczna (T = const.) jest przemianą
politropową o wykładniku m = 1, a więc
p·v = const.
Jest równocześnie przemianą przy stałej energii wewnętrznej, tj.
u = c
v
·T = const. lub du = c
v
·dt = 0
oraz przemianą przy stałej entalpii, tj.
i = c
p
·T = const. lub di = c
p
·dt = 0
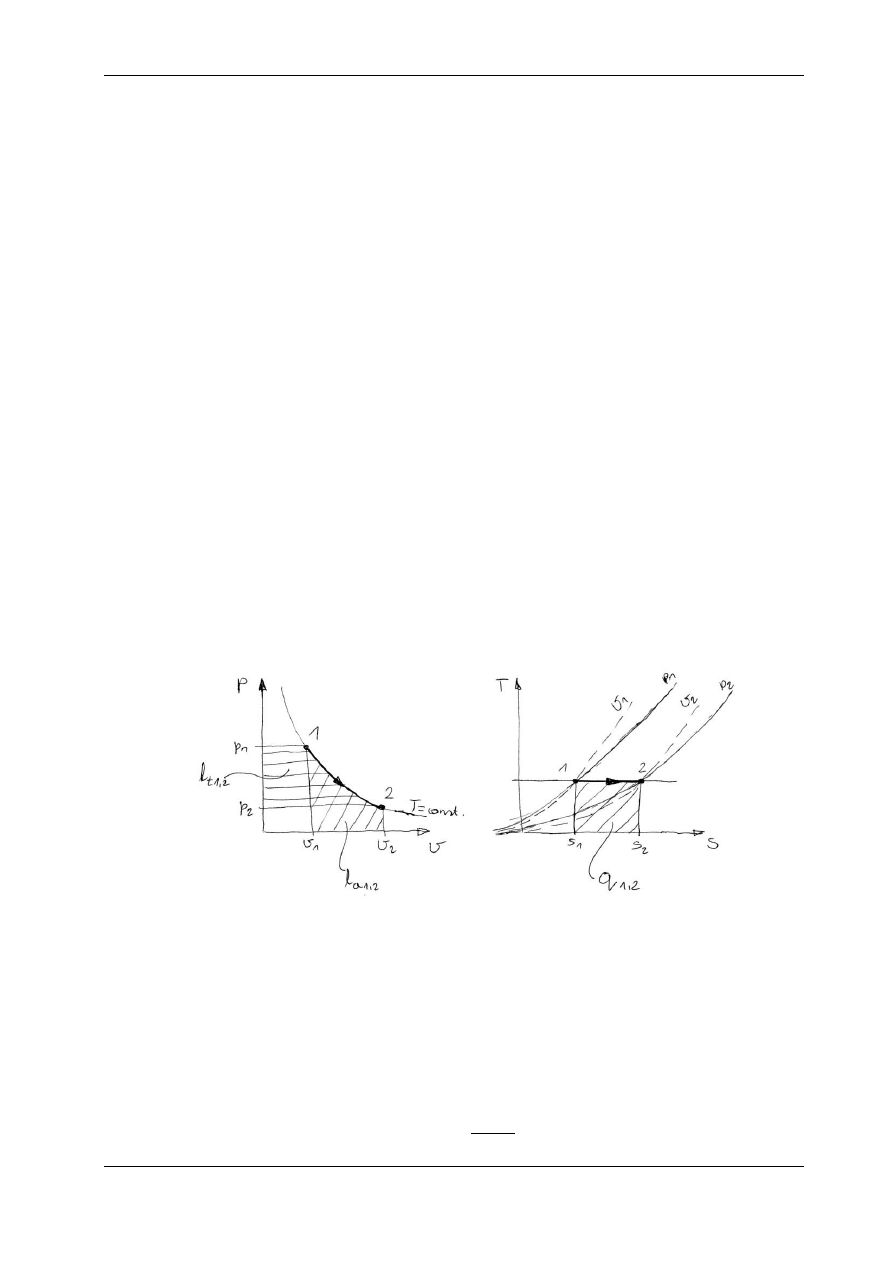
Linia przemiany przestawiającej przemianę o stałej temperaturze nosi nazwę izotermy i jest
przedstawiona na rys. 5.6.1 w układzie p – v i T – s. Parametry stanu gazu w tej przemianie
zmieniają się zgodnie z równaniem
T
R
v
p
v
p
2
2
1
1
Izoterma jest więc na wykresie p – v hiperbolą równoosiową.
Rys. 5.6.1. Przemiana izochoryczna na wykresie p – v i T – s
la
1,2
– praca absolutna, lt
1,2
– praca techniczna, q
1,2
- ciepło
Praca absolutna przemiany wynosi
2
1
2
,
1
dv
p
l
a
Z równania izotermy:
v
v
p
p
v
p
v
p
1
1
1
1
Przypadki szczególne przemiany politropowej
Opracowanie: Ewa Fudalej-Kostrzewa
5/6
A zatem
2
1
1
2
1
2
1
1
1
2
1
1
1
1
2
1
1
1
2
1
1
1
2
,
1
ln
ln
ln
ln
ln
ln
2
1
p
p
T
R
v
v
T
R
v
v
v
p
v
v
v
p
v
v
p
v
dv
v
p
v
dv
v
p
l
v
v
a
2
1
1
2
2
,
1
ln
ln
p
p
T
R
v
v
T
R
l
a
Praca techniczna wynosi
2
1
dp
v
l
t
Z równania izotermy:
p
v
p
v
v
p
v
p
1
1
1
1
A zatem
2
1
1
1
1
2
1
1
1
1
1
1
2
1
1
ln
ln
2
p
p
v
p
p
p
v
p
dp
p
v
p
p
dp
v
p
l
t
2
,
1
1
2
2
1
2
,
1
ln
ln
a
t
l
v
v
T
R
p
p
T
R
l
Przyrost energii wewnętrznej, zgodnie z definicją wynosi
)
(
1
2
2
,
1
T
T
c
u
v
Ponieważ :
2
1
T
T
przyrost energii wewnętrznej w przemianie izotermicznej:
0
2
,
1
u
Przyrost entalpii, zgodnie z definicją wynosi
)
(
1
2
2
,
1
T
T
c
i
p
Ponieważ :
2
1
T
T
przyrost entalpii w przemianie izotermicznej:
0
2
,
1
i
Ciepło przemiany można wyznaczyć z równania pierwszej zasady termodynamiki. Wobec tego, że
0
2
,
1
u
, z pierwszej postaci równania
Przypadki szczególne przemiany politropowej
Opracowanie: Ewa Fudalej-Kostrzewa
6/6
2
,
1
2
,
1
2
,
1
A
l
q
u
wynika
2
,
1
2
,
1
a
l
q
a wobec
0
2
,
1
i
, z drugiej postaci równania
2
,
1
2
,
1
2
,
1
t
l
q
i
wynika
2
,
1
2
,
1
t
l
q
A zatem, w przemianie izotermicznej
2
1
1
2
2
,
1
2
,
1
2
,
1
ln
ln
p
p
T
R
v
v
T
R
l
l
q
t
a
Przyrost entropii można wyznaczyć z definicji entropii:
T
dq
ds
a zatem:
2
1
1
2
1
2
,
1
2
,
1
ln
ln
p
p
R
v
v
R
T
q
s
5.7. Przemiana izentropowa
Jest to przemiana odbywająca się bez wymiany ciepła z otoczeniem, czyli przemiana
adiabatyczna, w której
dq = 0 oraz q= 0
Warunek ten powiązany ze wzorem definicyjnym na entropię, reprezentuje jednocześnie warunek
stałej entropii
dq = T·ds. = 0
Ponieważ T ≠ 0 to ds = 0, czyli s = const. przemiana przy stałej entropii nazywa się przemianą
izentropową a krzywa przedstawiająca tę przemianę nosi nazwę izentropy. Nie każda jednak
przemiana adiabatyczna jest przemianą izentropową. Równoważność obu przemian odnosi się tylko
do przemian odwracalnych gazu doskonałego bez wymiany ciepła z otoczeniem, gdy w układzie nie
ma wewnętrznych źródeł ciepła wynikłych np. z lepkości.
Pierwsze równanie termodynamiki w odniesieniu do przemiany adiabatycznej przybiera
postać
(5.7.1)
Przypadki szczególne przemiany politropowej
Opracowanie: Ewa Fudalej-Kostrzewa
7/6
Z równania
oraz
obliczone c
v
ma wartość
a po wstawieniu tej wartości do równania (5.7.1) otrzymuje się
a po przekształceniu
(5.7.2)
Różniczkując równanie pv=RT , otrzymuje się
p dv + v dp = R dT
i podstawiając do (5.7.2) wartość R dT otrzymuje się
Stąd
lub ostatecznie
Jest to równanie różniczkowe adiabaty. Całkując to równanie przy założeniu, że k = const.
otrzymuje się równanie
lub
skąd
= const.
(5.7.3)
A więc jest to postać przemiany politropowej, dla której m = k.
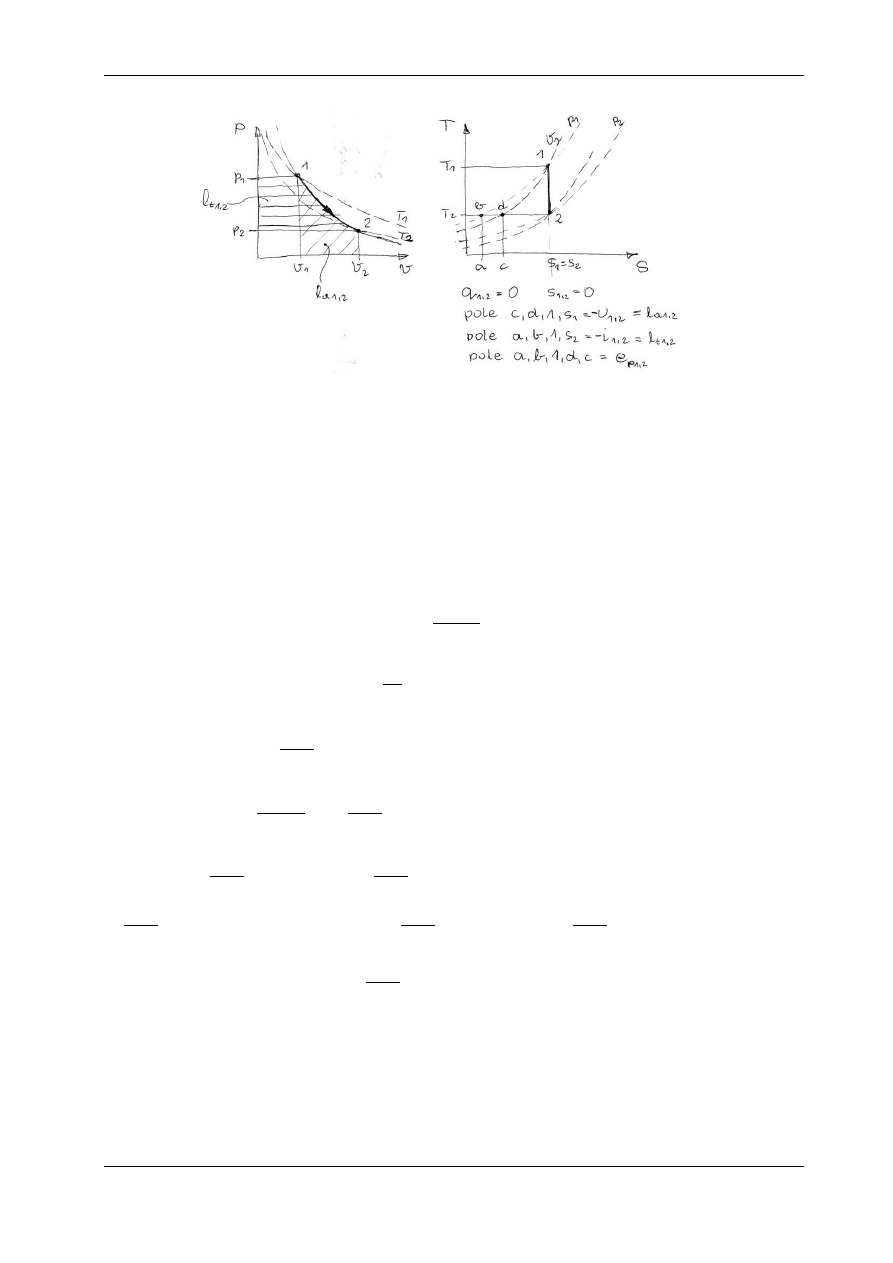
Adiabata w układzie p – v jest hiperbolą nierównoboczną przebiegającą bardziej stromo niż
izoterma. Jest przedstawiona na rys. 5.7.1 w układzie p – v i T – s.
Korzystając z równania stanu gazu można w równaniu (5.7.3) wyeliminować kolejno jeden
z parametrów i zastąpić go temperaturą. Po dokonaniu przekształceń otrzymuje się równanie
przemiany izentropowej w następujących postaciach
)
1
(
2
2
)
1
(
1
1
k
k
v
T
v
T
k
k
k
k
p
T
p
T
1
2
2
1
1
1
Przypadki szczególne przemiany politropowej
Opracowanie: Ewa Fudalej-Kostrzewa
8/6
Rys. 5.7.1. Przemiana izentropowa na wykresie p – v i T – s
la
1,2
– praca absolutna, lt
1,2
– praca techniczna, u
1,2
– przyrost energii wewnętrznej,
i
1,2
– przyrost entalpii, e
1,2
– przyrost energii przetłaczania
Praca absolutna przemiany wynosi
2
1
2
,
1
dv
p
l
a
Z równania izentropy
k
k
k
k
v
v
p
p
v
p
v
p
1
1
1
1
2
1
1
1
2
1
1
1
2
,
1
dv
v
v
p
v
dv
v
p
l
k
k
k
k
a
Wiadomo, że:
1
1
1
n
n
x
dx
x
n
n
A zatem:
1
1
1
2
2
1
1
2
1
1
1
1
k
k
v
v
k
k
v
v
k
k
v
dv
v
2
,.
1
1
2
1
2
1
1
2
2
1
1
1
1
1
2
2
2
1
1
1
1
1
2
1
1
1
1
1
2
1
1
2
,
1
1
1
1
1
1
1
1
1
1
u
T
T
c
T
T
k
R
v
p
v
p
k
v
v
p
v
v
p
k
v
v
p
v
v
p
k
v
v
k
v
p
l
v
k
k
k
k
k
k
k
k
k
k
k
a
2
,
1
1
2
2
,
1
1
u
T
T
k
R
l
a
Praca techniczna wynosi
2
1
dp
v
l
t
Przypadki szczególne przemiany politropowej
Opracowanie: Ewa Fudalej-Kostrzewa
9/6
Zrównania izentropy:
1
1
1
1
1
1
v
p
p
v
v
p
v
p
k
k
k
k
dp
p
v
p
p
dp
v
p
l
k
k
k
k
t
2
1
1
1
1
1
1
1
2
1
1
1
k
k
k
k
k
k
k
p
p
k
k
p
p
k
k
p
p
k
k
p
dp
p
1
1
1
2
1
1
1
1
1
2
1
1
2
1
1
1
1
1
1
1
1
2
1
2
,
1
1
2
1
2
1
1
2
2
1
1
2
2
1
1
1
1
1
1
2
1
1
1
1
1
1
2
1
1
1
2
,
1
)
(
1
1
1
1
1
i
T
T
c
T
T
R
k
k
v
p
v
p
k
k
v
p
v
p
k
k
p
v
p
p
v
p
k
k
p
p
k
k
v
p
l
p
k
k
k
k
k
k
k
k
k
k
k
t
2
,
1
2
,
1
1
2
2
,
1
1
i
u
k
T
T
k
R
k
l
t
Ciepło przemiany, zgodnie z definicją:
)
(
1
2
2
,
1
T
T
c
q
Wobec tego, że c =0:
0
2
,
1
q
Przyrost entropii, zgodnie z definicją:
T
dq
ds
Wobec tego, że c =0, q
1,2
=0:
0
2
,
1
s
Przyrost energii wewnętrznej, zgodnie z definicją:
)
(
1
2
2
,
1
T
T
c
u
v
Przyrost entalpii, zgodnie z definicją:
)
(
1
2
2
,
1
T
T
c
i
p