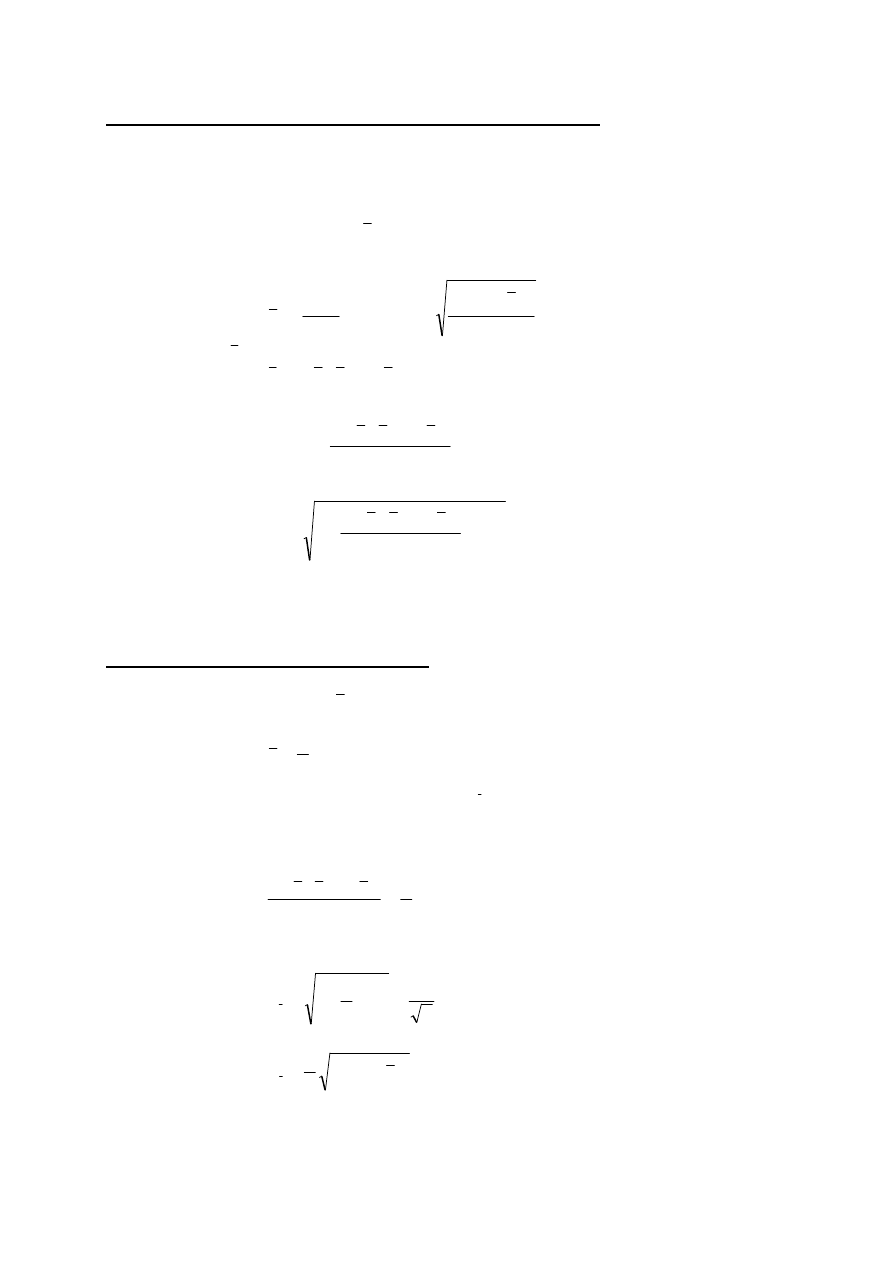
Pomiary pośrednie obarczone niepewnościami przypadkowymi.
Niech zmienna z będzie funkcją p niezależnych zmiennych x
i
(
)
p
x
x
x
f
z
,
,
,
2
1
K
=
Mierzymy zmienne x
q
, chcemy wyznaczyć wartość wielkości nie mierzonej z oraz jej
odchylenie standardowe S
z
. Niech
q
x
będzie średnią wartością wielkości x
q
, zaś
q
x
S
odchyleniem standardowym pojedynczego pomiaru wielkości x
q
:
(
)
m
x
x
S
m
x
x
m
l
q
l
q
q
x
m
l
l
q
q
∑
−
=
∑
=
=
=
1
2
1
Wartość średnią z wyznaczamy z równania
(
)
p
x
x
x
f
z
,
,
,
2
1
K
=
natomiast wariancję
2
z
S
z tzw. prawa przenoszenia wariancji
∑
∂
∂
=
=
p
q
q
x
q
p
z
S
x
x
x
x
f
S
1
2
2
1
2
)
,
,
,
(
K
Odchylenie standardowe S
z
oblicza się z tzw. prawa przenoszenia odchyleń standardowych
∑
∂
∂
=
=
p
q
q
x
q
p
z
S
x
x
x
x
f
S
1
2
2
1
)
,
,
,
(
K
( )
Odchylenie standardowe jest miarą niepewności pomiarowych poszczególnych wyników
wchodzących w skład próby. Jaka jest niepewność pomiarowa końcowego wyniku pomiaru,
czyli wartości średniej?
Niepewność pomiarowa wartości średniej
Zauważmy, że wartość średnią x można traktować formalnie jako wielkość mierzoną
pośrednio, obliczaną ze wzoru
(
)
n
x
x
x
n
x
+
+
+
=
K
2
1
1
Wtedy odchylenie standardowe wartości średniej
x
S
można obliczyć korzystając z prawa
przenoszenia odchyleń standardowych. W tym celu przyjmujemy, że
x
n
x
x
x
S
S
S
S
=
=
=
=
K
2
1
oraz
(
)
n
x
x
x
x
f
q
n
1
,
.
,
2
1
=
∂
∂
K
Podstawiając powyższe dwa wzory do prawa przenoszenia odchyleń standardowych
otrzymamy
x
n
q
x
x
S
n
S
n
S
1
1
1
2
2
=
∑
=
=
(∇)
Dla dużej próby otrzymamy zatem ostatecznie
(
)
∑
−
=
2
1
x
x
n
S
i
x
zaś dla małej próby
(
)
∑
−
−
=
2
)
1
(
1
x
x
n
n
S
i
x
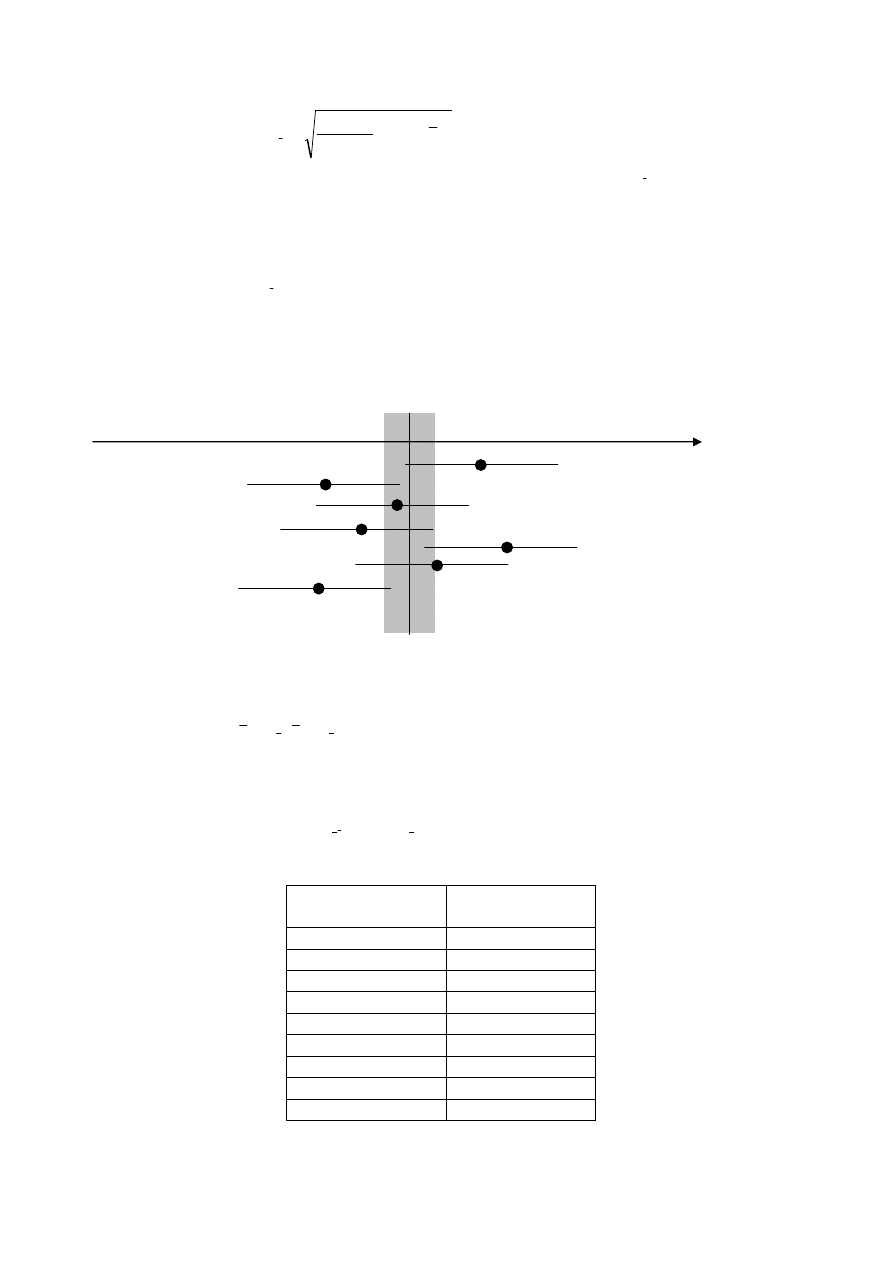
Jak więc widać z powyższych wzorów odchylenie standardowe średniej
x
S
jest mniejsze od
odchylenia standardowego S
x
pojedynczego pomiaru (niepewność średniej jest mniejsza niż
niepewność poszczególnego pomiaru). Ilustruje to poniższy rysunek, na którym wartości x
i
zaznaczone są punktami, długość odcinka ze środkowym punktem wynosi 2S
x
, średnia
arytmetyczna reprezentowana jest pionową linią, zaś długość krótszego boku zacieniowanego
prostokąta wynosi
x
S
2
(oś pionowa wprowadzona została jedynie dla zwiększenia
czytelności rysunku).
X
Dla bardzo małych prób wyniki pomiarów podlegają rozkładowi Studenta. Jaką niepewność
przypisać uzyskanej z próby wartości średniej? Przyjmując interpretacje probabilistyczną
odchylenia standardowego w rozkładzie normalnym (prawdopodobieństwo uzyskania wyniku
spoza przedziału
x
x
S
x
S
x
+
−
,
wynosi 31.74%), znajdujemy taką wartość krytyczną w
rozkładzie Studenta t
n,α
, dla której α=0.3174≈0.32. Wtedy dla bardzo małej próby
x
n
xt
S
t
S
32
.
0
,
=
x
n
t
x
S
t
S
32
.
0
,
=
Wartości krytyczne t
n,0.32
dla niektórych wartości n podane są w tabeli poniżej.
Liczebność próby n Wartość krytyczna
t
n,0.3174
3
1.3210
4
1.1966
5
1.1414
6
1.1103
7
1.0903
8
1.0765
9
1.0663
10
1.0585
15
1.0368

Odchylenie standardowe wielkości mierzonej pośrednio
otrzymamy podstawiając do wzoru
( ) wariancję średniej
2
q
x
S
zamiast wariancji poszczególnych pomiarów
2
q
x
S
∑
∂
∂
=
=
p
q
q
x
q
p
z
S
x
x
x
x
f
S
1
2
2
1
)
,
,
,
(
K
(
◊)
W przypadku gdy znamy tylko wariancje
2
q
x
S
oraz liczebności próby n
q
każdej zmiennej
losowej, wzór końcowy na odchylenie standardowe
z
S
otrzymamy przez podstawienie
wyrażenia (∇) do równania (
◊), uzyskując
∑
∂
∂
=
=
p
q
q
x
q
q
p
z
S
n
x
x
x
x
f
S
1
2
2
1
1
)
,
,
,
(
K
Niepewność całkowita pomiarów bezpośrednich
Zakładamy, że mierzona wielkość x obarczona jest zarówno R różnymi niepewnościami
systematycznymi
∆
r
x (r=1,2,...,R)
, jak i niepewnością przypadkową, opisaną odchyleniem
standardowym średniej
x
S
.Niepewności systematyczne poszczególnych przyczynków
∆
r
x
zamieniamy na odpowiadające im odchylenia standardowe S
r
za pomocą równania
3
x
S
r
r
∆
=
,
a niepewność całkowitą S
c
obliczymy z prawa przenoszenia odchyleń standardowych
(
)
(
)
(
)
(
)
(
)
2
2
1
2
2
1
2
2
2
1
2
/
1
2
2
2
2
2
1
3
3
q
x
R
r
r
x
R
x
R
c
S
x
S
x
x
x
S
S
S
S
S
+
∑ ∆
=
+
∆
+
+
∆
+
∆
=
+
+
+
+
=
=
L
L
Niepewność całkowita pomiarów pośrednich
Niepewność całkowita (całkowite odchylenie standardowe
y
S
) , na którą składają się
niepewności przypadkowe i systematyczne obliczymy korzystając ze wzoru (
◊) i ze wzoru
powyżej
(
)
∑
+
∑ ∆
∂
∂
=
=
=
p
q
q
x
R
r
r
q
p
y
S
x
x
x
x
x
f
S
1
2
2
2
1
2
1
3
,
,
,
(
L
Przykład: Wyznaczanie przyśpieszenia ziemskiego za pomocą wahadła matematycznego.
1.
Pomiary długości wahadła [m]: {1.241; 1.243; 1.240; 1.243; 1.242}
wartość średnia l =1.2418, odchylenie standardowe średniej długości
(
)
(
)
1
2
−
∑
−
=
n
n
l
l
S
i
l
=0.000583
000665
.
0
1414
.
1
=
⋅
=
l
t
l
S
S
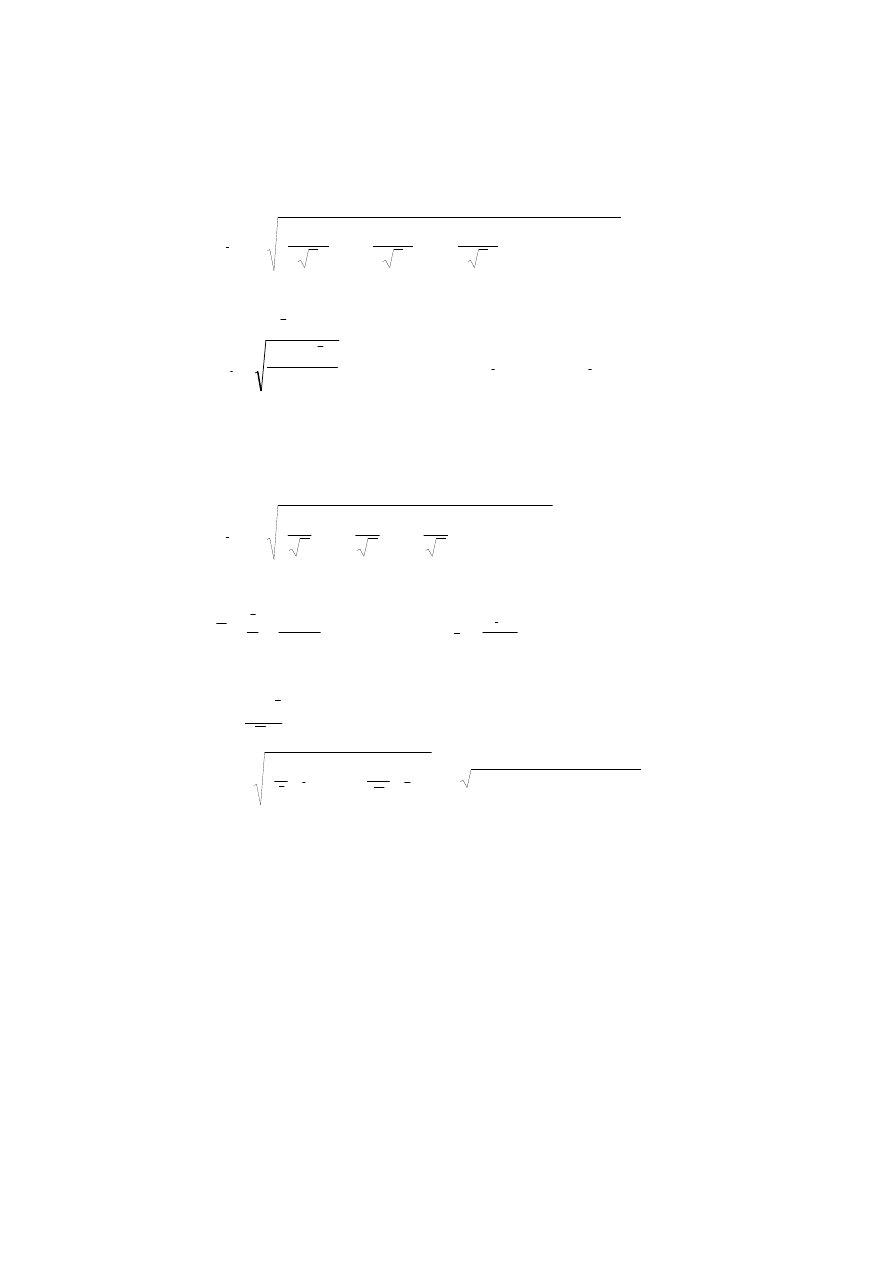
∆l
1
– niepewność systematyczna związana z dokładnością użytej miarki
0.001
∆l
2
– niepewność systematyczna związana z przyłożeniem początku miarki
0.001
∆l
3
– niepewność systematyczna związana z przyłożeniem końca miarki
0.001
Niepewność całkowita długości wahadła (odchylnie standardowe)
(
)
0012012
.
0
000665
.
0
3
001
.
0
3
001
.
0
3
001
.
0
2
2
2
2
)
(
=
+
+
+
=
ca
l
S
2.
Pomiary czasu k=30 wahnięć wahadła [s]: {66.1; 65.4; 66.0; 66.6; 65.5}
wartość średnia
9200
.
65
=
t
, odchylenie standardowe średniego czasu
(
)
(
)
1
2
−
∑
−
=
n
n
t
t
S
i
t
=0.2177
2485
.
0
1414
.
1
=
⋅
=
t
t
t
S
S
∆t
1
– niepewność systematyczna związana z dokładnością użytego stopera:
0.1
∆t
2
– niepewność systematyczna związana z włączeniem stopera:
0.2
∆t
3
– niepewność systematyczna związana z wyłączeniem stopera:
0.2
Niepewność całkowita czasu 30-tu wahnięć (odchylenie standardowe)
(
)
2
2
2
2
)
(
2485
.
0
3
2
.
0
3
2
.
0
3
1
.
0
+
+
+
=
ca
t
S
=0.30289
3.
Obliczenie okresu wahnięć i jego odchylenia standardowego:
010096
.
0
30
1973
.
2
30
92
.
65
)
(
=
=
=
=
=
ca
t
T
S
S
k
t
T
4.
Obliczenie przyśpieszenia ziemskiego i jego niepewności całkowitej
1539
.
10
4
2
2
=
=
T
l
g
π
0938
.
0
0087071
.
0
0000965
.
0
2
2
2
)
(
=
+
=
+
=
T
ca
l
g
S
T
g
S
l
g
S
Rezultat końcowy zapiszemy w postaci
g=10.15±0.09 m/s
2
Wyszukiwarka
Podobne podstrony:
06 niepewnosc calkowita, Prawo przenoszenia wariancji
06 niepewnosc calkowita, Prawo przenoszenia wariancji
NIEPEWNOŚĆ POMIARU
Wyk%c5%82ad Niepewno%c5%9b%c4%87 pomiaru
Podejmowanie decyzji w warunkach niepewnosci
19 rachunek calkowy 5 6 funkcje o wahaniu skonczonym
AMI 25 1 Rachunek calkowy podstawowe typy zadan id 59059 (2)
mierniki i niepewności pomiarowe
pm 3 4 szacowanie niepewnosci
RACHUNEK CAŁKOWY. CAŁKA OZNACZONA I JEJ ZASTOSOWANIA, SZKOŁA, Matematyka, Matematyka
Błąd i niepewność pomiaru
1 Rachunek niepew pom BSid 103 Nieznany (2)
Program calkow
więcej podobnych podstron