1

DYNAMIKA

Różniczkowe równania ruchu płynów nielepkich

Podstawowe równania dynamiki płynów nielepkich – Euler (1755 r)

Równania równowagi płynu w hydrostatyce np. dla kierunku Ox

0

1

x

p

q

x

Równanie równowagi dynamicznej płynu nielepkiego
dla kierunku Ox

0

1

dt

dv

x

p

q

x

x

2

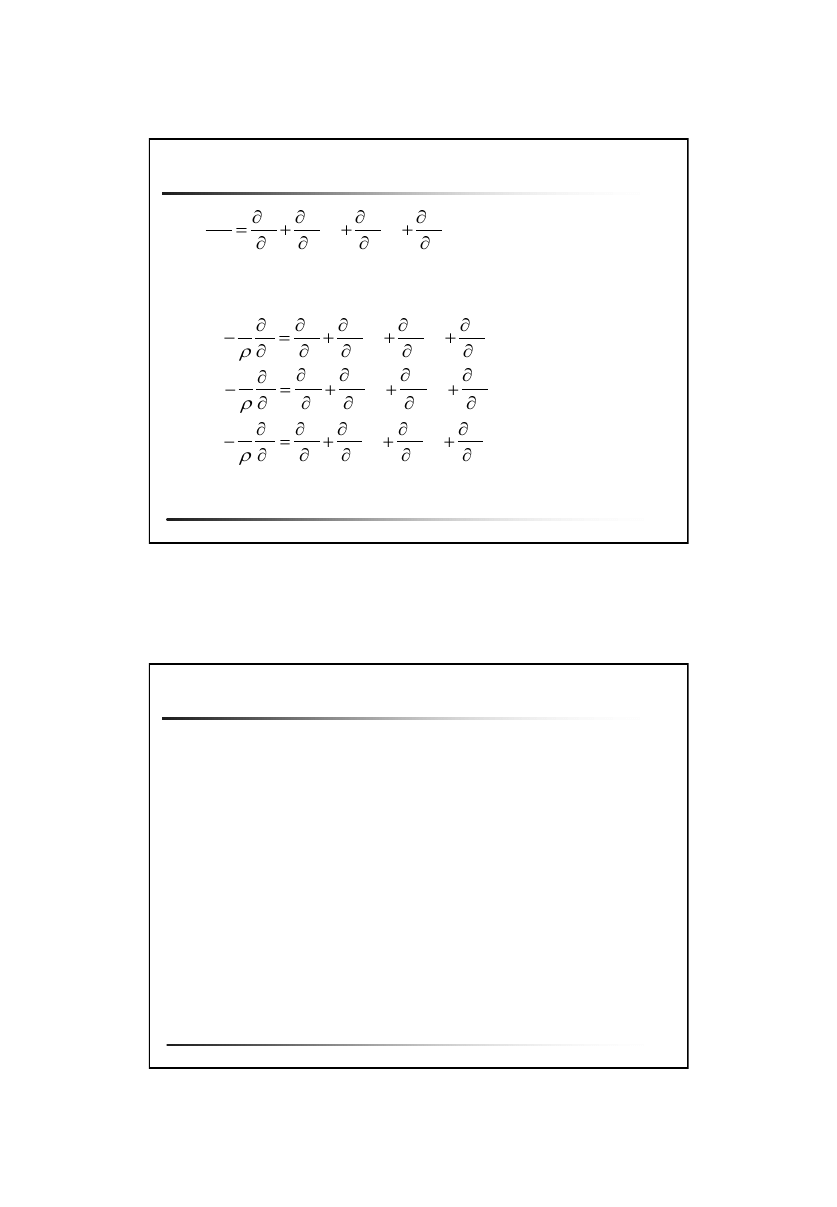
Różniczkowe równania ruchu płynów nielepkich

Pochodna substancjalna

z

x

y

x

x

x

x

x

v

z

v

v

y

v

v

x

v

t

v

dt

dv

z

x

y

x

x

x

x

x

v

z

v

v

y

v

v

x

v

t

v

x

p

q

1

Równania Eulera

z

z

y

z

x

z

z

z

z

y

y

y

x

y

y

y

v

z

v

v

y

v

v

x

v

t

v

z

p

q

v

z

v

v

y

v

v

x

v

t

v

y

p

q

1

1

Różniczkowe równania ruchu płynów nielepkich

Równania Eulera:



opisują przepływ nielepki,



są słuszne dla przepływu ściśliwego lub nieściśliwego

Rozwiązanie tych równań wymaga:



równania ciągłości



równania stanu (dla przepływu ściśliwego)



równania energii (np. dla przepływów z silnymi

zjawiskami falowymi)

3

Równanie Bernoulliego w przepływie ustalonym

Przepływ ustalony

pochodne lokalne

Siła masowa

ciężar

g

q

q

q

z

y

x

0

dz

dt

dv

dz

z

p

gdz

dy

dt

dv

dy

y

p

dx

dt

dv

dx

x

p

z

y

x

1

1

1

Równania Eulera
pomnożone odpowiednio przez dx, dy, dz

0

t

v

t

v

t

v

z

y

x

Równanie Bernoulliego w przepływie ustalonym

Prawą stronę można przekształcić pod warunkiem, że całkowanie

wykonamy wzdłuż linii prądu do postaci:

dz

dt

dv

dy

dt

dv

dx

dt

dv

dz

z

p

dy

y

p

dx

x

p

gdz

z

y

x

1

)

(

2

1

)

(

2

1

2

2

2

2

v

d

v

v

v

d

dv

v

dv

v

dv

v

dz

dt

dv

dy

dt

dv

dx

dt

dv

z

y

x

z

z

y

y

x

x

z

y

x

4

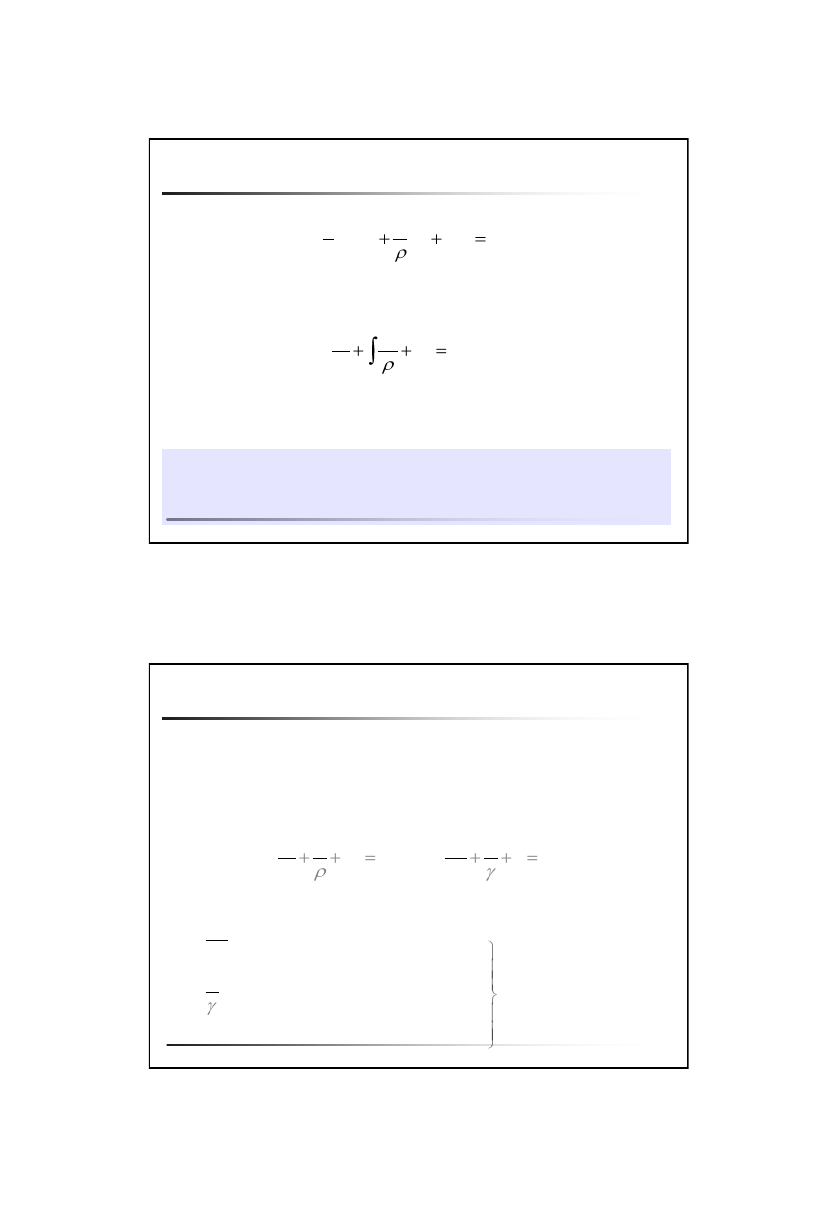
Równanie Bernoulliego w przepływie ustalonym

Po scałkowaniu otrzymujemy:

Wzdłuż linii prądu

0

1

)

(

2

1

2

gdz

dp

v

d

C

gz

dp

v

2

2

Równanie Bernoulliego

Równanie Bernoulliego jest całką równań Eulera wzdłuż linii

prądu dla ustalonego przepływu wirowego lub potencjalnego
w polu grawitacyjnym

.

Równanie Bernoulliego w przepływie ustalonym

Stosuje się do gazów i cieczy nielepkich
Wyprowadzone z równań ruchu - wyraża zasadę zachowania energii

mechanicznej

Dla płynu nieściśliwego mamy:

C

z

p

g

v

C

gz

p

v

2

lub

2

2

2

z

p

g

v

2

2

-

wysokość prędkości

-

wysokość ciśnienia

-

wysokość położenia

całkowita wysokość
hydrauliczna H

5

Równanie Bernoulliego w przepływie ustalonym

Prawo Bernoulliego

W ustalonym przepływie cieczy idealnej w polu

grawitacyjnym suma wysokości prędkości, wysokości

ciśnienia i wysokości położenia ma stałą wartość wzdłuż tej

samej linii prądu.

Równanie Bernoulliego w przepływie ustalonym

Wykres Ankony

1

1

1

2

1

2

z

p

g

v

2

2

2

2

2

2

z

p

g

v

h

s

1

2

poziom odniesienia

linia prądu

linia ciśnienia (piezometryczna)

linia energetyczna

linia strat energetycznych

1

1

1

2

1

2

z

p

g

v

2

2

2

2

2

2

z

p

g

v

h

s

1

2

poziom odniesienia

linia prądu

linia ciśnienia (piezometryczna)

linia energetyczna

linia strat energetycznych

6

Równanie Bernoulliego w przepływie ustalonym

W przepływie rzeczywistym dla dwóch punktów 1 i 2 leżących na jednej

linii prądu jest:

s

s

h

H

H

h

z

p

g

v

z

p

g

v

2

1

2

2

2

2

2

1

1

1

2

1

2

2

Zmianę wysokości całkowitej na jednostkę długości linii prądu

charakteryzującą intensywność strat możemy określić przez:

J

ds

dH

J - spadek hydrauliczny

Równanie Bernoulliego w przepływie ustalonym

Dla gazu:



musimy uwzględnić ściśliwość



możemy zaniedbać energię potencjalną

C

dp

v

2

2

Dla adiabatycznego i ustalonego

przepływu gazu

C

p

v

1

2

2

RT

p

-

dla gazu doskonałego - równanie stanu

Clapeyrona

d

C

dp

C

const

p

1

p

p

C

d

C

dp

1

1

1

1

1

1

2

- adiabata Poissona

wykładnik adiabaty

7

Ciśnienie dynamiczne. Metody pomiaru prędkości przepływu

Jeżeli przepływ cieczy odbywa się w płaszczyźnie poziomej lub jeżeli w

przepływie gazu możemy pominąć ściśliwość to :

Ciśnienie

całkowite

C

p

v

2

2

p

p

v

d

2

2

-

ciśnienie dynamiczne

-

ciśnienie statyczne

c

d

p

p

p

C

p

v

2

2

const

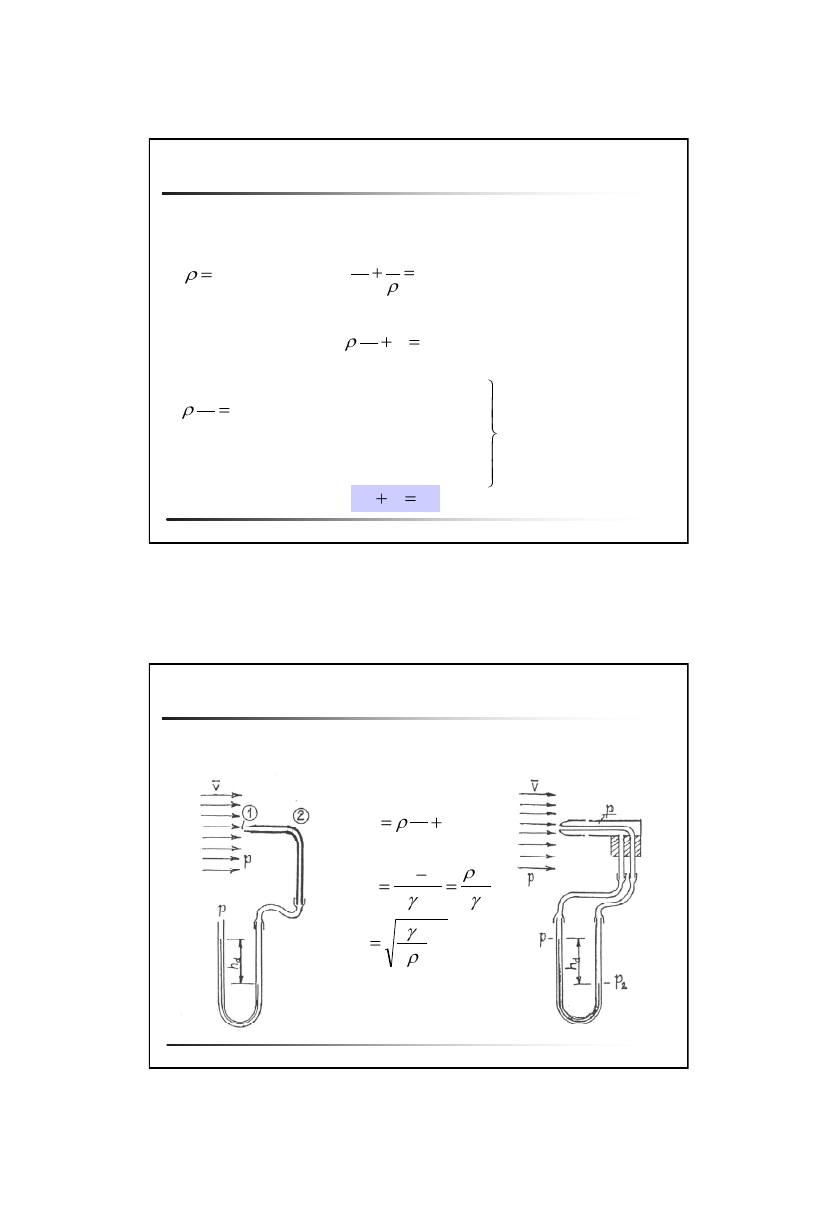
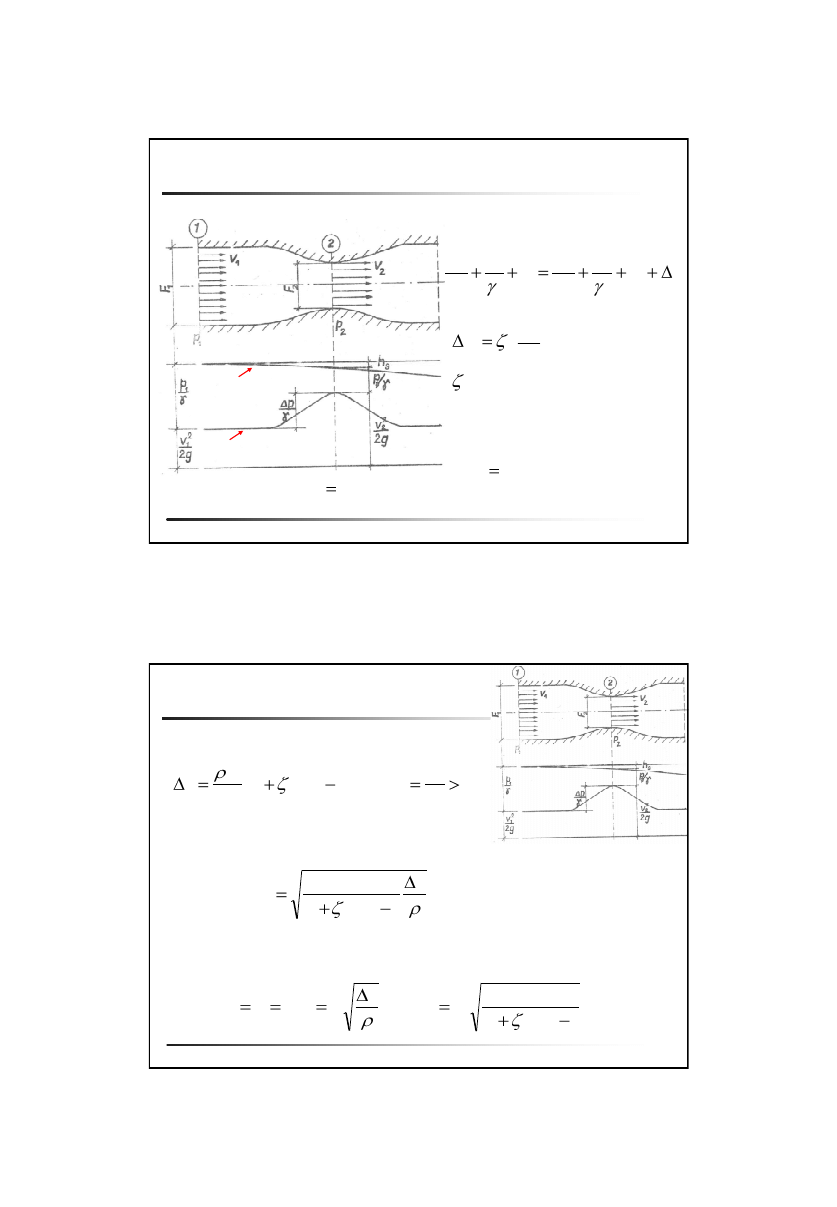
Metody pomiaru prędkości przepływu

Rurka Pitota

Rurka Prandtla

p

v

p

2

2

2

d

m

m

m

d

h

v

v

p

p

h

2

2

2

2

8

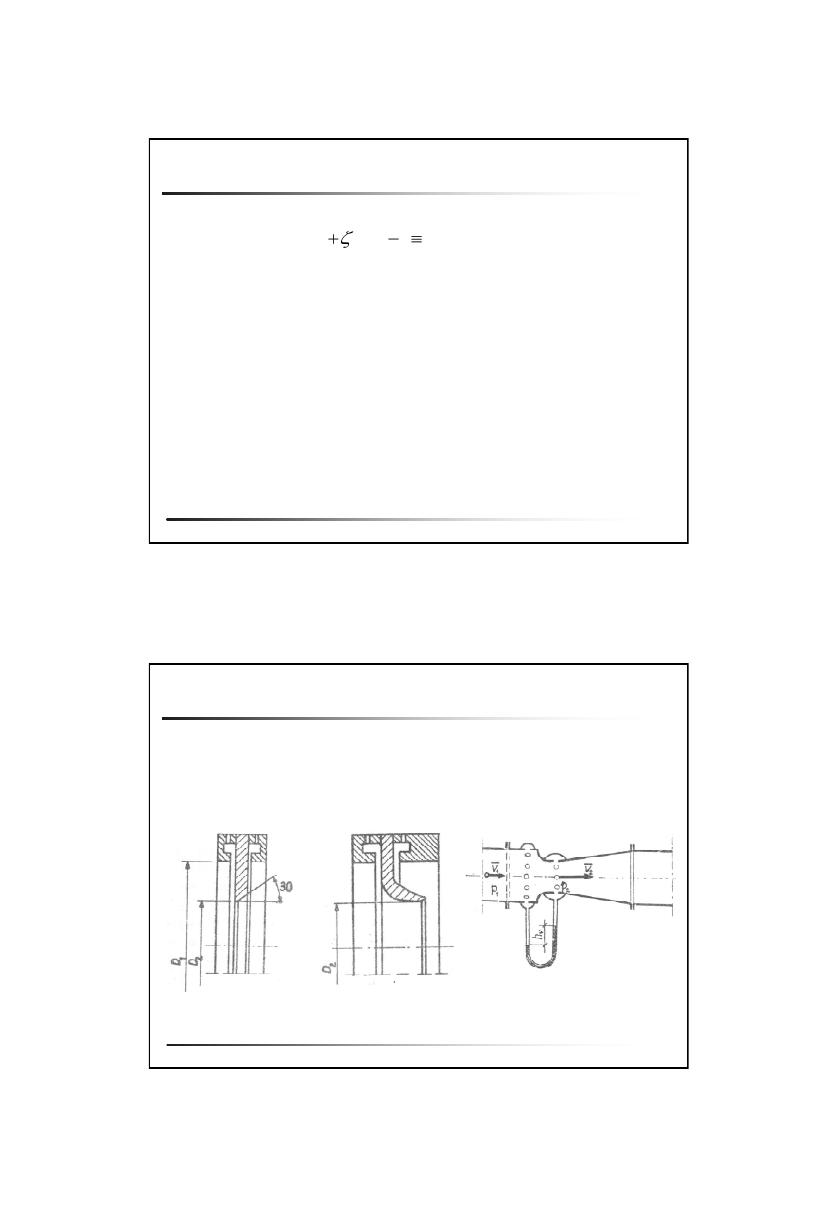
Metody pomiaru prędkości przepływu

Przepływomierze zwężkowe

s

h

z

p

g

v

z

p

g

v

2

2

2

2

2

1

1

1

2

1

2

2

)

(lokalnych

h

miejscowyc

strat

nik

wspólczyn

-

2

2

2

2

2

g

v

h

s

2

2

1

1

v

F

v

F

2

1

z

z

Wysokość prędkości

Wysokość ciśnienia

Metody pomiaru prędkości przepływu

Przepływomierze zwężkowe

Po przekształceniu:

1

]

1

)

1

[(

2

2

1

2

2

2

1

F

F

m

m

v

p

1

)

1

(

2

C

2

2

1

1

1

m

F

p

C

v

F

V

Q



Stąd

p

m

v

1

)

1

(

2

2

2

1

Strumień objętości przepływu:

9

Metody pomiaru prędkości przepływu

Przepływomierze zwężkowe

Wielkość:

1

)

1

(

2

2

k

m

Jest charakterystyczna dla danego przepływomierza

W zależności od sposobu realizacji przewężenia przepływomierze
można podzielić na:

•

kryzy

•

dysze

•

zwężki Venturiego

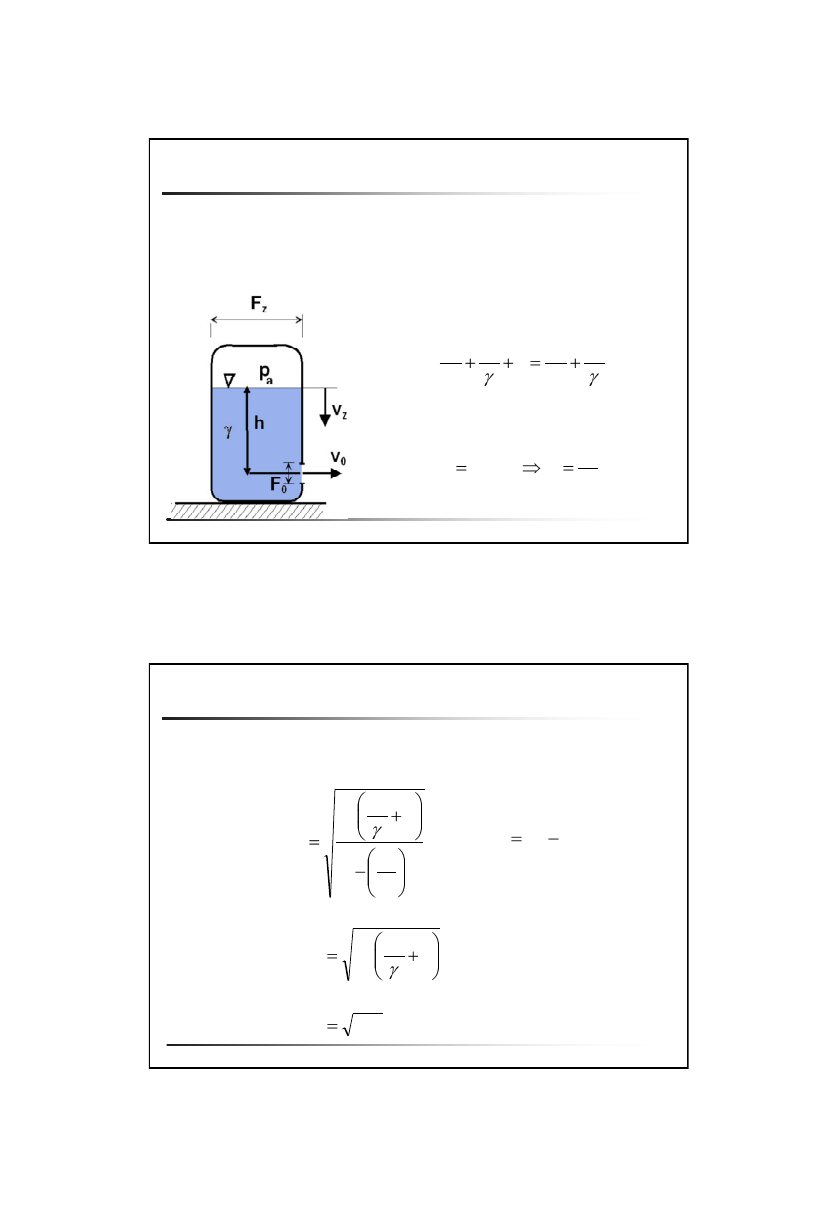
Metody pomiaru prędkości przepływu

Przepływomierze zwężkowe

Kryza

Zwężka Venturiego

Dysza

10

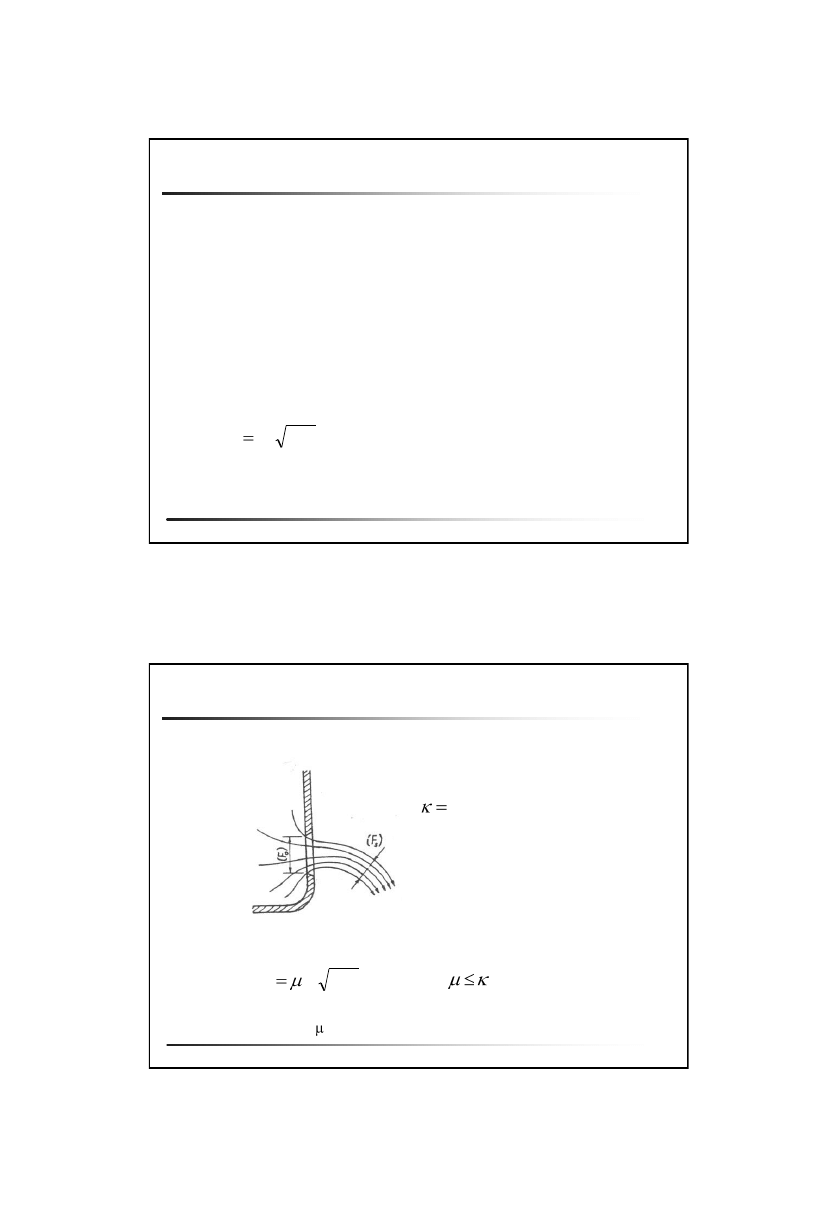
Wypływ cieczy ze zbiornika

Problem:
Wypływ przez mały otwór do atmosfery

Równanie Bernoulliego:

b

a

z

p

g

v

h

p

g

v

2

2

2

0

2

0

0

0

0

v

F

F

v

v

F

v

F

z

z

z

z

Równanie ciągłości:

Wypływ cieczy ze zbiornika

Prędkość wypływu:

2

0

0

1

2

z

n

F

F

h

p

g

v

b

a

n

p

p

p

Gdy F

0

/ F

z

<<1

h

p

g

v

n

2

0

Dla p

n

=0

gh

v

2

0

wzór Torricellego

11

Wypływ cieczy ze zbiornika

Wzór Torricellego stosujemy dla otworów małych tzn takich, że:



powierzchnia otworu jest mała w porównaniu z powierzchnią

zwierciadła cieczy,



gdy wymiar pionowy otworu jest mały w porównaniu z głębokością

zanurzenia

Przydatność do określania prędkości wypływu.

W przypadku określenia strumienia objętościowego:

gh

F

Q

2

0

błąd jest duży (wynosi ok. 40%).

Wypływ cieczy ze zbiornika

Zwężenie strugi (kontrakcja)

Ogólnie strumień objętościowy przez otwór określa się:

0

/ F

F

S

liczba kontrakcji

gh

F

Q

2

0

współczynnik przepływu

Dla otworu kołowego =0.59-0.64

12

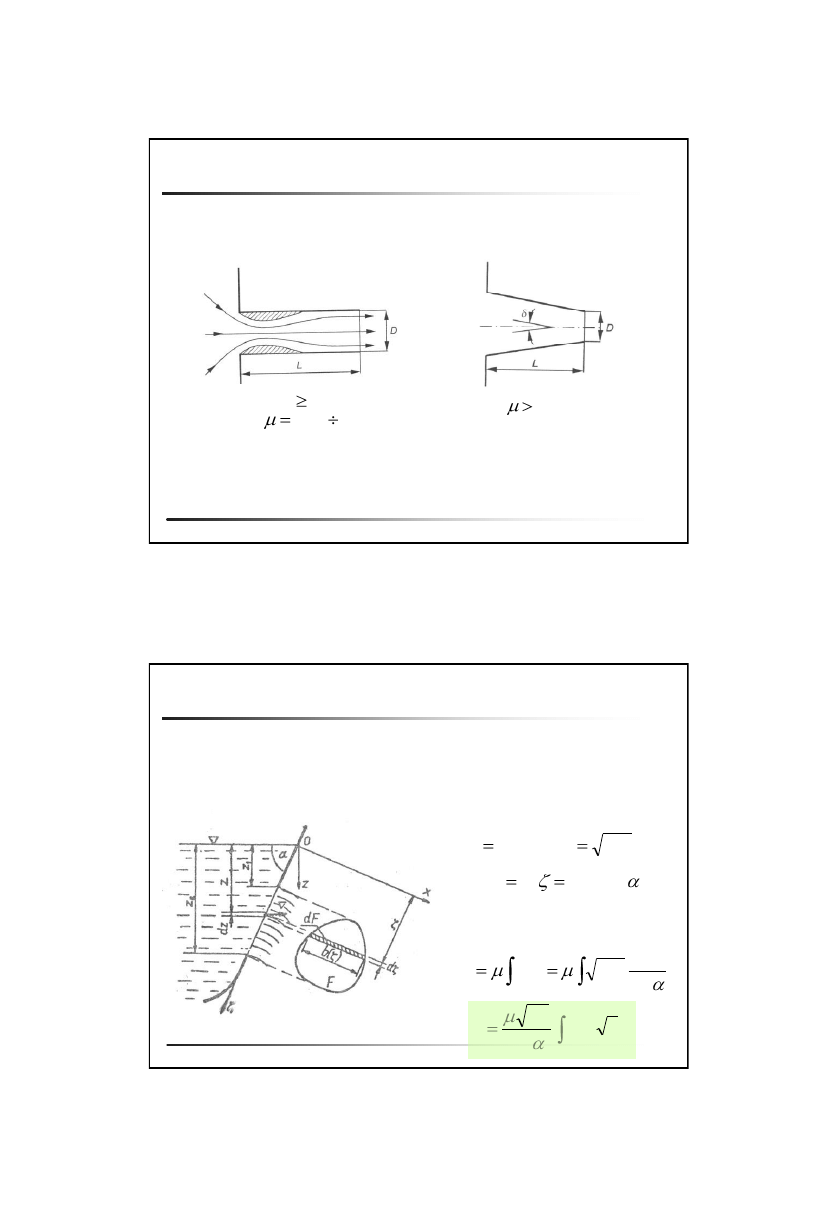
Wypływ cieczy ze zbiornika

Przystawki:

•

walcowe (wewnętrzne, zewnętrzne)

•

stożkowe (zbieżne, rozbieżne)

•

konoidalne

D

L

3

82

.

0

68

.

0

9

.

0

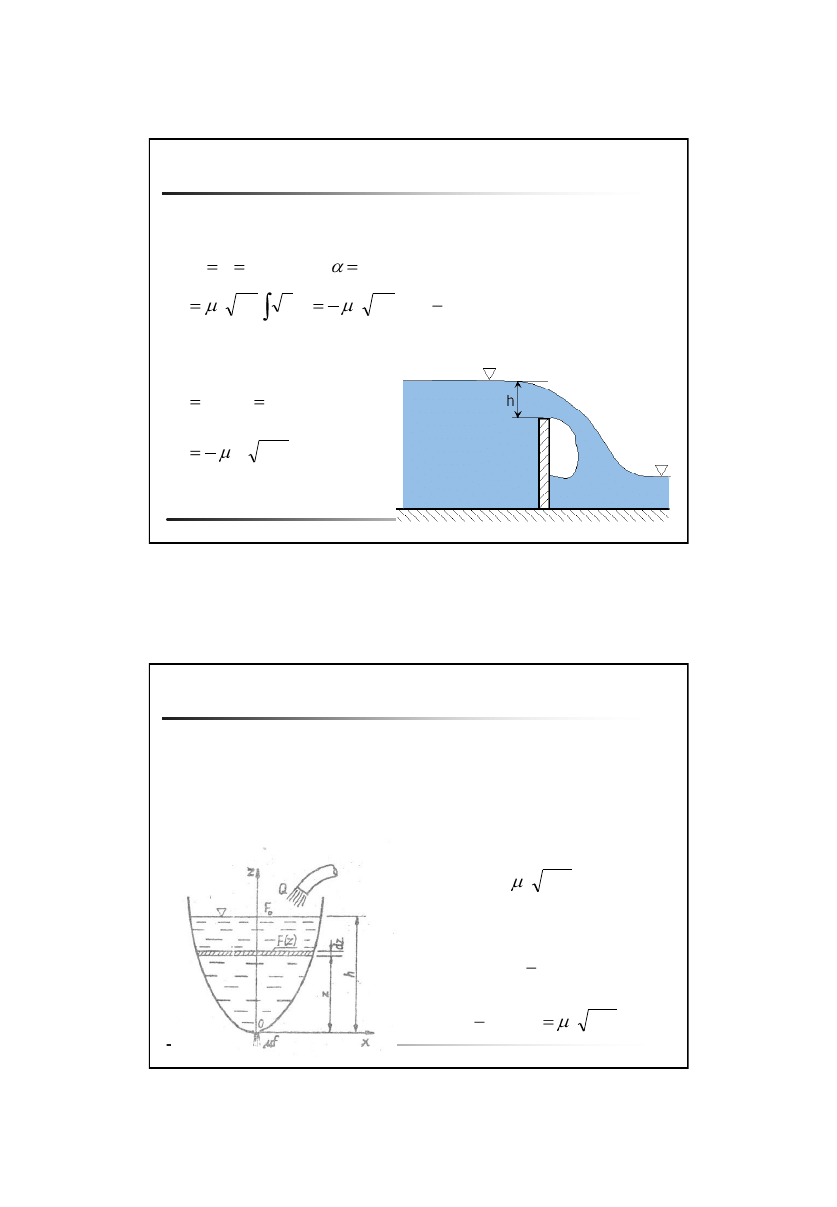
Wypływ cieczy przez duży otwór

Problem:
Określić strumień wypływu przez duży otwór do atmosfery (jego wymiar

jest tego samego rzędu co głębokość zanurzenia środka otworu)

vdF

dQ

gz

v

2

Strumień objętości wypływu z
uwzględnieniem kontrakcji:

sin

/

bdz

bd

dF

2

1

sin

)

(

2

z

z

F

dz

z

b

gz

vdF

Q

2

1

)

(

sin

2

z

z

dz

z

z

b

g

Q

13

Wypływ cieczy przez duży otwór

Otwór prostokątny w ścianie pionowej:

1

sin

,

)

(

const

b

z

b

)

(

2

3

2

2

2

/

3

1

2

/

3

2

2

1

z

z

g

b

dz

z

g

b

Q

z

z

h

z

z

2

1

,

0

gh

bh

Q

2

3

2

Przelew (prostokątny):

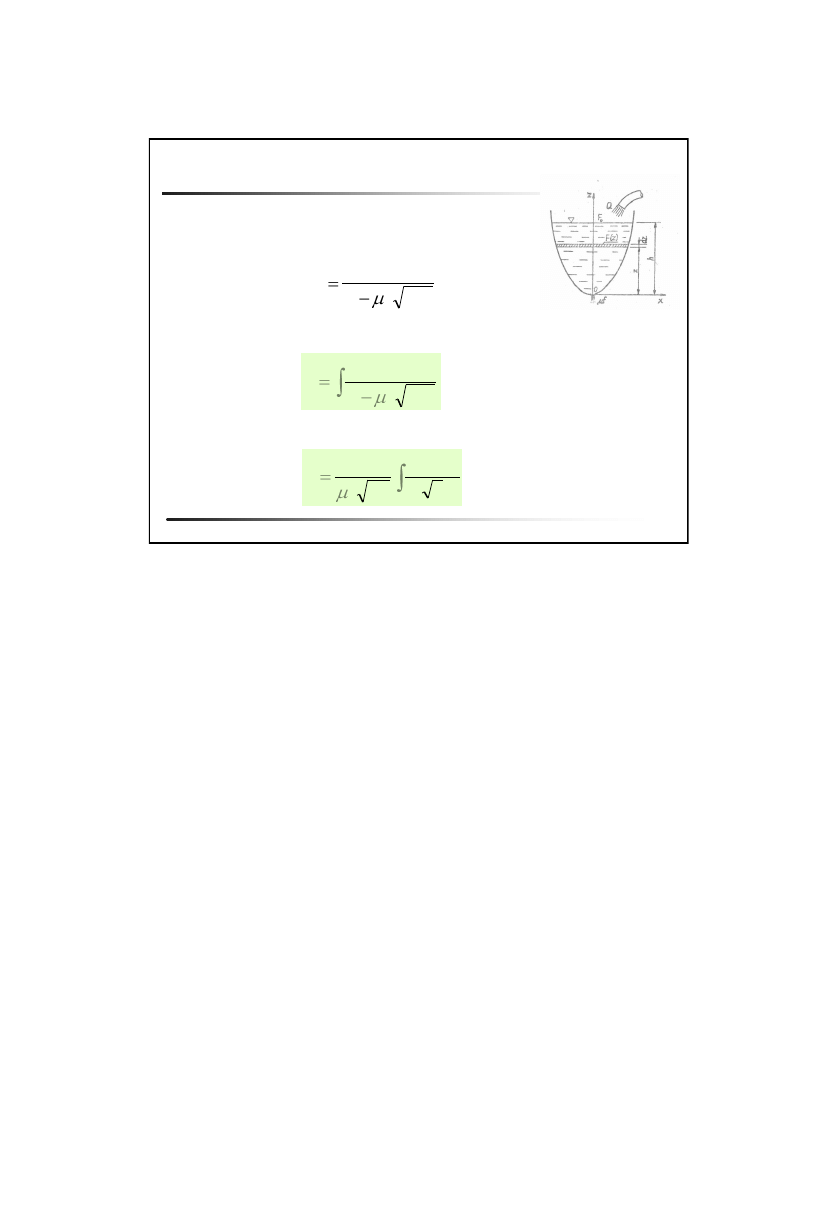
Czas opróżniania zbiornika

Problem:
Zasilany, otwarty zbiornik o zmiennym przekroju poziomym, napełniony

cieczą opróżniany jest przez mały otwór.Określić czas opróżniania

zbiornika.

dt

gz

f

2

W czasie dt

przez otwór przepływa ciecz

w ilości:

dz

z

F

Qdt

)

(

W czasie dt

zwierciadło obniża się o dz.

Ze zbiornika ubywa w czasie dt ciecz:

więc:

dt

gz

f

dz

z

F

Qdt

2

)

(

14

Czas opróżniania zbiornika

Po uporządkowaniu

Przy całkowitym opróżnianiu wysokość zmienia się od h do 0.

Jeżeli Q=0 to możemy zapisać:

gz

f

Q

dz

z

F

dt

2

)

(

0

0

2

)

(

h

gz

f

Q

dz

z

F

t

h

z

dz

z

F

g

f

t

0

0

)

(

2

1