Ćwiczenie 3
Temat:
BADANIE UKŁADÓW TRÓJFAZOWYCH
Z ODBIORNIKIEM POŁĄCZONYM
W GWIAZDĘ I TRÓJKĄT
I. ZAGADNIENIA
1.
Podstawowe właściwości, pojęcia i zależności dotyczące układów trój-
fazowych.
2.
Badanie rozkładu napięć, prądów i mocy układu trójfazowego symetrycz-
nego i niesymetrycznego odbiorników połączonych w gwiazdę i trójkąt.
II. WIADOMOŚCI PODSTAWOWE
Układem napięć (prądów) trójfazowych nazywamy skojarzenie trzech
napięć (prądów) tej samej częstotliwości i przesuniętych w fazie o pewien kąt.
Jeżeli amplitudy napięć (prądów) są równe, a przesunięcie fazowe wzajemne
wynosi 2/3 π , to taki układ trójfazowy nazywamy symetrycznym.
Symetryczny układ napięć trójfazowych sinusoidalnych zapisujemy nastę
pująco:
)
3
4
sin(
)
3
2
sin(
)
3
2
sin(
)
sin(
3
2
1
π
ω
π
ω
π
ω
ω
−
=
+
=
−
=
=
t
E
t
E
e
t
E
e
t
E
e
m
m
m
m
(3.1)
Przy założeniu, że źródłem zasilania jest symetryczny generator trój-
fazowy i że linia trójfazowa łącząca źródło z odbiornikiem jest również
symetryczna, o pracy układu trójfazowego decyduje rodzaj i charakter z2-
ążenia.
1. WŁASNOŚCI UKŁADU TRÓJFAZOWEGO Z GENERATOREM I OBIOR-
NIKIEM O FAZACH POŁĄCZONYCH W GWIAZDĘ
Jeżeli początki lub końce faz generatora (odbiornika) stanowią jeden punkt, to
otrzymuje się połączenie w gwiazdę. Punkt wspólny nazywamy punktem z2-
wym. Przewód łączący punkty zerowe źródła i odbiornika nazywamy przewo-
dem zerowym. Pozostałe przewody nazywamy przewodami fazowymi.
Układ trójfazowy mający przewód zerowy nazywamy układem trójfazowym s2-
zewodowym, natomiast układ mający tylko przewody fazowe nazywamy ukła-
dem trójfazowym trójprzewodowym.
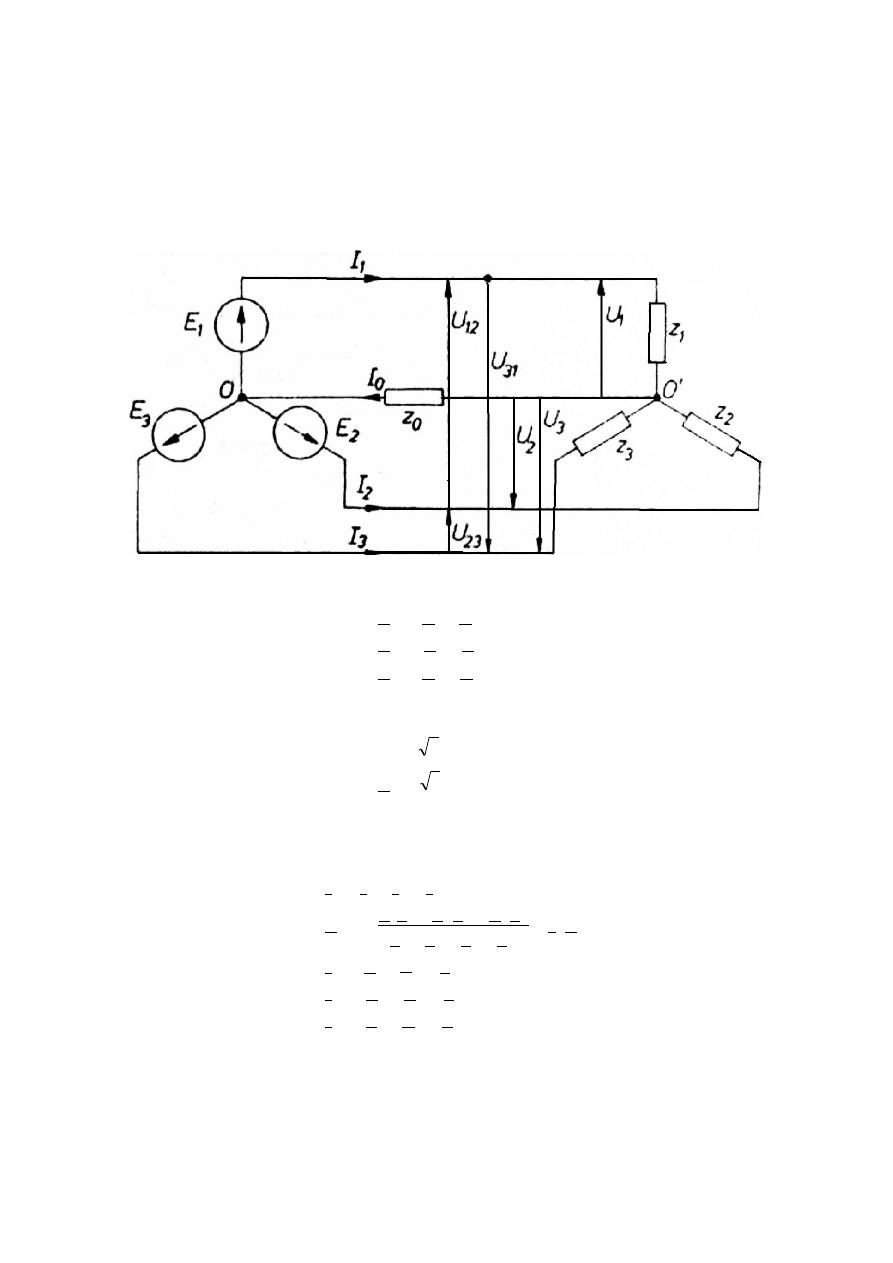
W układzie trójfazowym rozróżniamy: napięcia i prądy przewodowe, napięcia i
prądy fazowe, a w przypadku dołączenia w gwiazdę może wystąpić napięcie
między punktami zerowymi i prąd w przewodzie zerowym (rys. 3.1.):
Rys 3.1
1
3
31
3
2
23
2
1
12
U
U
U
U
U
U
U
U
U
−
=
−
=
−
=
(3.2)
W przypadku symetrycznego układu napięć spełniona jest następująca zależno-
ść:
0
,
3
,
3
0
30
0
=
=
=
I
e
U
U
U
U
j
f
P
f
P
(3.3)
Dla układu trójfazowego niesymetrycznego czteroprzewodowego otrzymujemy
zależności:
,
)
(
,
)
(
,
)
(
,
3
3
3
2
2
2
1
1
1
0
0
0
3
2
1
3
3
2
2
1
1
3
2
1
0
'
'
'
'
Y
U
E
I
Y
U
E
I
Y
U
E
I
Z
I
Y
Y
Y
Y
Y
E
Y
E
Y
E
U
I
I
I
I
O
O
O
O
O
O
O
O
−
=
−
=
−
=
=
+
+
+
+
+
=
+
+
=
(3.4)
W przypadku szczególnym niesymetria może być spowodowana przerwą fazy
obwodu lub zwarciem w obwodzie.
W układzie trójfazowym moc czynna, bierna i pozorna jest sumą mocy
poszczególnych faz i wynosi:
)
sin(
)
sin(
)
sin(
),
cos(
)
cos(
)
cos(
3
3
3
2
2
2
1
1
1
3
3
3
2
2
2
1
1
1
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
I
U
I
U
I
U
Q
I
U
I
U
I
U
P
+
+
=
+
+
=
(3.5a)
Dla obwodu symetrycznego:
),
sin(
3
),
cos(
3
)
cos(
3
f
p
p
f
p
p
f
f
f
I
U
Q
I
U
I
U
P
ϕ
ϕ
ϕ
=
=
=
(3.5b)
2.
WŁASNOŚCI UKŁADÓW TRÓJFAZOWYCH Z ODBIORNIKIEM
POŁĄCZONYM W TRÓJKĄT:
Połączenie generatora (odbiornika) w trójkąt powstaje przez połączenie kolejno
końca jednej fazy z początkiem następnej fazy. Układ taki może pracować tyl-
ko jako układ trójprzewodowy.
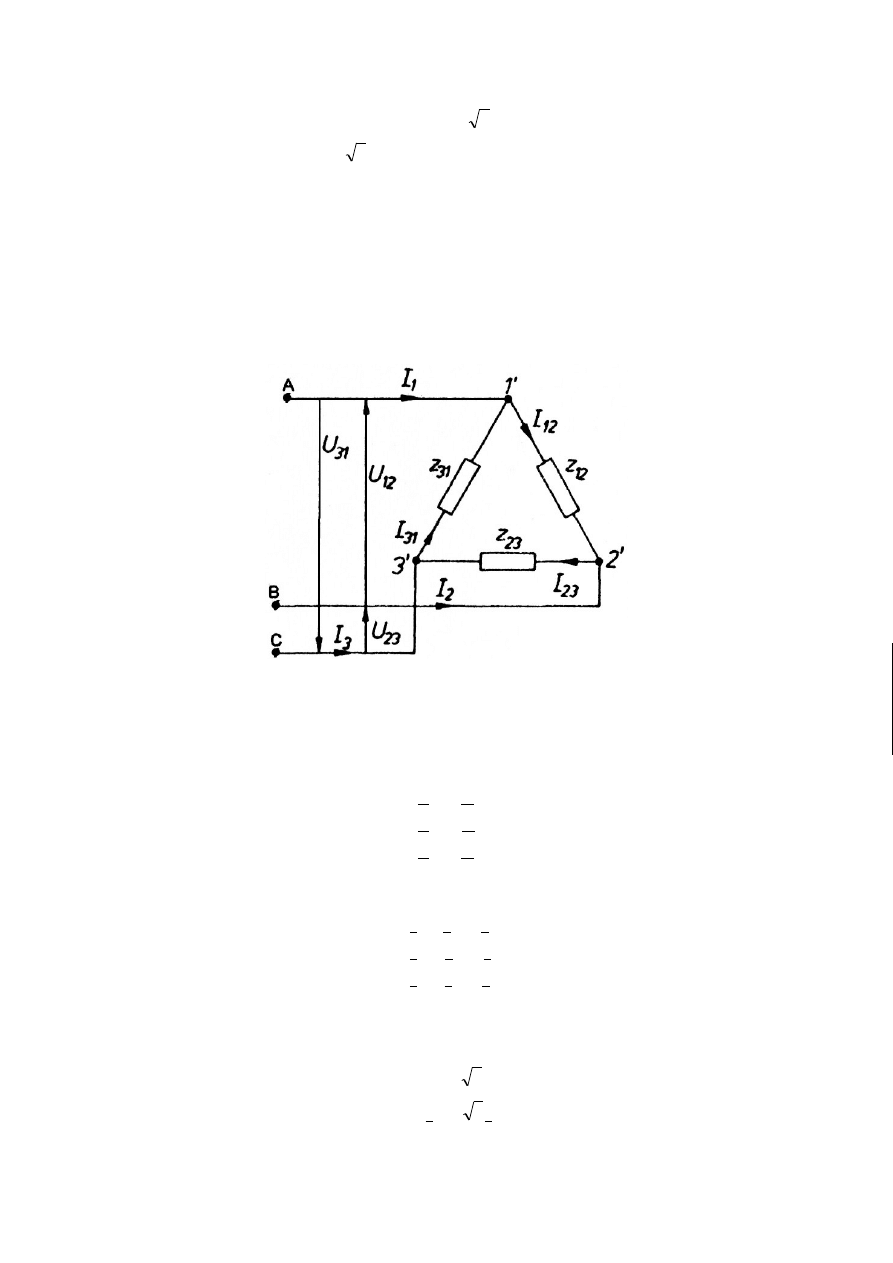
Rys 3.2
W układzie trójfazowym skojarzonym w trójkąt napięcia przewodowe są równe
napięciom fazowym (rys. 3.2.):
,
,
,
,
31
31
23
23
12
12
U
E
U
E
U
E
U
U
f
P
=
=
=
=
Prądy przewodowe związane są , zgodnie z prądowym prawem Kirchhoffa, z2-
żnościami:
,
,
,
23
31
3
12
23
2
31
12
1
I
I
I
I
I
I
I
I
I
−
=
−
=
−
=
(3.6)
W przypadku obwodu symetrycznego napięcia fazowe i prądy przewodowe są
przesunięte odpowiednio w fazie względem siebie o 2/3 π kąt a wartości
skuteczne odpowiednio równe:
,
3
,
3
0
30
j
f
P
f
P
e
I
I
I
I
−
=
=
(3.7)
Jeżeli układ trójfazowy skojarzony w trójkąt jest niesymetryczny, to w z2-
dku ogólnym prądy i napięcia poszczególnych faz są przesunięte w fazie
względem siebie o różne kąty, a ich wartości skuteczne są różne.
Prądy fazowe wyznacza się z zależności:
,
,
,
31
31
31
23
23
23
12
12
12
Z
U
I
Z
U
I
Z
U
I
=
=
=
(3.8)
Prądy przewodowe wyznacza się z wyrażeń (3.6).
Przy połączeniu odbiornika w trójkąt moc czynną w przypadku ogólnym
wyznacza się z zależności:
)
cos(
)
cos(
)
cos(
31
31
31
23
23
23
12
12
12
ϕ
ϕ
ϕ
I
U
I
U
I
U
P
+
+
=
(3.9)
W przypadku symetrii:
)
cos(
3
f
P
P
I
U
P
ϕ
=
(3.10)
Analogicznie moc bierna jest określona wyrażeniem:
)
sin(
3
)
sin(
)
sin(
)
sin(
31
31
31
23
23
23
12
12
12
f
P
P
I
U
Q
I
U
I
U
I
U
Q
ϕ
ϕ
ϕ
ϕ
=
+
+
=
(3.11)
III. Pomiary
1.
Badanie obwodu trójfazowego z odbiornikiem symetrycznym
połączonym w gwiazdę.
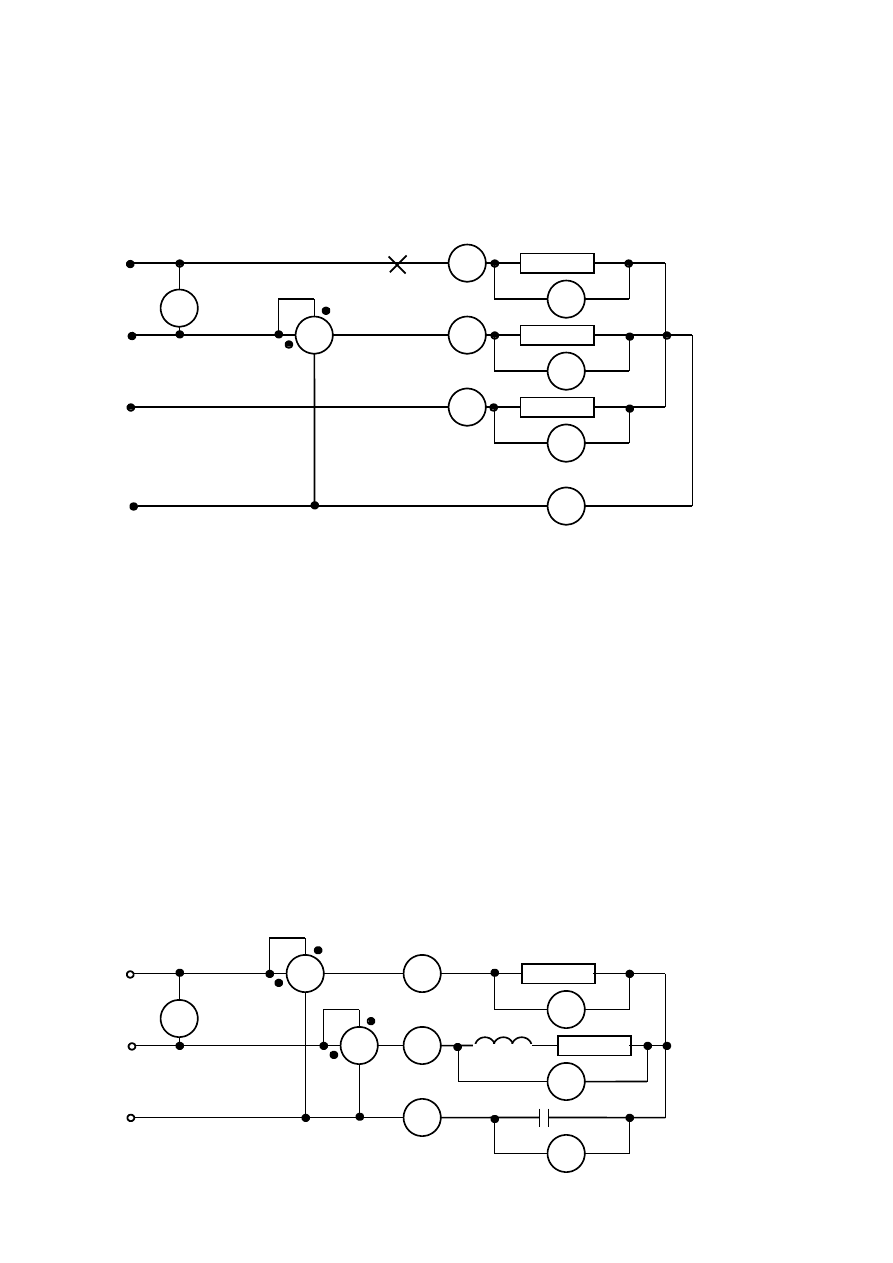
1.1 Układ symetrycznej i niesymetrycznej (w wyniku przerw) gwiazdy.
Schemat układu pomiarowego:
V
V
V
V
R
R
A
A
A
A
A
B
B
C
C
A
A
B
C
0
0
M
R
W
B
1.2 Przeprowadzić pomiary napięć fazowych i przewodowych, prądów z2-
dowych, prądu w przewodzie zerowym, mocy czynnej odbiornika za
pomocą trzech watomierzy.
1.3 Dokonać przerwy w pkt. M i wykonać pomiary wszystkich wielkości
wymienionych w pkt. 1.2.
1.4 Obliczyć teoretycznie prądy dla pkt.1.2 i1.3, przyjmując jako dane
wyjściowe napięcia zasilające i rezystancje odbiornika (które należy
dodatkowo zmierzyć).
1.5 Narysować w odpowiedniej skali pełne wykresy wektorowe.
2.
Badanie obwodu trójfazowego z odbiornikiem niesymetrycznym
połączonym w gwiazdę.
2.1 Schemat układu pomiarowego.
2.2 W układzie niesymetrycznej gwiazdy bez przewodu zerowego dokonać
pomiaru napięć przewodowych i fazowych, prądów przewodowych, mocy
czynnej odbiornika (metodą Arona).
V
V
V
V
L
R
R
W
W
A
A
A
A
B
C
A
B
C
1
2
L
C
R
L
C
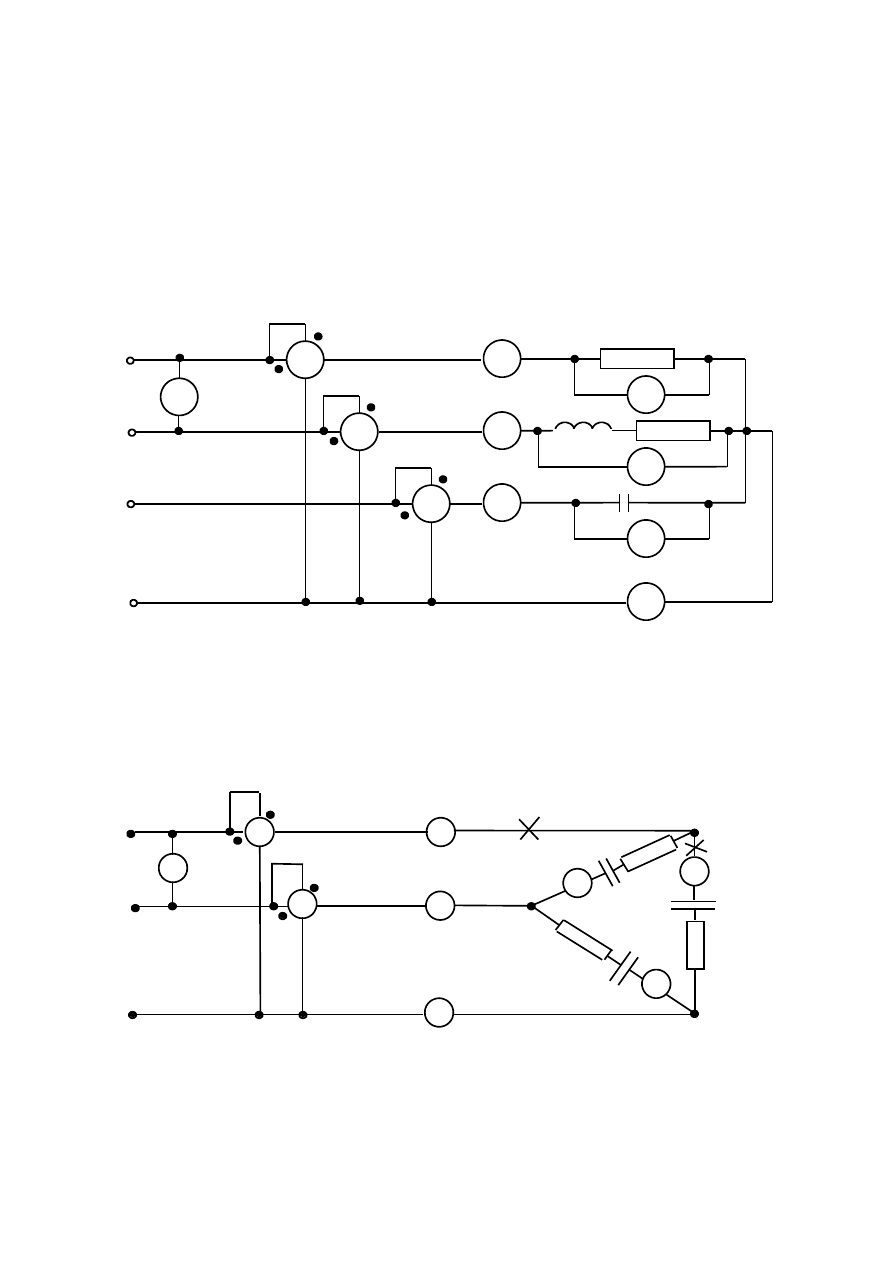
2.3 W układzie niesymetrycznej gwiazdy z przewodem zerowym dokonać
pomiaru napięć przewodowych i fazowych, prądów przewodowych i
prądu w przewodzie zerowym.
2.4 Wykonać teoretycznie obliczenia prądów przewodowych, mocy czynnej
i współczynnika mocy odbiornika przyjmując za dane wyjściowe napięcia
zasilające i impedancje odbiornika (wykonać odpowiednie pomiary impe-
dancji odbiornika).
2.5 Narysować w odpowiedniej skali pełne wykresy wektorowe.
2.6 Pomiary i obliczenia przeprowadzić tak jak dla układu 3-przewodowego.
V
V
V
V
L
R
R
W
W
A
A
A
A
B
C
A
B
C
0
1
2
L
C
A
0
R
L
C
W
2
UWAGA: w tym układzie nie można dokonywać pomiaru mocy metodą Arona.
3.
Badanie obwodu trójfazowego z odbiornikiem połączonym w trójkąt.
Układ symetrycznego i niesymetrycznego (w wyniku przerw) trójkąta.
3.1 Schemat układu pomiarowego.
W
W
1
2
A
C
A
B
A
A
A
A
A
R
R
R
C
C
C
M
N
V
A
B
C
2
1
3
3.2 Dokonać pomiaru napięć przewodowych, prądu przewodowego i fazo-
wego, mocy czynnej i biernej (metodą Arona).
3.3 Wykonać teoretycznie obliczenia prądów przewodowych, fazowych,
mocy czynnej, biernej, współczynnika mocy (dwukrotnie - raz na z2-
awie parametrów odbiornika, drugi raz na podstawie wskazań
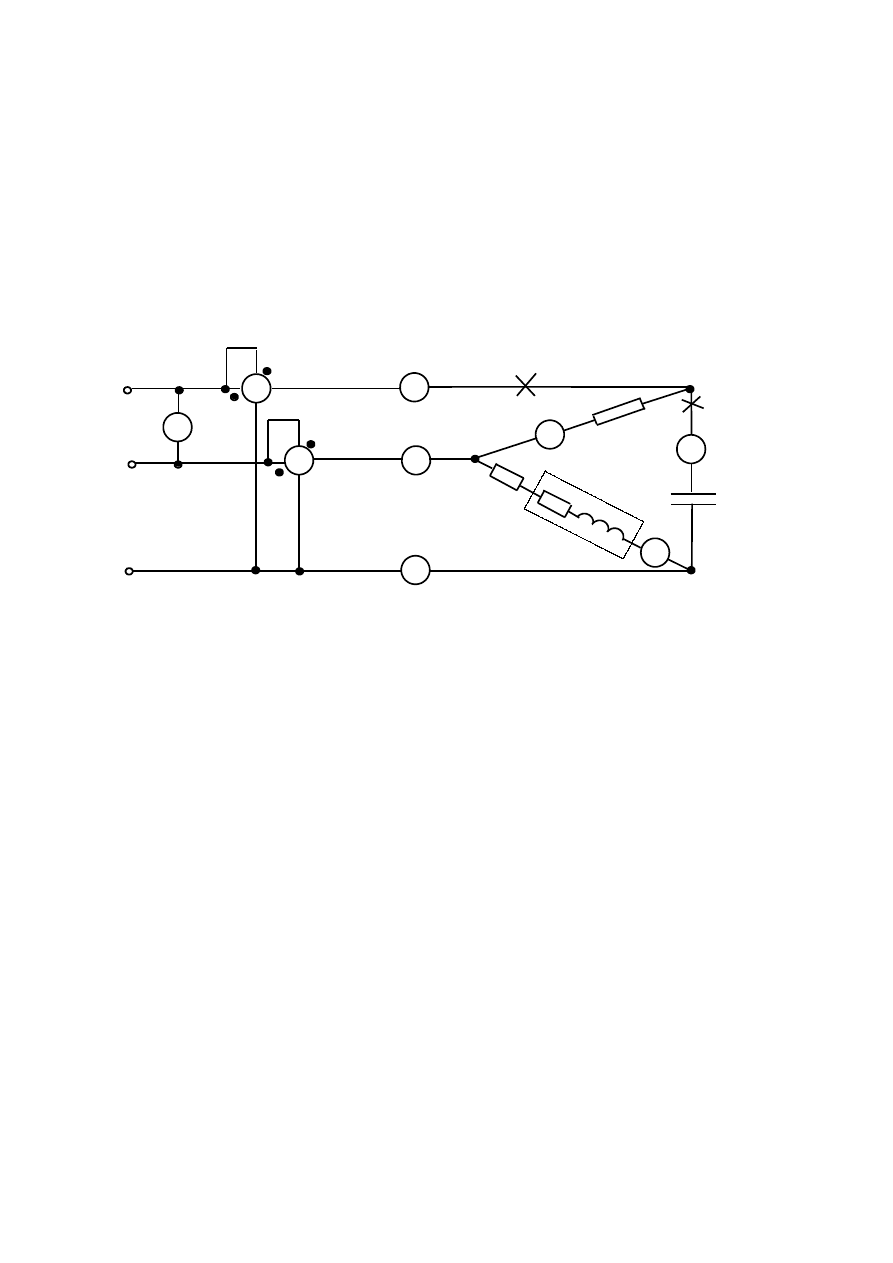
watomierzy) przyjmując jako dane napięcie zasilania i impedancje odbior-
nika.
3.4 Narysować w odpowiedniej skali pełne wykresy wektorowe.
3.5 Wykonać odpowiednie pomiary i obliczenia wg pkt. 3.2 i 3.3 gdy w
schemacie jak na rysunku wystąpi przerwa: a) w punkcie M, b) w punkcie
N. Zwrócić uwagę na poprawność pomiaru mocy biernej, obliczenie
współczynnika mocy na podstawie wskazań watomierzy.
4.
Układ trójkąta niesymetrycznego.
4.1 Schemat układu pomiarowego:
W
W
1
2
B
A
A
A
C
A
A
A
A
R
C
M
N
V
L
R
A
B
C
3
1
2
R
L
4.2 Wykonać pomiary i obliczenia dla układu przedstawionego na rysunku wg
pkt. 3.2-3.5 z odpowiednim uwzględnieniem uwag wymienionych
w pkt.3.5.