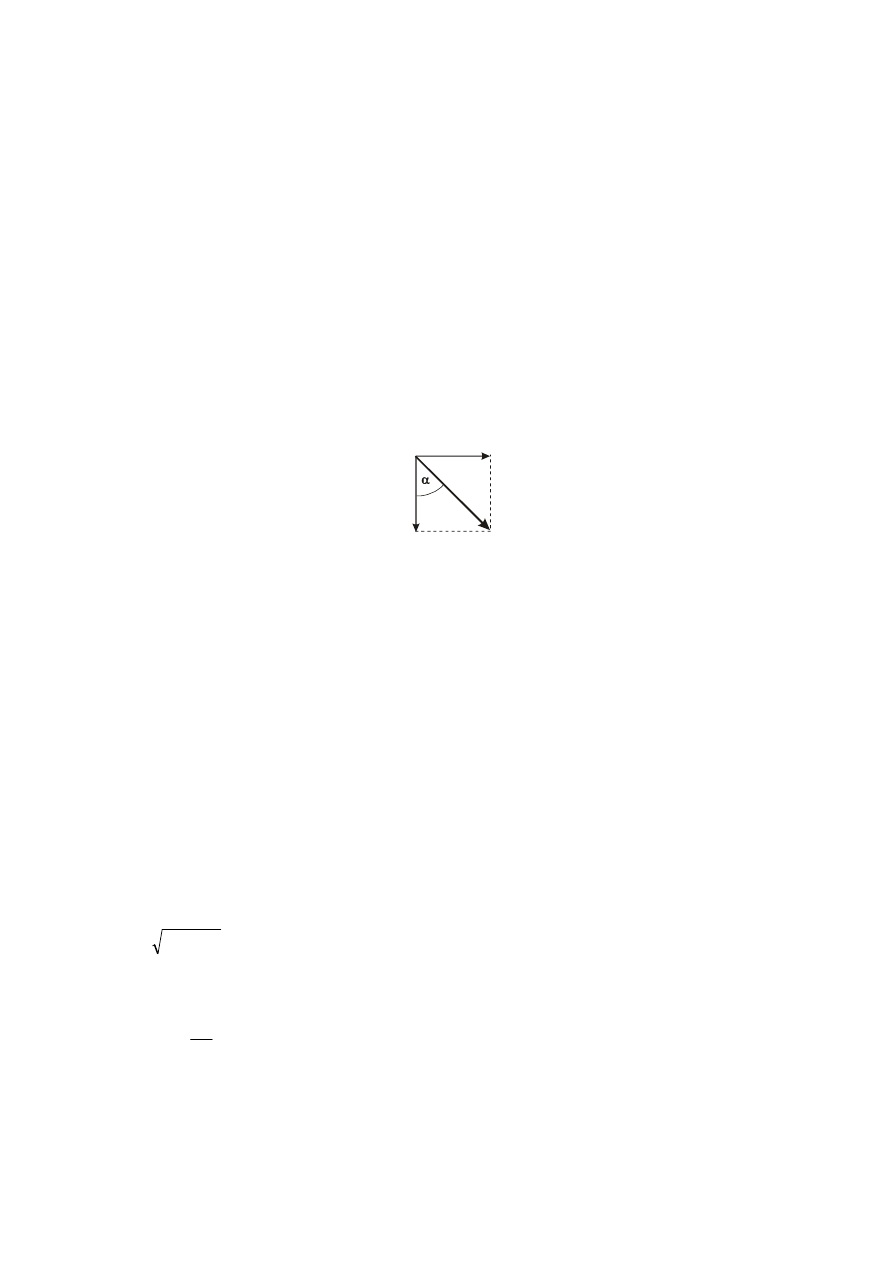
I.

HYDROSTATYKA-C.D.

I.1.

PARCIE NA ŚCIANY ZAKRZYWIONE

I.1.1.

Obliczenie wartości siły parcia

Elementarne powierzchnie d

A

tworzące rozpatrywaną powierzchnię krzywą mają różną orientację w

przestrzeni. Prostopadłe do nich, elementarne parcia d

P

i

nie są więc do siebie równoległe. Dlatego

wartość wypadkowej siły parcia P nie może być obliczona jako algebraiczna suma wartości
elementarnych sił.

Zatem siłę parcia całkowitego można rozłożyć na dwie składowe: pionową

P

V

i poziomą

P

H

.

P

P

H

P

V

Składowa pozioma parcia

P

H

Obliczenia wartości tej składowej parcia jest praktycznie obliczeniem wartości siły parcia na rzut
rozpatrywanej ściany na pionową ścianę (czyli na ścianę płaską), do jej obliczeń stosuje się metody
omówione w rozdziale I.2:

–

metodę graficzno – analityczną,

–

analityczną.

Składowa pozioma parcia jest prostopadła do rzutu rozpatrywanej powierzchni i działa zawsze od cieczy
w kierunku ściany.

Składowa pionowa parcia

P

V

Aby obliczyć wartość tej składowej, skorzystać można jedynie z metody graficzno-analitycznej
postępując następująco:

♦

wykonać prostokątny rzut ściany zakrzywionej na powierzchnię zwierciadła cieczy,

♦

dla tego rzutu skonstruować bryłę składowej pionowej parcia (bryła jest ograniczona: powierzchnią
ściany, zwierciadłem cieczy i tworzącymi pionowymi),

♦

obliczyć ciężar bryły parcia:

γ

⋅

=

V

V

V

P

.

Wektor

P

V

jest prostopadły do powierzchni zwierciadła cieczy i zwrócony jest: do góry (jeżeli ściana

znajduje się nad cieczą), a ku dołowi gdy ciecz jest nad ścianą na którą parcie liczymy.

Wartość całkowitej siły parcia

P

działającego na powierzchnię krzywą obliczyć można zatem jako:

2

2

V

H

P

P

P

+

=

Kierunek działania siły

P

jest zawsze prostopadły do powierzchni, a jej kąt nachylenia do poziomu

obliczyć można następująco:

H

V

P

P

arctg

=

α

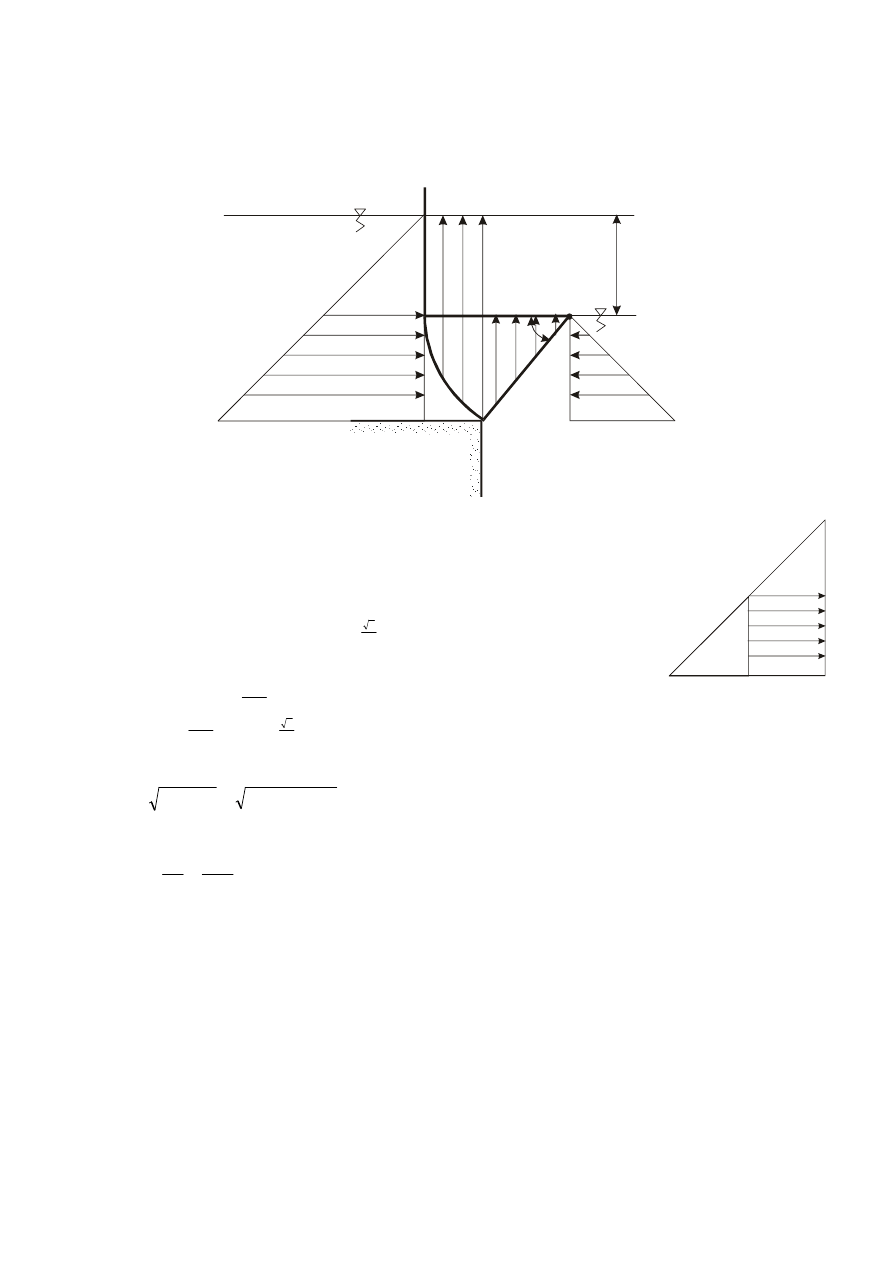
PRZYKŁAD I-1

Obliczyć wartość siły parcia na ścianę AB będącą ćwiartką walca o promieniu podstawy

R

i wysokości

b

Dane:

R, b,

γ

Szukane:

P

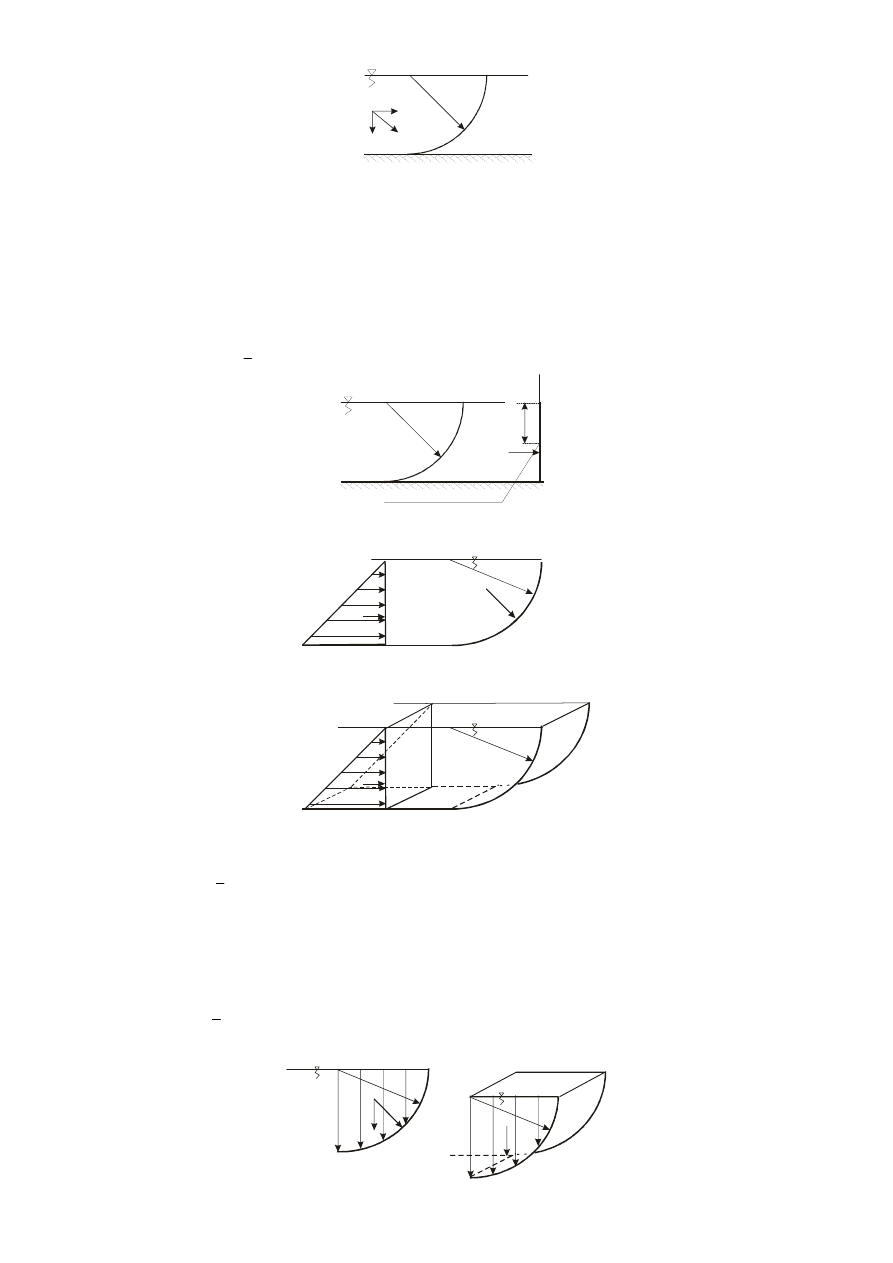
1

R

A

B

P

P

V

P

H

Rozw.:

Wypadkowe parcie

P

na ścianę AB należy rozłożyć na składowe:

P

H

i

P

V

.

1.

Składowa pozioma parcia

P

H

Wartość tej składowej obliczyć można dwoma metodami.

a)

metoda analityczna

A

z

P

S

H

⋅

⋅

=

γ

,

gdzie

A

jest powierzchnią ściany, a

z

S

- zagłębieniem środka ciężkości rzutu rozpatrywanej ściany na

dowolną powierzchnię pionową pod powierzchnią zwierciadła cieczy.

γ

γ

⋅

⋅

=

⋅

⋅

=

b

R

A

z

P

S

H

2

2

1

R

A

B

A'

B'

P

H

A'B' jest rzutem ściany AB

z

S

b) metoda graficzno – analityczna

.

R

R

b

Wykres składowej poziomej

parcia na na ćwiartkę walca

Bryła składowej poziomej

parcia na na ćwiartkę walca

R

R

b

R

R

P

P

H

P

H

Bryła parcia będzie graniastosłupem o wysokości

b

i podstawie będącej trójkątem równoramiennym o

boku

R

(rys. I-58).

γ

γ

b

R

V

P

H

H

2

2

1

=

⋅

=

2.

Składowa pionowa parcia

P

V

Bryła parcia składowej pionowej parcia jest ograniczona: ścianą, jej rzutem na powierzchnię zwierciadła
cieczy i płaszczyznami pionowymi, a zatem jest ćwiartką walca o promieniu

R

i wysokości

b

(rys I-59),

zatem wartość

P

V

wynosi:

γ

π

γ

b

R

V

P

V

V

2

4

1

=

⋅

=

Wykres składowej pionowej

parcia na ćwiartkę walca

R

P

P

V

Bryła składowej pionowej

parcia na na ćwiartkę walca

R

b

P

V

2

PRZYKŁAD I-2

Obliczyć parcie na segmentowe zamknięcie jazu. Szerokość segmentu wynosi

b

promień

R

, a kąt

pomiędzy ryglami

α

. Oś obrotu znajduje się na poziomie zwierciadła wody górnej.

Dane:

R

= 8 m

, b

= 6 m,

α

= 30

o

Szukane:

P

R

O

A

B

P

P

V

P

H

H

=

R

s

in

Rozw.:

1.

Składowa pozioma parcia

P

H

a) metoda analityczna

R

O

A

B

A'

B'

P

H

A'B' jest rzutem ściany AB

z

S

(

)

k

471

81

9

6

8

2

2

1

2

1

2

2

1

2

3

2

=

⋅

⋅

=

=

=

⋅

⋅

=

,

)

(

b

sin

R

b

H

A

z

P

S

H

γ

α

γ

γ

b)

graficzno - analityczna

Należy utworzyć bryłę składowej poziomej parcia, a następnie obliczyć jej ciężar:

kN

471

81

9

6

8

4

1

2

2

1

2

2

2

1

=

⋅

=

⋅

=

⋅

=

,

b

sin

R

V

P

H

H

γ

α

γ

H

H

H

b

H

Wykres składowej poziomej

parcia na segment

Bryła składowej poziomej

parcia na segment

2.

Składowa pionowa parcia

P

V

Na podstawie opisanej wcześniej metody, wyodrębnić należy bryłę składowej pionowej parcia, a
następnie obliczyć jej ciężar.

R

O

R

O

Wykres składowej pionowej

parcia na segment

Bryła składowej pionowej

parcia na segment

R

si

n

Rcos

(

)

(

)

kN

170

81

9

6

8

8

8

2

3

2

1

2

1

360

30

2

2

1

360

2

=

⋅

⋅

⋅

−

=

⋅

⋅

−

=

−

=

⋅

=

,

b

cos

R

sin

R

R

V

V

V

P

O

O

O

wyc

V

V

π

γ

α

α

π

γ

α

∆

Wektor całkowitego parcia ma długość:

kN

500

170

471

2

2

2

2

≅

+

=

+

=

V

H

P

P

P

i jest nachylony do poziomu pod kątem

o

70

77

2

170

471

=

⇒

=

=

=

α

α

,

P

P

tg

V

H

3

I.1.2.

Redukcja wykresów parcia

W celu skrócenia obliczeń, w przypadku, gdy na ścianę działa tylko jedna ciecz, wykresy parcia można
redukować. Na poniższych rysunkach przedstawiono kilka przykładów redukcji wykresów parcia
(poziomego i pionowego) na ścianę w kształcie fragmentu walca w przypadku, gdy:

a)

ciecz działa tylko od jednej strony ściany,

b)

na ścianę działa ciecz z obu jej stron.

a)

ciecz działa na ścianę tylko z jednej strony

P

H

P

V

P

woda po prawej stronie ćwiartki walca

woda po lewej stronie ćwiartki walca

P

H

P

V

P

P

H

P

V

P

woda po prawej stronie połówki walca

przed redukcją

po redukcji

P

H

P

V

P

woda po lewej stronie połówki walca

przed redukcją

po redukcji

Q

F

zwierciadło zastępcze

po redukcji wykresów

składowej pionowej parcia

ostateczna postać wykresu

składowej pionowej parcia

P

V

b) ciecz działa na ścianę w kształcie połówki walca z dwóch jego stron

wykresy parcia – przed redukcją

P

H

P

V

P

P

H

P

V

P

wykresy parcia – po redukcji

P

H

P

V

P

4

PRZYKŁAD I-3

Obliczyć parcie cieczy na segment będący wycinkiem walca o długości

L

i promieniu podstawy

r

.

Dane:

H

= 2 m

, r

= 5 m,

b

= 6 m,

α

= 45

o

Szukane

:

P

r

α

O

H

γ

γ

H

H+r sin

α

r sin

α

Rozw.:

1.

Składowa pozioma parcia

P

H

Ponieważ na segment działa tylko jedna ciecz, można dokonać redukcji
wykresów składowej poziomej parcia.

( )

kN

4

,

47

81

,

9

6

5

2

sin

2

2

2

=

⋅

⋅

⋅

⋅

=

⋅

=

⋅

=

γ

α

γ

b

HR

V

P

H

H

2.

Składowa pionowa parcia P

V

(

)

(

)

(

)

(

)

kN

5

,

76

81

,

9

6

5

5

2

5

cos

2

2

360

45

2

360

2

=

⋅

⋅

−

−

=

⋅

−

+

=

⋅

=

O

O

O

b

R

R

H

R

V

P

V

V

π

γ

α

π

γ

α

Wektor całkowitego parcia ma długość:

kN

90

4

,

47

5

,

76

2

2

2

2

≅

+

=

+

=

V

H

P

P

P

i jest nachylony do poziomu pod kątem

o

58

6

,

1

4

,

47

5

,

76

=

⇒

=

=

=

α

α

V

H

P

P

tg

H

r sin

r

si

n

5

I.1.3.

Rozwiązywanie zadań z wykorzystaniem równowagi sił

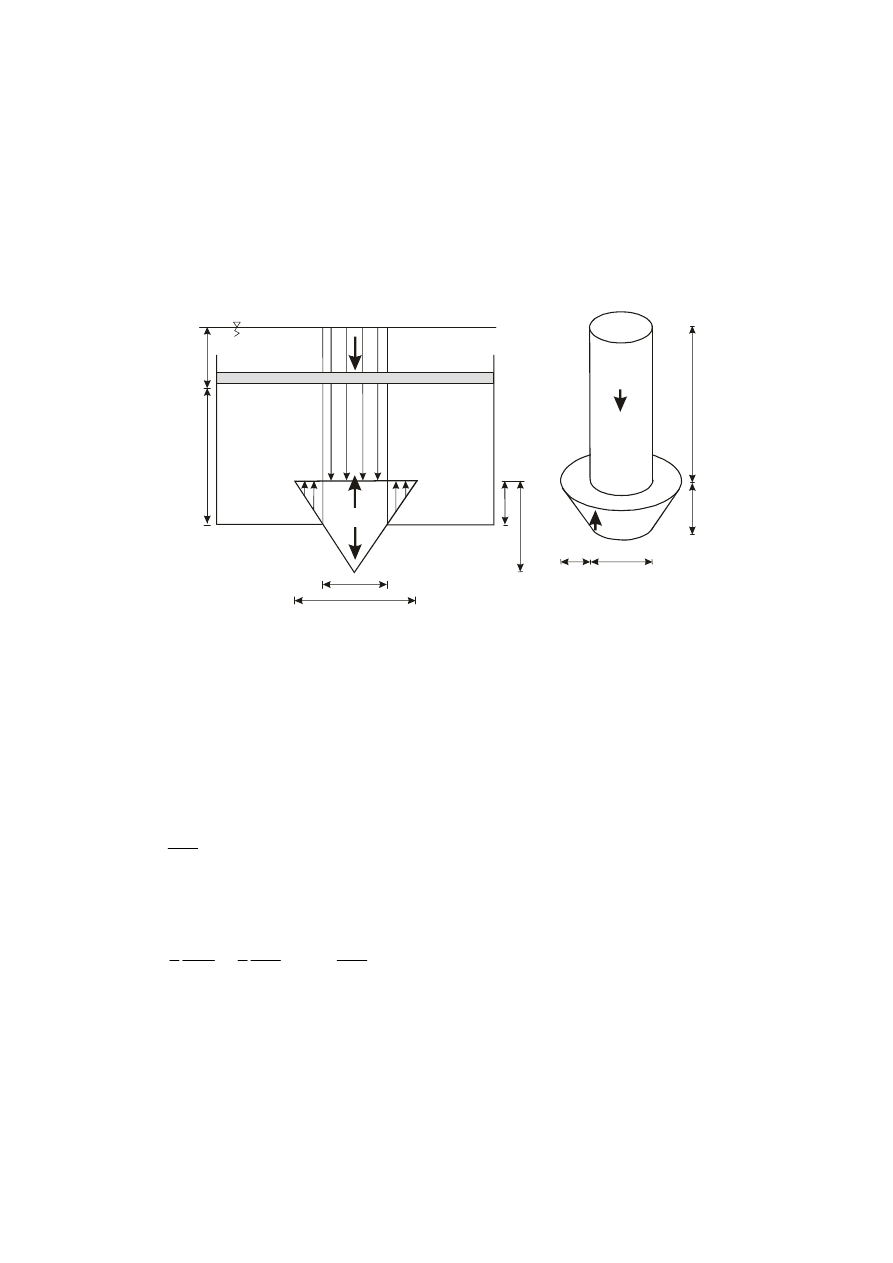
PRZYKŁAD I-4

Otwór o średnicy

d

w dnie zbiornika zamykany jest stożkiem o ciężarze

G

. Zbiornik jest wypełniony

cieczą do wysokości

H

, przy czym zwierciadło cieczy spoczywa szczelny tłok powierzchni

F

, obciążony

siłą

Q

. Obliczyć siłę

N

potrzebną do wyciągnięcia stożka z otworu.

Dane:

G, Q, F, D, d, H, t, γ

Szukane:

N

zwierciadło zastępcze

x =

Q/(F )

γ

H

N=?

G

Q

P

V1

P

V2

(D-d)/2

d

H-h+x

h

h

t

d
D

Rozw.:

Aby uwzględnić działanie tłoka, należy zamienić jego działanie na działanie warstwy cieczy o takim
samym ciężarze jak ciecz w zbiorniku i wysokości

x

=

Q

/(

F

—

γ

) ponad rzeczywistym zwierciadłem cieczy.

Aby zawór wyciągnąć, wartość szukanej siły

N

musi być większa od wartości sumy sił:

–

wypadkowego parcia (w tym przypadku parcie poziome redukuje się, a zatem uwzględniamy

jedynie składową pionową parcia

P

V

1

–

P

V

2

),

–

ciężaru

G

.

Warunek równowagi stożka ma zatem postać:

N

=

G

+

P

V

1

–

P

V

2

.

Bryła parcia siły

P

V

1

(patrz rys. I-72) jest walcem o wysokości (

H

–

h

+

x

):

(

)

γ

π















+

−

=

x

h

H

d

P

V

4

2

1

Bryła parcia siły

P

V

2

(patrz rys. I-72) jest częścią wspólną ściętego stożka o wysokości

h

i walca o

wysokości

h

:

(

)

γ

π

π

π















−

−

−

=

h

d

h

t

d

t

D

P

V

4

4

3

1

4

3

1

2

2

2

2

6

I.1.4.

Rozwiązywanie zadań w przypadku, gdy na daną ścianę

działają ciecze o różnych ciężarach właściwych

PRZYKŁAD I-5

Obliczyć parcie na połówkę walca znajdującego się w ścianie zbiornika wypełnionego dwoma cieczami
(rys. I-76).

Dane:

γ

1

,

γ

2

, h, R, b

Szukane:

P

γ

1

γ

2

Połówka walca
o wysokości b
i promieniu
podstawy R

h

x

zwierciadło zastępcze

P

VG

P

VD

P

HG

P

HD

Rozw.:

1.

Parcie na górną część (ćwiartkę) walca pochodzi tylko od cieczy o ciężarze właściwym

γ

1

:

(

)

1

γ

Rb

h

R

h

P

HG

+

−

=

(

)

1

2

4

1

γ

π

b

R

Rh

P

VG

−

=

2.

Parcie

na

dolną

część

(ćwiartkę)

walca

pochodzi

zarówno

od

cieczy

o ciężarze właściwym

γ

1

, jak i

γ

2.

Aby uwzglednić działanie górnej cieczy należy zamienić działanie

warstwy cieczy o

γ

1

, na działanie warstwy cieczy o

γ

2

, czyli utworzyć zwierciadło zastępcze na

wysokości

x

:

x

h

2

1

γ

γ

=

(

)

2

γ

Rb

R

x

x

P

HD

+

+

=

1

2

2

1

γ

π

b

R

P

VD

=

Parcie całkowite wynosi:

(

) (

)

2

2

VD

VG

VD

HG

P

P

P

P

P

−

+

+

=

7

I.1.5.

Wypór

Wypór jest to wypadkowe parcie cieczy działającej na ciało zanurzone częściowo lub całkowicie (czyli
skierowaną ku górze składową pionową parcia).

PRZYKŁAD I-6

Kula o ciężarze objętościowym

γ

K

pływa w cieczy. Obliczyć ciężar objętościowy

cieczy, przy którym zanurzy się ona tylko do połowy swej objętości.

Dane:

γ

K

= 7 kN/m

3

Szukane:

γ

C

Rozw.:

Ciężar kuli:

K

K

R

V

G

γ

π

γ

⋅

=

⋅

=

3

3

4

Wypór:

C

C

R

V

W

γ

π

γ

⋅

=

⋅

=

3

3

4

2

1

2

Kula będzie pływać w cieczy, gdy jej ciężar będzie zrównowarzony przez wypór, czyli:

G

=

W

, a zatem:

3

3

3

4

2

1

3

3

4

kN/m

14

2

=

⋅

=

⇒

⋅

=

⋅

K

C

C

K

R

R

γ

γ

γ

π

γ

π

PRZYKŁAD I-7

Określić najmniejszą powierzchnię kry lodowej o średniej grubości

h

, zdolnej utrzymać bałwanka o masie

m

. Gęstość lodu wynosi 0,92 g/cm

3

.

Dane:

h

= 0,5 m,

m

= 70 kg,

ρ

L

= 0,92 g/cm

3

Szukane:

F

h

x

Rozw.:

Warunek równowagi:

W = G

L

+G

czł

,

gdzie:

wypór:

W

x

F

W

γ

⋅

⋅

=

ciężar lodu:

L

L

h

F

G

γ

⋅

⋅

=

ciężar bałwanka:

g

m

G

czl

⋅

=

Przyjmując, że bałwanek zacznie tonąć, gdy kra całkowicie się zanurzy, czyli

h = x

otrzymujemy:

g

m

h

F

h

F

L

W

⋅

+

⋅

⋅

=

⋅

⋅

γ

γ

Skąd:

(

)

(

)

2

m

75

,

1

81

,

9

920

1000

5

,

0

81

,

9

70

=

⋅

−

⋅

⋅

==

−

⋅

⋅

=

g

h

g

m

F

L

W

ρ

ρ

K

W

8

PRZYKŁAD I-8

W którym położeniu (pionowym czy poziomym) dębowa bela w kształcie prostopadłościanu o wymiarach

a

×

a

×

b

zanurzy się głębiej?

Dane:

a

= 0,5 m,

b

= 2 m,

ρ

dębu

= 700 kg/m

3

Szukane:

x, y

x

a

b

a

b

y

Rozw.:

Ciężar beli:

kN

72

,

1

81

,

9

700

2

5

,

0

2

2

=

⋅

⋅

⋅

=

⋅

⋅

⋅

=

g

b

a

G

debu

ρ

Wypór w położeniu pionowym (rys. I-82):

]

kN

[

45

,

2

81

,

9

5

,

0

2

2

1

x

x

x

a

W

W

⋅

=

⋅

⋅

=

⋅

⋅

=

γ

Warunek równowagi:

W

1

=

G

m

0,70

kN

72

,

1

45

,

2

=

⇒

=

⋅

x

x

Wypór w położeniu poziomym (rys. I-82):

kN]

[

81

,

9

81

,

9

2

5

,

0

2

y

y

y

b

a

W

W

⋅

=

⋅

⋅

⋅

=

⋅

⋅

⋅

=

γ

Warunek równowagi:

W

2

=

G

m

0,18

kN

72

,

1

81

,

9

=

⇒

=

⋅

x

y

Bela zanurzy się głębiej gdy jest ustawiona pionowo o:

cm

52

,

0

=

−

y

x

.

9

II.

HYDRAULIKA

RUROCIĄGÓW

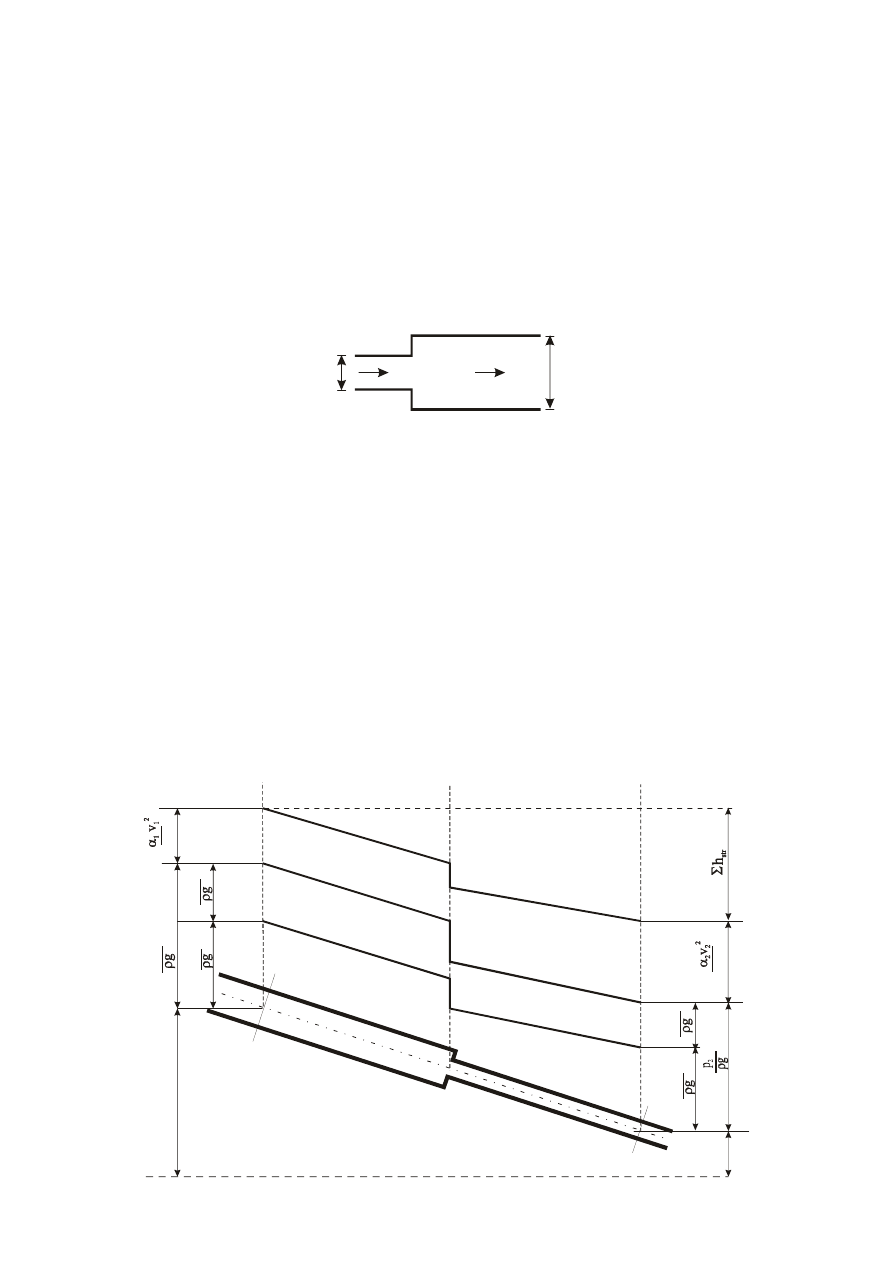
10

W zamkniętych przewodach całkowicie wypełnionych cieczą, ruch cieczy odbywa się dzięki różnicy
ciśnień panujących w dwóch przekrojach strumienia.

Zawarte w niniejszym rozdziale obliczenia dotyczą ustalonego przepływu cieczy w rurociągach pod
ciśnieniem (z pominięciem pomp i turbin), co oznacza, że parametry ruchu (prędkość i ciśnienie w
przewodzie) zależą tylko od położenia przekroju, natomiast nie zmieniają swych wartości w czasie.

II.1.

RÓWNANIE CIĄGŁOŚCI PRZEPŁYWU

Równanie ciągłości wynika z zasady zachowania masy. W sztywnym przewodzie w ujęciu
jednowymiarowym przy ruchu ustalonym cieczy nieściśliwej, równanie to ma postać:

Q

= const

v

1

v

2

d

1

d

2

Dla przypadku rurociągu o zmiennej średnicy oznacza to, że:

const

2

2

1

1

=

⋅

=

⋅

=

υ

υ

A

A

Q

gdzie:

υ

1

,

υ

2

–

średnie w przekroju prędkości przepływu na odcinkach rurociągów o średnicach

d

1

i

d

2

;

A

1

,

A

2

–

pola powierzchni przekrojów.

II.2.

RÓWNANIE BERNOULLIEGO

Równanie Bernoulliego wynika z zasady zachowania energii. Można go sformułować następująco:
W przepływie cieczy rzeczywistej energia mechaniczna strumienia płynącej cieczy maleje w
kierunku ruchu o wysokość strat hydraulicznych.
Graficznym obrazem przebiegu zmian energii mechanicznej na rozpatrywanym odcinku strumienia,
opisanych równaniem Bernoulliego jest

linia energii

.

Przebieg zmian energii potencjalnej strumienia obrazuje

linia ciśnień

obniżona w stosunku do linii

energii o wysokość energii kinetycznej

υ

2

/

2g

.

Linia ciśnień piezometrycznych

przebiega poniżej linii ciśnień o wartość

p

a

/γ

. Jest to linia na której

układa się zwierciadło cieczy piezometrach podłączonych w przekrojach rurociągu.

h

1

h

2

2

g

2

g

p

1

p

1

n

p

2

n

linia en

ergii

inia. ci

śnień b

ezwzgl

. (całko

witych

)

linia ci

śnień p

iezom

etryczn

ych

p

a

p

a

1

1

2

2

pp

11

Przy przyjętym poziom porównawczym i dwóch przekrojach przewodu jak na II-2 równanie Bernoulliego
można zapisać następująco:

const

2

2

str

2

2

2

2

2

2

1

1

1

1

=

∑

+

+

+

=

+

+

h

g

p

z

g

p

z

υ

α

γ

υ

α

γ

gdzie:

z

1

, z

2

– wysokość położenia środków ciężkości przekrojów 1-1 i 2-2 przewodu ponad

przyjęty poziom porównawczy,

p

1

,

p

2

– ciśnienie w środku ciężkości przekrojów 1-1 i 2-2,

γ

γ

2

1

p

,

p

– wysokości ciśnienia w przekrojach 1-1 i 2-2 przewodu ,

g

,

g

2

2

2

2

2

1

υ

υ

– wysokości energii kinetycznej (wysokości średnich prędkości przepływu) w

przekrojach 1-1 i 2-2,












+

+

γ

γ

2

2

1

1

p

z

p

z

–

wysokości energii potencjalnej cieczy w przekrojach 1-1 i 2-2,

str

∑

h

– suma wysokości strat energii na pokonanie oporów ruchu między

przekrojami 1-1 i 2-2,

α

1

,

α

2

– współczynniki St. Venanta wynikające ze stosowania wartości prędkości

średnich w przekrojach przewodu. W przypadku ruchu burzliwego
współczynniki te można pomiąć, gdyż ich wartości są bliskie 1.

II.3.

OBLICZENIE WYSOKOŚCI STRAT ENERGII

Człon

str

∑

h

w równaniu Bernoulliego (II-3) wyraża sumę wysokości strat energii:

–

lokalnych wynikających z pokonywania oporów miejscowych (np. na poszerzeniu rurociągu),

–

na długości przewodu związane wywołane tarciem cieczy o ścianki rurociągu.

II.3.1.

Straty lokalne

Straty lokalne są związane z przeszkodami występującymi na drodze płynącego strumienia, np.: nagłe
poszerzenie lub zwężenie rurociągu, zawory, kryzy, wodomierze, kolanka itp.

Wielkość tych strat oblicza się ze wzoru Weissbacha:

g

h

2

2

lok

υ

ζ

⋅

=

gdzie:

υ

–

średnia prędkość przepływu za przeszkodą wywołującą lokalną stratę energii
(wyjątek stanowi strata na wylocie z rurociągu, gdzie

υ

oznacza prędkość tuż

przed przekrojem wylotu),

ζ

–

bezwymiarowy współczynnik straty lokalnej zależny od rodzaju przeszkody,
geometrii rurociągu itp. Wartości tych współczynników zawiera norma PN-76/M-
34034. Można je także znaleźć w tablicach [10].

II.3.2.

Straty na długości

Straty na długości (liniowe) wywołane są tarciem cieczy o ściany przewodu. Wysokość tych strat można
ją obliczyć korzystając z formuły Darcy'ego-Weissbacha:

g

d

l

h

dl

2

2

υ

λ

⋅

⋅

=

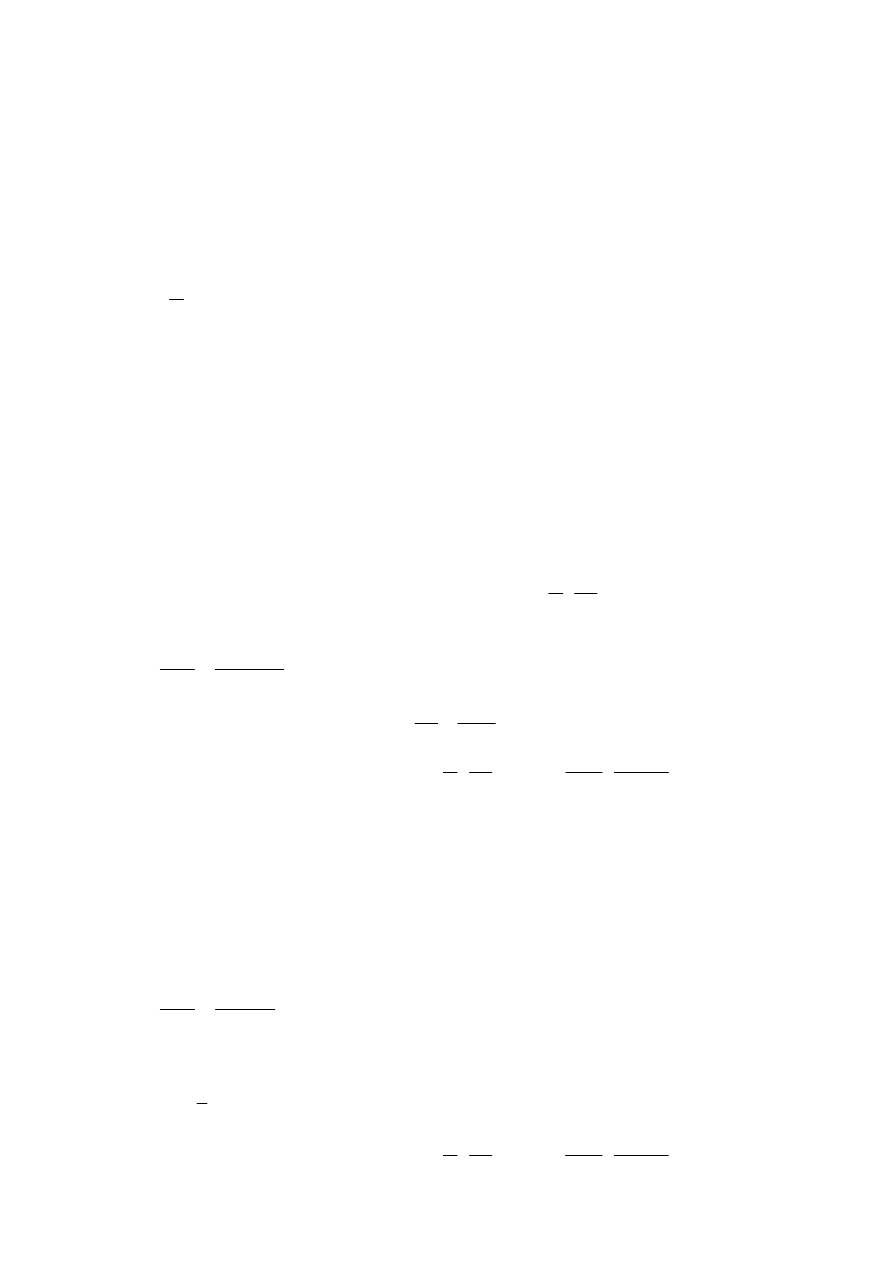
12

gdzie:

l

– długość rozpatrywanego odcinka rurociągu,

d

– średnica rurociągu,

υ

– średnia prędkość przepływu w rurociągu,

λ

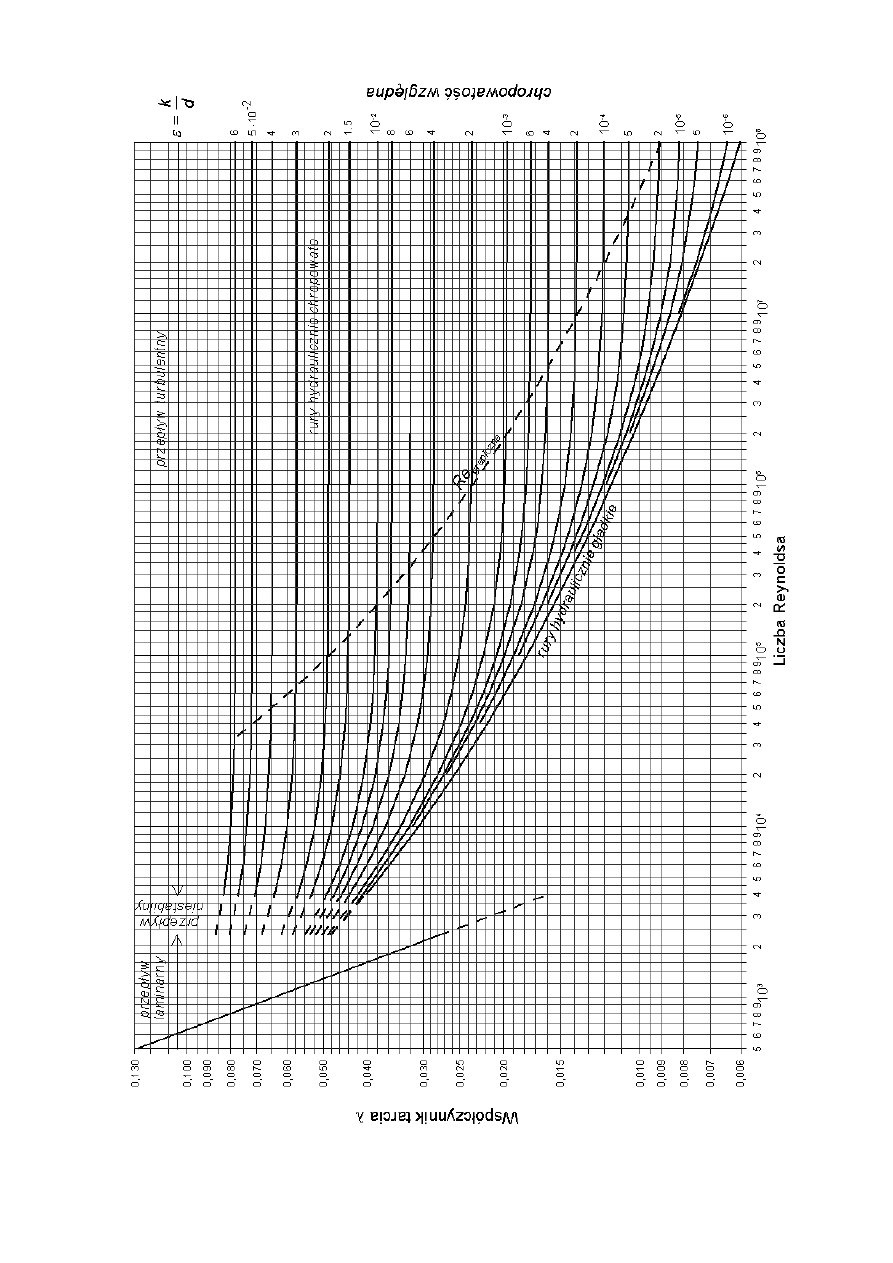
– bezwymiarowy współczynnik tarcia będący funkcją:

Dla przewodów o przekroju kołowym współczynnik

λ

w ruchu laminarnym jest odwrotnie proporcjonalny

do liczny Reynoldsa i oblicza się wg wzoru Hagena – Poiseuille’a:

λ

= 64/

Re

Na wartość oporów przepływu w ruchu turbulentnym wpływa także chropowatość powierzchni
przewodu. Wartość współczynnika oporów liniowych jest funkcją:













=

Re

,

d

k

f

λ

gdzie:

k

– chropowatość bezwzględna przewodu (średnia wysokość nierówności ścian przewodu),

v

d

Re

/

⋅

=

υ

– liczba Reynoldsa,

ν

– kinematyczny współczynnik lepkości cieczy,

Wartość współczynnika

λ

dla przewodów o przekroju kołowym odczytać można z nomogramu Moody'ego

PRZYKŁAD Straty liniowe w ruchu laminarnym

Obliczyć wysokość strat liniowych w rurociągu o długości

L

i średnicy

d

.

Dane:

L

= 1000 m,

d

= 0,1 m,

υ

= 0,02 m/s,

t

= 20

°

C

Szukane:

h

dl

Rozw.:

Wysokość strat energii na długości oblicza się ze wzoru:

g

d

L

h

dl

2

2

υ

λ

⋅

⋅

=

Aby wyliczyć wartość współczynnika

λ

, należy ustalić reżim ruchu, czyli obliczyć liczbę Reynoldsa:

2320

2000

10

1

0

02

0

6

<

=

⋅

=

⋅

=

−

,

,

d

Re

ν

υ

Ruch jest laminarny, czyli:

032

0

2000

64

64

,

Re

=

=

=

λ

Straty liniowe wynoszą zatem:

m

01

0

81

9

2

02

0

1

0

1000

032

0

2

2

2

,

,

,

,

,

g

d

L

h

dl

≅

⋅

⋅

⋅

=

⋅

⋅

=

υ

λ

PRZYKŁAD Straty liniowe w ruchu turbulentnym

Obliczyć wysokość strat liniowych w rurociągu o długości

L

i średnicy

d

.

Dane:

L

= 1000 m,

d

= 0,1 m,

υ

= 0,5 m/s,

t

= 20

°

C,

k

= 0,4 mm

Szukane:

h

dl

Rozw.:

Aby wyznaczyć współczynnik

λ

konieczny do obliczenia wielkości strat energii, należy określić reżim

ruchu, czyli obliczyć wartość liczby Reynoldsa:

2320

000

50

10

1

0

5

0

6

>

=

⋅

=

⋅

=

−

,

,

d

Re

ν

υ

Ruch jest turbulentny, czyli wartość współczynnika strat liniowych odczytać należy z nomogramu
Moody’ego.

(

)

(

)

031

0

004

0

000

50

,

,

;

f

,

Re

f

d

k

=

=

=

λ

Szukane straty liniowe wynoszą zatem:

m

95

3

81

9

2

5

0

1

0

1000

031

0

2

2

2

,

,

,

,

,

g

d

L

h

dl

=

⋅

⋅

⋅

=

⋅

⋅

=

υ

λ

13

N

o

m

o

g

ra

m

M

o

o

d

y

’e

g

o