Fizyka Ogólna

Wyk³ad 13

1

Polaryzacja œwiat³a

Równania Maxwella wymagaj¹ aby fala elektromagnetyczna
by³a fal¹ poprzeczn¹.

Przyk³ad:
Fale akustyczne s¹ pod³u¿nymi falami ciœnienia powietrza (lub
innego oœrodka, w którym rozchodzi siê dŸwiêk).

Doœwiadczalnym dowodem na poprzecznoœæ fal
elektromagnetycznych jest zjawisko polaryzacji.

Œwiat³o pochodz¹ce z konwencjonalnych Ÿróde³ na ogó³ nie jest
spolaryzowane: wystêpuj¹ w nim fale elektromagnetyczne
pochodz¹ce z wielu niespójnych dipoli drgaj¹cych w ró¿nych
p³aszczyznach (lub te¿ z przejœæ kwantowych - ka¿de wysy³a
falê o ró¿nych w³asnoœciach).

Istniej¹ oœrodki, w których padaj¹ca fala œwietlna wywo³uje
drganie anizotropowe tj. ró¿ne w ró¿nych kierunkach. Dzieje siê
tak gdy¿ polaryzacja dielektryczna wywo³ana wektorem
elektrycznym œwiat³a jest anizotropowa tj. zachodzi ³atwiej w
pewnych kierunkach ni¿ w innych. Takie oœrodki mog¹
doprowadziæ do spolaryzowania œwiat³a.

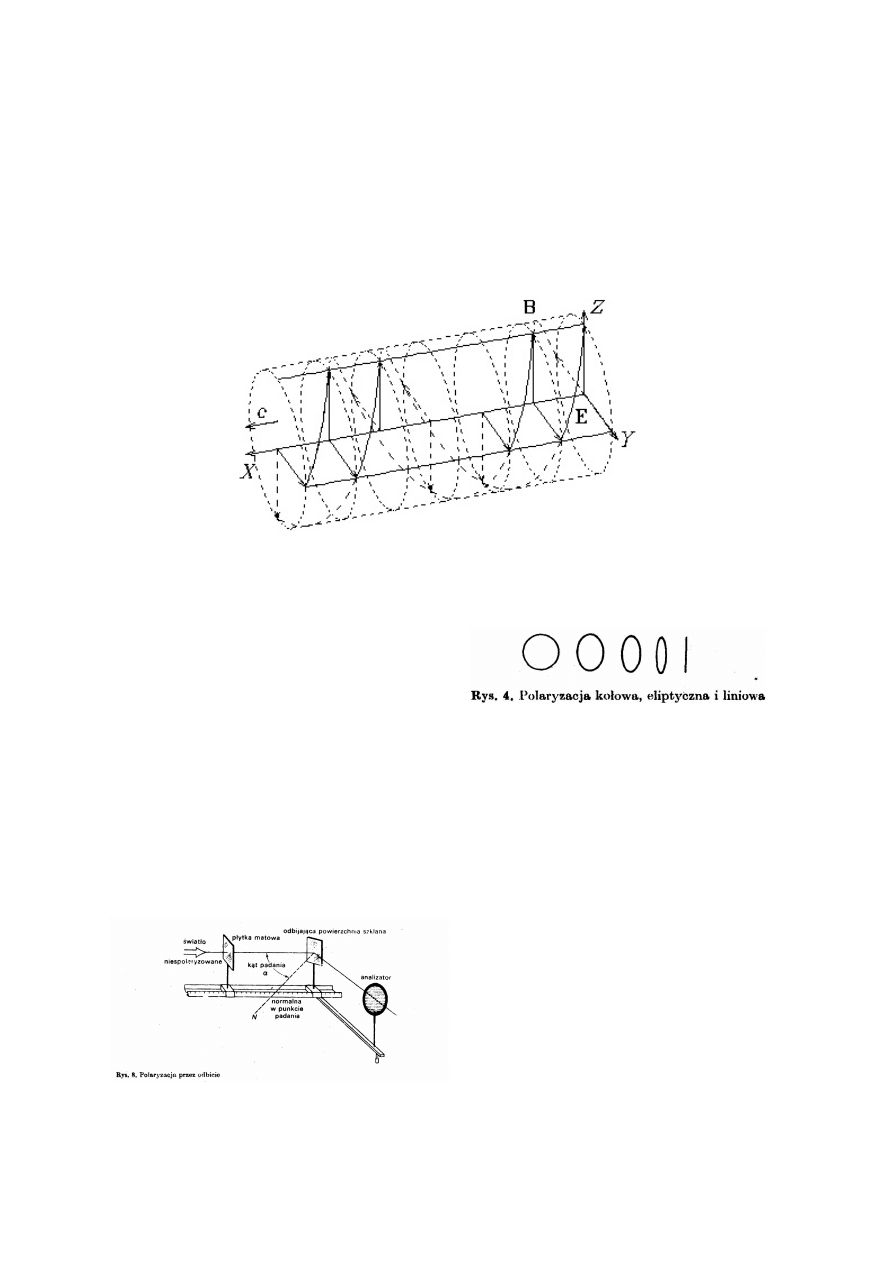
Skrajnym przyk³adem jest polaryzacja liniowa kiedy wektor
elektryczny ograniczony jest tylko do jednej p³aszczyzny.

Fizyka Ogólna

Wyk³ad 13

2

Przeciwstawnym skrajnym przypadkiem polaryzacji (nie myliæ
ze œwiat³em niespolaryzowanym !) jest polaryzacja ko³owa, w
której wektor elektryczny fali œwietlnej obraca siê w pewn¹
prêdkoœci¹ nie zmieniaj¹c swojej amplitudy.

Poœrednim typem polaryzacji jest polaryzacja eliptyczna, w
k t ó r e j k o n i e c w e k t o r a
elektrycznego fali zakreœla elipsê.

Dowodzi siê, ¿e polaryzacja liniowa jest z³o¿eniem dwóch
przeciwbie¿nych polaryzacji ko³owych. Efekt ten wykorzystuje
siê w urz¹dzeniach, w których zmienia siê p³aszczyznê
polaryzacji liniowej.

Otrzymywanie polaryzacji œwiat³a:

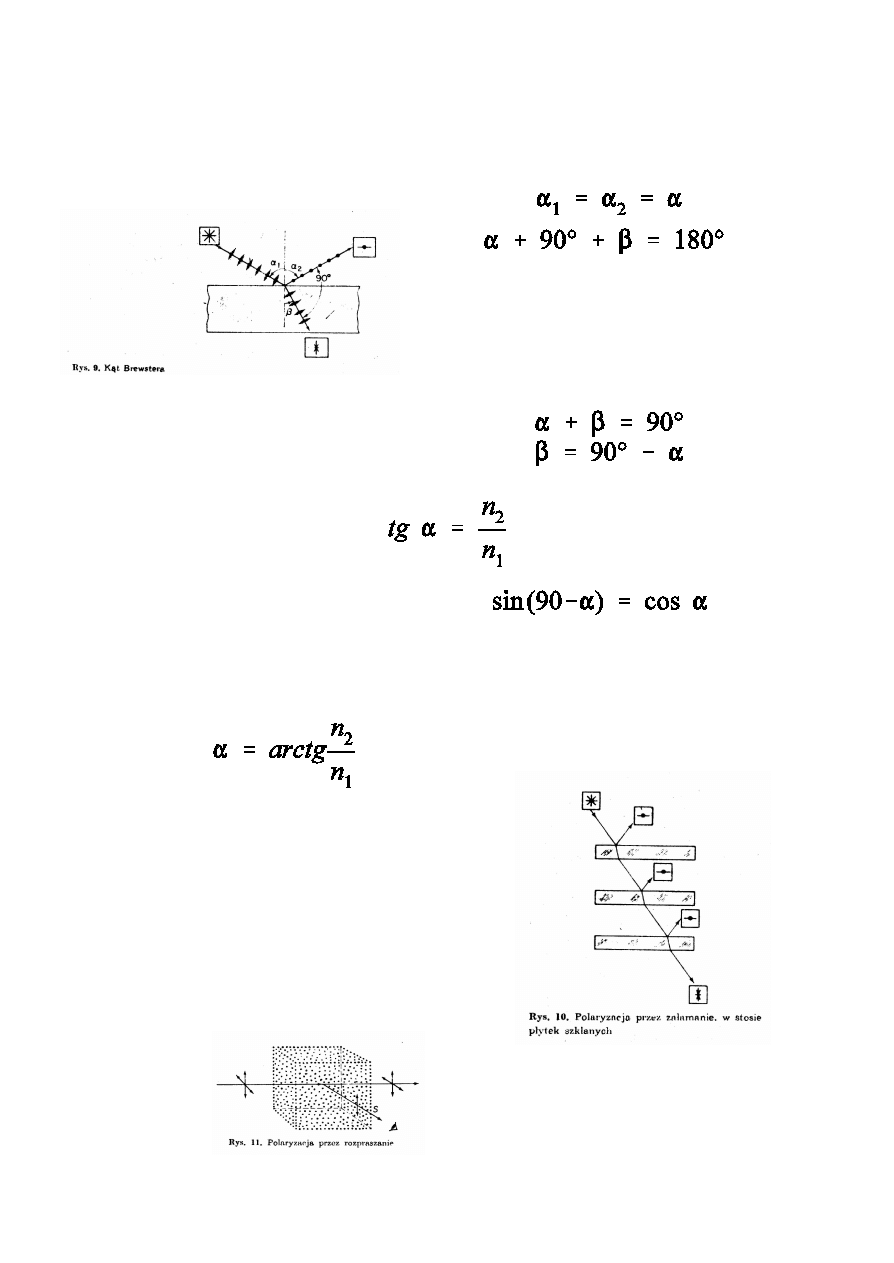
1) polaryzacja przez odbicie od
g r a n i c y o œ r o d k ó w j e s t
najsilniejsza gdy wiazka odbita
i wi¹zka za³amana tworz¹ kat
prosty

Fizyka Ogólna

Wyk³ad 13

3

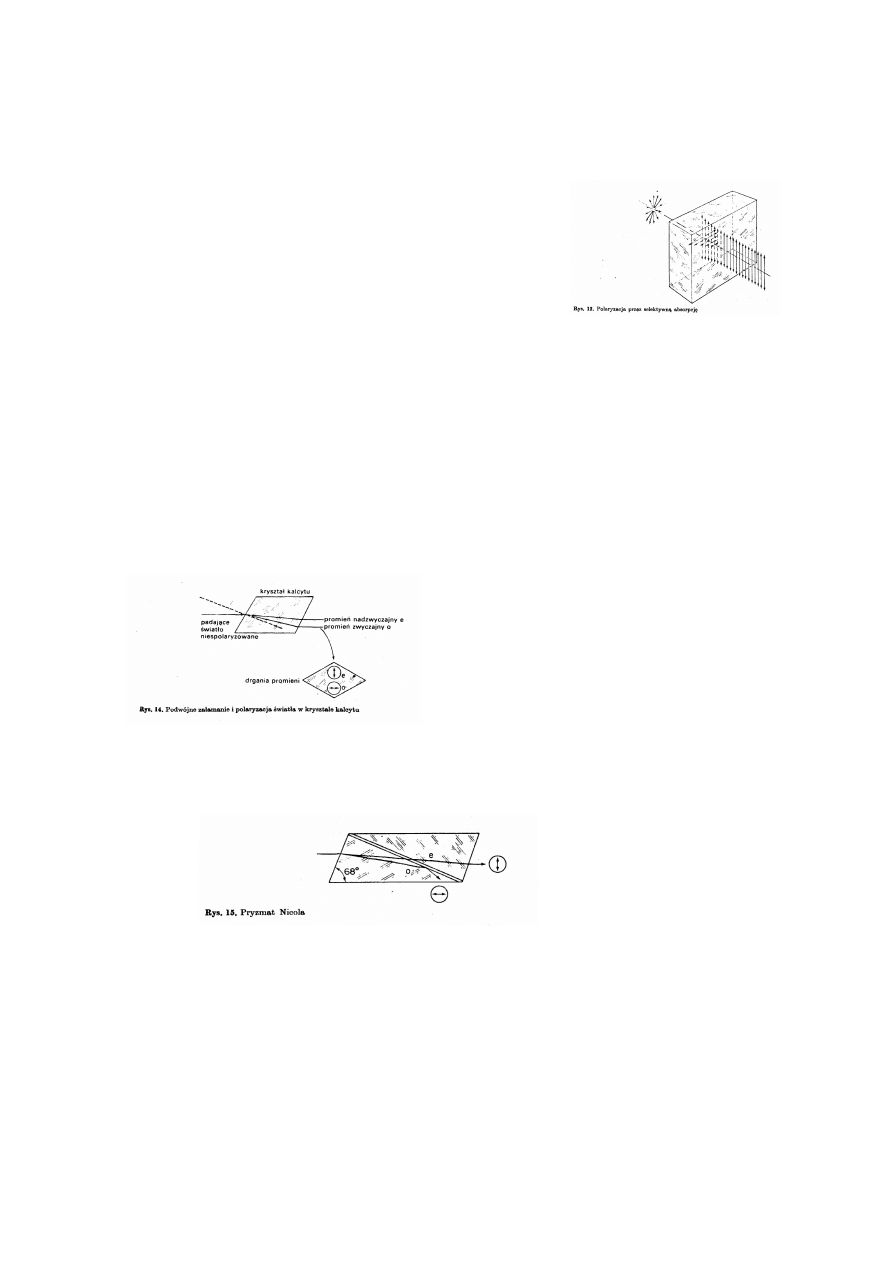
Na rysunku powy¿ej k¹t padania równa siê k¹towi odbicia
Z konstrukcji wynika te¿, ¿e

a st¹d

Wobec tego prawo Snelliusa
za³amania œwiat³a mo¿na
zapisaæ jako

gdzie skorzystaliœmy z to¿samoœci

Tak wiêc maksymaln¹ polaryzacjê przy odbiciu uzyskuje siê dla
k¹ta Brewstera

2) polaryzacja przez za³amanie

3) Polaryzacja przez rozpraszanie

Fizyka Ogólna

Wyk³ad 13

4

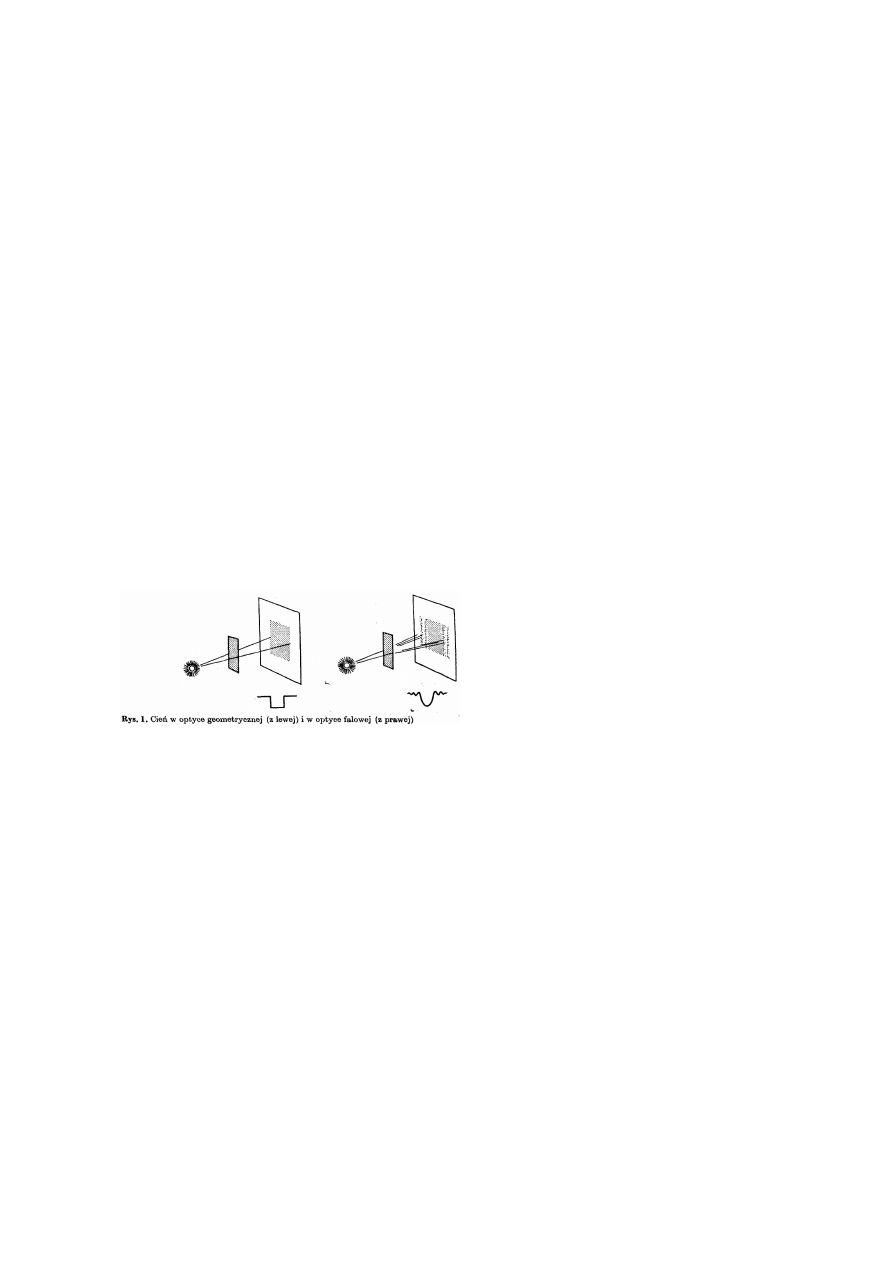
4) polaryzacja przez selektywn¹ absorpcjê

5) polaryzacja przez podwójne za³amanie
Kryszta³y s¹ oœrodkami anizotropowymi - posiadaj¹ ró¿ne
w³asnoœci w ró¿nych kierunkach.
Wœród kryszta³ów wyró¿nia siê grupê kryszta³ów dwój³omnych
(m.in. kalcyt, kwarc, turmalin, cukier, mika i lód). W
kryszta³ach tych zale¿nie od kierunku drgañ wektora
elektrycznego œwiat³o rozdziela siê na 2 wi¹zki rozchodz¹ce siê
w 2 ró¿nych kierunkach i o prostopad³ych polaryzacjach.

Wi¹zki te maj¹ ró¿ne prêdkoœci a
wiêc s¹ inaczej za³amywane przez
kryszta³ dwój³omny.

Zjawisko dwój³omnoœci ma wiele zastosowañ:
a) do otrzymywania œwiat³a spolaryzowanego liniowo

b) defektoskopia i badanie naprê¿eñ w oœrodkach
przezroczystych (modele maszyn !).

Fizyka Ogólna

Wyk³ad 13

5

c) w mikroskopach polaryzacyjnych wykorzystuje siê fakt, ¿e
2 wi¹zki œwiat³a o prostopad³ej polaryzacji nie interferuj¹.
Wykorzystuj¹c wiêc œwiat³o spolaryzowane mo¿na w pewnych
warunkach uzyskaæ poprawê kontrastu. Ponadto u¿ywa siê
takich mikroskopów do identyfikacji kry szta³ów
przezroczystych (daj¹ one charakterystyczne obrazy
inteferencyjne czyli uk³ady pr¹¿ków). W ten sposób odró¿nia
siê sztucznie chodowane cyrkonie od naturalnych kryszta³ów
stosowanych w bi¿uterii.

Ponadto
w zakresie takim jak mikrofale i i zakres optyczny
!

du¿e znaczenie ma zjawisko Faradaya (przy
przechodzeniu fali spolaryzowanej przez oœrodek
magnetyczny)

!

oraz zjawisko Kerra (przy odbiciu fali od oœrodka)

W obu tych zjawiskach p³aszczyzna polaryzacji liniowej ulega
obrotowi o pewien k¹t zale¿ny od w³asnoœci oœrodka Kerra lub
Faradaya.
S¹ to dwa nieliniowe zjawiska wykorzystywane w przyrz¹dach
pomiarowych (np. pomiar stê¿enia cukru w cieczy za pomoc¹
zjaiska Kerra) lub do manipulacji p³aszczyzn¹ polaryzacji w
uk³adach mikrofalowych (efekt Faradaya).

Fizyka Ogólna

Wyk³ad 13

6

Dyfrakcja

Zasada Huygensa:

Ka¿dy punkt, do którego dotar³a fala staje siê Ÿród³em fali
kulistej

W efekcie:
obserwujemy fale, które s¹ superpozycj¹ fal kulistych
(wtórnych).
Kiedy wiêc zas³onimy czêœæ frontu falowego (powstawanie
cienia) to ujawnia siê kulista (cylindryczna) natura fal
cz¹stkowych. Prowadzi do dyfrakcji tj.

ka¿dego odchylenia od prostoliniowego biegu fali, które
nie jest wynikiem ani odbicia ani za³amania.

Rozró¿nia siê dwa typy dyfrakcji:
dyfrakcjê Fraunhofera: gdy mo¿na uznaæ, ¿e Ÿród³o fali znajduje
siê nieskoñczenie daleko (fala jest fal¹ p³ask¹)
dyfrakcjê Fresnela - gdy tak za³ao¿yæ nie mo¿na i trzeba
uwzglêdniaæ w opisie krzywiznê powierzchni sta³ej fazy.

Dyfrakcja Fraunhofera na pojedyñczej szczelinie

Aby zobaczyæ obraz dyfrakcyjny szczeliny (tj. uzyskaæ
interferencjê na ekranie) w przypadku dyfrakcji Fraunhofera
(fala p³aska !) musimy wstawiæ za szczelinê soczewkê.

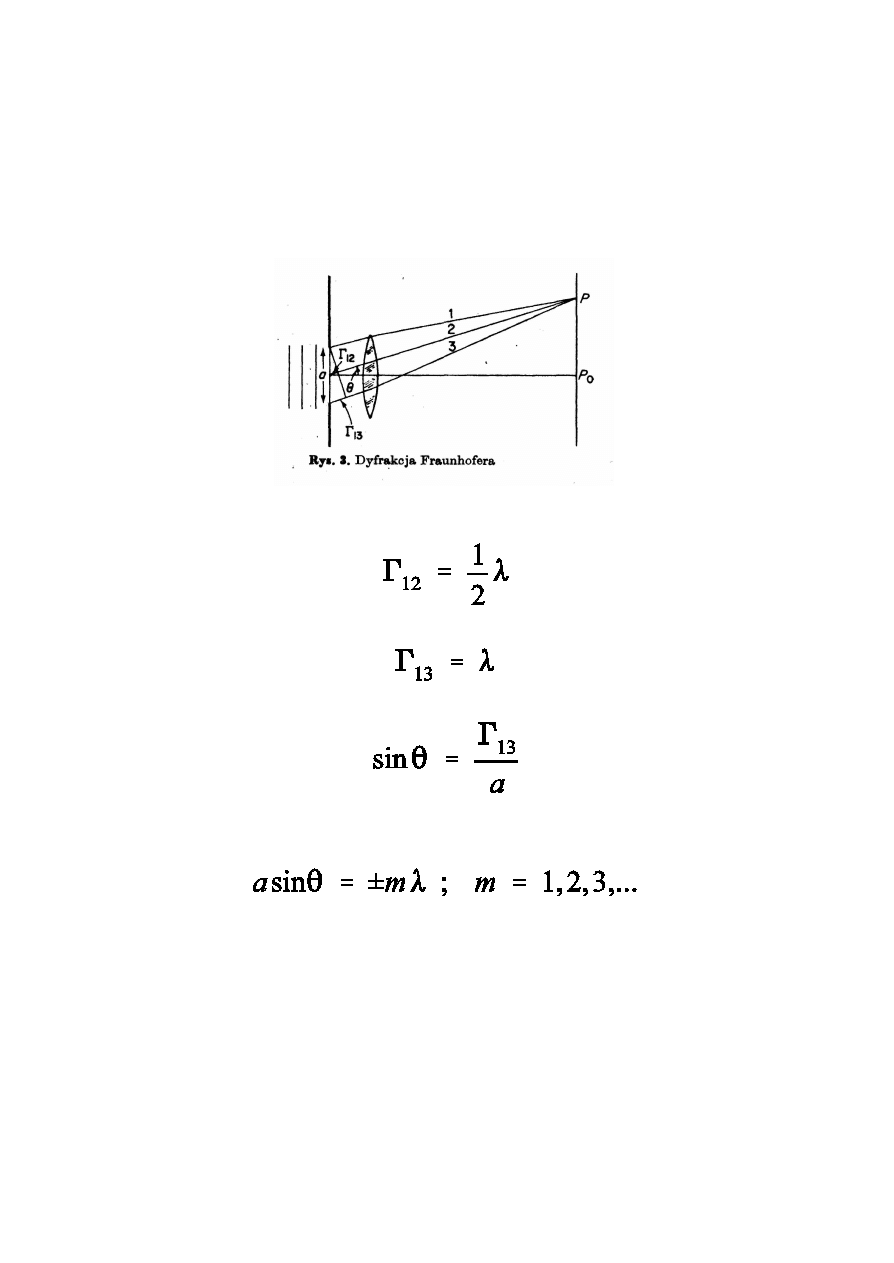
Fizyka Ogólna

Wyk³ad 13

7

Pozosta³e pr¹¿ki powstaj¹ tam gdzie drogi optyczne
poszczególnych promieni bêd¹ odpowiednio przesuniête
wzglêdem siebie.

Minimum pierwszego rzêdu powstaje tam gdzie

albo

Jednoczeœnie

Warunek na minima

gdzie a to jest szerokoϾ szczeliny.
Uwaga: formalnie to jest ten sam wzór co dla siatki dyfrakcyjnej
z t¹ ró¿nic¹, ¿e sta³a stoj¹ca przed funkcj¹ sinus ma inne
znaczenie !
W dyfrakcji Fraunhofera odlegloœæ od ekranu nie wp³ywa na
po³o¿enie minimów

.

Fizyka Ogólna

Wyk³ad 13

8

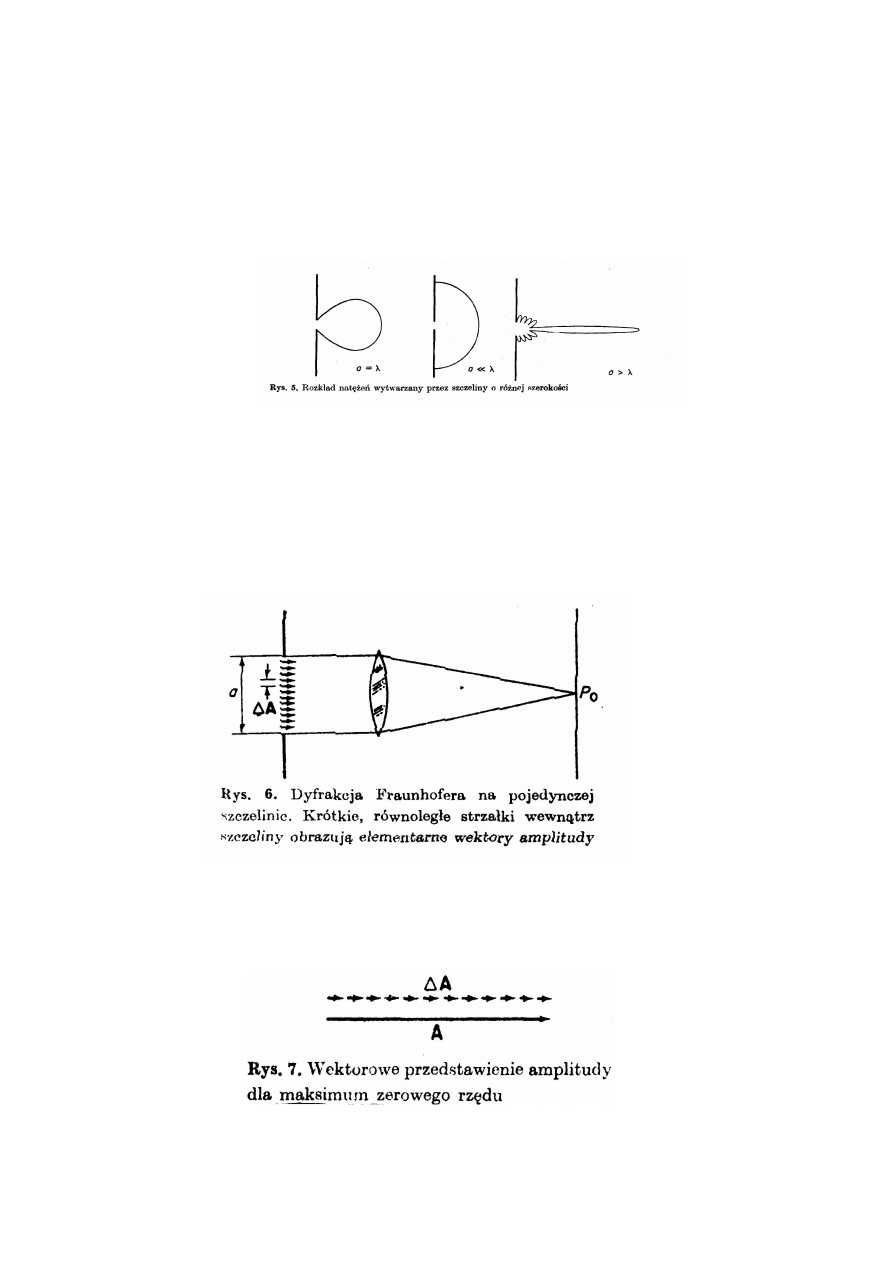
Z warunku na minimum wynikaj¹ w³asnoœci obrazu
dyfrakcyjnego dla ró¿nych d³ugoœci fali w stosunku do
szerokoœci szczeliny:

Wyznaczanie amplitudy i natê¿enia œwiat³a w dyfrakcji
Fraunhofera na pojedyñczej szczelinie

Podzielmy szczelinê na jednakowe strefy. Dla ustalenia uwagi
niech ich bêdzie 12

Cz¹stkowe amplitudy dodaj¹ siê wtedy wektorowo w pr¹zku
centralnym z jednakowymi fazami:

Fizyka Ogólna

Wyk³ad 13

9

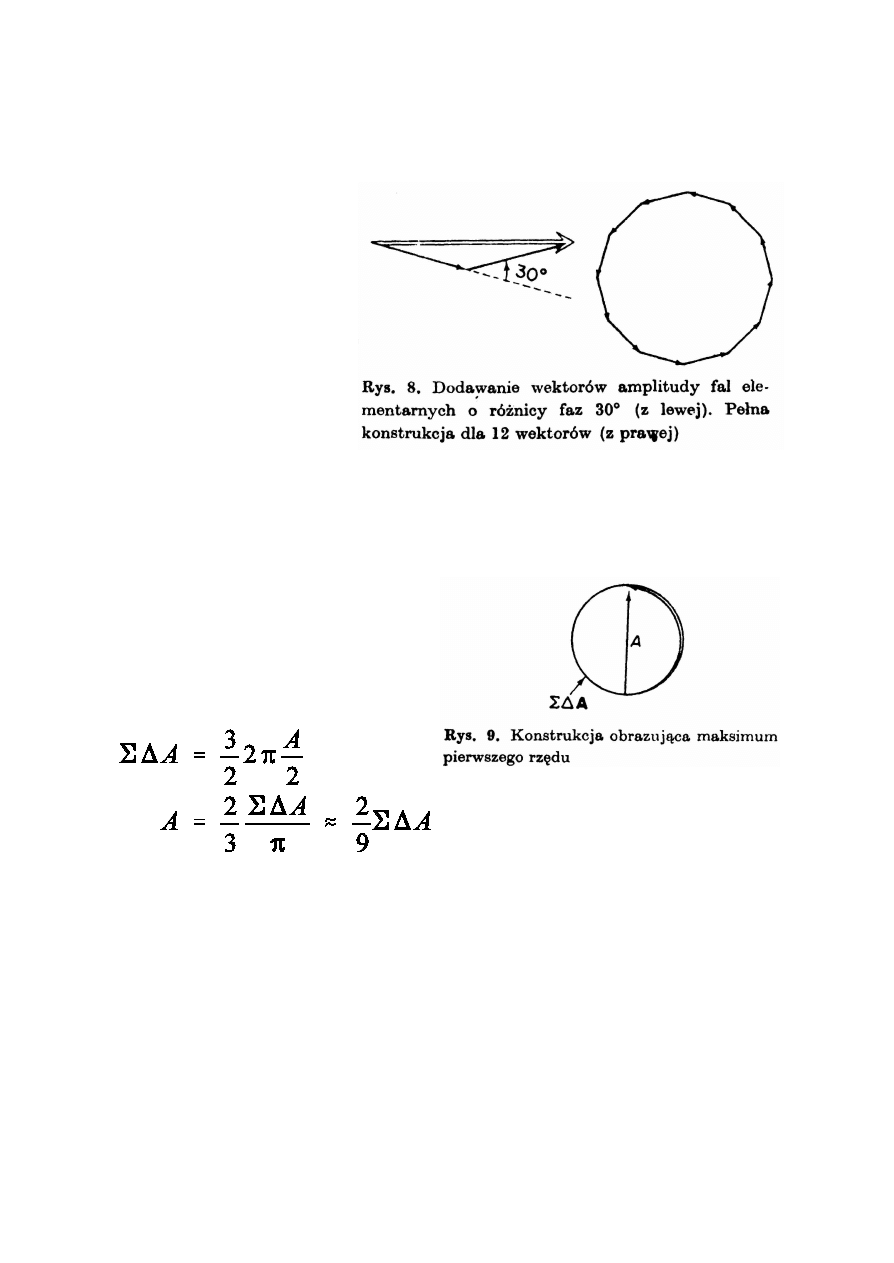
Gdyby punkt P na ekranie odpowiada³ pierwszemu minimum
:to wtedy ró¿nica faz
pomiêdzy skrajnymi
promieniami by³aby
r ó w n a 3 6 0 ° ( a
pomiêdzy centralnym
promieniem a skrajnym
180°). Odpowiada to
w y p a d k o w e j
ampltudzie A = 0.

Natomiast dla pierwszego
maksimum konstrukcja ta
wygl¹da³aby tak

Odpowiada to amplitudzie

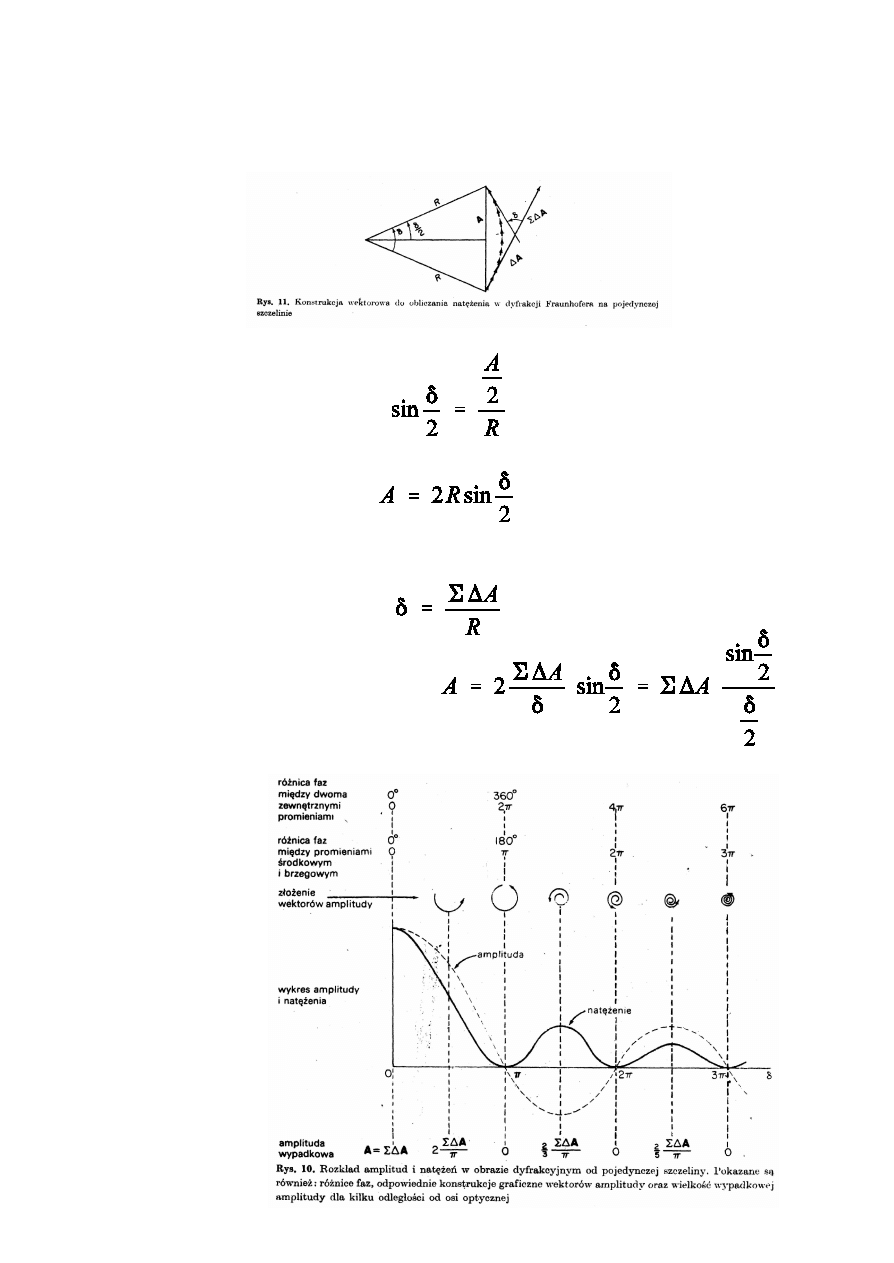
Zale¿noœæ natê¿enia na ekranie od przesuniêcia fazy *

Fizyka Ogólna

Wyk³ad 13

10

W dowolnym punkcie na elranie wypadkowa amplituda A jest
równa d³ugoœci ciêciwy:

w mierze ³ukowej przesuniêcie fazy

Po wyznaczeniu st¹d R

Natê¿enie
I = A2

Fizyka Ogólna

Wyk³ad 13

11

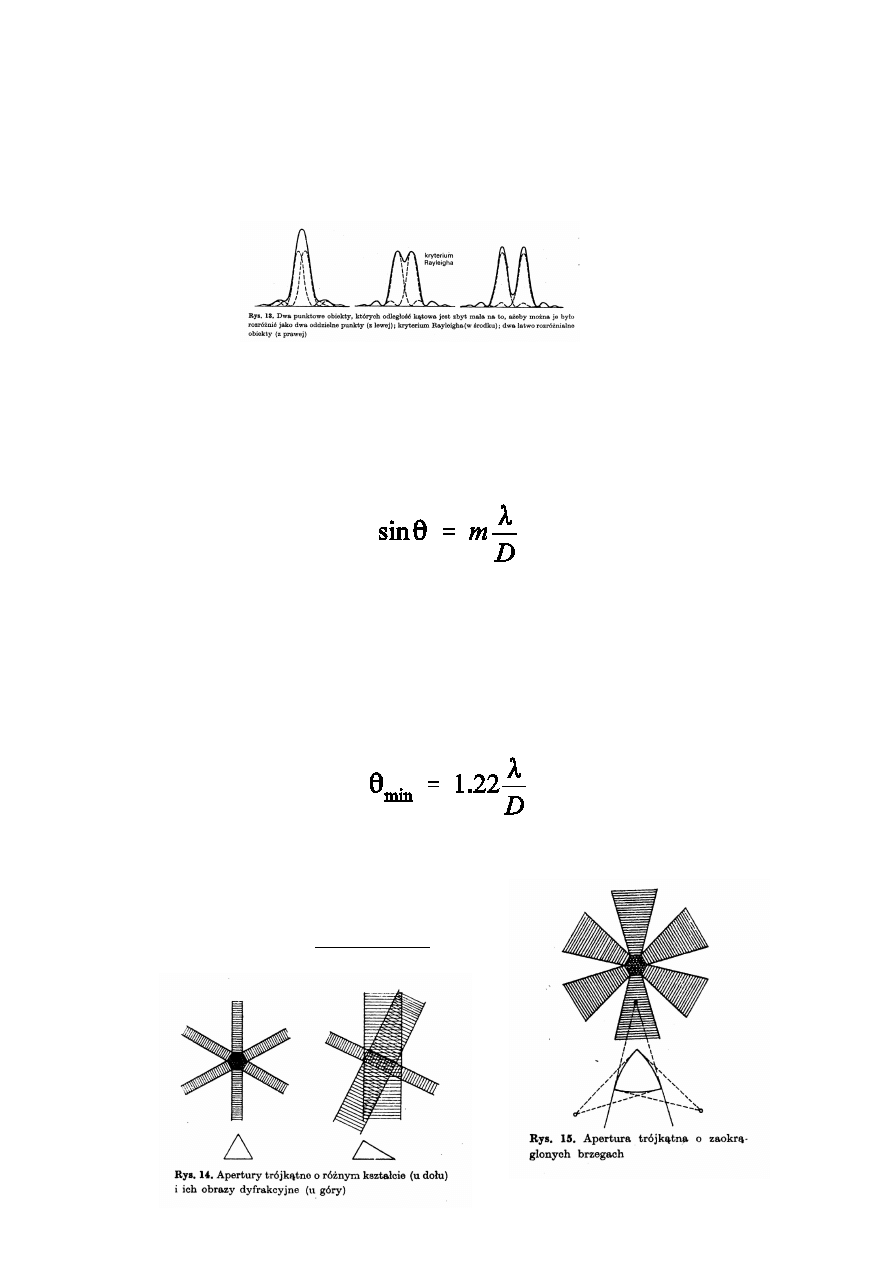
Kryterium zdolnoœci rozdzielczej Rayleigha

Dwie linie na rysunku s¹ rozró¿nialne (np. w mikrokopie
lub przez lunetê) gdy ich maksima dyfrakcyjne s¹
rozró¿nialne.

Gdy szczelina jest okr¹g³a (tak jak np. soczewka mikroskopu) i
ma œrednicê D to warunek na minimum w obrazie dyfrakcyjnym
ma formalnie tak¹ sam¹ postaæ jak dla szczeliny liniowej

gdzie 8 jest d³ugoœci¹ fali. Tym razem jednak m nie jest
wielkoœcia ca³kowit¹ i dla pierwszego minimum wynosi 1.22.

Poniewa¿ przy rozpatrywaniu rozdzielczoœci przyrz¹dów

optycznych k¹ty 2 s¹ ma³e wiêc minimalny rozdzielczoœæ
k¹towa wynosi:

W zale¿noœci od kszta³tu
szczeliny obrazy dyfrakcyjne
mog¹ byæ ró¿ne. Przyk³ad: