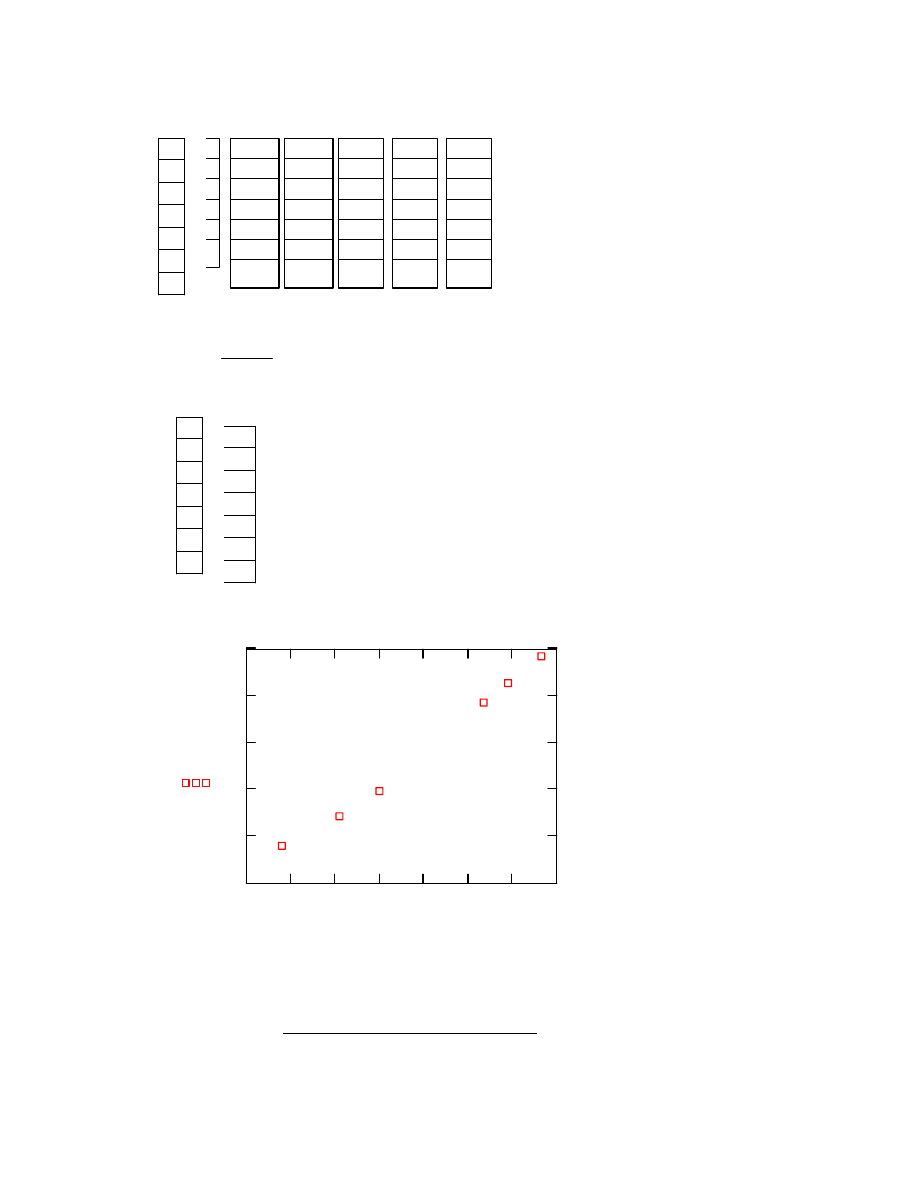
a
Lp
Lp
C
Lp
∑
⎛
⎜
⎝
⎞
⎠
Lp
Tsr
Lp
∑
⋅
Lp
Lp
C
Lp
Tsr
Lp
⋅
∑
⋅
−
Lp
C
Lp
∑
⎛
⎜
⎝
⎞
⎠
2
Lp
Lp
C
Lp
( )
2
∑
⎡
⎢
⎣
⎤
⎥
⎦
⋅
−
:=
3.Obliczam współczynniki a oraz b metodą Gaussa najmniejszych kwadratów
.
4
6
8
10
12
14
16
18
6
8
10
12
14
16
Tsr
Lp
C
Lp
2.Wykreślenie zależności T = f ( C )
:wartość średnia okresu
dla 1000 impulsów pojemności Cx
Tsr
i
7.59
8.86
9.93
13.72
14.55
15.69
11.41
=
i
1
2
3
4
5
6
7
=
Tsr
i
n
T
i n
,
∑
5
:=
:zmierzone wartości okresów (w sekundach)
dla wartości C pojemności (w nanofaradach)
T
i 5
,
7.592
9.01
10.001
13.652
14.436
15.594
11.383
:=
T
i 4
,
7.619
8.82
9.974
13.662
14.352
15.794
11.326
:=
T
i 3
,
7.629
8.822
9.914
13.686
14.421
15.66
11.365
:=
T
i 2
,
7.608
8.825
9.92
13.664
14.679
15.637
11.371
:=
T
i 1
,
7.523
8.8
9.847
13.919
14.851
15.788
11.584
:=
C
i
5.6
8.2
10
14.7
15.8
17.3
:=
i
1
2
3
4
5
6
7
=
1.Obliczenie wartości średnich zmierzonych okresów dla różnych pojemności
R3 = 500 k
Ω
asr
Lp
a
Lp
∑
6
:=
asr
1.04
=
b
Lp
Lp
C
Lp
∑
⎛
⎜
⎝
⎞
⎠
Lp
C
Lp
Tsr
Lp
⋅
∑
⎛
⎜
⎝
⎞
⎠
⋅
Lp
Tsr
Lp
∑
⎛
⎜
⎝
⎞
⎠
Lp
C
Lp
( )
2
∑
⎡
⎢
⎣
⎤
⎥
⎦
⋅
−
Lp
C
Lp
∑
⎛
⎜
⎝
⎞
⎠
2
Lp
Lp
C
Lp
( )
2
∑
⎡
⎢
⎣
⎤
⎥
⎦
⋅
−
:=
bsr
Lp
b
Lp
∑
6
:=
bsr
1.22
−
=
y x
( )
asr x
⋅
bsr
+
:=
x
0 0.01
,
18
..
:=
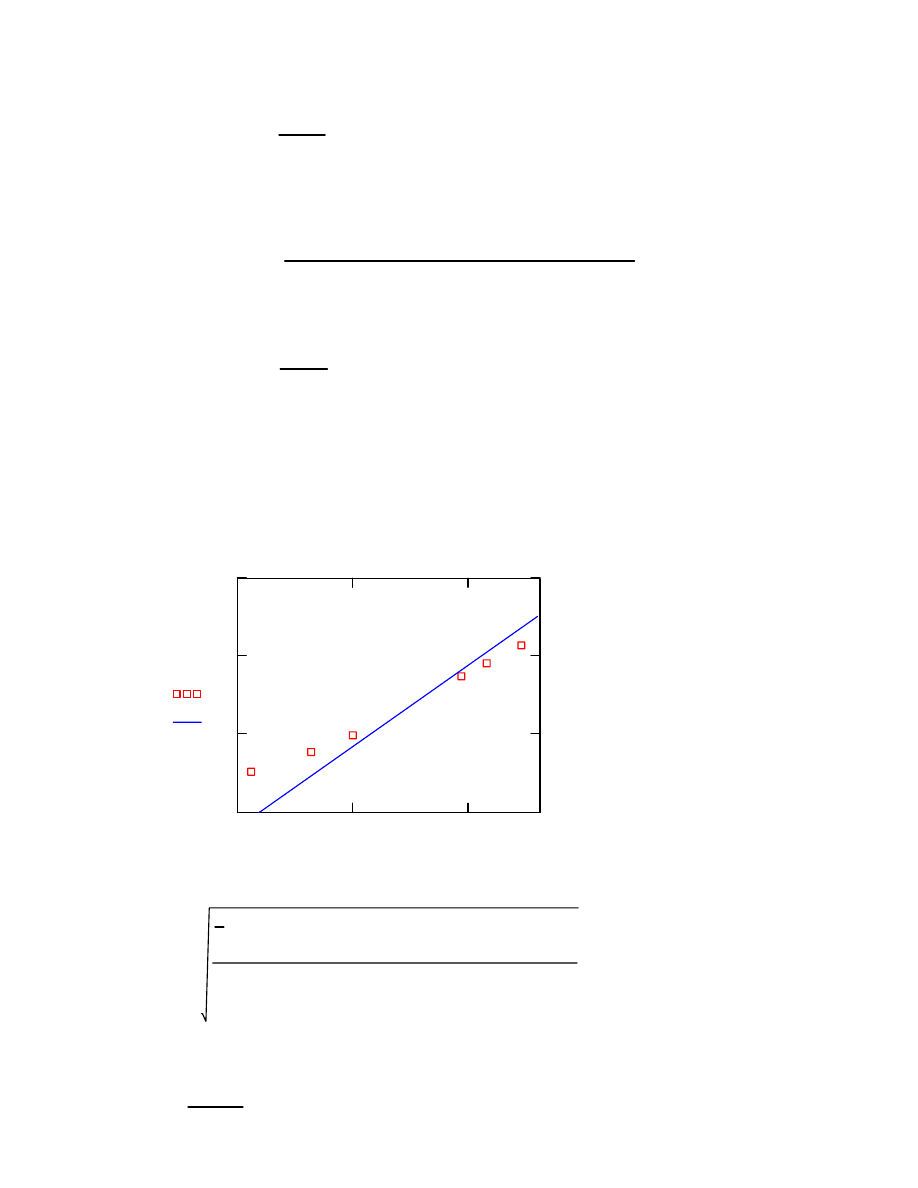
Wykres przedstawiający naniesione punkty eksperymentalne oraz doświadczalni
wyznaczoną prostą.
5
10
15
5
10
15
20
Tsr
Lp
y x
( )
C
Lp
x
,
4.Obliczenie odchyleń standardowych
σ
a
oraz
σ
b
σa
Lp
6
4
Lp
Tsr
Lp
( )
2
∑
asr
Lp
C
Lp
Tsr
Lp
⋅
∑
⎛
⎜
⎝
⎞
⎠
⋅
−
bsr
Lp
Tsr
Lp
∑
⎛
⎜
⎝
⎞
⎠
⋅
−
⎡
⎢
⎣
⎤
⎥
⎦
⋅
Lp
Lp
C
Lp
( )
2
∑
⎡
⎢
⎣
⎤
⎥
⎦
⋅
Lp
C
Lp
∑
⎛
⎜
⎝
⎞
⎠
2
−
:=
σa
Lp
σa
Lp
∑
6
:=
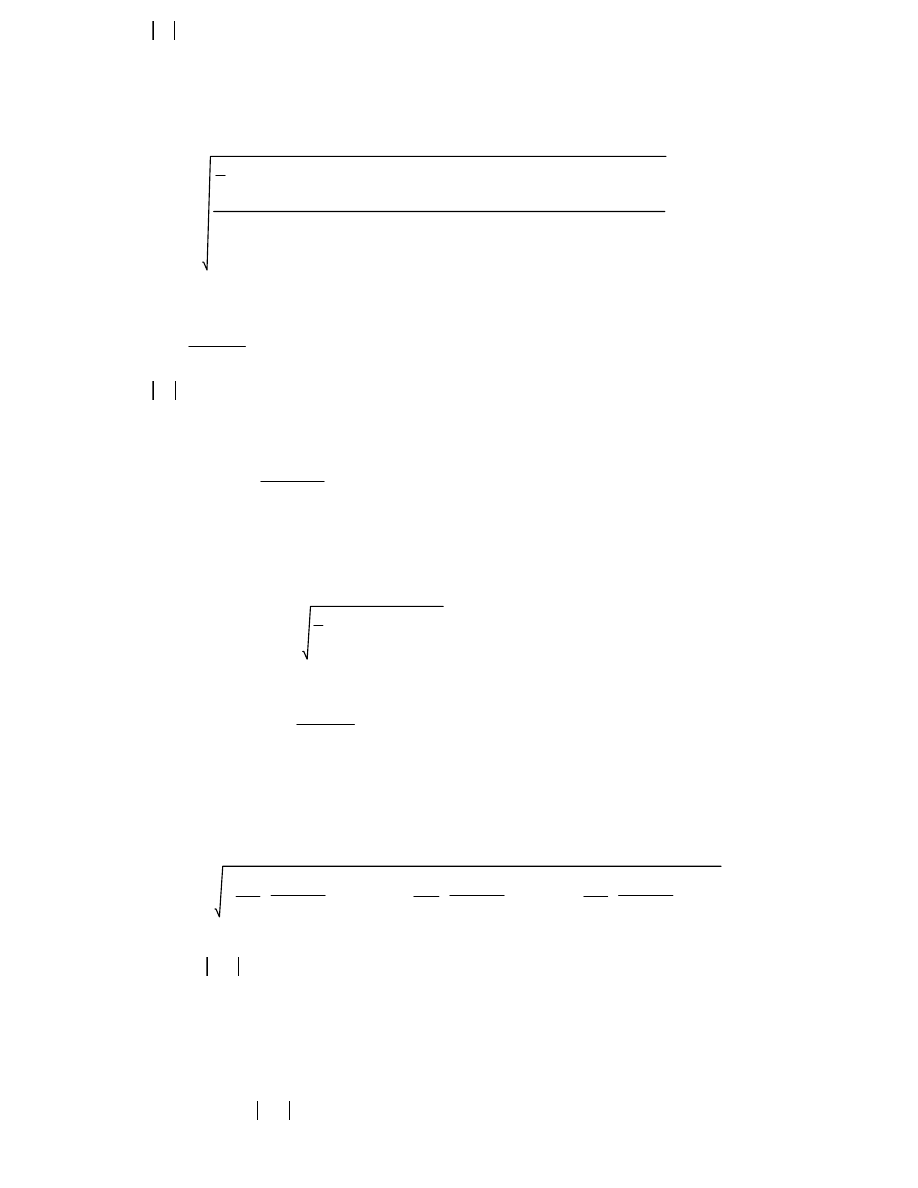
∆Cx
p
σCx
⋅
:=
:p - zadany przedział ufności
p
0.98
:=
8. Wyznaczenie przedziału ufności
∆
Cx
nF
σCx
1.56
=
σCx
Tx
Tx
bsr
−
asr
⎛⎜
⎝
⎞
⎠
d
d
⎡
⎢
⎣
⎤
⎥
⎦
σTx
⋅
⎡
⎢
⎣
⎤
⎥
⎦
2
bsr
Tx
bsr
−
asr
⎛⎜
⎝
⎞
⎠
d
d
⎡
⎢
⎣
⎤
⎥
⎦
σb
⋅
⎡
⎢
⎣
⎤
⎥
⎦
2
+
asr
Tx
bsr
−
asr
⎛⎜
⎝
⎞
⎠
d
d
⎡
⎢
⎣
⎤
⎥
⎦
σa
⋅
⎡
⎢
⎣
⎤
⎥
⎦
2
+
:=
7.Obliczenie średniego błędu kwadratowego
σ
C
x
σTx
0.08
=
σTx
n
σTx
n
∑
5
:=
σTx
n
1
5
i
T
7 n
,
Tsr
7
−
(
)
2
∑
⋅
:=
6. Obliczenie średniego błędu kwadratowego
σ
Tx
nF
C
x
12.11
=
C
x
Tsr
7
bsr
−
asr
:=
5. Obliczenie nieznanej pojemności Cx.
σb
1.18
=
σb
Lp
σb
Lp
∑
6
:=
σb
Lp
1
4
Lp
Tsr
Lp
(
)
2
∑
asr
Lp
C
Lp
Tsr
Lp
⋅
∑
⎛
⎜
⎝
⎞
⎠
⋅
−
bsr
Lp
Tsr
Lp
∑
⎛
⎜
⎝
⎞
⎠
⋅
−
⎡
⎢
⎣
⎤
⎥
⎦
⋅
Lp
C
Lp
( )
2
∑
⎡
⎢
⎣
⎤
⎥
⎦
⋅
Lp
Lp
C
Lp
( )
2
∑
⎡
⎢
⎣
⎤
⎥
⎦
⋅
Lp
C
Lp
∑
⎛
⎜
⎝
⎞
⎠
2
−
:=
σa
0.09
=
11.Obliczam współczynniki a oraz b metodą Gaussa najmniejszych kwadratów
.
4
6
8
10
12
14
16
18
10
15
20
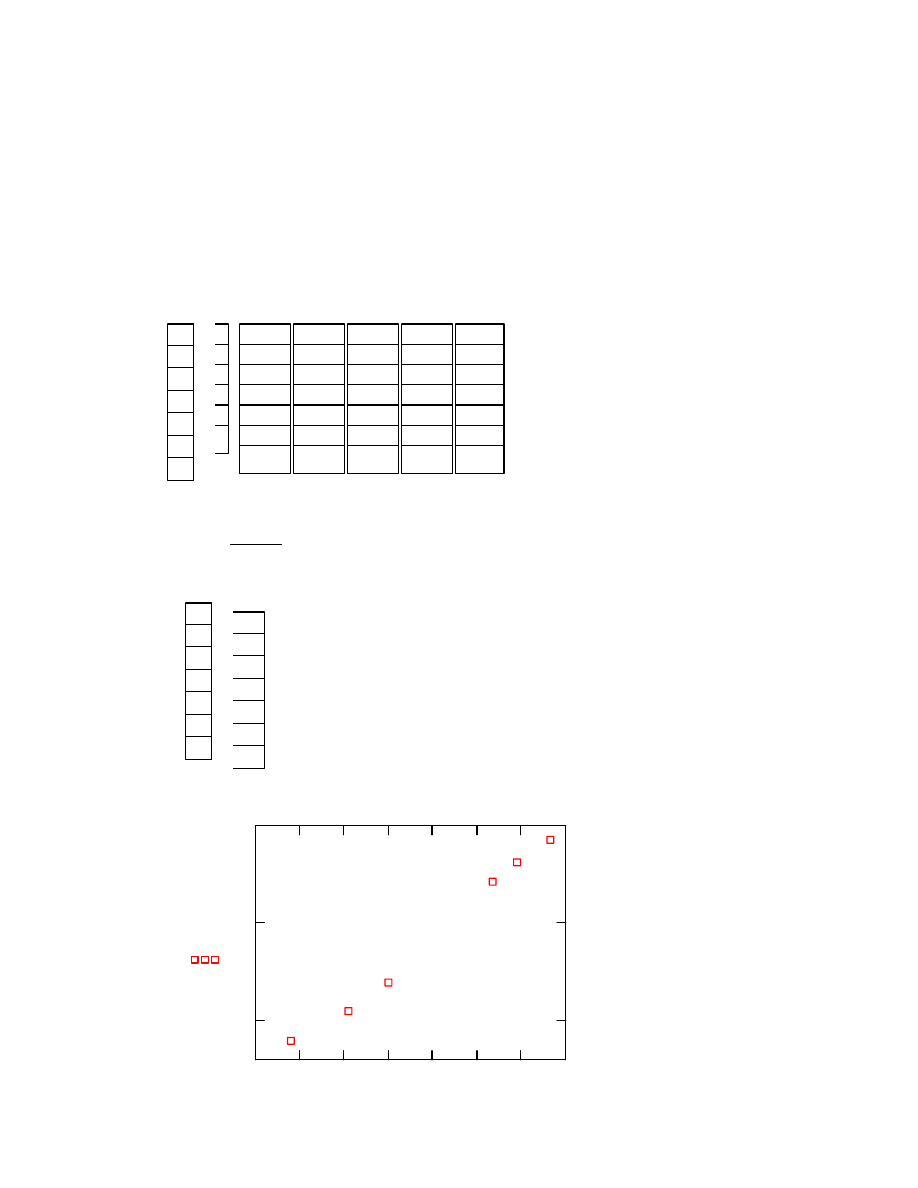
Tsr
Lp
C
Lp
10.Wykreślenie zależności T = f ( C )
:wartość średnia okresu
dla 1000 impulsów pojemności Cx
Tsr
i
8.96
10.49
11.96
17.13
18.12
19.28
14.65
=
i
1
2
3
4
5
6
7
=
Tsr
i
n
T
i n
,
∑
5
:=
:zmierzone wartości okresów (w sekundach)
dla wartości C pojemności (w nanofaradach
T
i 5
,
8.99
10.39
11.976
17.353
18.389
19.128
14.362
:=
T
i 4
,
9.014
10.425
11.885
17.284
17.878
19.345
14.73
:=
T
i 3
,
8.999
10.466
12.05
17.045
17.872
19.275
14.713
:=
T
i 2
,
8.921
10.549
11.923
16.893
18.203
19.196
14.713
:=
T
i 1
,
8.901
10.622
11.954
17.061
18.249
19.436
14.726
:=
C
i
5.6
8.2
10
14.7
15.8
17.3
:=
i
1
2
3
4
5
6
7
=
9.Obliczenie wartości średnich zmierzonych okresów dla różnych pojemności
R3 = 600 k
Ω
∆Cx 1.53
=
a
Lp
Lp
C
Lp
∑
⎛
⎜
⎝
⎞
⎠
Lp
Tsr
Lp
∑
⋅
Lp
Lp
C
Lp
Tsr
Lp
⋅
∑
⋅
−
Lp
C
Lp
∑
⎛
⎜
⎝
⎞
⎠
2
Lp
Lp
C
Lp
( )
2
∑
⎡
⎢
⎣
⎤
⎥
⎦
⋅
−
:=
asr
Lp
a
Lp
∑
6
:=
asr
1.26
=
b
Lp
Lp
C
Lp
∑
⎛
⎜
⎝
⎞
⎠
Lp
C
Lp
Tsr
Lp
⋅
∑
⎛
⎜
⎝
⎞
⎠
⋅
Lp
Tsr
Lp
∑
⎛
⎜
⎝
⎞
⎠
Lp
C
Lp
( )
2
∑
⎡
⎢
⎣
⎤
⎥
⎦
⋅
−
Lp
C
Lp
∑
⎛
⎜
⎝
⎞
⎠
2
Lp
Lp
C
Lp
( )
2
∑
⎡
⎢
⎣
⎤
⎥
⎦
⋅
−
:=
bsr
Lp
b
Lp
∑
6
:=
bsr
1.22
−
=
y x
( )
asr x
⋅
bsr
+
:=
x
0 0.01
,
18
..
:=
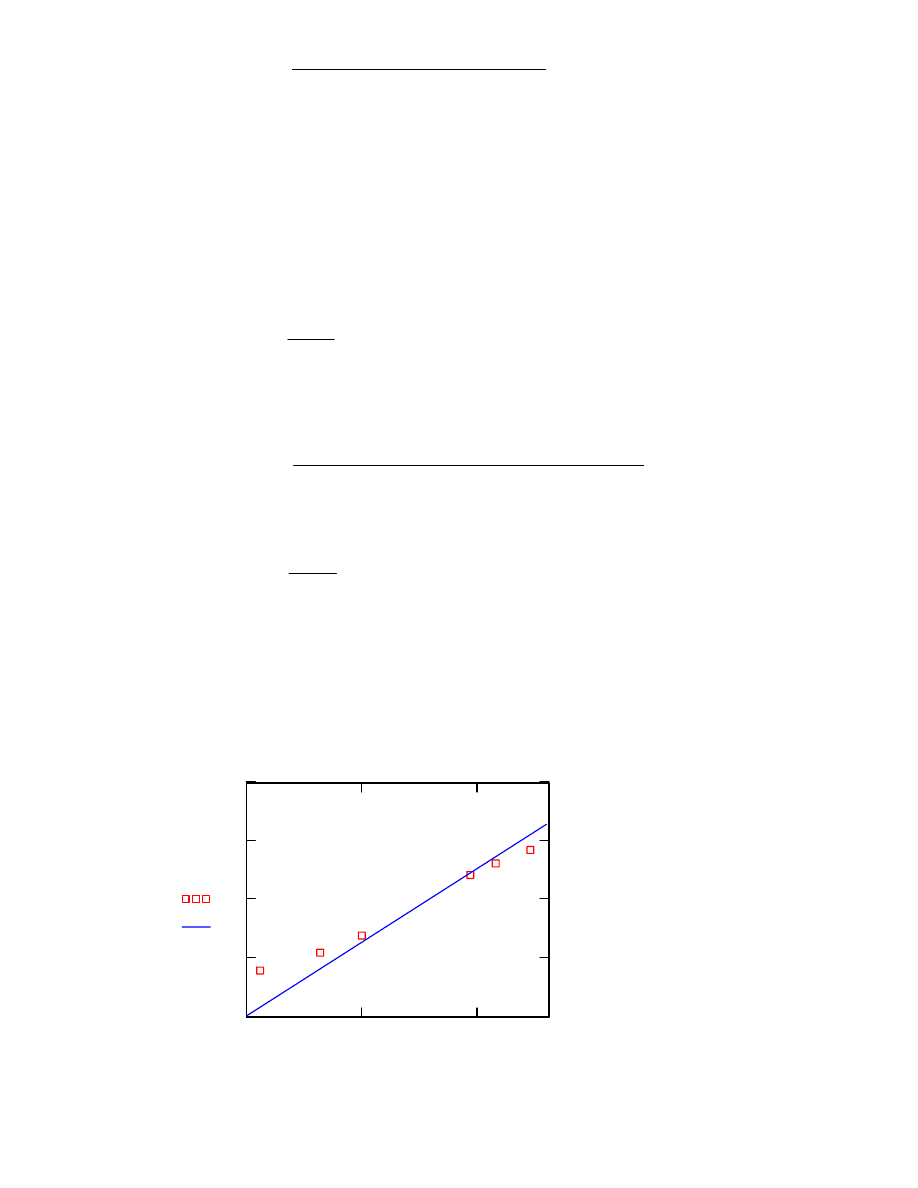
Wykres przedstawiający naniesione punkty eksperymentalne oraz doświadczalnie
wyznaczoną prostą.
5
10
15
5
10
15
20
25
Tsr
Lp
y x
( )
C
Lp
x
,
12.Obliczenie odchyleń standardowych
σ
a
oraz
σ
b
σa
Lp
6
4
Lp
Tsr
Lp
( )
2
∑
asr
Lp
C
Lp
Tsr
Lp
⋅
∑
⎛
⎜
⎝
⎞
⎠
⋅
−
bsr
Lp
Tsr
Lp
∑
⎛
⎜
⎝
⎞
⎠
⋅
−
⎡
⎢
⎣
⎤
⎥
⎦
⋅
Lp
Lp
C
Lp
( )
2
∑
⎡
⎢
⎣
⎤
⎥
⎦
⋅
Lp
C
Lp
∑
⎛
⎜
⎝
⎞
⎠
2
−
:=
σa
Lp
σa
Lp
∑
6
:=
σa
0.1
=
σb
Lp
1
4
Lp
Tsr
Lp
(
)
2
∑
asr
Lp
C
Lp
Tsr
Lp
⋅
∑
⎛
⎜
⎝
⎞
⎠
⋅
−
bsr
Lp
Tsr
Lp
∑
⎛
⎜
⎝
⎞
⎠
⋅
−
⎡
⎢
⎣
⎤
⎥
⎦
⋅
Lp
C
Lp
( )
2
∑
⎡
⎢
⎣
⎤
⎥
⎦
⋅
Lp
Lp
C
Lp
( )
2
∑
⎡
⎢
⎣
⎤
⎥
⎦
⋅
Lp
C
Lp
∑
⎛
⎜
⎝
⎞
⎠
2
−
:=
σb
Lp
σb
Lp
∑
6
:=
σb
1.21
=
13. Obliczenie nieznanej pojemności Cx.
C
x
Tsr
7
bsr
−
asr
:=
C
x
12.59
=
nF
14. Obliczenie średniego błędu kwadratowego
σ
Tx
σTx
n
1
5
i
T
7 n
,
Tsr
7
−
(
)
2
∑
⋅
:=
σTx
n
σTx
n
∑
5
:=
σTx
0.14
=
15.Obliczenie średniego błędu kwadratowego
σ
C
x
σCx
Tx
Tx
bsr
−
asr
⎛⎜
⎝
⎞
⎠
d
d
⎡
⎢
⎣
⎤
⎥
⎦
σTx
⋅
⎡
⎢
⎣
⎤
⎥
⎦
2
bsr
Tx
bsr
−
asr
⎛⎜
⎝
⎞
⎠
d
d
⎡
⎢
⎣
⎤
⎥
⎦
σb
⋅
⎡
⎢
⎣
⎤
⎥
⎦
2
+
asr
Tx
bsr
−
asr
⎛⎜
⎝
⎞
⎠
d
d
⎡
⎢
⎣
⎤
⎥
⎦
σa
⋅
⎡
⎢
⎣
⎤
⎥
⎦
2
+
:=
σCx
1.35
=
nF
16. Wyznaczenie przedziału ufności
∆
Cx
p
0.98
:=
:p - zadany przedział ufności
∆Cx
p
σCx
⋅
:=
∆Cx 1.32
=
WNIOSKI I OCENA OTRZYMANYCH WYNIKÓW
a b Cx σa σb σTx σCx p ∆Cx
1.R = 500 kΩ 1.04 -1.22 12.11 0.09 1.18 0.08 1.56 0.98 1.53
2.R = 600 kΩ 1.26 -1.22 12.59 0.1 1.21 0.14 1.35 0.98 1.32
Pomiary przeprowadzone zostały dla dwóch rezystancji 600kΩ i 500kΩ. Dla każdej
pojemności kondensatora przeprowadzonych zostało pięć pomiarów okresów drgań. Czasy
zamieszczone są w tabeli wyników pomiarów i podane są dla 1000 impulsów. Na ich podst
przeprowadzone zostały obliczenia.W powyższej tabeli podane są wyniki obliczeń dla niez
pojemności kondensatora. Przeprowadzono pięć pomiarów czasu i na ich podstawie
wyznaczono pojemność tego kondensatora.
WNIOSKI
Z rysunków wynika,że dla wszystkich pojemności kondensatorów okresy drgań układają si
na prostej.Na podstawie wykresów można stwierdzić, że wzrost rezystancji powoduje takż
wzrost okresu drgań; dla kondensatora o pojemności 5.6 nF okres drgań dla rezystora
o rezystancji 500kΩ okres dla 1000 impulsów wynosi 7.594 s, a dla rezystora o rezystan
600K dla tej samej ilości impulsów wynosi 8.965 s, czyli wzrost okresu nastąpił o 1.37 s;
podobnie się układają pozostałe okresy .
Przy zwiększaniu rezystancji i pojemności zwiększa się okres, czyli na podstawie wzoru T=
częstotliwośćdrgań maleje.
Na błąd pomiarów miała wpływ także dokładność urządzeń pomiarowych, które podają cza
dokładnością do 0.001s; w celu uzyskania dokładnych pomiarów należałoby podawać czasy
dużą dokładnością.Obliczane wartości pojemności dla dwóch rezystancji wynoszą :
12.11 1.56 nF i 12.59 1.35 nF.
