Egzamin z matematyki dla student´
ow chemii, 5 lutego 2008, 9:10 – 12:15
Rozwia
,
zania r´o˙znych zada´
n maja
,
znale´z´c sie
,
na r´o˙znych kartkach, bo sprawdza´c je be
,
da
,
r´o˙zne osoby.
Ka˙zda kartka musi by´c podpisana w LEWYM G ´
ORNYM ROGU nazwiskiem i imieniem pisza
,
cego, jego nr. indeksu oraz
nr. grupy ´cwiczeniowej i nazwiskiem osoby prowadza
,
cej ´cwiczenia .
Nie wolno korzysta´
c z kalkulator´
ow, telefon´
ow kom´
orkowych ani innych urza
,
dze´
n elektronicznych; je´sli
kto´s ma, musza
,
by´
c schowane i wy la
,
czone! Nie dotyczy rozrusznik´ow serca.
Nie wolno korzysta´c z tablic ani notatek! Wszystkie stwierdzenia nale˙zy uzasadnia´c. Wolno i NALE ˙ZY powo lywa´c sie
,
na twierdzenia, kt´ore zosta ly pojawi ly sie
,
na wyk ladzie lub na ´cwiczeniach.
1. Zdefiniowa´c log
c
b pamie
,
taja
,
c o za lo˙zeniach o c i b .
Wykaza´c, ˙ze 0,4 + log
10
6 > log
10
15 > 1,2 log
10
12 − log
10
5
√
4 .
2. Poda´c definicje
,
kosinusa i sinusa dowolnego ka
,
ta.
Rozwia
,
za´c nier´owno´s´c: tg t + ctg t >
4
√
3
3
. Zilustrowa´c jej rozwia
,
zanie na okre
,
gu x
2
+ y
2
= 1 .
3. Niech f (x) =
3
p
x
4
(x + 5)
2
· (x
2
+ 1)
−1
.
Je´sli 0 6= x 6= −5 , to zachodza
,
r´owno´sci
f
0
(x) = −
2
3
(5x
2
− 3x − 10)(x
2
+ 1)
−2
3
q
x
x+5
oraz
f
00
(x) =
4
9
15x
5
+49x
4
−135x
3
−358x
2
+30x+25
(x
2
+1)
3 3
√
x
2
(x+5)
4
.
Wielomian 5x
2
− 3x − 10 ma dwa pierwiastki: x
1
=
1
10
(3 −
√
209) ≈ −1,15 i x
2
=
1
10
(3 +
√
209) ≈ 1,75 . Wielomian
15x
5
+ 49x
4
− 135x
3
− 358x
2
+ 30x + 25 ma pie
,
´c pierwiastk´ow rzeczywistych x
3
≈ −4,00 , x
4
≈ −2,14 , x
5
≈ −0,24 ,
x
6
≈ 0,29 oraz x
7
≈ 2,82 .
Znale´z´c przedzia ly, na kt´orych funkcja f maleje, na kt´orych ro´snie.
Znale´z´c przedzia ly, na kt´orych funkcja f jest wypuk la, na kt´orych jest wkle
,
s la.
Obliczy´c granice funkcji f przy x −→ ±∞ , oraz granice f
0
przy x −→ ±∞ i przy x −→ −5
±
.
Na podstawie uzyskanych informacji naszkicowa´c wykres funkcji f .
4. Obliczy´c
wyznacznik
3 0 0 1
0 1 0 0
0 0 1 0
2 0 0 1
, sume
,
3 0 0 1
0 1 0 0
0 0 1 0
2 0 0 1
+
1 0 0 −1
0 1 0
0
0 0 1
0
−2 0 0
3
, iloczyn
3 0 0 1
0 1 0 0
0 0 1 0
2 0 0 1
·
1 0 0 −1
0 1 0
0
0 0 1
0
−2 0 0
3
.
5. Niech A = (1, 0, 0) , B = (0, 2, 2) , C = (15, 5, 2) , O = (0, 0, 0) .
Znale´z´c obje
,
to´s´c czworo´scianu OABC .
Znale´z´c jakikolwiek wektor ~v 6= ~0 =
−−−−→
[0, 0, 0] prostopad ly do p laszczyzny ABC .
Znale´z´c pole tr´ojka
,
ta ABC i wyja´sni´c, czy ten tr´ojka
,
t jest ostroka
,
tny, prostoka
,
tny czy rozwartoka
,
tny.
Znale´z´c r´ownanie p laszczyzny ABC .
Znale´z´c kosinusy obu ka
,
t´ow utworzonych przez p laszczyzne
,
ABC i p laszczyzne
,
o r´ownaniu x + y + z = 1 .
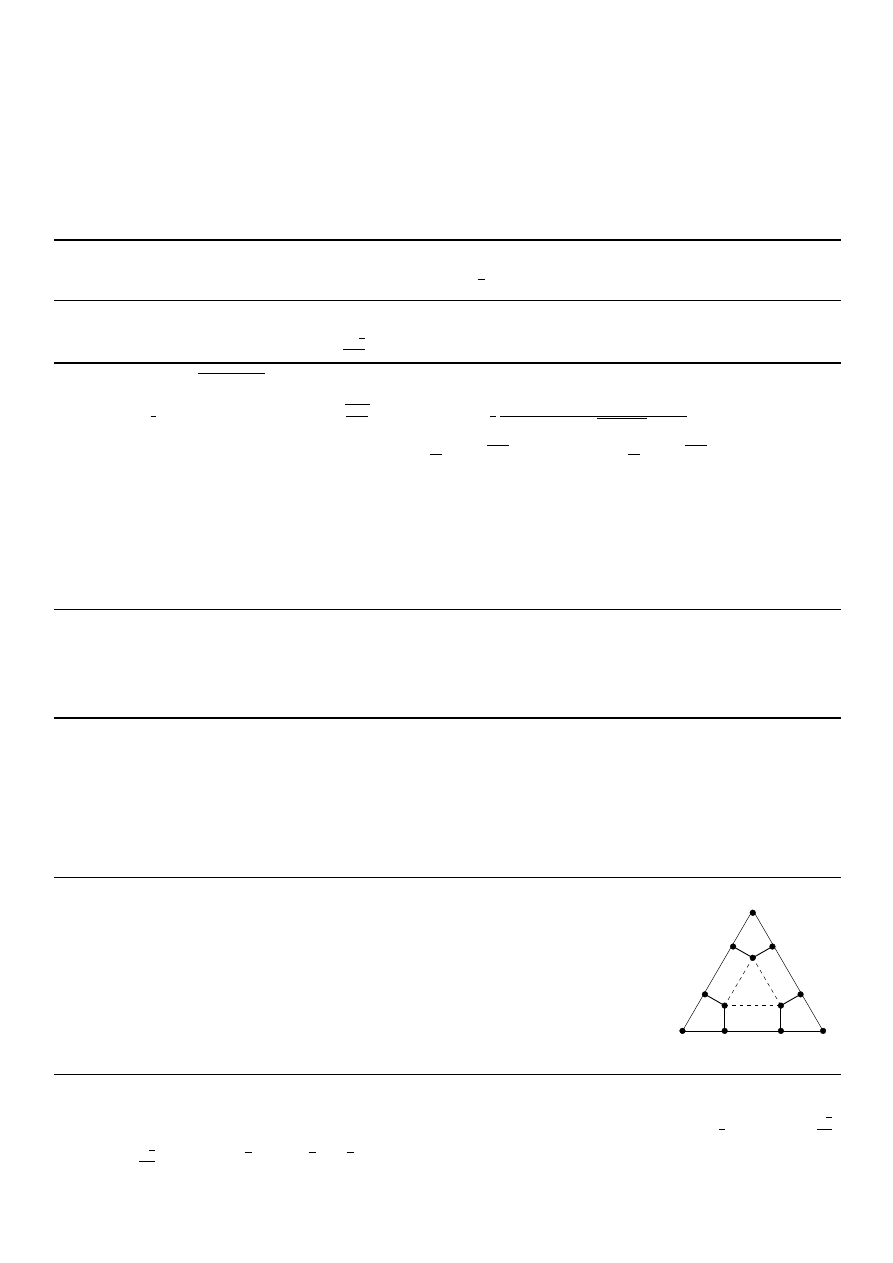
6. Z tekturowego tr´ojka
,
ta r´ownobocznego ABC o boku a odcie
,
to trzy deltoidy AEF G ,
BHIJ , CKLM przy czym: punkty E, J le˙za
,
na boku AB , punkty H, M — na
boku BC , punkty KG na boku CA , za´s punkty F, I, L — wewna
,
trz tr´ojka
,
ta ABC ;
odcinki F E oraz IJ sa
,
prostopad le do boku AB , odcinki IH oraz LM — do boku
BC , odcinki LK oraz F G — do boku CA ; d lugo´s´c ka˙zdego odcink´ow z tych sze´sciu
odcink´ow jest r´owna x . Naste
,
pnie zagie
,
to tekture
,
uzyskuja
,
c pude lko o wysoko´sci x ,
otwarte z g´ory, kt´orego denkiem jest tr´ojka
,
t F IL . Dla jakiego x pojemno´s´c po-
wsta lego pude lka jest najwie
,
ksza?
A
B
C
E
F
G
H
I
J
K
M
L
x
x
x
x
x
x
Informacje po˙zyteczne lub zbe
,
dne: 5
3
= 125 , 5
4
= 625 , 5
5
= 3125 , 5
6
= 15625 , 5
7
= 78125 , 3
2
= 9 , 3
3
= 27 ,
3
4
= 81 , 3
5
= 243 , 3
6
= 729 , 2
6
= 64 , 2
7
= 128 , 2
8
= 256 , 2
9
= 512 , 2
10
= 1024 , sin 210
◦
= −
1
2
, cos 330
◦
=
√
3
2
,
cos 135
◦
= −
√
2
2
, tg 7,5
◦
=
√
6 − 2 −
√
3 +
√
2 .