Fizyka - Literatura

Autor

Tytuł

Wyd.

D. Halliday,

R. Resnick,

J. Walker

Podstawy fizyki, cz. 1-5, PWN, Warszawa

2003

A. Rogalski

Podstawy fizyki dla elektroników,

Skrypt WAT

2002

J. Orear

Fizyka, cz. 1 i 2, WNT, Warszawa

1997

Cz. Bobrowski Fizyka, WNT, Warszawa

1997

Raszewski i

inni

Fizyka ogólna. Przykłady i zadania z fizyki, cz. I.

Rozwiązania i odpowiedzi do zadań z fizyki, cz.II.

Skrypt WAT

1994

T. Kostrzyński

i inni

Ćwiczenia laboratoryjne z fizyki, Skrypt WAT

2007

WWW

www.wtc.wat.edu.pl/ift/dydaktyka.html

 

Istota fizyki

poszukiwanie i poznawanie

podstawowych praw przyrody
fizyka klasyczna – opis makroświata
fizyka współczesna – opis mikroświata
kamienie milowe: teoria względności

i mechanika kwantowa

 

FIZYCZNE PODSTAWY

MECHANIKI

Kinematyka zajmuje się

opisem ruchu ciał bez

uwzględniania przyczyn

które ten ruch wywołały
(Galileusz, XVII w.)

 

Podstawowe definicje

„

układ odniesienia - kartezjański

układ współrzędnych prostokątnych

„

punkt materialny- ciało o znikomo

małych rozmiarach o danej masie i

położeniu

„

położenie cząstki – podanie

współrzędnych cząstki (wektor

położenia)

„

ruch – zmiana położenia względem

układu odniesienia

„

tor (trajektoria) cząstki – linia którą

zakreśla poruszająca się cząstka

„

przemieszczenie

k

z

j

y

i

x

z

y

x

r

r

r

r

r

⋅

+

⋅

+

⋅

=

=

)

,

,

(

ϕ

θ

)

,

,

(

θ

ϕ

r

r =

r

ϕ

θ

cos

sin

r

x =

ϕ

θ

sin

sin

r

y =

θ

cos

r

z =

w układzie sferycznym

X

Y

Z

A

r

z

y

x

k

r

j

r

i

r

A

B

r

r

r

r

r

r

−

=

Δ

B

 

Prędkość

cząstka porusza się po krzywoliniowym torze z

punktu A do B w czasie Δt przebywając drogę Δs

„

prędkość średnia

„

prędkość chwilowa

„

wartość liczbowa prędkości

jest równa pochodnej drogi

względem czasu

t

r

v

Δ

Δ

=

r

r

dt

r

d

t

r

v

t

r

r

r

=

Δ

Δ

=

→

Δ

lim

0

dt

ds

t

s

v

t

=

Δ

Δ

=

→

Δ

lim

0

k

dt

dz

j

dt

dy

i

dt

dx

dt

r

d

v

r

r

r

r

r

+

+

=

=

y

x

A

B

( )

t

rr

(

)

r

r

t

t

r

r

r

r

Δ

+

=

Δ

+

rr

Δ

s

Δ

vr

tor

 

Przyspieszenie

dt

v

d

t

v

a

t

r

r

r

=

Δ

Δ

=

→

Δ

lim

0

2

2

dt

r

d

dt

r

d

dt

d

dt

v

d

a

r

r

r

r

=

⎟

⎠

⎞

⎜

⎝

⎛

=

=

t

i

v

v

r

r =

( )

v

dt

i

d

i

dt

dv

i

v

dt

d

a

t

t

t

r

r

r

r

+

=

=

n

t

a

a

a

r

r

r

+

=

dt

dv

a

t

=

r

v

v

dt

di

a

t

n

2

=

=

przyspieszenie styczne

szybkość zmiany wartości v

przyspieszenie normalne

szybkość zmiany kierunku ruchu

(r – promień krzywizny)

i

t

wektor jedn.

styczny do toru

y

x

( )

t

rr

ar

t

ar

tor

n

ar

 

Ruch po okręgu

Ruch po okręgu - przypadek ruchu krzywoliniowego,

gdy promień jest stały r=const

r

v

r

r

r

×

=

ω

ω - prędkość kątową
ε - przyspieszenie kątowe

Przyspieszenie liniowe:

dt

d

α

ω

r

r =

dt

d

ω

ε

r

r =

dt

r

d

r

dt

d

dt

v

d

a

r

r

r

r

r

r

×

+

×

=

=

ω

ω

Przyspieszenie styczne i normalne (dośrodkowe)

r

r

a

a

a

n

t

r

r

r

r

r

r

⋅

−

×

=

+

=

2

ω

ε

)

(

)

(

)

(

b

a

c

c

a

b

c

b

a

r

r

r

r

r

r

r

r

r

⋅

−

⋅

=

×

×

tożsamość

(

)

(

)

(

)

r

r

r

r

v

dt

r

d

r

r

r

r

3

2

1

r

r

r

r

r

r

r

r

r

r

2

0

ω

ω

ω

ω

ω

ω

ω

ω

ω

−

=

⋅

⋅

−

⋅

⋅

=

×

×

=

×

=

×

=

r

s

⋅

Δ

=

Δ

α

r

v

⋅

=

ω

W układzie biegunowym do opisu ruchu stosujemy:

α - położenie kątowe

r

v

Δs

Δα

ω

ε

a

t

a

n

r

r

r

v

r

r

v

a

n

r

r

r

2

2

2

−

=

−

=

 

Dynamika – badanie przyczyn

ruchu (Newton, XVIII w.)

Oddziaływania fundamentalne

Oddziaływania

Źródło

Intensywność

względna

Promień

działania

Grawitacyjne

Masa

10

-39

Daleko-

zasięgowe

Słabe

Cząstki elementarne

10

-15

Krótko-

zasięgowe

(10

-15

m)

Elektro-

magnetyczne

Ładunki elektryczne

10

-2

Daleko-

zasięgowe

Jądrowe (silne)

Hadrony (protony,

neutrony, mezony)

1

Krótko-

zasięgowe

(10

-15

m)

 

Zasady dynamiki Newtona

„

Ciało pozostaje w spoczynku lub porusza się

ruchem jednostajnym prostoliniowym dopóki nie

zostanie zmuszone za pomocą odpowiednich sił do

zmiany tego stanu (zasada bezwładności)

„

Szybkość zmiany pędu ciała jest równa sile

wypadkowej działającej na to ciało

„

Gdy dwa ciała oddziaływują wzajemnie to siła

wywierana przez ciało drugie na ciało pierwsze jest

równa i przeciwnie skierowana do siły z jaką ciało

pierwsze działa na ciało drugie

A

B

B

A

F

F

⇐

⇐

−

=

r

r

wyp

F

dt

p

d

r

r

=

wyp

F

a

m

dt

v

d

m

dt

v

dm

r

r

r

r

=

=

=

 

(

)

t

v

r

F

F

,

, r

r

r

r

=

dt

v

d

m

a

m

F

r

r

r

=

=

dt

m

F

v

∫

=

r

r

Z równania ruchu można otrzymać prędkość i tor ciała w

dowolnej chwili czasu , odtworzyć ruch przeszły i przewidzieć

poruszanie się w przyszłości ⇒ charakter deterministyczny

Jeżeli znamy masę i siłę działającą na ciało to

II zasada Newtona określa tzw. równanie ruchu

dt

v

r

∫

= r

r

Równanie ruchu

(

)

dt

r

d

t

r

v

v

r

r

r

r

=

=

,

 

Przykład rozwiązywania

równania ruchu

gdzie stałą C

1

wyznaczamy z warunków

początkowych: x

0

, v

0

– położenie i

prędkość w początkowej chwili czasu t

0

=0

Z równania ruchu otrzymujemy wyrażenia prędkość i tor ciała

Rozpatrzmy ruch jednowymiarowy pod wpływem stałej siły F

masa ciała m, przyspieszenie a=F/m=const.

Oś OX wybieramy w kierunku działania siły, więc

(

)

0

,

0

,

x

r

=

r

2

2

dt

x

d

dt

dv

a

=

=

1

C

at

dt

a

v

+

=

=

∫

( )

1

1

0

0

0

C

C

a

v

v

=

+

⋅

=

=

0

v

at

v

+

=

(

)

2

0

2

0

2

C

t

v

at

dt

v

at

dt

v

x

+

+

=

+

=

=

∫

∫

( )

2

0

0

C

x

x

=

=

0

0

2

2

x

t

v

at

x

+

+

=

(

)

0

,

0

,

F

F

=

r

dt

v

d

a

r

r =

(

)

0

,

0

,

v

v

=

r

 

Zasady zachowania –

najbardziej

fundamentalne prawa

wyrażają stałość danej wielkości

fizycznej w trakcie określonych

procesów fizycznych
zasady zachowania: pędu, momentu

pędu, energii;
ładunku, liczby nukleonów, liczby

leptonowej

 

Prawo zachowania energii

mechanicznej

„

Energia mechaniczna układu jest sumą energii potencjalnej

i kinetycznej wszystkich jego składników

„

gdy układ jest izolowany od otoczenia i siła zachowawcza

wykonuje pracę W

AB

nad jednym z ciał układu to zachodzi

zmiana energię kinetycznej ciała w energię potencjalną układu

„

jeżeli wszystkie siły działające na cząstkę są zachowawcze, to

całkowita energia cząstki w każdym jej położeniu jest

wielkością stałą, zwaną całkowitą energią mechaniczną

AB

W

K =

Δ

AB

W

U

−

=

Δ

U

+

K

E

mech

=

mech

B

B

A

A

E

const

=

U

+

K

=

U

+

K

=

(

)

A

B

A

B

U

U

=

K

K

−

−

−

 

Zasada zachowania energii

„

jeżeli w układzie oprócz sił zachowawczych działa siła

niezachowawcza (rozpraszająca) np. siła tarcia, to zmiana

energii kinetycznej cząstek jest równa:

„

korzystając z definicji energii potencjalnej otrzymujemy, że

praca sił rozpraszających jest <0 i równa zmianie E

mech

„

energia układu izolowanego może przekształcać się z jednej

postaci w inną, jednak energia całkowita w jej różnorodnych

formach nie może być ani stworzona z niczego, ani też

unicestwiona

„

całkowita energia układu izolowanego nie może się zmieniać

mech

A

B

A

B

AB

E

U

K

U

U

K

K

rozp

W

Δ

=

Δ

+

Δ

=

−

+

−

=

)

(

)

(

)

(

)

(

)

(

rozp

W

zach

W

W

K

AB

AB

AB

+

=

=

Δ

0

=

Δ

+

Δ

+

Δ

wew

E

U

K

(

)

rozp

W

E

bo

AB

wew

−

=

Δ

 

Zasada zachowania pędu

„

całkowity pęd izolowanego i zamkniętego układu cząstek pozostaje

stały

(jeśli na układ cząstek nie działają siły zewnętrzne lub ich wypadkowa

jest równa zeru, to całkowity pęd układu nie ulga zmianie)

„

pęd początkowy jest równy pędowi końcowemu

„

jeśli wypadkowa sił zewnętrznych jest wzdłuż pewnej osi równa zeru,

to składowa pędu w tym kierunku nie ulega zmianie

const

v

m

v

m

v

m

v

m

N

i

i

i

N

N

=

=

+

+

+

∑

=1

2

2

1

1

r

r

L

r

r

konc

pocz

p

p

r

r

=

konc

x

pocz

x

p

p

=

const

p

dt

dp

F

=

⇒

=

⇒

=

0

0

 

Przykład:

Zderzenie niesprężyste (idealne)

1

1

V

m

2

2

V

m

1

2

1

u

m

m

+

Zasada zachowania pędu

Zasada zachowania energii

(

)

1

2

1

2

2

1

1

u

m

m

V

m

V

m

⋅

+

=

+

(

)

E

u

m

m

V

m

V

m

Δ

+

⋅

+

=

+

2

2

2

2

1

2

1

2

2

2

2

1

1

E

Δ

2

1

2

2

1

1

1

m

m

v

m

v

m

u

+

+

=

strata energii

 

Momentu pędu

„

moment pędu (kręt) cząstki o pędzie p i znajdującej się w

punkcie określonym wektorem wodzącym r wynosi:

„

wektor momentu pędu jest prostopadły do płaszczyzny

wyznaczonej przez p i r przedstawiamy go w postaci:

p

r

v

m

r

=

L

r

r

r

r

r

×

=

×

(

)

(

)

(

)

x

y

z

x

y

z

z

y

x

yp

xp

k

xp

zp

j

zp

yp

i

p

p

p

z

y

x

k

j

i

L

−

+

−

+

−

=

=

=

r

r

r

r

r

r

r

p

sin

mv

r

=

L

⊥

= r

φ

φ

L

r

rr

p

r

x

z

y

⊥

r

r

 

Zachowanie momentu pędu

„

moment siły

„

zmiana momentu pędu w czasie

„

jeżeli wypadkowy moment sił zewnętrznych

działających na układ jest równy zeru, to

całkowity moment pędu tego układu jest stały

0

F

r

T

=

×

=

r

r

r

∑

const

=

L

r

F

r

T

r

r

r

×

=

(

)

T

=

F

r

=

F

r

dt

p

r

d

=

dt

L

d

r

r

r

r

r

3

2

1

r

r

r

r

r

×

×

+

×

=

×

=0

p

v

T=0 gdy: r=0, lub F=0, lub F || r

 

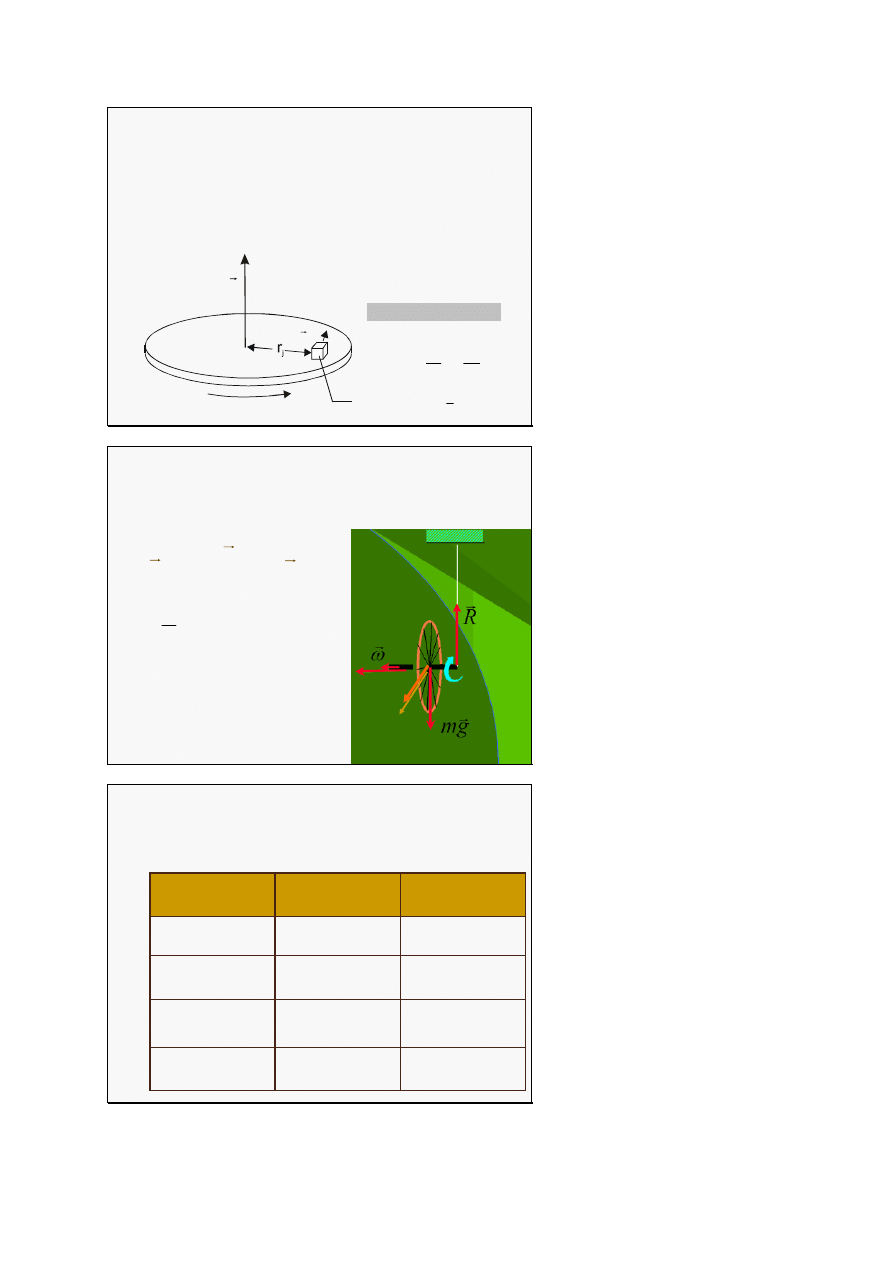
Obracający się dysk

rozważmy ciało obracające się z prędkością

ω

wokół osi przechodzącej przez środek masy ciała

m

j

Δ

L

j

v

( )

(

)

ω

ω

∑ Δ

=

Δ

∑

=

Δ

∑

j

2

j

j

j

j

j

j

j

m

r

r

m

r

v

m

r

=

L

ω

I

=

L

mj

r

=

I

2

j

Δ

∑

∫

dm

2

r

=

I

gdzie

nazywamy momentem bezwładności

ε

ω

r

r

r

r

I

dt

d

I

=

dt

L

d

=

=

T

2

I

2

1

ω

=

K

konc

pocz

ω

ω

konc

pocz

I

I

=

Dzielimy ciało na małe elementy o masie Δm

j

 

Precesja pod wpływem siły

ciężkości

F

r

T

r

r

r

×

=

dt

L

d

T

r

r =

t

T

L

Δ

=

Δ

r

r

gr

r

r

m

r

T

×

=

L

L

L

r

r

r

Δ

+

=

'

Lr

Tr

Lr

Δ

moment siły, tak więc i zmiana

momentu pędu jest skierowana

w naszą stronę w płaszczyźnie

poziomej powodując precesję

g

m

R

r

r

−

=

Na obracające się koło o

momencie pędu L działa moment

siły T powodujący zmianę ΔL

 

Analogia ruchu

postępowego i obrotowego

Ruch

postępowy

Ruch

obrotowy

Wielkości

m, v, a

I, ω, ε

Energia

kinetyczna

mv

2

/2

Iω

2

/2

II Zasada

dynamiki

F=ma

F=dp/dt

T=Iε

T=dL/dt

pęd, moment

pędu

p=mv

L=Iω