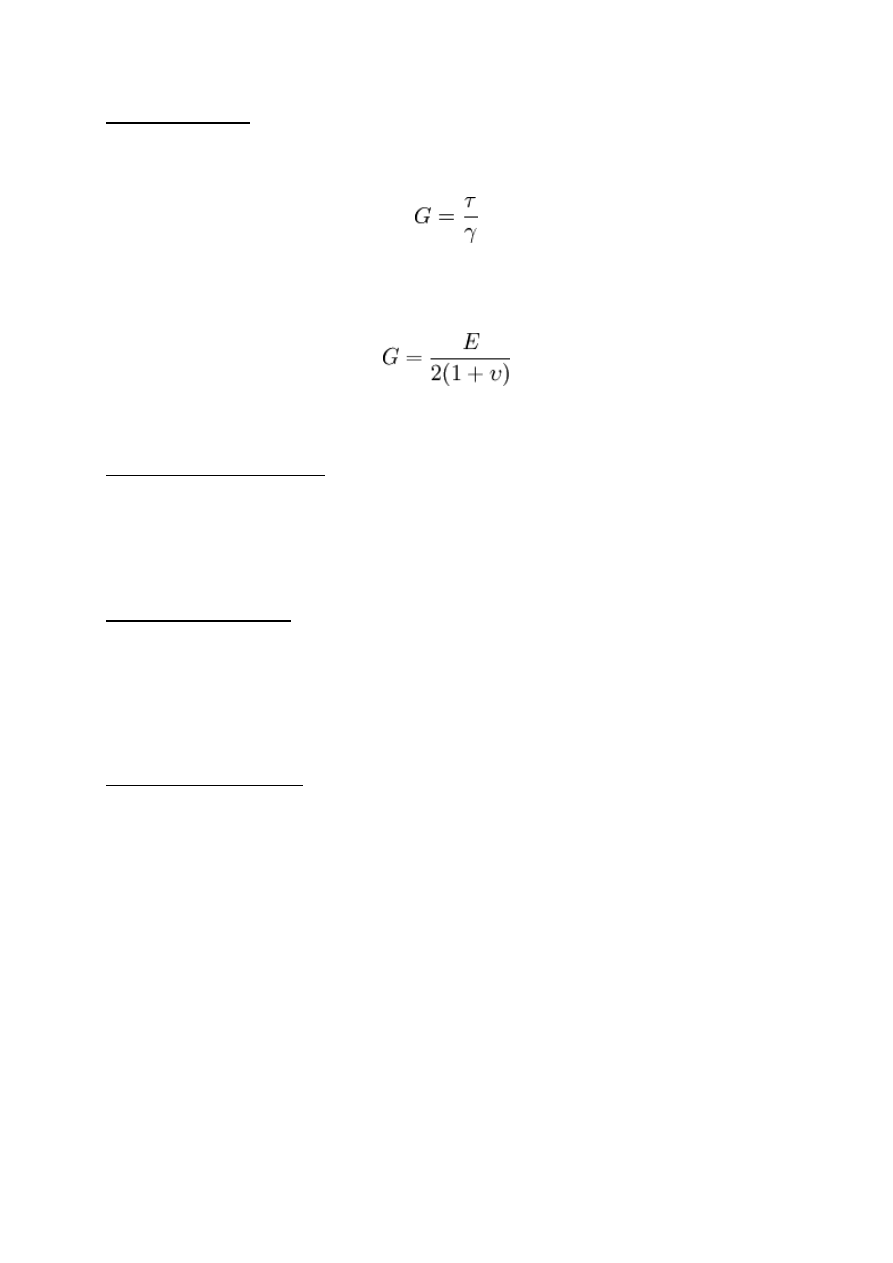
Moduł Kirchhoffa (G) (inaczej moduł odkształcalności postaciowej albo moduł
sprężystości poprzecznej) - współczynnik uzależniający odkształcenie postaciowe

materiału od naprężenia, jakie w nim występuje. Jednostką modułu Kirchhoffa jest
paskal. Jest to wielkość określająca sprężystość materiału.

gdzie τ - naprężenia ścinające, γ - odkształcenie postaciowe

Moduł Kirchhoffa dla materiałów izotropowych bezpośrednio zależy od modułu Younga i

współczynnika Poissona:

gdzie υ - współczynnik Poissona, E - moduł Younga

Odkształcenie postaciowe to zmiana kształtu (odkształcenie) ośrodka ciągłego przy
zachowaniu długości odcinków równoległych do osi układu współrzędnych.

Przykładem odkształcenia postaciowego może być ścinanie lub skręcanie
Należy zwrócić uwagę, że można mówić o odkształceniu postaciowym tylko w odniesieniu

do konkretnego układu odniesienia. Przy jego zmianie odkształcenie może okazać się
odkształceniem liniowym bądź ich złożeniem.

Odkształcanie liniowe - to zmiana kształtu wzdłuż jednego z wymiarów ciała.
Odkształcenia liniowe mogą nastąpić pod wpływem siły zewnętrznej, zmiany temperatury

lub innego czynnika fizycznego. Siła wewnętrzna (siła sprężystości) może spowodować
odkształcenie będące reakcją na wcześniejsze odkształcenie ciała przez siły zewnętrzne.
Odkształcenia liniowe podłużne dzieli się na odkształcenia spowodowane ściskaniem i

odkształcenia spowodowane rozciąganiem.
Przykładem odkształcenia liniowego jest wydłużanie się rozciąganego drutu, pręta,

sprężyny.

Współczynnik Poissona (ν) jest stosunkiem odkształcenia poprzecznego do

odkształcenia podłużnego przy osiowym stanie naprężenia. Współczynnik Poissona jest
wielkością bezwymiarową i nie określa sprężystości materiału, a jedynie sposób w jaki się
on odkształca.

Materiał

Współczynnik Poissona

Guma

~ 0,50

Magnez 0,35
Tytan

0,34

Miedź

0,33

Aluminium 0,33
Glina

0,30-0,45

Stal nierdzewna

0,30-0,31

Stal

0,27-0,30

Żeliwo

0,21-0,26

Piasek

0,20-0,45

Beton

0,20

Szkło

0,18-0,3

Korek

~ 0,00

Moduł Younga (E) – inaczej moduł odkształcalności liniowej albo moduł sprężystości
podłużnej (w układzie jednostek SI) – wielkość uzależniająca odkształcenie liniowe ε

materiału od naprężenia σ, jakie w nim występuje w zakresie odkształceń sprężystych.
Jednostką modułu Younga jest paskal. Jest to wielkość określająca sprężystość materiału.
Moduł Younga jest hipotetycznym naprężeniem, które wystąpiłoby przy dwukrotnym

wydłużeniu próbki materiału, przy założeniu, że jej przekrój nie ulegnie zmianie
(założenie to spełnione jest dla hipotetycznego materiału o współczynniku Poissona υ =
0).

Prawo Hooke'a – prawo mechaniki określające zależność odkształcenia od naprężenia.

Głosi ono, że odkształcenie ciała pod wpływem działającej na niego siły jest wprost
proporcjonalne do tej siły. Współczynnik między siłą a odkształceniem jest często
nazywany współczynnikiem (modułem) sprężystości.

Ta prawidłowość, sformułowana przez Roberta Hooke'a (1635-1703) w formie "ut tensio

sic vis", pozostaje prawdziwa tylko dla niezbyt dużych odkształceń, nie przekraczających
tzw. granicy Hooke'a (zwanej też granicą proporcjonalności), i tylko dla niektórych
materiałów. Prawo Hooke'a zakłada też, że odkształcenia ciała, w reakcji na działanie sił,

następują w sposób natychmiastowy i całkowicie znikają, gdy przyłożone siły przestają
działać. Takie uproszczenie jest wystarczające jedynie dla ciał o pomijalnie małej
lepkości.

Najprostszym przykładem zastosowania prawa Hooke'a jest rozciąganie statyczne pręta.
Względne wydłużenie takiego pręta jest wprost proporcjonalne do siły przyłożonej do

pręta, do jego długości i odwrotnie proporcjonalne do pola przekroju poprzecznego pręta.
Współczynnikiem proporcjonalności jest moduł Younga E

Prawo Hooke’a dla ogólnego, trójwymiarowego układu naprężeń w przypadku materiału
izotropowego może być zapisane w postaci układu równań:

dla odkształceń liniowych

dla odkształceń kątowych własnych

gdzie:
ε - odkształcenie liniowe w punkcie,

σ - naprężenie liniowe w punkcie,
γ - odkształcenie postaciowe (kątowe) w punkcie,

τ - naprężenie kątowe w punkcie,
G – współczynnik sprężystości postaciowej (poprzecznej) lub moduł Kirchhoffa.

E - moduł Younga
ν - współczynnik Poissona

Rozciąganie osiowe - w wytrzymałości materiałów definiujemy dwa podstawowe
przypadki rozciągania osiowego:
Rozciąganie czyste pręta, w którym do ścianek poprzecznych jednorodnego i

izotropowego pręta pryzmatycznego przyłożone jest obciążenie o stałej gęstości σ o
zwrocie zgodnym z wektorem normalnym powierzchni ścianki poprzecznej (prostopadłym
do ścianki, skierowanym na zewnątrz). Dla tego przypadku wytrzymałościowego znane

jest rzeczywiste rozwiązanie zagadnienia brzegowego liniowej teorii sprężystości.

Rozciąganie proste pręta, które różni się od rozciągania "czystego" tym, że obciążenie

zastępujemy dwójką przeciwnie skierowanych, równych co do wartości i współliniowych
sił skupionych, działających w osi tego pręta. Analityczne rozwiązanie tego przypadku

jest praktycznie niemożliwe, dlatego stosujemy zgodnie z zasadą de Saint-Venanta
rozwiązanie zagadnienia czystego rozciągania przyjmując, że

gdzie A oznacza pole przekroju poprzecznego pręta.

Zasada de Saint-Venanta – uproszczenie powszechnie przyjmowane w wytrzymałości

materiałów. Zasada mówi, że jeśli na sprężyste ciało działa układ sił statycznych
przyłożonych na powierzchni małej w stosunku do powierzchni całego ciała i zastąpimy
ten układ sił dowolnym innym układem – jednak statycznie mu równoważnym (o równej

sumie układu i sumie momentów sił układu względem dowolnego punktu) – to istnieje
taki przekrój tego ciała, dostatecznie odległy od miejsca przyłożenia sił, że różnice w
naprężeniach, odkształceniach i przemieszczeniach, pochodzących od obu przypadków

obciążenia, są dowolnie małe (tzn. wpływ działających sił uśrednia się).

Ilustracją zasady jest rysunek. Pokazuje on pręt rozciągany przez parę sił przyłożonych
punktowo na obu końcach. W bezpośredniej bliskości końców stan naprężenia odpowiada
rzeczywistemu stanowi obciążenia. W dostatecznej odległości od końców uśrednia się i

równy jest sumie sił podzielonej przez pole przekroju pręta.

Ściskanie osiowe - w wytrzymałości materiałów definiujemy dwa podstawowe

przypadki ściskania osiowego:
Ściskanie czyste pręta, w którym do ścianek poprzecznych jednorodnego i izotropowego
pręta pryzmatycznego przyłożone jest obciążenie o stałej gęstości σ o zwrocie

przeciwnym do wektora normalnego powierzchni ścianki poprzecznej (prostopadłym do
ścianki, skierowanym do wewnątrz). Dla tego przypadku wytrzymałościowego znane jest
rzeczywiste rozwiązanie zagadnienia brzegowego liniowej teorii sprężystości.

Ściskanie proste pręta, które różni się od ściskania "czystego" tym, że obciążenie

zastępujemy dwójką przeciwnie skierowanych, równych co do wartości i współliniowych
sił skupionych, działających w osi tego pręta. Analityczne rozwiązanie tego przypadku
jest praktycznie niemożliwe, dlatego stosujemy zgodnie z zasadą de Saint-Venanta

rozwiązanie zagadnienia czystego ściskania przyjmując, że

gdzie A oznacza pole przekroju poprzecznego pręta.

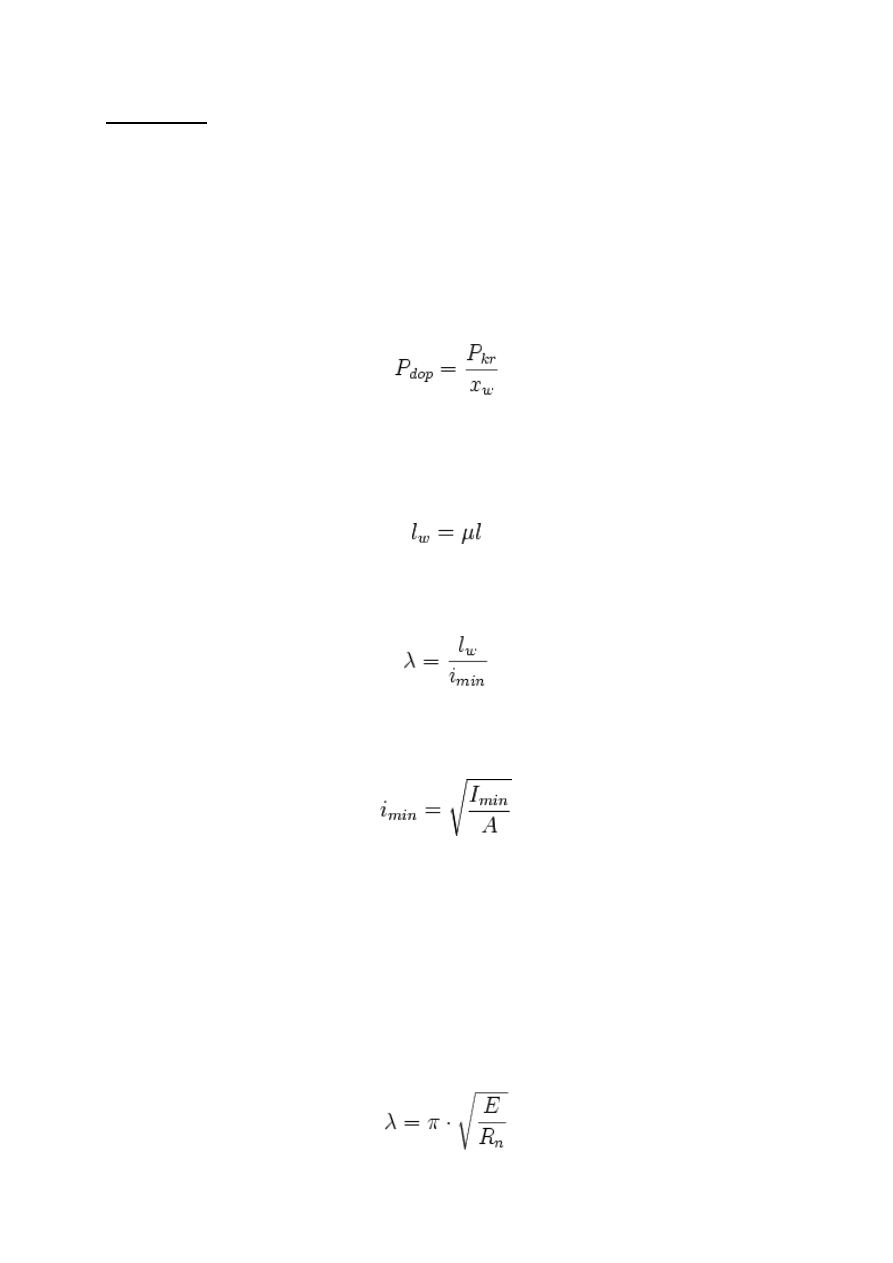
Wyboczenie – w wytrzymałości materiałów odkształcenie (wygięcie) osiowo ściskanego
pręta.

Teoretycznie, gdy pręt jest idealnie symetryczny, a siła ściskająca idealnie osiowa i
centryczna, wyboczenie nie ma prawa wystąpić. W rzeczywistych układach taki warunek

jest jednak bardzo rzadko spełniony. Pręty zawsze mają pewne niedokładności
wykonania, siły mogą być przykoszone lub obciążać pręty ekscentrycznie. W takiej
sytuacji przy odpowiednio dużym obciążeniu, większym niż obciążenie dopuszczalne

Pdop, istnieje niebezpieczeństwo wyboczenia. Wyboczenie może być sprężyste, to znaczy
takie, gdy po odciążeniu pręta wraca on do pierwotnego, wyprostowanego kształtu, lub
niesprężyste, gdy pręt utrzymuje swój wyboczony kształt także po odciążeniu.

Obciążenie dopuszczalne oblicza się ze wzoru:

gdzie:
Pkr – obciążenie krytyczne
xw – współczynnik bezpieczeństwa

Innym ważnym parametrem ściskanego pręta, ze względu na wyboczenie jest jego
długość wyboczeniowa

gdzie:

μ – współczynnik zależny od sposobu podparcia (mocowania pręta) na obu końcach.
l – długość pręta
oraz smukłość pręta

gdzie:

imin – najmniejszy promień bezwładności przekroju wyznaczany ze wzoru:

gdzie:

Imin – najmniejszy główny centralny moment bezwładności przekroju
A – pole powierzchni przekroju.

Dla większości materiałów, smukłością graniczna dla wyboczenia niesprężystego jest

gdzie:

E – współczynnik sprężystości wzdłużnej
Rn – maksymalne naprężenie, dla którego można przyjąć ważność prawa Hooke’a.

Dla wyboczenia sprężystego można wyznaczyć siłę krytyczną z zależności:

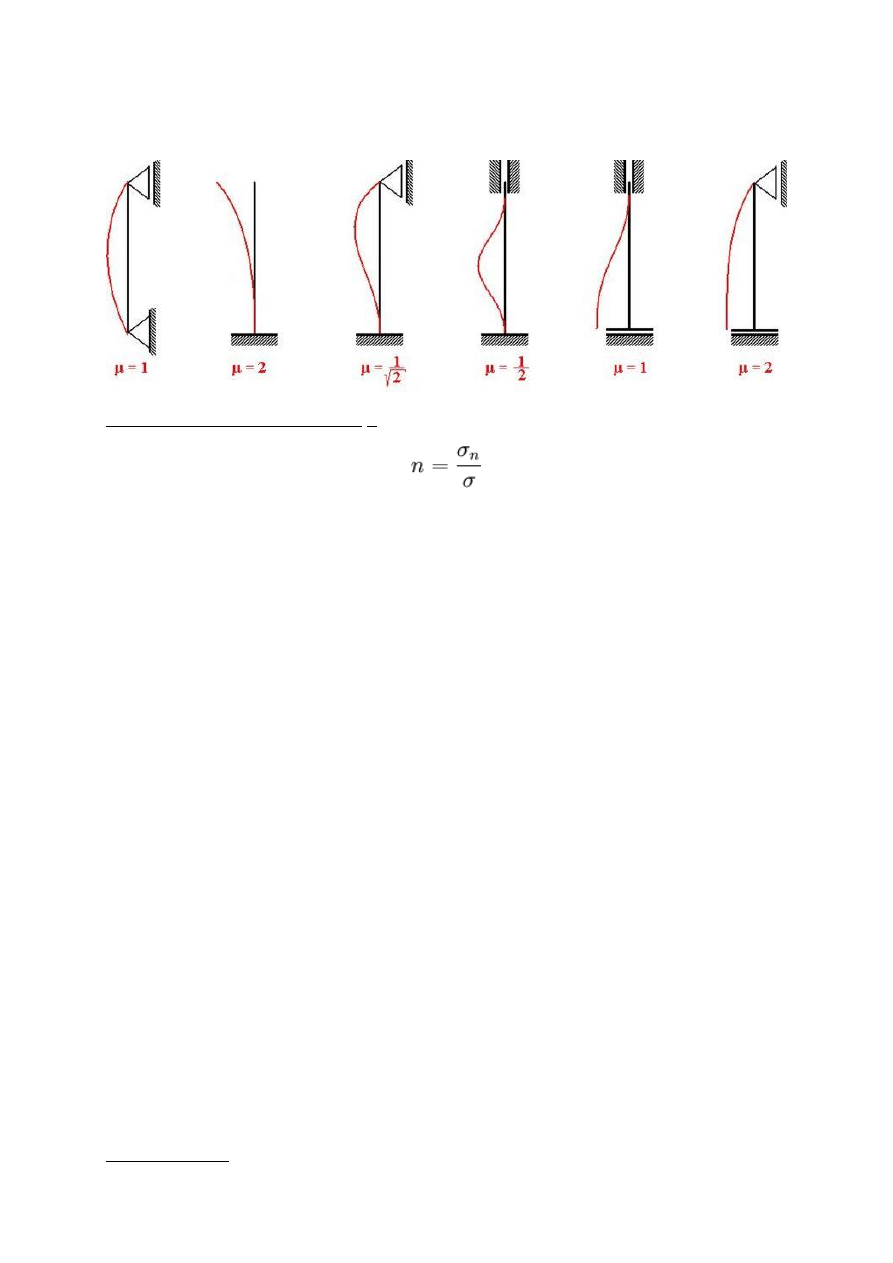
Współczynniki μ oraz sposoby wyboczenia pręta przy różnych rodzajach podparcia
pokazane są na poniższym rysunku:

Współczynnik bezpieczeństwa n - liczba mówiąca, ile razy naprężenie σ występujące
podczas normalnej pracy konstrukcji jest mniejsze od naprężenia niebezpiecznego σn.

Podczas projektowania wprowadza się współczynnik bezpieczeństwa, ponieważ z reguły

nie jest możliwe dokładne określenie wszystkich możliwych obciążeń konstrukcji, metody
obliczeniowe cechuje pewien błąd, materiały nie są idealnie jednorodne a ich parametry

cechuje pewien rozrzut, mogą wystąpić niedokładności związane z technologią
wykonania, a elementy ulegają zużyciu, korozji itp.

Współczynnik bezpieczeństwa jest to liczba większa od jedności mówiąca ile razy wielkość
dopuszczalna jest mniejsza od wielkości uznawanej za niebezpieczną. Stosowany jest do
naprężeń obciążeń i stanowi przedmiot szeregu norm, szczególnie duże wartości osiąga w

obliczeniach stateczności. Współczynnik bezpieczeństwa jest zmienny i wynosi od 1,5 do
3 dla materiałów plastycznych i od 8 do 12 dla materiałów kruchych, uwzględnia wartości
technologiczne, warunki pracy i dopuszczalne błędy.

Warunki współczynników bezpieczeństwa: -jednorodność materiału -jakość wykonania -

naprężenia wstępne w czasie procesu technologicznego np. kucia, odlewu, spawania -
obciążenia przewidywane i przypadkowe -czynnik niedoskonałości ludzkiej -
niedoskonałość metod obliczeniowych -wpływ czasu pracy- procesy korozji, ścierania,

wietrzenia -zmęczenie materiału -spiętrzenie naprężeń

Współczynnik bezpieczeństwa dla obciążeń stałych dobiera się: -dla stali konstrukcyjnej

x=2,0-2,3 -dla stali sprężynowej x=1,6 -dla żeliwa x=3,5

Aby określić współczynnik bezpieczeństwa należy ustalić następujące czynniki: -stopień

znaczenia części dla pewności działania maszyny -poprawność przyjętego schematu
obciążeń przy obliczeniach wytrzymałościowych -prawidłowość uwzględnienia rodzaju
obciążenia (stale, zmienne) -pewność odnośnie do materiału -przewidywana jakość

wykonania Kształt części i stan jej powierzchni

Współczynnik bezp. zależy od rodzaju zastosowanego materiału, przeznaczenia
zastosowanego elementu, czasu pracy, warunków pracy, grubości materiału itd.
Obliczeniowy wsp. wytrzymałościowy złącza spawanego składa się z dwóch elementów

z=z1*zdop z1 zależy od rodzaju połączenia spawanego, zdop zależy od technologii
wykonania spoiny. Wsp. ten przyznawany jest poszczególnym zakładom przez Urząd
Dozoru Technicznego.

Moment gnący w dowolnym przekroju belki zginanej to algebraiczna suma momentów
sił zewnętrznych działających po jednej stronie (lewej lub prawej) rozważanego przekroju

względem środka masy tego przekroju.

Moment skręcający – w mechanice moment pary sił, którego wektor jest równoległy do
osi elementu skręcanego, najczęściej pręta lub wału.

O wielkości skręcenia na jednostkę długości pręta, wywołanego przez dany moment
skręcający decydują:

- wytrzymałość materiału, z którego wykonany jest poddany skręcaniu element,
- charakteryzowana przez moduł Kirchhoffa,
- "sztywność" przekroju konkretnego pręta, wyrażana przez wskaźnik wytrzymałości na

skręcanie.