Zad 1. Wykaż, że jeżeli g, h są holomorficzne w punkcie z

0

i h ma w nim

zero jednokrotne, to

res

z=z

0

g(z)

h(z)

=

g(z

0

)

h

0

(z

0

)

.

Zad 2. Oblicz całki:

a)

Z

C(0,2)

tg πzdz;

b)

Z

C(0,1)

cosh

1
z

dz;

c)

Z

C(i,3)

cos

1

z − i

dz;

d)

Z

C(1,4)

sin z

e

iz

+ 1

dz;

e)

Z

C(1/2π,1/5π)

1

sin 1/z

dz;

f) dla jakich n ∈ N

Z

C(0,1)

(e

z

−

1

z

n

)

−1

dz = 0?

Zad 3. Oblicz całkę:

Z

C(0,10)

|z|e

1

z−1

dz.

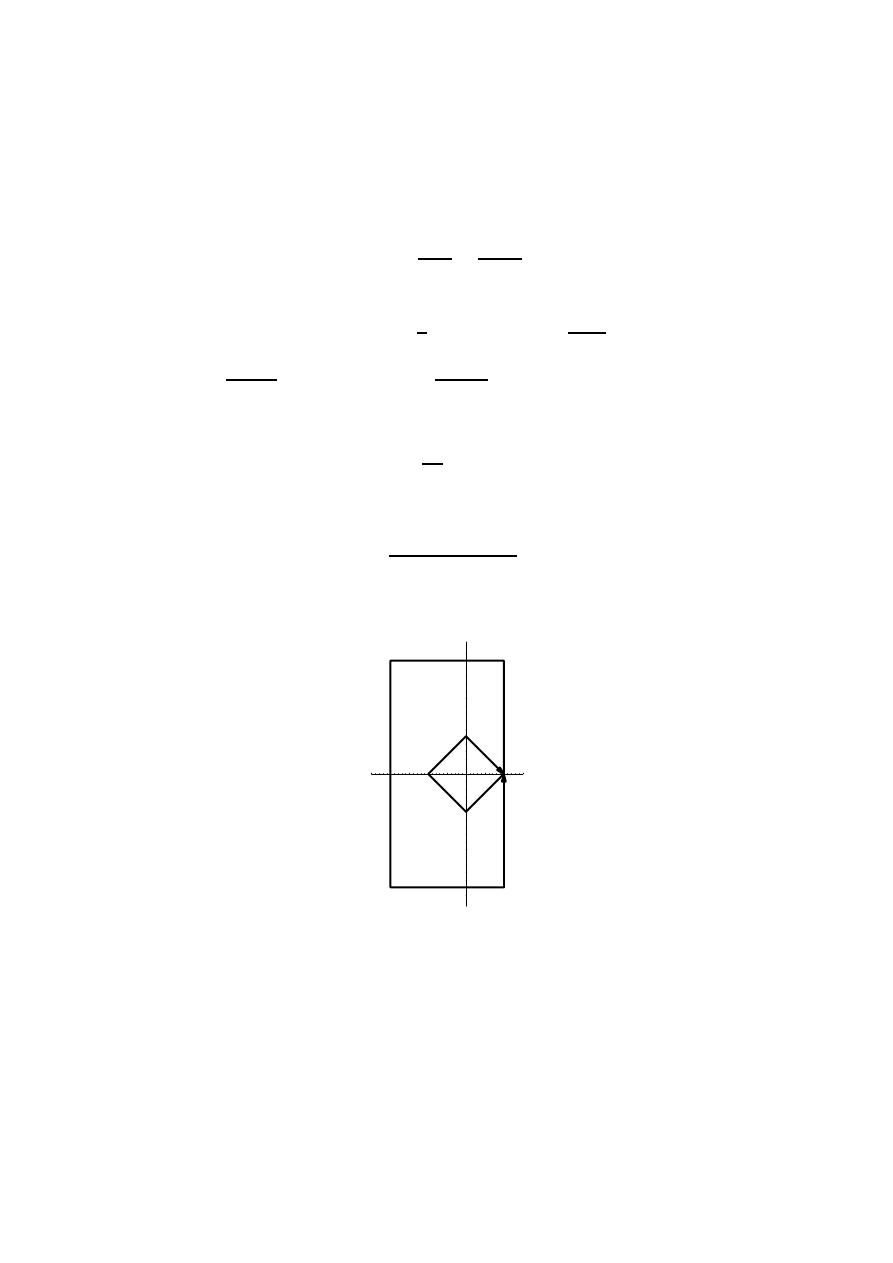
Zad 4

∗

. Oblicz całkę

Z

Γ

dz

(z

2

+ 4) cos(1/z)

,

gdzie Γ zaznaczono na rys.

-2.5 -2 -1.5 -1 -0.5

0.5

1

1.5

-3

-2

-1

1

2

3