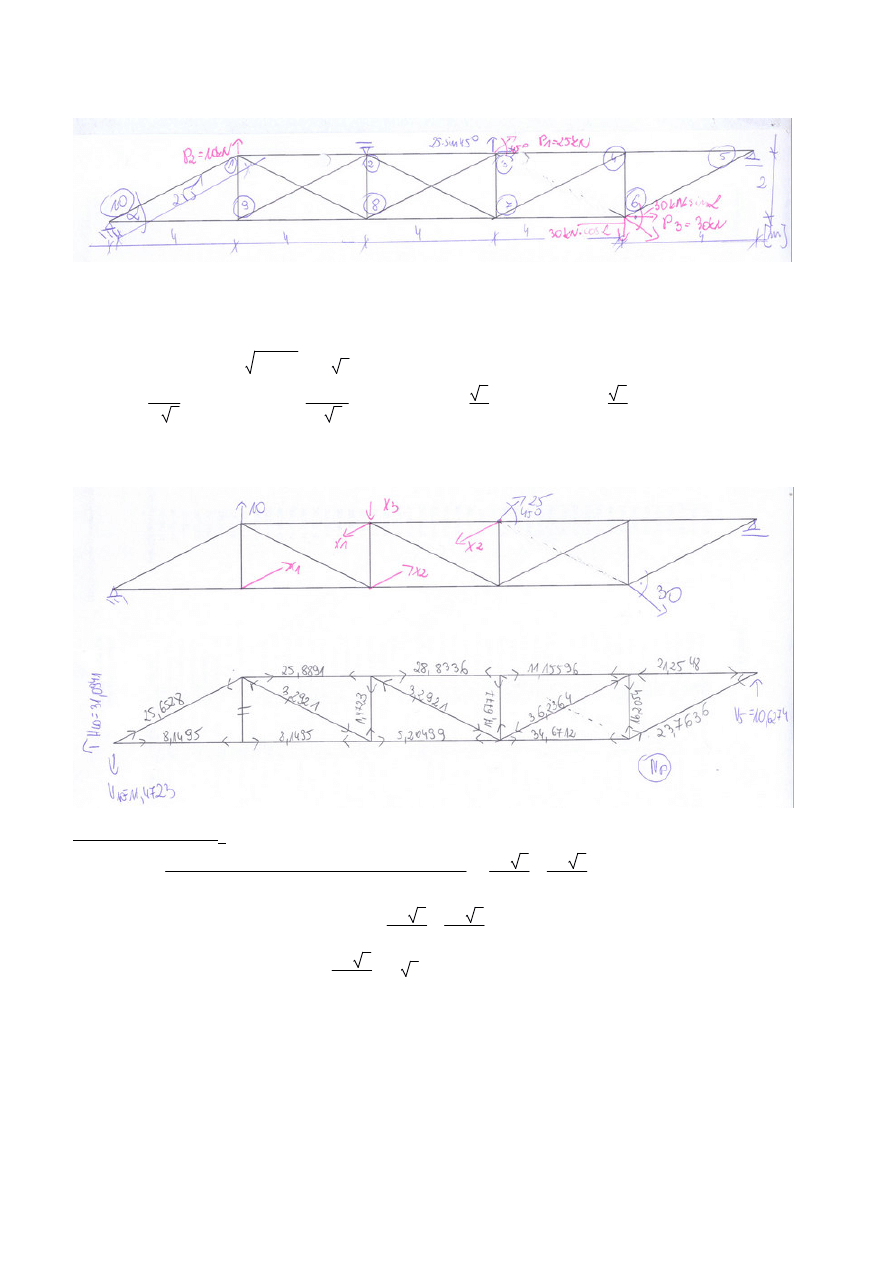
Zało
ż
enia:
EA
const
=
a
4
:=
h
2
:=
2
2
4
2
+
2
5
⋅
→
sin
α
2
2
5
⋅
:=
cos
α
4
2
5
⋅
(
)
:=
sin45
2
2
:=
cos45
2
2
:=
Układ podstawowy:
Reakcje do wykresy N
P
:
Σ
M10
V5
10
−
a
⋅
25 sin45
⋅
3
⋅
a
⋅
−
25 cos45
⋅
h
⋅
+
30 cos
α
⋅
4
⋅
a
+
5 a
⋅
48
5
⋅
5
25
2
⋅
4
−
2
−
→
:=
kN
V5 10.62741782
=
kN
Σ
Y
V10
10
25 sin45
⋅
+
30 cos
α
⋅
−
V5
+
(
)
25
2
⋅
4
12
5
⋅
5
−
8
+
→
:=
kN
V10
11.47227162
=
kN
Σ
X
H10
30 sin
α
⋅
25 cos45
⋅
+
25
2
⋅
2
6
5
⋅
+
→
:=
kN
H10
31.09407739
=
kN
1
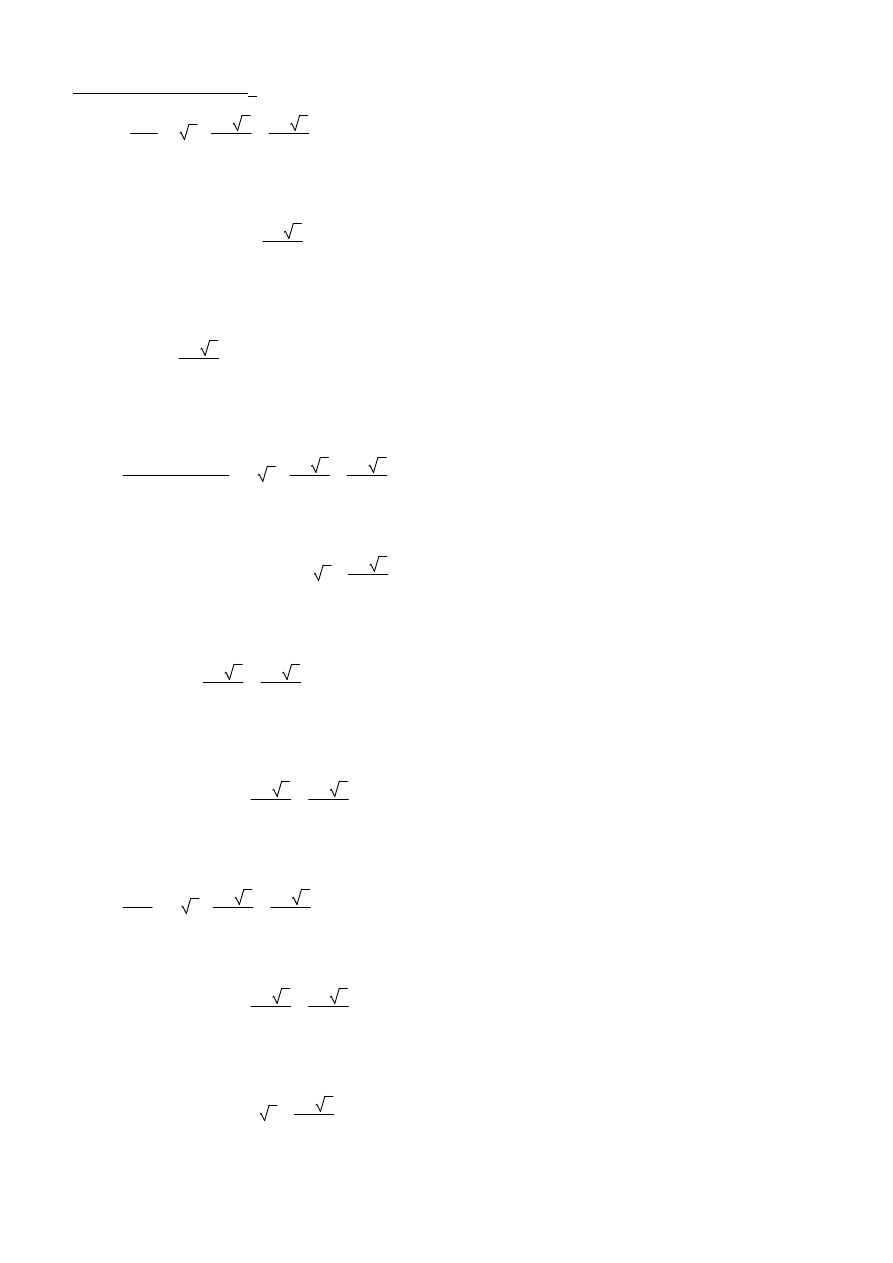
Obliczenia sił do wykresy N
P
P10.1
V10
sin
α
5
25
2
⋅
4
12
5
⋅
5
−
8
+
⋅
→
:=
kN
P10.1 25.6527792
=
kN
P10.9
H10 P10.1 cos
α
⋅
−
54
5
⋅
5
16
−
→
:=
kN
P10.9 8.14953416
=
kN
P9.8
P10.9
54
5
⋅
5
16
−
→
:=
kN
P9.8
8.14953416
=
kN
P1.8
10
−
P10.1 sin
α
⋅
+
sin
α
5
12
5
⋅
5
25
2
⋅
4
−
2
+
⋅
−
→
:=
kN
P1.8
3.29209942
=
kN
P1.2
P10.1 cos
α
⋅
P1.8 cos
α
⋅
+
25
2
⋅
48
5
⋅
5
−
12
+
→
:=
kN
P1.2
25.88908648
=
kN
P2.8
P1.8 sin
α
⋅
25
2
⋅
4
12
5
⋅
5
−
2
−
→
:=
kN
P2.8
1.47227162
=
kN
kN
P8.7
P9.8 P1.8 cos
α
⋅
−
78
5
⋅
5
25
2
⋅
2
−
12
−
→
:=
P8.7
5.20499092
=
kN
P2.7
P2.8
sin
α
5
12
5
⋅
5
25
2
⋅
4
−
2
+
⋅
−
→
:=
kN
P2.7
3.29209942
=
kN
P2.3
P1.2 P2.7 cos
α
⋅
+
75
2
⋅
2
72
5
⋅
5
−
8
+
→
:=
kN
P2.3
28.83362971
=
kN
P3.4
P2.3 25 sin45
⋅
−
25
2
⋅
72
5
⋅
5
−
8
+
→
:=
kN
P3.4
11.15596018
=
kN
2
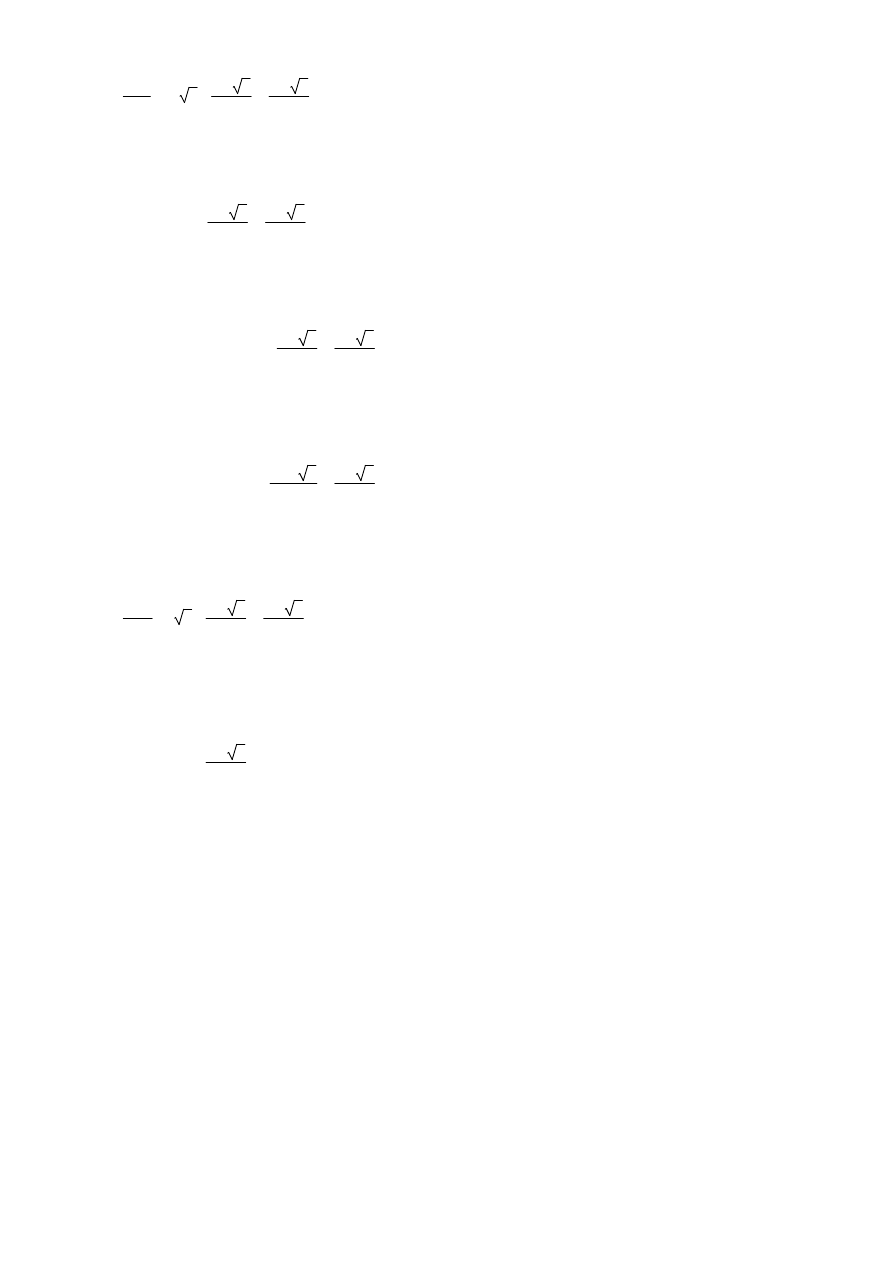
P6.5
V5
sin
α
5
25
2
⋅
4
48
5
⋅
5
−
2
+
⋅
−
→
:=
P6.5
23.76362867
=
kN
P4.5
P6.5 cos
α
⋅
96
5
⋅
5
25
2
⋅
2
−
4
−
→
:=
kN
P4.5
21.25483564
=
kN
P4.6
P6.5
−
sin
α
⋅
30 cos
α
⋅
+
25
2
⋅
4
12
5
⋅
5
+
2
+
→
:=
kN
P4.6
16.20539791
=
kN
P7.6
P6.5 cos
α
⋅
30 sin
α
⋅
+
126
5
⋅
5
25
2
⋅
2
−
4
−
→
:=
kN
P7.6
34.6712435
=
kN
P4.7
P4.6
sin
α
5
25
2
⋅
4
12
5
⋅
5
+
2
+
⋅
→
:=
kN
P4.7
36.23637133
=
kN
P3.7
25 sin45
⋅
25
2
⋅
2
→
:=
kN
P3.7
17.67766953
=
kN
3

Reakcje do wykresy N
3
:
Σ
M10
V5
1 2
⋅
a
⋅
5 a
⋅
2
5
→
:=
Σ
M5
V10
1 3
⋅
a
⋅
5 a
⋅
3
5
→
:=
Obliczenia sił do wykresy N
3
P10.1
V10
sin
α
3
5
⋅
5
→
:=
P10.9
P10.1 cos
α
⋅
6
5
→
:=
P1.8
P10.1
3
5
⋅
5
→
:=
P1.2
P10.1 cos
α
⋅
P10.1 cos
α
⋅
+
12
5
→
:=
P2.8
P1.8 sin
α
⋅
3
5
→
:=
P2.7
3
5
−
1
+
sin
α
2
5
⋅
5
→
:=
P2.3
P1.2 P2.7 cos
α
⋅
−
8
5
→
:=
P3.7
P2.7 sin
α
⋅
2
5
→
:=
P3.6
P3.7
sin
α
2
5
⋅
5
→
:=
4

P6.5
P3.6
2
5
⋅
5
→
:=
P7.6
P3.6 cos
α
⋅
P6.5 cos
α
⋅
+
8
5
→
:=
P4.5
P6.5 cos
α
⋅
4
5
→
:=
P8.7
P7.6 P2.7 cos
α
⋅
+
12
5
→
:=
5

Układ równa
ń
i jego rozwi
ą
zanie:
δ
11 X1
⋅
δ
12 X2
⋅
+
δ
13 X3
⋅
+
∆
1P
+
0
=
δ
21 X1
⋅
δ
22 X2
⋅
+
δ
23 X3
⋅
+
∆
2P
+
0
=
δ
31 X1
⋅
δ
32 X2
⋅
+
δ
33 X3
⋅
+
∆
3P
+
0
=
X1
7.18372635
:=
kN
X2
12.15084239
:=
kN
X3
3.47097683
:=
kN
Rozwi
ą
zanie ko
ń
cowe
Reakcje:
V2
X3 3.47097683
=
:=
kN
Σ
M10
V5
10
−
a
⋅
25 sin45
⋅
3
⋅
a
⋅
−
25 cos45
⋅
h
⋅
+
30 cos
α
⋅
4
⋅
a
+
V2 2
⋅
a
+
5 a
⋅
12.01580855
=
:=
kN
Σ
Y
V10
10
25 sin45
⋅
+
30 cos
α
⋅
−
V5
+
V2
−
9.38968552
=
:=
kN
Σ
X
H10
30 sin
α
⋅
25 cos45
⋅
+
31.09407739
=
:=
kN
Sprawdzenie zgodno
ś
ci odkształce
ń
przez obliczenie przemieszczenia w
ę
zła 5 (pionowe)
V10
3
2
:=
V2
5
2
:=
P10.1
V10
sin
α
3
5
⋅
2
→
:=
P10.9
P10.1 cos
α
⋅
3
→
:=
6

P1.8
P10.1
3
5
⋅
2
→
:=
P1.2
P10.1 cos
α
⋅
P10.1 cos
α
⋅
+
6
→
:=
P2.8
P1.8 sin
α
⋅
3
2
→
:=
P8.7
P10.9 P1.8 cos
α
⋅
+
6
→
:=
P2.7
P2.8
−
V2
+
sin
α
5
→
:=
P2.3
P1.2 P2.7 cos
α
⋅
−
4
→
:=
P3.7
P2.7 sin
α
⋅
1
→
:=
P4.7
P3.7
sin
α
5
→
:=
P6.5
1
sin
α
5
→
:=
P7.6
P6.5 cos
α
⋅
2
→
:=
P4.5
P6.5 cos
α
⋅
2
→
:=
P2.3 P4.5
−
P4.7 cos
α
⋅
−
0
→
7
Wyszukiwarka
Podobne podstrony:
Mathcad Sprzeglo id 287200
Mathcad straty zbiornik id 287204
Mathcad JB beton wersja 2 id 287131
projekt Mathcad KOMIN moj id 829609
Mathcad 14 (1) id 287078
Eurokody mostowe mathcad nosnosc sworzni id 165476
MathCAD Cwiczenia praktyczne id 287096
instrukcja Mathcad1 2012 id 216 Nieznany
Mathcad KOMIN id 287138
Mathcad Zbyszek obliczenia1 id 287222
Mathcad filarek zew III id 287126
Mathcad projekt 2 moj poprawiony id 287
Mathcad Schody tuuu id 287191
Mathcad stal slup280 id 287201
Mathcad cwiczenia cwmcad id 287 Nieznany
Mathcad projekt metal spawy id 287178
Mathcad Sprzeglo id 287200
więcej podobnych podstron