komin

bmp

komin

bmp

Dane ogólne.

strefa wiatrowa

II A

wysoko

ść

trzonu nad terenem

H

38 m

⋅

:=

ś

rednica zewn

ę

trzna

D

z

1 m

⋅

:=

nominalna temperatura gazów spalinowych

T

n

423 K

⋅

:=

pr

ę

dko

ść

gazów spalinowych

v

10

m

s

⋅

:=

liczba czopuchów

n

c

2

:=

poziomy czopuchów

h

c1

4.5 m

⋅

:=

h

c2

7 m

⋅

:=

stal płaszcza

St4V

wyposa

ż

enie

wg obowi

ą

zuj

ą

cych przepisów

warunki gruntowe

piasek drobny

okres eksploatacji komina

T

e

10 lat

⋅

:=

liczba segmentów

n

s

6

:=

wysko

ść

najni

ż

szego segmentu (cokołu)

h

c

8 m

⋅

:=

wysoko

ś

ci pzostałych segmentów

h

s

6 m

⋅

:=

grubo

ś

ci

ś

cianek i pozimy ko

ń

ców poszczególnych segmentów ( od podstawy komina )

segment najni

ż

szy

i

1

:=

t

i

16 mm

⋅

:=

z

i

h

c

:=

z

i

8 m

=

segment

i

2

:=

t

i

10 mm

⋅

:=

z

i

z

1

i

1

−

(

) h

s

⋅

+

:=

z

i

14 m

=

segment

i

3

:=

t

i

9 mm

⋅

:=

z

i

z

1

i

1

−

(

) h

s

⋅

+

:=

z

i

20 m

=

segment

i

4

:=

t

i

8 mm

⋅

:=

z

i

z

1

i

1

−

(

) h

s

⋅

+

:=

z

i

26 m

=

segment

i

5

:=

t

i

7 mm

⋅

:=

z

i

z

1

i

1

−

(

) h

s

⋅

+

:=

z

i

32 m

=

segment

i

6

:=

t

i

6 mm

⋅

:=

z

i

z

1

i

1

−

(

) h

s

⋅

+

:=

z

i

38 m

=

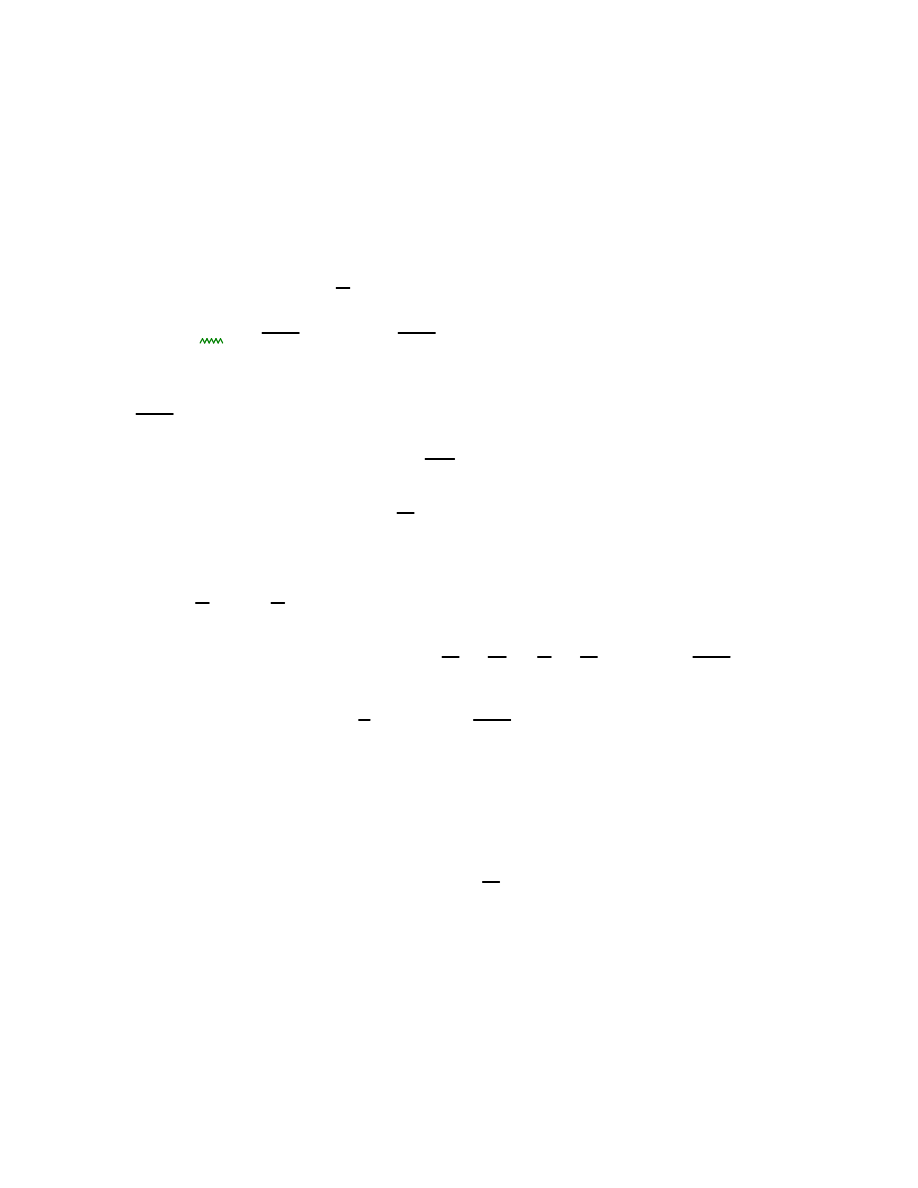
1. Wpływy termiczne na wła

ś

ciwo

ś

ci mechaniczne stali.

Trzon komina jest jednowarstwowy i nie posiada izolacji termicznej.

temperatura awaryjna

T

w

1.2 T

n

⋅

:=

T

w

507.6 K

=

Wyznacznie współczynnika przenikania ciepła.

współczynnik napływu ciepła

v

10

m

s

=

<

16 m/s

α

n

2 v

⋅

8

+

:=

α

n

α

n

W

m

2

K

⋅

⋅

:=

α

n

28

W

m

2

K

⋅

=

współczynnik odpływu ciepła

H

38 m

=

<

40 m

α

o

26

W

m

2

K

⋅

⋅

:=

współczynnik przenikania ciepła dla stali

λ

1

58

W

m K

⋅

⋅

:=

promie

ń

zewn

ę

trzny

r

z

D

z

2

:=

r

z

500 mm

=

r

1

r

z

:=

współczynnik uwzgl

ę

dniaj

ą

cy wpływ krzywizny

ś

cianki

χ

1

0.49

0.57

r

z

r

1

⋅

+

0.06

r

z

r

1













2

⋅

−

:=

χ

1

1

=

odwrotno

ść

współczynnika przenikania ciepła

k'

1

α

n

t

1

λ

1

χ

1

⋅

r

z

r

1

⋅













+

1

α

o

+

:=

k'

0.07

m

2

K

⋅

W

=

współczynnik przenikania ciepła

k

1

k'

:=

k

13.43

W

m

2

K

⋅

=

Temperatura płaszcza w okresie letnim.

przyj

ę

ta temperatura zewn

ę

trzna letnia

T

zl

308 K

⋅

:=

ró

ż

nica temperatur po obu stronach przeszkody

∆

T

T

w

T

zl

−

:=

∆

T

199.6 K

=

spadek temperatury przy napływie ciepła

∆

T

n

k

1

α

n

⋅

∆

T

⋅

:=

∆

T

n

95.75 K

=

temperatura na wewn

ę

trznej powierzchni płaszcza

T

pl

T

w

∆

T

n

−

:=

T

pl

411.85 K

=

Temperatura płaszcza w okresie zimowym.

przyj

ę

ta temperatura zewn

ę

trzna letnia

T

zz

241 K

⋅

:=

ró

ż

nica temperatur po obu stronach przeszkody

∆

T

T

w

T

zz

−

:=

∆

T

266.6 K

=

spadek temperatury przy napływie ciepła

∆

T

n

k

1

α

n

⋅

∆

T

⋅

:=

∆

T

n

127.89 K

=

temperatura na wewn

ę

trznej powierzchni płaszcza

T

pz

T

w

∆

T

n

−

:=

T

pz

379.71 K

=

Wpływ temperatury na wytrzymało

ść

obliczeniow

ą

stali.

normowa wytrzymało

ść

obliczeniowa stali

f

d

235 MPa

⋅

:=

maksymalna temperatura na wewn

ę

trznej powierzchni płaszcza

T

pl

411.85 K

=

>

343 K

Nale

ż

y uwzgl

ę

dni

ć

zmniejszenie si

ę

wytrzymało

ś

ci obliczeniowej stali.

T

T

pl

K

273

−

:=

f

dT

f

d

1.022

0.197 10

3

−

⋅

T

⋅

−

1.590 10

6

−

⋅

T

2

⋅

−

(

)

⋅

:=

f

dT

226.54 MPa

=

Wpływ temperatury na moduł spr

ęż

ysto

ś

ci podłu

ż

nej stali.

warto

ść

normowa

E

205000 MPa

⋅

:=

E

T

E 0.987

0.300 10

3

−

⋅

T

⋅

+

1.857 10

6

−

⋅

T

2

⋅

−

(

)

⋅

:=

E

T

203534.82 MPa

=

2. Wpływ korozji na wytrzymało

ść

stli.

planowany czas u

ż

ytkowania komina

T

e

10 lat

=

stopie

ń

zagro

ż

enia korozyjnego wg tablicy 2 normy

ze wzgl

ę

du na silnie agresywn

ą

atmosfer

ę

zewn

ę

trzn

ą

s

1

1

:=

ze wzgl

ę

du na zasiarczenie w

ę

gla

s

2

3

:=

ze wzgl

ę

du na mo

ż

liwo

ść

wykroplenia kondensatu

s

3

4

:=

∆

t

0.1

1

3

i

s

i

∑

=

⋅

:=

∆

t

0.8

=

współczynnik korozyjny

α

kor

1

1

0.04 T

e.

⋅

∆

t

⋅

+

:=

α

kor

0.76

=

3. Obci

ąż

enie wiatrem w I sytuacji projektowej.

strefa wiatrowa II

teren A

charakterystyczne ci

ś

nienie pr

ę

dko

ś

ci wiatru

q

k

350 Pa

⋅

:=

współczynnik dla czasu eksploatacji 3 lata

D

T

0.65

:=

Współczynnik ekspozycji.

współczynnik przeliczeniowy zale

ż

ny od rodzaju terenu

k

1

:=

wysko

ść

nad poziomem terenu

z

H

m

:=

z

38

=

wykładnik zale

ż

ny od rodzaju terenu

α

0.14

:=

współczynnik ekspozycji

C

e

k

z

10













2

α

⋅

⋅

:=

C

e

1.45

=

Współczynnik aerodynamiczny dla komina stalowego z drabin

ą

włazow

ą

.

H

D

z

38

=

> 25

D

z

H

0.03

=

< 0.04

⇒

C

xo

0.7

:=

( tablica Z2-3 )

pole rzutu bocznego drabiny na płaszczyzn

ę

symetrii

A

d

0.1

m

2

m

⋅

:=

liczba przewodów kominowych

n

1

:=

ś

rednica zewn

ę

trzna komina

D

z

1 m

=

współczynnik aerodynamiczny

C

x

C

xo

2.4

A

d

n D

z

⋅

⋅

+

:=

C

x

0.94

=

3.1. Współczynnik działania porywów wiatru.

podstawowego okres drga

ń

własnych

T

1

0.001

H

2

D

⋅

:=

T

1

1.44

=

cz

ę

stotliwo

ść

drga

ń

własnych

n

1

T

1

:=

n

0.69

=

Współczynnik szczytowej warto

ś

ci obci

ąż

enia.

Ψ

2 ln 600 n

⋅

(

)

⋅

0.577

2 ln 600 n

⋅

(

)

⋅

+

:=

Ψ

3.64

=

Wyznacznie współczynnika

δδδδ

s

.

współczynnik chropowato

ś

ci dla terenu A

r

0.08

:=

współczynnik pozarezonansowego oddziaływania turbulentnego

k

b

2.25

0.227 1

3.24

D

H

⋅

+













⋅

ln H

( )

⋅

−

:=

k

b

1.35

=

logarytmiczny dekrement tłumienia drga

ń

wg tablicy Z3-2

dla komina spawanego jednoprzewodowego bez wykładziny

δ

s

1

0.015

:=

dodatek na poł

ą

czenia kołnierzowe

δ

s

2

0.015

:=

δ

s

1

2

i

δ

s

i

∑

=

:=

δ

s

0.03

=

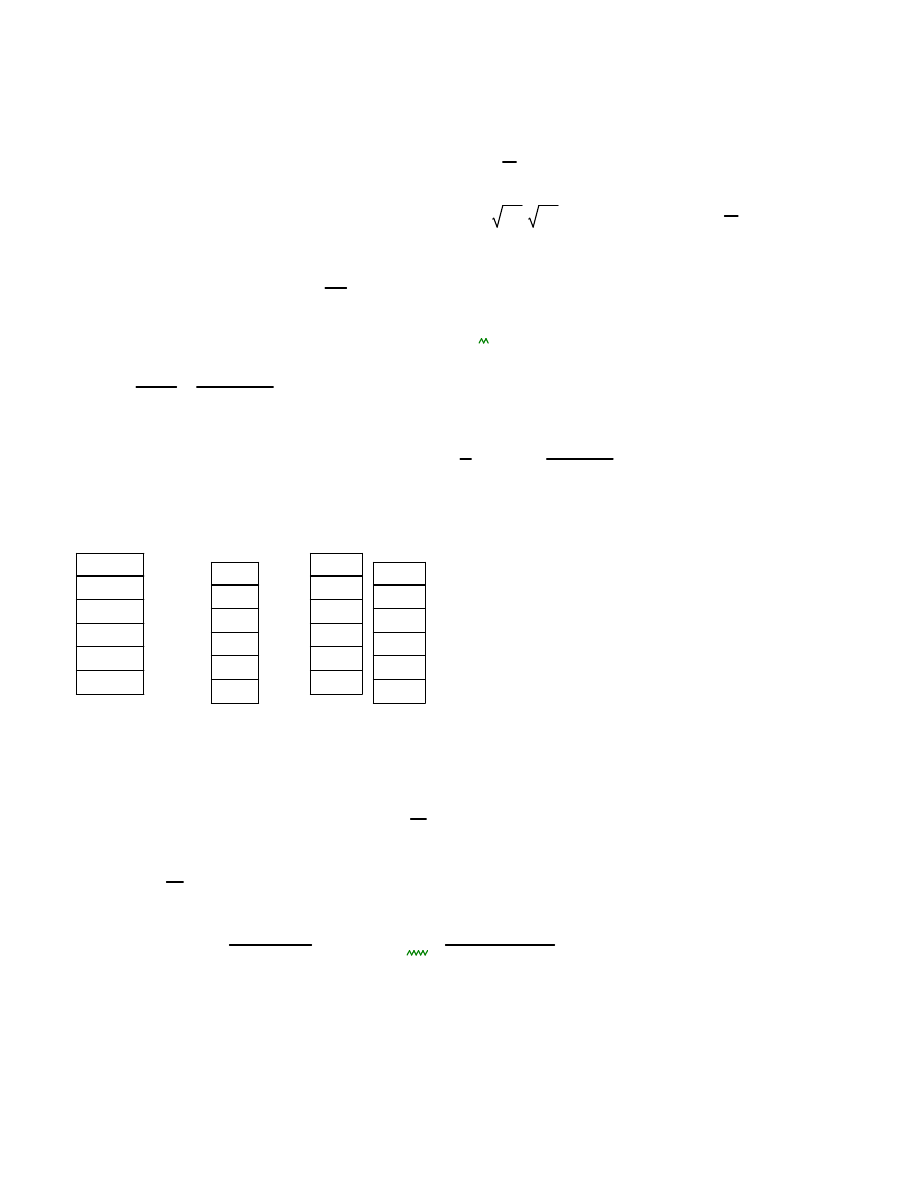
pr

ę

dko

ść

charakterystyczna dla II strefy wiatrowej

v

k

24

m

s

⋅

:=

pr

ę

dko

ść

wiatru na wysoko

ś

ci wierzchołka komina

v

H

v

k

D

T

⋅

C

e

⋅

:=

v

H

23.33

m

s

=

Masa równowa

ż

na komina.

g

ę

sto

ść

masy stali

ρ

7850

kg

m

3

⋅

:=

masy poszczególnych segmentów na jednostk

ę

długo

ś

ci

i

1 n

s

..

:=

j

1 n

s

..

:=

m

I

i

ρ

π

D

z

2

⋅

4

π

D

z

t

i

−

(

)

2

⋅

4

−









⋅

:=

bezwymiarowe współrz

ę

dne komina

ζ

i

z

i

H

:=

ζ

1

j

z

j

1.5 m

⋅

−

H

:=

masa skupiona jest tylko na najwy

ż

szym elemencie

M

ns

300 kg

⋅

:=

m

I

i

195.71

122.69

110.48

98.25

86.01

73.76

kg m

1

−

⋅

=

M

j

0

0

0

0

0

300

kg

=

ζ

i

0.21

0.37

0.53

0.68

0.84

1

=

ζ

1

j

0.17

0.33

0.49

0.64

0.8

0.96

=

masa równowa

ż

na komina

m

e1

1

n

s

i

m

I

i

ζ

i

( )

4.2

ζ

i 1

−

( )

4.2

+









⋅









∑

=

4.2

1

n

s

j

M

j

H

ζ

1

j

( )

3.2

⋅













∑

=

⋅

+

:=

m

e1

236.04

kg

m

=

współczynnik

δ

a

T

1

v

H

⋅

C

x

⋅

D

z

⋅

2 m

e1

⋅

:=

δ

a

δ

a

kg

1

−

m

3

⋅

sec

1

−

⋅

:=

δ

a

0.07

=

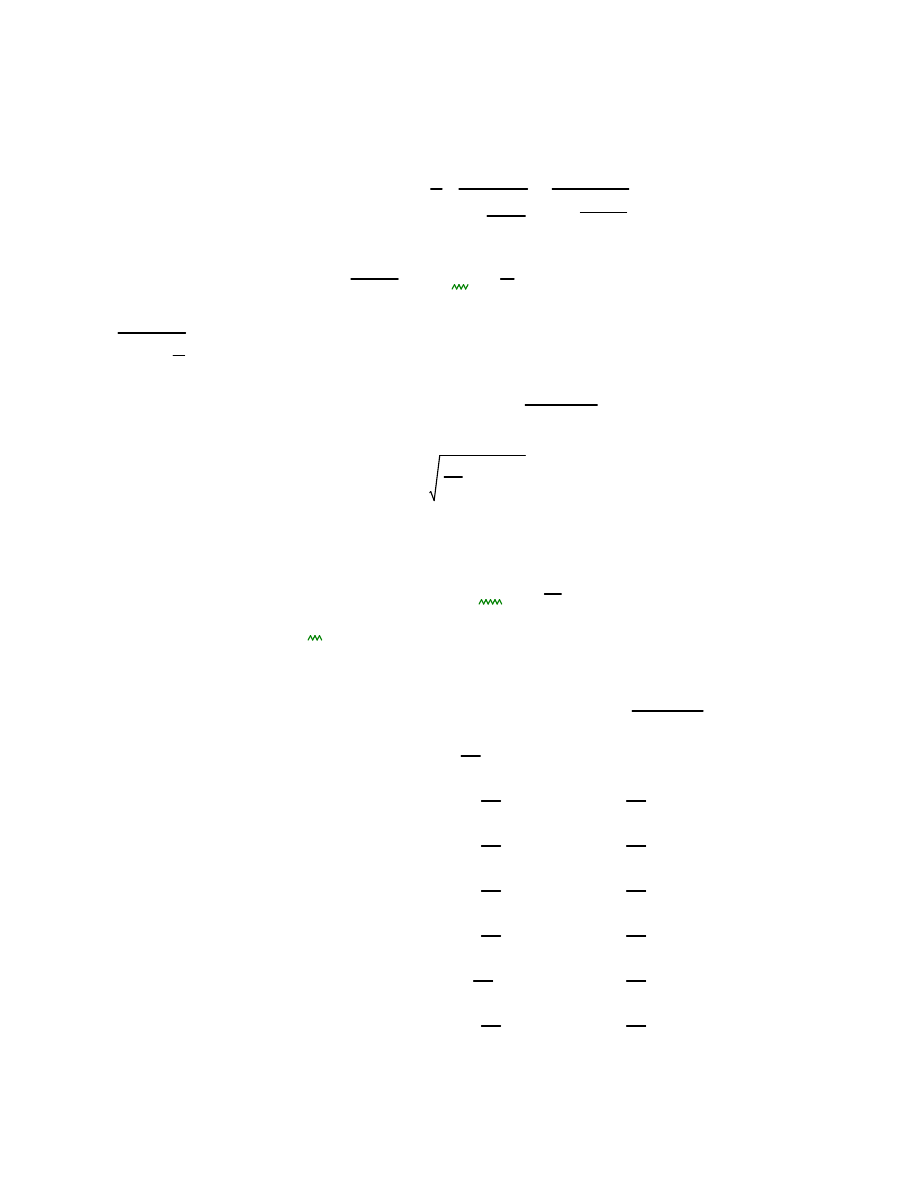
Wyznacznie współczynnika

δδδδ

b

.

współczynnik oddziaływania rezonansowego

K

L

π

3

1

1

8 n

⋅

H

⋅

3 v

H.

⋅

+

















⋅

1

1

10 n

⋅

D

⋅

v

H.

+

















⋅

:=

K

L

0.2

=

współczynnik energii porywów

χ

1200 n

⋅

v

H

:=

χ

χ

m

s

⋅

:=

χ

35.63

=

K

O

χ

2

1

χ

2

+

(

)

4

3

:=

K

O

0.09

=

współczynnik rezonansowego oddziływania turbulentnego

k

r

2

π

⋅

K

L

⋅

K

O

⋅

δ

s

δ

a

+

:=

k

r

1.2

=

współczynnik działania porywów wiatru

β

1

Ψ

r

C

e

k

b

k

r

+

(

)

⋅

⋅

+

:=

β

2.37

=

> 1.8

3.2. Obci

ąż

enie wiatrem poszczególnych segmentów w I sytuacji projektowej.

współczynnik ekspozycji dla poszczególnych segmentów

C

e

i

k

z

i

10













2

α

⋅

⋅

:=

liczba przewodów kominowych

n

1

:=

obci

ąż

enie charakterystyczne wiatrem na górnej kraw

ę

dzi segmentów

p

Ik

i

q

k

D

T

⋅

C

e

i

⋅

C

x

⋅

n

⋅

D

z

⋅

β

⋅

:=

ś

rednie obci

ąż

enie charakterystyczne poszczególnych segmentów

p

Iksr

i

p

Ik

i 1

−

p

Ik

i

+

2

:=

z

0

0 m

=

C

e

0

0

=

p

Ik

0

0

kN

m

=

segment 1

z

1

8 m

=

C

e

1

0.94

=

p

Ik

1

0.48

kN

m

=

p

Iksr

1

0.24

kN

m

=

segment 2

z

2

14 m

=

C

e

1

0.94

=

p

Ik

2

0.56

kN

m

=

p

Iksr

2

0.52

kN

m

=

segment 3

z

3

20 m

=

C

e

1

0.94

=

p

Ik

3

0.61

kN

m

=

p

Iksr

3

0.58

kN

m

=

segment 4

z

4

26 m

=

C

e

1

0.94

=

p

Ik

4

0.66

kN

m

=

p

Iksr

4

0.64

kN

m

=

segment 5

z

5

32 m

=

C

e

1

0.94

=

p

Ik

5

0.7

kN

m

=

p

Iksr

5

0.68

kN

m

=

segment 6

z

6

38 m

=

C

e

1

0.94

=

p

Ik

6

0.74

kN

m

=

p

Iksr

6

0.72

kN

m

=

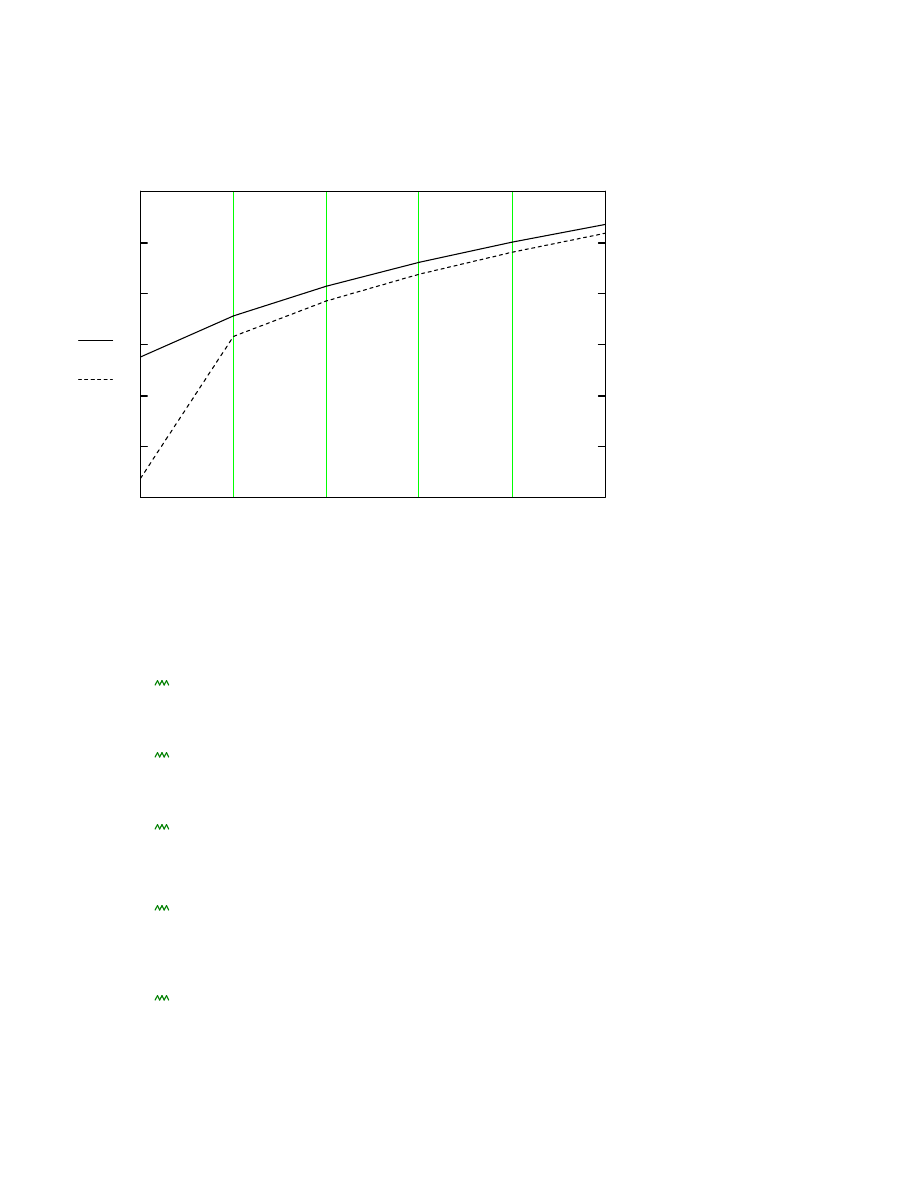
Warto

ś

ci obci

ąż

enia wiatrem poszczególnych segmentów.

1

2

3

4

5

6

200

300

400

500

600

700

800

p

Ik

i

p

Iksr

i

i

.

4. Siły wewn

ę

trzne w podstawach segmentów komina od obc. wiatrem.

4.1. Siły poprzeczne.

segment 6

n

1

:=

P

7 n

−

1

n

n

p

Iksr

7 n

−

h

s

⋅

(

)

∑

=

:=

P

7 n

−

4.31 kN

=

segment 5

n

2

:=

P

7 n

−

1

n

n

p

Iksr

7 n

−

h

s

⋅

(

)

∑

=

:=

P

7 n

−

8.39 kN

=

segment 4

n

3

:=

P

7 n

−

1

n

n

p

Iksr

7 n

−

h

s

⋅

(

)

∑

=

:=

P

7 n

−

12.22 kN

=

segment 3

n

4

:=

P

7 n

−

1

n

n

p

Iksr

7 n

−

h

s

⋅

(

)

∑

=

:=

P

7 n

−

15.73 kN

=

segment 2 n

5

:=

P

7 n

−

1

n

n

p

Iksr

7 n

−

h

s

⋅

(

)

∑

=

:=

P

7 n

−

18.82 kN

=

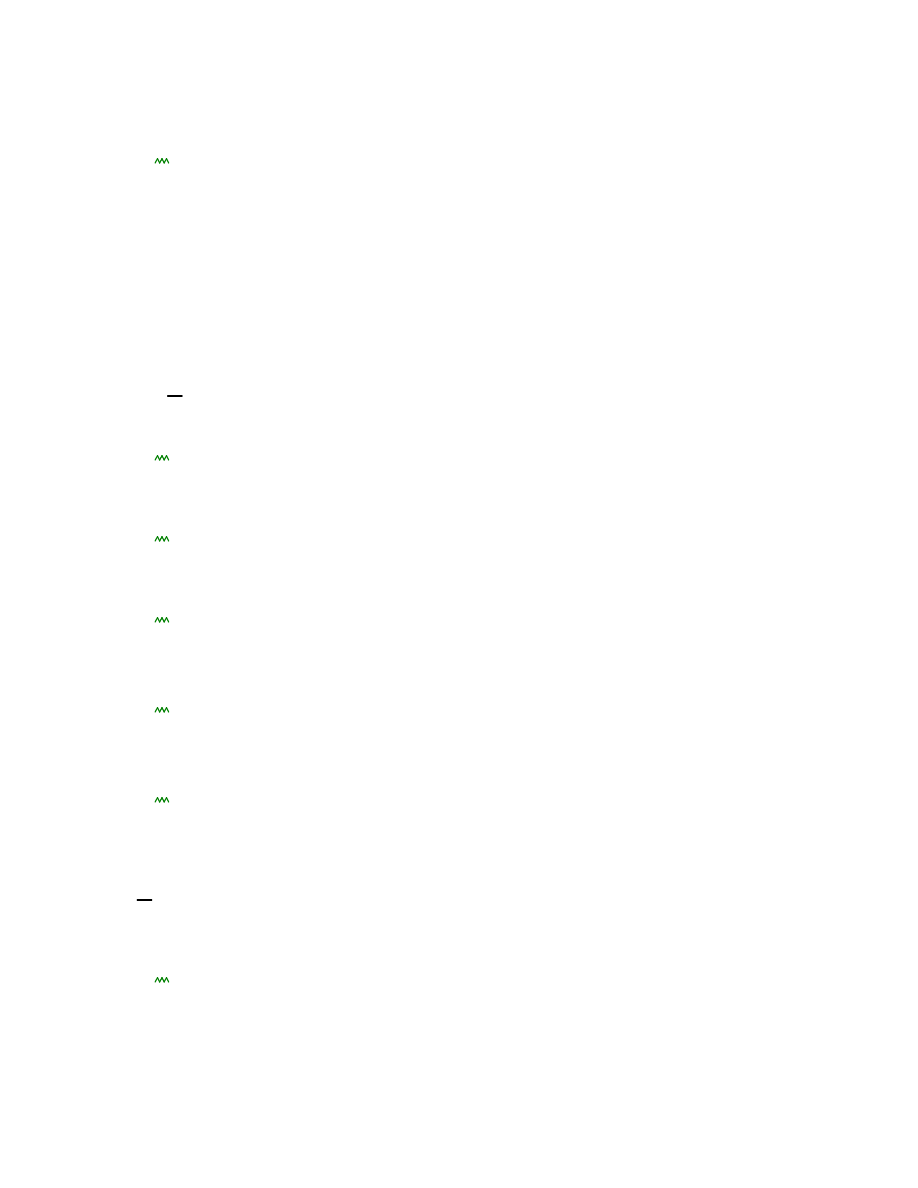
segment 1

n

6

:=

P

7 n

−

P

2

p

Iksr

7 n

−

h

c

⋅

+

:=

P

7 n

−

20.72 kN

=

4.2. Momenty zginaj

ą

ce.

i

1 n

s

..

:=

Siły poziome na poszczególnych segmentach.

p

i

p

Iksr

ns i

−

1

+

h

s

⋅

:=

p

n

s

p

Iksr

1

h

c

⋅

:=

Ś

rodki ci

ęż

ko

ś

ci segmentów.

x

i

H

h

c

−

h

s

2

−

n

s

1

−

i

−

(

)

h

s

⋅

−

:=

segment 6

n

1

:=

M

I

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

I

7 n

−

12.92 kN m

⋅

=

segment 5

n

2

:=

M

I

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

I

7 n

−

51.01 kN m

⋅

=

segment 4

n

3

:=

M

I

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

I

7 n

−

112.83 kN m

⋅

=

segment 3

n

4

:=

M

I

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

I

7 n

−

196.66 kN m

⋅

=

segment 2

n

5

:=

M

I

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

I

7 n

−

300.29 kN m

⋅

=

Ś

rodki ci

ęż

ko

ś

ci segmentów.

x

i

H

h

s

2

−

n

s

i

−

(

)

h

s

⋅

−

:=

segment 1

n

6

:=

M

I

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

I

7 n

−

460.35 kN m

⋅

=

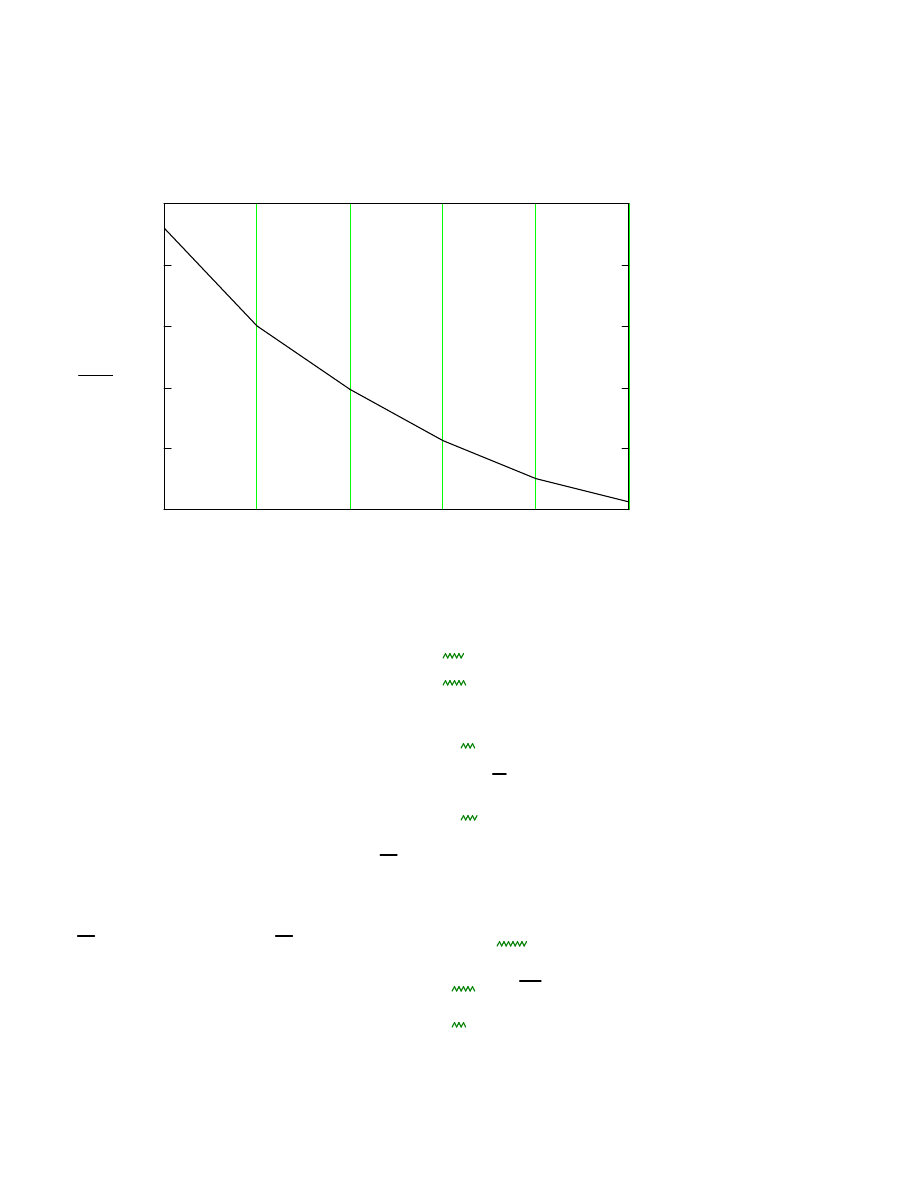
Momnty zginaj

ą

ce w kominie od obci

ąż

enia wiatrem.

1

2

3

4

5

6

0

1 10

5

×

2 10

5

×

3 10

5

×

4 10

5

×

5 10

5

×

M

I

i

i

.

5. Obci

ąż

enie wiatrem w II sytuacji projektowej.

strefa wiatrowa II

teren A

charakterystyczne ci

ś

nienie pr

ę

dko

ś

ci wiatru

q

k

350 Pa

⋅

:=

współczynnik dla czasu eksploatacji

T

e

10 lat

=

D

T

0.8

:=

Współczynnik ekspozycji.

współczynnik przeliczeniowy zale

ż

ny od rodzaju terenu

k

1

:=

wysko

ść

nad poziomem terenu

z

H

m

:=

z

38

=

wykładnik zale

ż

ny od rodzaju terenu

α

0.14

:=

współczynnik ekspozycji

C

e

k

z

10













2

α

⋅

⋅

:=

C

e

1.45

=

Współczynnik aerodynamiczny dla komina stalowego z drabin

ą

włazow

ą

.

H

D

z

38

=

> 25

D

z

H

0.03

=

< 0.04

⇒

C

xo

0.7

:=

( tablica Z2-3 )

pole rzutu bocznego drabiny na płaszczyzn

ę

symetrii

A

d

0.1

m

2

m

⋅

:=

liczba przewodów kominowych

n

1

:=

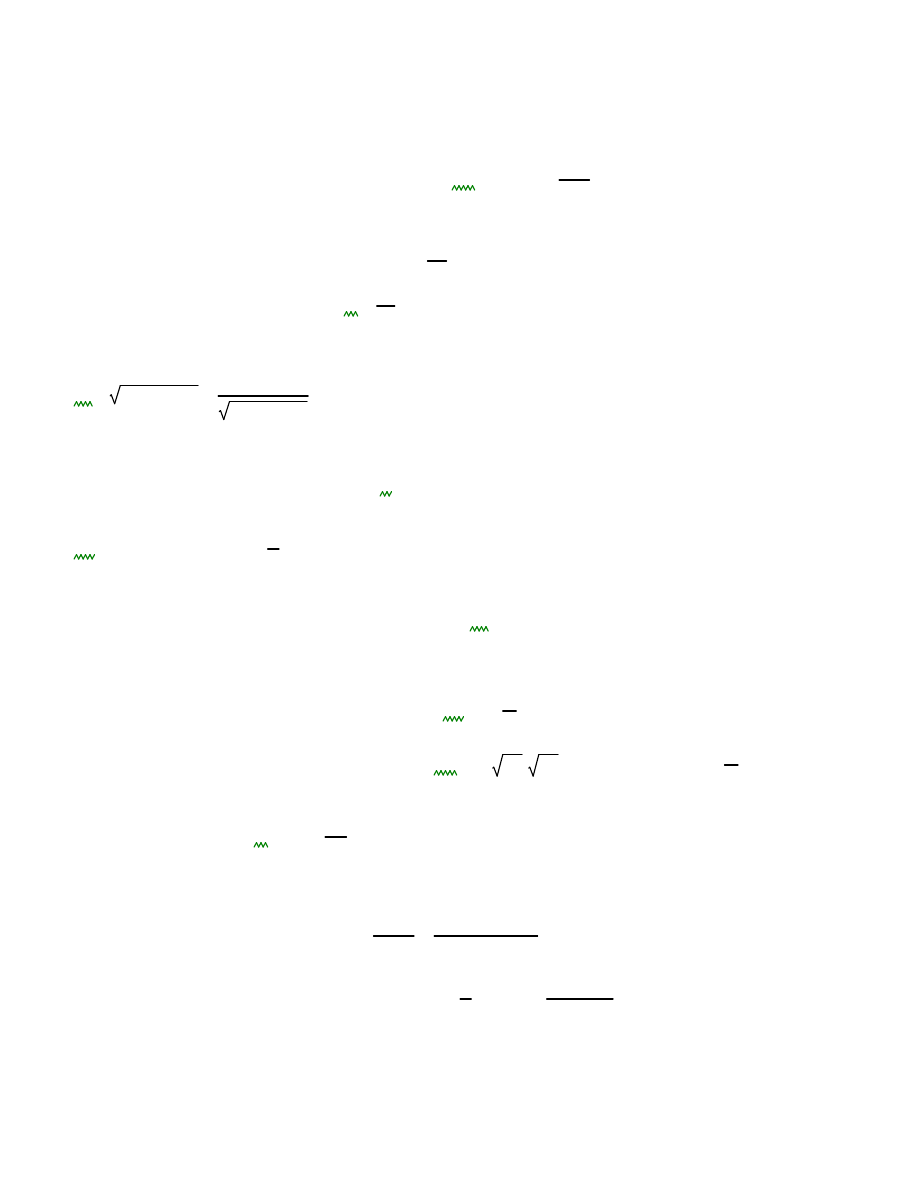
ś

rednica zewn

ę

trzna komina

D

z

1 m

=

współczynnik aerodynamiczny

C

x

C

xo

2.4

A

d

n D

z

⋅

⋅

+

:=

C

x

0.94

=

5.1. Współczynnik działania porywów wiatru.

podstawowego okres drga

ń

własnych

T

1

0.001

H

2

D

⋅

:=

T

1

1.44

=

cz

ę

stotliwo

ść

drga

ń

własnych

n

1

T

1

:=

n

0.69

=

Współczynnik szczytowej warto

ś

ci obci

ąż

enia.

Ψ

2 ln 600 n

⋅

(

)

⋅

0.577

2 ln 600 n

⋅

(

)

⋅

+

:=

Ψ

3.64

=

Wyznacznie współczynnika

δδδδ

s

.

współczynnik chropowato

ś

ci dla terenu A

r

0.08

:=

współczynnik pozarezonansowego oddziaływania turbulentnego

k

b

2.25

0.227 1

3.24

D

H

⋅

+













⋅

ln H

( )

⋅

−

:=

k

b

1.35

=

logarytmiczny dekrement tłumienia drga

ń

wg tablicy Z3-2

dla komina spawanego jednoprzewodowego bez wykładziny

δ

s

1

0.015

:=

dodatek na poł

ą

czenia kołnierzowe

δ

s

2

0.015

:=

δ

s

1

2

i

δ

s

i

∑

=

:=

δ

s

0.03

=

pr

ę

dko

ść

charakterystyczna dla II strefy wiatrowej

v

k

24

m

s

⋅

:=

pr

ę

dko

ść

wiatru na wysoko

ś

ci wierzchołka komina

v

H

v

k

D

T

⋅

C

e

⋅

:=

v

H

25.88

m

s

=

Masa równowa

ż

na komina.

g

ę

sto

ść

masy stali

ρ

7850

kg

m

3

⋅

:=

masy poszczególnych segmentów na jednostk

ę

długo

ś

ci z uwzgl

ę

dniniem dodatków na korozj

ę

i

1 n

s

..

:=

j

1 n

s

..

:=

t

k

T

e.

∆

t

⋅

mm

⋅

:=

t

k

8 mm

=

m

II

i

ρ

π

D

z

2

⋅

4

π

D

z

t

i

−

t

k

−

(

)

2

⋅

4

−









⋅

:=

bezwymiarowe współrz

ę

dne komina

ζ

i

z

i

H

:=

ζ

1

j

z

j

1.5 m

⋅

−

H

:=

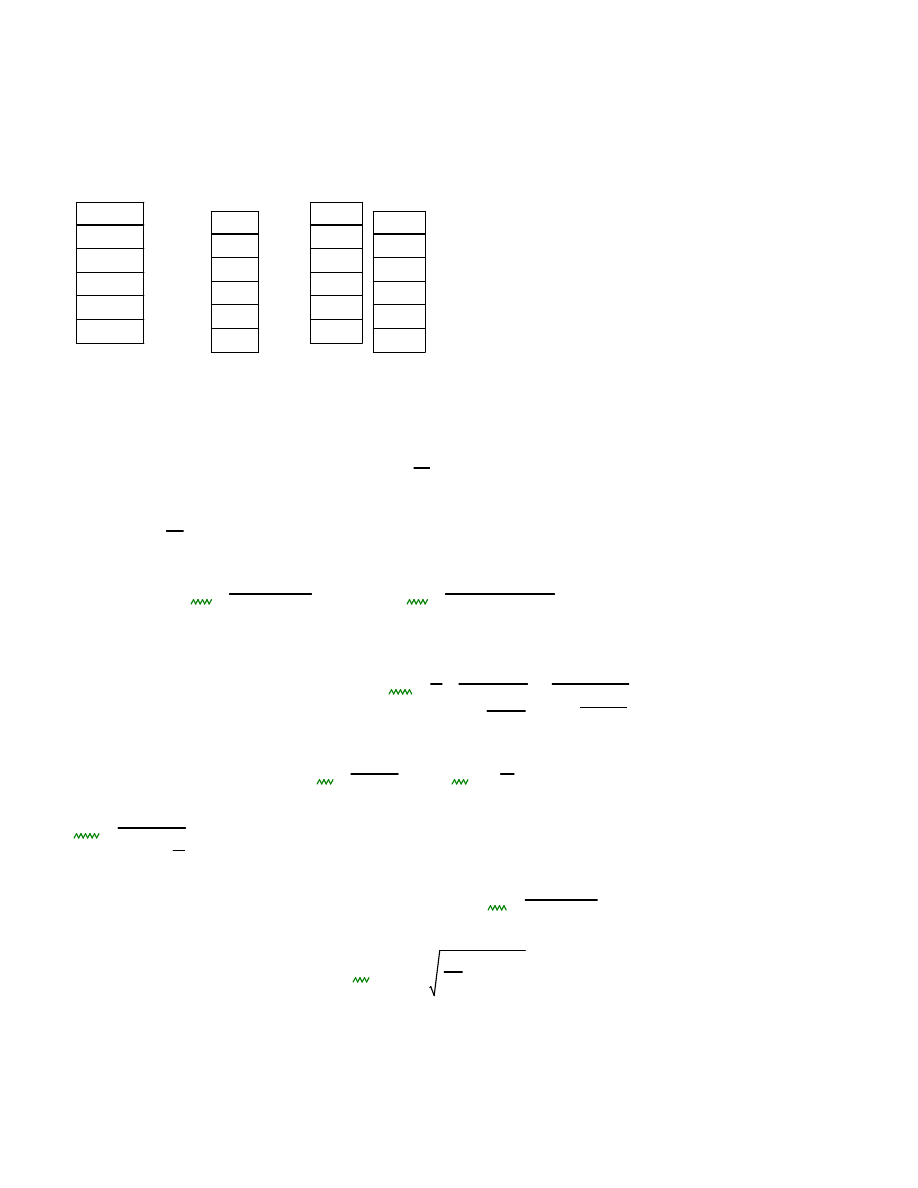
masa skupiona jest tylko na najwy

ż

szym elemencie

M

ns

300 kg

⋅

:=

m

II

i

292.39

219.96

207.84

195.71

183.57

171.42

kg m

1

−

⋅

=

M

j

0

0

0

0

0

300

kg

=

ζ

i

0.21

0.37

0.53

0.68

0.84

1

=

ζ

1

j

0.17

0.33

0.49

0.64

0.8

0.96

=

masa równowa

ż

na komina

m

e2

1

n

s

i

m

II

i

ζ

i

( )

4.2

ζ

i 1

−

( )

4.2

+









⋅









∑

=

4.2

1

n

s

j

M

j

H

ζ

1

j

( )

3.2

⋅













∑

=

⋅

+

:=

m

e2

484.54

kg

m

=

współczynnik

δ

a

T

1

v

H

⋅

C

x

⋅

D

z

⋅

2 m

e1

⋅

:=

δ

a

δ

a

kg

1

−

m

3

⋅

sec

1

−

⋅

:=

δ

a

0.07

=

Wyznacznie współczynnika

δδδδ

b

.

współczynnik oddziaływania rezonansowego

K

L

π

3

1

1

8 n

⋅

H

⋅

3 v

H.

⋅

+

















⋅

1

1

10 n

⋅

D

⋅

v

H.

+

















⋅

:=

K

L

0.22

=

współczynnik energii porywów

χ

1200 n

⋅

v

H

:=

χ

χ

m

s

⋅

:=

χ

32.11

=

K

O

χ

2

1

χ

2

+

(

)

4

3

:=

K

O

0.1

=

współczynnik rezonansowego oddziływania turbulentnego

k

r

2

π

⋅

K

L

⋅

K

O

⋅

δ

s

δ

a

+

:=

k

r

1.32

=

współczynnik działania porywów wiatru

β

1

Ψ

r

C

e

k

b

k

r

+

(

)

⋅

⋅

+

:=

β

2.4

=

> 1.8

5.2. Obci

ąż

enie wiatrem poszczególnych segmentów w II sytuacji projektowej.

współczynnik ekspozycji dla poszczególnych segmentów

C

e

i

k

z

i

10













2

α

⋅

⋅

:=

liczba przewodów kominowych

n

1

:=

obci

ąż

enie charakterystyczne wiatrem na górnej kraw

ę

dzi segmentów

p

IIk

i

q

k

D

T

⋅

C

e

i

⋅

C

x

⋅

n

⋅

D

z

⋅

β

⋅

:=

ś

rednie obci

ąż

enie charakterystyczne poszczególnych segmentów

p

IIksr

i

p

IIk

i 1

−

p

IIk

i

+

2

:=

segment 1

z

1

8 m

=

C

e

1

0.94

=

p

IIk

1

0.59

kN

m

=

p

IIksr

1

0.3

kN

m

=

segment 2

z

2

14 m

=

C

e

1

0.94

=

p

IIk

2

0.69

kN

m

=

p

IIksr

2

0.64

kN

m

=

segment 3

z

3

20 m

=

C

e

1

0.94

=

p

IIk

3

0.77

kN

m

=

p

IIksr

3

0.73

kN

m

=

segment 4

z

4

26 m

=

C

e

1

0.94

=

p

IIk

4

0.82

kN

m

=

p

IIksr

4

0.8

kN

m

=

segment 5

z

5

32 m

=

C

e

1

0.94

=

p

IIk

5

0.87

kN

m

=

p

IIksr

5

0.85

kN

m

=

segment 6

z

6

38 m

=

C

e

1

0.94

=

p

IIk

6

0.92

kN

m

=

p

IIksr

6

0.9

kN

m

=

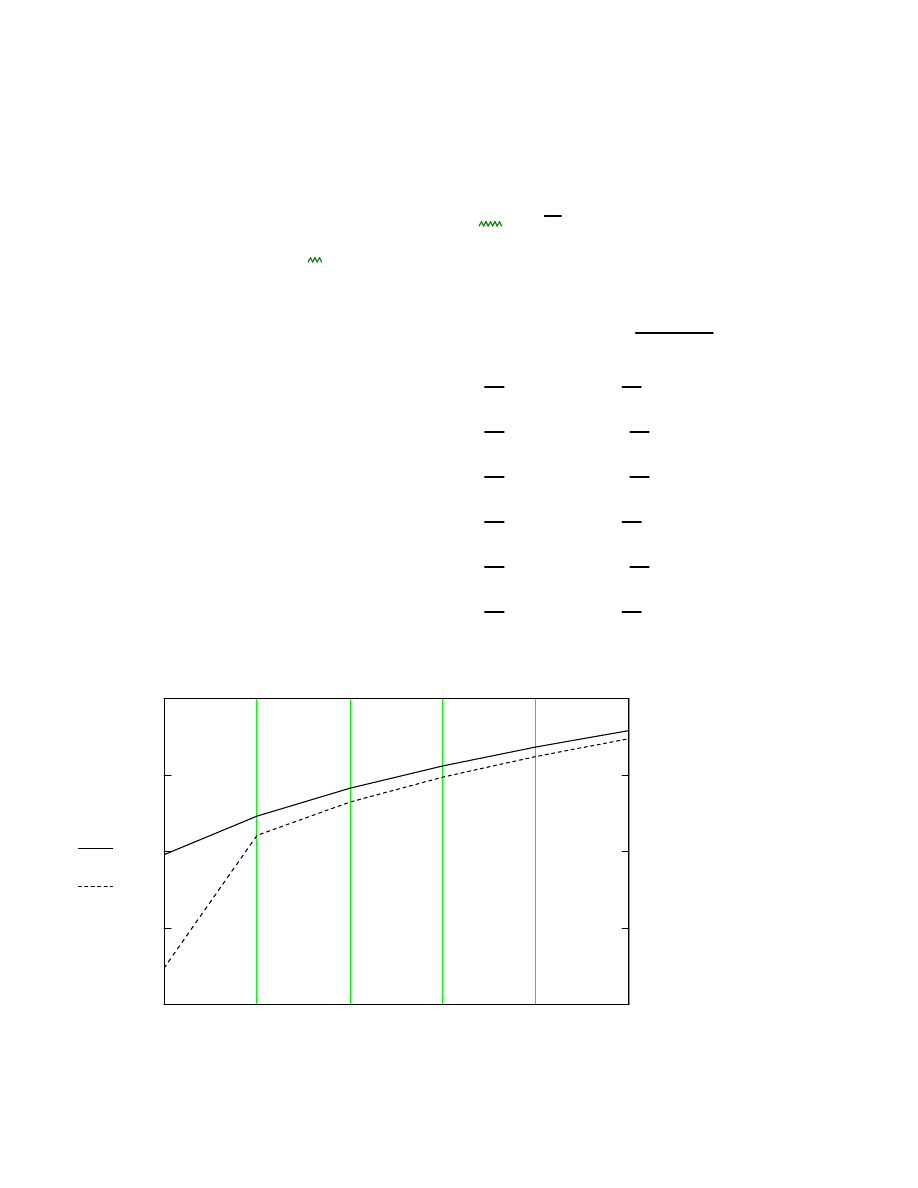
Warto

ś

ci obci

ąż

enia wiatrem poszczególnych segmentów.

1

2

3

4

5

6

200

400

600

800

1 10

3

×

p

IIk

i

p

IIksr

i

i

.

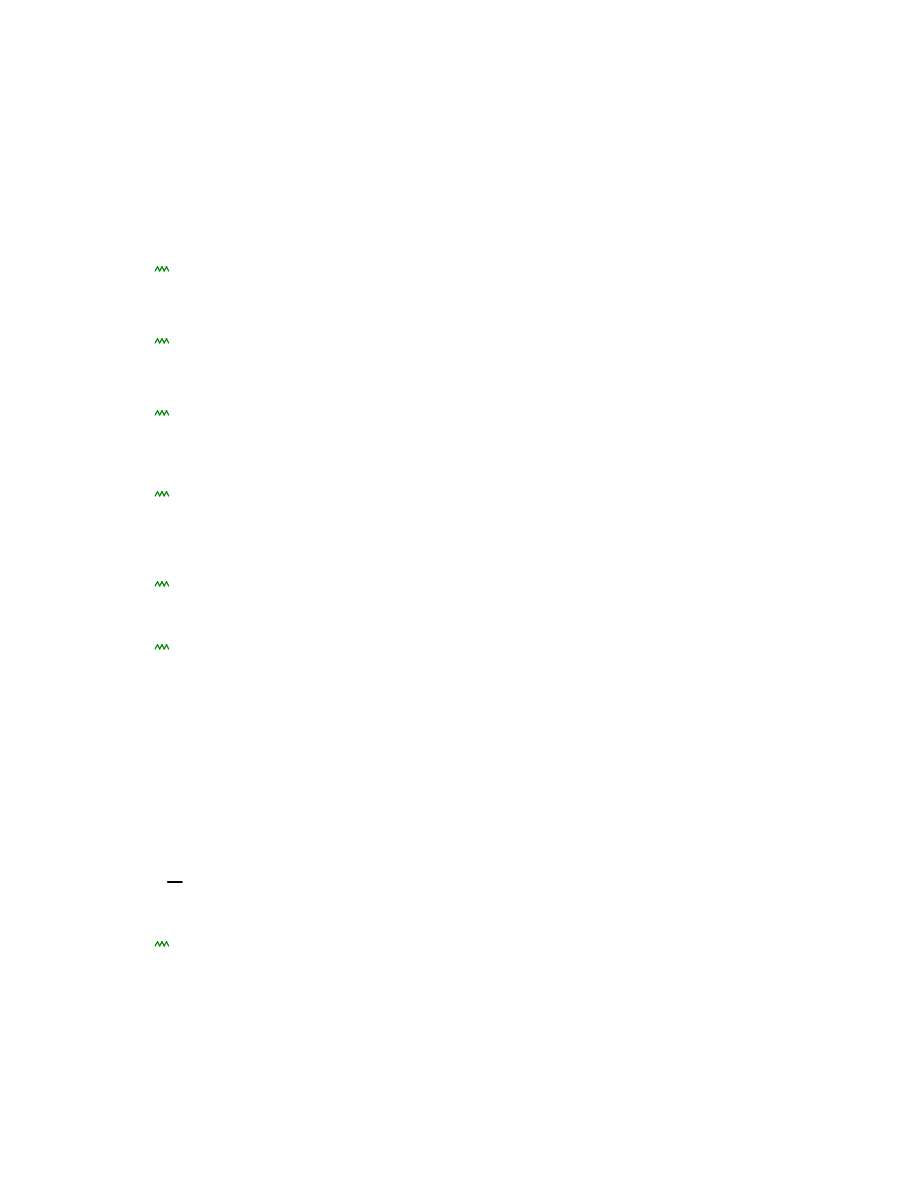
6. Siły wewn

ę

trzne w podstawach segmentów komina od obc. wiatrem.

6.1. Siły poprzeczne.

segment 6

n

1

:=

P

7 n

−

1

n

n

p

IIksr

7 n

−

h

s

⋅

(

)

∑

=

:=

P

7 n

−

5.37 kN

=

segment 5

n

2

:=

P

7 n

−

1

n

n

p

IIksr

7 n

−

h

s

⋅

(

)

∑

=

:=

P

7 n

−

10.47 kN

=

segment 4

n

3

:=

P

7 n

−

1

n

n

p

IIksr

7 n

−

h

s

⋅

(

)

∑

=

:=

P

7 n

−

15.24 kN

=

segment 3

n

4

:=

P

7 n

−

1

n

n

p

IIksr

7 n

−

h

s

⋅

(

)

∑

=

:=

P

7 n

−

19.62 kN

=

segment 2 n

5

:=

P

7 n

−

1

n

n

p

IIksr

7 n

−

h

s

⋅

(

)

∑

=

:=

P

7 n

−

23.47 kN

=

segment 1

n

6

:=

P

7 n

−

P

2

p

IIksr

7 n

−

h

c

⋅

+

:=

P

7 n

−

25.84 kN

=

6.2. Momenty zginaj

ą

ce.

i

1 n

s

..

:=

Siły poziome na poszczególnych segmentach.

p

i

p

IIksr

ns i

−

1

+

h

s

⋅

:=

p

n

s

p

IIksr

1

h

c

⋅

:=

Ś

rodki ci

ęż

ko

ś

ci segmentów.

x

i

H

h

c

−

h

s

2

−

n

s

1

−

i

−

(

)

h

s

⋅

−

:=

segment 6

n

1

:=

M

II

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

II

7 n

−

16.12 kN m

⋅

=

segment 5

n

2

:=

M

II

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

II

7 n

−

63.63 kN m

⋅

=

segment 4

n

3

:=

M

II

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

II

7 n

−

140.75 kN m

⋅

=

segment 3

n

4

:=

M

II

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

II

7 n

−

245.31 kN m

⋅

=

segment 2

n

5

:=

M

II

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

II

7 n

−

374.58 kN m

⋅

=

Ś

rodki ci

ęż

ko

ś

ci segmentów.

x

i

H

h

s

2

−

n

s

i

−

(

)

h

s

⋅

−

:=

segment 1

n

6

:=

M

II

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

II

7 n

−

574.23 kN m

⋅

=

Momnty zginaj

ą

ce w kominie od obci

ąż

enia wiatrem.

1

2

3

4

5

6

0

2 10

5

×

4 10

5

×

6 10

5

×

M

II

i

i

.

7. Obci

ąż

enia prostopadłe do linii wiatru.

Obliczenia wykonano w I sytuacj projektowej.

Pr

ę

dko

ść

krytyczna przy której nast

ę

puje wzbudzenie wirowe.

liczba Strouhala

S

t

0.2

:=

odległo

ść

mi

ę

dzy osiami przewodów komina wieloprzewodowego

a

0

:=

okres dega

ń

własnych komina

T

1

1.44

=

pr

ę

dko

ść

krytyczna

v

cr

a

D

+

T

1

S

t

⋅

:=

v

cr

3.46

=

[ m/s ]

Liczba Scrutona.

masa równowa

ż

na

m

e1

236.04

kg

m

=

logarytmiczny dekrement tłumienia

δ

s

0.03

=

g

ę

sto

ść

powietrza

ρ

p

1.25

kg

m

3

⋅

:=

liczba Scrutona

S

c

2 m

e1

⋅

δ

s

⋅

ρ

p

D

z

2

⋅

:=

S

c

11.33

=

< 15

oraz

v

cr

3.46

=

Nale

ż

y uwzgl

ę

dni

ć

obci

ąż

enie wzbudzeniem wirowym.

7.1. Obci

ąż

enie wzbudzeniem wirowym wg procedury uproszczonej.

Obci

ąż

enie charakterystyczne w płaszczy

ź

nie prostopadłej do wiatru.

moduł współczynnika aerodynamicznej pulsacyjnej siły bocznej

c

lat

1

0.1 v

cr

⋅

D

⋅

−

:=

c

lat

0.65

=

warto

ść

obci

ąż

enia

p

y

0.05

ρ

p

⋅

T

1

( )

2

δ

s

⋅

c

lat

⋅

D

3

⋅

:=

p

y

p

y

kN

m

⋅

:=

p

y

0.65

kN

m

=

Obci

ąż

enie przyłozono na odcinku

l

o

0.25 H

⋅

:=

l

o

9.5 m

=

>

6 D

z

⋅

6 m

=

7.2. Momenty zginaj

ą

ce wywołane przyło

ż

onym obci

ąż

eniem.

segment 6

i

6

:=

M

y

i

p

y

h

s

2

⋅

2

:=

M

y

i

11.76 kN m

⋅

=

wypadkowa warto

ść

obci

ąż

enia

P

y

p

y

l

o

⋅

:=

P

y

6.21 kN

=

odległo

ść

od dołu komina

z

w

H

l

o

2

−

:=

z

w

33.25 m

=

Momenty w pozostałych segmentach.

i

1 n

s

1

−

..

:=

M

y

i

P

y

z

w

z

i

−

h

c

+

(

)

⋅

:=

i

1

2

3

4

5

=

z

i

8

14

20

26

32

m

=

M

y

1

206.32 kN m

⋅

=

M

y

2

169.09 kN m

⋅

=

i

1 n

s

..

:=

M

y

3

131.86 kN m

⋅

=

M

y

4

94.63 kN m

⋅

=

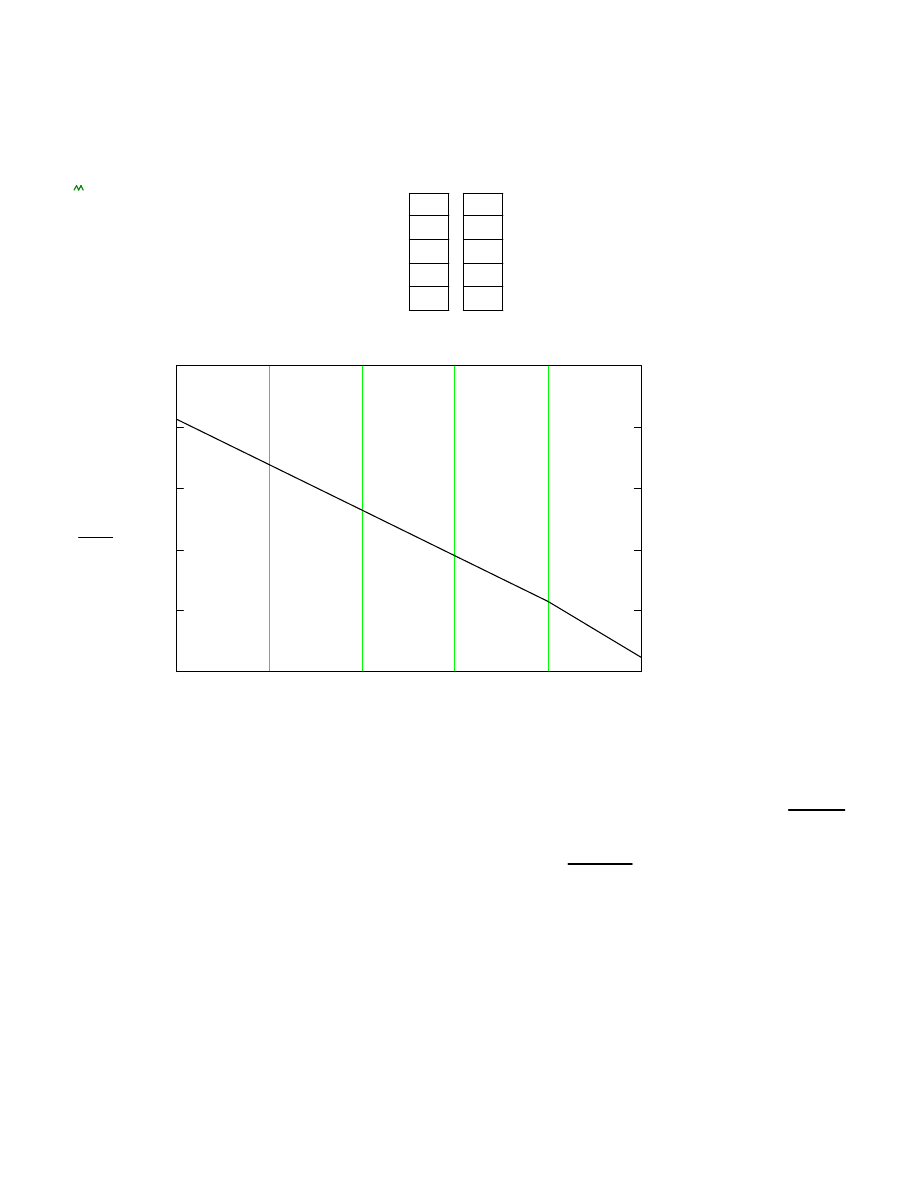
Momenty zginaj

ą

ce:

M

y

5

57.4 kN m

⋅

=

1

2

3

4

5

6

0

5 10

4

×

1 10

5

×

1.5 10

5

×

2 10

5

×

2.5 10

5

×

M

y

i

i

8. Obci

ąż

enia stałe.

wielko

ść

naddatkuu korozyjnego

t

k

8 mm

=

ci

ęż

ary poszczególnych segmentów

i

2 n

s

..

:=

G

I

i

m

I

i

h

s

⋅

:=

G

II

i

m

II

i

h

s

⋅

:=

G

III

i

G

I

i

G

II

i

+

2

:=

ci

ęż

ar cokoła

G

I

1

m

I

1

h

c

⋅

:=

G

II

1

m

II

1

h

c

⋅

:=

G

III

1

m

I

1

m

I

2

+

2

h

c

⋅

:=

ci

ęż

ar galeri

M

ns

300 kg

=

siły podłu

ż

ne w poszczególnych przekrojach

i

1 n

s

..

:=

N

I

i

i

n

s

n

G

III

n

M

ns

+









∑

=

:=

N

II

i

i

n

s

n

G

II

n

M

ns

+









∑

=

:=

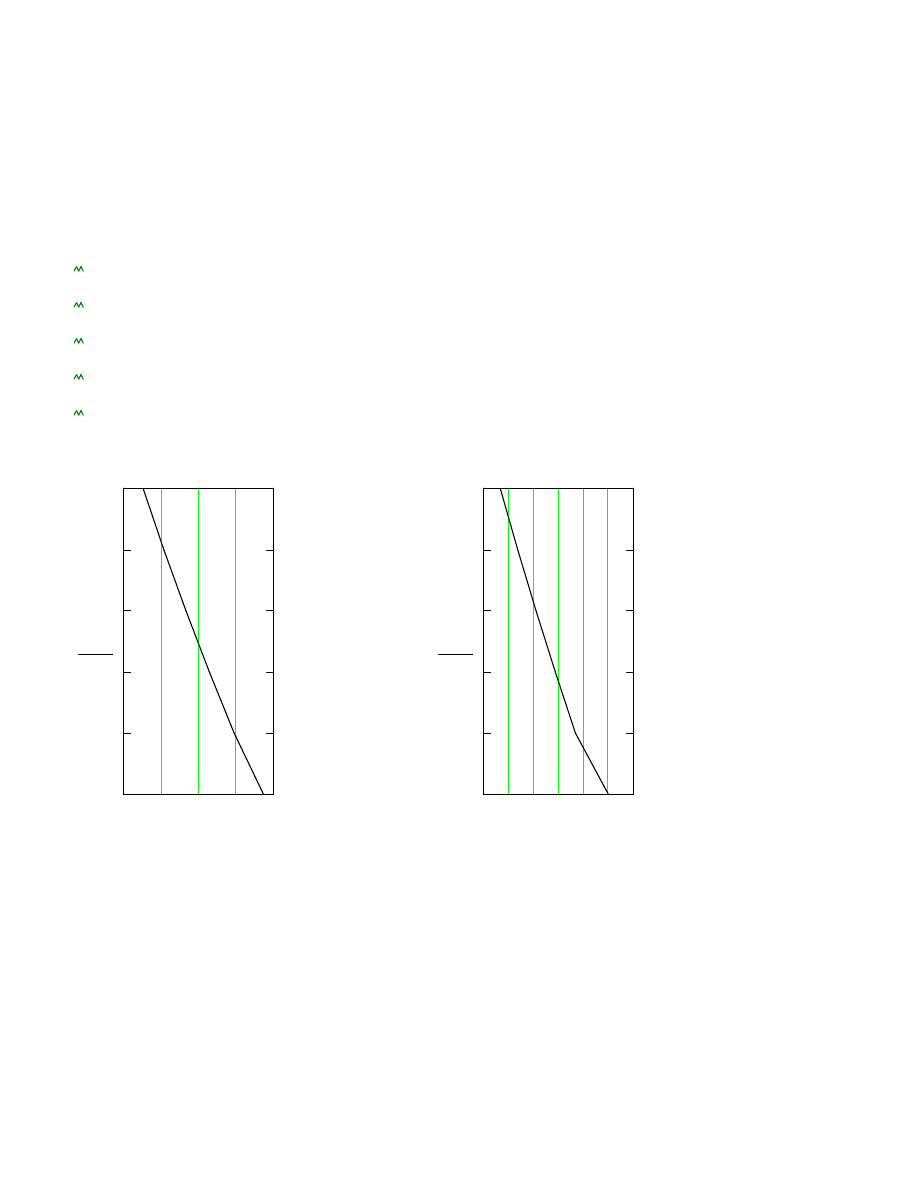
Siły podłu

ż

ne w podstawach poszczególnych segmentów.

segment

wysoko

ść

grubo

ść

wyj

ś

ciowa

ci

ęż

ar z połow

ą

naddatku

ci

ęż

ar z całym naddatkiem

i

1

:=

z

i

8 m

=

t

i

16 mm

=

N

I

i

7482.73 kg

=

N

II

i

10010.13 kg

=

i

2

:=

z

i

14 m

=

t

i

10 mm

=

N

I

i

5909.11 kg

=

N

II

i

7371.04 kg

=

i

3

:=

z

i

20 m

=

t

i

9 mm

=

N

I

i

4581.17 kg

=

N

II

i

5751.3 kg

=

i

4

:=

z

i

26 m

=

t

i

8 mm

=

N

I

i

3326.21 kg

=

N

II

i

4204.26 kg

=

i

5

:=

z

i

32 m

=

t

i

7 mm

=

N

I

i

2144.32 kg

=

N

II

i

2729.98 kg

=

i

6

:=

z

i

38 m

=

t

i

6 mm

=

N

I

i

1035.55 kg

=

N

II

i

1328.53 kg

=

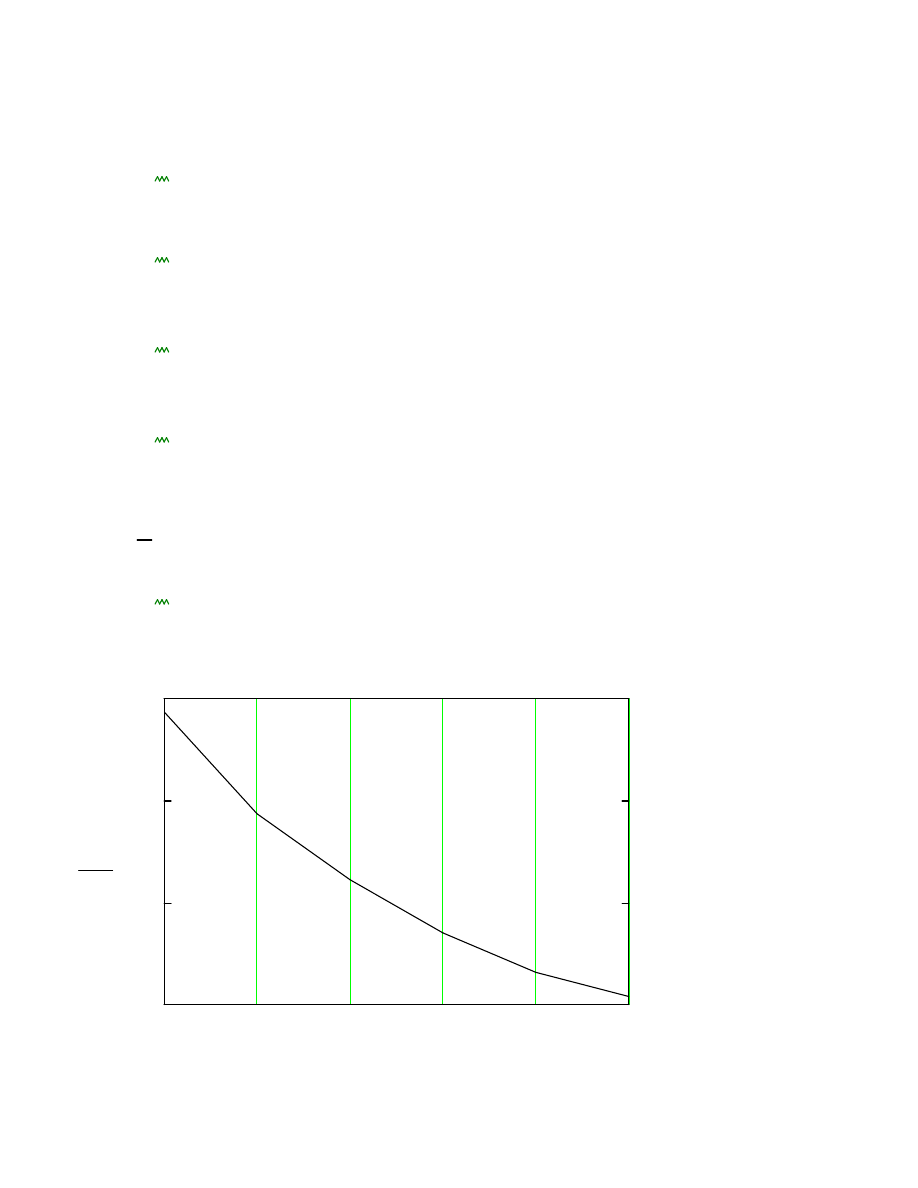
Siły podłu

ż

ne w trzonie.

0

4 10

3

×

8 10

3

×

1

2

3

4

5

6

i

N

I

i

0

6 10

3

×

1.2 10

4

×

1

2

3

4

5

6

i

N

II

i

połowa naddatku na korozj

ę

cały naddatek na korozj

ę

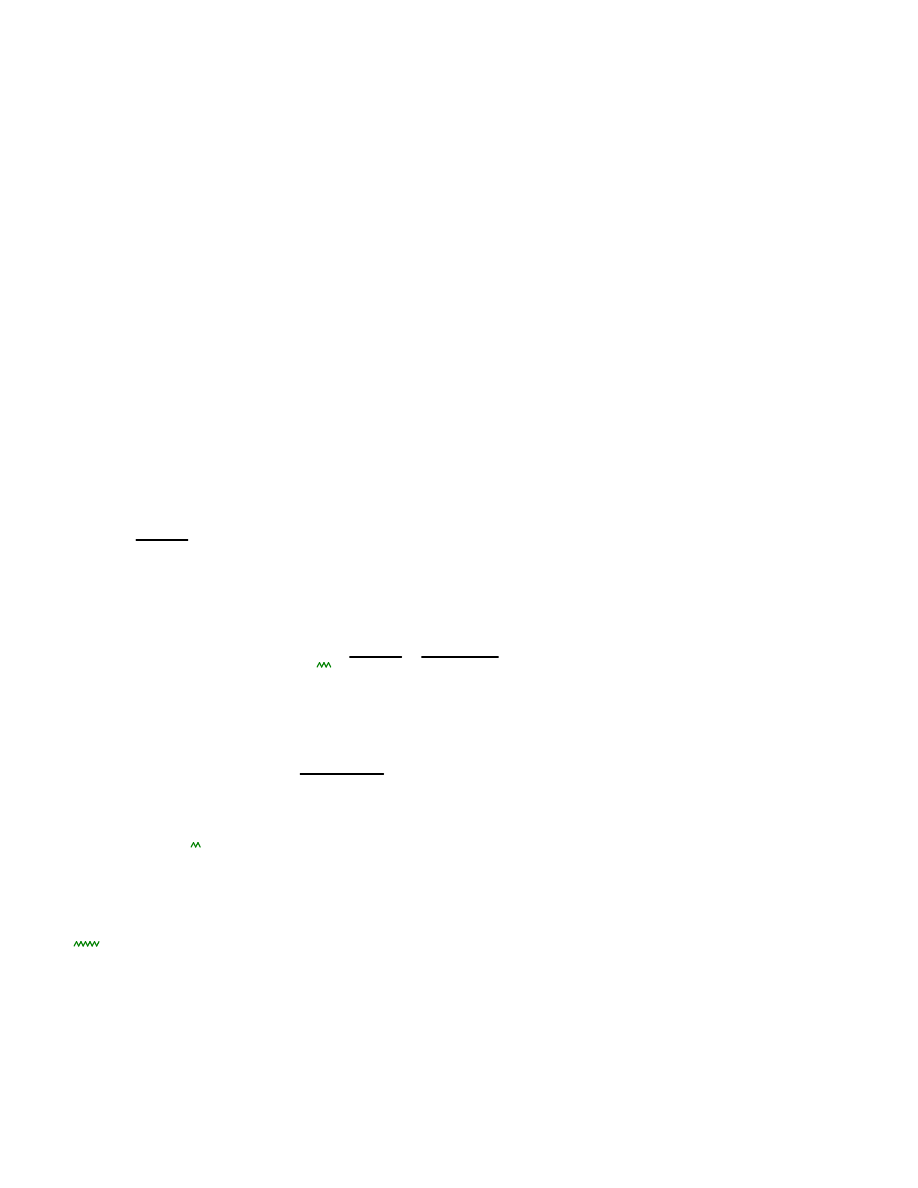
9. Spr

ęż

yste wychylenie wierzchołka trzonu komina.

Ugi

ę

cie wierzchołka obliczono metod

ą

Maxwella-Mohra wyra

ż

on

ą

wzorem:

y

w

=

∑

∫

[(

M

r

*M

p

)]/EJ dx

gdzie M

r

-funkcja momentów zginaj

ą

cych rzeczywistych od obci

ąż

enia poziomego

M

p

-funkcja momentów zginaj

ą

cych od obci

ąż

enia wirtualnego

na poszczególnych segmentach komina

9.1. Ugi

ę

cie w I sytuacji projektowej.

Obci

ąż

enie jednostkowe jest przyło

ż

one w wierzchołku komina.

Segment 6.

i

6

:=

wysoko

ść

segmentu

x

0 m

⋅

h

s

..

:=

h

s

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

:=

grubo

ść

ś

cianki trzonu

t

i

6 mm

=

ś

rednica zewn

ę

trzna

D

z

1000 mm

=

moment bezwładno

ś

ci przekroju

J

π

D

z

( )

4

⋅

64

π

D

z

t

i

−

(

)

4

⋅

64

−

:=

J

116753.67 cm

4

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

s

( )

:=

M

rk

M

r

h

s

( )

:=

M

rk

12.92 m kN

=

M

pk

6 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

s

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠





⌡

d

:=

u

i

0.49 mm

=

Segment 5.

i

5

:=

wysoko

ść

segmentu

x

0 m

⋅

h

s

..

:=

h

s

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

M

pk

+

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

i 1

+

n

s

n

p

Iksr

n

h

s

2

⋅

1

2

n

+

i

−













⋅













∑

=

+

:=

grubo

ść

ś

cianki trzonu

t

i

7 mm

=

ś

rednica zewn

ę

trzna

D

z

1000 mm

=

moment bezwładno

ś

ci przekroju

J

π

D

z

( )

4

⋅

64

π

D

z

t

i

−

(

)

4

⋅

64

−

:=

J

136008.23 cm

4

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

s

( )

:=

M

rk

M

r

h

s

( )

:=

M

rk

51.01 m kN

=

M

pk

12 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

s

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠




⌡

d

:=

u

i

8.43 mm

=

Segment 4.

i

4

:=

wysoko

ść

segmentu

x

0 m

⋅

h

s

..

:=

h

s

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

M

pk

+

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

i 1

+

n

s

n

p

Iksr

n

h

s

2

⋅

1

2

n

+

i

−













⋅













∑

=

+

:=

grubo

ść

ś

cianki trzonu

t

i

8 mm

=

ś

rednica zewn

ę

trzna

D

z

1000 mm

=

moment bezwładno

ś

ci przekroju

J

π

D

z

( )

4

⋅

64

π

D

z

t

i

−

(

)

4

⋅

64

−

:=

J

155204.71 cm

4

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

s

( )

:=

M

rk

M

r

h

s

( )

:=

M

rk

112.83 m kN

=

M

pk

18 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

s

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠




⌡

d

:=

u

i

29.86 mm

=

Segment 3.

i

3

:=

wysoko

ść

segmentu

x

0 m

⋅

h

s

..

:=

h

s

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

M

pk

+

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

i 1

+

n

s

n

p

Iksr

n

h

s

2

⋅

1

2

n

+

i

−













⋅













∑

=

+

:=

grubo

ść

ś

cianki trzonu

t

i

9 mm

=

ś

rednica zewn

ę

trzna

D

z

1000 mm

=

moment bezwładno

ś

ci przekroju

J

π

D

z

( )

4

⋅

64

π

D

z

t

i

−

(

)

4

⋅

64

−

:=

J

174343.22 cm

4

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

s

( )

:=

M

rk

M

r

h

s

( )

:=

M

rk

196.66 m kN

=

M

pk

24 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

s

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠





⌡

d

:=

u

i

66.94 mm

=

Segment 2.

i

2

:=

wysoko

ść

segmentu

x

0 m

⋅

h

s

..

:=

h

s

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

M

pk

+

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

i 1

+

n

s

n

p

Iksr

n

h

s

2

⋅

1

2

n

+

i

−













⋅













∑

=

+

:=

grubo

ść

ś

cianki trzonu

t

i

10 mm

=

ś

rednica zewn

ę

trzna

D

z

1000 mm

=

moment bezwładno

ś

ci przekroju

J

π

D

z

( )

4

⋅

64

π

D

z

t

i

−

(

)

4

⋅

64

−

:=

J

193423.88 cm

4

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

s

( )

:=

M

rk

M

r

h

s

( )

:=

M

rk

300.29 m kN

=

M

pk

30 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

s

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠





⌡

d

:=

u

i

120.23 mm

=

Segment 1.

i

1

:=

wysoko

ść

segmentu

x

0 m

⋅

h

c

..

:=

h

c

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

M

pk

+

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

i 1

+

n

s

n

p

Iksr

n

h

s

⋅

5 m

⋅

n

1

−

(

) h

s

⋅

+





⋅









∑

=

+

:=

grubo

ść

ś

cianki trzonu

t

i

16 mm

=

ś

rednica zewn

ę

trzna

D

z

1000 mm

=

moment bezwładno

ś

ci przekroju

J

π

D

z

( )

4

⋅

64

π

D

z

t

i

−

(

)

4

⋅

64

−

:=

J

306699.55 cm

4

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

c

( )

:=

M

rk

M

r

h

c

( )

:=

M

rk

458.45 m kN

=

M

pk

38 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

c

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠





⌡

d

:=

u

i

196.2 mm

=

Ugi

ę

cie wierzchołka komina

u

w

1

n

s

i

u

i

∑

=

:=

u

w

0.42 m

=

Dopusczalne ugi

ę

ci wierzchołka komina

u

dop

H

75

:=

u

dop

0.51 m

=

( jak dla komina jednopowłokowego )

u

w

0.42 m

=

<

u

dop

0.51 m

=

u

w

0.42 m

=

>

0.01 H

⋅

0.38 m

=

Nale

ż

y w I sytuacji projektowej uwzgl

ę

dni

ć

efekty II rz

ę

du.

obliczeniowa siła osiowa w przekroju zamocowania

N

o

N

I

1

1.1

⋅

g

⋅

:=

N

o

80.72 kN

=

sztywno

ść

komina w przekroju zamocowania

EJ

o

E J

⋅

:=

EJ

o

628734.07 kN m

2

⋅

=

ε

H

N

o

EJ

o

⋅

:=

ε

0.43

=

< 0.8

zgodnie z norm

ą

oblicznia wg teorii II rz

ę

du przeprowadzono sposobem przybli

ż

onym

Zast

ę

pcze momenty wg teorii II rz

ę

du

N

o

N

o

kN

⋅

:=

N

o

80718.52 s

2

−

kg m

⋅

⋅

kN

=

EJ

o

E J

⋅

:=

EJ

o

628734.07 kN m

2

⋅

=

i

1 n

s

..

:=

M'

I

i

M

I

i

1

ε

2

8

+













⋅

:=

9.1. Ugi

ę

cie w II sytuacji projektowej.

Obci

ąż

enie jednostkowe jest przyło

ż

one w wierzchołku komina.

Segment 6.

i

6

:=

wysoko

ść

segmentu

x

0 m

⋅

h

s

..

:=

h

s

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

:=

grubo

ść

ś

cianki trzonu

t

i

t

i

t

k

+

:=

t

i

14 mm

=

ś

rednica zewn

ę

trzna

D

z

1000 mm

=

moment bezwładno

ś

ci przekroju

J

π

D

z

( )

4

⋅

64

π

D

z

t

i

−

(

)

4

⋅

64

−

:=

J

269170.37 cm

4

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

s

( )

:=

M

rk

M

r

h

s

( )

:=

M

rk

12.92 m kN

=

M

pk

6 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

s

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠





⌡

d

:=

u

i

0.21 mm

=

Segment 5.

i

5

:=

wysoko

ść

segmentu

x

0 m

⋅

h

s

..

:=

h

s

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

M

pk

+

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

i 1

+

n

s

n

p

Iksr

n

h

s

2

⋅

1

2

n

+

i

−













⋅













∑

=

+

:=

grubo

ść

ś

cianki trzonu

t

i

t

i

t

k

+

:=

t

i

15 mm

=

ś

rednica zewn

ę

trzna

D

z

1000 mm

=

moment bezwładno

ś

ci przekroju

J

π

D

z

( )

4

⋅

64

π

D

z

t

i

−

(

)

4

⋅

64

−

:=

J

287963.53 cm

4

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

s

( )

:=

M

rk

M

r

h

s

( )

:=

M

rk

51.01 m kN

=

M

pk

12 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

s

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠





⌡

d

:=

u

i

3.98 mm

=

Segment 4.

i

4

:=

wysoko

ść

segmentu

x

0 m

⋅

h

s

..

:=

h

s

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

M

pk

+

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

i 1

+

n

s

n

p

Iksr

n

h

s

2

⋅

1

2

n

+

i

−













⋅













∑

=

+

:=

grubo

ść

ś

cianki trzonu

t

i

8 mm

=

ś

rednica zewn

ę

trzna

D

z

1000 mm

=

moment bezwładno

ś

ci przekroju

J

π

D

z

( )

4

⋅

64

π

D

z

t

i

−

(

)

4

⋅

64

−

:=

J

155204.71 cm

4

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

s

( )

:=

M

rk

M

r

h

s

( )

:=

M

rk

112.83 m kN

=

M

pk

18 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

s

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠





⌡

d

:=

u

i

29.86 mm

=

Segment 3.

i

3

:=

wysoko

ść

segmentu

x

0 m

⋅

h

s

..

:=

h

s

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

M

pk

+

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

i 1

+

n

s

n

p

Iksr

n

h

s

2

⋅

1

2

n

+

i

−













⋅













∑

=

+

:=

grubo

ść

ś

cianki trzonu

t

i

t

i

t

k

+

:=

t

i

17 mm

=

ś

rednica zewn

ę

trzna

D

z

1000 mm

=

moment bezwładno

ś

ci przekroju

J

π

D

z

( )

4

⋅

64

π

D

z

t

i

−

(

)

4

⋅

64

−

:=

J

325378.52 cm

4

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

s

( )

:=

M

rk

M

r

h

s

( )

:=

M

rk

196.66 m kN

=

M

pk

24 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

s

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠




⌡

d

:=

u

i

35.87 mm

=

Segment 2.

i

2

:=

wysoko

ść

segmentu

x

0 m

⋅

h

s

..

:=

h

s

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

M

pk

+

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

i 1

+

n

s

n

p

Iksr

n

h

s

2

⋅

1

2

n

+

i

−













⋅













∑

=

+

:=

grubo

ść

ś

cianki trzonu

t

i

t

i

t

k

+

:=

t

i

18 mm

=

ś

rednica zewn

ę

trzna

D

z

1000 mm

=

moment bezwładno

ś

ci przekroju

J

π

D

z

( )

4

⋅

64

π

D

z

t

i

−

(

)

4

⋅

64

−

:=

J

344000.58 cm

4

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

s

( )

:=

M

rk

M

r

h

s

( )

:=

M

rk

300.29 m kN

=

M

pk

30 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

s

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠




⌡

d

:=

u

i

67.6 mm

=

Segment 1.

i

1

:=

wysoko

ść

segmentu

x

0 m

⋅

h

c

..

:=

h

c

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

M

pk

+

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

i 1

+

n

s

n

p

Iksr

n

h

s

⋅

5 m

⋅

n

1

−

(

) h

s

⋅

+





⋅









∑

=

+

:=

grubo

ść

ś

cianki trzonu

t

i

t

i

t

k

+

:=

t

i

24 mm

=

ś

rednica zewn

ę

trzna

D

z

1000 mm

=

moment bezwładno

ś

ci przekroju

J

π

D

z

( )

4

⋅

64

π

D

z

t

i

−

(

)

4

⋅

64

−

:=

J

454544.1 cm

4

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

c

( )

:=

M

rk

M

r

h

c

( )

:=

M

rk

458.45 m kN

=

M

pk

38 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

c

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠





⌡

d

:=

u

i

132.39 mm

=

Ugi

ę

cie wierzchołka komina

u

w

1

n

s

i

u

i

∑

=

:=

u

w

0.27 m

=

Dopusczalne ugi

ę

ci wierzchołka komina

u

dop

H

75

:=

u

dop

0.51 m

=

( jak dla komina jednopowłokowego )

u

w

0.27 m

=

<

u

dop

0.51 m

=

u

w

0.27 m

=

<

0.01 H

⋅

0.38 m

=

Obliczenia dla II sytuacji projektowej mo

ż

na przeprowadzi

ć

wg teorii I rz

ę

du.

10. Sprawdzanie trzonu w I sytuacji projektowej.

10.1. Pierwsza kombinacja podstawowa obci

ąż

e

ń

.

Pierwsza kombinacja obejmuje:
- obci

ąż

enie stałe powi

ę

kszone o ci

ęż

ar połowy naddatku korozyjnego

- obci

ąż

enie wiatrem w linii wiatru dla 3-letniego czasu u

ż

ytkowania

- obci

ąż

enia technologiczne z pomini

ę

ciem obci

ąż

enia pomostu i drabin

No

ś

no

ść

w dolnym przekroju segmentu I (najni

ż

szego).

i

1

:=

długo

ść

oblczeniowa komina

l

c

1.12 H

⋅

:=

l

c

42.56 m

=

poziom

z

z

i

h

c

−

:=

z

0 m

=

promie

ń

zewn

ę

trzny trzonu

R

D

z

2

:=

R

500 mm

=

grubo

ść

segmentu z uwzgl

ę

dnieniem połowy naddatku korozyjnego

g

t

t

i

t

k

2

−

:=

g

t

20 mm

=

pole przekroju poprzecznego pier

ś

cienia

A

π

D

z

2

⋅

4

π

D

z

g

t

−

(

)

2

⋅

4

−

:=

A

311.02 cm

2

=

moment bezwładno

ś

ci przekroju

J

π

4

D

z

2













4

D

z

g

t

−

2













4

−









⋅

:=

J

381074.4 cm

4

=

wska

ź

nik wytrzymało

ś

ci przekroju

W

J

0.5 D

z

⋅

:=

W

7621.49 cm

3

=

obliczeniowa siła

ś

ciskaj

ą

ca

N

o

1.1 N

I

i

⋅

g

⋅

:=

N

o

80.72 kN

=

obliczeniowy moment zginaj

ą

cy

M

o

1.3 M

I

i

⋅

:=

M

o

598.45 kN m

⋅

=

smukło

ść

wzgl

ę

dna przekroju

λ

'

p

R

g

t

1.59

⋅

f

dT

E

T













2

3

⋅

:=

λ

'

p

0.17

=

współczynnik niestateczno

ś

ci ogólnej

ϕ

p

1

λ

'

p

2.4

+









0.625

−

:=

ϕ

p

0.99

=

obliczeniowa no

ś

no

ść

przekroju na

ś

ciskanie

N

R

ϕ

p

α

kor

⋅

A

⋅

f

dT

⋅

:=

N

R

5291.5 kN

=

obliczeniowa no

ś

no

ść

przekroju na zginanie

M

R

1.2

ϕ

p

⋅

α

kor

⋅

W

⋅

f

dT

⋅

:=

M

R

1556.02 kN m

⋅

=

Współczynnik wyboczeniowy.

promie

ń

bezwładno

ś

ci

i

J

A

:=

i

350.04 mm

=

smukło

ść

λ

l

c

i

:=

smukło

ść

porównawcza

λ

'

λ

ϕ

p

⋅

2.73

f

dT

E

T

⋅

:=

λ

'

1.48

=

współczynnik niestateczno

ś

ci ogólnej

ϕ

1

λ

'

3.2

+

(

)

0.625

−

:=

ϕ

0.39

=

Oblczeniowa no

ś

no

ść

przekroju:

N

o

ϕ

N

R

⋅

M

o

M

R

+

0.42

=

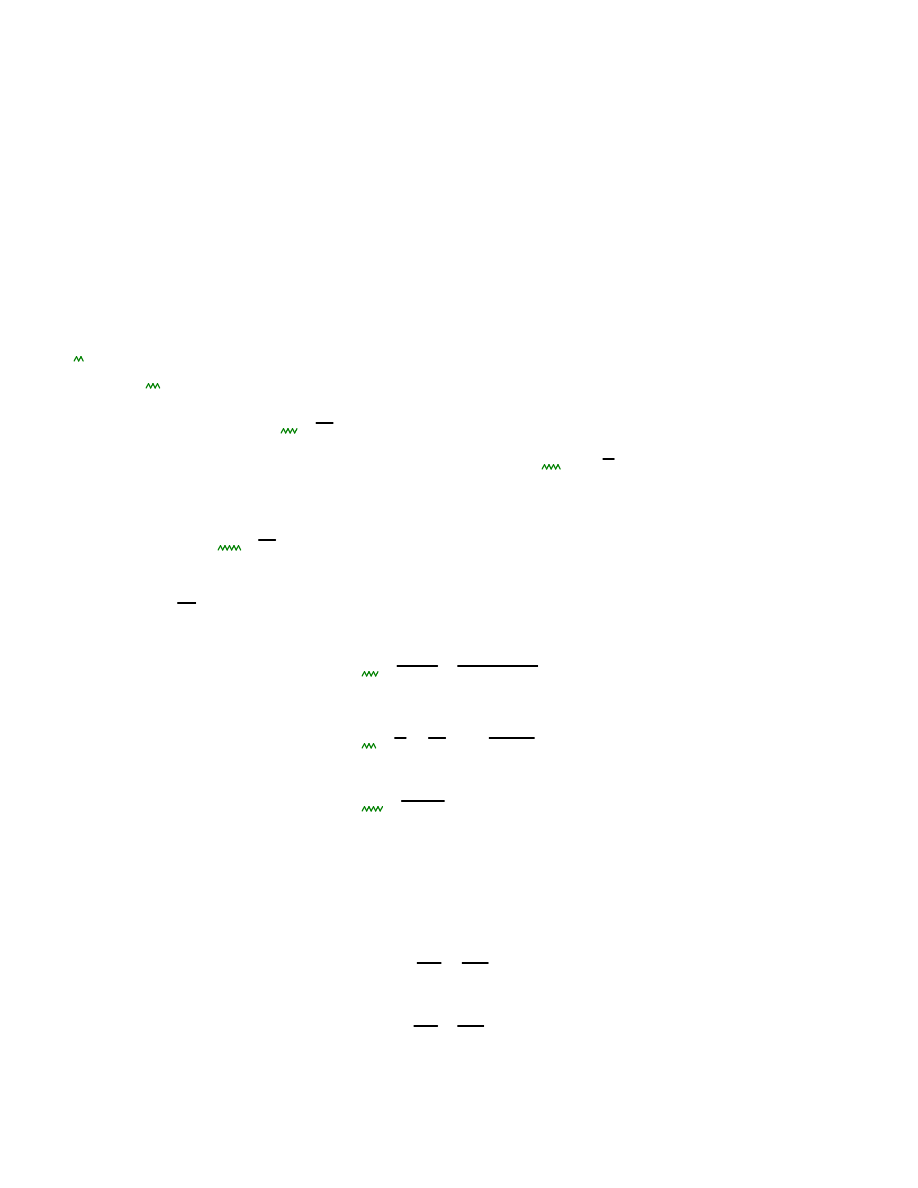
10.1. Druga kombinacja podstawowa obci

ąż

e

ń

.

Druga kombinacja obejmuje warto

ś

ci charakterystyczne:

- obci

ąż

enie stałe powi

ę

kszone o połow

ę

naddatku korozyjnego

- obci

ąż

enie wiatrem w płaszczy

ź

nie prostopadłej do linii wiatru

- obci

ąż

enie technologiczne z pomini

ę

ciem obci

ąż

enia pomostów i drabin

No

ś

no

ść

w dolnym przekroju segmentu I (najni

ż

szym).

i

1

:=

poziom

z

z

i

h

c

−

:=

z

0 m

=

promie

ń

zewn

ę

trzny trzonu

R

D

z

2

:=

R

500 mm

=

grubo

ść

segmentu z uwzgl

ę

dnieniem połowy naddatku korozyjnego

g

t

t

i

t

k

2

−

:=

g

t

20 mm

=

liczba cykli obci

ąż

enia wzbudzeniem wirowym

okres eksploatacji

T

e

T

e

lat

:=

T

e

10

=

N

wz

5.1 10

6

⋅

T

e

T

1

⋅

e

0.16 v

cr

⋅

(

)

2

−

e

0.2 v

cr

⋅

(

)

2

−

−









⋅

:=

N

wz

4120214.58

=

pole przekroju poprzecznego pier

ś

cienia

A

π

D

z

2

⋅

4

π

D

z

g

t

−

(

)

2

⋅

4

−

:=

A

311.02 cm

2

=

moment bezwładno

ś

ci przekroju

J

π

4

D

z

2













4

D

z

g

t

−

2













4

−









⋅

:=

J

381074.4 cm

4

=

wska

ź

nik wytrzymało

ś

ci przekroju

W

J

0.5 D

z

⋅

:=

W

7621.49 cm

3

=

charakterystyczna siła

ś

ciskaj

ą

ca

N

ch

N

I

i

g

⋅

:=

N

ch

73.38 kN

=

charakterystyczny moment zginaj

ą

cy

M

ch

M

y

i

:=

M

ch

206.32 kN m

⋅

=

maksymalne napr

ęż

enie w trzonie

σ

max

N

ch

A

M

ch

W

+

:=

σ

max

29.43 MPa

=

minimalne napr

ęż

enia w trzonie

σ

min

N

ch

A

M

ch

W

−

:=

σ

min

24.71

−

MPa

=

zakres zmiennoi

ś

ci napr

ęż

e

ń

∆σ

σ

min

σ

max

+

:=

∆σ

54.14 MPa

=

dla

N

wz

4120214.58

=

<

m

3

:=

kategoria zm

ę

czeniowa

∆σ

c

56 MPa

⋅

:=

wytrzymało

ść

zm

ę

czeniowa trzonu

∆σ

R

0.735

∆σ

c

⋅

5 10

6

⋅

N

wz









1

m

⋅

:=

∆σ

R

43.9 MPa

=

ś

rednia temperatura zewn

ę

trzna

T

z

T

zl

T

zz

+

2

:=

T

z

274.5 K

=

nie uwzgl

ę

dnia si

ę

wpływów temperatury gazów wewn

ą

trz komina na wytrzymało

ść

stali płaszcza

α

T

1

:=

∆σ

54.14 MPa

=

<

α

T

α

kor

⋅

∆σ

R

⋅

33.26 MPa

=

11. Sprawdzanie trzonu w II sytuacji projektowej.

11.1. Podstawowa kombinacja obci

ąż

e

ń

.

W II sytuacji projektowej uwzgl

ę

dnia si

ę

warto

ś

ci obliczeniowe:

- obci

ąż

enia stałego

- obci

ąż

enia wiatrem w linii wiatru (dla całego okresu eksploatacyjneg)

- obci

ąż

enia technologiczne z pomini

ę

ciem obci

ąż

enia pomstów i drabin

- obci

ąż

enie temperatur

ą

No

ś

no

ść

w dolnym przekroju segmentu I (najni

ż

szego).

i

1

:=

długo

ść

oblczeniowa komina

l

c

1.12 H

⋅

:=

l

c

42.56 m

=

poziom

z

z

i

h

c

−

:=

z

0 m

=

promie

ń

zewn

ę

trzny trzonu

R

D

z

2

:=

R

500 mm

=

grubo

ść

segmentu z uwzgl

ę

dnieniem połowy naddatku korozyjnego

g

t

t

i

:=

g

t

24 mm

=

pole przekroju poprzecznego pier

ś

cienia

A

π

D

z

2

⋅

4

π

D

z

g

t

−

(

)

2

⋅

4

−

:=

A

372.47 cm

2

=

moment bezwładno

ś

ci przekroju

J

π

4

D

z

2













4

D

z

g

t

−

2













4

−









⋅

:=

J

454544.1 cm

4

=

wska

ź

nik wytrzymało

ś

ci przekroju

W

J

0.5 D

z

⋅

:=

W

9090.88 cm

3

=

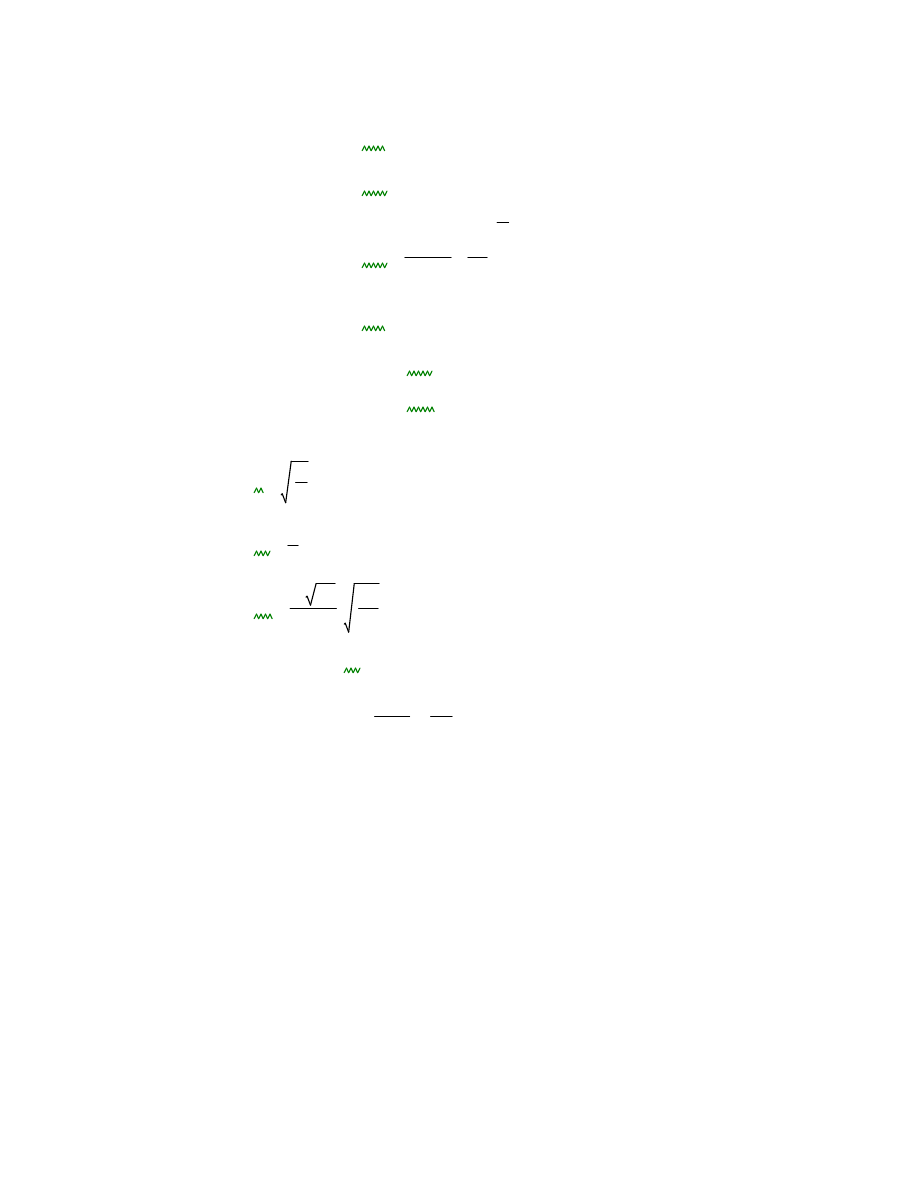
obliczeniowa siła

ś

ciskaj

ą

ca

N

o

1.1 N

II

i

⋅

g

⋅

:=

N

o

107.98 kN

=

obliczeniowy moment zginaj

ą

cy

M

o

1.3 M

II

i

⋅

:=

M

o

248.83 m kN m

⋅

=

smukło

ść

wzgl

ę

dna przekroju

λ

'

p

R

g

t

1.59

⋅

f

dT

E

T













2

3

⋅

:=

λ

'

p

0.14

=

współczynnik niestateczno

ś

ci ogólnej

ϕ

p

1

λ

'

p

2.4

+









0.625

−

:=

ϕ

p

0.99

=

obliczeniowa no

ś

no

ść

przekroju na

ś

ciskanie

N

R

ϕ

p

α

kor

⋅

A

⋅

f

dT

⋅

:=

N

R

6356.42 kN

=

obliczeniowa no

ś

no

ść

przekroju na zginanie

M

R

1.2

ϕ

p

⋅

α

kor

⋅

W

⋅

f

dT

⋅

:=

M

R

620.57 m kN m

⋅

=

Współczynnik wyboczeniowy.

promie

ń

bezwładno

ś

ci

i

J

A

:=

i

349.34 mm

=

smukło

ść

λ

l

c

i

:=

smukło

ść

porównawcza

λ

'

λ

ϕ

p

⋅

2.73

f

dT

E

T

⋅

:=

λ

'

1.48

=

współczynnik niestateczno

ś

ci ogólnej

ϕ

1

λ

'

3.2

+

(

)

0.625

−

:=

ϕ

0.39

=

Oblczeniowa no

ś

no

ść

przekroju:

N

o

ϕ

N

R

⋅

M

o

M

R

+

0.44

=

kN

10

3

newton

⋅

:=

MPa

10

6

Pa

⋅

:=

s

sec

:=

W

watt

:=

lat

yr

:=

v

v s

⋅

m

:=

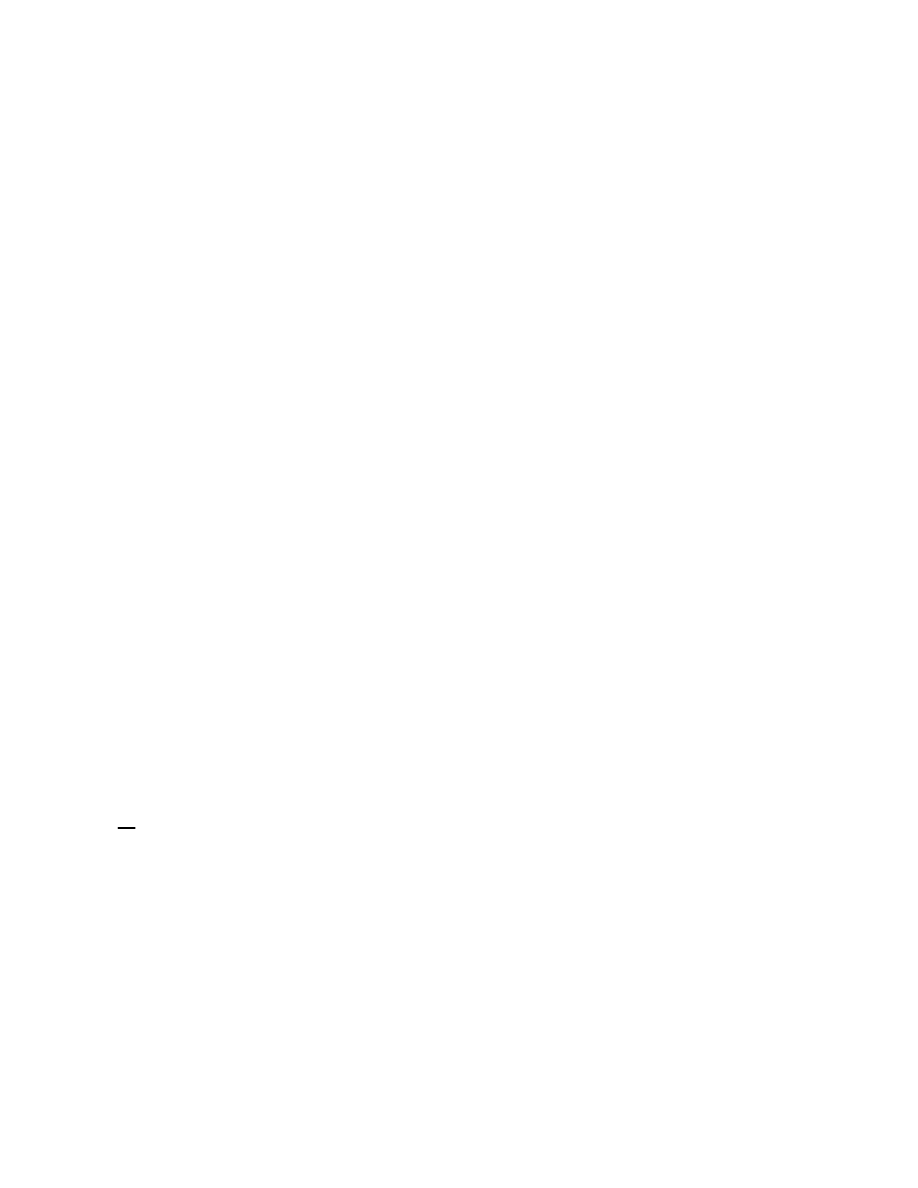
T

e.

T

e

lat

:=

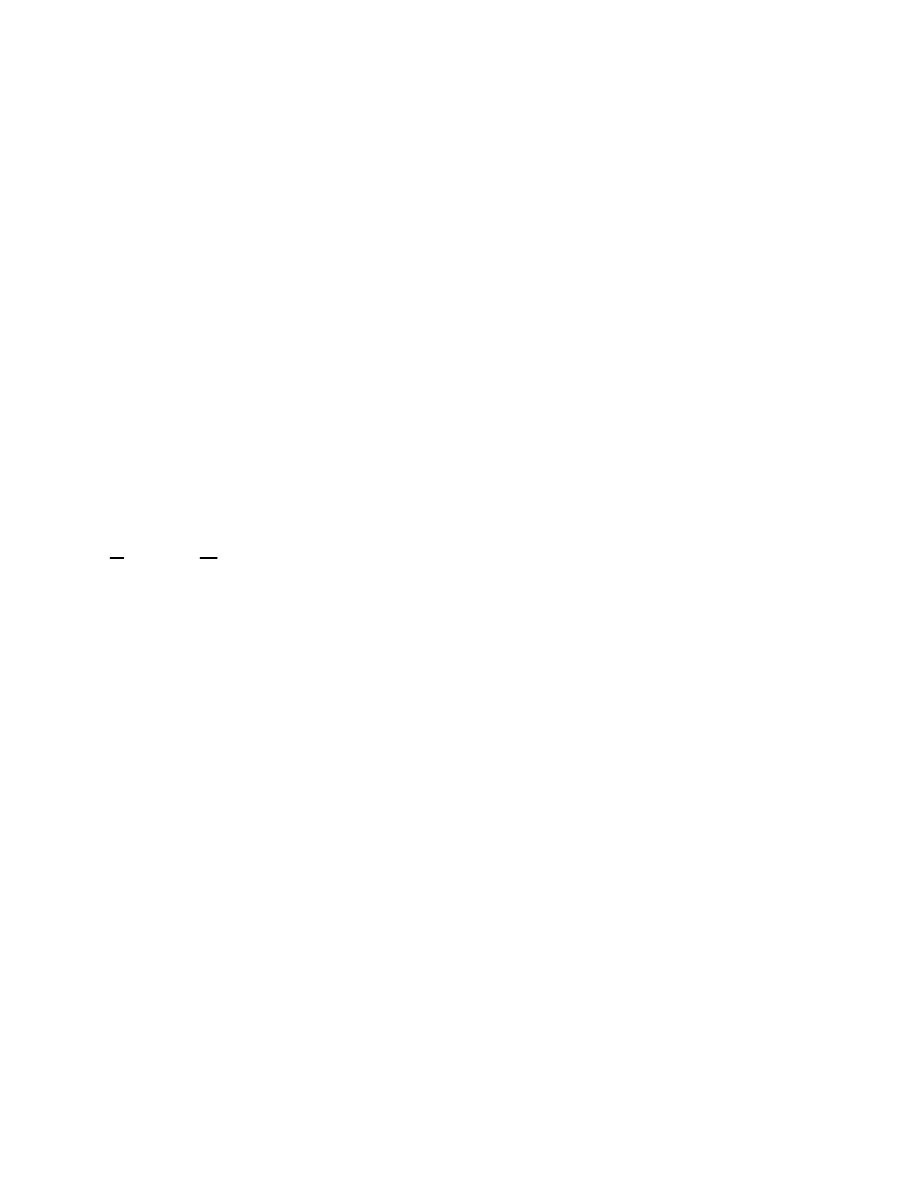
H

H

m

:=

D

D

z

m

:=

v

v

H

:=

v

H.

H

m s

1

−

⋅

:=

z

i

z

i

m

:=

H

H

m

:=

D

D

z

m

:=

v

H.

v

H

m s

1

−

⋅

:=

z

i

z

i

m

:=

ρ

p

ρ

p

m

3

−

kg

⋅

:=

i

1 n

s

..

:=