13. Elektrodyfuzja

W ramach tych zajęć, postaramy się przybliżyć zjawisko elektrodyfuzji. Jak sugeruje sama nazwa,

elektrodyfuzja jest procesem łączącym dwa zjawiska - transport dyfuzyjny (masy) oraz transport ładunku
elektrycznego w polu elektrycznym. Ponieważ nośniki ładunku również obdarzone są masą, oba te procesy
możemy połączyć poprzez odpowiednie sformułowanie wyrażenia na strumień masy.

13.1.Teoria Wagnera

Założenia i podstawowe równanie teorii:

(13.1)

lub zapisane w innej postaci:

(13.2)

znają państwo z poprzednich zajęć. Teraz pokażemy tylko jak sformułować granice całkowania. Przyjrzyjmy się
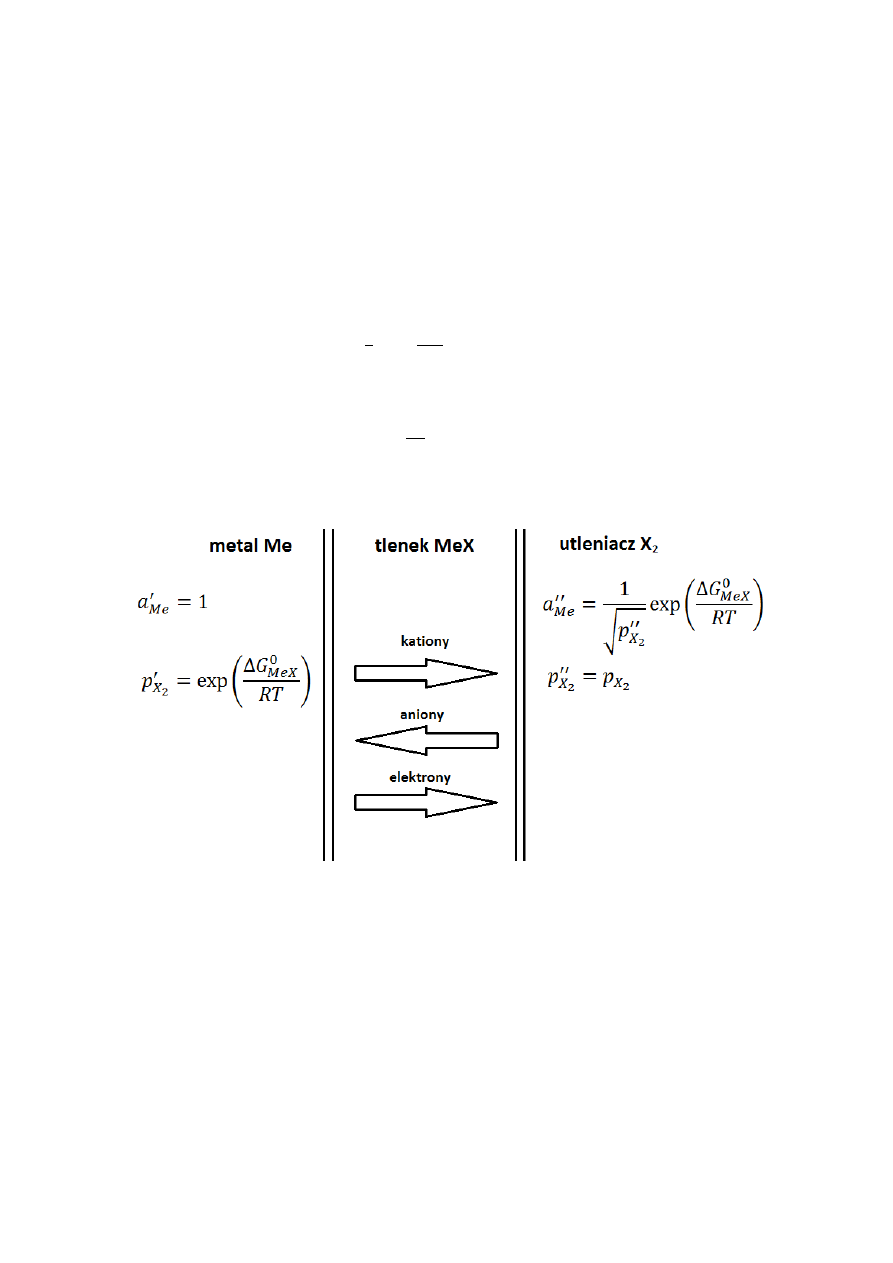
naszemu układowi:

Po lewej stronie, znajduje się czysty metal, którego aktywność wynosi 13. Przejście metalu do zgorzeliny wiąże
się z wytworzeniem jonu, który docierając na drugą stronę zgorzeliny, ma już nieco inną aktywność. Podobnie
ma się sprawa z ciśnieniem - o ile na zewnętrznej powierzchni ciśnienie jest równe ciśnieniu parcjalnemu, o tyle
na powierzchni rozdzielającej metal od zgorzeliny, wartość ta będzie już zupełnie inna.

Zapiszmy teraz równanie reakcji:

(133)

Zmiana entalpii swobodnej Gibbsa wyniesie:

(13.4)

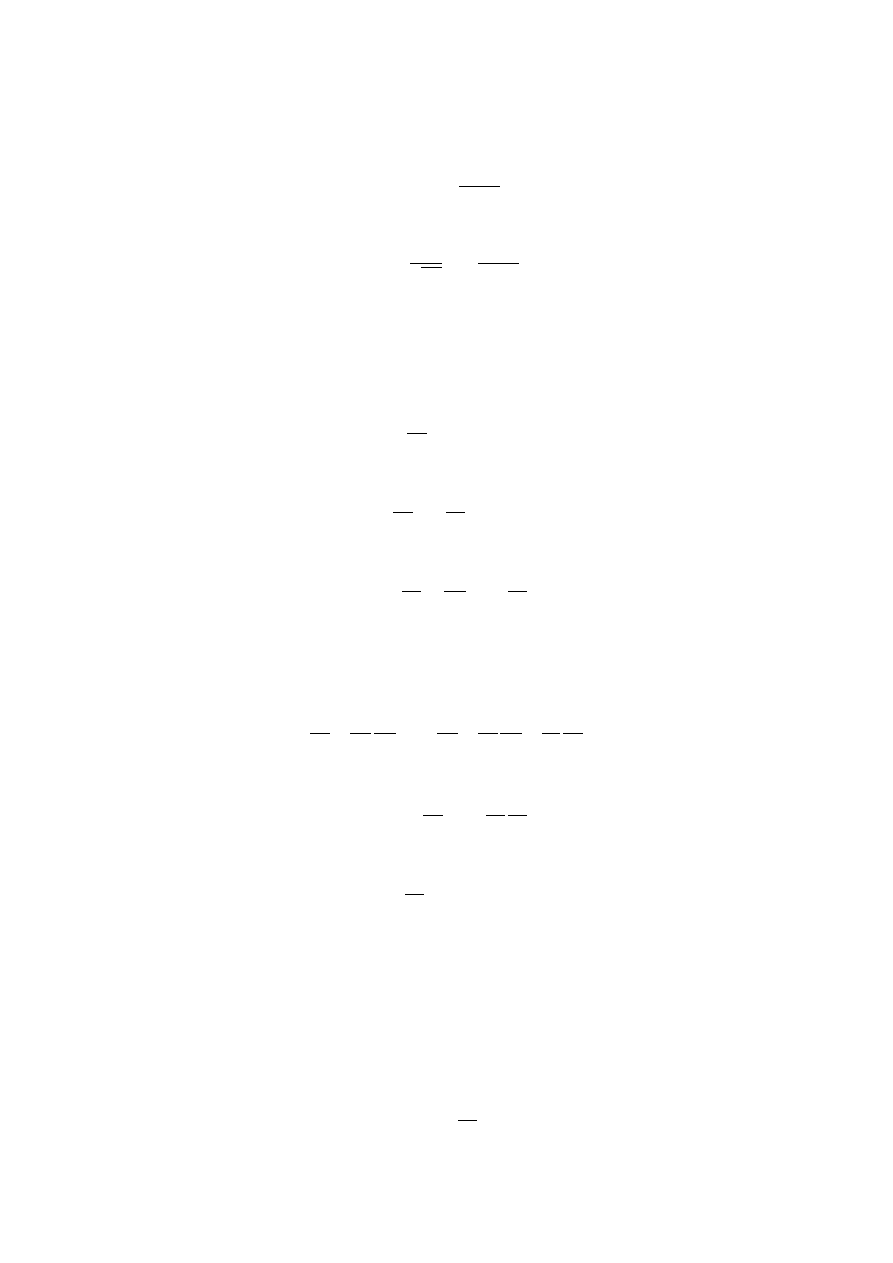
zwróćmy tutaj uwagę, że w członie związanym z metalem uwzględniamy fakt, iż aktywność metalu na granicy
tlenek/utleniacz może być różna od 13. W rezultacie, możemy obliczyć wartości

i

:

(13.5)

(13.6)

13.2. Model Nernsta-Plancka-Poissona (NPP)

Układ równań Nernsta-Plancka-Poissona służy do opisu ruchu jonów w czasie i przestrzeni. Załóżmy układ n-
składnikowy. Dla każdego i-tego składnika obowiązuje nas prawo zachowania o postaci:

(13.7)

Po zredukowaniu zagadnienia do jednego wymiaru:

(13.8)

Ponieważ znowu rozważamy transport masy i ładunku, to ponownie wykorzystamy strumień Nernsta-Plancka:

(13.9)

Aby przejść z potencjału chemicznego na stężenia, wykorzystujemy zależność:

(13.10)

Przy założeniu a

i

= c

i

, możemy obliczyć odpowiednie pochodne:

(13.11)

Po wstawieniu (13.11) do (13.9) otrzymujemy:

(13.12)

W przypadku trójwymiarowym, równanie (13.9) przyjmuje postać:

(13.13)

Po uzyskaniu wyrażenia na strumień dyfuzyjny, następnym krokiem jest odpowiednie wyrażenie gradientu
potencjału elektrycznego. Gdy pole elektryczne jest potencjalne, spełniona jest zależność:

(13.14)

Gdzie: E – natężenie pola elektrycznego

Wyrażenie (14.14) jest prawdziwe, gdy rozważamy pola w sytuacji stacjonarnej lub kwazistacjonarnej, czyli gdy
na podstawie prawa Faradaya możemy zapisać:

(13.15)

Gdzie: B – natężenie pola magnetycznego

Wprowadźmy teraz prawo Gaussa, pozwoli ona na powiązanie pola elektrycznego i gęstości ładunku, którą z
kolei będziemy mogli powiązać ze stężeniem jonów w układzie. Ma ono postać:

(13.16)

Gdzie: ρ – gęstość ładunku

ε – przenikalność elektryczna ośrodka

Podstawiając (13.14) do (13.16) otrzymujemy:

(13.17)

Równanie (13.17) nazywamy równaniem Poissona.

Gęstość ładunku możemy wyrazić, jako sumę iloczynów stężeń poszczególnych jonów i ich ładunków (ponieważ
rozważamy stężenia molowe, musimy uwzględnić dodatkowo stałą Faradaya):

(13.18)

Uwzględniając (13.13), (13.14), (13.16) i (13.18), dla przypadku jednowymiarowego otrzymamy układ równań:

(13.19)

Ze względów obliczeniowych, wygodniejsze jest przedstawienie ostatniego równania z układu (13.19), za
pomocą pochodnej czasowej. W tym celu różniczkujemy to równanie obustronnie po czasie:

(13.20)

Z twierdzenia Schwarza wiemy, że (przy odpowiednich założeniach):

(13.21)

zatem:

(13.22)

Widać, że pochodna po prawej stronie może być zapisana jako drugie prawo Fick’a (równanie ciągłości):

(13.23)

Całkując obustronnie po „x”:

(13.24)

Gdzie: C – stała całkowania

Dobór stałej całkowania podyktowany jest przez analogię do uogólnionego prawa Ampera:

(13.25)

Po przekształceniu (13.25) otrzymamy:

(13.26)

Jak widać, równania (13.26) i (13.24) są w pełni analogiczne. Wyrażenie po lewej stronie równania (13.26),
nazywamy prądem przesunięcia. Nie jest prąd w sensie przepływu ładunków, jednak podobnie jak zwykły prąd
przewodzenia wywołuje on wirowe pole magnetyczne.

Jak wynika z dotychczasowych rozważań, drugi człon po prawej stronie równania (13.26) ma wymiar prądu,
więc przez analogię możemy napisać równanie (13.24) w postaci:

(13.27)

Gdzie: I – całkowita gęstość prądu

Korzystając z dotychczasowych wyprowadzeń, możemy teraz zapisać pełny układ równań Nernsta-Plancka-
Poissona:

(13.28)

13.3. Model Nernsta-Plancka-Poissona-Darkena (NPPD)

W przypadku układów opisywanych przez model NPP możliwe jest wprowadzenie członu związanego z
prędkością Darkena, czyli będącego wynikiem obecności niekompensujących się strumieni składników,
płynących w przeciwne strony. Wtedy równanie na strumień, zaprezentowane w układzie (13.28) przybierze
postać:

(13.29)

Pozostałe równania nie wymagają dodatkowych zmian, jednak pojawia się problem innego rodzaju. W
poprzednio rozpatrywanym przypadku mieliśmy r+1 zmiennych („r” stężeń oraz E) i r+1 równań („r” równań
ciągłości oraz wyrażenie na prąd przesunięcia). Przy uwzględnieniu dryftu pojawia się kolejna niewiadoma: v

drift

,

przy tej samej liczbie równań. Konieczne zatem jest wprowadzenie do układu jeszcze jednego równania. Będzie
nim założenie stałego stężenia molowego w układzie:

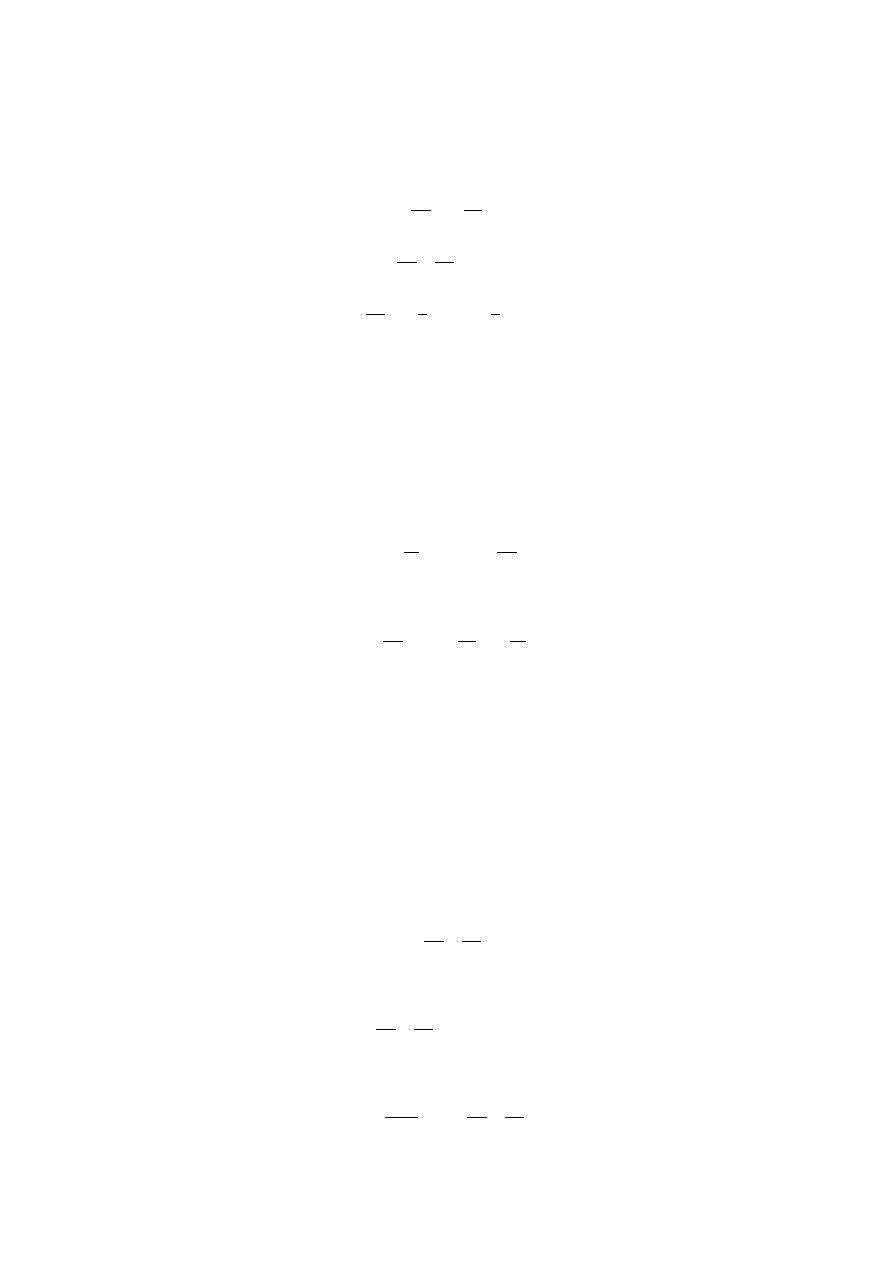
(13.30)

Kompletny układ równań będzie się zatem prezentował następująco:

(13.31)

Rozważmy teraz układ zamknięty. Oznacza to, iż strumienie na brzegach układu wynoszą 0 (warunki brzegowe
Neumanna):

(13.32)

Zróżniczkujmy stronami po czasie równanie (13.30):

(13.33)

Widzimy, że po prawej stronie możemy ponownie wstawić równanie ciągłości:

(13.34)

Ponieważ pochodna przestrzenna z sumy strumieni wynosi zero, oznacza to, iż sama suma strumieni musi być
wartością stałą, zależną co najwyżej od czasu:

(13.35)

Ponieważ wartość stałej K(t) nie zależy od położenia, warunek (13.35) musi być zachowany także na brzegach
układu, co po uwzględnieniu warunków (13.32) prowadzi do wniosku:

(13.36)

Wstawmy do (13.36) nasze wyrażenie na strumień (13.29):

(13.37)

Na podstawie (13.33):

(13.38)

W rezultacie otrzymujemy zależność na prędkość Darkena:

(13.39)