1. WSTĘP TEORETYCZNY.

Większość zjawisk towarzyszących przepływowi prądu elektrycznego nie zależy od znaku nośników prądu. Dlatego przez długie lata fizycy nie byli w stanie stwierdzić, jego znaku ładunek podlega ruchowi podczas przepływu prądu w przewodniku.

W roku 1879 E.H. Hall wymyślił doświadczenie, które pozwoliło określić znak ładunku poruszającego się w przewodniku.

Zjawisko Halla dotyczy ruchów nośników ładunków w metalach i półprzewodnikach w obecności pola magnetycznego. Na poruszające się dziury i elektrony w płytce półprzewodnika (hallotronie) działa siła Lorentza

gdzie:

siła Lorentza,

17. B - indukcja magnetyczna,

5. q - ładunek,

5. V - prędkość unoszenia,

E - natężenie pola elektrycznego,

która odchyla je w kierunku prostopadłym do wektorów B i V. W ten sposób powstaje poprzeczna różnica potencjałów w hallotronie - napięcie Halla między punktami A i B.

Proces rozdzielania się ładunków trwa tak długo, aż powstaje w wyniku rozdzielania, poprzeczne pole elektryczne o natężeniu E, które spowoduje wytworzenie siły elektrostatycznej, która zrównoważy siłę Lorentza.

Zjawisko charakteryzuje stała R_H zwaną stałą Halla. Stwierdzono doświadczalnie, że różnica potencjałów U jest wprost proporcjonalna do natężenia prądu I oraz indukcji B pola magnetycznego a odwrotnie do szerokości płytki.

U - napięcie Halla

Z wyżej wymienionego równania wynika, że napięcie Halla, dla geometrii przedstawionej na rys.1, jest proporcjonalne do natężenia prądu i_a, do indukcji pola magnetycznego B i do stałej Halla. Jest natomiast odwrotnie proporcjonalne do grubości d płytki przewodzącej prąd. Dlatego stosuje się płytki bardzo cienkie, często naparowane dla uzyskania dużego napięcia Halla przy wybranym metalu.

gdzie:

e - elektron,

n - gęstość nośników prądu.

Jak widać znak stałej odpowiada znakowi elektronu. Na podstawie jej pomiaru można określić rodzaj przewodnictwa. Jeżeli R_H<0 wtedy przewodnictwo elektronowe, gdy R_H>0 to przewodnictwo dziurowe. W przypadku gdy w półprzewodniku mamy do czynienia z oboma rodzajami przewodnictwa to znak R_H pokaże który rodzaj przeważa.

Wyjaśnione jest to na rysunku przedstawiającym model zjawiska Halla w metalu:

Rys.1. Zjawisko Halla w metalu.

W przewodniku lub półprzewodniku siły działające w polu. Spowoduje to powstanie poprzecznego pola elektrycznego Halla E_H, które przeciwstawia się dalszemu przesuwaniu ładunków w poprzek przewodnika. Kierunek pola jest różny dla różnych znaków nośników prądu, co pozwala na określenie ich znaku w konkretnych przewodnikach.

W osiągniętym stanie równowagi siła Lorentza będzie równa 0 czyli:

Po uwzględnieniu gęstości prądu
otrzymamy:

Zatem w kierunku poprzecznym pojawi się między krawędziami płytki różnica potencjałów, którą łatwo obliczyć zakładając, że pole poprzeczne jest jednorodne.

gdzie:

U_H - napięcie Halla,

E_H - natężenie pola elektrycznego Halla,

d - grubość płytki,

j - gęstość prądu,

B - indukcja magnetyczna,

n - koncentracja nośników,

e - elektron.

Hallotrony znajdują szerokie zastosowanie w technice: od zastosowań do pomiaru natężenia pól magnetycznych, badania własności materiałów magnetycznych, pomiaru prądu i mocy w urządzeniach elektroenergetycznych, do zastosowań w elementach liczących i logicznych. Efekt Halla spełnia także ważną rolę poznawczą w badaniach struktury półprzewodników.

2. OPIS STANOWISKA.

W ćwiczeniu źródłem pola magnetycznego był solenoid (zasilany napięciem stałym 120V) o całkowitej liczbie zwojów n = 1500 i długości l = 95 cm, przez który płynął prąd o natężeniu I. Dla wyznaczenia rodziny charakterystyk hallotronu był on zmieniany (dla każdej charakterystyki inny). Hallotron był umieszczony wewnątrz solenoidu tak, że wektor natężenia pola magnetycznego był prostopadły do powierzchni płytki. Pole solenoidu można uważać za stałe. Do hallotronu był przyłączony prąd sterujcy i_a, a do punktów A i B miliwoltomierz. W celu wyznaczenia charakterystyki dla danego pola magnetycznego zmieniano prąd sterujący i odczytywano napięcie Halla dla kolejnych wartości I.

Łączymy obwód wg schematu przedstawionego w punkcie pierwszym przebiegu ćwiczenia. Ustalamy warunki początkowe: najniższe zakresy napięciowe zasilacza i prostownika oraz maksymalne rezystancje opornic. Zmieniamy natężenie prądu sterującego i_a w zakresie od 0 do 26 mA, co 2 mA. Przy wyłączonym obwodzie cewki nastawiamy zadaną wartość natężenia prądu sterującego i_a i kompensujemy napięcie asymetrii elektrod, włączamy prostownik i notujemy wskazanie miliwoltomierza, wyłączamy prostownik. Charakterystyki hallotronu wykonujemy dla trzech różnych pól magnetycznych solenoidu odpowiadających natężeniu prądu np. I= 3, 5 i 7 [A].

UWAGA:

Pomiary należało wykonywać w miarę szybko i sprawnie, bo własności półprzewodnikowego hallotronu bardzo silnie zależą od temperatury, duży prąd płynący przez cewkę nagrzewał ją.

3. PRZEBIEG ĆWICZENIA.

1. Łączymy obwody wg schematu podanego na rys.2.

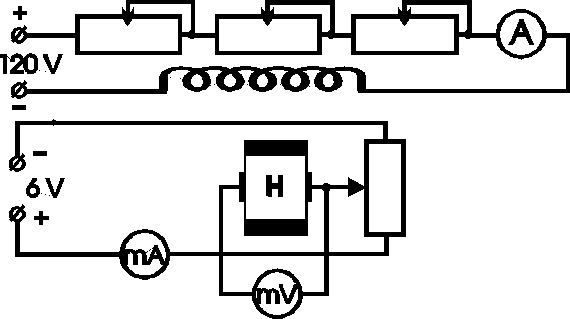
Rys.2. Schemat obwodu do wyznaczania czułości hallotronu.

2. Ustalamy warunki początkowe: najniższe zakresy napięciowe zasilacza i prostownika oraz maksymalne rezystancje opornic.

3. Wyznaczamy rodzinę charakterystyk U_H=f(i_a) hallotronu zmieniając natężenie prądu sterującego i_a w zakresie 0 - 26 [mA] co 2[mA].

Tok postępowania:

- przy włączonym obwodzie cewki nastawiamy zadaną wartość natężenia prądu sterującego i_a i kompensujemy napięcie asymetrii elektrod,

- włączamy prostownik i notujemy wskazanie miliwoltomierza,

- włączamy prostownik.

4. Charakterystyki hallotronu wykonujemy dla pięciu różnych pól magnetycznych solenoidu odpowiadających natężeniu prądu I = 3, 5, 7 [A].

W tabeli 1 przedstawiono wyniki pomiarów.

Tabela pomiarowa 1.

Lp.	is	Napięcie Halla UH [mV] dla prądu I [A]
	[mA]	I1=3 [A]	I2= 5[A]	I3=7 [A]
1	2	0,9	1,2	1,8
2	4	1,8	2,1	3,7
3	6	2,0	3,3	5,6
4	8	2,8	4,4	7,3
5	10	4,4	5,6	9,5
6	12	5,6	7,0	11,4
7	14	6,5	8,2	13,0
8	16	7,8	9,5	15,0
9	18	9,0	10,9	15,4
10	20	10,1	12,0	17,1
11	22	11,1	13,4	18,3
12	24	12,1	15,1	20,2
13	26	13,0	16,1	22,3

3. OBLICZENIA.

1. Rysujemy rodzinę charakterystyk hallotronu U_H=f(i_s).

Na podstawie tabelarycznego zestawienia wyników pomiarów oraz regresji liniowej narysowano wykresy dla poszczególnych natężeń prądu I.

- wyk.1., dla I=3 [A],

- wyk.2., dla I=5 [A],

- wyk.3., dla I=7 [A].

2. Metodą regresji liniowej obliczamy nachylenie charakterystyk U_H=k⋅i_s.

- dla I =3 [A]	k=(5,32±0,14)⋅10 ^-1
- dla I =5 [A]	k=(6,34±0,9)⋅10 ^-1
- dla I =7 [A]	k=(8,27±0,21)⋅10 ^-1

3. Obliczamy czułość hallotronu dla I = 3, 5, 7 [A].

gdzie:

k - współczynnik regresji,

l - długość solenoidu (95 cm),

μ₀ - przenikalność magnetyczna próżni,

N - całkowita liczba zwoji (1500),

I - prąd płynący przez solenoid.

Wyprowadzamy jednostkę:

⇒ dla I = 3 [A]

⇒ dla I = 5 [A]

⇒ dla I = 7 [A]

4. Obluiczamy błąd czułości hallotronu Δγ metodą różniczki zupełnej.

Pomiar prądu przeprowadziliśmy miernikiem Multimetr V561, którego dokładność dla prądu stałego wynosi:

1,5%⋅wskazanie+3⋅waga ostatniej cyfry,

więc dokładność pomiaru wyniesie:

dla 3 [A]	ΔI=1,5%⋅3+3⋅0,01=0,08 [A]
dla 5 [A]	ΔI=1,5%⋅5+3⋅0,01=0,1 [A]
dla 7 [A]	ΔI=1,5%⋅7+3⋅0,01=0,14 [A]

czyli:

⇒ dla 3 [A]

Ostatecznie

γ=89±5

⇒ dla 5 [A]

Ostatecznie

γ=64±10

⇒ dla 7 [A]

Ostatecznie

γ=60±3

5. Obliczamy średnią ważoną czułości hallotronu.

Obliczamy wagi pomiarów wg wzoru:

c - dowolna liczba większa od zera, przyjmujemy c=100,

Δx_i - błąd pomiaru,

5. Obliczamy średnią ważoną czułości hallotronu.

Wyszukiwarka