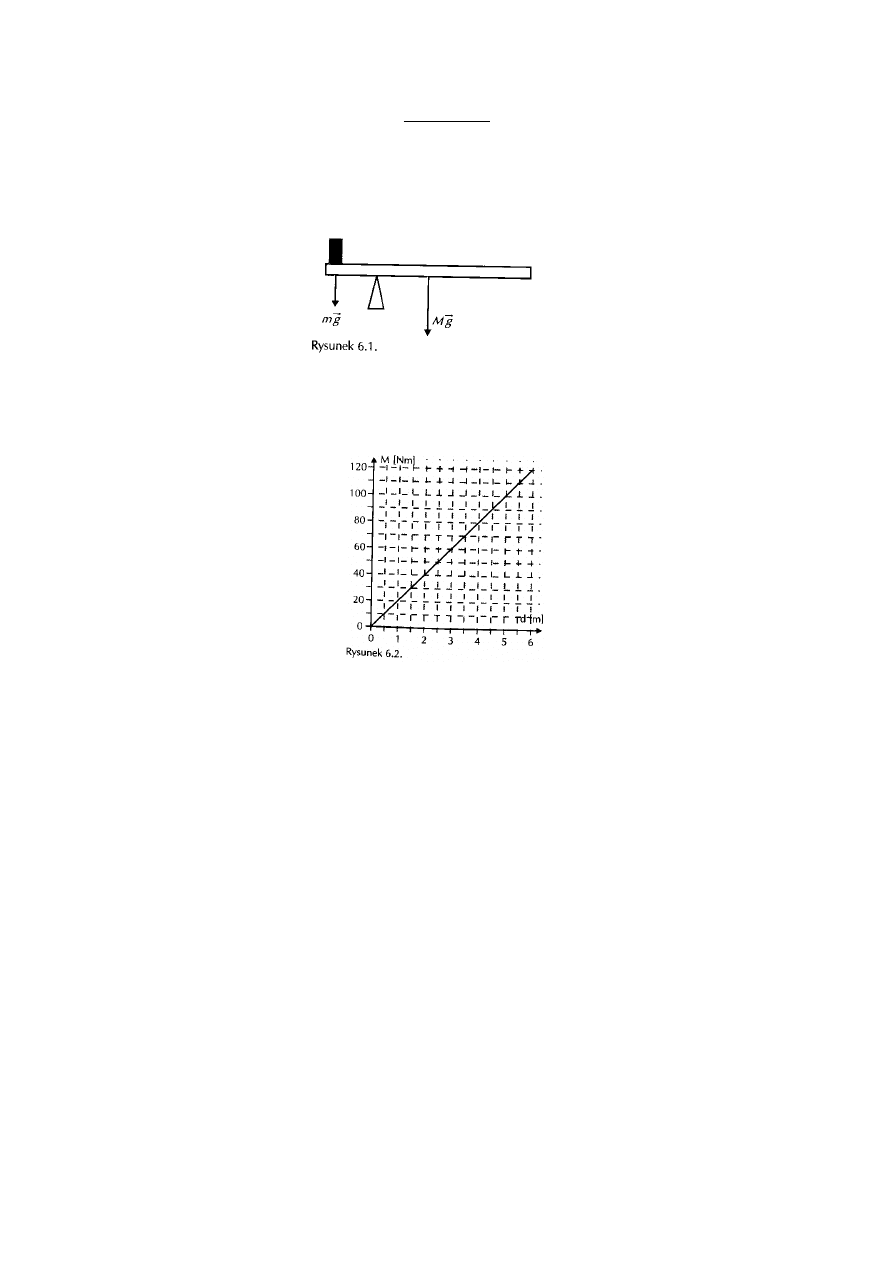
MOMENTY SIŁ
Zadanie 6.1
Na końcu jednorodnej, metalowej listwy o długości l umieszczono ciężarek o masie m = 120 g i kiedy podparto
ją w odległości x = ¼ l od końca z ciężarkiem (rysunek 6.1.), listwa pozostała w równowadze. Oblicz masę M
listwy.
Odp. M = 120 g
Zadanie 6.2
Na rysunku 6.2. pokazano zależność momentu pary sił (M) od odległości między prostymi działania sił (d).
Oblicz wartość każdej z sił.
Odp. F = 20 N
Zadanie 6.3
Jednorodna drewniana belka leży na platformie tak, że
1
/
5
jej długości wystaje poza platformę. Gdy na
wystający koniec belki zacznie działać skierowana pionowo w dół siła o wartości F ≥1500 N, to drugi koniec
belki zacznie się unosić. Belka ma ciężar:
a) 1000 N b) 1500 N
c) 2000 N d) 2500 N
Zadanie 6.4
Dwaj robotnicy nieśli rurę długości l = 4 m i masie m = 40 kg. Jeden z nich trzymał rurę za jej koniec, natomiast
drugi trzymał ją w odległości a = 0,8 m od drugiego końca. Jaki ciężar dźwigał każdy z robotników?
Odp. F
1
= 147 N; F
2
= 245 N
Zadanie 6.5
Stalowa belka o długości l = 5 m i masie m
1
= 1 t jest podparta na obu końcach. Na belce, w odległości
a = 1 m od jednego z końców stoi metalowy obciążnik dźwigu budowlanego o masie m
2
= 100 kg. Jaką siłą
reaguje każda z podpór?
Odp. F
1
= 5690 N; F
2
= 5100 N
Zadanie 6.6
Metalowa szyna o długości l = 12 m i masie m = 1500 kg leży na dwu podporach. Jedna podpora umieszczona
jest w odległości a
1
= 2 m od końca szyny, a druga w odległości a
2
= 4 m od drugiego końca szyny. Jaką siłą F
trzeba naciskać ten koniec szyny, aby przeciwny uniósł się do góry?
Odp. F = 7357,5 N
Zadanie 6.7
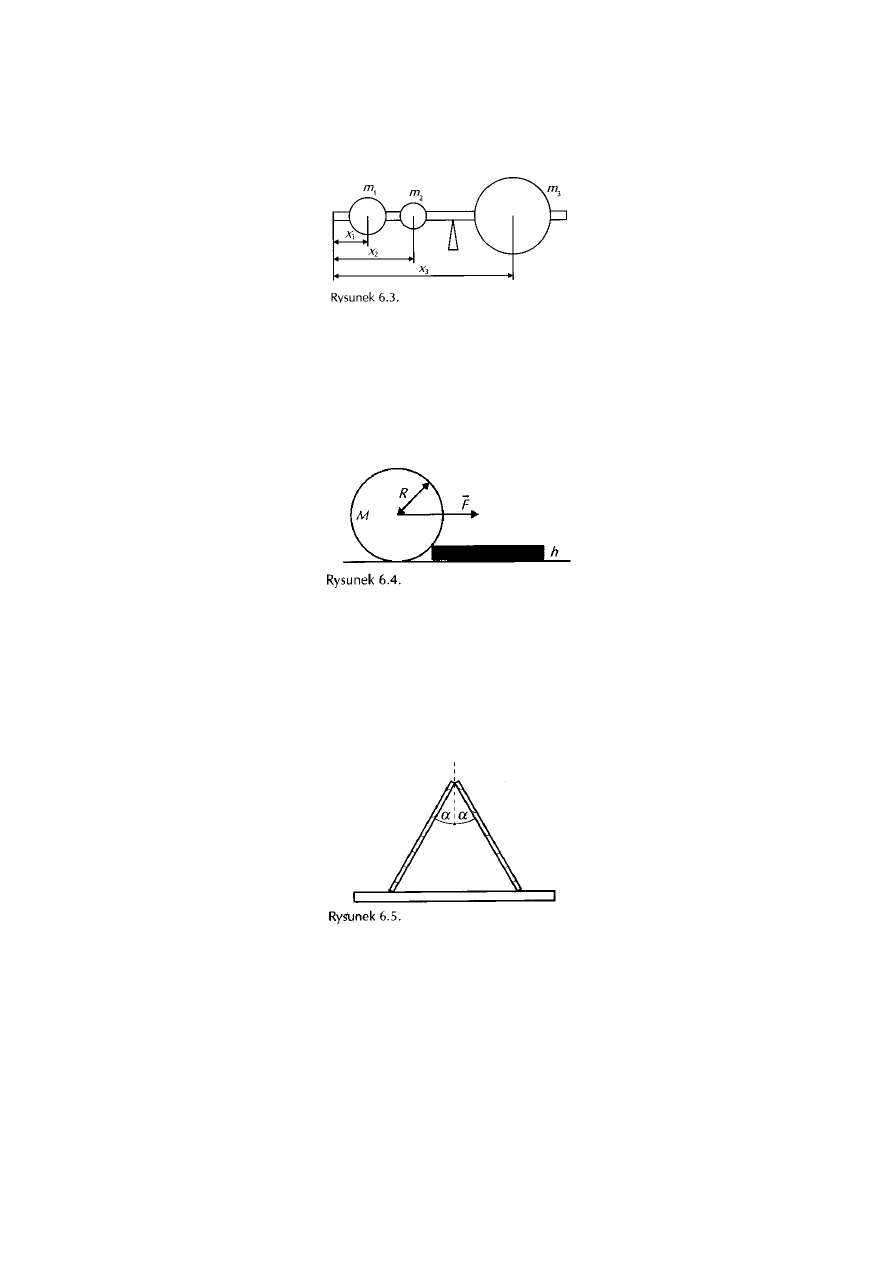
Na cienkiej rurce, której ciężar można zaniedbać, umieszczono trzy metalowe kule o masach m
1
, m
2
i m
3
tak, że
środki ich mas odległe są od lewego końca rurki odpowiednio o x
1,
x
2
i x
3
, jak na rysunku 6.3. W jakiej odległości
x od tego końca należy podeprzeć rurkę, aby układ był w równowadze?
Zadanie 6.8
Do ściany przystawiono drabinę o masie m pod kątem α do pionu. Drabina jest niejednorodna i w rezultacie
środek jej masy znajduje się na wysokości x = l od dolnego końca drabiny. Jaką siłę skierowaną poziomo
⅓
należałoby przyłożyć w środku wysokości drabiny, aby jej górny koniec nie wywierał żadnego nacisku na ścianę?
Zadanie 6.9
Metalowy wałek o masie M i promieniu R trzeba wtoczyć na niewielki stopień o wysokości h (rysunek 6.4.}. Jaką
co najmniej wartość musi mieć siła F przyłożona do osi O walca, aby walec znalazł się na stopniu? Tarcie można
zaniedbać.
Zadanie 6.10
Jednorodna drabina, której środek masy znajduje się w połowie jej wysokości, opiera się o gładką ścianę.
Współczynnik tarcia drabiny o podłogę wynosi f. Oblicz najmniejszy kąt α pomiędzy drabiną a podłogą, przy
którym drabina będzie w równowadze.
Zadanie 6.11
Dwie jednakowe deseczki, między którymi nie występuje siła tarcia, oparto wzajemnie o siebie, jak pokazano
na rysunku 6.5. Każda deseczka tworzy kąt α z pionem. Jaką co najmniej wartość musi mieć współczynnik
tarcia f między deseczkami a stołem, na którym stoją, aby nie ześlizgnęły się?
Zadanie 6.12
Jednorodny metalowy walec stoi na równi pochyłej o kącie nachylenia α do poziomu. Wysokość walca jest
dwukrotnie większa od promienia jego podstawy. Pod jakim co najwyżej kątem może być nachylona równia,
aby walec się nie przewrócił? Współczynnik tarcia ma wystarczająco dużą wartość.
a) 22,5° b) 30°
c) 45° d) 60°
Zadanie 6.13
Drabina o długości l = 4 m oparta jest o idealnie gładką ścianę pod kątem α = 60°do poziomu. Na jaką wy-
sokość może wejść człowiek na tę drabinę, aby nie zaczęła dolnym końcem ześlizgiwać się po podłodze? Współ-
czynnik tarcia drabiny o podłogę wynosi f = 0,3. Drabina jest bardzo lekka i masę jej można zaniedbać.
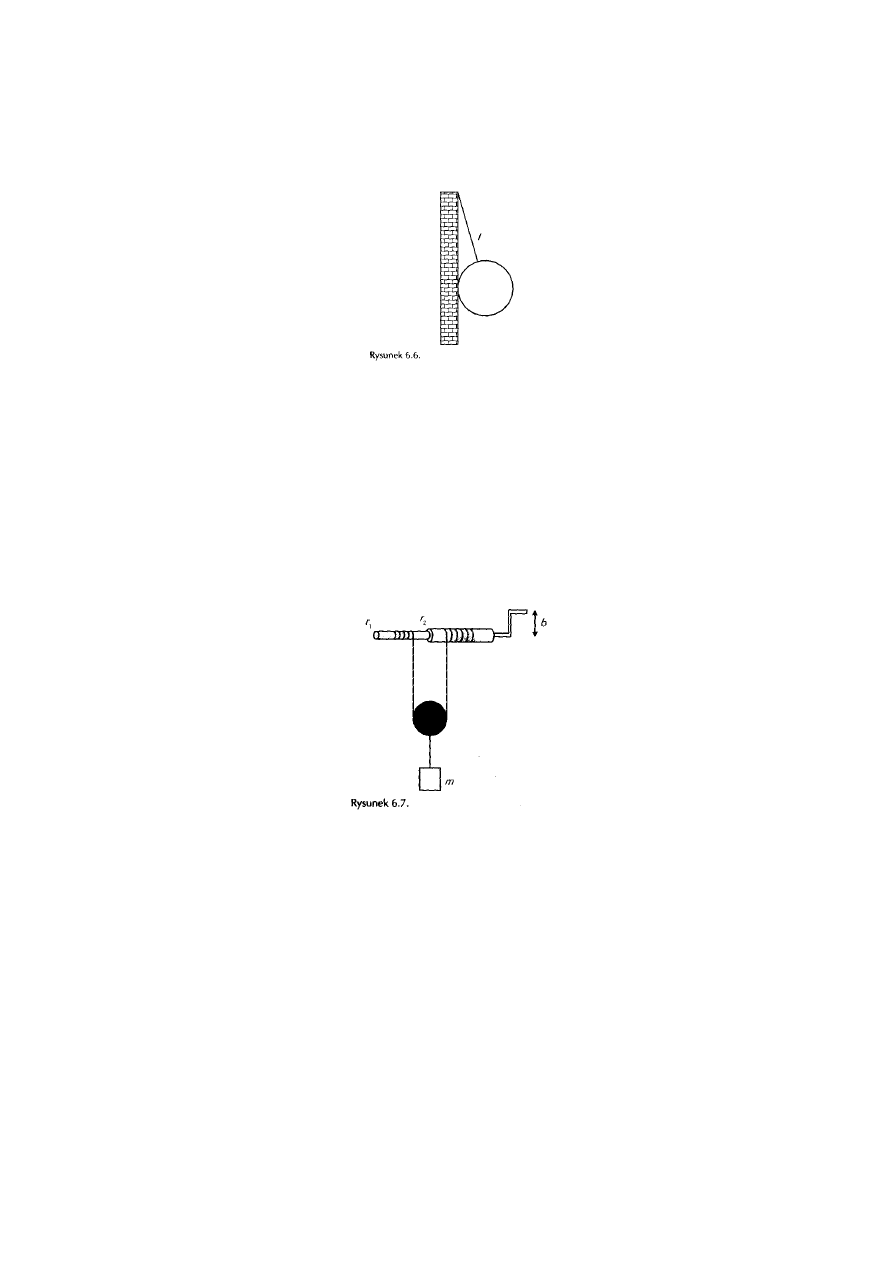
Zadanie 6.14
Na nici o długości l = 10 cm przyczepiono do ściany kulę o masie m = 500 g i promieniu r = 5 cm (rysunek 6.6.).
Między ścianą i kulą nie występują siły tarcia. Jaką siłą N kula naciska na ścianę?
Odp. N = 1,73 N
Zadanie 6.15
Na cienką listwę działają dwie siły równoległe o wartościach F
1
=15 N i F
2
= 25 N, o przeciwnych zwrotach.
Odległość między prostymi, wzdłuż których działają siły wynosi a = 1 m. Oblicz wartość siły równoważącej układ
(tzn. takiej, która spowoduje, że listewka będzie w spoczynku) oraz miejsce jej przyłożenia i kierunek. Ciężar
listwy można zaniedbać.
Zadanie 6.16
Kołowrót składa się z dwóch umieszczonych na wspólnej osi wałków o promieniach r
1
= 15 cm i
r
2
= 25 cm {rysunek 6.7.). Obrót korbą kołowrotu powoduje, że lina z jednego wałka się odwija, a na drugi
nawija. Na linie umieszczony jest bloczek ruchomy, do którego przyczepiono ciężarek o masie
m = 5 kg. Jaką siłą trzeba obracać korbę kołowrotu, której ramię ma długość b = 50 cm, aby podnosić ciężarek
ruchem jednostajnym?
Odp. F = 4,9 N