Józef Szymczak
Granica funkcji w punkcie
(notatki z wykładu)
Definicja granicy funkcji
Funkcja
)
(x
f
ma w punkcie
0
x
granicę równą g gdy dla każdego ciągu argumentów
)
(
n
x
, gdzie
0
x
x
n
≠
i
f
n
D
x
∈
dla każdego n,
jeżeli
0
lim
x
x
n
n
=
∞
→
, to
g
x
f
n
n
=
∞
→
)
(
lim
.
Zapisujemy ten fakt symbolicznie:
g
x
f
x
x
=
→
)
(
lim
0
.
Granica w punkcie
0
x
może być w szczególności granicą niewłaściwą. Można też rozpatry-
wać granicę w punkcie niewłaściwym (
∞
+
∞
−
lub
).
W celu stwierdzenia, że w punkcie
0
x
funkcja nie ma granicy, wystarczy wskazać dwa
różne ciągi argumentów zbieżne do punktu
0
x
takie, że odpowiednie ciągi wartości funkcji są
zbieżne do różnych granic.
Przykład 1. Wykażemy na podst. definicji, że
2
lim
2
3
2
1
=
−
→
x
x
x
.
Wybierając dowolny ciąg
)
(
n
x
argumentów taki, że
1
lim
=
∞
→
n
n
x
, otrzymujemy następującą
granicę ciągu wartości funkcji:
2
2
3
2
2
1
3
1
2
2
3
2
lim
(
lim
)
=
=
−
−
⋅
⋅
=
−
=
∞
→
∞
→
n
n
x
x
x
f
n
n
n
.
Przy obliczaniu granic funkcji w punkcie
0
x
ważnymi pojęciami są granice jednostronne:
lewostronna i prawostronna.
Funkcja
)
(x
f
ma w punkcie
0
x
granicę lewostronną (właściwą lub niewłaściwą) równą g,
co zapisujemy symbolicznie
g
x
f
x
x
=
−
→
)
(
lim
0
,
gdy dla każdego ciągu argumentów
)
(
n
x
należących do dziedziny funkcji takich, że
0
x
x
n
<
,
jeżeli
0
lim
x
x
n
n
=
∞
→
, to
g
x
f
n
n
=
∞
→
)
(
lim
.
Analogicznie definiujemy
granicę prawostronną funkcji
)
(x
f
w punkcie
0
x
, którą
zapisujemy symbolicznie:
g
x
f
x
x
=
+
→
)
(
lim
0
.
Uwaga.
g
x
f
g
x
f
g
x
f
x
x
x
x
x
x
=
∧
=
⇔
=
+
→
−
→
→
)
)
)
(
lim
(
lim
(
lim
0
0
0
Jeśli granice jednostronne funkcji
)
(x
f
w punkcie
0
x
są różne, to mówimy, że funkcja nie
ma granicy w tym punkcie.
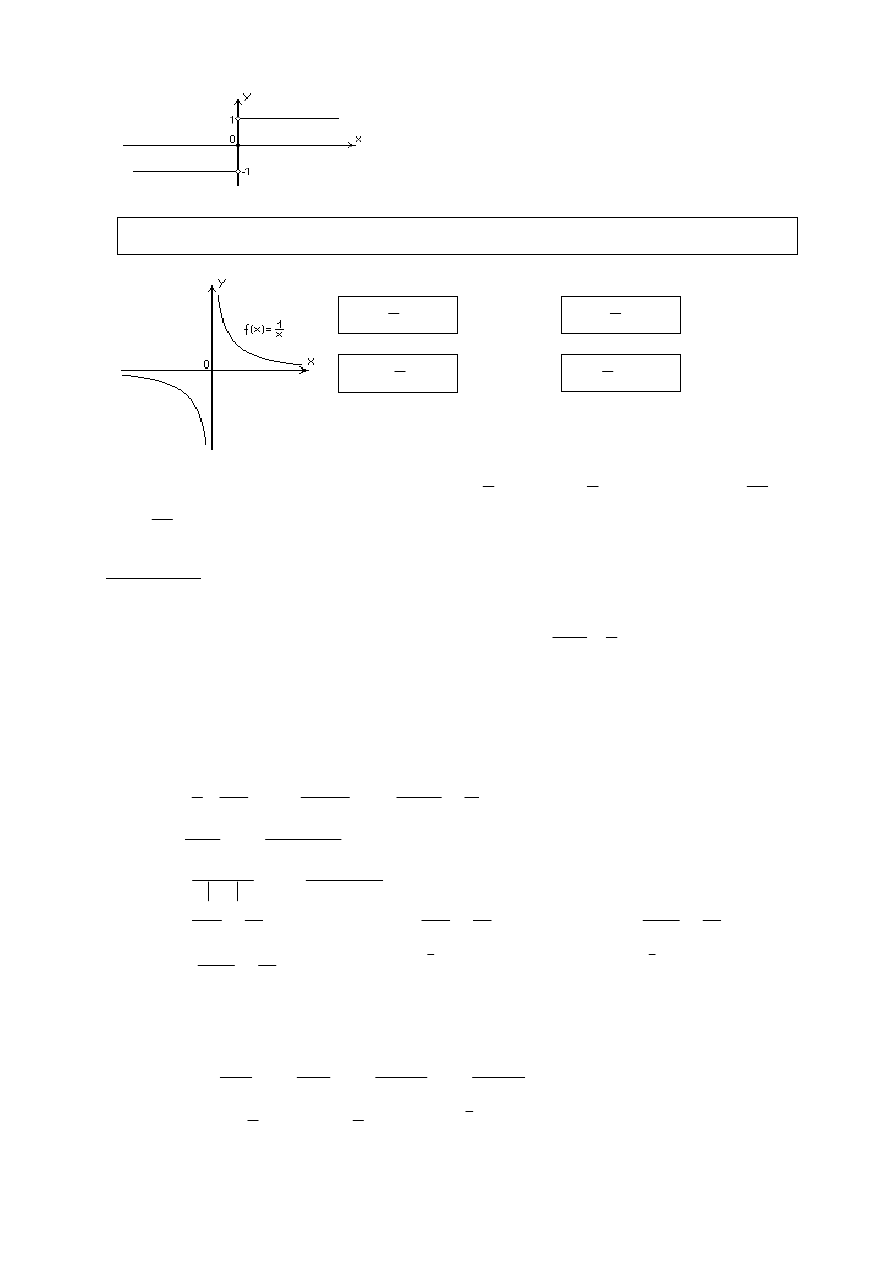
1
sgn
)
(
lim
0
−
=
−
→
x
x
,
1
sgn
)
(
lim
0
=
+
→
x
x
.
Funkcja
)
(
sgn x
nie ma zatem granicy w punkcie
0
0
=
x
.
Zauważmy, że dla funkcji stałej
c
x
f
=
)
(
mamy
c
c
x
x
=
→
0
lim
w każdym punkcie
R
x
∈
0
.
−∞
=
−
→
x
x
1
0
lim
∞
=
+
→
x
x
1
0
lim
0
1
lim
=
−∞
→
x
x
0
1
lim
=
∞
→
x
x
Ogólnie możemy zauważyć, że jeżeli
0
>
a
, to
−∞
=
−
→
x
a
x
0
lim
i
∞
=
+
→
x
a
x
0
lim
natomiast
∞
=
−
−
→
x
a
x
0
lim
i
−∞
=
−
+
→
x
a
x
0
lim
.
Twierdzenie (o granicy sumy, iloczynu i ilorazu funkcji)
Jeżeli
a
x
f
x
x
=
→
)
(
lim
0
oraz
b
x
g
x
x
=
→
)
(
lim
0
, to
b
a
x
g
x
f
x
x
+
=
+
→
))
(
)
(
(
lim
0
;
b
a
x
g
x
f
x
x
⋅
=
⋅
→
))
(
)
(
(
lim
0
;
b
a
x
g
x
f
x
x
=
→
)
(
)
(
0
lim
(
0
,
0
)
(
≠
≠
g
x
g
).
Uwaga. Granice funkcji przy warunku, gdy
∞
→
x
lub gdy
−∞
→
x
obliczamy podobnie jak dla
ciągów. Zapamiętać przy tym trzeba też zachowanie się podstawowych funkcji elementarnych,
gdy argument zmierza do nieskończoności.
Przykłady.
1.
0
]
3
[
3
3
)
3
(
3
)
3
1
1
(
2
lim
lim
lim
=
∞
=
+
=
+
−
+
=
+
−
∞
→
∞
→
∞
→
x
x
x
x
x
x
x
x
x
x
x
.
2.
6
)
3
(
lim
lim
lim
3
3
2
3
3
)
3
)(
3
(
3
9
=
+
→
→
→
=
−
−
+
=
−
−
x
x
x
x
x
x
x
x
x
.
3.
1
)
3
)(
(
lim
lim
lim
1
2
)
3
)(
2
(
2
6
5
2
2
2
2
=
−
−
=
−
−
−
=
−
+
−
−
→
−
→
−
→
x
x
x
x
x
x
x
x
x
x
.
4.
−∞
=
=
−
+
−
+
→
]
[
lim
0
3
2
1
2
x
x
x
. 5.
−∞
=
=
−
−
+
−
→
]
[
lim
0
2
-
3
1
3
x
x
x
. 6.
∞
=
=
−
+
−
→
]
[
lim
0
5
2
2
4
5
x
x
.
7.
−∞
=
=
−
−
−
−
→
]
[
lim
0
5
2
2
4
5
x
x
. 8.
∞
=
=
∞
+
→
]
[
1
0
lim
e
e
x
x
. 9.
0
]
[
1
0
lim
=
=
∞
−
−
→
e
e
x
x
.
10.
∞
=
∞
→
x
x
ln
lim
. 11.
−∞
=
+
→
x
x
ln
lim
0
.
W przypadku granic funkcji zachodzą następujące wzory (tożsamości):
1
arctan
arcsin
tan
sin
0
0
0
0
lim
lim
lim
lim
=
=
=
=
→
→
→
→
x
x
x
x
x
x
x
x
x
x
x
x
;
e
x
x
x
x
x
x
x
x
x
=
+
=
+
=
+
→
−∞
→
∞
→
1
0
)
1
(
)
1
1
(
)
1
1
(
lim
lim
lim
.
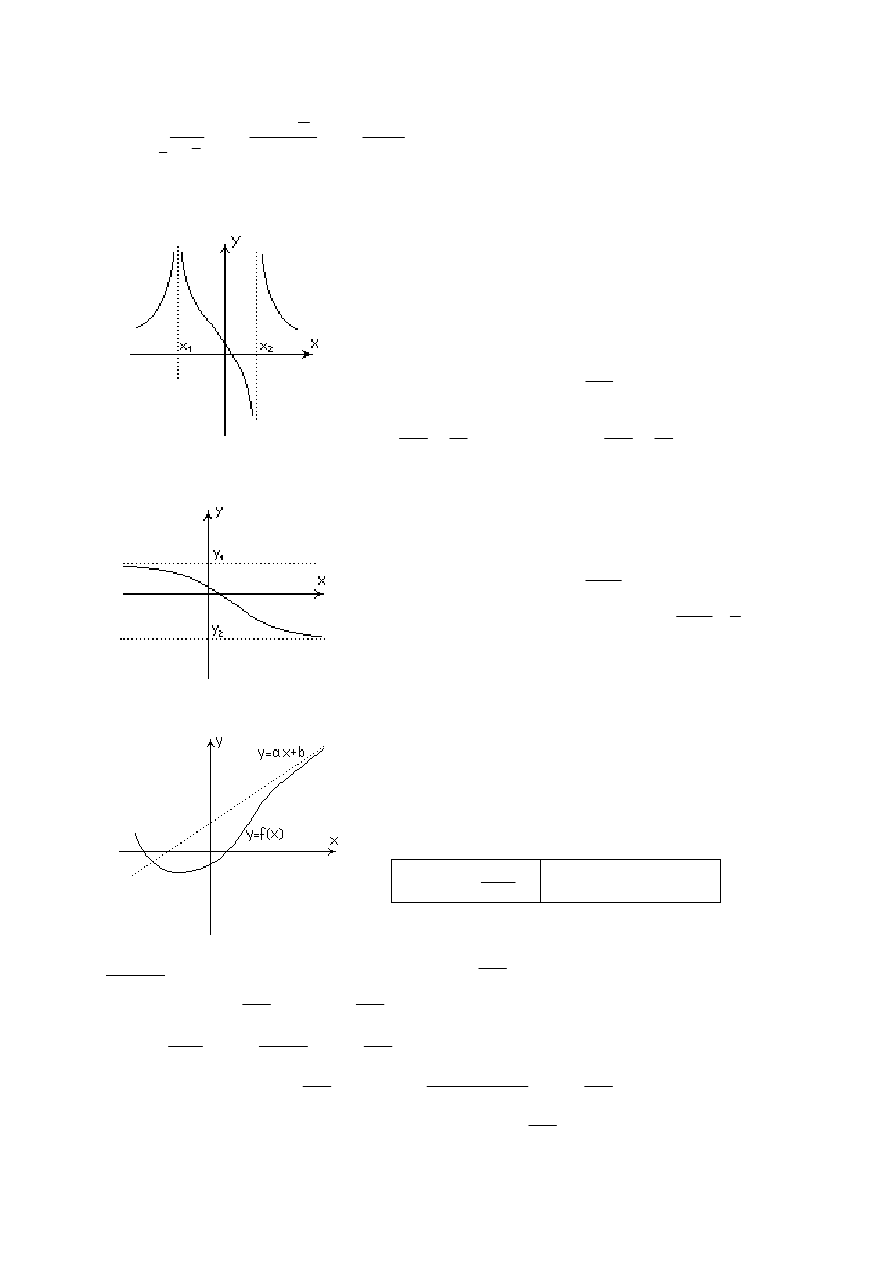
Przykład.
1
lim
lim
lim
sin
)
cos(
cos
0
2
0
2
2
−
=
−
=
+
=
−
→
→
→
y
y
y
y
x
x
y
y
x
π
π
π
.
Asymptoty funkcji
Prosta
0
x
x
=
, gdzie
f
D
x
∉
0
, jest asymptotą pionową
funkcji f, gdy przynajmniej jedna z granic jednostronnych
)
(
lim
0
x
f
x
x
−
→
lub
)
(
lim
0
x
f
x
x
+
→
jest niewłaściwa.
Asymptota pionowa może być zatem jednostronna lub
obustronna.
Na przykład funkcja
3
2
)
(
−
=
x
x
x
f
ma asymptotę pionową
obustronną o równaniu
3
=
x
, ponieważ
−∞
=
−
−
−
=
→
]
[
lim
0
9
3
2
3
x
x
x
oraz
∞
=
−
+
+
=
→
]
[
lim
0
9
3
2
3
x
x
x
.
Prosta
0
y
y
=
, jest
asymptotą poziomą funkcji f, gdy
0
)
(
lim
y
x
f
x
=
−∞
→
lub
0
)
(
lim
y
x
f
x
=
∞
→
.
Na przykład funkcja
3
2
4
)
(
−
=
x
x
x
f
ma asymptotę
poziomą o równaniu
2
=
y
, ponieważ
2
2
4
3
2
4
lim
=
−
=
±∞
→
x
x
x
.
Asymptota pozioma jest szczególnym przypadkiem
asymptoty ukośnej
Prosta
b
ax
y
+
=
, jest
asymptotą ukośną funkcji f, gdy
0
))
(
)
(
(
lim
=
+
−
∞
→
b
ax
x
f
x
(lub gdy
0
))
(
)
(
(
lim
=
+
−
∞
−
→
b
ax
x
f
x
)
Z powyższej zależności wynikają wzory na wyznaczanie
współczynników asymptoty ukośnej (jeśli istnieją odpowiednie
granice):
x
x
f
x
a
)
(
lim
±∞
→
=
)
)
(
(
lim
ax
x
f
b
x
−
=
±∞
→
Przykład. Wyznaczyć asymptotę ukośną funkcji
3
2
2
)
(
−
=
x
x
x
f
. Dziedziną tej funkcji jest zbiór
}
3
{
-
R
.
Zauważmy, że
∞
=
−
∞
→
3
2
lim
x
x
x
,
−∞
=
−
−∞
→
3
2
lim
x
x
x
, czyli funkcja nie ma asymptoty poziomej.
2
3
2
)
3
(
2
)
(
lim
lim
lim
2
=
−
=
−
=
±∞
±∞
±∞
→
→
→
x
x
x
x
x
x
x
f
x
x
x
, skąd wynika, że
2
=
a
.
6
3
6
3
6
2
2
2
3
2
)
)
(
(
lim
lim
)
(
lim
lim
2
2
2
=
−
=
−
+
−
=
−
−
=
−
±∞
±∞
±∞
±∞
→
→
→
→
x
x
x
x
x
x
x
x
x
ax
x
f
x
x
x
x
, więc
6
=
b
.
Prosta
6
2
+
=
x
y
jest zatem asymptotą ukośną funkcji
3
2
2
)
(
−
=
x
x
x
f
.
Ciągłość funkcji w punkcie
Definicja funkcji ciągłej
Funkcja
)
(x
f
jest ciągła w punkcie
a
, jeżeli
1.
funkcja ta jest określona w pewnym otoczeniu punktu
a
,
2.
istnieje granica
)
(
lim
x
f
a
x
→
,
3.
granica ta jest równa wartości funkcji w punkcie
a
, tzn.
)
(
)
(
lim
a
f
x
f
a
x
=
→
.
Funkcja jest ciągła w każdym punkcie pewnego przedziału, jeżeli jest ciągła w każdym punkcie
wewnętrznym tego przedziału oraz prawostronnie ciągła na jego lewym końcu i lewostronnie ciągła na
jego prawym końcu, pod warunkiem, że końce te należą do danego przedziału.
Punkt, w którym naruszone są warunki ciągłości, nazywamy punktem nieciągłości danej funkcji.
Obok przedstawione są
graficznie przykłady różnych
punktów nieciągłości.
Punkty
3
2
1
,
,
x
x
x
to tzw.
punkty nieciągłości I rodzaju.
W punktach nieciągłości II
rodzaju nie istnieje przynajmniej
jedna granica jednostronna
Uwaga.
Każda funkcja elementarna jest ciągła na całej swojej dziedzinie.
Suma i iloczyn funkcji ciągłych jest funkcją ciągłą.
Iloraz funkcji ciągłych jest funkcją ciągłą we wszystkich punktach, w których mianownik nie
przyjmuje wartości zerowej.
Złożenie funkcji ciągłych jest funkcją ciągłą.
Przykład. Zbadać ciągłość funkcji
≥
<
−
=
0
dla
0
dla
1
)
(
/
1
x
x
x
e
x
f
x
.
W przypadku tej funkcji należy sprawdzić jej ciągłość w punkcie
0
=
x
, ponieważ dla wszystkich
niezerowych argumentów funkcje składowe są ciągłe (jako funkcje elementarne). Mamy więc:
0
)
0
(
=
f
,
1
0
1
/
1
0
0
1
lim
(
lim
)
=
−
=
=
−
−
→
−
→
x
e
x
x
x
f
,
0
0
0
lim
(
lim
)
=
=
+
→
+
→
x
x
f
x
x
.
Widzimy, że badana funkcja ma różne granice
jednostronne dla
0
=
x
, a więc nie jest ciągła w
tym punkcie (graficznie następuje przeskok
wykresu przy przejściu przez ten punkt).
Zadanie. Zbadać ciągłość funkcji
≥
−
<
=
0
dla
1
0
dla
)
(
x
e
x
x
x
f
x
.
Twierdzenie (własność Darboux o wartościach pośrednich funkcji ciągłej)
Funkcja
)
(x
f
y
=
ciągła na przedziale
>
<
b
a
;
, dla której
)
(
)
(
b
f
a
f
≠
, przyjmuje
na tym przedziale wszystkie wartości zawarte pomiędzy
)
(a
f
i
)
(b
f
.
Z twierdzenia Darboux wynika następujący
Wniosek. Jeżeli funkcja
)
(x
f
y
=
jest ciągła na przedziale
>
<
b
a
;
oraz
0
)
(
)
(
<
⋅
b
f
a
f
(czyli funkcja przyjmuje na końcach tego przedziału wartości o
różnych znakach), to istnieje przynajmniej jeden punkt
)
;
(
b
a
c
∈
taki, że
0
)
(
=
c
f
(miejsce zerowe funkcji).
Wniosek ten jest wykorzystywany przy obliczaniu przybliżonych wartości rozwiązań równań
postaci
0
)
(
=
x
f
.
Przykład. Sprawdzić, czy istnieje rozwiązanie równania
0
2
2
=
−
x
x
w przedziale
>
−
<
0
;
1
.
Jeśli rozważymy lewą stronę równania jako funkcję
x
x
x
f
2
)
(
2
−
=
, to widzimy, że
2
1
1
2
1
)
1
(
=
−
=
−
−
f
,
1
2
0
)
0
(
0
−
=
−
=
f
. Dana funkcja jest ciągła, ma na końcu tego przedziału wartości
o różnych znakach, a więc musi istnieć w tym przedziale punkt będący miejscem zerowym rozważanej
funkcji, czyli istnieje rozwiązanie wyjściowego równania.
Zadanie. Sprawdzić, czy równanie
0
2
ln
=
−
+
x
x
ma rozwiązanie w przedziale
>
<
2
;
1
.