Ewelina Dudek

8.04.2008 r.

Rok I, chemia podstawowa

dr Bogusław Kosturek

Wtorek, 12

45

-15

00

Dokładność pomiaru długości

.

1.Pomiary

Wszystkie pomiary i obliczenia zostały zamieszczone na dołączonym arkuszu.

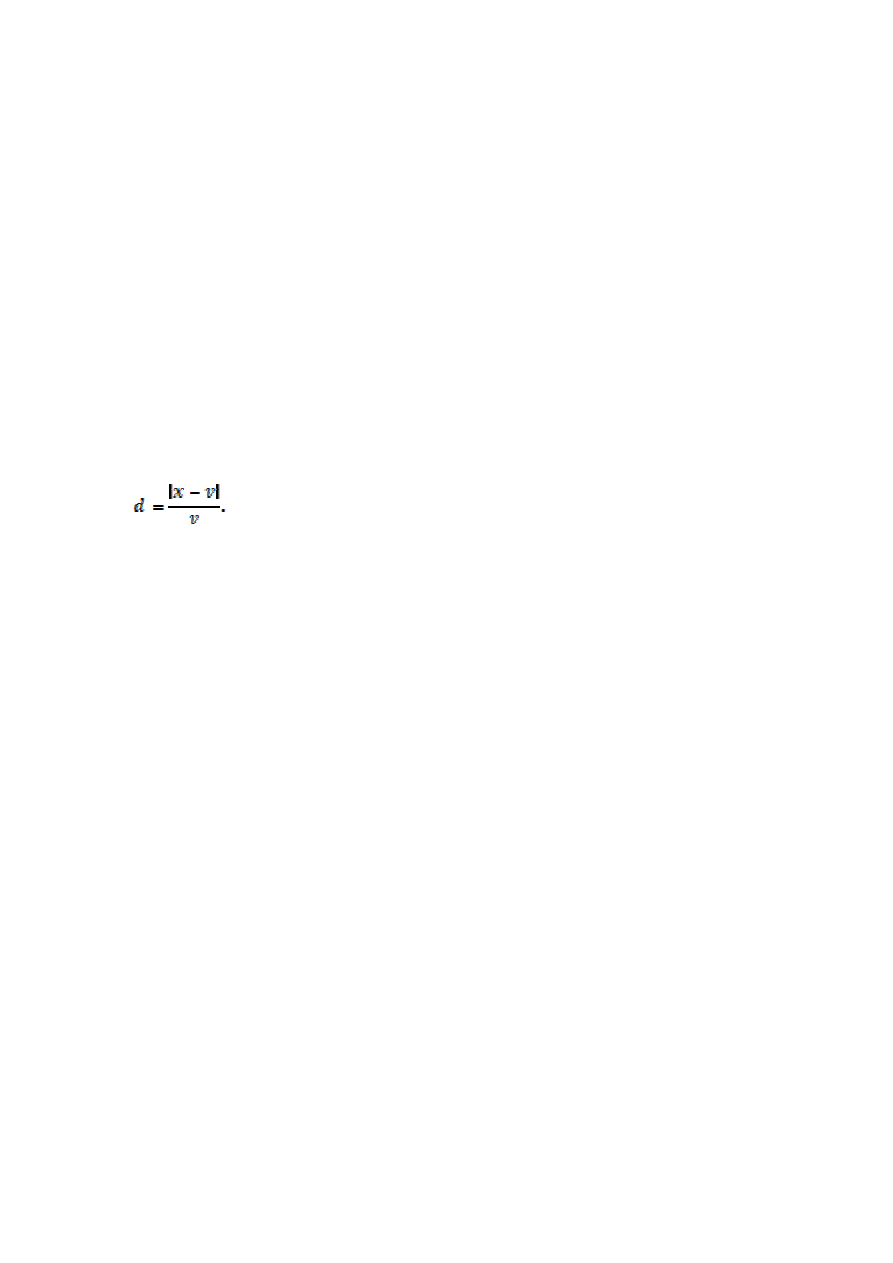
2. Wstęp teoretyczny

2.1 Klasyfikacja błędów

Błędy pomiarowe mogą wynikać z ograniczonej dokładności narzędzia
pomiarowego (wskazanie narzędzi różni się od wartości prawdziwej mierzonej
wielkości) oraz niepoprawnego pomiaru.
Błąd bezwzględny D – wyraża różnicę między wynikiem pomiaru x a wartością
prawdziwą mierzonej wielkości v, czyli x-v; jest wyrażony w jednostkach pomiaru.
Problem jest nieznajomości wartości v, którą w praktyce można zastąpić względnie
dokładnym przybliżeniem, tzn. wartością poprawną xp – wyznaczoną za pomocą
wzorcowego narzędzia pomiarowego.
Błąd względny d - wyraża stosunek wartości bezwzględnej błędu względnego D
do wielkości mierzonej:

Pozwala na porównanie dokładności pomiarowych przyrządów różnych typów i o
odmiennych zakresach.
Błąd przypadkowy jest błędem pomiaru, którego nie da się z góry przewidzieć na
podstawie pojedynczego pomiaru. Błędy tego rodzaju zmieniają się w sposób
losowy i są one niemożliwe do usunięcia. Na podstawie serii pomiarów i rachunku
prawdopodobieństwa ustala się granice w których znajdują się błędy przypadkowe
(przedział niepewności końcowego wyniku pomiaru). Np. skończona dokładność
przyrządu pomiarowego.
Błąd systematyczny jest błędem wynikającym z zastosowanej metody pomiaru
lub innych przyczyn. Przy wielu pomiarach tej samej wartości określanej
wielkości, wykonywanych w tych samych warunkach, błędy systematyczne są
stałe lub zmieniają się wg określonego prawa wraz ze zmianą warunków. Mogą
powstawać na przykład w wyniku obrania innego układu odniesienia. Wielokrotne
powtarzanie pomiarów nie umożliwia ich wykrycia ani wyeliminowania. Istnienie
błędów systematycznych można stwierdzić w wyniku zastosowania innej metody
pomiarowej lub zastosowania innego narzędzia pomiarowego. Np. ważenie przy
pomocy źle wyskalowanej wagi; pomiar czasu stoperem, który się śpieszy.

2.2 Niepewności pomiaru

Niepewność standardowa jest parametrem związanym z wynikiem pomiaru
charakteryzującym rozrzut wartości, który można w uzasadniony sposób przypisać
wielkości mierzonej.
Niepewność standardowa wyniku pomiaru bezpośredniego u – parametr
związany z rezultatem pomiaru określający możliwy rozrzut wyników. Przy
pomiarach rzeczywistego zjawiska fizycznego występuje zwykle kilka źródeł
niepewności pomiaru i dlatego niepewność standardowa całkowita pomiaru jest

zwykle złożona z kilku pojedynczych niepewności standardowych pomiaru. Przy
czym to nie jest prosta suma algebraiczna.
Złożona niepewność standardowa pomiaru u

c

(y) – jest niepewnością wyników

pomiarów pośrednich y= f(x

1

,…., x

n

), gdzie x

1

….x

n

oznaczają wielkości mierzone

bezpośrednio. Jest ona wyznaczana z prawa przenoszenia niepewności pomiaru.

2.3 Przedstawianie wyników pomiaru

Wygodnym sposobem zapisu eksperymentu jest przedstawienie ich w tabeli, tak,
ż

e wartości jednej wielkości zapisujemy w kolumnie. Nagłówek kolumny powinien

zawierać symbol wielkości i jednostkę. Wielkość jednostki dobieramy tak, by
zapisywane liczby mieściły się w zakresie 0,1 do 1000.
Jeżeli jakiś pomiar powtarzamy wielokrotnie, to przedstawiamy średnią z tych
pomiarów z taką samą dokładnością, co niepewność. W przypadku wyznaczania
błędów – zapisujemy tylko dwie znaczące cyfry oraz zawsze zaokrąglamy do góry.

2.4 Zaokrąglanie wyników pomiaru oraz ich niepewności

Cyframi znaczącymi danej liczby różnej od zera nazywamy wszystkie jej cyfry z
wyjątkiem występujących na początku zer. Do cyfr znaczących zalicza się również
zera końcowe, jeśli są one wynikiem obliczeń, a nie zaokrągleń.
Cyfry pewne – jeśli błąd spowodowany przybliżeniem liczby dziesiętnej jest
mniejszy od jedności na ostatnim miejscu dziesiętnym mówimy, że wszystkie jej
cyfry są pewne.
Zaokrąglanie wyników i błędów – przy zaokrąglaniu wyniku pomiaru stosowane
są powszechnie przyjęte zasady zaokrągleń:
- liczbę kończącą się cyframi 0-4 zaokrąglamy w dół, a 5-9 w górę lub
- liczby 0-4 zaokrąglamy w dół, 6-9 w górę, a cyfrę 5 w dół, jeśli poprzedza ją
cyfra parzysta, zaś w górę, jeśli poprzedzą ją cyfra nieparzysta.
Można stosować dowolną z tych zasad, ale w jednym opracowaniu wyników
należy konsekwentnie stosować jedną z nich.
Oszacowania błędów - zaokrąglamy zawsze w górę, ponieważ w żadnym
przypadku nie wolno zmniejszać błędów. Zawsze lepiej podać zawyżoną wartość
błędu niż go niedoszacować.

Obliczenia wykonujemy zawsze z większą liczbą cyfr, niż chcemy podać wynik.
Zaokrągleń dokonujemy dopiero po zakończeniu obliczeń.
Błędy pomiarów zaokrąglane są do pierwszej cyfry znaczącej. Ostatnia cyfra
znacząca w każdym wyniku pomiaru powinna stać na tym samym miejscu
dziesiętnym, co błąd pomiaru.

2.5 Statystyczny rozrzut danych

Najbardziej znaną miarą rozrzutu jest odchylenie standardowe, czyli pierwiastek z
wariancji. Jest to jednak miara bardzo czuła na obserwacje odstające i czasem

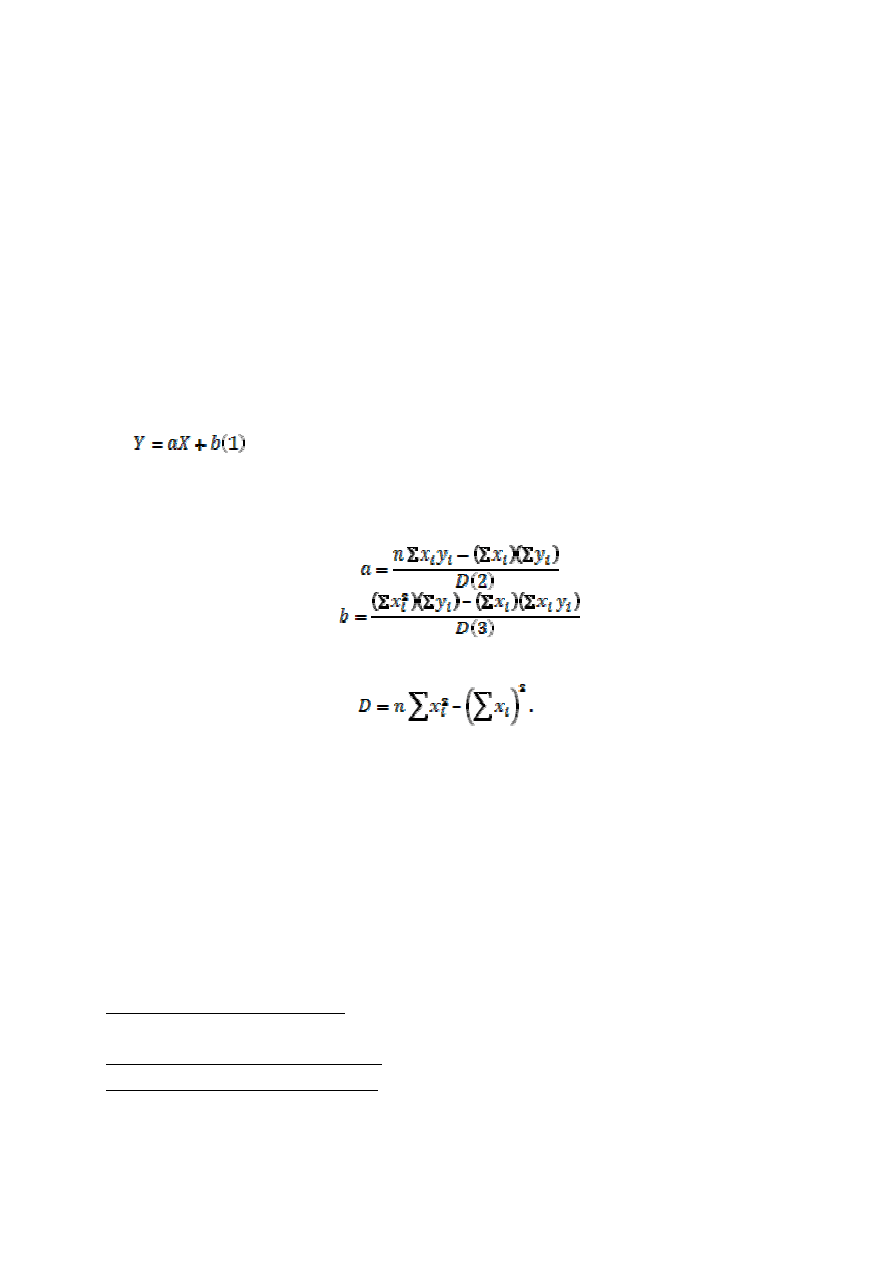
zaleca się stosowanie bardziej odpornych wersji jak na przykład różnica miedzy 3 i
2 kwartylem.

2.6 Graficzne metody przedstawienia wyników

Wyniki eksperymentu wygodnie jest przedstawić przy pomocy wykresu. Daje nam
to poglądowe przedstawienie wyników oraz wychwycenie pewnych zależności,
które można potem dokładniej badać. Na wykresie często łatwiej wychwycić
niektóre zależności.

2.7 Regresja liniowa

Regresją liniową zmiennej Y względem zmiennej X jest prosta

Której parametry a, b dobiera się w ten sposób, by minimalizować sumę
kwadratów odchyleń współrzędnych y

1

…..y

n

zbioru n o współrzędnych

(x

1

,y

1

),…,(x

n

, y

n

). Gdy niepewności przypisane punktom eksperymentalnym są

jednakowe, otrzymujemy wzory:

gdzie:

3. Opis doświadczeń

3.1 Wyznaczanie wymiarów i objętości kostki metalowej

Pomiary zostały wykonane przy pomocy różnych technik i przyrządów, stąd wynikają
różne dokładności.

Pomiar z dokładności do 1mm – wykonany przez przyłożenie kostki na papierze
milimetrowym i odczytanie wartości.
Pomiar z dokładnością do 0,05 mm – wykonany za pomocą suwmiarki.
Pomiar z dokładnością do 0,01mm – wykonany za pomocą śruby mikrometrycznej.

3.2 Wymiary i pole powierzchni płaskiego metalowego pierścienia

Pomiar z dokładnością do 0,05mm – wykonany za pomocą suwmiarki.
Pomiar z dokładnością do 0,01 mm – wykonanego za pomocą mikroskopu
warsztatowego.

3.3 Szacowanie pola powierzchni kwadratu na papierze milimetrowym

Pomiar został wykonany za pomocą mikroskopu warsztatowego z dokładnością do
0,01mm.

3.4 Wyznaczanie odległości na linijce między kreskami podziałki

Pomiar wykonany za pomocą mikroskopu warsztatowego z dokładnością do 0,01mm.

4. Pomiary i ocena niepewności pomiarowej

Obliczenia do zadań 1-4 zostały zamieszczone w dołączonym arkuszu.

5. Wnioski

Dokładność pomiaru długości zależy głównie od techniki jaką stosujemy i

dobiera się ją w zależności od potrzeb. Podstawowymi narzędziami są: papier
milimetrowy oraz linijka ( dokładność 1mm), suwmiarka ( dokładność 0,05 mm),

ś

ruba mikrometryczna oraz mikroskop warsztatowy ( dokładność 0,01mm). Stosując

większą dokładność jesteśmy w stanie wychwycić pewne zjawiska. Przykładowo na
początek kostka wydawała się sześcianem ( przy dokładności 1mm) , potem okazało
się, że wcale sześcianem nie jest. Przy dokładności 0,05mm okazała się
prostopadłościanem natomiast przy dokładności 0,01mm okazywało się że ścianki nie
są wcale równe. Precyzja jest ważna, gdyż możemy wyciągnąć różne wnioski z
wykonanych obliczeń. Dokładność pomiaru jest bardzo istotna przy wyznaczaniu na
przykład pola powierzchni czy objętości. O ile w przypadku wymiarów bezpośrednich,
czyli na przykład długości boku, średnicy okręgu, różnice nie są duże. Natomiast
potęgują się, gdy wymnażamy przez siebie te wymiary – błędy rosną wykładniczo.
Dla uzyskania lepszej dokładności najlepiej wykonać kilka pomiarów i wziąć z nich

ś

rednią arytmetyczną. Wtedy korzystając z praw statystyki, błąd będzie mniejszy niż

przy jednym pomiarze. Wyniki powinno podawać się z precyzją, na jaką pozwalają
przyrządy pomiarowe. Przykładowo linijki nie można stosować dokładniej niż do
1mm, gdyż okazuje się, że nie zawsze odległości między kreskami są dokładne,

podobnie jak w przypadku papieru milimetrowego. Są to drobne różnice, ale możliwe
do

znalezienia

przy

pomocy

przyrządów

o

większej

dokładności.

Wpisz tutaj równanie.

Sprawozdanie z wykonania ćwiczenia nr 1

Zadanie 1 (Kostka metalowa)
Pomiar za pomocą linijki z podziałką milimetrową lub papieru milimetrowego:

a)

Długość boku metalowej kostki a = (14

±

1) mm

b) Objętość kostki:

V

obl

= 2,7 cm

3

V

min

= 2,2 cm

3

V

max

= 3,4 cm

3

∆

V = max ( V

obl

- V

min

, V

max

- V

obl

) = 0,5 cm

3

Po zaokrągleniu : V = 2,7

±

0,5 cm

3

c)

δ

=

∆

V

V

⋅

100

% = 18,5 %

Pomiar za pomocą suwmiarki

d)

Długości boków metalowej kostki:
a = (14,1

±

0,05) mm

b = (14,3

±

0,05) mm

c = (14,4

±

0,05) mm

e)

Objętość kostki:
V

obl

= 2,9 cm

3

V

min

= 2,8 cm

3

V

max

= 3,0 cm

3

∆

V = max ( V

obl

- V

min

, V

max

- V

obl

) = 0,1

cm

3

.

Po zaokrągleniu : V = (2,8

±

0,1) cm

3

f)

δ

=

∆

V

V

⋅

100

% = 3,6%

Pomiar za pomocą śruby mikrometrycznej

g)

Długości boków metalowej kostki:
a = 14,20; 14,21; 14,17 mm

a

śr

= (14,19

±

0,01) mm

b = 14,00; 14,10; 14,13 mm

b

śr

= (14,08

±

0,01) mm

c = 14,30; 14,30; 14,22 mm

c

śr

= (14,27

±

0,01) mm

h)

Objętość kostki
V

obl

= 2,9 cm

3

V

min

= 2,8 cm

3

V

max

= 3,0 cm

3

∆

V = max ( V

obl

- V

min

, V

max

- V

obl

) = 0,1 cm

3

.

Po zaokrągleniu : V = (2,9

±

0,1) cm

3

i)

δ

=

∆

V

V

⋅

100

% = 3,4 %

Zadanie 2. (Pierścień)
Pomiar za pomocą suwmiarki z dokładnością do 0,05 mm.

a)

Φ

zewn

= (22,2

±

0,05) mm

Φ

wewn

= (11,0

±

0,05) mm

b) Pole powierzchni S =

π

4

2

2

(

)

Φ

Φ

zewn

wewn

-

S

obl

=2,92 cm

2

S

min

= 2,89 cm

2

S

max

= 2,95 cm

2

∆

S = max ( S

obl

- S

min

, S

max

- S

obl

) = 0,03 cm

2

Po zaokrągleniu : S = (2,92

±

0,03) cm

2

δ

=

∆

S

S

⋅

100

% = 1,0%

Pomiar za pomocą mikroskopu warsztatowego
d)

Φ

zewn

= (

23,89

±

0,01

) mm

przyjęłam te wartości co Ty bo nie

wiem jak to policzyć ☺
e)

Φ

wewn

= (

12,90

±

0,01

) mm

f) Pole powierzchni S =

π

4

2

2

(

)

Φ

Φ

zewn

wewn

-

S

obl

=3,18 cm

2

S

min

=3,17 cm

2

S

max

=3,19 cm

2

∆

S = max ( S

obl

- S

min

, S

max

- S

obl

) =0,01cm

2

Po zaokrągleniu : S = (3,18

±0,01

) cm

2

δ

=

∆

S

S

⋅

100

% =0,03%

Zadanie 3. (Kwadraty na arkuszu papieru milimetrowego)
Wybrany kwadrat

a= (9,91

±

0,01) mm

b= (10,01

±

0,01) mm

S

obl

= 0,99 cm

2

S

min

= 0,98 cm

2

S

max

= 1,0 cm

2

∆

S = max ( S

obl

- S

min

, S

max

- S

obl

) = 0,01 cm

2

Po zaokrągleniu : S = (0,99

±

0,01) cm

2

δ

=

∆

S

S

⋅

100

% = 1,0 %

Zadanie 4. (Odcinki o długości 1 cm zmierzone za pomocą mikroskopu)

a1 = 10,37 mm ; a2 = 8,63 mm ;
średnia długość a = 9,5

±

0,87

mm tego na czerwono nie jestem pewna

δ

=

∆

a

a

⋅

100

% = 9,2 %