
Stanisław Kowalski,
Wykłady z matematyki –
Granica funkcji
– wykład 6.
59
31
Granica funkcji
Definicja.
Niech
R
∈
a
(
C
∈
a
). Otoczeniem punktu a nazywamy dowolny zbiór
)
,
( r
a
K
b d cy kołem otwartym o rodku a i
promieniu r, a s siedztwem punktu a nazywamy zbiór punktów
)
,
( r
a
S
otrzymany z jego otoczenia
)
,
( r
a
K
przez wy-
rzucenie rodka:
}
{
\
)
,
(
)
,
(
a
r
a
K
r
a
S
=
.
Definicja – charakterystyka otoczeniowa punktu skupienia.
Punkt a jest punktem skupienia zbioru
A ⊂ R (piszemy:
A
∈
a
) wtedy i tylko wtedy, gdy w dowolnym jego s siedztwie
s elementy zbioru
A:
∅
≠
∩
∀
>
ε
A
S
)
,
(
0
a
, gdzie
)
(
)
(
)
,
(
ε
+
∪
ε
−
=
ε
a
a
a
S
.
Definicja – charakterystyka ci gowa punktu skupienia.
Punkt a jest punktem skupienia zbioru
A, je li istnieje ci g
)
(
n
a taki, e:
1
°
A
N
∈
∀
∈
n
n
a
,
2
°
a
a
n
n
≠
∀
∈N
,
3
°
a
a
n
n
=
∞
→
lim
.
Ci g
)
(
n
a o własno ciach 1
°−3° nazywamy
ci giem Heinego
(1)
dla punktu a i zbioru
A.
Granica funkcji mo e by okre lona jedynie w punktach skupienia dziedziny tej funkcji.
Definicja granicy funkcji.
g
x
f
x
x
=
→
)
(
lim
0
⇔ dla ka dego ci gu Heinego
)
(
n
x dla punktu
0
x i zbioru
f
D ci g
(
)
)
(
n
x
f
jest zbie ny do g.
1. Przykład
2
1
1
lim
2
1
=
−
−
→
x
x
x
2. Przykład
1
sin
lim
0
=
→
x
x
x
(
x
x
x
tan
sin
<
<
→
x
x
x
cos
1
sin
1
<
<
→
1
sin
cos
<
<
x
x
x
)
3. Zadanie
Niech b dzie dana funkcja
)
4
(
+
=
x
x
f
oraz ci g liczbowy
)
(
n
x , gdzie
n
n
x
n
+
= 1
. Utworzy ci g
(
)
)
(
n
x
f
warto-
ci funkcji oraz obliczy jego granic .
Rozwi zanie.
n
n
n
n
x
x
f
n
n
5
1
4
1
4
)
(
+
=
+
+
=
+
=
.
5
)
5
(
lim
)
5
(
lim
5
1
lim
)
(
lim
1
1
=
+
=
+
=
+
=
→∞
→∞
→∞
→∞
n
n
n
n
n
n
n
n
n
n
n
x
f
.
(1)
Edward Heine (1821
−1881): matematyk niemiecki.
Stanisław Kowalski,
Wykłady z matematyki –
Granica funkcji
– wykład 6.
60
4. Zadanie
Obliczy
)
4
2
(
lim
3
+
→
x
x
.
Rozwi zanie.
Skorzystamy z definicji Heinego funkcji w punkcie skupienia jej dziedziny.
Niech
)
(
n
x b dzie ci giem Heinego dla punktu
3
0
=
x
i zbioru
R
D
f
= :
f
n
D
x
∈
≠
3
,
3
lim
=
→∞
n
n
x
. Wówczas
10
4
3
2
)
4
2
(
lim
)
(
lim
=
+
⋅
=
+
⋅
=
∞
→
∞
→
n
n
n
n
x
x
f
.
Wykorzystali my tu twierdzenia o granicy iloczynu i granicy sumy ci gów.
5. Zadanie
Obliczy
x
x
x
x
2
4
lim
2
2
2
−
−
→
.
Rozwi zanie.
Skorzystamy z definicji Heinego funkcji w punkcie skupienia jej dziedziny.
Niech
)
(
n
x b dzie ci giem Heinego dla punktu
2
0
=
x
i zbioru
}
2
,
0
{
\
R
D
f
=
:
f
n
D
x
∈
≠
2
,
2
lim
=
∞
→
n
n
x
. Wówczas
=
⋅
−
−
=
→∞
→∞
n
n
n
n
n
n
x
x
x
x
f
2
)
(
4
)
(
lim
)
(
lim
2
2
0
0
2
2
2
2
2
lim
)
2
(
)
2
)(
2
(
lim
=
+
=
+
=
−
+
−
=
∞
→
∞
→
n
n
n
n
n
n
n
n
x
x
x
x
x
x
.
Wykorzystali my tu twierdzenia o granicy ilorazu i granicy sumy ci gów.
6. Zadanie
Obliczy
9
15
2
lim
2
2
3
−
−
+
→
x
x
x
x
.
Rozwi zanie.
Skorzystamy z definicji Heinego funkcji w punkcie skupienia jej dziedziny.
Niech
)
(
n
x b dzie ci giem Heinego dla punktu
3
0
=
x
i zbioru
}
3
,
3
{
\
−
= R
D
f
:
f
n
D
x
∈
≠
3
,
3
lim
=
→∞
n
n
x
. Wówczas
=
−
−
⋅
+
=
→∞
→∞
9
)
(
15
2
)
(
lim
)
(
lim
2
2
n
n
n
n
n
n
x
x
x
x
f
0
0
3
4
6
8
3
3
5
3
3
5
lim
)
3
)(
3
(
)
5
)(
3
(
lim
=
=
+
+
=
+
+
=
+
−
+
−
=
∞
→
∞
→
n
n
n
n
n
n
n
n
x
x
x
x
x
x
.
Wykorzystali my tu twierdzenia o granicy ilorazu i granicy sumy ci gów.
7. Zadanie
Obliczy
x
x
x
1
1
lim
0
+
−
→
.
Rozwi zanie.
Skorzystamy z definicji Heinego funkcji w punkcie skupienia jej dziedziny.
Niech
)
(
n
x b dzie ci giem Heinego dla punktu
0
0
=
x
i zbioru
)
;
0
(
)
0
;
1
[
∞
∪
−
=
f
D
:
f
n
D
x
∈
≠
0
,
0
lim
=
→∞
n
n
x
.
Wówczas
=
+
−
=
∞
→
∞
→
n
n
n
n
n
x
x
x
f
1
1
lim
)
(
lim
0
0
=
+
+
+
−
=
+
+
+
+
+
−
=
∞
→
∞
→
)
1
1
(
)
1
(
1
lim
)
1
1
(
)
1
1
)(
1
1
(
lim
n
n
n
n
n
n
n
n
n
x
x
x
x
x
x
x
=
+
+
−
∞
→
)
1
1
(
lim
n
n
n
n
x
x
x
2
1
1
1
1
lim
−
=
+
+
−
=
∞
→
n
n
x
Wykorzystali my tu wzór
)
)(
(
2
2
b
a
b
a
b
a
+
−
=
−
oraz twierdzenia o arytmetyce granic ci gów.

Stanisław Kowalski,
Wykłady z matematyki –
Granica funkcji
– wykład 6.
61
Definicja granicy cz
ciowej:
Liczba g jest granic cz ciow funkcji f w punkcie
0
x
⇔ istnieje ci g Heinego
)
(
n
x dla punktu
0
x i zbioru
f
D taki,
e ci g
(
)
)
(
n
x
f
jest zbie ny do g.
F
AKT
.
Je li g jest granic funkcji f w punkcie
f
D
x
∈
0
, to wszystkie granice cz ciowe funkcji f w punkcie
0
x s równe licz-
bie g.
F
AKT
.
Je li funkcja f ma dwie ró ne granice cz ciowe w punkcie
0
x , to funkcja f nie ma granicy w tym punkcie.
8. Przykład
Dla funkcji
)
|
|
(
x
x
x
x
f
+
=
nie istnieje
)
(
lim
0
x
f
x
→
.
①
Niech
)
(
n
x b dzie dowolnym ci giem o wyrazach
0
>
n
x
i takim, e
0
lim
=
∞
→
n
n
x
. Wówczas
1
1
)
(
→
+
=
n
n
x
x
f
.
②
Niech
)
(
n
y b dzie dowolnym ci giem o wyrazach
0
<
n
y
i takim, e
0
lim
=
∞
→
n
n
y
. Wówczas
1
1
)
(
−
→
+
−
=
n
n
y
y
f
.
9. Przykład
Dla funkcji
)
sin
(
x
x
f
=
nie istnieje
)
(
lim
x
f
x
∞
→
.
①
Niech
)
(
n
x b dzie ci giem o wyrazach
π
= n
x
n
. Wówczas
0
0
)
sin(
)
(
→
=
π
=
n
x
f
n
.
②
Niech
)
(
n
y b dzie ci giem o wyrazach
π
+
π
=
n
y
n
2
2
. Wówczas
1
1
)
2
2
sin(
)
(
→
=
π
+
π
=
n
y
f
n
.
③
Niech
)
(
n
z b dzie ci giem o wyrazach
π
+
π
−
=
n
z
n
2
2
. Wówczas
1
1
)
2
2
sin(
)
(
−
→
−
=
π
+
π
−
=
n
z
f
n
.
Definicja granicy prawostronnej:
g
x
f
x
x
=
+
→
)
(
lim
0
⇔
=
=
>
∈
∀
∞
→
∞
→
g
x
f
x
x
x
x
x
n
n
n
n
n
f
n
x
n
)
(
lim
lim
0
0
)
(
D
Definicja granicy lewostronnej:
g
x
f
x
x
=
−
→
)
(
lim
0
⇔
=
=
<
∈
∀
∞
→
∞
→
g
x
f
x
x
x
x
x
n
n
n
n
n
f
n
x
n
)
(
lim
lim
0
0
)
(
D
10. Przykład
1
|
2
|
2
3
lim
2
2
=
−
+
−
+
→
x
x
x
x
,
1
|
2
|
2
3
lim
2
2
−
=
−
+
−
−
→
x
x
x
x
Stanisław Kowalski,
Wykłady z matematyki –
Granica funkcji
– wykład 6.
62
Ilustracja do przykładu 10.
11. Przykład
1
|
1
|
lim
2
3
1
−
=
−
−
−
−
→
x
x
x
x
,
1
|
1
|
lim
2
3
1
=
−
−
+
−
→
x
x
x
x
,
1
|
1
|
lim
2
3
1
−
=
−
−
−
→
x
x
x
x
,
1
|
1
|
lim
2
3
1
=
−
−
+
→
x
x
x
x
,
Ilustracja do przykładu 11.
12. Przykład
1
|
1
|
lim
2
2
4
1
=
−
−
−
−
→
x
x
x
x
,
1
|
1
|
lim
2
2
4
1
−
=
−
−
+
−
→
x
x
x
x
,
1
|
1
|
lim
2
2
4
1
−
=
−
−
−
→
x
x
x
x
,
1
|
1
|
lim
2
2
4
1
=
−
−
+
→
x
x
x
x
.
Ilustracja do przykładu 12.
F
AKT
.
=
∧
=
⇔
=
−
+
→
→
→
g
x
f
g
x
f
g
x
f
x
x
x
x
x
x
)
(
lim
)
(
lim
)
(
lim
0
0
0
Kontrapozycj tego twierdzenia stosujemy, gdy chcemy wykaza , e funkcja nie ma granicy:
Stanisław Kowalski,
Wykłady z matematyki –
Granica funkcji
– wykład 6.
63
F
AKT
.
)
(
lim
)
(
lim
0
0
x
f
x
f
x
x
x
x
−
+
→
→
≠
nie istnieje
)
(
lim
0
x
f
x
x
→
13. Zadanie
Badaj c granice jednostronne rozstrzygn istnienie granicy dla funkcji f w punkcie
0
x , je li:
2
1
1
)
(
−
⋅
+
+
=
x
x
x
x
f
,
1
0
−
=
x
.
Rozwi zanie.
Warunkiem koniecznym i wystarczaj cym na to, aby funkcja miała granic w punkcie jest istnienie i równo jej granic
jednostronnych. Wspólna warto granic jednostronnych jest wówczas granic funkcji. Dla granic jednostronnych mamy
1
)
2
(
lim
2
1
)
1
(
lim
2
1
1
lim
)
(
lim
1
1
1
1
−
=
−
−
=
−
⋅
+
+
−
=
−
⋅
+
+
=
−
−
−
−
−
→
−
→
−
→
−
→
x
x
x
x
x
x
x
x
f
x
x
x
x
,
3
)
2
(
lim
2
1
1
lim
2
1
1
lim
)
(
lim
1
1
1
1
−
=
−
=
−
⋅
+
+
=
−
⋅
+
+
=
+
+
+
+
−
→
−
→
−
→
−
→
x
x
x
x
x
x
x
x
f
x
x
x
x
.
Poniewa granice jednostronne s ró ne, wi c badana granica nie istnieje.
14. Zadanie
Badaj c granice jednostronne rozstrzygn istnienie granicy dla funkcji f w punkcie
0
x , je li:
x
x
f
+
=
1
1
)
(
arctg
,
1
0
−
=
x
.
Rozwi zanie.
Dla granic jednostronnych mamy
2
-
)
arctg(-
arctg
arctg
π
=
∞
=
=
+
=
−
−
→
−
→
−
→
−
−
−
0
1
lim
1
1
lim
)
(
lim
1
1
1
x
x
x
x
x
f
,
2
)
arctg(
arctg
arctg
π
=
∞
=
=
+
=
+
−
→
−
→
−
→
+
+
+
0
1
lim
1
1
lim
)
(
lim
1
1
1
x
x
x
x
x
f
.
Poniewa granice jednostronne s ró ne, wi c badana granica nie istnieje.
15. Zadanie
Badaj c granice jednostronne rozstrzygn istnienie granicy dla funkcji f w punkcie
0
x , je li:
>
<
+
=
0
cos
0
1
)
(
2
x
x
x
x
x
f
dla
dla
,
0
0
=
x
.
Rozwi zanie.
Dla granic jednostronnych mamy
1
)
1
(
lim
)
(
lim
2
0
0
=
+
=
−
−
→
→
x
x
f
x
x
,
1
cos
lim
)
(
lim
0
0
=
=
+
+
→
→
x
x
f
x
x
Poniewa granice jednostronne s równe, wi c badana granica jest równa 1.
32
Niesko czenie małe (wielkie)
Funkcj f nazywamy niesko czenie mał
w s siedztwie punktu
f
D
x
∈
0
, je li
0
)
(
lim
0
=
→
x
f
x
x
.
Niesko czenie małe
nazywamy
równowa nymi
, je li
1
)
(
)
(
lim
0
=
→
x
g
x
f
x
x
.

Stanisław Kowalski,
Wykłady z matematyki –
Granica funkcji
– wykład 6.
64
16. Przykład
1
sin
lim
0
=
→
x
x
x
17. Przykład
1
lim
0
=
→
x
x
x
tg
18. Przykład
1
sin
lim
0
=
→
x
x
x
arc
Stanisław Kowalski,
Wykłady z matematyki –
Granica funkcji
– wykład 6.
65
19. Przykład
1
lim
0
=
→
x
x
x
arctg
20. Przykład
1
)
1
ln(
lim
0
=
+
→
x
x
x
21. Przykład
1
1
lim
0
=
−
→
x
e
x
x
22. Przykład
7
°
(
)
=
+
=
=
+
∞
=
→
→
→
→
e
x
f
x
f
e
x
f
x
f
x
f
x
x
x
x
x
f
x
x
x
x
)
(
/
1
)
(
)
(
1
lim
0
)
(
lim
)
(
1
1
lim
)
(
lim
0
0
0
0
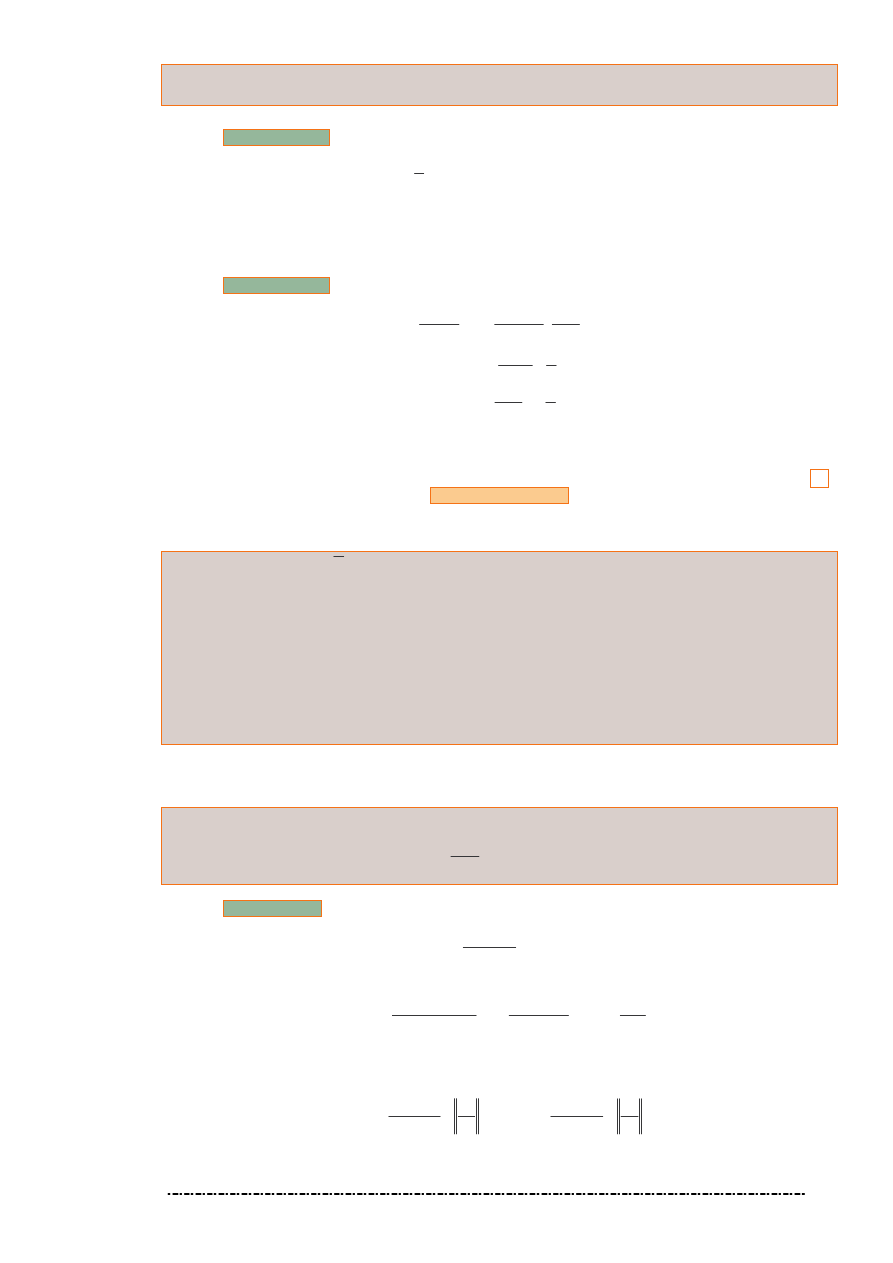
Stanisław Kowalski,
Wykłady z matematyki –
Granica funkcji
– wykład 6.
66
Funkcj f nazywamy niesko czenie wielk w danym przej ciu granicznym
, je li
∞
=
→
|
)
(
|
lim
0
x
f
x
x
.
23. Przykłady
)
1
(
x
x
f
=
jest niesko czenie wielk , gdy
0
→
x
,
)
ln
(
x
x
f
=
jest niesko czenie wielk , gdy
+
→ 0
x
,
)
ln
(
x
x
f
=
jest niesko czenie wielk , gdy
∞
→
x
.
24. Przykłady
1
sin
)
1
(
lim
sin
1
lim
0
0
=
⋅
−
−
=
−
−
→
−
→
x
x
x
e
x
e
x
x
x
x
,
3
2
1
cos
lim
0
π
=
−
→
x
e
x
x
arc
;
4
|
|
sin
lim
0
π
−
=
−
→
x
x
x
arctg
.
33
Asymptoty funkcji
1°°°°
Prosta
0
x
x
=
, gdzie
f
f
x
D
D \
0
∈
, jest
asymptot pionow
funkcji f, gdy przynajmniej jedna z granic jednostron-
nych:
)
(
lim
0
x
f
x
x
+
→
lub
)
(
lim
0
x
f
x
x
−
→
jest niewła ciwa. Je li jest to granica prawostronna
− asymptot nazywamy prawo-
stronn , je li lewostronna
− asymptota równie jest lewostronna. Asymptot pionowych szukamy na ko cach prze-
działów okre lono ci funkcji.
2°°°°
Asymptot uko nych szukamy w
∞ i w −∞ (o ile
f
a
D
⊂
−∞ )
,
(
lub
f
a
D
⊂
∞)
,
(
). Prosta okre lona równaniem
n
mx
y
+
=
jest
asymptot uko n
funkcji w
∞, je li
[
]
0
)
(
)
(
lim
=
+
−
+∞
→
n
mx
x
f
x
.
T
WIERDZENIE
.
Warunkiem koniecznym i wystarczaj cym na to, aby prosta
n
mx
y
+
=
była asymptot funkcji f w
∞ jest, aby
[
]
mx
x
f
n
x
x
f
m
x
x
−
=
=
∞
→
∞
→
)
(
lim
,
)
(
lim
.
25. Przykład
R
R
→
−
+
+
=
}
1
(
\
:
)
1
1
(
2
x
x
x
x
f
Poniewa
1
3
2
1
3
)
1
(
2
1
1
2
)
1
(
)
(
−
+
+
=
−
+
−
+
=
−
+
+
−
=
x
x
x
x
x
x
x
x
x
x
f
wi c prosta
2
+
= x
y
jest asymptot uko n funkcji f w
∞. Ta sama prosta jest asymptot uko n funkcji f w −∞.
Poniewa
−∞
=
=
−
+
+
−
→
−
0
3
1
1
lim
2
1
x
x
x
x
,
∞
=
=
−
+
+
+
→
+
0
3
1
1
lim
2
1
x
x
x
x
,
wi c prosta
1
=
x
jest asymptot pionow funkcji f.
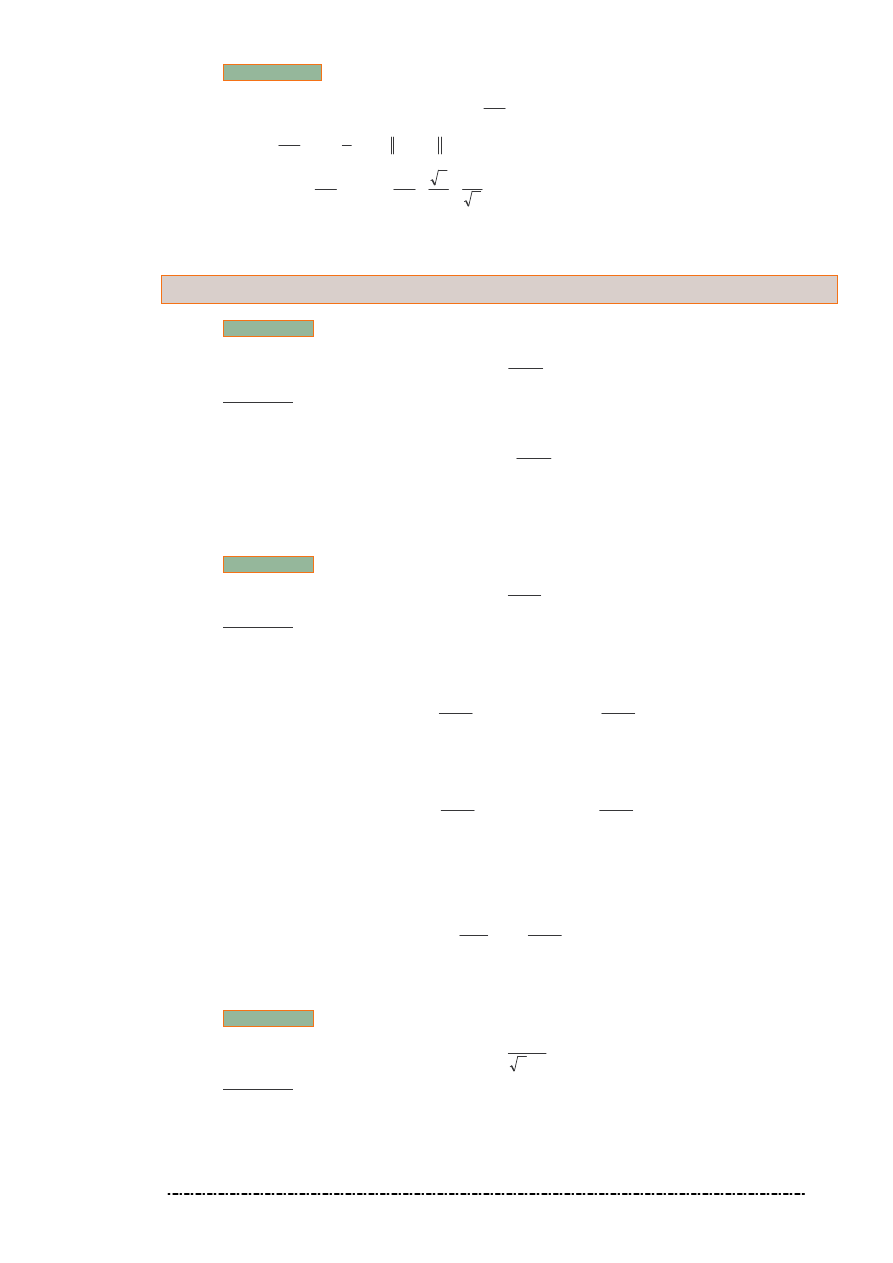
Stanisław Kowalski,
Wykłady z matematyki –
Granica funkcji
– wykład 6.
67
26. Przykład
R
R →
=
>0
:
)
ln
(
x
x
x
f
−∞
=
−∞
⋅
∞
=
⋅
=
+
+
→
→
)
(
ln
1
lim
ln
lim
0
0
x
x
x
x
x
x
→
→
→
→
prosta
0
=
x
jest asymptot pionow prawostronn .
0
ln
lim
=
+∞
→
x
x
x
,
=
<
<
x
x
x
x
x
1
ln
0
→
→
→
→
prosta
0
=
y
jest asymptot poziom w
∞.
Asymptoty w
−∞ nie szukamy, gdy
)
,
0
(
+∞
=
f
D
.
FAKT.
Funkcje wymierne (ilorazy wielomianów) nie mog mie ró nych asymptot w
∞ i w −∞.
27. Zadanie
Wyznaczy asymptoty funkcji danej za pomoc wzoru
1
1
)
(
2
2
+
−
=
x
x
x
f
.
Rozwi zanie.
Dziedzin funkcji jest zbiór
R liczb rzeczywistych. Zatem funkcja nie ma asymptot pionowych. Obliczymy granic
1
1
1
lim
)
(
lim
2
2
=
+
−
=
→∞
→∞
x
x
x
f
x
x
.
Z powy szego wynika, e prosta
1
=
y
jest asymptot poziom prawostronn (w plus niesko czono ci). Poniewa funk-
cja f jest wymierna, wi c prosta
1
=
y
jest te asymptot poziom lewostronn (w minus niesko czono ci).
28. Zadanie
Wyznaczy asymptoty funkcji danej za pomoc wzoru
x
e
x
f
x
1
)
(
−
=
.
Rozwi zanie.
Dziedzin funkcji jest zbiór
}
0
{
\
R
D
f
=
. Asymptot pionow mogłaby by jedynie prosta
0
=
x
. Obliczamy granice
jednostronne
1
1
lim
)
(
lim
0
0
=
−
=
+
+
→
→
x
e
x
f
x
x
x
,
1
1
lim
)
(
lim
0
0
=
−
=
−
−
→
→
x
e
x
f
x
x
x
.
Poniewa obie granice jednostronne s wła ciwe, wi c funkcja f nie ma asymptoty pionowej.
Wyznaczymy asymptoty w niesko czono ciach. Obliczamy przede wszystkim granice
0
1
lim
)
(
lim
=
−
=
−∞
→
−∞
→
x
e
x
f
x
x
x
,
∞
=
−
=
∞
→
∞
→
x
e
x
f
x
x
x
1
lim
)
(
lim
.
Z powy szego wynika, e prosta
0
=
y
jest asymptot poziom lewostronn funkcji (w
−∞ ); nie jest ona asymptot
poziom prawostronn , W
∞ funkcja mo e mie ewentualnie asymptot uko n . Wyliczamy współczynniki asymptoty
uko nej
∞
=
−
=
=
→∞
→∞
2
1
lim
)
(
lim
x
e
x
x
f
m
x
x
x
.
Poniewa współczynnik m nie jest sko czony, wi c funkcja f nie ma asymptoty uko nej prawostronnej.
29. Zadanie
Wyznaczy asymptoty funkcji danej za pomoc wzoru
3
)
(
−
=
x
x
x
f
.
Rozwi zanie.
Dziedzin funkcji jest zbiór
)
;
9
(
)
9
;
0
[
∞
∪
=
f
D
. Asymptot pionow mogłaby by jedynie prosta
9
=
x
. Obliczamy
granice jednostronne
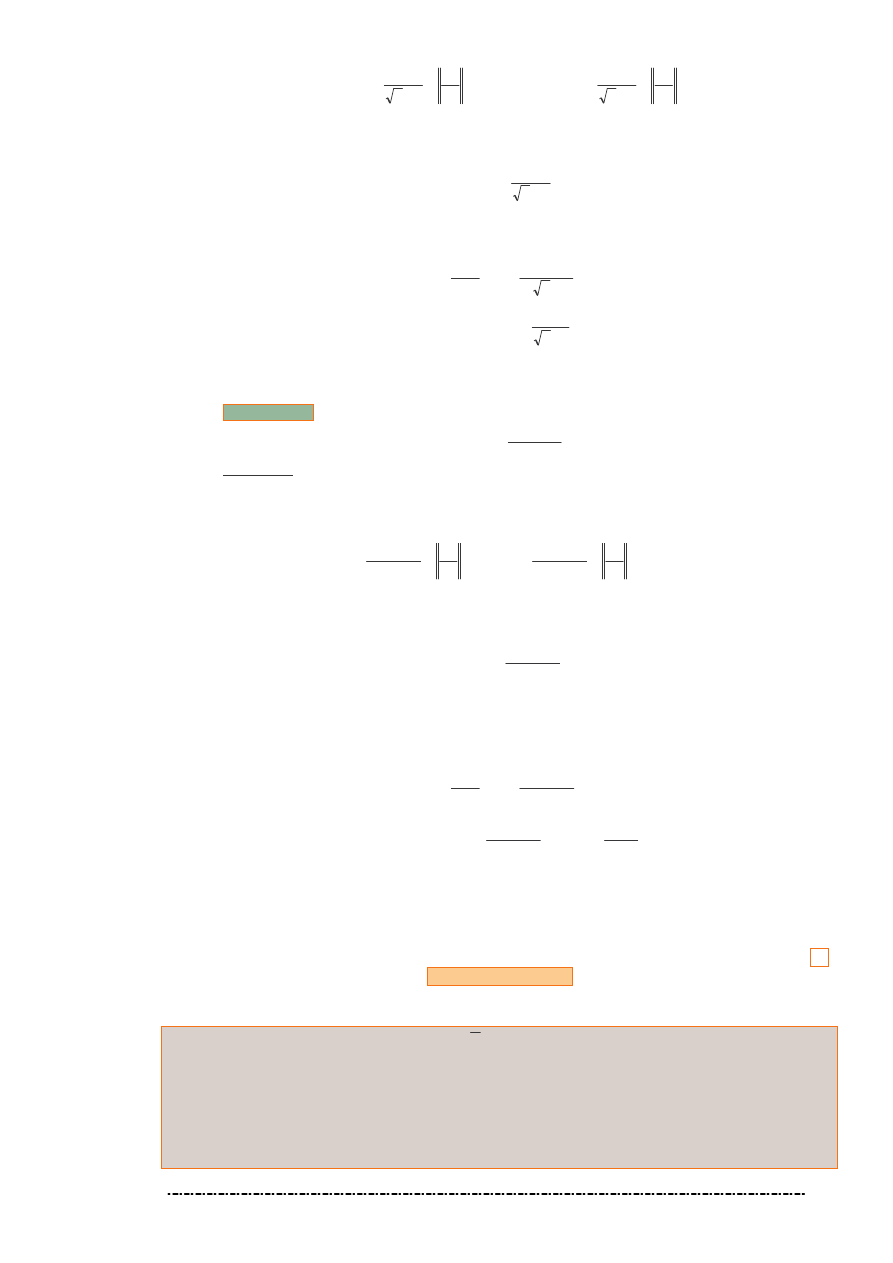
Stanisław Kowalski,
Wykłady z matematyki –
Granica funkcji
– wykład 6.
68
∞
=
=
−
=
+
→
→
+
+
0
9
3
lim
)
(
lim
9
9
x
x
x
f
x
x
,
−∞
=
=
−
=
−
→
→
−
−
0
9
3
lim
)
(
lim
9
9
x
x
x
f
x
x
.
Poniewa obie granice jednostronne s niewła ciwe, wi c prosta
9
=
x
jest asymptot pionow obustronn .
Ewentualna asymptota uko na mo e by jedynie lewostronna. Obliczamy przede wszystkim granic
∞
=
−
=
→∞
→∞
9
lim
)
(
lim
x
x
x
f
x
x
.
Z powy szego wynika, e funkcja nie ma asymptoty poziomej prawostronn . Wyliczamy współczynniki asymptoty
uko nej
0
)
1
(
lim
)
(
lim
=
−
=
=
→∞
→∞
x
x
x
x
x
f
m
x
x
,
[
]
∞
=
−
−
=
−
=
→∞
→∞
]
0
1
[
lim
)
(
lim
x
x
mx
x
f
n
x
x
Poniewa współczynnik n nie jest sko czony, wi c funkcja f nie ma asymptoty uko nej prawostronnej.
30. Zadanie
Wyznaczy asymptoty funkcji danej za pomoc wzoru
1
1
)
(
2
−
+
+
=
x
x
x
x
f
.
Rozwi zanie.
Asymptot pionowych szukamy na ko cach przedziałów okre lono ci funkcji. Poniewa
}
1
{
\
R
D
f
=
oraz obie granice
jednostronne
−∞
=
=
−
+
+
−
→
−
0
3
1
1
lim
2
1
x
x
x
x
,
+∞
=
=
−
+
+
+
→
+
0
3
1
1
lim
2
1
x
x
x
x
s niewła ciwe, wi c prosta
1
=
x
jest asymptot pionow obustronn funkcji f.
Poniewa
∞
=
−
+
+
=
→∞
→∞
1
1
lim
)
(
lim
2
x
x
x
x
f
x
x
wi c funkcja nie ma asymptoty poziomej prawostronnej (w plus niesko czono ci) ani lewostronnej, gdy funkcje wy-
mierne (ilorazy wielomianów) nie mog mie ró nych asymptot w
∞ i w −∞.
Asymptot uko n funkcji w
∞ jest prosta okre lona równaniem
n
mx
y
+
=
, gdzie
1
1
lim
)
(
lim
2
2
=
−
+
+
=
=
→∞
→∞
x
x
x
x
x
x
f
m
x
x
,
[
]
2
1
1
2
lim
]
1
1
[
lim
)
(
lim
2
=
−
+
=
−
−
+
+
=
−
=
→∞
→∞
→∞
x
x
x
x
x
x
mx
x
f
n
x
x
x
.
Prosta
2
+
= x
y
jest asymptot uko n funkcji f w
∞. Ta sama prosta jest asymptot uko n funkcji f w −∞ (gdy f jest
funkcj wymiern ).
34
Ci gło
funkcji
Funkcja f jest okre lona w otoczeniu
0
x
U punktu
f
x
D
∈
0
(a tym samym i w punkcie
0
x ).
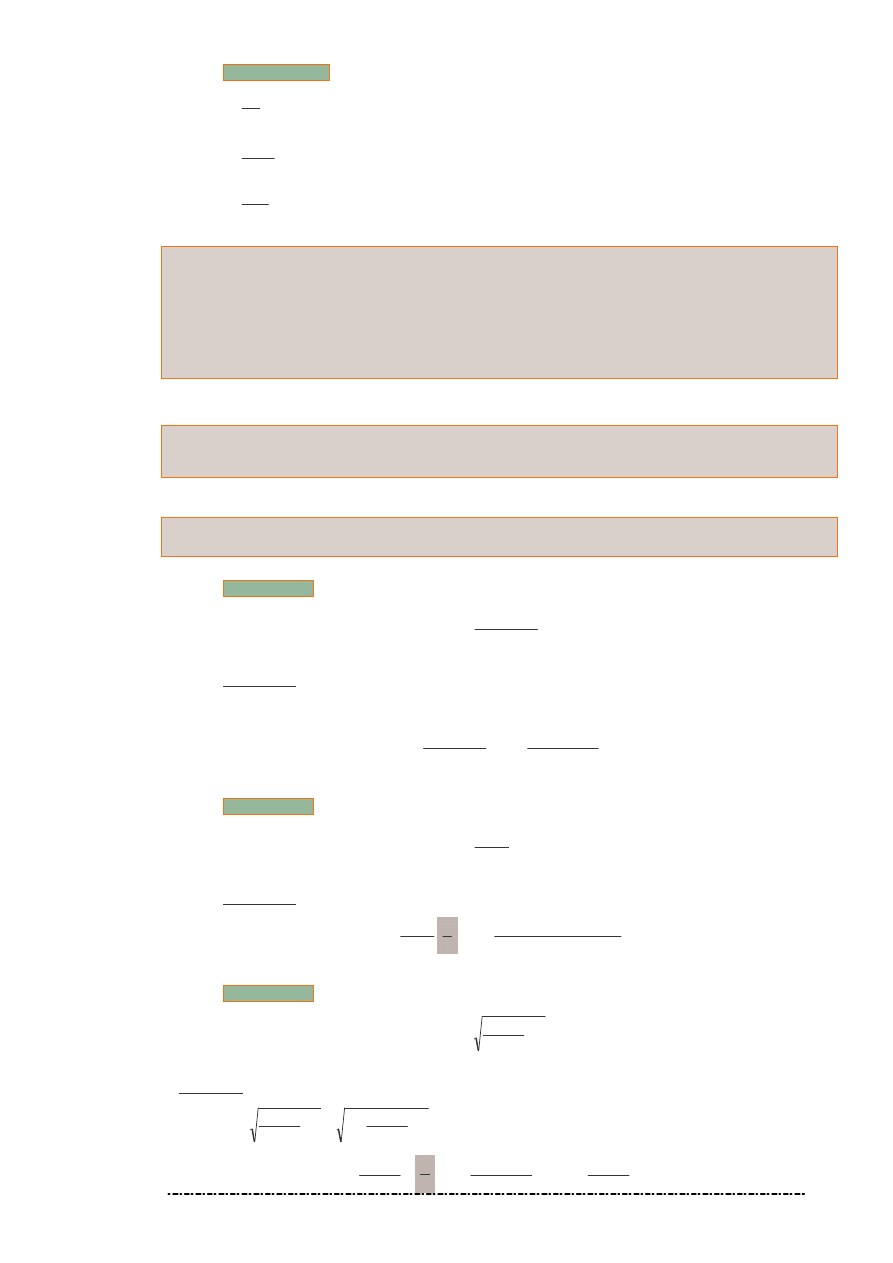
Funkcja f jest ci gła w punkcie
0
x wtedy i tylko wtedy, gdy
)
(
)
(
lim
0
0
x
f
x
f
x
x
=
→
.
Funkcja f jest ci gła prawostronnie w punkcie
0
x wtedy i tylko wtedy, gdy
)
(
)
(
lim
0
0
x
f
x
f
x
x
=
+
→
.
Funkcja f jest ci gła lewostronnie w punkcie
0
x wtedy i tylko wtedy, gdy
)
(
)
(
lim
0
0
x
f
x
f
x
x
=
−
→
.
Stanisław Kowalski,
Wykłady z matematyki –
Granica funkcji
– wykład 6.
69
31. Przykłady
1°°°°
R
R
→
=
{0}
\
:
)
|
|
(
x
x
x
f
jest ci gła. Nie daje si przedłu y do funkcji ci głej na
R.
2°°°°
R
R
→
−
−
=
{1}
\
:
)
1
1
(
2
x
x
x
f
jest ci gła i daje si przedłu y do funkcji ci głej na
R.
3°°°°
R
R
→
=
{0}
\
:
)
sin
(
x
x
x
f
jest ci gła i daje si przedłu y do funkcji ci głej na
R.
•
Funkcja f jest ci gła wtedy i tylko wtedy, gdy jest ci gła w ka dym punkcie swej dziedziny.
•
Suma, ró nica, iloczyn oraz iloraz (tam, gdzie jest sensowny) funkcji ci głych jest funkcj ci gł .
•
Zło enie funkcji ci głych jest funkcj ci gł .
•
Funkcja odwrotna funkcji ci głej jest funkcj ci gł .
Twierdzenie. Weierstrasse’a
- twierdzenie o osi ganiu kresów:
Je li
0
]
,
[ b
a
C
f
∈
, to f jest ograniczona w [a,b] oraz
=
∧
=
∃
∈
∈
∈
)
(
sup
)
(
)
(
inf
)
(
]
,
[
2
]
,
[
1
]
,
[
,
2
1
x
f
c
f
x
f
c
f
b
a
x
b
a
x
b
a
c
c
Własno Darboux
- twierdzenie o przyjmowaniu warto ci po rednich:
Je li
0
]
,
[ b
a
C
f
∈
,
)
(
)
(
b
f
a
f
≠
,
α jest zawarte mi dzy f(a) i f(b), to
α
=
∃
∈
)
(
)
,
(
c
f
b
a
c
.
32. Zadanie
Dla jakiej warto ci A funkcja f jest ci gła, je li
=
≠
−
+
−
=
.
3
,
3
3
3
4
)
(
2
x
A
x
x
x
x
x
f
dla
dla
Rozwi zanie.
Funkcja f jest ci gła w punkcie
0
x , gdy jej warto równa jest granicy w tym punkcie. Dlatego
=
−
+
−
=
→
3
3
4
lim
2
3
x
x
x
A
x
2
3
)
1
)(
3
(
lim
3
=
−
−
−
→
x
x
x
x
.
33. Zadanie
Dla jakiej warto ci A funkcja f jest ci gła, je li
=
≠
−
−
=
.
1
,
1
1
1
)
(
4
x
A
x
x
x
x
f
dla
dla
Rozwi zanie.
1
1
lim
4
1
−
−
=
→
x
x
A
x
0
0
4
1
)
1
)(
1
(
lim
2
3
1
=
−
+
+
+
−
=
→
x
x
x
x
x
x
34. Zadanie
Dla jakiej warto ci A funkcja f jest ci gła, je li
=
≠
+
=
.
0
,
0
5
20
sin
)
(
x
A
x
x
x
x
f
dla
dla
Rozwi zanie.
Poniewa
5
20
sin
lim
5
20
sin
lim
0
0
+
=
+
→
→
x
x
x
x
x
x
, wi c wystarczy obliczy
=
→
x
x
x
20
sin
lim
0
0
0
20
20
20
sin
lim
20
20
20
sin
20
lim
0
0
=
⋅
=
⋅
=
→
→
x
x
x
x
x
x
H
.

Stanisław Kowalski,
Wykłady z matematyki –
Granica funkcji
– wykład 6.
70
Funkcja f jest ci gła dla
5
=
A
.
35. Zadanie
Dla jakiej warto ci A funkcja f jest ci gła, je li
=
≠
=
.
0
,
0
2
)
(
x
A
x
x
x
f
dla
dla
arcctg
Rozwi zanie.
x
2
arcctg
0
lim
→
=
x
A
nie istnieje, gdy
π
=
−∞
=
=
=
−
→
−
−
)
(
0
2
lim
0
arcctg
arcctg
2
arcctg
x
x
A
,
0
)
(
0
2
lim
0
=
∞
=
=
=
+
→
+
+
arcctg
arcctg
2
arcctg
x
x
A
.
Funkcja f mo e by ci gła jedynie jednostronnie: dla
π
=
A
jest ci gła lewostronnie, za dla
0
=
A
jest ci gła prawo-
stronnie.
Wyszukiwarka
Podobne podstrony:
AiSD Wyklad4 dzienne id 53497 Nieznany (2)
3 Wyklad OiSE id 33284 Nieznany
or wyklad 4b id 339029 Nieznany
Materialy do wykladu nr 5 id 28 Nieznany
Finanse Wyklady FiR id 172193 Nieznany
AiSD Wyklad9 dzienne id 53501 Nieznany
Folie wyklad2 Krakow id 286699 Nieznany
OP wyklad nr 3 id 335762 Nieznany
prc wyklad zagad 5 id 388963 Nieznany
hydrologia wyklad 06 id 207845 Nieznany
hydrologia wyklad 05 id 207839 Nieznany
F II wyklad 11 id 167234 Nieznany
BHP Wyklad 10 id 84576 Nieznany (2)
AiSD Wyklad11 dzienne id 53494 Nieznany
elektro wyklad 03b id 157928 Nieznany
fcs wyklad comment 2 2 id 16907 Nieznany
5 wyklad ciagi id 40772 Nieznany (2)
więcej podobnych podstron