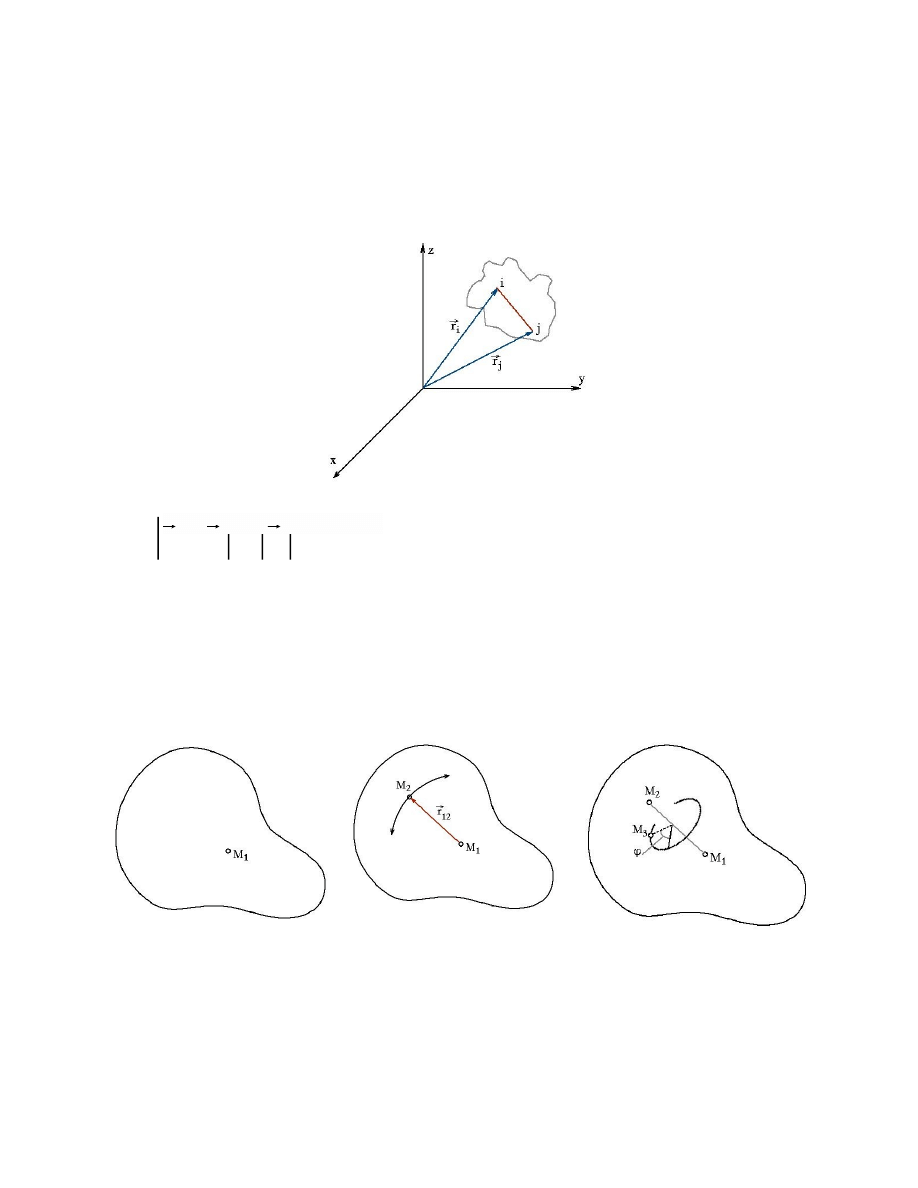
1

DYNAMIKA BRYŁY SZTYWNEJ

Bryłą sztywną nazywamy takie ciało, w którym wszystkie punkty mają zawsze
względem siebie stałą odległość.

Rys. 3.1 Bryła sztywna

i

j

ij

ij

r r

r

r









nie zależy od czasu

Stąd wynika, ze podczas ruchu układ punktów materialnych składających się
na bryłę sztywną porusza się jako całość o nie zmieniającej się postaci i
objętości

Bryła sztywna ma 6 stopni swobody w ruchu swobodnym.

Rys. 3.2

Rys. 3.3

Rys. 3.4

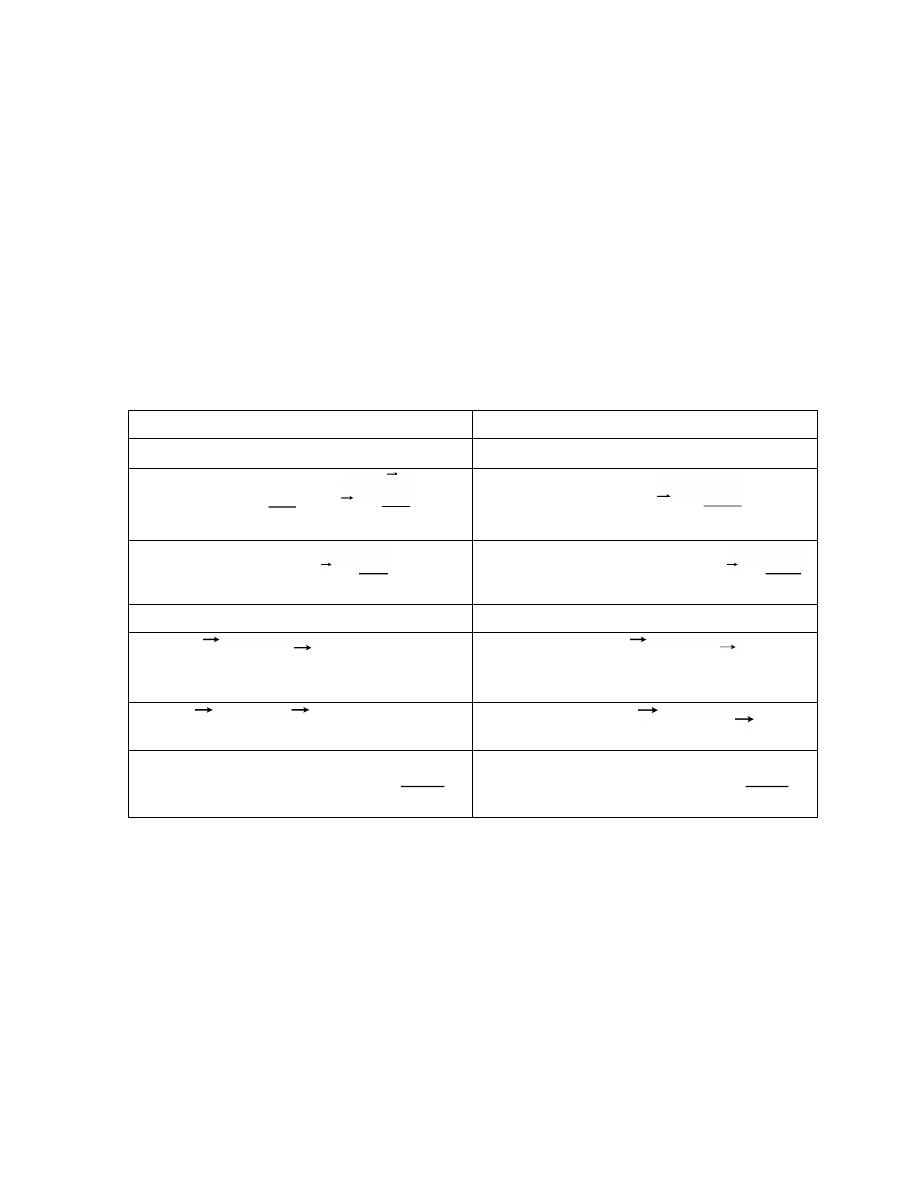
Rys. 3.2 – Wybieramy dowolny punkt

1

M

bryły sztywnej. Ma on trzy stopnie

swobody

2

Rys. 3.3 – Wybieramy układ w którym punkt

1

M

jest nieruchomy; wówczas

punkt

2

M

ma tylko dwa stopnie swobody, gdyż może poruszać się po

powierzchni kuli o promieniu

12

r

Rys. 3.4 – Wybieramy układ, w którym

1

M

oraz

2

M

są nieruchome . Dowolny

punkt lub cząstka

3

M

w tym układzie ma tylko jeden stopień swobody, gdyż

może się poruszać tylko po okręgu.

Gdy na ruch bryły sztywnej nałożymy więzy, wówczas ruch nie traktowany jako
swobodny. Dla

p

niezależnych więzów (równań więzów) ilość stopni swobody

wynosi:

6

f

p

 

(3.1)

W ogólnym przypadku bryła sztywna porusza się dwoma rodzajami ruchów:
postępowym i obrotowym.

Ruch postępowy:
dowolna prosta przeprowadzona przez bryłę sztywną przesuwa się
równolegle do samej siebie, wektory prędkości wszystkich punktów bryły
sztywnej są w danej chwili jednakowe.


Ruch obrotowy:
wszystkie punkty bryły sztywnej poruszają się po okręgach, których środki
leżą na jednej wspólnej prostej zwanej chwilową osią obrotu.


Dla n-tego punktu o wektorze wodzącym

n

r

, relacja między prędkością liniową

n

v

oraz prędkością kątową (obrotową)



jest opisana związkiem:

n

n

v

r



 

(3.2)

3

Podstawowe wielkości charakteryzujące ruch postępowy oraz
obrotowy

Ruch prostoliniowy

Ruch obrotowy

Przesunięcie:

x

(

r

)

Kąt obrotu



Prędkość:

dx

v

dt



(

dr

v

dt



)

Prędkość kątowa :

d

dt







Przyspieszenie :

dv

a

dt



Przyspieszenie kątowe:

d

dt







Masa :

m

Moment bezwładności :

I

Siła :

F ma



Moment siły:

M

I





Pęd:

p mv



Moment pędu:

L I





Energia kinetyczna:

2

2

k

mv

E



Energia kinetyczna:

2

2

k

I

E





Dla każdej bryły sztywnej, niezależnie od jej kształtu, istnieją trzy ortogonalne
(prostopadłe) kierunki, dla których moment pędu

L



jest równoległy do osi

obrotu



 

(

L









). Osie te noszą nazwę osi głównych. Gdy bryła sztywna

posiada jakąś symetrię, to osie główne pokrywają się z osiami symetrii.

Równanie ruchu obracającego się ciała

4

Ruch obrotowy punktu materialnego jest opisany wzorem:

dL

M

dt



(3.3)

gdzie:

L



jest momentem pędu,

M



jest momentem wypadkowej siły.

Obie wielkości muszą być odniesione do wspólnego początku układu, którym
jest zwykle środek masy (ale nie zawsze).

Jeżeli potraktuje się bryłę sztywną jako układ punktów materialnych, to moment
pędu możemy zapisać :

n

n

n

n

v

r

m

L













(3.4)

związek między prędkością liniową

v

dla n-tego elementu bryły sztywnej i

prędkością kątową



jest następujący:

n

n

v

r



 

(3.5)

Przyjmujemy:

( ,

,

)

x

y

z

   

( , , )

n

n

n

n

r

x y z

( , , )

x

y

z

L L L L

Wstawiając równanie (3.5) do (3.4) otrzymujemy:

)

(

n

n

n

n

r

r

m

L



















(3.6)

Stosujemy tożsamość wektorową:

5

(

)

(

)

(

)

A B C

B A C

C A B

 









(3.7)

w której przy zastąpieniu :

n

A

r



,

B





,

n

C

r



wzór (3.6) przyjmuje postać:

2

[

(

)]

n

n

n

n

n

L

m

r

r r













(3.8)

Wektorowe równanie (3.8) można rozpisać na trzy równania skalarne dla
składowym momentu pędu

L



, korzystamy przy tym z rozpisania iloczynu

skalarnego:

n

n

x

n

y

n

z

r

x

y

z









 





. Wówczas dostajemy układ trzech równań

skalarnych:

2

2

(

)

n

n

n

n

y

n n n

z

n n n

L

m r

x

m x y

m x z

x

n

n

n





















2

2

(

)

x

n n n

y

n

n

n

z

n n n

L

m x y

m r

y

m y z

y

n

n

n







 













2

2

(

)

x

n n n

y

n n n

z

n

n

n

L

m z x

m z y

m r

z

z

n

n

n







 













(3.9a-c)

W równaniach (3.9a-c), przy składowych wektora prędkości





, występują

wielkości, które zależą od rozkładu masy ciała względem chwilowej osi obrotu i
orientacji w stosunku do układu współrzędnych. Wielkości te nie zależą od czasu i
noszą nazwę współczynników bezwładności lub momentów bezwładności.
Zapisujemy je następująco:

2

2

2

2

(

)

(

)

xx

n

n

n

n

n

n

n

n

I

m r

x

m y

z



















n

n

n

n

xy

y

x

m

I

(3.10a-c)

6







n

n

n

n

xz

z

x

m

I

2

2

2

2

(

)

(

)

yy

n

n

n

n

n

n

n

n

I

m r

y

m x

z



















n

n

n

n

yx

x

y

m

I

(3.11a-c)







n

n

n

n

yz

z

y

m

I

2

2

2

2

(

)

(

)

zz

n

n

n

n

n

n

n

n

I

m r

z

m x

y













zx

n n n

n

I

m z x

 



(3.12a-c)

zy

n n n

n

I

m z y

 



Równania od (3.10a-c) do (3.12a-c) stanowią definicję 9–ciu składowych
momentu bezwładności lub inaczej tensora momentu bezwładności

Trzy równania skalarne (3.9a-c) można teraz zapisać w postaci:

x

xx

x

xy

y

xz

z

L

I

I

I













y

yx

x

yy

y

yz

z

L

I

I

I













(3.13a-c)

z

zx

x

zy

y

zz

z

L

I

I

I













Ogólnie wektor momentu pędu

L



nie ma kierunku wektora prędkości kątowej





.

Najprostszą bryłą sztywną jest kula, dla niej zawsze

L









.

Tensor momentu bezwładności zapisujemy w postaci macierzowej:

7

xx

xy

xz

yx

yy

yz

zx

zy

zz

I

I

I

I

I

I

I

I

I





















(3.14)

Człony

xx

I

yy

I

zz

I

nazywają się przekątnymi macierzy lub wyrazami na diagonali,

inne wyrazy są poza przekątnymi.
Zapis całkowy: jeżeli przez

( )

r



jest gęstością bryły w punkcie odległym o

r

od

osi obrotu to składowe momentu bezwładności są zapisane przykładowo w
następującej postaci:

2

2

( )(

)

xx

I

r r

x dV









( )

xy

I

r xydV



 



(3.15a-c)

( )

xz

I

r xzdV



 



Mamy następujące związki:

2

2

2

2

( )

xx

yy

zz

n n

n

I

I

I

m r

r r dV















(3.16)

Wzór (3.16) przedstawia izotropowe wielkości niezależne od orientacji ciała
względem układu współrzędnych.


Własności tensora momentu bezwładności:

Wyrazy poza przekątną są symetryczne:

8

xy

yx

I

I



xz

zx

I

I



yz

zy

I

I



Z własności macierzy symetrycznych wynika, że dla każdej bryły sztywnej można
tak dobrać osie obrotu, że znikną wszystkie wyrazy poza diagonalne.

0

xy

xz

yz

I

I

I







Wówczas pozostaną tylko wyrazy na diagonali, które przy tak szczególnie
wybranych osiach obrotu i układzie współrzędnych można zapisać:

1

( )

xx

x

I

I

I



2

( )

yy

y

I

I

I



(3.17)

3

( )

zz

z

I

I

I



Tensor momentu bezwładności można zapisać w postaci macierzy diagonalnej:

0

0

0

0

0

0

x

y

z

I

I

I





















(3.18)

9

Moment bezwładności posiada tyko składowe w odniesieniu do kierunków
głównych.

1

2

3

, ,

I I I



główne momenty bezwładności, a odpowiednie osie

nazywamy głównymi osiami bezwładności ciała (bryły sztywnej)

Dla jednorodnego ciała o symetrii sferycznej jest spełniona
zależność:

1

2

3

I

I

I

I







(3.19)

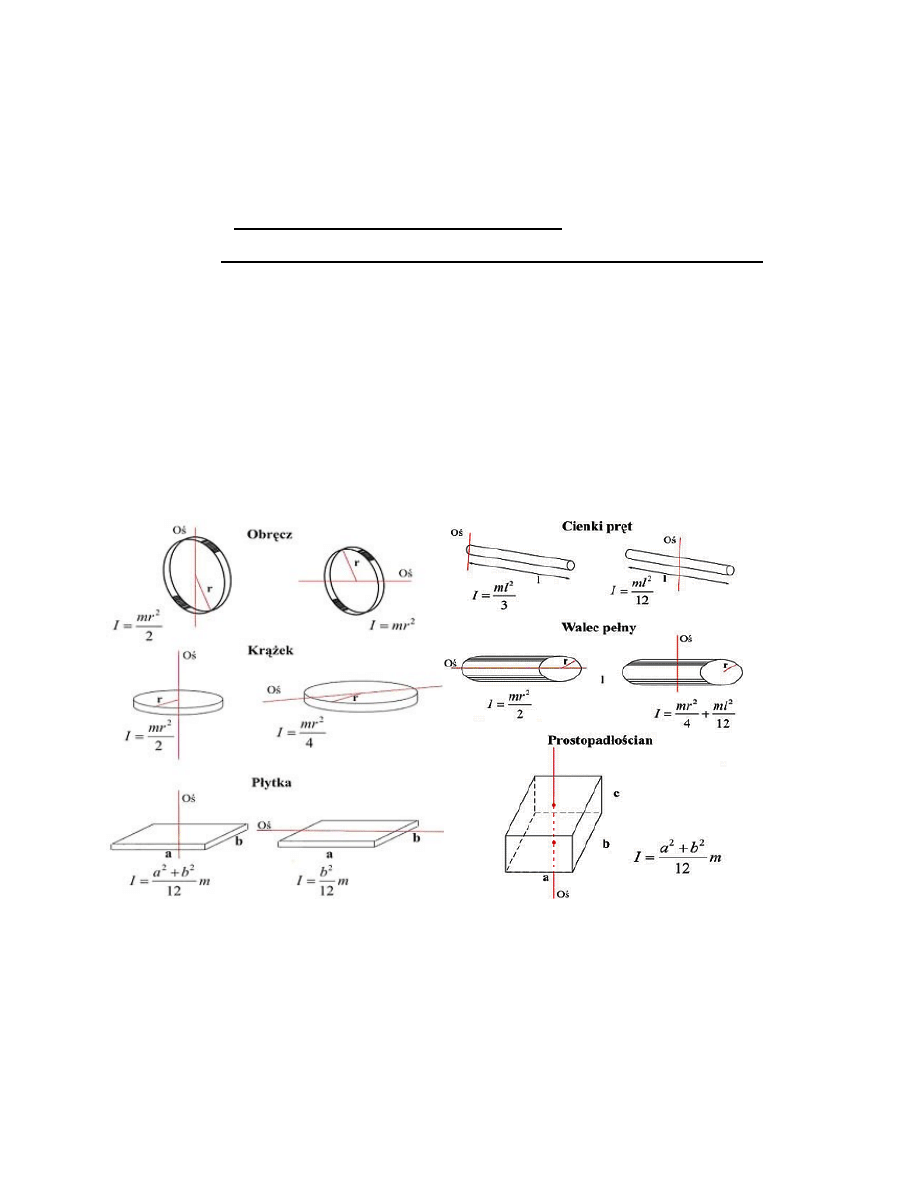
Rys. 3.5 Momenty bezwładności dla brył o prostych kształtach

geometrycznych

10

Twierdzenie o osiach równoległych Twierdzenie Steinera

2

xx

xx

n

I

I

a m





 

(3.20)

xx

I

moment bezwładności dowolnej bryły sztywnej wirującej dookoła osi

równoległej do osi x-ów i oddalonej o odcinek

a

od środka masy

(np. wzdłuż

osi y-ów),

0

xx

I

– moment bezwładności

liczony względem osi przechodzącej

przez środek masy.

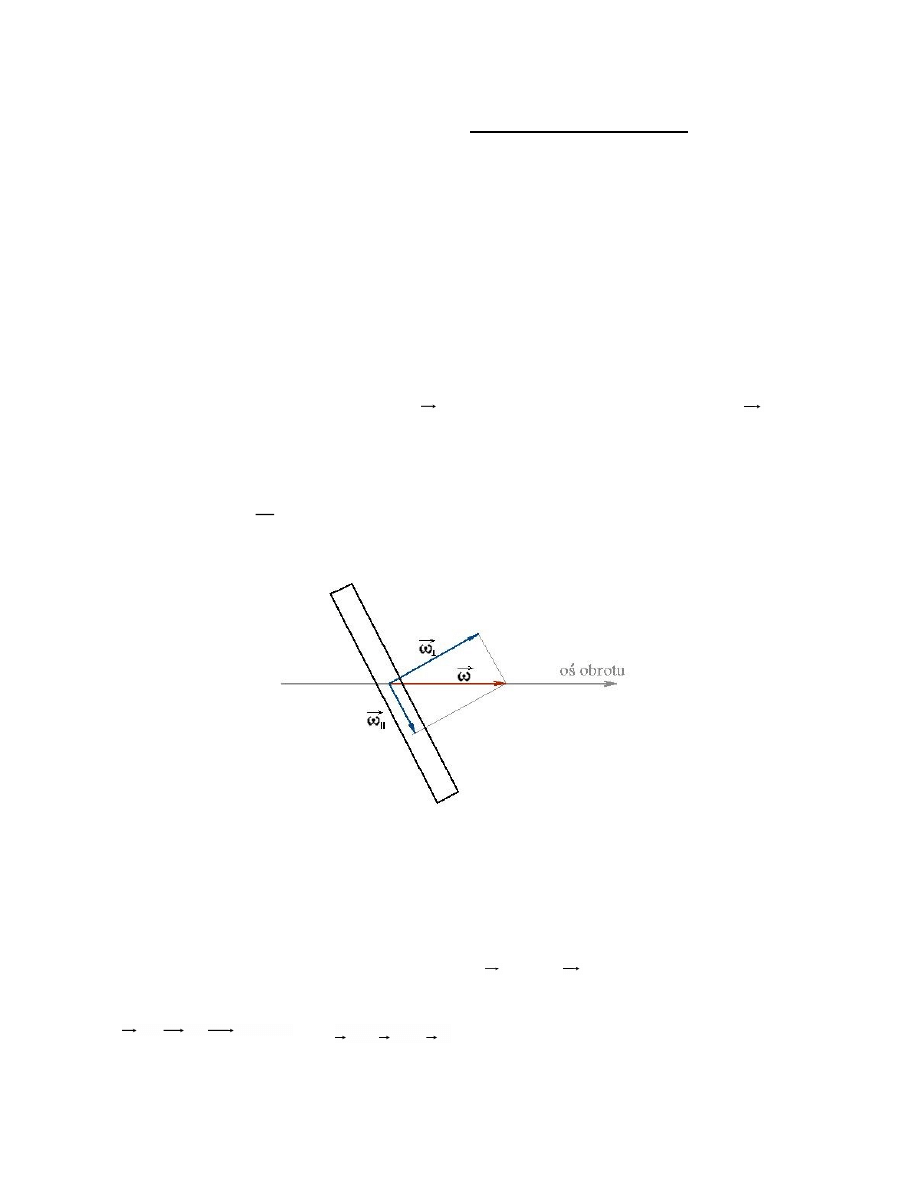
Przykład, w którym moment pędu

L

nie jest równoległy do osi obrotu



:

Obręcz obraca się wokół osi przechodzącej przez środek masy lecz tworzącej

kąt mniejszy od

2



z płaszczyzną obręczy

Rys. 3.6 Bryła sztywna z osią obrotu nie będącą jej osią symetrii

Każda oś przechodząca przez środek masy ciała nazywa się osią środkową.
Wybrana w przykładzie oś jest osią środkową lecz nie jest osią symetrii.

Szukamy relacji między kierunkiem

L

oraz



||

||

L L

L

  





 





11

Korzystamy ze związków:

||

|| ||

L

I

L

I







 





Znane są zależności :

2

2

||

2

mr

I

I

mr







Szukamy związku miedzy składowymi

L

i



. Musimy znaleźć relacje między

ich składowymi:

2

2

1

1

2

2

mr

L

I

L

I

mr















 









 

oznacza to, że te dwa wektory nie są do siebie równoległe gdyż stosunki ich
składowych nie są sobie równe



Energia kinetyczna ruchu obrotowego bryły sztywnej (energia rotacyjna)

Korzystamy ze znanego związku na energię kinetyczną:

2

2

1

1

(

)

2

2

k

n n

n

n

E

m v

m

r













(3.21)

lub w innym zapisie:

2

1

( )(

)

2

k

E

r

r dV











(3.22)

12

Przykład (B1):

Energia kinetyczna jednorodnej kuli:

|| z





równoległe do osi z

(0,0, )





Obliczamy :

2

2

2

2

2

2

2

(

)

(

) (

)

(

)

(

)

(

)

(

)

n

n

n

y n

z n

z n

x n

x n

y n

n

n

r

r

r

z

y

x

z

y

x

x

y



















































(B1.1)

Wstawiając równanie (B1.1) do (3.21) i (3.22) otrzymujemy:

2

2

2

1

(

)

2

k

n

n

n

E

m

x

y



 



(B1.2)

2

2

2

1

( )

(

)

2

k

E

r

x

y dV

 







(B1.3)

Korzystamy z wyrażenia na

zz

I

(

3

I

) dla jednorodnej kuli:

2

2

2

2

3

(

)

(

)

zz

I

I

r

z dV

x

y dV



















(B1.4)

2

2

3

(

)

zz

n

n

n

I

I

m x

y



 



(B1.5)

Wówczas równania (B1.2) oraz (B1.3) przyjmą postać.

2

3

1

2

k

E

I





(B1.6)

13

Ogólnie dla ciała o dowolnym kształcie energia kinetyczna jest zapisana w
postaci:

2

2

2

1

(

2

2

2

2

)

k

x

xx

y

yy

z

zz

x

y xy

x

z xz

y

z yz

E

I

I

I

I

I

I







 

 

 















(B1.7)

Dla układu odniesienia pokrywającego się

z osiami głównymi

wykorzystujemy zapis:

1

xx

I

I



,

2

yy

I

I



,

3

zz

I

I



0

xy

xz

yz

I

I

I







Wówczas wyrażenie (B1.7) na energię kinetyczną przyjmuje postać:

2

2

2

1 1

2

2

3

3

1

(

)

2

k

E

I

I

I













(B1.8)

RÓWNANIE RUCHU EULERA

Dla ruchu obrotowego punktu materialnego równanie ruchu ma postać:

dL

M

dt



(3.23)

gdzie

L



jest momentem pędu,

M



jest momentem sił zewnętrznych

Współczynnik bezwładności

ij

I

najwygodniej jest określić w układzie osi, które są

sztywno związane z obracającym się ciałem, czyli w układzie nieinercjalnym.
Korzystamy ze wzorów na przekształcenie przy transformacji wektora z układu
inercjalnego do nieinercjalnego.

14

(

)

iner

dL

dL

L

dt

dt





 

(3.24)

Prawa strona równania odnosi się do układu wirującego z prędkością kątową



,

Równanie ruchu bryły sztywnej pod wpływem działania momentu sił zewnętrznych
ma postać:

dL

L M

dt



  

(3.25)

Rozważamy przykład, gdzie układ odniesienia pokrywa się z osiami głównymi 1,
2, 3 wirującej bryły, składowe wektora momentu siły wynoszą

1

M

,

2

M

,

3

M

natomiast momentu pędu

1

L

,

2

L

,

3

L

i mogą być zapisane:

1

1 1

L

I





2

2

2

L

I





(3.26a-c)

3

3

3

L

I





Przy tak przyjętych założeniach, równanie wektorowe (3.25) zapisujemy w postaci
trzech równań skalarnych:

1

2 3

3 2

1

(

)

dL

L

L

M

dt











2

3 1

1 3

2

(

)

dL

L

L

M

dt











(3.27a-c)

2

1 2

2 1

3

(

)

dL

L

L

M

dt











15

Wykorzystując związki (3.26a-c) otrzymujemy:

1

1

2

3

3

2

1

(

)

d

I

I

I

M

dt

  







2

2

1 3

1

3

2

(

)

d

I

I

I

M

dt



 







(3.28a-c)

3

3

2 1

2

1

3

(

)

d

I

I

I

M

dt



 







Równania (3.28a-c) stanowią układ skalarnych równań Eulera. Stosuje się je do
rozwiązywania różnych zagadnień dotyczących ruchu bryły sztywnej.


Przykład (B2):


Precesja jednorodnej kuli swobodnej.
Dla kuli jednorodnej mamy :

1

2

3

I

I

I

I







, natomiast swobodnie wirująca

kula oznacza:

1

2

3

0

M

M

M







Przy tak przyjętych założeniach równania (3.28a-c) mają postać:

1

0

d

I

dt





2

0

d

I

dt





(B2.1a-c)

3

0

d

I

dt





Oznacza to, że:

1

const





,

16

2

const





,

3

const





,

czyli

const





– jest to szczególna cecha swobodnie wirującej kuli.

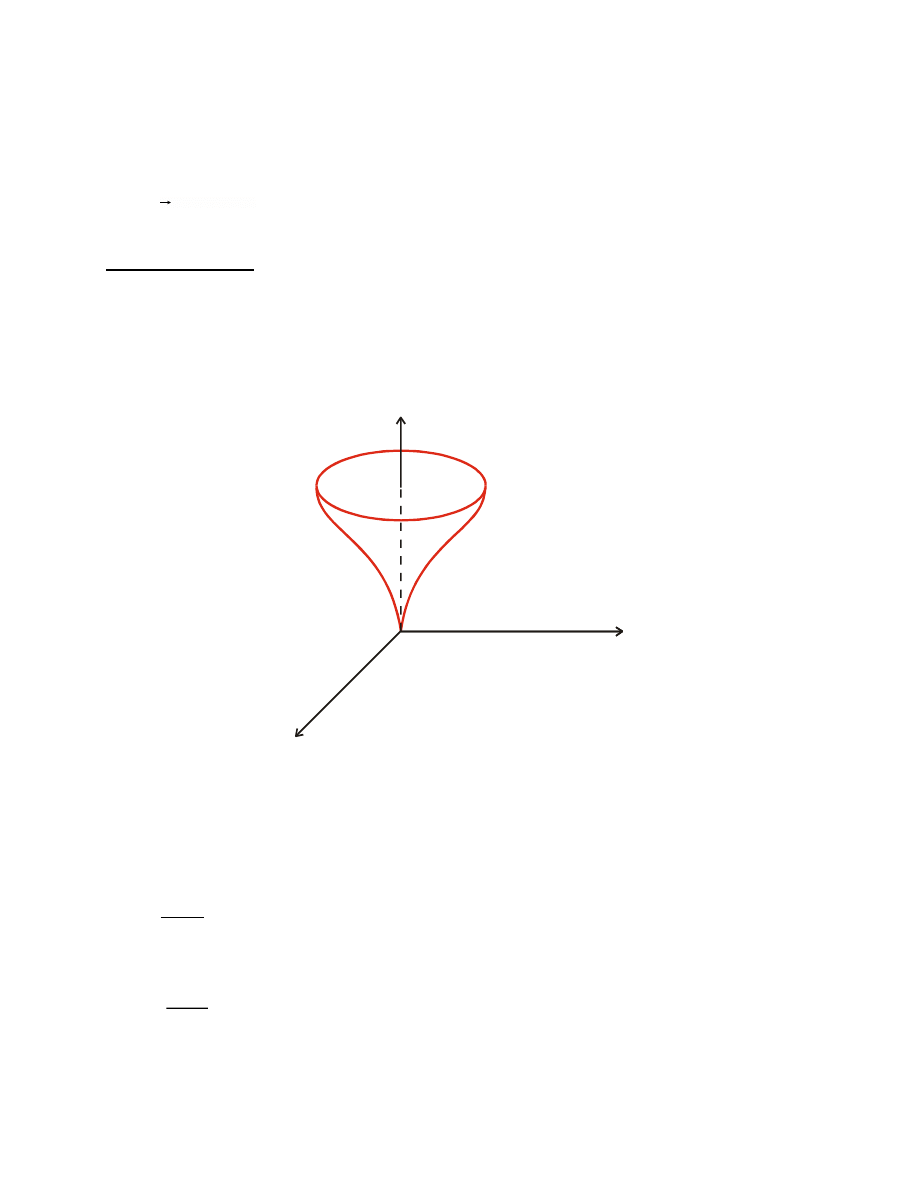
Przykład (B3.1):

Precesja swobodnego, symetrycznego bąka
Dla symetrycznego bąka mamy :

1

2

3

I

I

I





, natomiast swobodnie wirujący

bąk oznacza:

1

2

3

0

M

M

M







y

x

z

Skalarne równania (3.28a-c) mają postać:

3

3

0

d

I

const

dt











1

1

2

3

3

2

(

) 0

d

I

I

I

dt

  







(B3.1a-c)

17

2

2

1 3

1

3

(

) 0

d

I

I

I

dt



 







Definiujemy:

3

3

2

2

(

)

I

I

I





 

, które jest parametrem stałym dla tego zagadnienia.

Wykorzystując założenia rozważanego zagadnienia oraz po przekształceniu,
równania (B3.1b,c) mają postać:

1

2

0

d

dt

 

  

(B3.2a,b)

2

1

0

d

dt





  

Dla układu równań (B3.2a,b) rozwiązanie jest dane w następującej postaci:

 

1

cos

A

t







(B3.3a,b)

 

2

sin

A

t







Z uzyskanych rozwiązań na składowe wektora prędkości kątowej wynika, że:

Składowe

1



,

2



prostopadłe do osi symetrii (oś 3-cia) wirującego bąka

swobodnego obracają się ze stałą prędkością



, czyli wektor



wiruje

jednostajnie z prędkością



dookoła osi bąka.

WNIOSEK:
Bąk wirujący dookoła swej osi symetrii z prędkością kątową

3



, w

18

przestrzeni wolnej od działania momentu sił, wiruje kołysząc się jednorodnie z
prędkością



określoną wzorem:

3

3

2

2

(

)

I

I

I





 