Elementy animacji – sterowanie manipulatorem

1

Cel zadania

Wykształcenie umiej˛etno´sci korzystania z szablonów std::vector<> i std::list<>.

2

Opis zadania

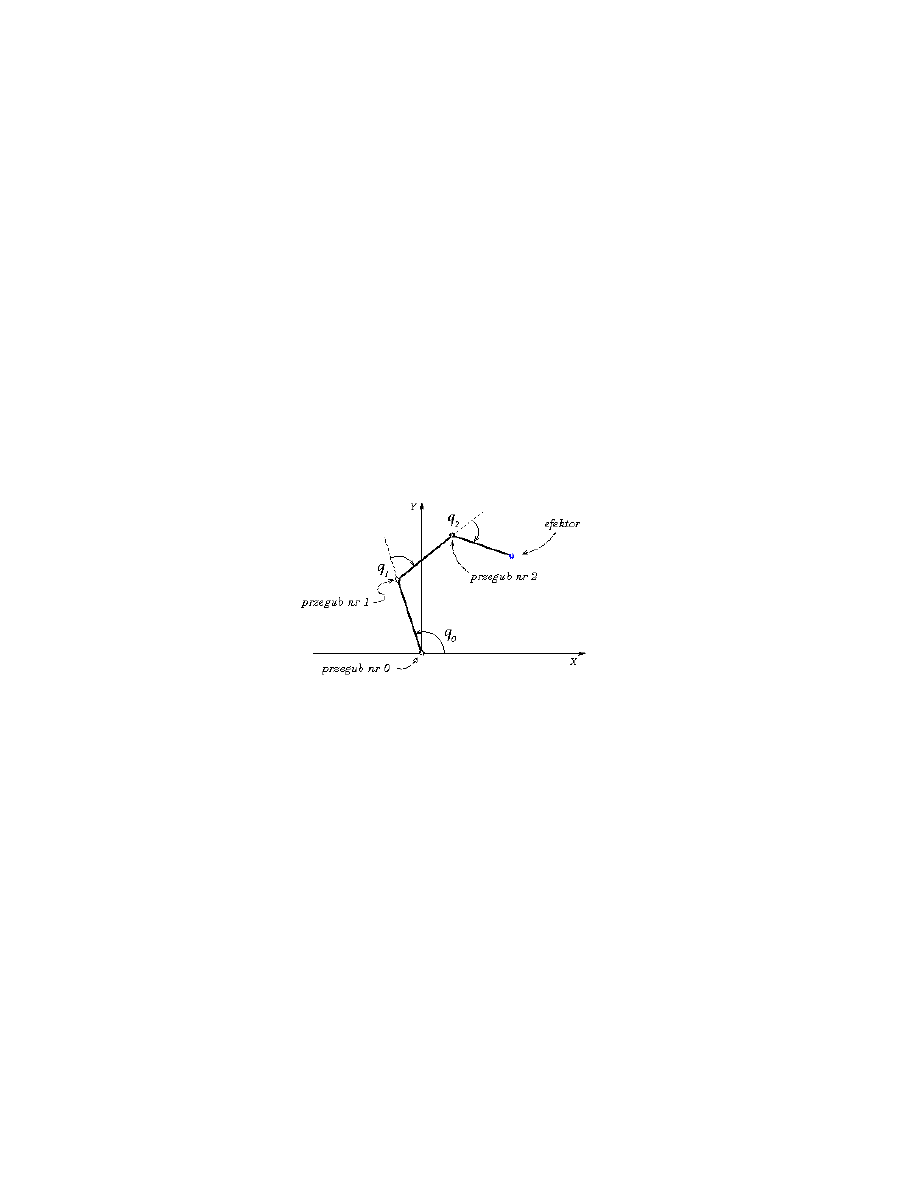
Nale˙zy napisa´c program, który umo˙zliwi wyznaczenie konfiguracji (postury) manipulatora. Za-
kładamy, ˙ze manipulator przedstawiony jest schematycznie w postaci łamanej (patrz rysunek
poni˙zej). Ka˙zdy z segmentów łamanej ma symbolizowa´c pojedynczy segment ramienia mani-
pulatora. Tak wi˛ec w ten sposób przedstawione zadanie sprowadza si˛e do wyznaczenia poło˙ze-
nia poszczególnych przegubów manipulatora i jego efektora. Postura manipulatora jest zadana
poprzez warto´sci k ˛

atów q

0

, q

1

, q

2

, . . . mi˛edzy jego kolejnymi segmentami ramienia. Dla uprosz-

czenia, postury manipulatora b˛ed ˛

a rozwa˙zane tylko w jednej płaszczy´znie X OY . Zakłada si˛e,

Rysunek 1: Szkielet manipulatora i zaznaczonymi k ˛

atami pozwalaj ˛

acymi sterowanie nachyle-

niem poszczególnych segmentów manipulatora.

˙ze ilo´s´c segmentów ramienia nie jest ograniczona (w uproszczonej wersji zadania – słabiej oce-

nianej – mo˙zna przyj ˛

a´c, ˙ze liczba ta jest stała i wynosi 3). Ponadto przyjmuje si˛e, ˙ze długo´s´c

wszystkich segmentów jest jednakowa. Warto´s´c parametru okre´slaj ˛

acego długo´s´c mo˙ze by´c

zmieniana w trakcie działania programu. Wyznaczone współrz˛edne maj ˛

a by´c zapisane do pliku

o ustalonej nazwie manipulator.dat.

3

Format zapisu współrz˛ednych

Przyjmuje si˛e, ˙ze współrz˛edne kolejnych przegubów zapisywane s ˛

a w pliku tekstowym. Ka˙zda

para współrz˛ednych zapisana zostaje w osobnej linii. W pierwszej linii zapisane s ˛

a zawsze

współrz˛edne pocz ˛

atku układu współrz˛ednych. Przykładowa posta´c pliku ze współrz˛ednymi

przedstawiona jest poni˙zej.

0

0

-2.4

10.23

7.3

20.14

15.1

16.23

18.21

23.19

1

4

Wizualizacja

Chc ˛

ac zobaczy´c, postur˛e manipulatora w ´srodowisku systemu Unix/Linux mo˙zna skorzysta´c z

programu gnuplot (znajduje si˛e on w ka˙zdej dystrybucji Linuksa). Program ten jest dost˛epny
równie˙z dla systemu MS Windows. Adres strony umo˙zliwiaj ˛

acej pobranie programu to:

http://sourceforge.net/project/showfiles.php?group_id=2055

4.1

Wersja uproszczona

W tej wersji zadania mo˙zna ograniczy´c si˛e do r˛ecznego uruchamiania programu gnuplot po
ka˙zdorazowym przeliczeniu współrz˛ednych przegubów. Program gnuplot uruchamiamy w
osobnym okienku terminala graficznego po wcze´sniejszym przej´sciu do podkatalogu, w którym
znajduje si˛e plik manipulator.dat.

4.1.1

Uruchomienie rysowania z linii polecenia

Przykładowy sposób uruchomienia programu:

echo "plot ’manipulator.dat’; pause 999" | gnuplot

Przerwanie działania programu realizujemy poprzez naci´sni˛ecie przycisków Ctrl-C, gdy focus
znajduje si˛e w okienku, w którym on został uruchomiony.

4.1.2

Uruchomienie rysowania z w trybie interakcjnym

Z programem gnuplot mo˙zna pracowa´c w trybie interakcyjny. Uruchamiamy go poleceniem
gnuplot

, nast˛epnie wydajemy polecenie plot ’manipulator.dat’. Wyj´scie z programu po-

przez polecenie exit.
Uwaga: W przypadku pracy w trybie interakcyjnym nie ma sensu ko´nczy´c jego działanie po jed-
nokrotnym narysowaniu łamanej. Po ponownym przeliczeniu współrz˛ednych mo˙zna powtórzy´c
polecenie plot ’manipulator.dat’ (program gnuplot pami˛eta histori˛e polece´n, przej´scie
do poprzedniego polecenia dokonuje si˛e poprzez naci´sni˛ecie strzałki w gór˛e), które spowoduje
zaktualizowanie poprzedniego rysunku. Przykład sesji z programem gnuplot.

diablo@jkowalsk> gnuplot

G N U P L O T

Version 4.0 patchlevel 0

last modified Thu Apr 15 14:44:22 CEST 2004

System: SunOS 5.10

...

gnuplot>

plot ’manipulator.dat’

gnuplot>

plot ’manipulator.dat’

...

gnuplot>

plot ’manipulator.dat’

gnuplot>

exit

diablo@jkowalsk> _

2

4.2

Wersja podstawowa

W tej wersji proponuje si˛e u˙zycie zewn˛etrznego modułu lacze_do_gnuplota. Znajduje si˛e
on kartotece ˜bk/edu/po/zad/z-manipulator1/przyklad_2D wraz z przykładem jego wy-
korzystania. Wspomniany moduł pozwala uruchomi´c program gnuplot z poziomu własnego
programu i przesła´c do niego polecenie wykonania rysunku. Ponadto umo˙zliwia na ustalenie
zakresu osi współrz˛ednych OX i OY .

5

Przykład działania programu

Niniejszy przykład nie obejmuje widoku okienka z rysunkiem wygenerowanym przez program
gnuplot

.

jkowalsk@panamint: rozwiazanie> ./manipulator

Aktualne wspolrzedne i parametry:

q0 =

105

Przegub_0: (0, 0)

q1 =

-70

Przegub_1: (-2.59, 9.66)

q2 =

-60

Przegub_2: (5.6, 15.4)

Efektor: (14.7, 11.2)

l = 10

Menu:

0 - Zmiana kata q0

1 - Zmiana kata q1

2 - Zmiana kata q2

z - zmiana ilosc segmentow

l - zmiana dlugosci segmentu

? - ponowne wyswietlenie menu

k - koniec programu

Twoj wybor?> 0

Wprowadz q0: 82

Aktualne wspolrzedne i parametry:

q0 =

82

Przegub_0: (0, 0)

q1 =

-70

Przegub_1: (1.39, 9.9)

q2 =

-60

Przegub_2: (11.2, 12)

Efektor: (17.9, 4.55)

l = 10

Menu:

0 - Zmiana kata q0

1 - Zmiana kata q1

2 - Zmiana kata q2

z - zmiana ilosc segmentow

l - zmiana dlugosci segmentu

? - ponowne wyswietlenie menu

k - koniec programu

3

Twoj wybor?> k

jkowalsk@panamint: rozwiazanie> _

6

Rozszerzenie (nieobowi ˛

azkowe)

W wersji rozszerzonej proponuje si˛e dodatkowe elementy:

• Animacj˛e zmiany pozycji danego segmentu. Chodzi o zapewnienie płynnej zmiany po-

zycji segmentu (tak jak to jest zrealizowane w dostarczonym przykładzie).

• Skonstruowanie trójwymiarowego rysunku manipulatora. Mo˙zna tego dokona´c wykorzy-

stuj ˛

ac moduł lacze_do_gnuplota. Przykład jego u˙zycia dla wersji 3D jest umieszczony

w kartotece

˜bk/edu/po/zad/z-manipulator1/przyklad_3D

Wspomniany moduł pozwala uruchomi´c program gnuplot z poziomu programu i prze-
sła´c do niego polecenie wykonania rysunku. W tej wersji programu zakłada si˛e, ˙ze kon-
strukcja manipulatora jest w programie zaszyta na sztywno (bez mo˙zliwo´sci zmiany ilo´sci
segmentów i ich długo´sci). Przykład wizualizacji manipulatora znajduje si˛e na zamiesz-

Rysunek 2: Przykład wizualizacji manipulatora zrealizowany w ramach studenckich zaj˛e´c la-
boratoryjnych

czonym rysunku.

7

Obliczanie współrz˛ednych przegubów

Wyznaczanie współrz˛ednych przegubów i efektora najłatwiej jest zrealizowa´c ł ˛

acz ˛

ac z ka˙zdym

z przegubów i efektorem lokalny układ współrz˛ednych. Przeguby znajduj ˛

a si˛e w pocz ˛

atku ta-

kich układów współrz˛ednych. Dzi˛eki temu i-ty przegub (oznaczony jako punkt P

i

) w swoim

lokalnym układzie współrz˛ednych X

i

OY

i

ma współrz˛edne P

i

i

= (0, 0). Zastosowane oznacze-

nie P

i

i

odzwierciedla fakt, ˙ze s ˛

a to współrz˛edne punktu P

i

w układzie współrz˛ednych i-tego

przegubu. To samo dotyczy efektora.

Naszym zadaniem jest wyliczenie współrz˛ednych poszczególnych punktów w układzie glo-

balnym X

O

OY

O

. W przedstawionym przykładzie mo˙zna to zrealizowa´c dokonuj ˛

ac nast˛epuj ˛

a-

4

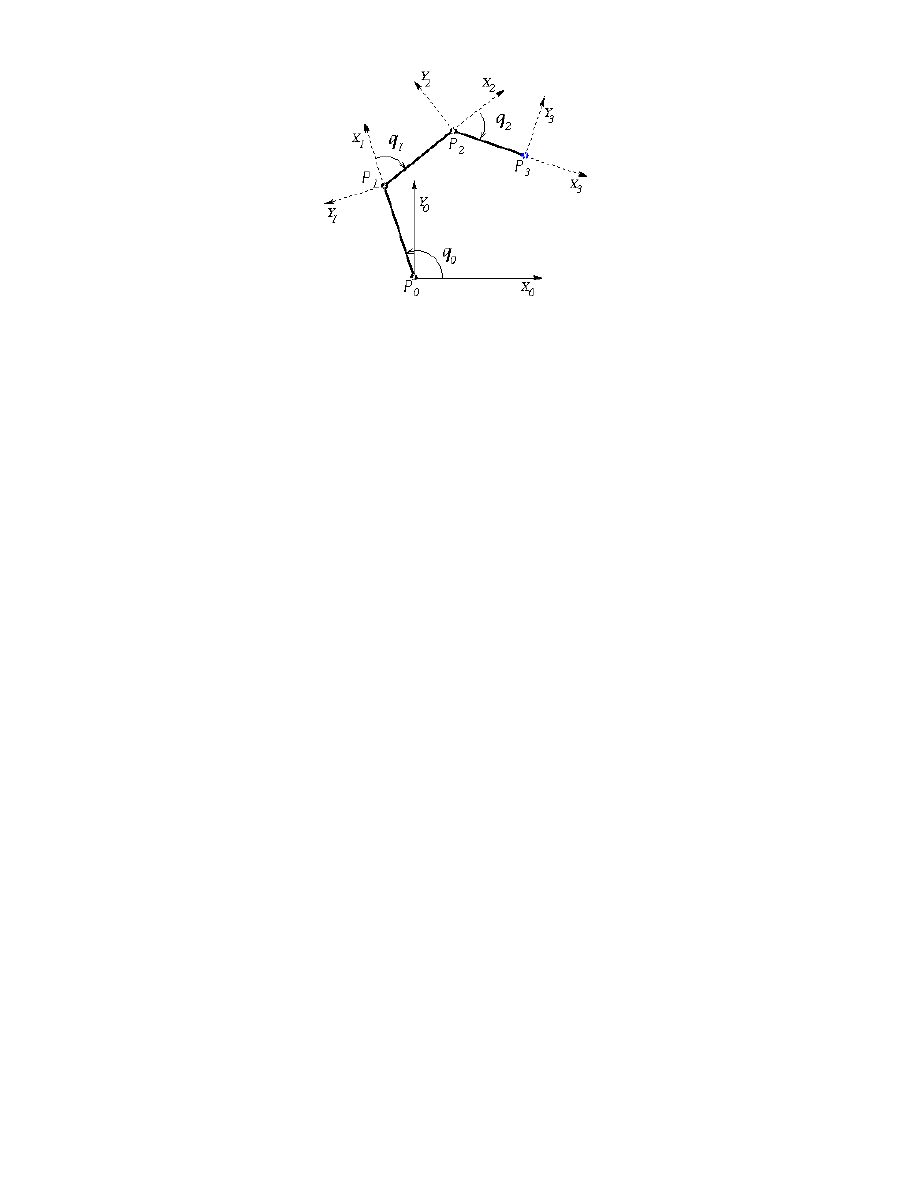
Rysunek 3: Lokalne układy współrz˛ednych zwi ˛

azane z ka˙zdym z przegubów.

cych transformacji:

P

0

0

= [0 0]

T

,

P

1

0

= R(q

0

) · (P

1

1

+ T ),

P

2

0

= R(q

0

) ·

³

R

(q

1

) · (P

2

2

+ T ) + T

´

,

P

3

0

= R(q

0

) ·

³

R

(q

1

) ·

³

R

(q

2

) · (P

3

3

+ T ) + T

´

+ T

´

.

(1)

Współrz˛edne punktu we wzorze przedstawionym powy˙zej reprezentowane s ˛

a jako macierz jed-

nokolumnowa. Natomiast T to wektor translacji reprezentowany przez macierz jednokolum-
now ˛

a [l 0]

T

, gdzie l jest długo´sci ˛

a segmentu. R(q

i

) jest macierz ˛

a rotacji w współczynnikach

postaci:

R

(q

i

) =

· cos q

i

− sin q

i

sin q

i

cos q

i

¸

(2)

Nale˙zy zauwa˙zy´c, ˙ze wyliczanie współrz˛ednych przegubu np. P

2

jest ci ˛

agiem transformacji

do układów współrz˛ednych kolejnych przegubów reprezentowanych przez punkty P

1

i P

0

. Po-

dobnie dla P

3

jest to ci ˛

ag transformacji do układów współrz˛ednych zwi ˛

azanych z przegubami

reprezentowanych przez punkty P

2

, P

1

oraz P

0

. Tak wi˛ec wyliczenie współrz˛ednych przegubu

P

3

mo˙zna byłoby rozpisa´c nast˛epuj ˛

aco:

P

3

2

= R(q

2

) · (P

3

3

+ T ),

P

3

1

= R(q

1

) · (P

3

2

+ T ),

P

3

0

= R(q

0

) · (P

3

1

+ T ).

(3)

To spostrze˙zenie nale˙zy wykorzysta´c przy implementacji rozwi ˛

azania zadania.

8

Materiały pomocnicze

Dodatkowe pomocnicze elementy ułatwiaj ˛

ace rozpocz˛ecie realizacj˛e zadania znale´z´c mo˙zna na

serwerze diablo lub panamint w katalogu ˜bk/edu/po/zad/z-manipulator1. W katalogu
tym znajduj ˛

a si˛e nast˛epuj ˛

ace podkatalogi i pliki:

˜bk/edu/po/zad/z-manipulator1/.

bin.diablo/manipulator

bin.panamint/manipulator

przyklad_2D/Makefile

5

przyklad_2D/src/start.cpp

przyklad_2D/src/lacze_do_gnuplota.cpp

przyklad_2D/inc/lacze_do_gnuplota.hh

przyklad_3D/Makefile

przyklad_3D/src/start.cpp

przyklad_3D/src/lacze_do_gnuplota.cpp

przyklad_3D/inc/lacze_do_gnuplota.hh

przyklad_3D/inc/prostopadloscian1.dat

przyklad_3D/inc/prostopadloscian2.dat

przyklad_3D/inc/prostopadloscian3.dat

bin.diablo/manipulator, bin.panamint/manipulator

S ˛

a to programy binarne. Stanowi ˛

a one

przykład realizacji programu, w wersji podstawowej (z dodatkiem animacji), który został skom-
pilowany odpowiednio na serwerze diablo i na serwerze panamint.

przyklad_2D

Katalog zawiera przykład u˙zycia modułu lacze_do_gnuplota pozwalaj ˛

acego

uruchomi´c program gnuplot z poziomu własnego programu i nawi ˛

aza´c z nim komunikacj˛e. W

przykładzie pokazane jest rysowanie z wykorzystaniem grafiki 2D.

przyklad_3D

Katalog zawiera przykład u˙zycia modułu lacze_do_gnuplota pozwalaj ˛

acego

uruchomi´c program gnuplot z poziomu własnego programu i nawi ˛

aza´c z nim komunikacj˛e. W

przykładzie pokazane jest rysowanie z wykorzystaniem grafiki 3D.

6