8.
Analiza danych przestrzennych
Treścią niniejszego rozdziału będą analizy danych przestrzennych. Analiza, ogólnie
mówiąc, jest procesem poszukiwania (wydobywania) informacji ukrytej w zbiorze danych.
Najprostszym przypadkiem analizy danych przestrzennych jest wzrokowa ocena ich
rozmieszczenia na podstawie zobrazowania w postaci tradycyjnej mapy. W opisanym
przypadku analizy dokonuje człowiek patrząc na mapę. W systemach informacji
przestrzennej zadanie to wykonuje komputer przy pomocy odpowiedniego oprogramowania
na podstawie zbioru danych, który zgodnie z przyjętym modelem opisuje rzeczywistość.
Analiza realizowana jest z zastosowaniem metod matematycznych, które stają się
„wzrokiem” komputera pozwalającym wyciągać wnioski. Wzrok komputera zbudowany jest
z elementarnych procedur matematycznych dostarczających odpowiedzi na najprostsze
pytania związane z relacjami obiektów w przestrzeni typu: czy odcinki się przecinają, po
której stronie odcinka leży punkt, czy punkt leży wewnątrz wielokąta itp.. W rezultacie
wymienione elementarne procedury po wykonaniu stosownych obliczeń dają odpowiedzi na
postawione pytania. Początkiem każdej analizy jest wybór danych, na podstawie których w
dalszym jej etapie wykonane zostaną odpowiednie działania prowadzące do otrzymania
wyniku. Podejmowane w trakcie analizy działania mogą dotyczyć:
¾
geometrii obiektów,
¾
atrybutów opisowych,
¾
powiązania geometrii z atrybutami opisowymi.
Wynikiem analizy może być jedynie wybranie interesującej nas (spełniającej warunki
zadania) grupy obiektów, utworzenie nowych obiektów lub modyfikacja atrybutów obiektów
istniejących.
W dalszej części niniejszego rozdziału przedstawimy kilka najistotniejszych analiz
istotnych z punktu widzenia systemu informacji o terenie.
8.1. Wyszukiwanie
W zagadnieniu wyszukiwania obiektów możemy wyróżnić dwa podstawowe typy zadań.
Wyodrębnienie typów wynika z charakteru stawianych warunków.
• Pierwszą (najprostszą) grupę zadań stanowi wyszukiwanie obiektów spełniających
jedynie warunki dotyczące atrybutów opisowych. Jako przykład takiego zadania możemy
uznać znalezienie wszystkich budynków o określonej funkcji i liczbie kondygnacji. W
przypadku takiego wyszukiwania odpowiedź czy obiekt spełnia warunki czy nie jest
informacja zapisana w samym obiekcie bez konieczności analizowania związku z innymi
obiektami bazy danych.
Waldemar Izdebski - Wykłady z przedmiotu SIT 70
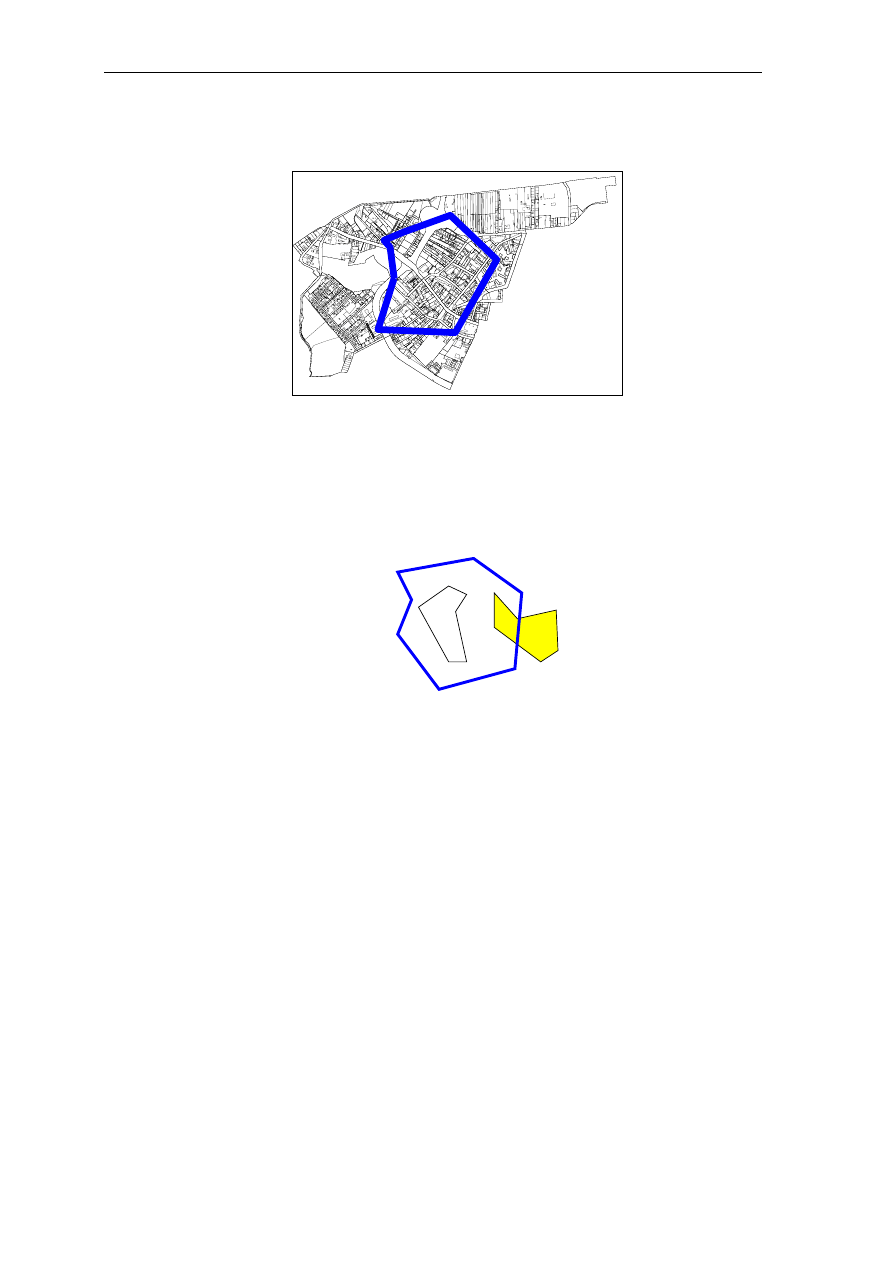
• Drugą grupę zadań stanowią sytuacje kiedy wśród postawionych warunków koniecznych
do wybrania obiektu znajdują się warunki przestrzenne np. konieczność położenia obiektu
wewnątrz zadanego wielokąta.
Rys. 8.1. Ilustracja wyszukiwania obiektów spełniających określone warunki
Pełne możliwości wyszukiwania uzyskuje się więc łącząc oba z wymienionych typów
wyszukiwania uzyskując wyszukiwanie z zastosowaniem warunków przestrzenno-opisowych.
Przy badaniu położenia obiektu wewnątrz obszaru warunek może być postawiony tak, że
cały badany obiekt musi się mieścić w dozwolonym obszarze lub wystarczające jest aby tylko
jego cześć wchodziła do zadanego obszaru.
A
B
Rys. 8.2. Ilustracja położenia obiektów względem obszaru zapytań.
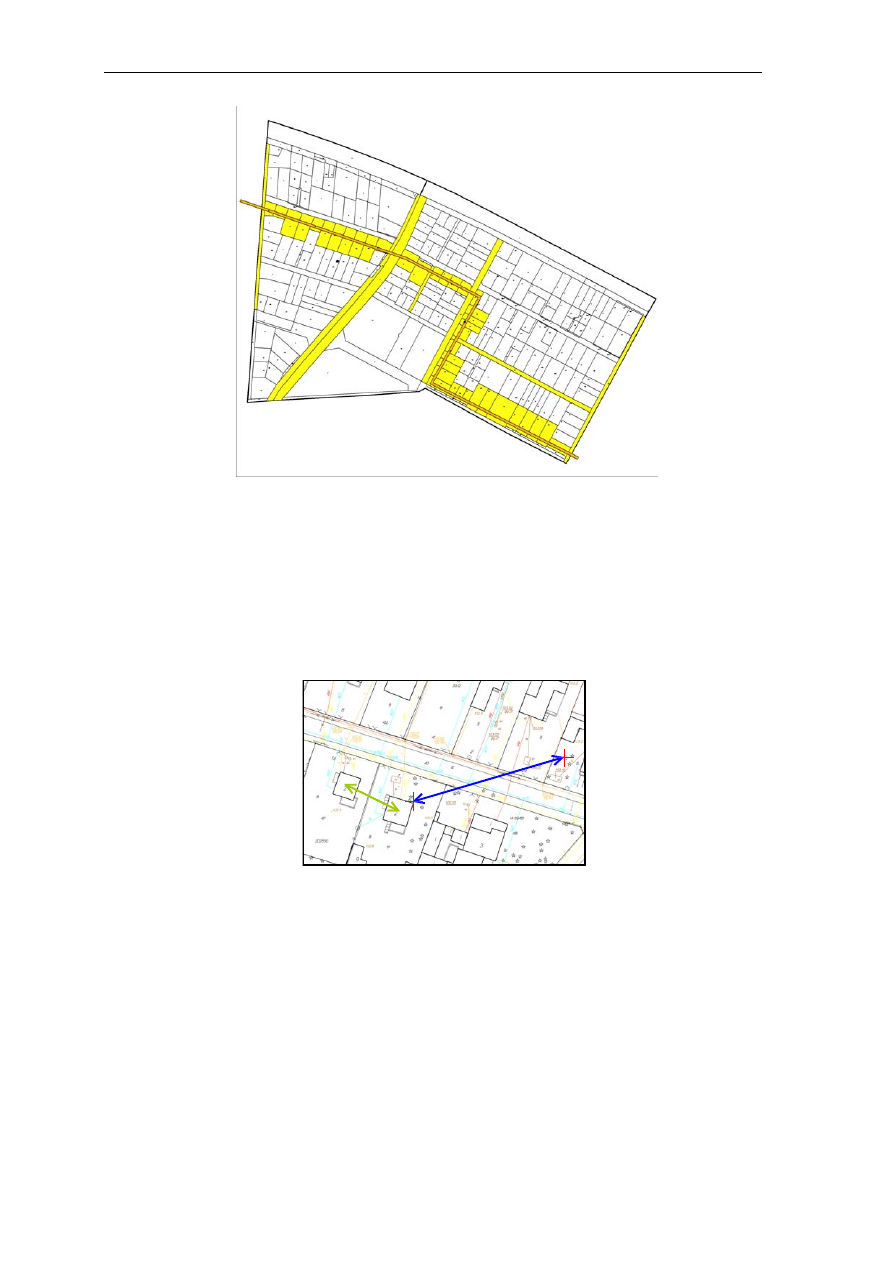
Czasami wręcz wymagamy aby wybierane obiekty były przecinane przez granice obszaru
lub pewien zadany obiekt liniowy. Szczególnie jest to istotne przy planowaniu inwestycji
liniowych w kontekście znalezienia właścicieli działek, których inwestycja będzie dotyczyła.
Waldemar Izdebski - Wykłady z przedmiotu SIT 71
Rys. 8.3. Ilustracja wybierania obiektów powierzchniowych przeciętych obiektem liniowym
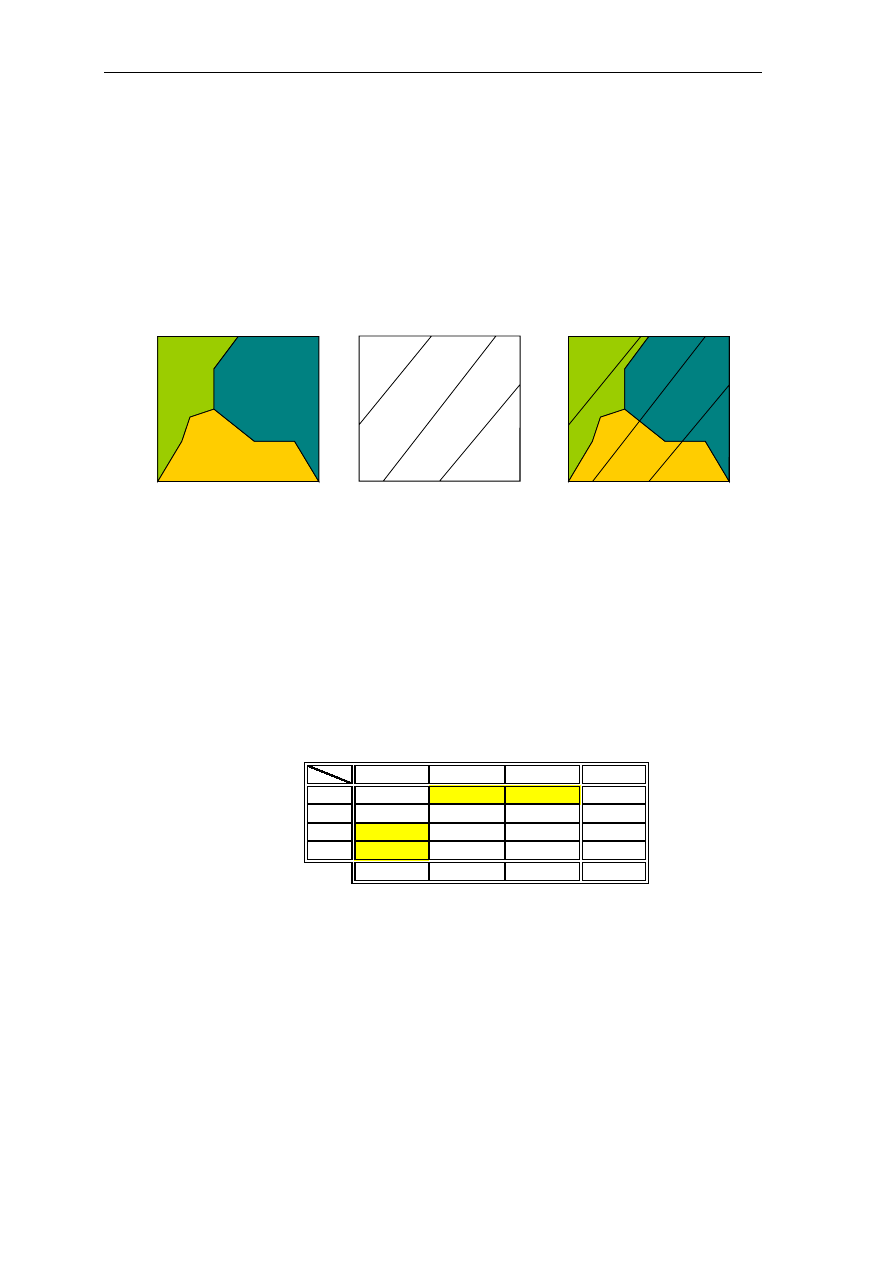
8.2. Pomiary wielkości geometrycznych
Pomiary wielkości geometrycznych są najprostszym przypadkiem analizy danych
przestrzennych. Na podstawie wskazywanych punktów pomiarowych obliczane są wartości
mierzonej wielkości (kąta, odległości, domiaru, itp.). Zadanie najczęściej realizowane jest w
trybie interaktywnym, podczas prezentacji graficznej gdzie operator dokonuje wskazania
punktów kursorem graficznym.
Rys. 8.4. Ilustracja pomiaru wielkości geometrycznych
Wskazanie graficzne punktu służy do znalezienia w bazie danych właściwego punktu i
wykorzystanie do obliczenia wartości jego współrzędnych. Powyższy rysunek ilustruje
pomiar odległości od narożnika budynku do drzewa. W przypadku dużego zagęszczenia
punktów w okolicy wskazanej kursorem mogą nastąpić problemy z wyborem właściwych
punktów z tego też względu w takich sytuacjach należy dokonywać odpowiedniego
powiększenia aby nie było wątpliwości co do identyfikacji punktów.
Innym wariantem pomiaru jest sytuacja kiedy nie daje się jednoznacznie wskazać
konkretnego punktu a możemy jedynie określić w sposób przybliżony lokalizację punktu
używając kursora. Sytuacja taka jest zbliżona do pomiaru na mapie klasycznej, gdzie punkt
przyłożenia przymiaru (tak jak i właściwe ustawienie kursora) jest sprawą subiektywnej
Waldemar Izdebski - Wykłady z przedmiotu SIT 72
oceny mierzącego. Sytuację przedstawiono na powyższym rysunku pokazując pomiar
odległości między wzrokowo (subiektywnie) wyznaczonymi środkami budynków.
8.3. Nakładanie obszarów
Zadanie niniejsze często bywa również nazywane nakładaniem warstw czy
przecięciem warstw. Jest dosyć powszechnie wykorzystywane w systemach informacji o
terenie do różnych analiz. Efektem działania funkcji jest utworzenie nowej grupy obiektów
będących częścią wspólną obiektów wchodzących do zbiorów P i Q.
A
B
C
1
2
3
4
A
B
C
1
2
3
4
+
=
P
Q
Rys. 8.5. Ilustracja nakładania obszarów
Innym efektem działania funkcji może być jedynie modyfikacja atrybutów
poszczególnych obszarów. Jeśli przyjmiemy, że zbiór P zawiera kontury klasyfikacji gruntów
a zbiór Q działki ewidencyjne to realizując zadanie nałożenia obszarów uzyskujemy tzw.
rozliczenie użytków w działkach. Z punktu widzenia tego właśnie zadania wcale nie jest
konieczne aby tworzyć nowe obiekty powierzchniowe. Istotne jest jedynie obliczenie jakie
powierzchnie poszczególnych konturów znajdują się w poszczególnych działkach.
A
B
C
Suma
1
1,1250
1,1250
2
1,7018
1,0745
1,3486
4,1249
3
2,7747
2,4754
5,2501
4
0,8739
0,6261
1,5000
2,8268
4,7231
4,4501 12,0000
Na analogicznej zasadzie można dokonać analizy obszarów zabudowy na działkach
ewidencyjnych nakładając działki na budynki.
8.4. Agregacja
Funkcja agregacji łączy ze sobą obiekty charakteryzujące się równością wybranych
atrybutów tworząc obszary po zewnętrznym obrysie przylegających do siebie obiektów.
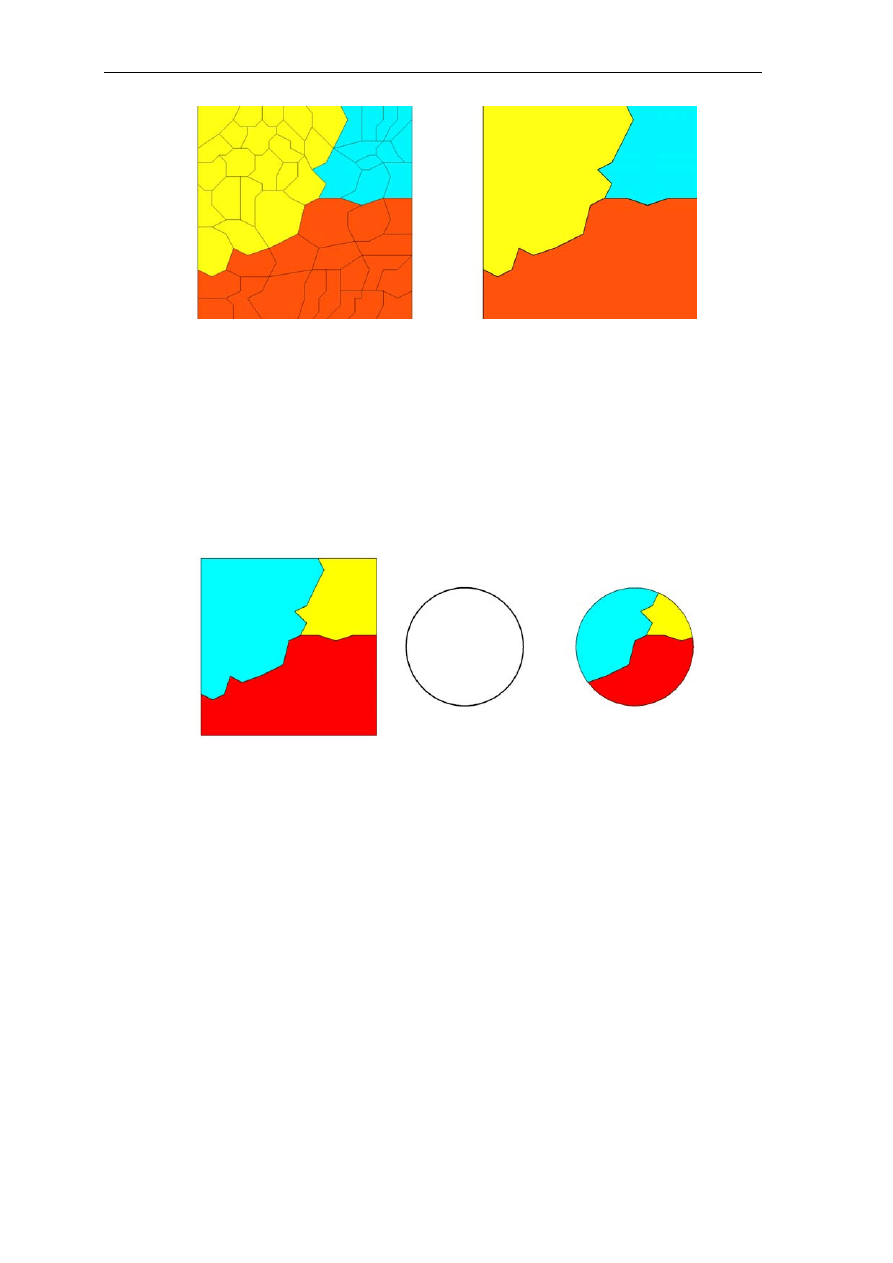
Waldemar Izdebski - Wykłady z przedmiotu SIT 73
Rys. 8.6. Ilustracja agregacji
Przykładem wykorzystania funkcji może być automatyczne utworzenie granic
obrębów na podstawie działek posiadających wpis o numerze obrębu z którego pochodzą.
Analogicznie możemy utworzyć granicę gminy na podstawie obrębów itp..
8.5. Wycinanie
Funkcja wycinania powoduje wybranie (przycięcie) wskazanej treści przez obiekt
ograniczający. Schematycznie działanie wycinania przedstawiono na poniższym rysunku.
+
=
Rys. 8.7. Ilustracja wycinania
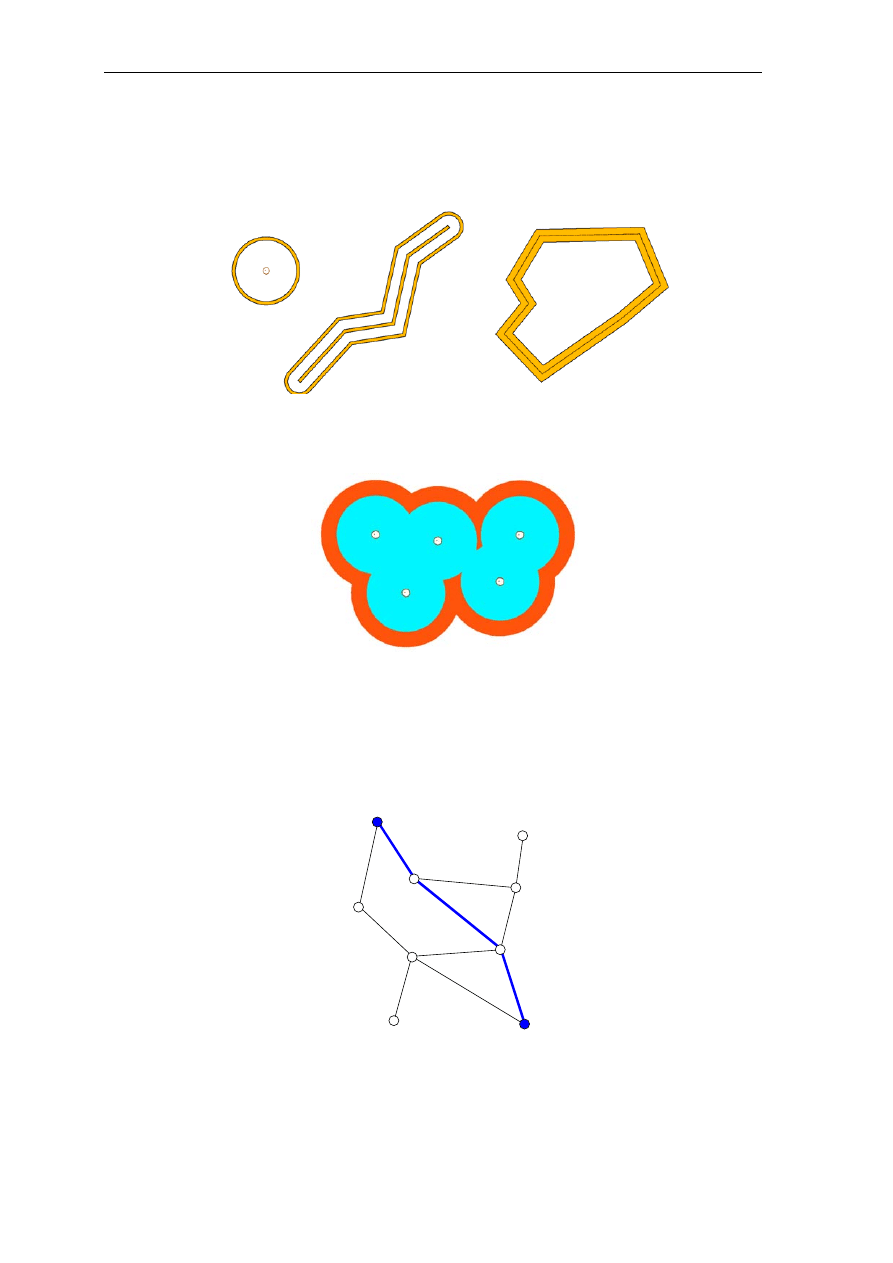
Waldemar Izdebski - Wykłady z przedmiotu SIT 74
8.6. Tworzenie stref buforowych
Funkcja służy do wyznaczenia stref buforowych wokół wskazanych obiektów. Strefy
buforowe mogą być tworzone wokół punktów, linii i obszarów.
Rys. 8.8. Ilustracja stref buforowych
Strefy buforowe można również tworzyć wokół grupy obiektów agregując ze sobą
powstałe wcześniej strefy indywidualne.
Rys. 8.9. Ilustracja strefy buforowej wokół grupy punktów
8.7. Analizy sieciowe
Analizy sieciowe to zestaw funkcji działających na obiektach liniowych
umożliwiających określenie np. najkrótszej drogi pomiędzy dwoma punktami czy
optymalizacja trasy przejazdu pomiędzy wieloma punktami.
A
B
Rys. 8.10. Ilustracja analizy sieciowej
Waldemar Izdebski - Wykłady z przedmiotu SIT 75
9.
Podstawowe narzędzia matematyczne analiz przestrzennych
Niniejszy rozdział służy ogólnemu przedstawieniu metod matematycznych
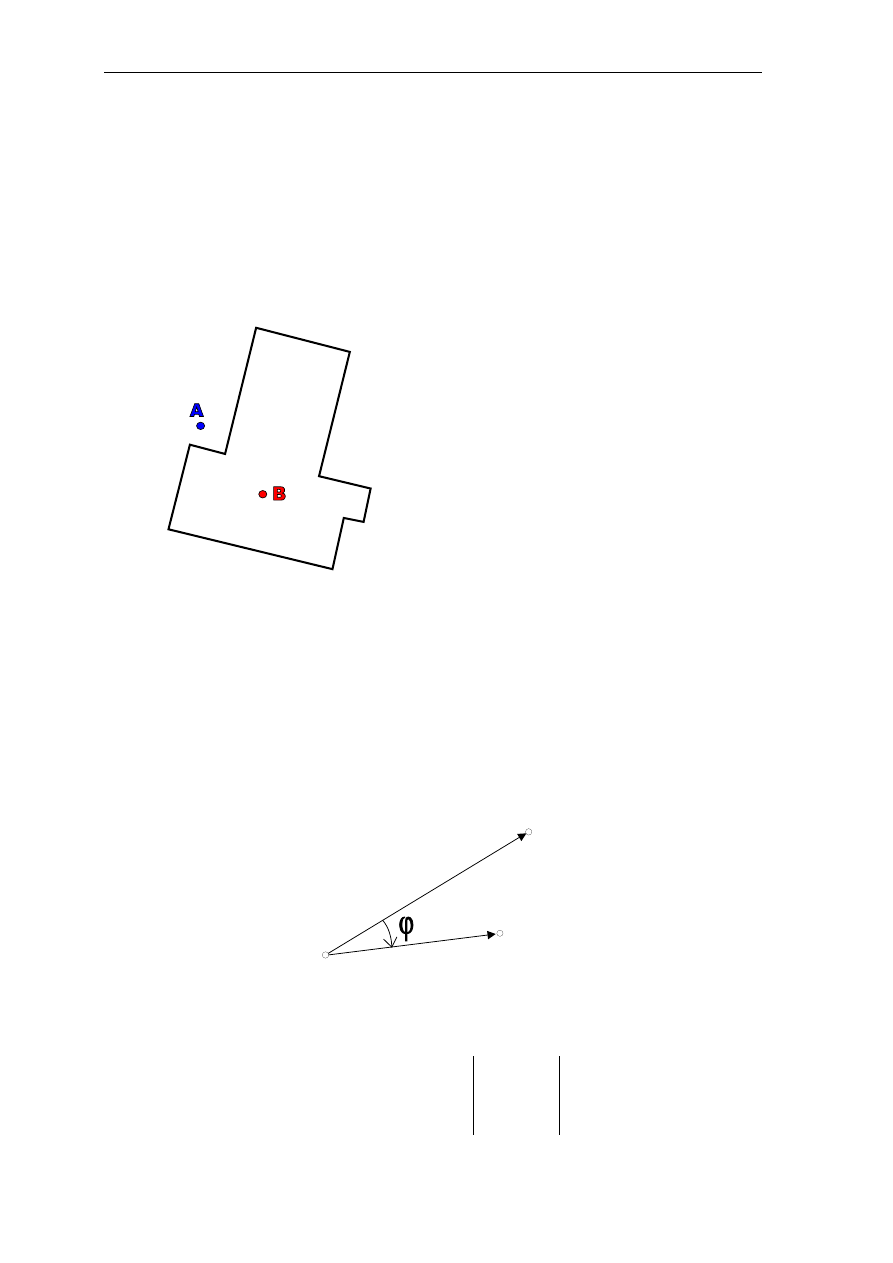
wykorzystywanych w zagadnieniu analizy przestrzennej. Człowiek patrzący na dane
przestrzenne przedstawione na mapie (w postaci graficznej) bezbłędnie ocenia położenie
punktów względem wielokąta. Przykład rysunku poniżej, na którym bez problemów
stwierdzamy, że punkt A leży na zewnątrz a punkt B wewnątrz wielokąta Q. W przypadku
kiedy korzystamy z danych w postaci współrzędnych (wykaz współrzędnych obok rysunku),
odpowiedzi nie są takie proste i wymagają wielu operacji obliczeniowych i logicznych.
Punkty wielokąta
Nr ---------X-- ---------Y--
1 5613399.248 4661287.044
2 5613395.479 4661302.143
3 5613375.501 4661297.209
4 5613373.441 4661305.470
5 5613368.028 4661304.187
6 5613368.702 4661301.214
7 5613360.444 4661299.332
8 5613366.870 4661273.000
9 5613380.442 4661276.294
10..5613378.991 4661282.115
Punkty do sprawdzenia
Nr ---------X-- ---------Y--
A 5613383.425 4661277.999
B 5613372.326 4661288.302
Poniżej przedstawiono ogólny zarys podstawowych operacji w analizie danych
przestrzennych tj. badania położenia punktu względem odcinka, wyznaczania punktu
przecięcia się dwóch odcinków oraz badaniu położenia punktu względem wielokąta.
Szczegółowe przedstawienie tematyki można znaleźć w pracy [Izdebski 1999].
9.1.1. Wyznaczenie położenia punktu względem odcinka
Pierwszym z analizowanych zagadnień będzie sprawdzenie, po której stronie danego
odcinka leży punkt posiadający określone współrzędne XY. Ilustrację zadania przedstawia
poniższy rysunek.
A
B
P
Rys. 9.1. Ilustracja zadania położenia punktu względem odcinka
Jednym ze sposobów rozwiązania postawionego zadania jest obliczenie wyznacznika
postaci:
det(A,B,P) =
1
1
1
P
P
B
B
A
A
Y
X
Y
X
Y
X