R ´

OWNANIA R ´

O ˙

ZNICZKOWE ZWYCZAJNE, SEMESTR LETNI 2012/2013

WYK LAD I ´

CWICZENIA W TYGODNIU ZACZYNAJA

¸ CYM SIE

¸ 11.03.2013

Wyk lad

1. Doko´

nczenie rozwi¸

azania r´

ownania zupe lnego metod¸

a czynnika ca lkuj¸

acego.

2. Sprowadzenie r´

ownania r´

o˙zniczkowego zwyczajnego stopnia n do uk ladu n-r´

owna´

n zwyczajnych stopnia

pierwszego, y

′

= F (t, y), gdzie y = ⃗

y = (y

1

, . . . , y

n

).

3. Twierdzenie Peano z dowodem metod¸

a lamanych Eulera. Wykorzystanie Twierdzenia Arzeli-Ascoli’ego

(bez dowodu).

4. Przyk lad zagadnienia pocz¸

atkowego y

′

= y

β

, y(t

0

) = 0, 0 < β < 1, z niejednoznacznym rozwi¸

azaniem.

5. Je´

sli czas pozwoli, Twierdzenie Picarda - Lindel¨

ofa z dowodem. Wykorzystanie Twierdzenia Banacha

o odwzorowaniu zw¸e˙zaj¸

acym (bez dowodu).

Sugerowane zadania do przerobienia na ´

cwiczeniach

(niekt´

ore zadania mog¸

a by´

c opuszczone, inne za´

s dodane)

1. Czy r´

ownanie (3xy + y

2

)dx + (x

2

+ xy)dy = 0 jest zupe lne?

2. Rozwi¸

aza´

c r´

ownanie r´

o˙zniczkowe 2x + y

2

+ 2xyy

′

= 0.

3. Znale´

z´

c czynnik ca lkuj¸

acy dla r´

ownania (3xy + y

2

)dx + (x

2

+ xy)dy = 0 i rozwi¸

aza´

c to r´

ownanie.

4. Znale´

z´

c czynnik ca lkuj¸

acy dla r´

ownania (2xy + x

2

y +

1
3

y

3

)dx + (x

2

+ y

2

)dy = 0.

5. Znale´

z´

c rozwi¸

azanie zagadnienia pocz¸

atkowego

{

(3x

2

+ 6xy

2

)dx + (6x

2

y + y

3

)dy = 0

y(2) = 1

6. Rozwi¸

aza´

c r´

ownanie

dy

dt

=

−r

(

1

−

y

A

) (

1

−

y

B

)

, gdzie r > 0, A, B (A < B) s¸

a danymi sta lymi.

R´

ownanie to r´

ownie˙z opisuje zachowanie si¸

e populacji w pewnych warunkach.

7. Sprowadzi´

c r´

ownanie Bernoulliego y

′

+ p(x)y = q(x)y

n

, (n

̸= 1) do postaci r´ownania liniowego bior¸ac

zamian¸

e zmiennej zale˙znej z = y

1

−n

.

8. Rozwi¸

aza´

c r´

ownanie y

′

− 2xy = 2x

3

y

2

.

9. Rozwi¸

aza´

c problem pocz¸

atkowy y

′

= y

2

, y(0) = 1, oraz wyznaczy´

c przedzia l na kt´

orym rozwi¸

azanie

istnieje.

10. Przeanalizowa´

c rozwi¸

azanie problemu y

′

= y

1/3

, y(0) = 0, szczeg´

olnie jednoznaczno´

s´

c.

Zadania domowe

1. Sprawdzi´

c czy r´

ownanie (2x + 3) + (2y

− 2)y

′

= 0 jest zupe lne. Je´

sli tak, znale´

z´

c rozwi¸

azanie og´

olne.

2. Sprawdzi´

c czy r´

ownanie (3x

2

− 2xy + 2)dx + (6y

2

− x

2

+ 3)dy = 0 jest zupe lne. Je´

sli tak, znale´

z´

c

rozwi¸

azanie og´

olne.

3. Sprawdzi´

c czy r´

ownanie (e

x

sin y + 3y)dx

− (3x − e

x

sin y)dy = 0 jest zupe lne.

Je´

sli tak, znale´

z´

c

rozwi¸

azanie og´

olne.

4. Rozwi¸

aza´

c zagadnienie pocz¸

atkowe (2x

− y)dx + (2y − x)dy = 0, y(1) = 3.

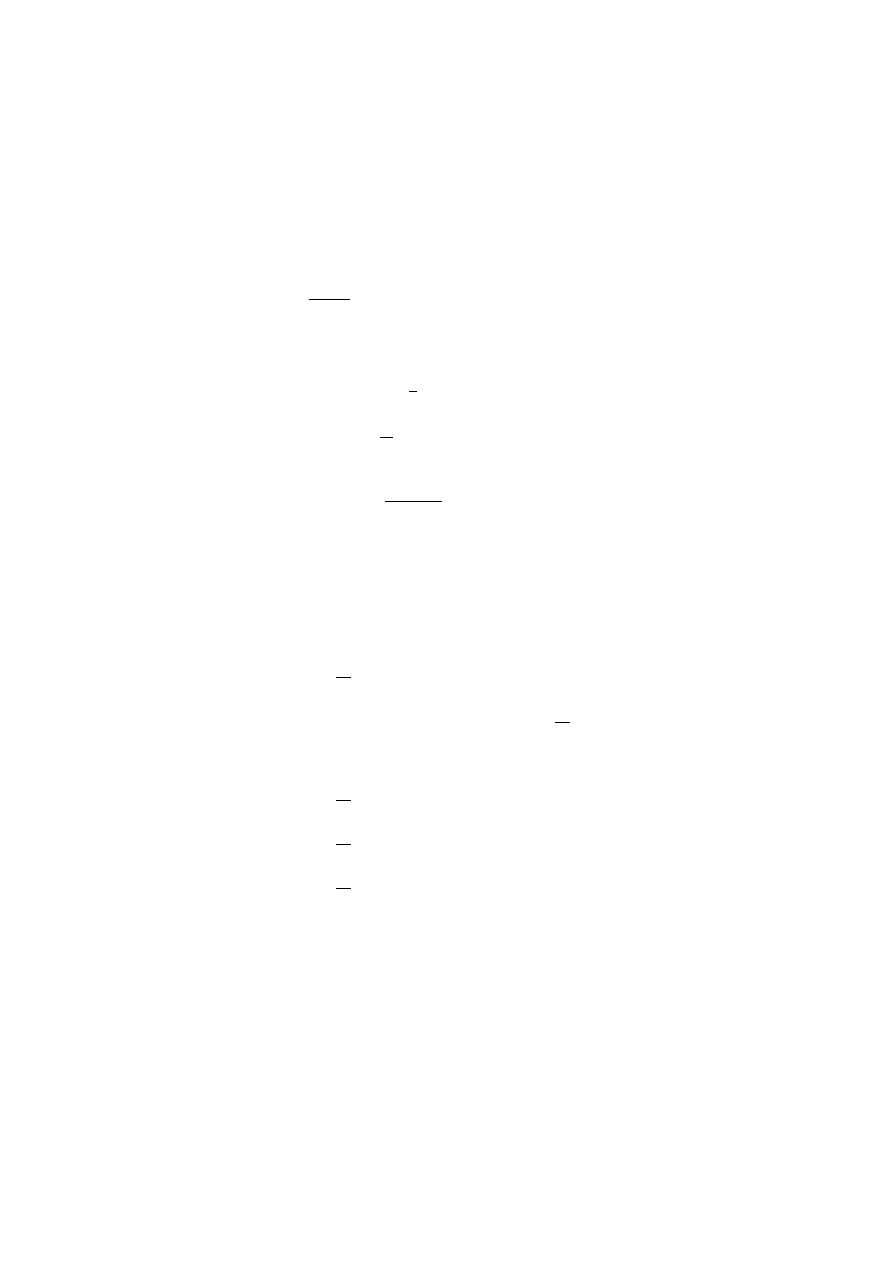
5. Znale´

z´

c warto´

s´

c b dla kt´

orej r´

ownanie (xy

2

+ bx

2

t) dx + (x + y)x

2

dy = 0 jest zupe lne.

6. Udowodni´

c, ˙ze r´

ownanie o zmiennych rozdzielonych M (x) + N (y)y

′

= 0 jest zupe lne.

7. Sprawdzi´

c czy µ(x, y) = 1/xy

3

jest czynnikiem ca lkuj¸

acym dla r´

ownania x

2

y

3

+ x(1 + y

2

)y

′

= 0. Je´

sli

tak, rozwi¸

aza´

c to r´

ownanie.

8. Sprawdzi´

c czy µ(x, y) = y jest czynnikiem ca lkuj¸

acym dla r´

ownania y dx + (2x

− ye

y

) dy = 0. Je´

sli

tak, rozwi¸

aza´

c to r´

ownanie.

9. Niech b¸

edzie dane r´

ownanie (

√

x

2

− y + 2x)dx − dy = 0. Znale´z´c czynnik ca lkuj¸acy dla tego r´ownania

je´

sli wiadome jest, ˙ze jest w postaci µ = µ(ξ(x, y)), gdzie ξ(x, y) = x

2

− y.

10. Znale´

z´

c czynnik ca lkuj¸

acy dla r´

ownania (3x

2

y + 2xy + y

3

) dx + (x

2

+ y

2

) dy = 0.

11. Znale´

z´

c czynnik ca lkuj¸

acy dla r´

ownania dx + (

x

y

− sin y) dy = 0.

12. Rozwi¸

aza´

c zagadnienie pocz¸

atkowe y

′

=

−

4t

y

, y(0) = y

0

i zbada´

c jak przedzia l na kt´

orym rozwi¸

azanie

istnieje zale˙zy od warto´

sci pocz¸

atkowej y

0

.

13. Rozwi¸

aza´

c zagadnienie pocz¸

atkowe y

′

=

t

2

y(1 + t

3

)

,

y(0) = y

0

i zbada´

c jak przedzia l na kt´

orym

rozwi¸

azanie istnieje zale˙zy od warto´

sci pocz¸

atkowej y

0

.

14. Pokaza´

c, ˙ze ϕ(t) = e

2t

jest rozwi¸

azaniem r´

ownania y

′

− 2y = 0 i ˙ze y = cϕ(t) jest tak˙ze rozwi¸azaniem

tego r´

ownania dla dowolnej sta lej c.

15. Pokaza´

c, ˙ze ϕ(t) = 1/t jest rozwi¸

azaniem r´

ownania y

′

+ y

2

= 0 dla t > 0 lecz y = cϕ(t) nie jest

rozwi¸

azaniem r´

ownania, chyba ˙ze c = 0 lub c = 1. Dlaczego w poprzednim zadaniu w lasno´

s´

c rozwi¸

aza´

n

r´

ownania z mno˙zeniem przez sta l¸

a zachodzi a w tym zadaniu nie zachodzi?

16. Rozwi¸

aza´

c r´

ownanie autonomiczne

dy

dt

= y(y

− 1)(y − 2), y > 0.

17. Innym modelem zachowania si¸e populacji jest r´

ownanie Gompertz’a

dy

dt

= r y ln(K/y), gdzie r i K s¸

a

dodatnimi sta lymi. Rozwi¸

aza´

c to r´

ownanie z warunkiem pocz¸

atkowym y(0) = y

0

. Wskaz´

owka: zrobi´

c

zamian¸

e funkcji szukanej u = ln(K/y).

18. Rozwi¸

aza´

c r´

ownanie autonomiczne

dy

dt

=

−(y − 1)

2

z warunkiem pocz¸

atkowym y(0) = y

0

.

19. Rozwi¸

aza´

c r´

ownanie autonomiczne

dy

dt

= y

2

(y

2

− 1) z warunkiem pocz¸atkowym y(0) = y

0

.

20. Rozwi¸

aza´

c r´

ownanie autonomiczne

dy

dt

= e

y

.