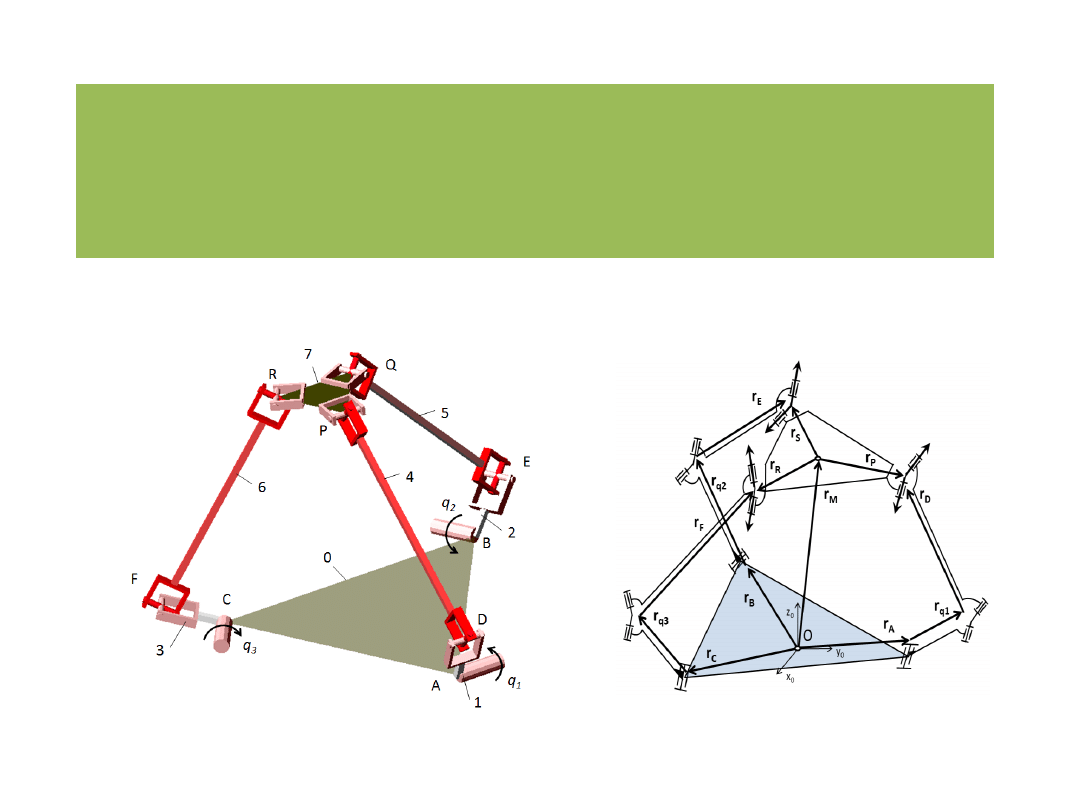
Analiza kinematyczna mechanizmów
Metoda wektorowych równań konturowych
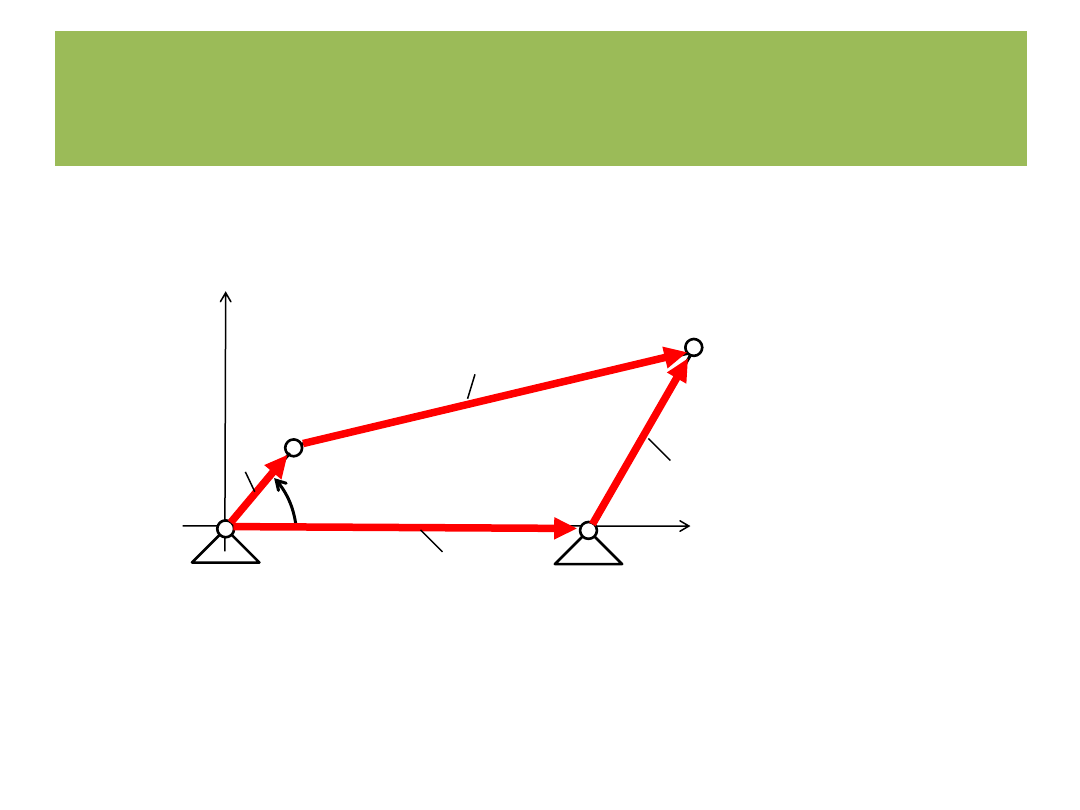
Metoda wektorowych równań konturowych
A
D
C
B
y
x
j
(
t
)
AB=a BC=b CD=c AD=d
d
c
b
a
r
a
+ r
b
- r
d
- r
c
= 0
Dane:
j
(t)
a
a
y
a
x
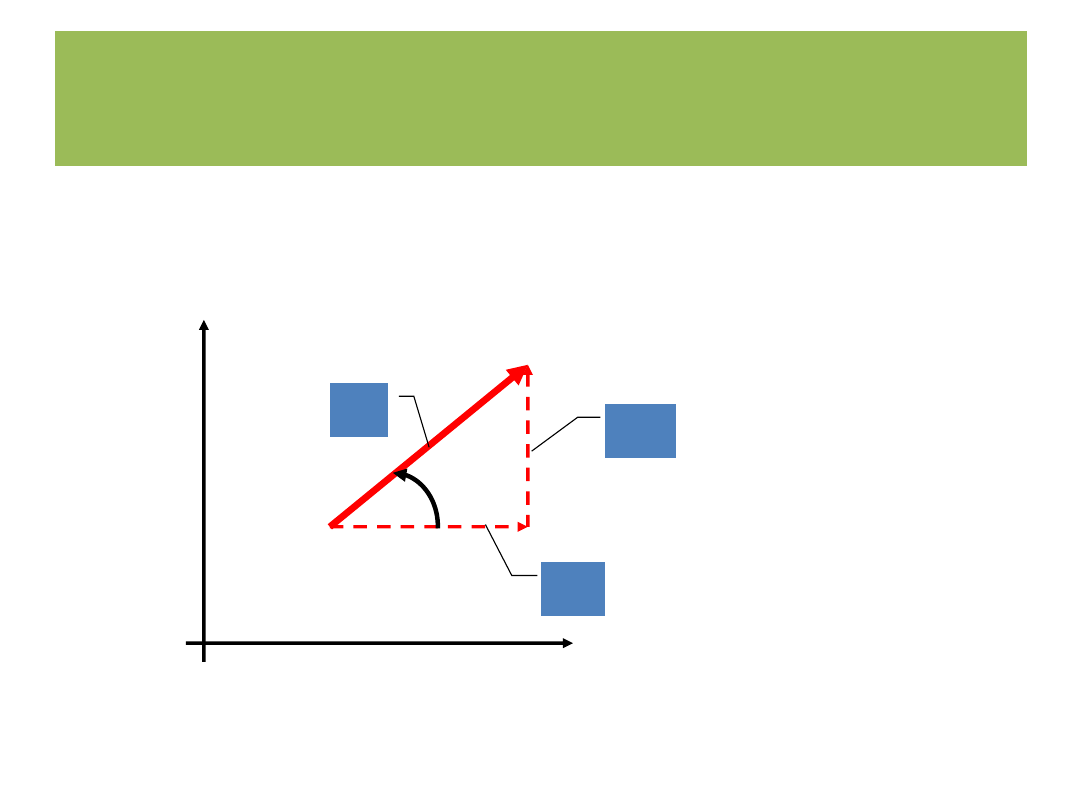
Metoda wektorowych równań konturowych
a
x
= a cos
a
y
= a sin
x
y
A
D
C
B
y
x
j(
t
)
AB=a BC=b CD=c AD=d
d
c
b
a
Dane:
j
(t)
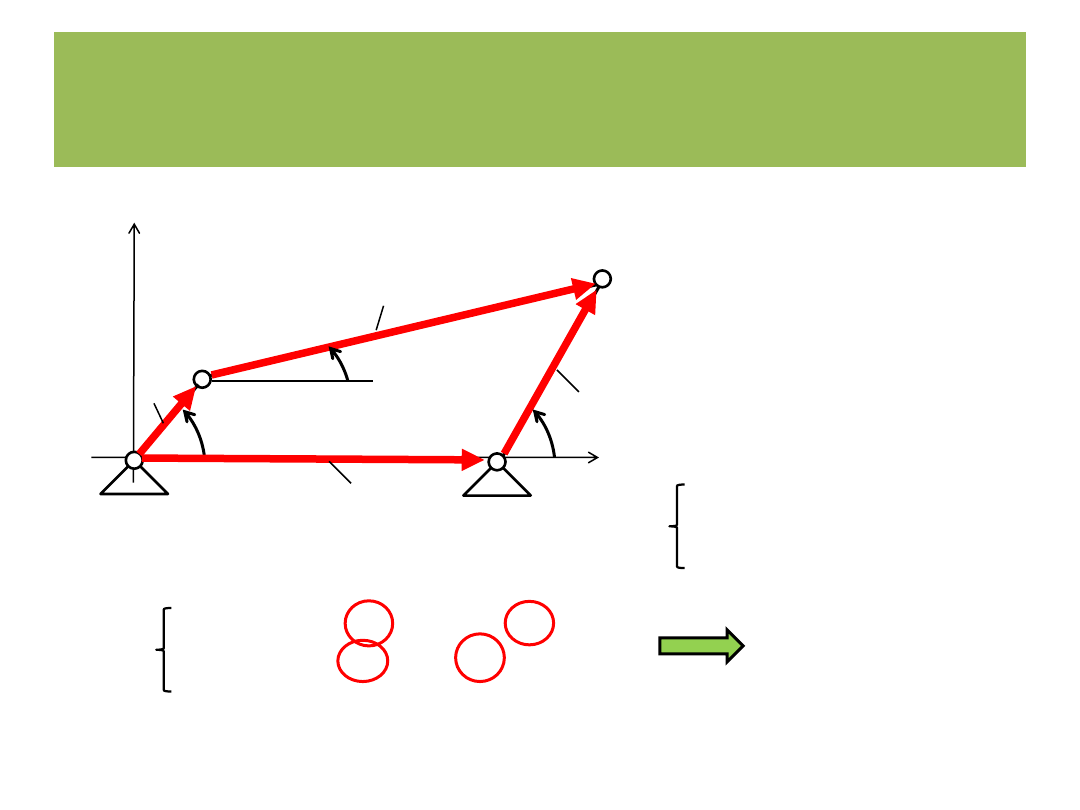
Metoda wektorowych równań konturowych
3
2
r
x
a
+ r
x
b
- r
x
d
- r
x
c
= 0
r
y
a
+ r
y
b
- r
y
d
- r
y
c
= 0
r
a
+ r
b
- r
d
- r
c
= 0
a cos
j
+ b cos
2
- d - c cos
3
= 0
a sin
j
+ b sin
2
- c sin
3
= 0
Szukane :
2
,
3
2
,
3
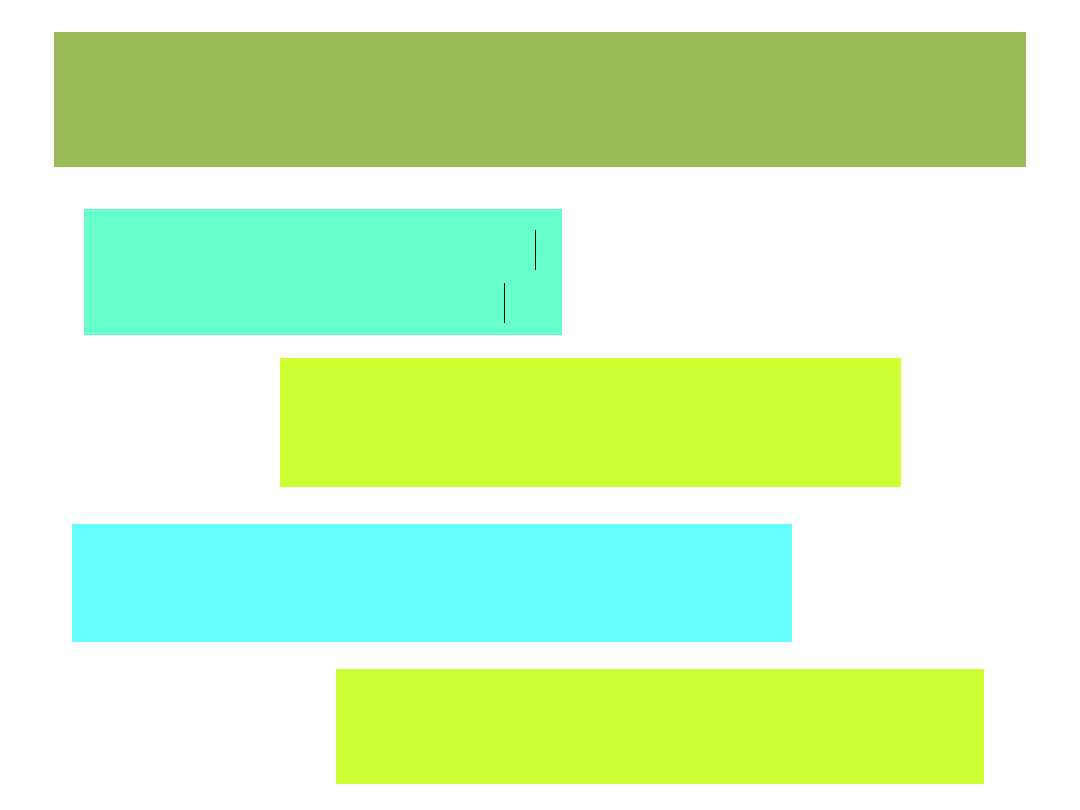
2
3
2
2
3
2
sin
sin
sin
cos
cos
cos
c
a
b
c
d
a
b
j
j
(
)
(
)
2
3
2
2
2
2
3
2
2
2
sin
sin
sin
cos
cos
cos
c
a
b
c
d
a
b
j
j
(
)
(
) (
)
2
3
2
3
2
2
2
2
2
sin
sin
cos
cos
sin
cos
c
a
c
d
a
b
j
j
(
)
3
3
3
2
2
2
2
cos
cos
sin
sin
2
cos
2
cos
2
j
j
j
ac
cd
ad
d
c
a
b
Metoda wektorowych równań konturowych
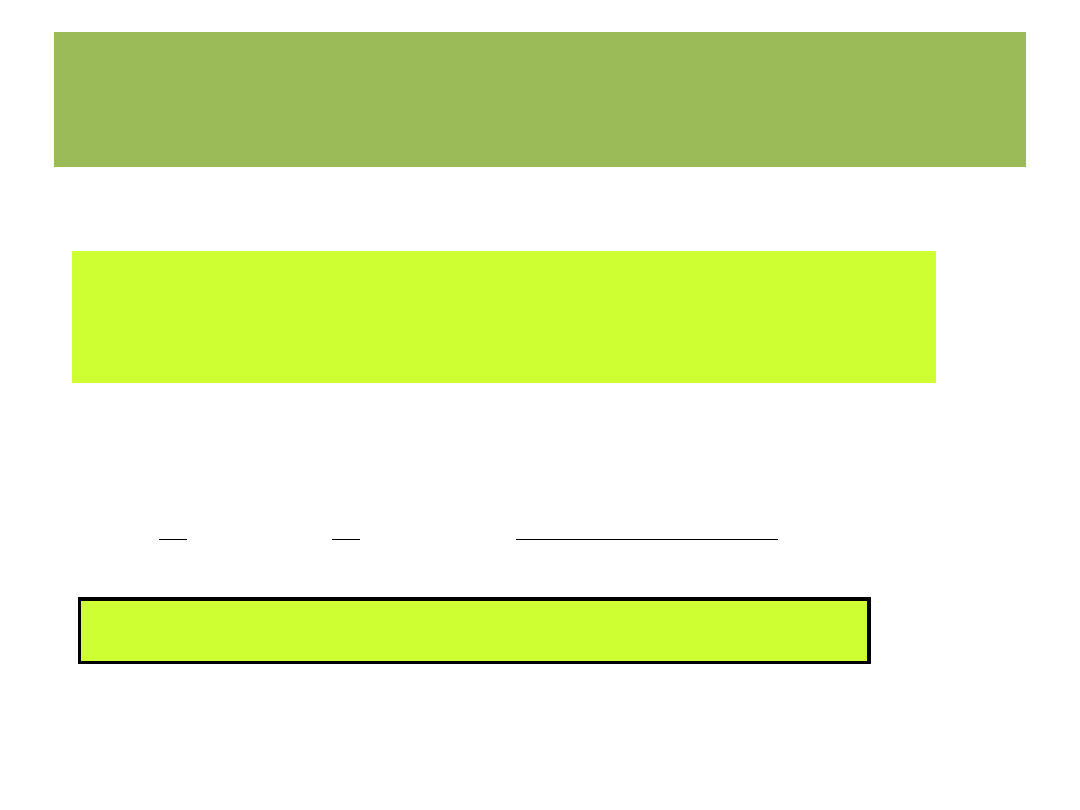
ac
d
c
b
a
k
c
d
k
a
d
k
2
2
2
2
2
3
2
1
(
)
3
3
3
2
3
1
cos
cos
sin
sin
cos
cos
j
j
j
k
k
k
Podstawienie:
Metoda wektorowych równań konturowych
(
)
3
3
3
2
2
2
2
cos
cos
sin
sin
cos
/
cos
/
2
/
)
(
j
j
j
c
d
c
d
ac
d
c
a
b
A. Gronowicz: Podstawy analizy
układów kinematycznych
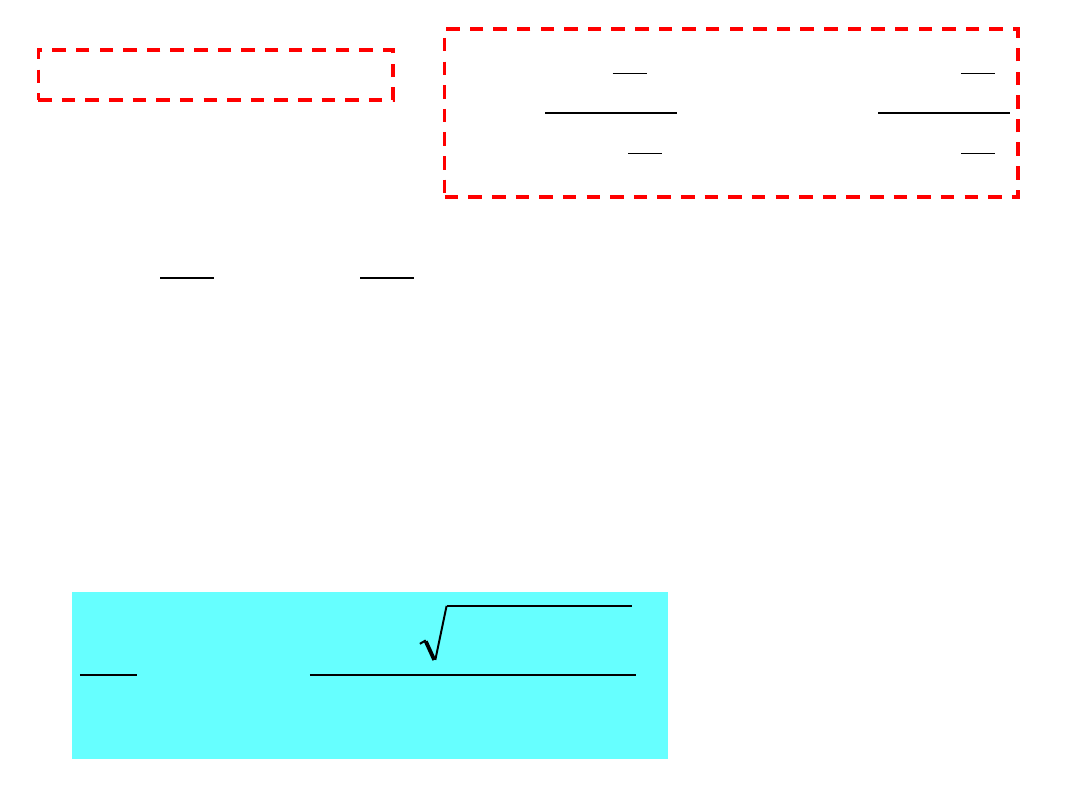
Podstawienie:
2
1
2
1
cos
2
1
2
2
sin
3
2
3
2
3
3
2
3
3
tg
tg
tg
tg
0
2
2
3
3
2
C
Btg
Atg
gdzie:
(
)
3
2
1
3
2
1
cos
1
sin
2
cos
cos
k
k
k
C
B
k
k
k
A
j
j
j
j
A
AC
B
B
arctg
2
4
2
2
3
2 rozwiązania

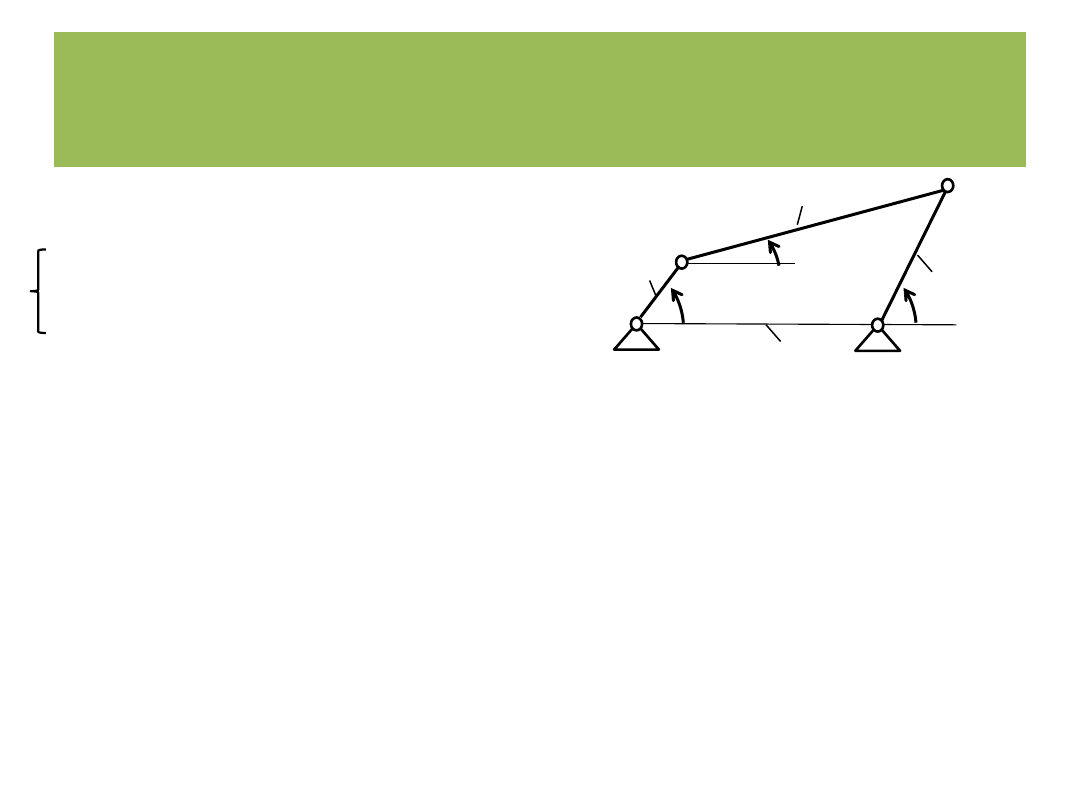
Metoda wektorowych równań konturowych
Algorytmizacja - Matlab
A
D
C
B
j(
t
)
d
c
b
a
3
2
a cos
j
+ b cos
2
- d - c cos
3
= 0
a sin
j
+ b sin
2
- c sin
3
= 0
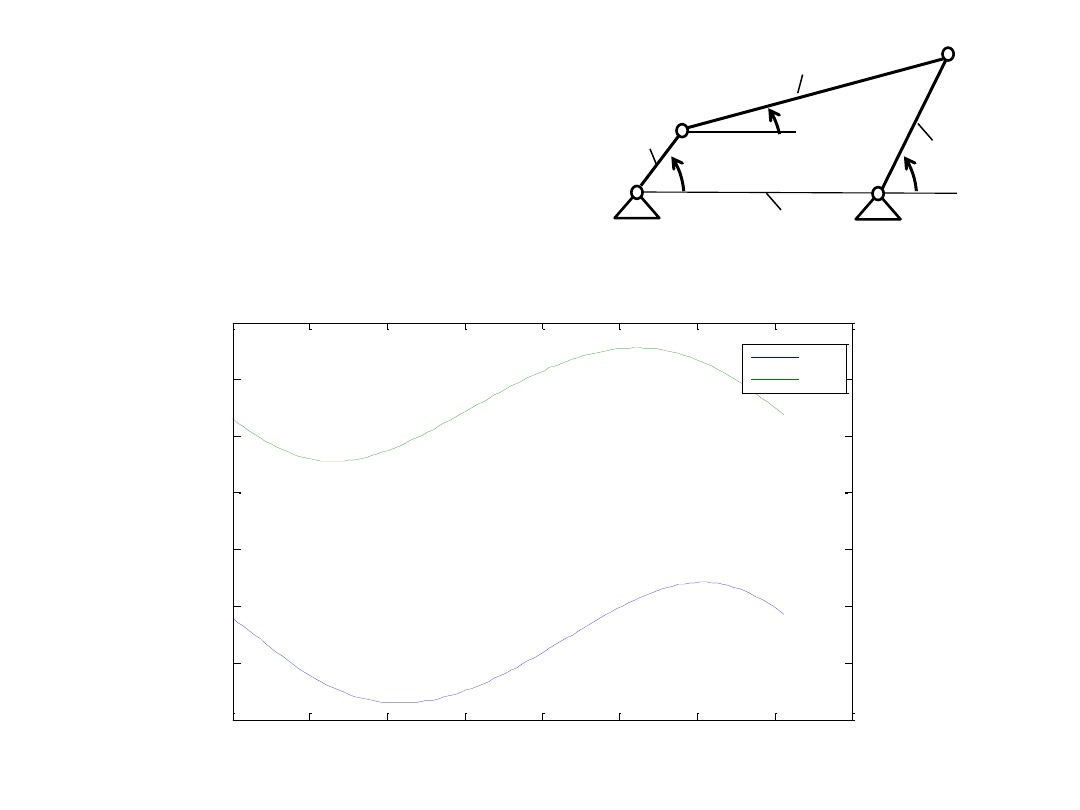
Czworobok.m
-------------------------------------------
function F=czworobok(teta);
global fi
a=0.1; b=0.8; c=0.85; d=0.6;
f1=a*cos(fi)+ b*cos(teta(1))- d-c*cos(teta(2));
f2=a*sin(fi)+ b*sin(teta(1)) - c*sin(teta(2));
F=[f1 f2];
Start.m
----------------------------------------
global fi
teta0=[1 1.5];
for i=1:100
fi=(i-1)*2*pi/100;
teta=fsolve(@czworobok, teta0);
fi1(i)=fi*180/pi;
teta2(i)=teta(1)*180/pi;
teta3(i)=teta(2)*180/pi;
teta0=teta;
end
0
50
100
150
200
250
300
350
400
60
70
80
90
100
110
120
130
fi
te
ta
2
,
te
ta
3
teta2
teta3
A
D
C
B
j(
t
)
d
c
b
a
3
2
a cos
j
+ b cos
2
- d - c cos
3
= 0
a sin
j
+ b sin
2
- c sin
3
= 0
a=0.1; b=0.8; c=0.85; d=0.6;
j
= 0 - 360
o
(0 - 2*pi)
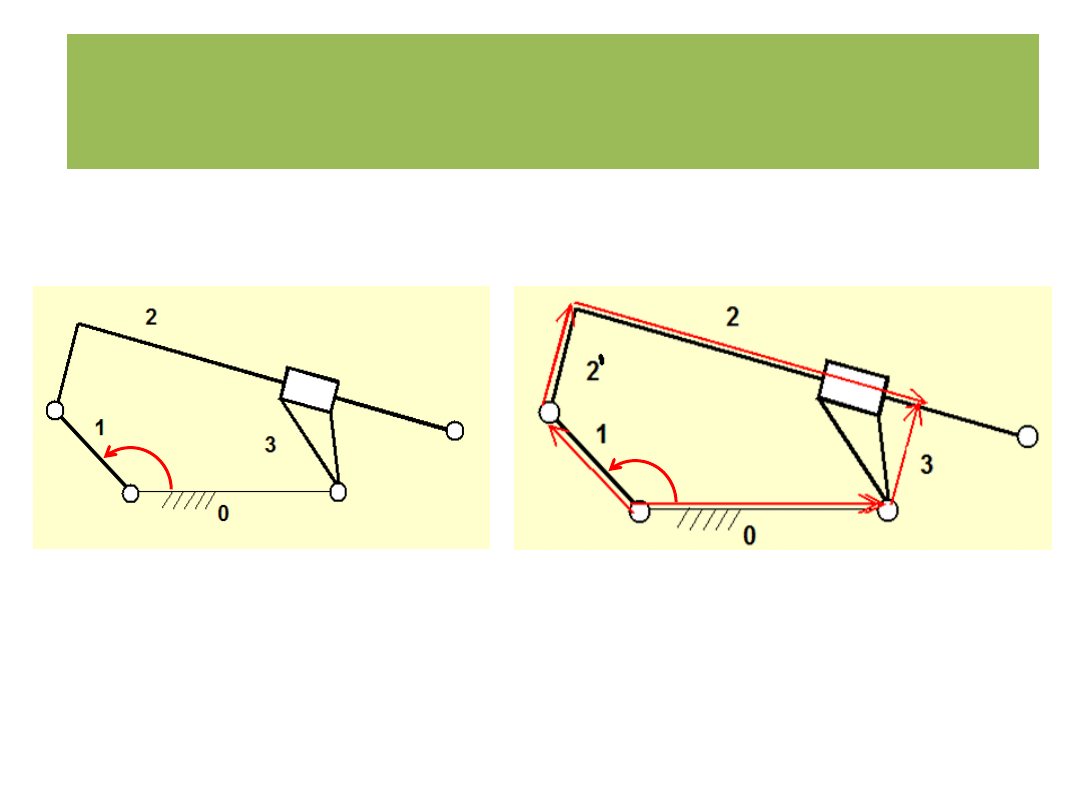
Analiza kinematyczna
Metoda wektorowych równań konturowych
r
1
+ r
2
‘ + r
2
- r
3
- r
0
= 0
j
1
j
1
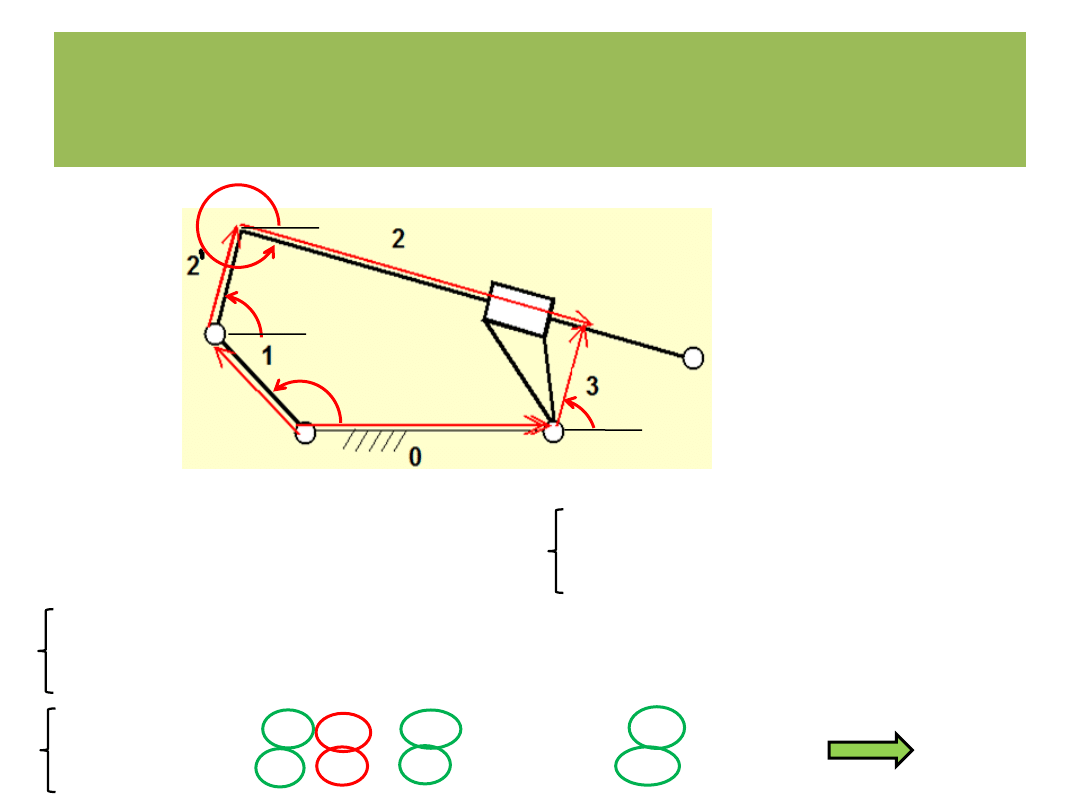
Analiza kinematyczna
Metoda wektorowych równań konturowych
r
1
x
+ r
2
x
’+ r
2
x
- r
3
x
- r
0
x
= 0
r
1
y
+ r
2
y
’+ r
2
y
- r
3
y
- r
0
y
= 0
j
1
j
3
j
2
'
j
2
Dane:
j
1
(t)
Szukane
:
j
2
‘
,
r
2
j
2
j
2
‘
270
o
j
3
j
2
‘
r
1
cos
j
1
+ r
2
‘ cos
j
2
‘ + r
2
cos
(j
2
‘
270
o
)
- r
3
cos
j
2
‘
- r
0
= 0
r
1
sin
j
1
+ r
2
‘ sin
j
2
‘ + r
2
sin
(j
2
‘
270
o
)
- r
3
sin
j
2
‘
= 0
r
1
+ r
2
‘ + r
2
- r
3
- r
0
= 0
r
1
cos
j
1
+ r
2
‘ cos
j
2
‘ + r
2
cos
j
2
- r
3
cos
j
3
- r
0
= 0
r
1
sin
j
1
+ r
2
‘ sin
j
2
‘ + r
2
sin
j
2
- r
3
sin
j
3
= 0
r
2
, j
2
’
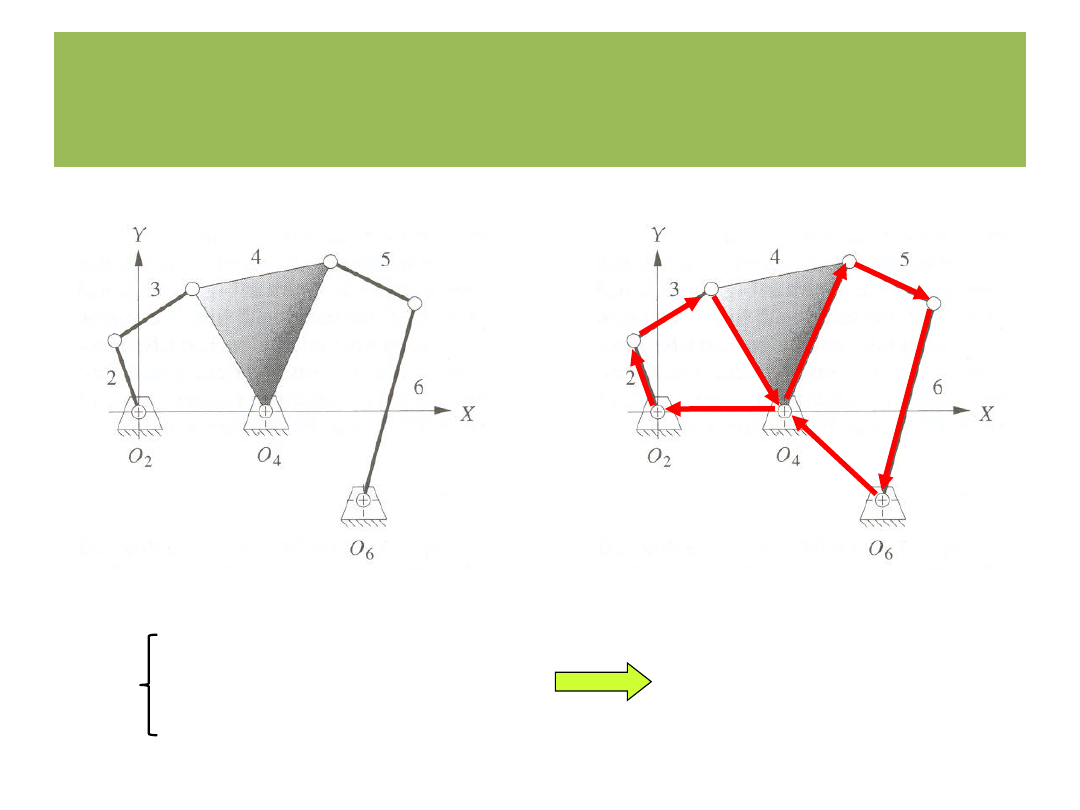
0
r
r
r
r
0
r
r
r
r
7
8
6
5
4
1
3
2
4 równania rzutów
Metoda wektorowych równań konturowych
r
2
r
3
r
4
r
1
r
5
r
6
r
7
r
8
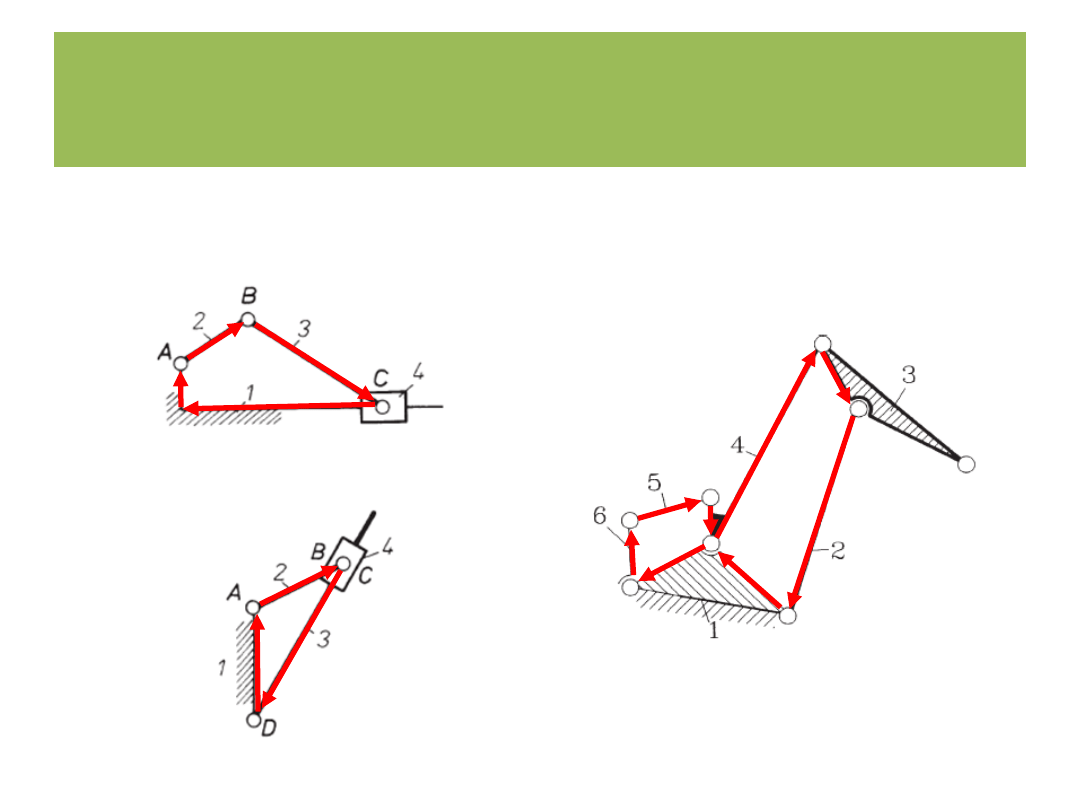
Metoda wektorowych równań konturowych
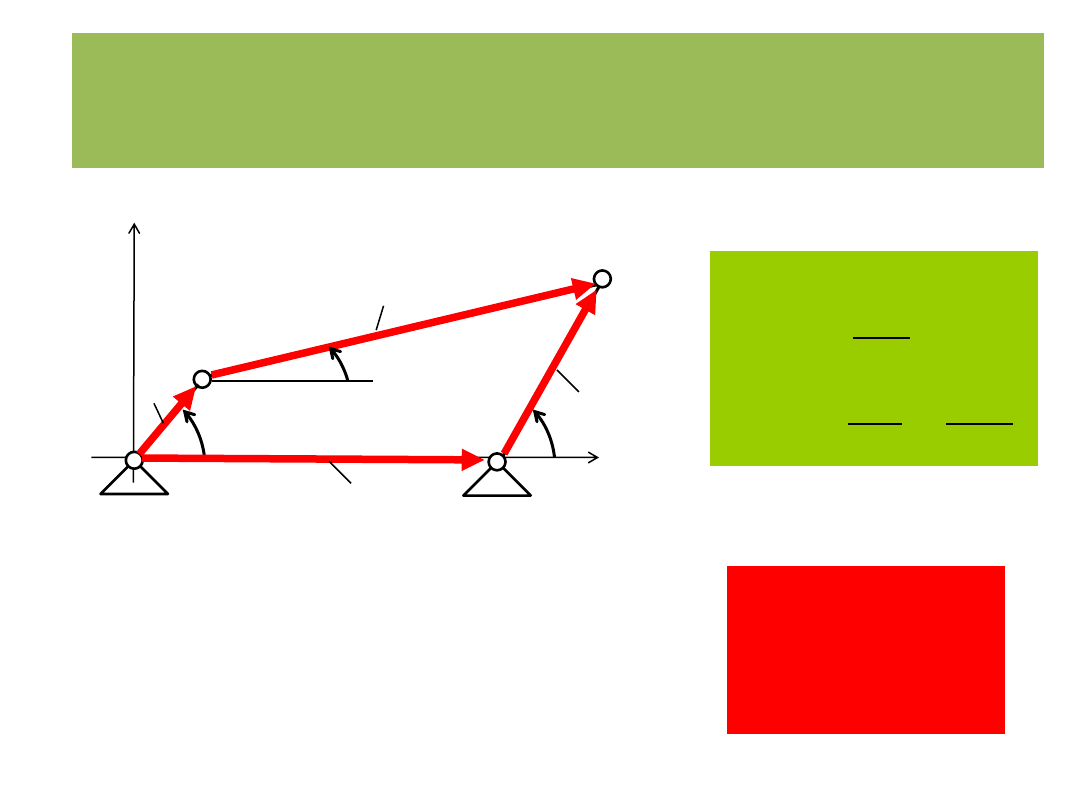
Metoda wektorowych równań konturowych
Położenia
prędkości
przyspieszenia
A
D
C
B
y
x
1
(
t
)
d
c
b
a
Dane:
3
2
r
a
+ r
b
- r
d
- r
c
= 0
Szukane :
2
1
2
1
1
1
1
1
1
1
)
(
dt
d
dt
d
dt
d
t
2
2
2
2
3
3
2
2
3
2
,
,
,
Równanie położeń:
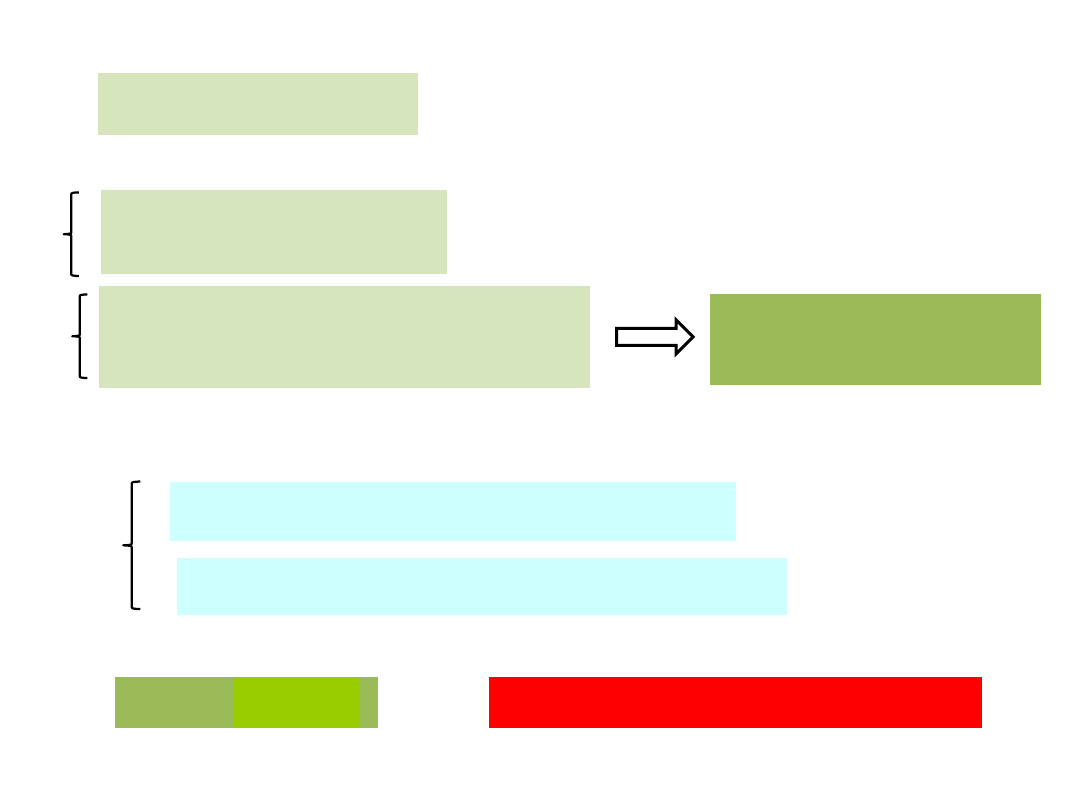
Szukane:
0
sin
sin
sin
0
cos
cos
cos
3
2
1
3
2
1
c
b
a
c
d
b
a
Równania rzutów:
Równania prędkości – 1-sza pochodna po czasie
0
sin
sin
sin
3
3
2
2
1
1
c
b
a
0
cos
cos
cos
3
3
2
2
1
1
c
b
a
r
a
+ r
b
- r
d
- r
c
= 0
Równanie położeń:
r
x
a
+ r
x
b
- r
x
d
- r
x
c
= 0
r
y
a
+ r
y
b
- r
y
d
- r
y
c
= 0
Dane:
1
,
Wyznaczone:
2
,
3
3
3
2
2
,
Dane:
1
1

Po uporządkowaniu:
0
cos
cos
sin
sin
cos
sin
3
2
3
2
3
2
1
1
1
c
b
c
b
a
a
1
1
1
1
3
2
cos
sin
a
a
A
1
1
1
3
2
3
2
3
2
cos
sin
cos
cos
sin
sin
a
a
c
b
c
b
3
2
3
2
cos
cos
sin
sin
c
b
c
b
A
1
1
1
3
2
cos
sin
a
a
A
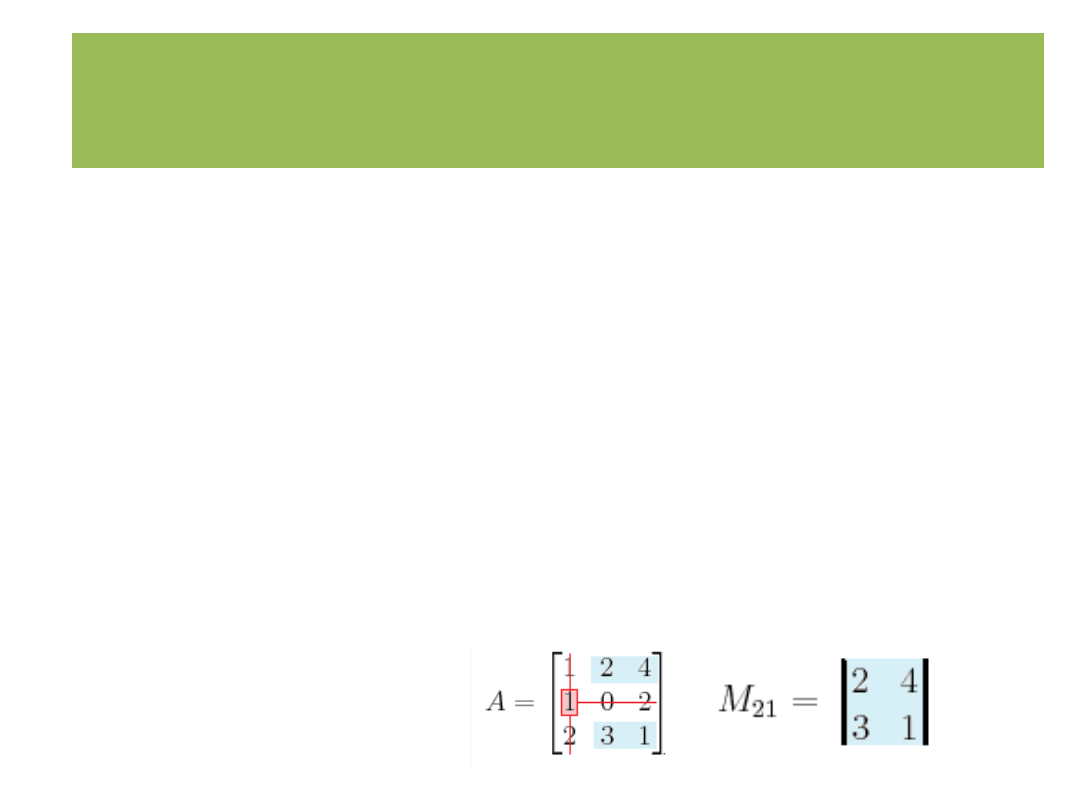
Metoda wektorowych równań konturowych
Prędkości – odwracanie macierzy A
3
2
3
2
cos
cos
sin
sin
c
b
c
b
A
Odwracanie macierzy:
A
-1
= 1/det(A) *A
T
dop
gdzie:
det(A) - wyznacznik macierzy
A
dop
- macierz dopełnień algebraicznych
a
dop
ij
= (-1)
i+j
M
ij
...
...
...
...
...
...
ij
dop
dop
a
A
Metoda wektorowych równań konturowych
Prędkości – odwracanie macierzy A
0
cos
cos
sin
sin
)
det(
3
2
3
2
c
b
c
b
A
)
sin(
)
sin
cos
cos
(sin
)
det(
3
2
3
2
3
2
bc
bc
A
2
2
3
3
3
2
1
sin
cos
sin
cos
)
sin(
1
b
b
c
c
bc
A

D=
Metoda wektorowych równań konturowych
Prędkości – odwracanie macierzy A
Warunek istnienia macierzy odwrotnej A
-1
:
det(A)
≠ 0
)
sin(
)
det(
3
2
bc
A
0
)
sin(
)
det(
3
2
bc
A
?
,
3
2
Jeżeli det(A) = 0, macierz A
-1
nie istnieje.
Co to oznacza?
Metoda wektorowych równań konturowych
Położenia osobliwe
0
)
sin(
)
det(
3
2
bc
A
1) b = 0 lub c =0
A
D
C
B
1
(
t
)
d
c
b
a
3
2
A
C=D
B
1
(
t
)
d
c=0
a
b
A
D
B =C
1
(
t
)
d
b=0
a
c
U
kłady zdegenerowane
Metoda wektorowych równań konturowych
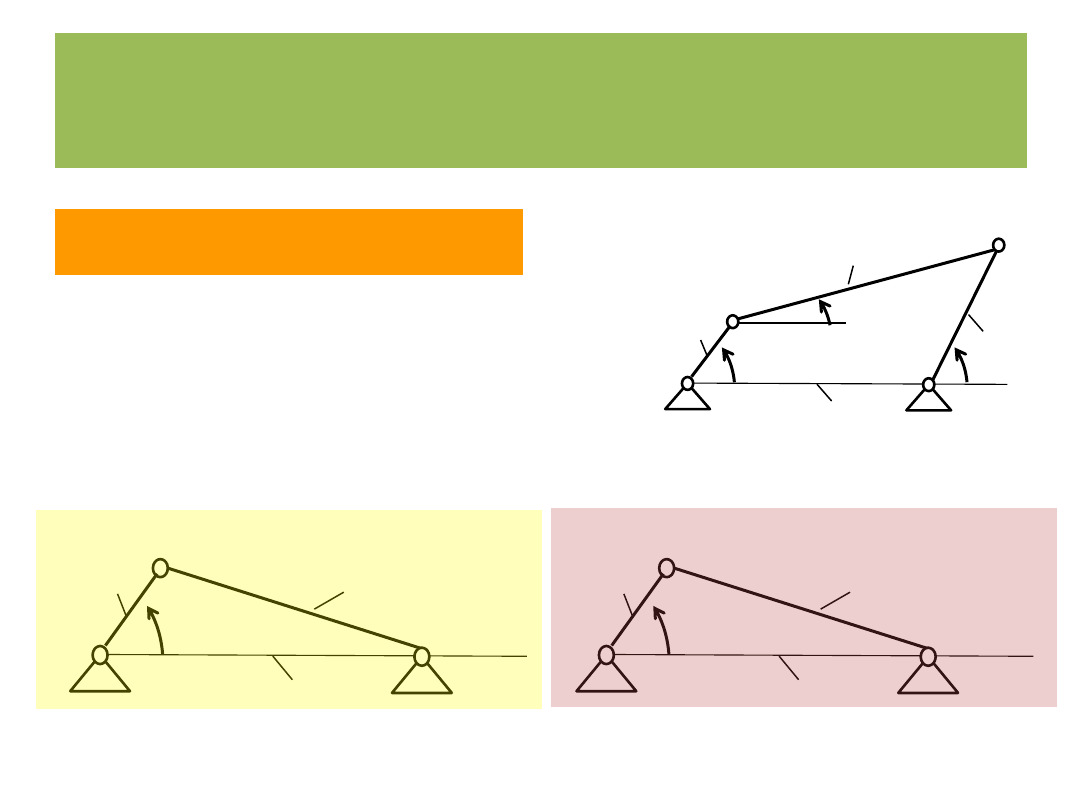
Położenia osobliwe
0
)
sin(
)
det(
3
2
bc
A
A
D
C
B
1
(
t
)
d
c
b
a
3
2
2)
2
3
A
D
C
B
3
2
3
2
1
(
t
)
Metoda wektorowych równań konturowych
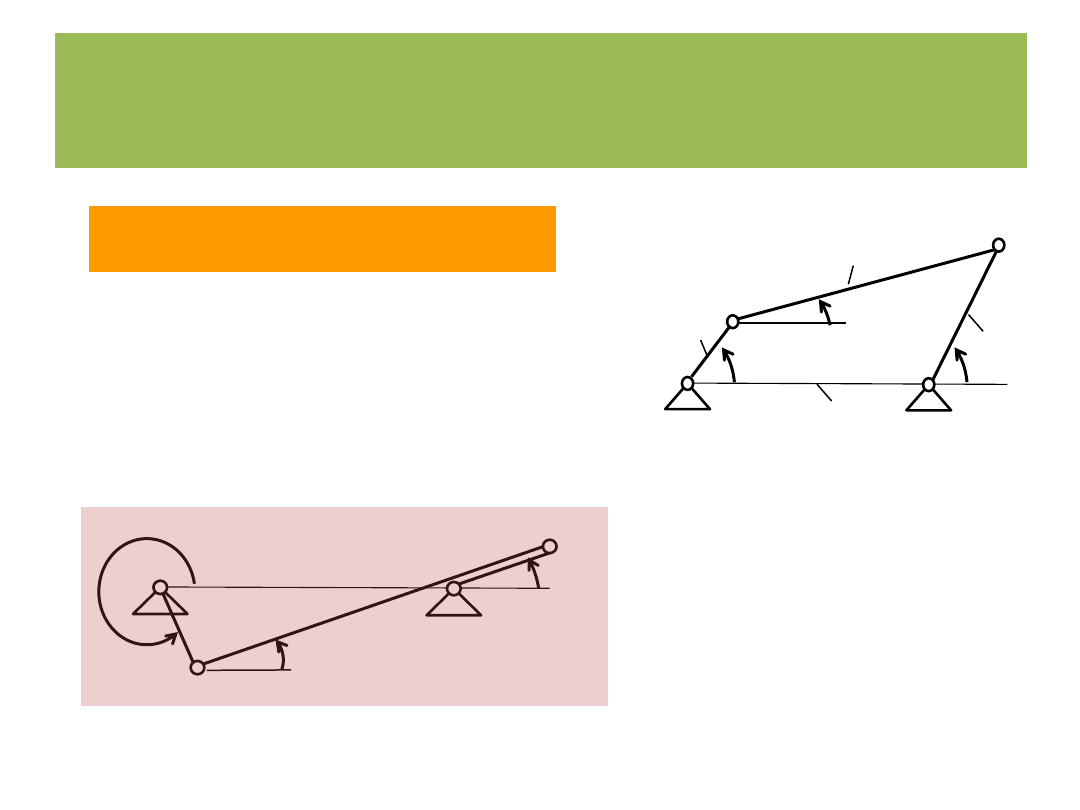
Położenia osobliwe
0
)
sin(
)
det(
3
2
bc
A
A
D
C
B
1
(
t
)
d
c
b
a
3
2
3)
2
3
p
2
3
p
4)
2
3
p
3
2
p
A
D
C
B
3
2
2
3
p
1
(
t
)
A
D
C
B
3
2
3
2
p
1
(
t
)
Metoda wektorowych równań konturowych
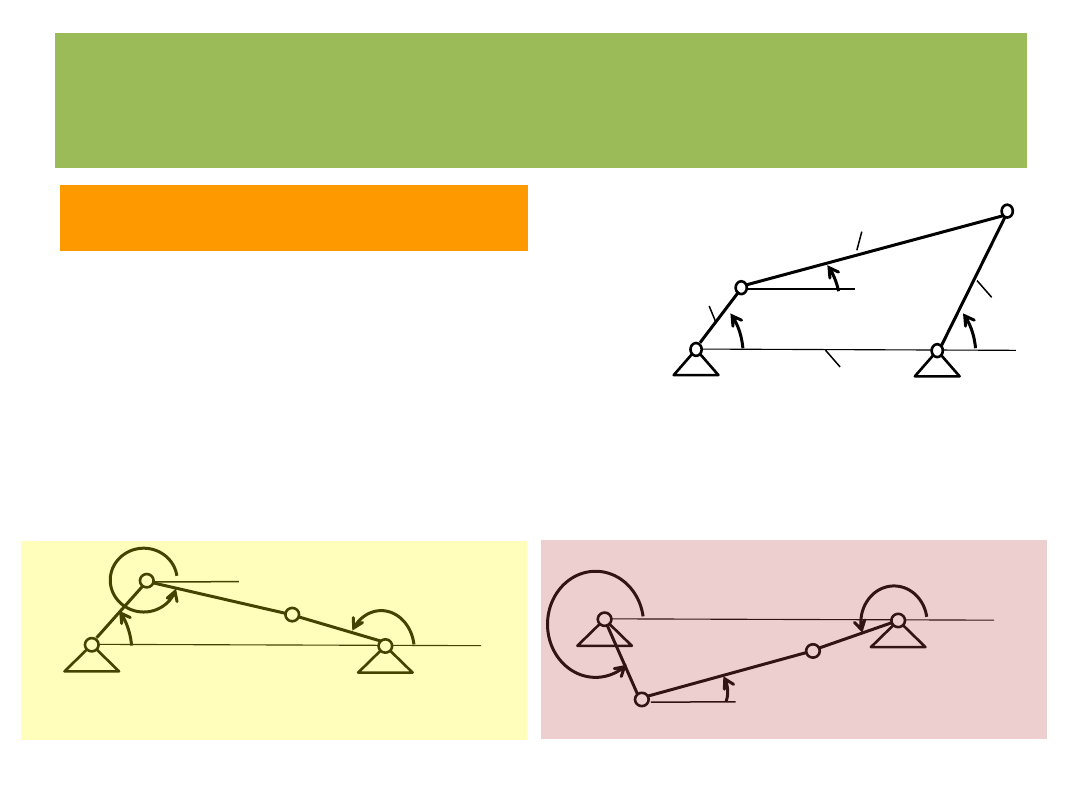
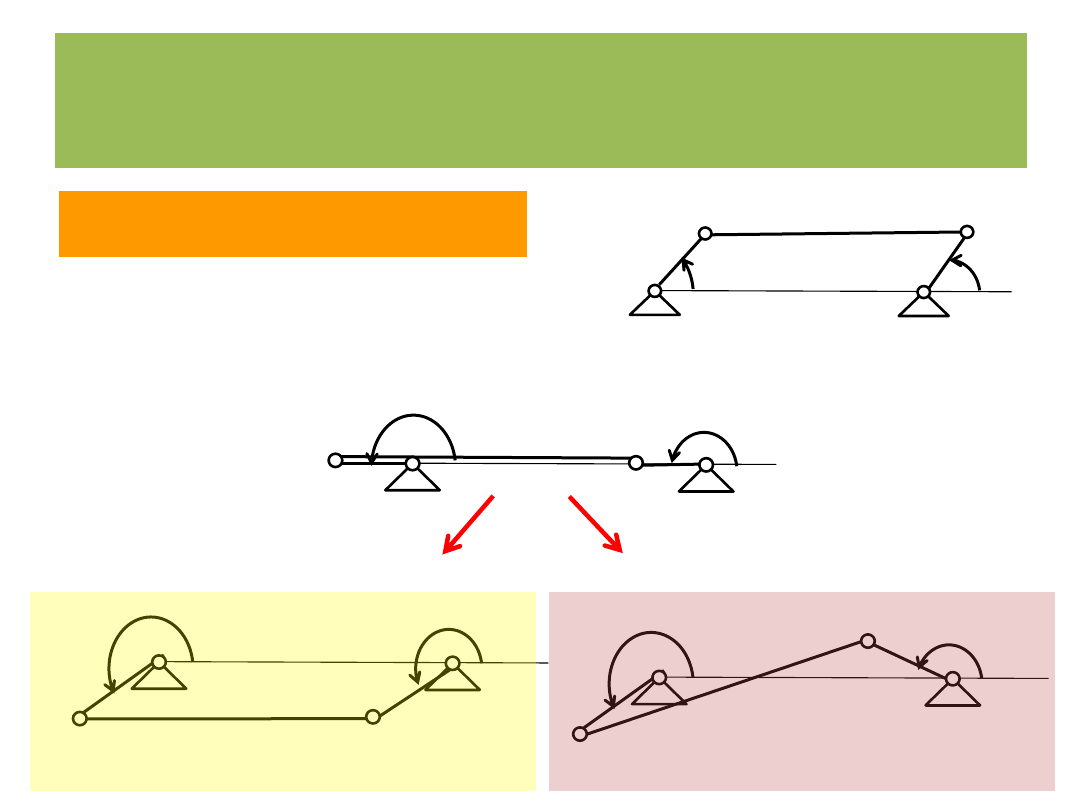
Położenia osobliwe
0
)
sin(
)
det(
3
2
bc
A
5)
2
p
3
2
0,
3
p
A
D
C
B
3
2
= 0
1
(
t
)
A
D
C
B
3
=
p
2
= 0
1
(
t
)
A
D
C
B
3
2
= 0
1
(
t
)
A
D
C
B
3
2
> 0
1
(
t
)
Równania prędkości
Równania przyspieszeń – 2 pochodna po czasie
0
sin
cos
sin
cos
sin
cos
0
cos
sin
cos
sin
cos
sin
3
2
3
3
3
2
2
2
2
2
1
2
1
1
1
3
2
3
3
3
2
2
2
2
2
1
2
1
1
1
c
c
b
b
a
a
c
c
b
b
a
a
3
,
2
,
1
2
2
i
dt
d
dt
d
i
i
i
i
Metoda wektorowych równań konturowych
Przyśpieszenia
0
cos
cos
cos
0
sin
sin
sin
3
3
2
2
1
1
3
3
2
2
1
1
c
b
a
c
b
a
Dane napęd:
Wyliczone położenia
i prędkości:
Szukane:
0
sin
sin
cos
cos
cos
cos
sin
sin
sin
cos
cos
sin
2
3
2
2
3
2
3
2
3
2
3
2
3
2
2
1
1
1
1
1
1
c
b
c
b
c
b
c
b
a
a
a
a
Po uporządkowaniu:
1
1
1
,
),
(
t
2
3
2
2
3
2
3
2
2
1
1
1
1
1
1
3
2
3
2
3
2
sin
sin
cos
cos
sin
cos
cos
sin
cos
cos
sin
sin
c
b
c
b
a
a
a
a
c
b
c
b
3
2
3
2
,
,
,
3
3
2
2
,
2
1
1
1
1
1
1
2
3
2
2
3
2
3
2
1
3
2
3
2
3
2
sin
cos
cos
sin
sin
sin
cos
cos
cos
cos
sin
sin
a
a
a
a
c
b
c
b
c
b
c
b
3
2
3
2
cos
cos
sin
sin
c
b
c
b
B
1
3
2
3
2
1
cos
cos
sin
sin
c
b
c
b
B
2
1
1
1
1
1
1
2
3
2
2
3
2
3
2
1
3
2
sin
cos
cos
sin
sin
sin
cos
cos
a
a
a
a
c
b
c
b
B
Wyszukiwarka
Podobne podstrony:
05 Analiza kinematyczna mechanizmów wyznaczanie prędkości i przyśpieszeń
ANALIZA KINEMATYCZNA MECHANIZMOW KRZYWKOWYCH v2011
Analiza kinematyczna mechanizmu różnicowego
04 Analiza kinematyczna mechanizmów wyznaczanie środków obrotów
Analiza kinematyczna i kinetostatyczna mechanizmu dźwigniowego
Analiza kinematyczna i kinetostatyczna mechanizmu dźwigniowego
WYKLAD MECHANIKA kinematyka dynamika PREZENTACJA
4A, 4Aa, TEMAT: Analiza kinematyczna i kinetostatyczna mechanizmu dźwigniowego
ANALIZA KINEMATYCZNA BELEK id 6 Nieznany (2)
04 Analiza kinematyczna manipulatorów robotów metodą macierz
Analiza ekon 08 w2 id 60028 Nieznany
analiza sem 2 lista nr5 id 6134 Nieznany (2)
Analiza Wyklad 01 Logika id 59757 (2)
J Ossowski Analiza czynnikow ujecie kwartale id 221447
Analiza Finansowa program szczegolowy id 60226 (2)
prezentacja 3 2 id 390139 Nieznany
więcej podobnych podstron