Całki

Całka nieoznaczona
Niech f(x) będzie określona na przedziale X.
Funkcję F(x) nazywamy funkcją pierwotną funkcji f(x) na przedziale X jeżeli:
F’(x) = f(x)

Twierdzenie I.
Jeżeli F(x) jest funkcją pierwotną f(x) na X to:
1.Funkcja ϕ(x)=F(x) + c c=cosnt jest też funkcją pierwotną funkcji f(x) na przedziale X.
2. Każda funkcja pierwotna ϕ(x) funkcji f(x) da się przedstawid w postaci sumy F(x) + c.

Wniosek
Jeżeli funkcja F(x) jest funkcja pierwotną funkcji f(x) na przedziale X to zbór wszystkich funkcji pierwotnych
funkcji f(x) jest postaci F(x) + c.

Obliczanie funkcji pierwotnych jest działaniem odwrotnym do obliczania pochodnych.

c=const

Twierdzenie II.
Każda funkcja ciągła na przedziale X ma na tym przedziale funkcję pierwotną.

Znajdowanie funkcji pierwotnych, czyli całkowanie, jest trudniejsze od liczenia pochodnych, gdyż definicja całki
nie podaje sposobu jej liczenia.

Reguły całkowania

Twierdzenie III.
Jeżeli funkcje f(x), g(x) mają na pewnym przedziale X funkcje pierwotne F(x), G(x) ( A – dowolna stała) to
f(x)±g(x) oraz A*f(x) mają także na tym przedziale funkcje pierwotne przy czym:
1.

2.

Jeżeli całkujemy sumę (różnicę) kilku funkcji to dopisujemy na koocu jedną stałą, gdyż suma dowolnych stałych
jest stałą.

Całkowanie przez podstawianie
Jeżeli funkcja f(t) jest całkowalna na przedziale (a,b) i funkcja t= φ(x) ma ciągłą pochodną na przedziale (α,β)
oraz funkcja f(x) jest zawarta w przedziale a<f(x)<b to:

gdzie t= (x) dt= ’(x)dx

Całkowanie przez części
Jeżeli funkcja u(x) i v(x) mają na pewnym przedziale X ciągłe pochodne (klacy c1) to zachodzi wzór

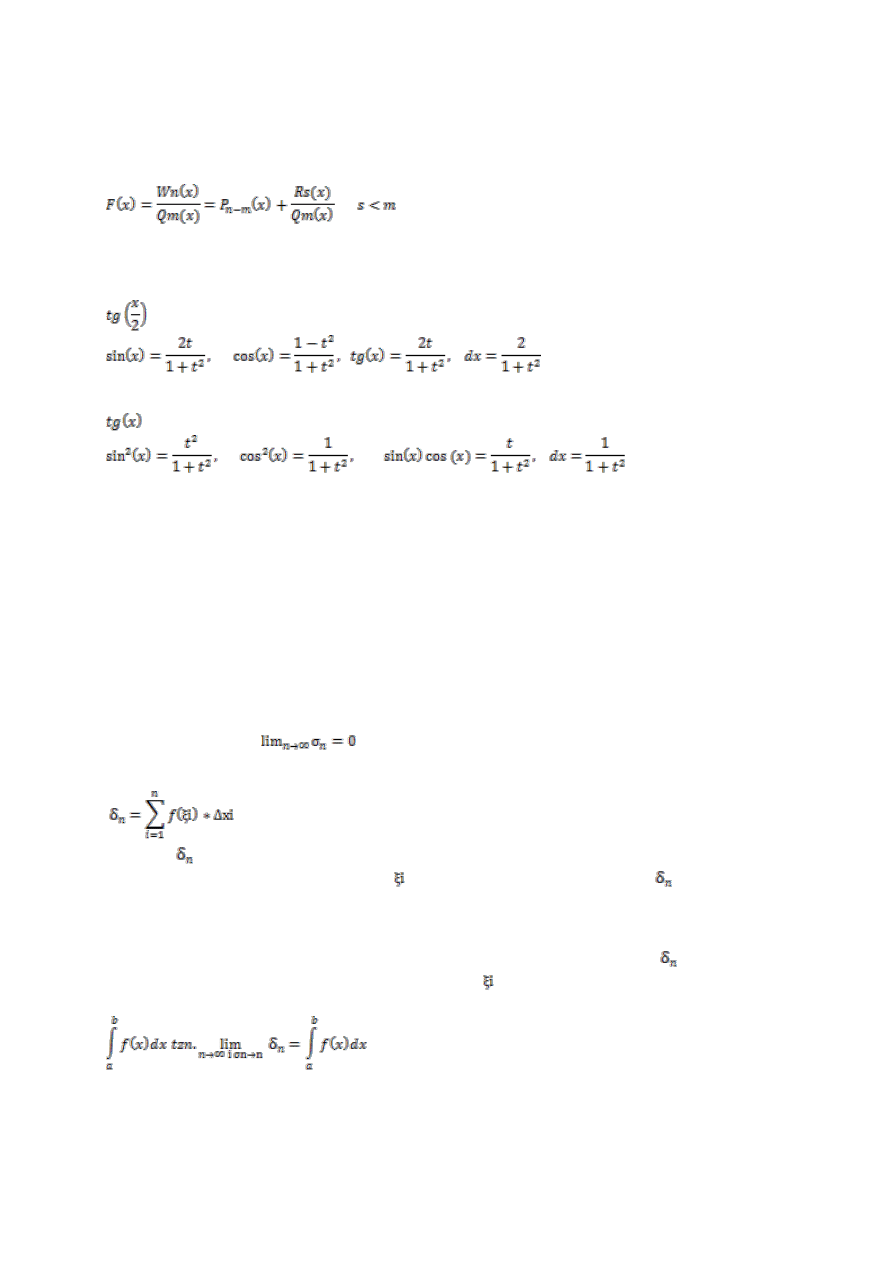
Całki z funkcji wymiernych

Jeżeli mamy do czynienia z funkcją F(x) niewłaściwą n>=m to każdą taką funkcję możemy zapisad w postaci
dwóch składników:

Pierwsze uniwersalne podstawienie

Drugie uniwersalne podstawienie

1) Rozważając całki z funkcji trygonometrycznych można zauważyd, że jeśli funkcja podcałkowa jest

nieparzysta względem sinx to podstawiamy cosx=t i na odwrót.

Całka oznaczona

Niech będzie funkcja f(x) określona i ograniczone na przedziale <a,b>.
1. Dzielimy przedział <a,b> na n podprzedziałów dowolnie wybranymi punktami x1,x2…xn (a=x0, b=xn) takie, że
x0<x1 , x1<x2 etc.
2. Długośd przedziałów <x

i-1

,x

i

> i=1,2,3,4… n-1 oznaczamy przez ∆x

i

. Największą z liczb ∆x

i

=σ

n

=max ∆x

i

nazywamy

średnicą przedziału.
3. Jeśli dla każdego n mamy pewien podział przedziałów to mówimy, że określony jest ciąg podziału
przedziałów <a,b>, a wraz z nim ciąg średnic ∆n.
4. Jeśli zachodzi warunek

to dokonaliśmy normalnego ciągu podziału przedziału <a,b>.

5. W każdym przedziale <x

i-1

,x

i

> wybieram po punkcie pośrednim ξ

i

i=1,2…n-1 i tworzę sumę

Sumy typy

dla danej funkci f(x) i danego ciągu σ

n

podziału przedziałów są zależne od sposobu dzielenia

przedziału <a,b> i wyboru punktów pośrednich

.

Tworzą one nieskooczony ciąg liczbowy

zwany ciągiem

sum całkowych.

Definicja:
Jeśli dla każdego n ormalnego ciągu podziałów przedziału <a,b> każdy ciąg sum całkowych

dąży do tej samej

skooczonej granicy i granica ta nie zależy od wyboru punktów

gdzie i=1,2…n to granicę tę nazywamy całką

oznaczoną funkcji f<a,b> i oznaczamy:

Jest to tak zwana całka Riemana
Wnioski:
Jeśli funkcja f(x) ma całkę oznaczoną to nazywamy ją całkowalną na przedziale <a,>

Twierdzenie:
Każda funkcja ciągła na przedziale <a,b> jest całkowalna na tym przedziale.

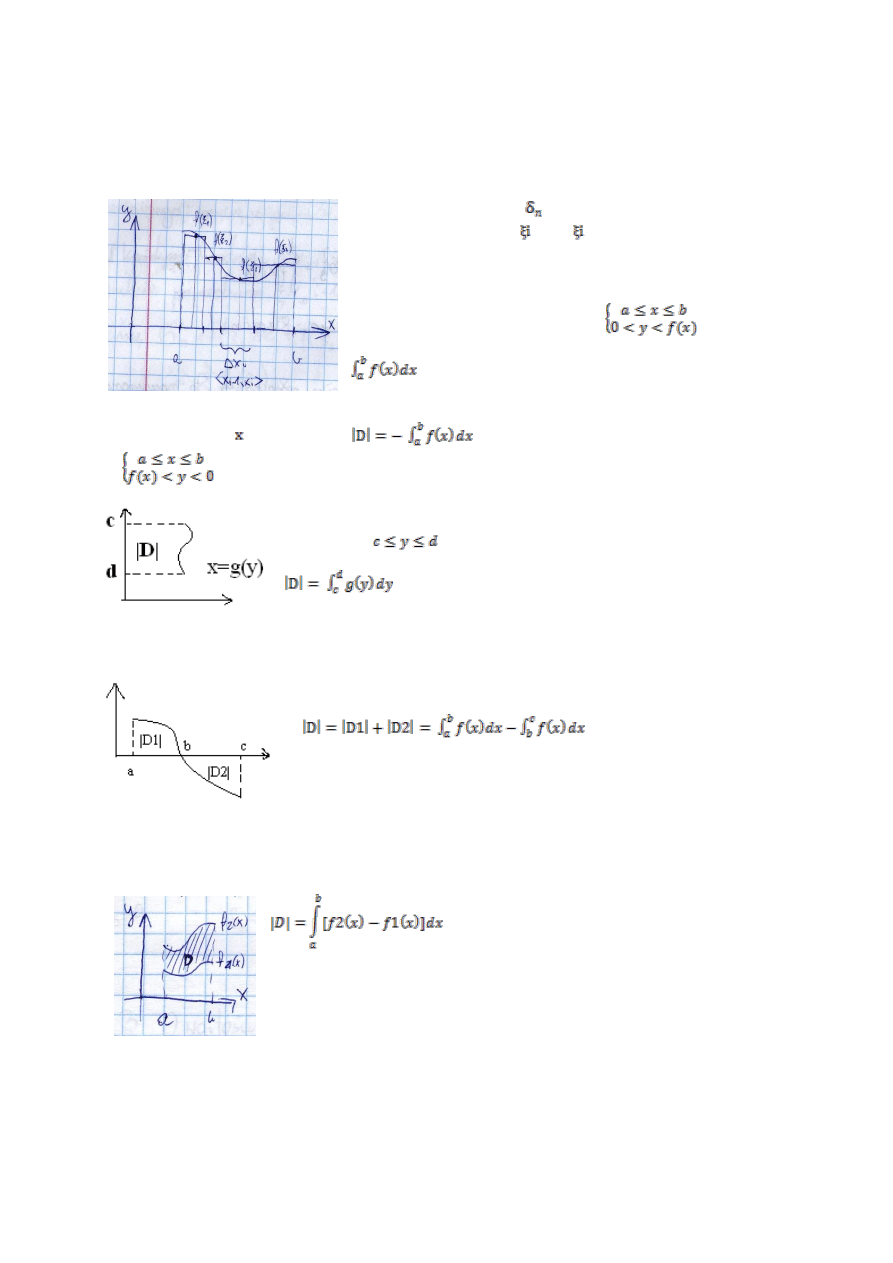
Interpretacja geometryczna całki oznaczonej:

Niech f(x) >0, sumy całkowe

określają sumy pól prostokątów o

podstawie ∆x

i

i wysokości f( ) gdzie €<x

i-1

,x

i

>.

Geometrycznie całka oznaczona z funkcji jako granica ciągu sum
całkowych określa pole obszaru płaskiego „D” ograniczonego krzywą

y=f(x), osią OX oraz rzędnymi x=a i x=b. D:

=|D| Pole obszaru płaskiego.

Uwaga I

Jeżeli funkcja f(x)<0 i €<a,b>. to wtedy

.

D:

Uwaga II
W przypadku gdy funkcja f(x) jest postaci
x=g(y), g(y)>0,

.

Uwaga III

Jeżeli częśd obszaru znajduje się powyżej OX, a częśd poniżej OX to:

.

Uwaga IV
Jeżeli obszar płaski D jest ograniczony przez dwie krzywe y

1

=f

1

(x) i y

2

=f

2

(x).

a) Krzywe są >0

b) Krzywe przecinają się

Własności całki oznaczonej

Twierdzenie I
Stałą można przenieśd przed znak całki.
Suma/różnica całek równa się sumie/różnicy całek.

Twierdzenie II
Zmiana granic całkowania powoduje zmianę znaku przed całką.

Twierdzenie III – o wartości średniej
Jeśli funkcja f(x) jest ciągła na przedziale <a,b> to istnieje taki punkt c należący do <a,b>, że

- wartośd średnia funkcji w przedziale <a,b>

Pole tego prostokąta to geometryczna interpretacja.

Twierdzenie IV
Jeżeli F(x) jest funkcją pierwotną funkcji f(x) ciągłej na przedziale <a,b> to:

Całki niewłaściwe I rodzaju

Rozważmy funkcję f(x) na przedziale <a,b), niech ta funkcja będzie nieograniczona w otoczeniu punktu x=b oraz
całkowalna na przedziale <a,b-ε> 0< ε< b-a
Wówczas całka ma postad:

Jeżeli istnieje granica to całkę nazywamy całką niewłaściwą I rodzaju.

Analogicznie jest w dolnym przedziale całkowania.

Całki niewłaściwe II rodzaju

a) Niech f(x) będzie określone i ciągłe na przedziale <a, ), wówczas zamieniamy taką całkę na całkę

oznaczoną.

b) Niech f(x) będzie określone i ciągłe na przedziale (

>, wówczas zamieniamy taką całkę na całkę

oznaczoną.

c) Niech f(x) będzie określone i ciągłe na przedziale (

), wówczas zamieniamy taką całkę na:

c€(

)

Uwaga:
Gdy istnieje skooczona granica to takie całki nazywamy zbieżnymi, w przeciwnym wypadku nazywamy
rozbieżnymi.

Geometryczne zastosowanie całki oznaczonej

1. Pole obszaru płaskiego

- krzywa dana w postaci jawnej
y=f(x) x€<a,b>

-krzywa dana równaniem parametrycznym
x=x(t), y=y(t) t€<t1,t2>
gdzie funkcje x(t), y(t) są ciągłe na przedziale <t1,t2> oraz funkcja x(t) jest klasy c1 na tym przedziale
przy czym a=x(t1), b=x(t2)

-krzywa dana w postaci biegunowej
Pole obszaru D ograniczonego łukiem krzywej r( ) oraz promieniami wodzącymi o amplitudach α ,β.

Przy czym:

o

2

D

1

2

r( )

2

d

2. Długośd łuku krzywej

-krzywa dana w postaci jawnej
y=f(x), x€<a,b>. Funkcja ciągła wraz z I pochodną klasy C1 na <a,b>

l

a

b

x

1

f'' x

( )

2

d

f''

f''

-krzywa dana w postaci parametrycznej
x=x(t), y=y(t) t€<t1,t2>
gdzie funkcje x(t), y(t) są ciągłe na przedziale <t1,t2> oraz funkcja x(t) jest klasy c1

-krzywa dana w postaci biegunowej
Pole obszaru D ograniczonego łukiem krzywej r( ) oraz promieniami wodzącymi o amplitudach α ,β.

Przy czym:

o

2

3. Objętośd bryły powstałej poprzez obrót krzywej dookoła osi OX

4. Pole powierzchni bryły (gdy istnieje pierwsza pochodna i jest ciągła)

Uwaga:
Jeżeli krzywa jest dana w postaci x=g(y) jest ciągła i ograniczone y€<c,d> to obracamy dookoła OY.

l

t

1

t

2

t

x' t

( )

2

y' t

( )

2

d

x'

x'

l

r( )

2

r'( )

2

d

r

V

a

b

x

f x

( )

2

d

P

2

a

b

x

f x

( )

1

f'' x

( )

2

d

f''

f''

P

2

c

d

y

x y

( )

1

x' y

( )

2

d

x

V

c

d

y

x y

( )

2

d

x

x

Funkcje wielu zmiennych

Niech będą dane dwa zbiory A, Z. Jeśli każdemu punktowi (x,y) ze zbioru A przyporządkujemy według pewnego
przepisu liczbę ze zbioru Z to mówimy, że w zbiorze A została zdefiniowana określona funkcja dwóch zmiennych
x i y o wartości € Z.

(x,y)Z z=f(x,y)

Zbiór A nazywamy polem lub dziedziną funkcji. Zbiór Z nazywamy przeciwdziedziną funkcji lub zakresem. W
przypadku funkcji dwóch zmiennych dziedziną jest zbór płaski. W przypadku funkcji trzech zmiennych dziedziną
jest zbiór przestrzenny.

Definicja granicy funkcji dwóch zmiennych.
Mówimy, że funkcja f(x,y) ma w pkt xo,yo granicę g taką, że dla każdego epsilona>0 istnieje taka delta dodatnia,
że dla każdej pary x,y należącej do dziedziny spełniona jest nierównośd

Definicja ciągłości funkcji wielu zmiennych.
Mówimy, że funkcja f(x,y) jest ciągła w pkt xo,yo jeżeli istnieje w tym punkcie granica i ta granica równa się
wartości funkcji w punkcie.

Funkcję ciągła w każdym punkcie pewnego zbioru nazywamy funkcją ciągłą w tym zbiorze.

Pochodne cząstkowe funkcji dwóch zmiennych
a) Weźmy funkcję dwóch zmiennych f(x,y) w otoczeniu pewnego punktu (x,y) i nadajmy zmiennej y stałą
wartośd yo. Wówczas moja funkcja będzie funkcją jednej zmiennej x. Jeżeli funkcja (x)=f(x,yo) ma w pkt xo

pochodną to nazywamy ją pochodną cząstkową funkcji f(x,y) względem zmiennej x.
b) Analogicznie definiujemy pochodną cząstkową względem y.

Niech będzie dana funkcja n zmiennych. Pochodną cząstkową funkcji względem zmiennej xi nazywamy zwykłą
pochodną tej funkcji przy założeniu, że pozostałe zmienne są stałe.

Pochodne cząstkowe wyższych rzędów
Podobnie jak dla pochodnej funkcji jednej zmiennej wprowadza się pochodne cząstkowe wielu zmiennych. N-
ta pochodna cząstkowa będzie istnied jeśli będzie istniej pochodna rzędu n-1.

Twierdzenie Schwarza (o pochodnych mieszanych)

Założenie:
Jeżeli istnieje funkcja f(x,y) posiada pochodne mieszane i są ciągłe w punkcie to są one również równe w tym
punkcie.

x

xo

(

)

2

y

yo

(

)

2

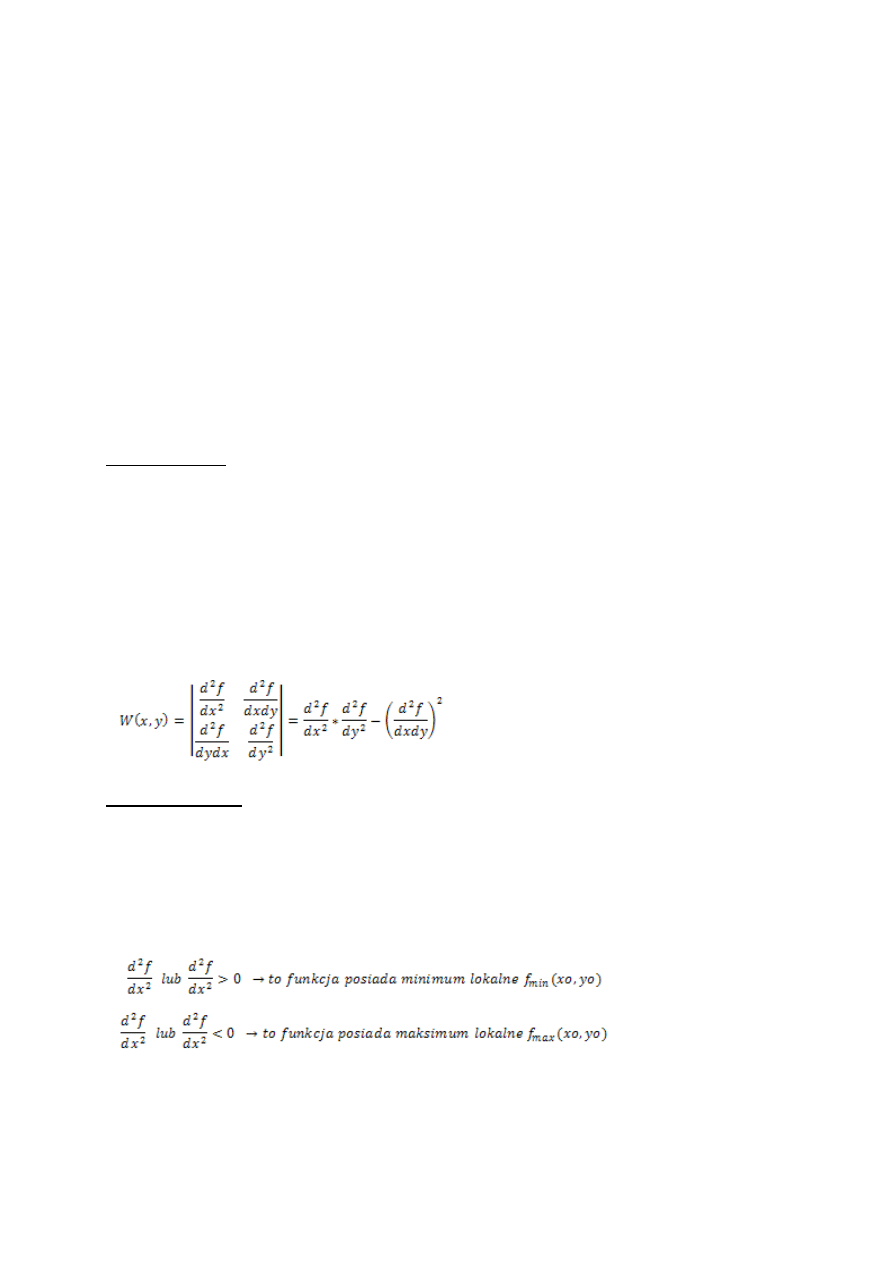
Twierdzenie Schwarza jest prawdziwe dla pochodnych cząstkowych wyższych rzędów.

Mówimy, że funkcja jest klasy Cn w pewnym obszarze D jeśli ma w tym obszarze wszystkie pochodne cząstkowe
rzędu n i są ciągłe.

Ekstrema lokalne funkcji dwóch zmiennych.

Weźmy dowolną funkcję f(x,y) określoną na (x,y)€D.

Def I
Mówimy, że funkcja f(x,y) ma w punkcie Po(xo,yo)€D maksimum lokalne jeśli istnieje takie otoczenie U(Po,r)€D,
że wartośd funkcji w punkcie Po jest f(Po)≥f(p) P€U(Po,r)

Def II
Mówimy, że funkcja f(x,y) ma w punkcie Po(xo,yo)€D minimum lokalne jeśli istnieje takie otoczenie U(Po,r)€D,
że wartośd funkcji w punkcie Po jest f(Po)≤f(p) P€U(Po,r)

Twierdzenie I
Warunek konieczny istnienia ekstremum funkcji dwóch zmiennych, mających pierwsze pochodne cząstkowe w
Po(xo,yo) jest znikanie tych pochodnych w tym punkcie.

Wniosek
Ekstrema lokalne funkcji f(x,y) mające pierwsze pochodne mogą wystąpid, ale nie muszą tylko w tych punktach
będących rozwiązaniem układu równao – pierwsze pochodne cząstkowe przyrównane do 0.
Jeżeli ten układ nie ma rozwiązao to funkcja nie ma ekstremum.

Definicja

Wyróżnikiem funkcji f(x,y) nazywamy taki wyznacznik funkcyjny:

Warunek dostateczny istnienia ekstremum:
Jeśli funkcja f(x,y) jest klasy C2 na obszarze D oraz Po(xo,yo)€D wraz z pewnym otoczeniem U(Po,r) oraz
spełnione są warunki:
1. Pierwsze pochodne są = 0
2. Wyróżnik funkcji jest większy od 0.

To nasza funkcja posiada ekstremum lokalne w pkt Po.

Uwaga
:Jeżeli wyróżnik funkcji jest <0 to nie ma ekstremum, a jeżeli jest = 0 to jest to przypadek wątpliwy.

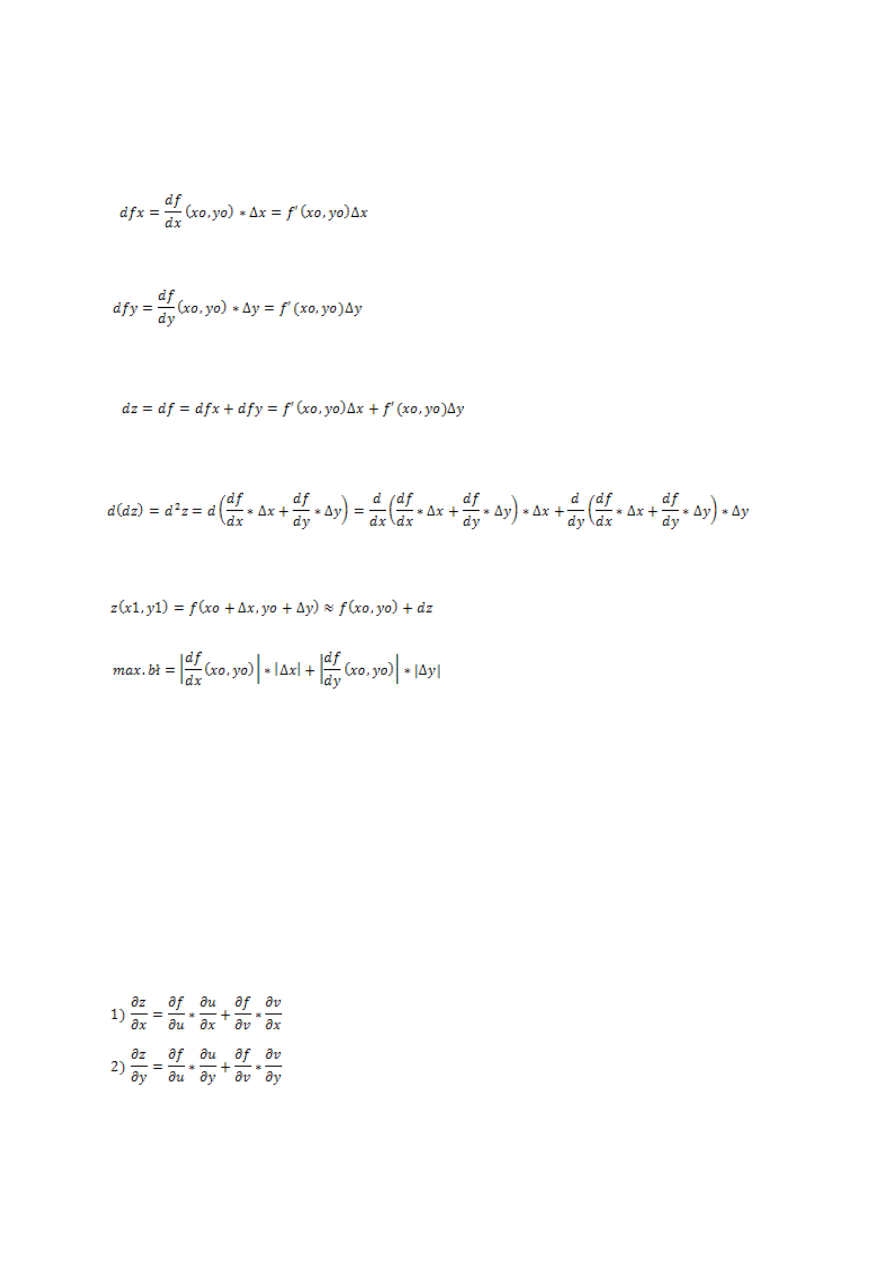
Różniczka zupełna funkcji dwóch zmiennych

Def I
Różniczką cząstkową funkcji f(x,y) w pkt (xo,yo) dla ∆x=x-xo względem zmiennej x nazywamy:

Def II
Różniczką cząstkową funkcji f(x,y) w pkt (xo,yo) dla ∆y=y-yo względem zmiennej y nazywamy:

Def III
Różniczką zupełną funkcji f(x,y) nazywamy sumę różniczek cząstkowych

Def IV
Różniczką rzędu drugiego nazywamy różniczkę różniczki tej funkcji

Zastosowanie różniczki zupełnej:
1. Przybliżona wartośd pewnego wyrażenia z=f(x,y).

2. Błąd maksymalny

Pochodne cząstkowe funkcji złożonej funkcji dwóch zmiennych

Niech będzie dana funkcja z=f(u,v) na pewnym obszarze płaskim G oraz dwie funkcje (u,v)€G.
u=u(x,y)
v=v(x,y) x,y€D

Jeśli dla każdego punktu (x,y)€D przyposządkowana jest para (u,v)€G to funkcję Z można uważad jako funkcję
złożoną zmiennych x i y.
Z=f[u(x,y),v(x,y)]

Twierdzenie
Jeśli funkcja z=f(u,v) ma na obszarze G ciągłe pochodne cząstkowe oraz funkcja u i v ma na obszarze D
pochodne cząstkowe względem x i y to funkcja złożona Z ma na tym obszarze również pochodne cząstkowe
względem zmiennej x,y określone wzorami:

Uwaga I
Jeżeli funkcję u i v dla funkcji Z zależą tylko od zmiennej x tzn. u=u(x) i v=v(x) to funkcja Z zależy tylko od
zmiennej x i wzór przyjmuje postad Z=f*u(x),v(x)+. W tym przypadku niektóre pochodne cząstkowe są zwykłymi
pochodnymi i wzór przyjmuje postad:

Uwaga II
Jeżeli u=x, v=y(x) to funkcja Z jest postaci Z=f*x,y(x)+ stąd pochodna:

Funkcja uwikłana funkcji jednej zmiennej

Załóżmy, że jest dane równanie F(x,y)=0, F określone na zbiorze D. Jeżeli istnieje taka funkcja y=f(x) spełniająca
w każdym x€X równanie F(x,y)=0 to nazywamy ją funkcją uwikłaną określoną równaniem F(x,y)=0.

Interesowad nas będą funkcje, które mają pochodne. Zagadnienie istnienia i jednoznaczności funkcji uwikłanej
rozstrzyga następujące twierdzenie.

Twierdzenie

Jeżeli funkcja f(x,y) spełnia następujące warunki
1) Istnieje punkt xo,yo, w którym wartośd F(xo,yo)=0

2) Pochodna cząstkowa

jest różna od 0.

3) Pochodne cząstkowe po x i y są ciągłe w otoczeniu punkt xo,yo

To istnieje w pewnym przedziale zawierającym punkt xo funkcja y=f(x) spełniająca dla każdego x tego przedziału
równanie F(x,f(x))=0.
Warunek: f(xo)=yo

Pochodna funkcji uwikłanej

Zakładając dodatkowo w twierdzeniu, że funkcja jest klasy C2 można znaleźd drugą pochodną y’’ funkcji
uwikłanej.

Analogicznie otrzymujemy pochodne wyższych rzędów. Znajdowanie pochodnych funkcji uwikłanych jest
szczególnie istotne w przypadku, gdy metodami rachunkowymi nie można wyznaczyd funkcji uwikłanej
określonej równaniem F(x,y)=0.

Jeśli równanie F(x,y)=0 wyznacza funkcję uwikłaną f(x) to można znaleźd jej ekstrema o ile istnieją bez
znajomości postaci jawnej funkcji f.

Równania różniczkowe

1. Równaniem różniczkowy zwyczajnym nazywamy równanie, w którym niewiadoma jest funkcja y(x) i w

którym występują pochodne tej funkcji y’,y’’,y’’’….y

zapisane w postaci *f(x,y,y’,y’’….y

n

)=0

2. Rzędem równania różniczkowego nazywamy najwyższy stopieo pochodne występujący w tym

równaniu.

3. Całką albo rozwiązaniem równania różniczkowego nazywamy każdą funkcję różniczkowalną y= (x),

która wraz z pochodnymi do rzędu n włącznie, spełnia w rozpatrywanym przedziale równanie
f[x, (x), ’(x)….

n

(x)]=0

Rozwiązanie równania różniczkowego rzędu n najczęściej uzyskujemy n-krotnym całkowaniem. Wynikiem
rozwiązania równania różniczkowego jest tzw krzywa całkowa lub linia całkowa.

Całką ogólna równania różniczkowego nazywamy funkcję postaci y=F(x,C1,C2….Cn) która zawiera n dowolnych
stałych niezależnych C1-Cn, która po wstawieniu liczb k1, k2, k3 wybranych dowolnie z naszego przedziału
będzie spełniad to równanie.

Funkcję postaci y= (x) spełniającą dane równanie różniczkowe nazywamy całką szczególną lub rozwiązaniem

szczególnym.

Zagadnienie Couch’iego dla równania różniczkowego * polega na znalezieniu takiego równania szczególnego,
które dla zadanego z góry argumentu x=xo oraz liczb yo,y1,…y

n-1

spełnia tzw. Warunki początkowe.

y(xo)=xo
y’(xo)=y1
y’’(xo)=y2
…
y

n

(xo)=y

n-1

Liczby yo,y1,…y

n-1

nazywamy warunkami początkowymi.

Równania różniczkowe pierwszego rzędu

F(x,y,y’)=0
y=F(x,C) – całka ogólna

Całką ogólną jest jednoparametrowa rodzina krzywych całkowych tego równania.

Zagadnienie Couch’iego dla równao różniczkowych pierwszego rzędu (mając całkę ogólną) polega na
wyznaczaniu takiej całki szczególnej, która dla pewnej z góry danej wartości zmiennej niezależnej x=xo przyjmie
z góry ustalone yo tzn. y(xo)=yo.

Uwzględniając w całkę ogólnej warunki początkowe, stad obliczymy stałą C. Wstawiając obliczoną wartośd do
równania ogólnego otrzymamy szukaną całkę szczególną.

W interpretacji geometrycznej zagadnienie Couch’iego polega na wybraniu z rodziny krzywych całkowych jedną
krzywą, która przechodzi przez z góry zadany punkt (xo,yo).

Klasyfikacja równao różniczkowych I rzędu.

Jednorodne

1) y’=f(x), f(x) - ciągła

2) y’=g(y), g(y) - ciągła

3) y’=f(x)*g(x), f(x),g(x) – ciągła

4) y’=f(x/y), f(x/y) – ciągła

y/x=u, y=x*u, y’=u’*x + u

Niejednorodne

5) y’+p(x)*y=f(x), f(x),p(x) – ciągła

6) Bernoulliego y’+p(x)*y=f(x)*y

n

n€R, n≠0, n≠1 y

1-n

=k

Równania różniczkowe drugiego rzędu

1) f(x,y,y’,y’’….y

n

)=0

2) Całka ogólna równania y=F(x,C1,C2) C1,C2 – const

3) y= (x)

Zagadnienie Couch’iego polega na znalezieniu takiej całki szczególnej y(x) x€(a,b) spełniającej w tym przedziale
równanie 1, a ponadto warunki początkowe y(xo)=yo, y’(xo)=y1.

W interpretacji geometrycznej zagadnienie Couchiego dla równania 1) polega na wybraniu z rodziny krzywych
całkowych jedną krzywą, która przechodzi przez punkt xo,yo i ma określony w tym punkcie kierunek.

Zagadnienie brzegowe dla równania 1 polega na wyznaczeniu takiego rozwiązania y(x) tego równania, które w
przedziale <a,b> spełnia warunki

y(x1)=y1
y(x2)=y2
x1,x2 € (a,b)

Geometrycznie zagadnienie brzegowe polega na znalezieniu takiej całki równania 1), której wykres przechodzi
przez 2 pkt.

Równania różniczkowe drugiego rzędu liniowe niejednorodne

1) y’’+p(x)y’+g(x)*y=f(x), p(x), g(x), f(x) – ciągłe

f(x)=0

2) y’’+p(x)y’+g(x)*y=0 równanie różniczkowe drugiego rzędu liniowe jednorodne

Własności równania 2.

a) Jeżeli y1(x) jest c. szczególną równania 2 dla x€(a,b) to funkcja jest też całką równania 2???

y=y(x)=c*y1(x) c=const

b) Jeżeli y1(x) i y2(x) są całkami szczególnymi równania 2 w przedziale (a,b) to suma y1(x) + y2(x) jest też

całką równania 2.

c) Jeżeli y1(x) i y2(x) są całkami szczególnymi równania 2 w przedziale (a,b) to funkcja

* y(x)=C1*y1(x)+C2*y2(x) C1, C2 = const
jest też rozwiązaniem równania 2.

Rozwiązanie równania * zawiera dwie dowolne stałe C1 i C2, będzie ono rozwiązaniem ogólnym równania jeśli
całki szczególne y1(x) i y2(x) są liniowo niezależne.

Definicja liniowej niezależności całek szczególnych

Dwie funkcje y1(x) i y2(x) są liniowo niezależne w przedziale (a,b) jeśli żadna z nich nie jest = 0 na tym przedziale
i stosunek y2(x)/y1(x) nie jest stałą.

Jeśli założymy różniczkowalnośd funkcji to warunek liniowej nie zależności można wyrazid w postaci

Ten wyznacznik funkcyjny nazywamy Wrooskim albo wyznacznikiem Wrooskiego

Twierdzenie

Jeżeli y1(x) i y2(x) są całkami szczególnymi równania linowo niezależnymi to funkcja y(x)=C1*y1(x)+C2*y2(x)
jest całką ogólną równania 2.

Równania różniczkowe drugiego rzędu liniowe jednorodne o stałych współczynnikach

1) y’’+ p*y’ + g*y=0 p,q = const

Zakładamy, że rozwiązanie tego równania jest postaci
2) y = e

rx

r- dowolna stała którą należy dobrad aby równanie 2 spełniało równanie 1

y’ = r * e

rx

, y’’ = r

2

* e

rx

wstawiam to do równania i dziele przez e

rx

bo to zawsze >0 i powstaje

3) r

2

+ p*r + q = 0

Równanie 3 jest zwykłym równaniem kwadratowym i w zależności od delty wartośd r się zmienia.

a) ∆>0 r1≠r2 y1(x)= e

r1x

y2(x)= e

r2x

b) ∆=0

c) ∆<0 r

1

=a+bi, r

2

=a-bi

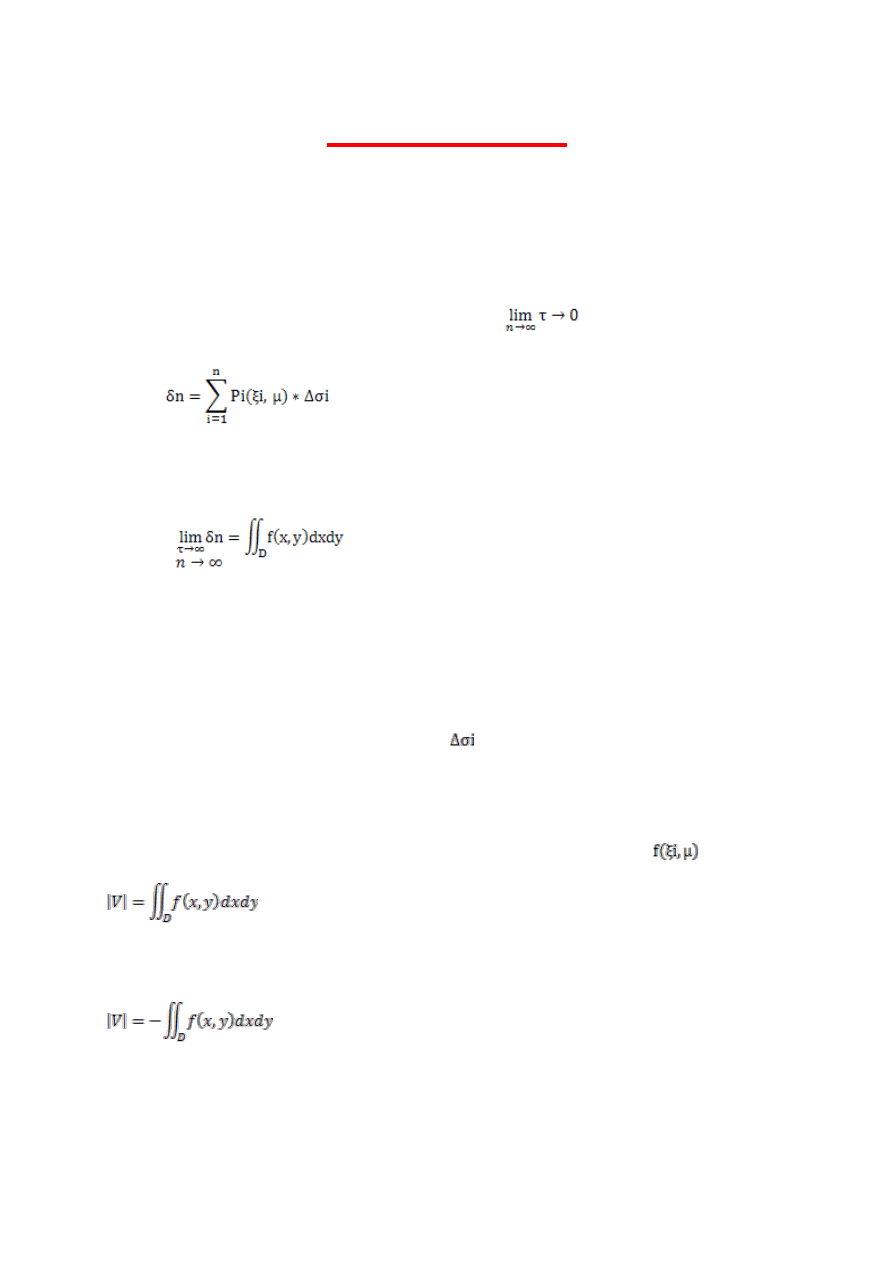
Całka podwójna

Niech będzie dana funkcja f(x,y) określona I ograniczone w obszarze płaskim |D| jak w przypadku całki
oznaczonej:

a) Dzielimy obszar D na dowolny sposób na n podprzedziałów Di o polach ∆

δ

i

i=1,2…n

b) W każdym podobszarze Di dobieramy punkt pośredni o współrzędnych Pi(ksi

i

, ni

i

).

c) Dokonujemy normalnego ciągu podziału obszaru Di tzn.

d)

- suma całkowa

e) Jeżeli funkcja f(x,y) ma tę własnośd, że przy każdym ciągu normalnym podziału obszaru D i przy każdym

wyborze punktów pośrednich ciąg sum całkowych jest zbierzny do tej samej granicy to funkcję f(x,y)
nazywamy całkowalną w sensie Riemanna w obszarze D, a tę granice oznaczamy

i nazywamy całką podwójną funkcji f(x,y) w obszarze D.

Twierdzenie

Funkcja ograniczona w obszarze D jest w nim całkowalna jeśli jest ciągła wszędzie z wyjątkiem pkt leżących na
skooczonej ilości wykresów funkcji ciągłych. y=y(x), x=x(y)

Interpretacja geometryczna

Geometrycznie wartośd funkcji w punkcie i podobszarze

przedstawia V walca.

Zatem suma całkowa jest objętością figury złożonej z n walców o podstawach D1,D2…Dn.

Wniosek:

Jeżeli całka podwójna istnieje to jest ona miarą objętości bryły o podstawie Di i wysokości

.

Uwaga

Jeżeli funkcja podcałkowa f(x,y) jest <0 w obszarze D to

Uwaga II

Jeżeli funkcja podcałkowa tożsamościowo = 1 to całka podwójna przedstawia pole obszaru płaskiego

Uwaga III

Jeżeli f(x,y) zmienia znak w obszarze całkowania D to całka podwójna równa się sumie algebraicznej objętości
leżących na i pod osią OXY.

Uwaga IV

Własności całki podwójnej są jak w pojedynczej.

Obliczanie całki podwójnej w obszarze normalnym za pomocą całki iterowanej

Def I

Obszar domknięty D określony nierównościami

gdzie f(x),g(x) są ciągłe dla x€<a,b> i f(x)<g(x)

Obszar normalny względem osi OX.

Całka iterowana

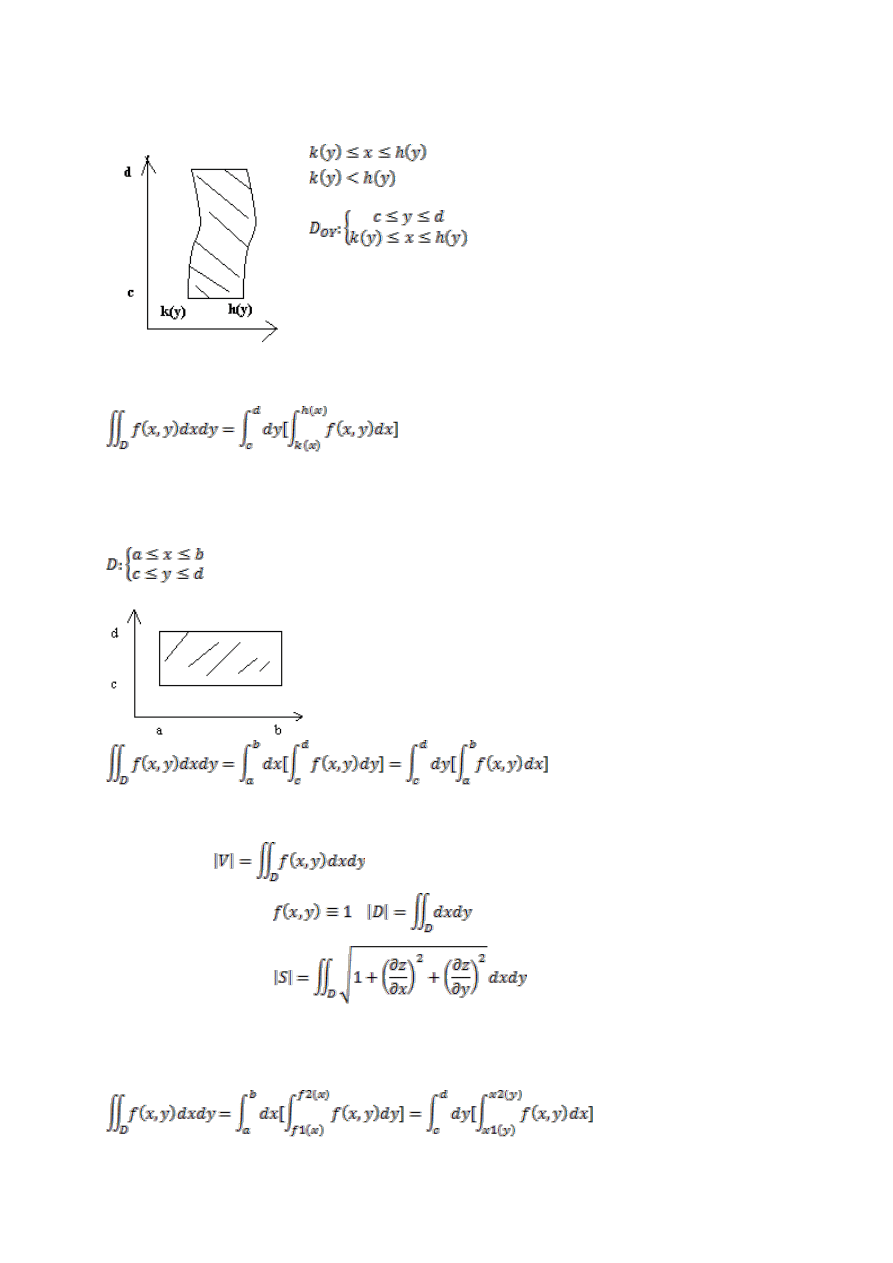
Def II

Całka iterowana

Uwaga

Jeżeli obszar jest prostokątem

Zastosowanie całki podwójnej

Objętośd bryły

Pole obszaru płaskiego

Pole płata powierzchni

Gdy obszar D jest normalny względem oby osi współrzędnych to wynik dwukrotnego całkowania nie
zależy od kolejności całkowania.

Jeśli obszar D można rozłożyd na n obszarów normalnych D1…Dn względem osi OX lub OY to całka w
obszarze D jest równa sumie całek w tych obszarach.

Zamiana zmiennych w całce podwójnej

*

x=x(u,v), y=y(u,v) (u,v)€∆

Załóżmy, że te równania przyporządkowujemy każdemu P€∆ punkt Q(x,y) obszaru D w ten sposób,
że różnym punktom obszaru ∆ odpowiadają punkty obszaru D i odwrotnie.

Obszar D jest obrazem obszaru ∆.
Przekształcenie dane równaniami * jest wzajemnie jednoznacznym, a więc istnieje do niego
przekształcenie odwrotne u=u(x,y), v=v(x,y).

Jeśli funkcje * są określone i różniczkowalne to wyznacznik funkcyjny:

Nazywamy go Jakobianem przekształcenia.

Twierdzenie, które służy do obliczania całki podwójnej za pomocą zamiany zmiennych:
1. Jeśli funkcje x(u,v), y(u,v) są klasy C1 w obszarze ∆.
2. Przekształcenie obszaru ∆ na D jest wzajemnie jednoznaczne.
3. Jakobian przekształcenia ≠ 0.

To całkę w obszarze D z funkcji zapisujemy

Obliczanie całki podwójnej w obszarze biegunowym

W przypadku gdy obszar D jest kołem, pierścieniem lub wycinkiem jednej z tych figur, a także w
innych przypadkach, gdy krzywa jest dana w postaci uwikłanej współrzędnych biegunowych to
wygodnie jest wprowadzid do obliczeo całki podwójnej współrzędne biegunowe.

x=x(r,

)=rcos

y=y(r, )=rsin

Uwaga I

Uwaga II

Jeśli obszar D jest ograniczony promieniami tworzącymi z osią biegunową kąty 1 i 2 i krzywymi

r1=r1( ) i r2=r2( ) r1( )<r2( )
wówczas obszar D jest określony równaniami:

Uwaga III

Jeżeli obszar D zawiera początek układu współrzędnych to obszar określają nierówności:

Przy funkcji wielu zmiennych pozamieniajcie sobie po wydrukowaniu w niektórych miejscach
wzory, bo zamiast jest tam zwykłe d.

Ogólnie bierzcie na to poprawkę, bo pisałem to po całej nocy pracy i kilku godzinach snu.

Jak widzicie jakieś bledy to się nimi pochwalcie.

Życzę wam powodzenia i zaliczenia Baśki.

Tomek M.

وأد ر برا با يي ق ت لام