www.it.pw.edu.pl/ztkut Laboratorium

Metrologii

1

Ćwiczenie nr 5

1. Tytuł ćwiczenia

WYZNACZANIE CHARAKTERYSTYK LICZBOWYCH ZMIENNYCH

LOSOWYCH NA PODSTAWIE DANYCH DOŚWIADCZALNYCH

2. Cel ćwiczenia
Celem ćwiczenia jest zapoznanie studentów z podstawowymi metodami statystycznej oceny
wyników pomiarów otrzymanych na stanowisku kontroli produkcji.
W produkcji wielkoseryjnej i masowej jest niemożliwe sprawdzanie dokładności wykonania
każdego detalu, dlatego też sprawdzana jest dokładnie tylko pewna próbka n-elementowa
wybrana losowo z całej produkcji np. w danym dniu.
Ten sposób postępowania nazywa się statystyczną kontrolą jakości i stąd też wynika potrzeba
nabycia umiejętności wyznaczania charakterystyk liczbowych zmiennych losowych.
W ćwiczeniu dokonujemy analizy statystycznej określonej partii detali, o której chcemy się
dowiedzieć jak najwięcej czyli odpowiedzieć na pytania:

- czy wymiar poszczególnych detali mieści się w założonym polu tolerancji,
- czy rozkład wymiarów detali ma charakter rozkładu normalnego (w przybliżeniu).

W tym celu określamy charakterystyki statystyczne wyników pomiarów i weryfikujemy
hipotezy parametryczne o wartości przeciętnej i wariancji czyli testujemy hipotezy statystyczne.
Hipoteza statystyczna – dowolne przypuszczenia co do rozkładu populacji generalnej (jego

postaci funkcji lub wartości parametrów).

Test statystyczny – reguła postępowania, która każdej możliwej próbie przyporządkowuje

decyzje przyjęcia lub odrzucenia hipotezy.

3. Wprowadzenie teoretyczne
Rozważmy uzyskany w wyniku pomiarów ciąg n-elementowy wartości pewnej wielkości x,
którą będziemy utożsamiać ze zmienną losową. Wartości (x

1

, x

2

, .. x

n

) zmiennej losowej x

nazywamy próbą n-elementową .
Zadaniem opracowującego wyniki pomiarów jest znalezienie ocen (wartości przybliżonych) dla
charakterystyk liczbowych danej zmiennej losowej. Charakterystykami tymi są:

- wartość oczekiwana x,
- odchylenie standardowe

σ

x

,

- wariancja

σ

x

2

,

- momenty wyższych rzędów

µ

s

, m

s

,

- współczynnik asymetrii i spłaszczenia

γ

1

,

γ

2

.

Oceny tych charakterystyk, uzyskane na podstawie wyników pomiarów, oznaczamy tymi
samymi literami, co szukane charakterystyki, lecz z „wężykiem” u góry

2

~

,

~

,

~

x

x

x

σ

σ

itp.

Przy nieograniczonym wzroście liczebności próby n ocena powinna być zbieżna wg.
prawdopodobieństwa do ocenianego parametru.
Mając liczna próbę, elementy próby łączymy, grupując w klasach tworzących tzw.
uporządkowany szereg rozdzielczy

)

)

)

mcx

g

x

x

x

x

x

x

,

,

,

,

,

2

1

1

min

K

tablica.4.1.

Oceny wartości oczekiwanej wariancji i momentów wyższych rzędów dokonuje się wtedy w
sposób przybliżony korzystając ze wzorów:

(

)

i

n

i

i

i

n

i

i

P

x

x

P

x

x

⋅

−

=

⋅

=

∑

∑

=

∗

=

∗

2

1

1

~

~

,

~

σ

(4.1)

gdzie:

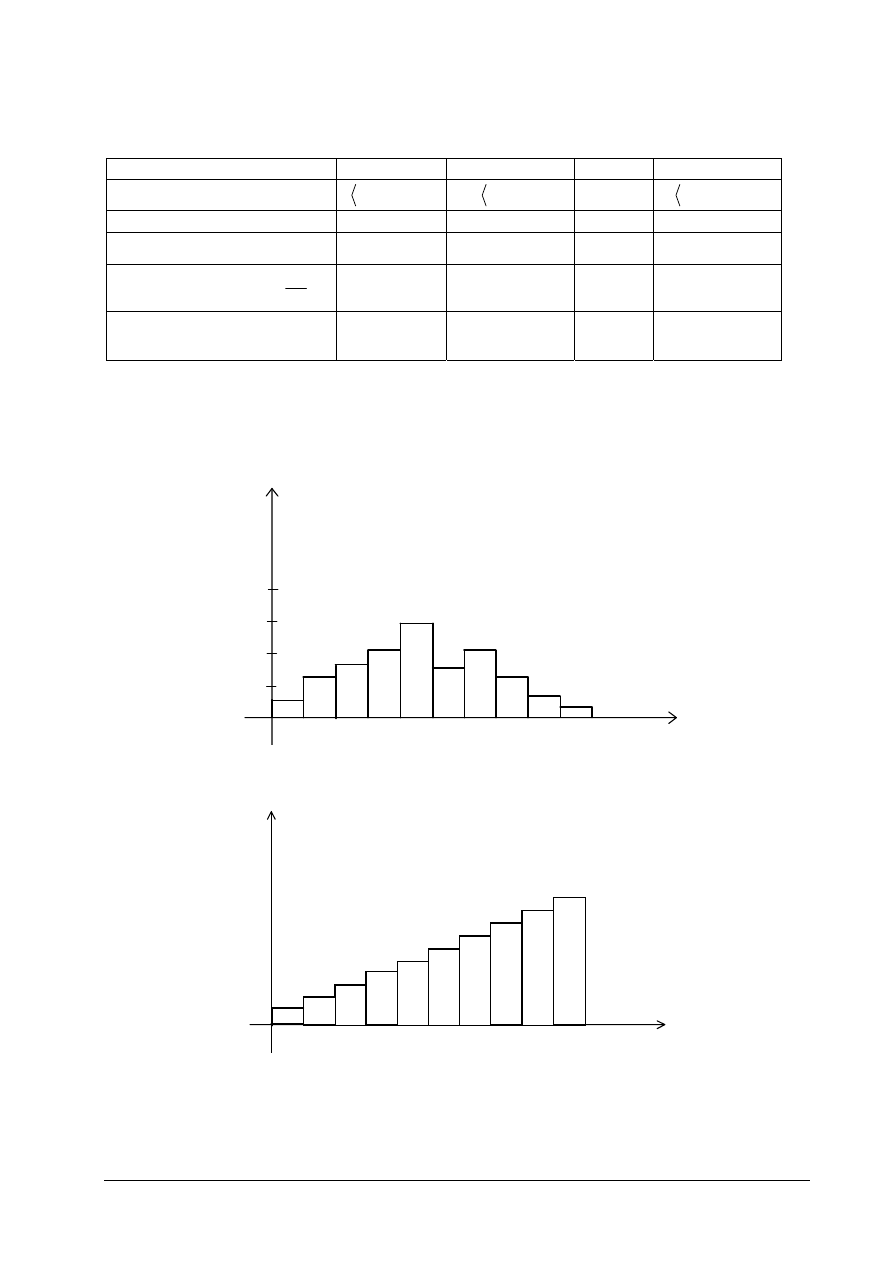
www.it.pw.edu.pl/ztkut Laboratorium Metrologii

2

∗

i

x - wartość średnia w i-tej klasie

P

i

– częstość (prawdopodobieństwo) zdarzeń w i-tej klasie

Tablica 4.1.

Nr klasy

1

2

....

10

Granice klasy

)

1

min

x

x

÷

2

1

x

x

÷

)

max

9

x

x

÷

Liczba elementów w klasie

m

1

m

2

m

10

Wartość średnia w klasie

∗

1

x

∗

2

x

∗

10

x

Częstość w klasie

n

m

P

i

i

=

P

1

P

2

P

10

Dystrybuanta w klasie

i

i

P

P

P

W

+

+

+

=

K

2

1

W

1

W

2

W

10

Korzystając z danych uzyskanych przy tworzeniu uporządkowanego szeregu rozdzielczego
wykonujemy wykresy (histogramy) empirycznych funkcji:

- gęstości prawdopodobieństwa (wykres zależności P

i

)

- dystrybuanty empirycznej W

i

1

2

3

4

5

6

7

8

9

10

n

Pi

0,25

0,5

0,75

1

Rys. 4.1. Przykładowy wykres gęstości prawdopodobieństwa

Wi

n

1

2 3 4 5 6 7

9

10

8

Rys. 4.2. Przykładowy rozkład dystrybuanty empirycznej

Dalszym etapem analizy jest weryfikacja hipotezy o wartości przeciętnej oraz weryfikacja
hipotezy o wariancji wraz ze znalezieniem przedziału ufności dla wartości przeciętnej.

www.it.pw.edu.pl/ztkut Laboratorium Metrologii

3

Weryfikacja hipotez
l. Weryfikacja hipotezy o wartości przeciętnej w populacji generalnej.

Hipotezę orzekającą, że wartość przeciętna m jest równa liczbie m

0

, zapisujemy

H

(m = m

0

). Jeśli zmienna losowa x ma rozkład normalny N (m,

σ

), przy czym

σ

jest znane

i przyjmujemy poziom istotności

α

, to korzystając z tabl. II [l], wyznaczamy

ε

α

takie, by:

α

ε

σ

α

≈

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

≥

−

n

m

x

P

~

Jeśli zaobserwowana (obliczona) w n-elementowej próbie wartość

x~

jest taka, że:

n

m

x

σ

ε

α

~

0

≥

−

,

to hipotezę H (m = m

0

) odrzucamy.

W przypadku, gdy:

n

m

x

σ

ε

α

~

0

<

−

,

to nie ma podstaw do odrzucenia hipotezy H (m = m

0

).

Jeżeli nie ma podstaw do przyjęcia założenia, że cecha ma rozkład normalny, ale n > 30,
to w celu zweryfikowania hipotezy H (m = m

0

) można stosować postępowanie analogiczne jak

omówione wyżej, przy czym jako

σ

2

można przyjąć

2

~

σ

2. Weryfikacja hipotezy o wariancji.

Niech zmienna losowa x ma rozkład normalny, przy czym

σ

jest nie znane. Hipotezę

(

)

2

0

2

σ

σ

=

H

, tzn. że wariancja jest równa liczbie

2

0

σ

,

weryfikujemy, korzystając z faktu, że

zmienna losowa

(

)

2

1

2

0

2

0

2

2

~

1

~

∑

=

−

=

=

n

i

i

x

x

n

σ

σ

σ

χ

ma rozkład

χ

2

o n - l stopniach swobody. Przyjmujemy poziom istotności

α

. W tabl. IV [l]

znajdujemy

χ

2

α

takie, że

(

)

,

2

2

α

χ

χ

α

≈

≥

P

czyli

α

χ

σ

σ

α

=

≥

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

2

2

0

2

~

n

P

.

Hipotezę odrzucamy, jeśli

n

2

2

0

2

~

α

χ

σ

σ

≥

W przeciwnym przypadku hipotezę przyjmujemy.
3. Przedział, ufności.
Znajdowanie przedziału ufności dla wartości przeciętnej w rozkładzie normalnym, gdy jest
nieznana wariancja. Jeśli zmienna losowa x ma rozkład normalny N(m,

σ

) i

σ

jest nieznane, to

przedział ufności dla nieznanego również parametru m, wyznaczamy, korzystając z faktu, że
zmienna losowa

1

~

~

−

−

=

n

m

x

T

σ

ma rozkład

t Studenta, który jest stablicowany (tabl. III [l]).

www.it.pw.edu.pl/ztkut Laboratorium Metrologii

4

Dla prawdopodobieństwa 1-

α

(

α

- dany poziom istotności z tabl. III [l]) odczytujemy takie

ε

α

, że

α

ε

σ

α

−

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

≤

−

−

1

1

~

n

m

x

P

Przedziałem ufności dla parametru

m jest

.

~

1

~

;

~

1

~

⎥⎦

⎤

⎢⎣

⎡

+

−

+

−

−

x

n

x

n

σ

ε

σ

ε

α

α

4. Przebieg ćwiczenia
Ćwiczenie wykonujemy w dwóch etapach

Etap pierwszy

1. Przy pomocy czujnika indukcyjno-analogowego Vistronik wykonać pomiar średnicy 50

wałeczków ø15 i 50 wałeczków ø10.

1

2

3

4

Czujnik indukcyjny
analogowy
Vistronik A1

Rys. 4.3

Schemat blokowy stanowiska pomiarowego: 1 – kontrolowany detal,

2 – czujnik indukcyjny, 3- podstawa pomiarowa, 4 – stół pomiarowy

2. Na podstawie pomiarów utworzyć uporządkowany szereg rozdzielczy próby składający

się z 10-ciu klas (tablica 4.1) szerokość klasy:

10

min

max

x

x

−

3. Narysować wykresy (histogramy) gęstości prawdopodobieństwa (częstość wystąpienia

wymiaru w danej klasie) oraz dystrybuanty empirycznej.

4. Na podstawie wzorów 4.1 obliczyć (oszacować) wartość oczekiwaną i wariancję

(wartości z tablicy 4.1).

Etap drugi

Weryfikując hipotezy parametryczne o wartości przeciętnej i wariancji oszacować, czy
wszystkie wyniki populacji generalnej (przy założonym poziomie istotności

α

) zawierają się w

założonym polu tolerancji

m

0

± ∆m

gdzie:

∆m = 3

σ

0

Wartości:

m

0

,

∆m i

α

- podaje prowadzący.

5. Wymagania dotyczące sprawozdania

- Podstawowe definicje
- Tabela wyników pomiarów
- Wykresy gęstości prawdopodobieństwa i dystrybuanty empirycznej
- Weryfikacja hipotez
- Wnioski

6. Wymagania dotyczące zaliczenia ćwiczenia
Znajomość charakterystyk liczbowych zmiennej losowej. Znajomość pojęcia „uporządkowany
szereg rozdzielczy”. Znajomość sposobu weryfikacji hipotez o wartości przeciętnej i wariancji
7. Literatura
[1] Praca zbiorowa pod redakcją Jerzego Kisilowskiego:

Podstawy pomiarów wielkości stałych i

zmiennych w czasie, Laboratorium, Oficyna Wydawnicza PW, Warszawa 1995.