Strona 1

Zakład TKUT

www.it.pw.edu.pl/ztkut

Laboratorium Metrologii

Ćwiczenie nr 4

1. Tytuł ćwiczenia

POMIARY KĄTÓW

2. Cel ćwiczenia

Celem ćwiczenia jest praktyczna nauka pomiaru kąta metodą bezpośrednią i pośrednią

oraz wyznaczenie błędu pomiary. Błędy te należy wyznaczyć, traktując pomiary jako zmienne
losowe.

3. Wprowadzenie teoretyczne
Do pomiarów kątów, nachyleń i stożków stosuje się:

- uniwersalne przyrządy pomiarowe mechaniczne i sprzęt pomocniczy, jak kątomierze

uniwersalne, kątowniki nastawne, liniały sinusowe, skośnice sinusowe, kątomierze z
poziomicami, przyrządy czujnikowe, kulki i wałeczki pomiarowe,

- uniwersalne i specjalne przyrządy optyczne, jak kątomierze optyczne, optyczne

poziomice kątowe, głowice podziałowe optyczne, stoły podziałowe, mikroskopy
warsztatowe, goniometry, teodolity.

Wśród metod pomiarowych rozróżnia się:

- metody bezpośrednie,
- metody pośrednie.

4. Opis stanowiska
Bezpośrednie pomiary kątów z użyciem kątomierza uniwersalnego i optycznego

Pomiar kąta kątomierzem polega na przyłożeniu (bez szczelin) do powierzchni

przedmiotu obu ramion kątomierza, które tworzą mierzony kąt. Przykłady pomiarów kątów
kątomierzem uniwersalnym i optycznym zilustrowano na rys. 1 i 2.

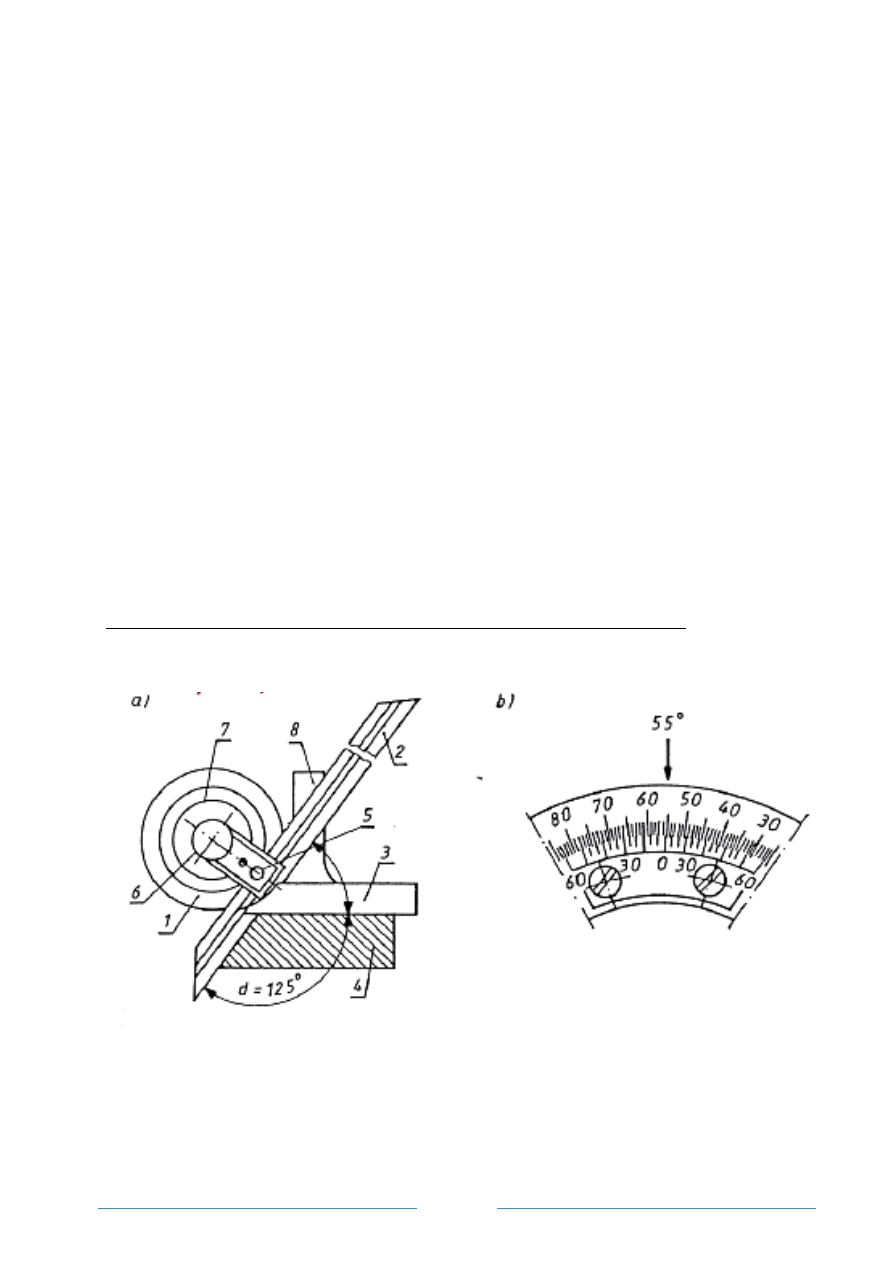
Rys. 1.

Kątomierz uniwersalny: a) przykład pomiaru kata, b) podziałka z noniuszem kątowym (wartość

dziatki elementarnej noniusza 5', moduł noniusza m = 2): 1- tarcza z podziałka główną,

2 - ramię ruchome, 3 - ramię stałe, 4 - przedmiot mierzony, 5 - zacisk ustalający wysunięcie ramienia

ruchomego, 6 - zacisk ustalający położenie kątowe ramienia ruchomego, 7 - noniusz kątowy,

8- poprzeczka ramienia stałego

Strona 2

Zakład TKUT

www.it.pw.edu.pl/ztkut

Laboratorium Metrologii

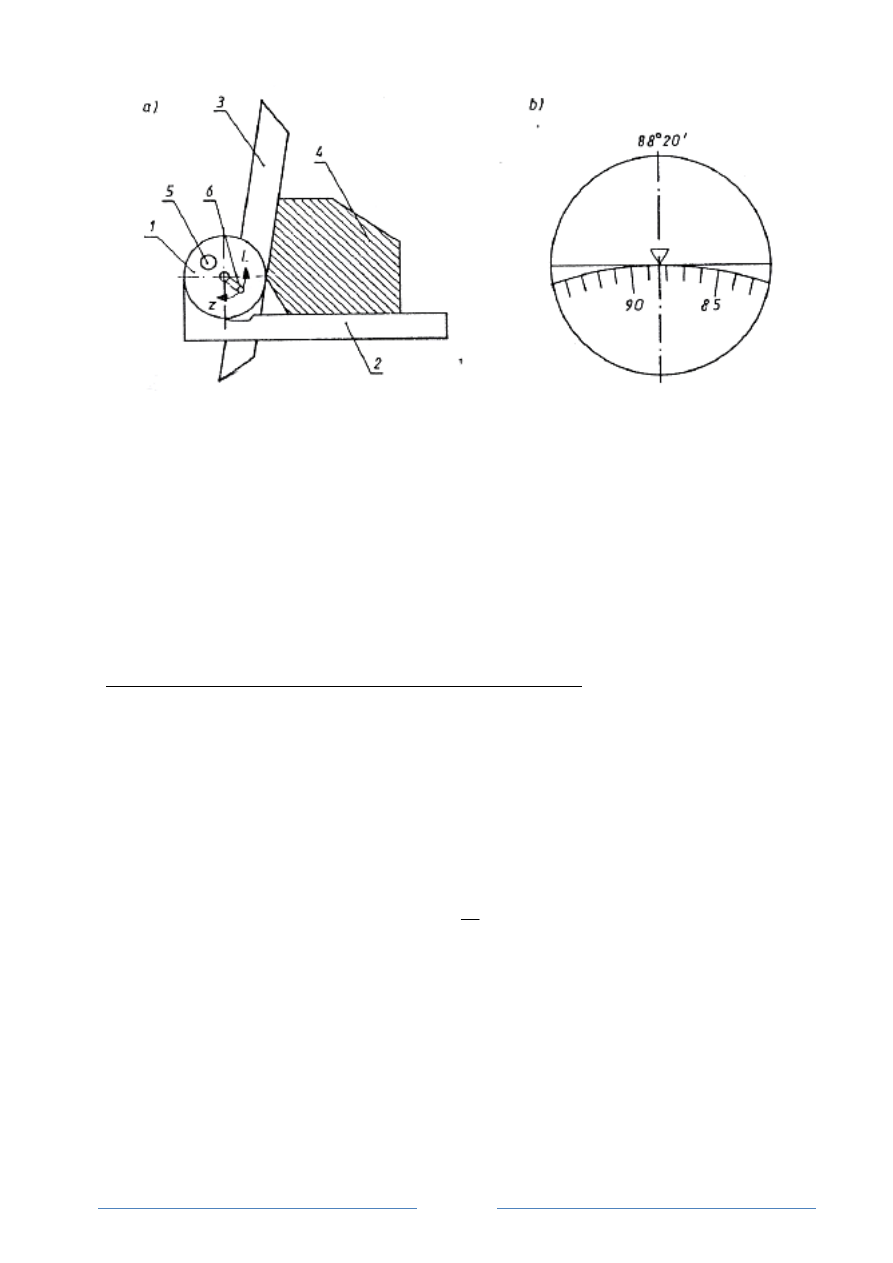
Rys.2 Kątomierz optyczny: a) przykład pomiaru kąta, b) podziałka ze wskazówką;

1

÷6 jak na rys. l

Wskazanie kątomierza uniwersalnego odczytuje się z podziałki kreskowej umieszczonej

na tarczy 1 (rys. 1). Zakres pomiarowy podziałki kątowej wynosi 0

÷360° (cztery razy 0÷90°).

Wartość działki elementarnej wynosi 1°.

Dwustronny noniusz kątowy pokazany na rys. 1 umożliwia odczytanie kąta o wartości

±5'. Przy pomiarze kątów rozwartych wskazanie kątomierza jest kątem dopełniającym do 180°.
Kąt mierzony jest

odczyt.

mierz.

180

α

α

−

=

o

Według rys. 1.

o

o

o

125

55

180

mierz.

=

−

=

α

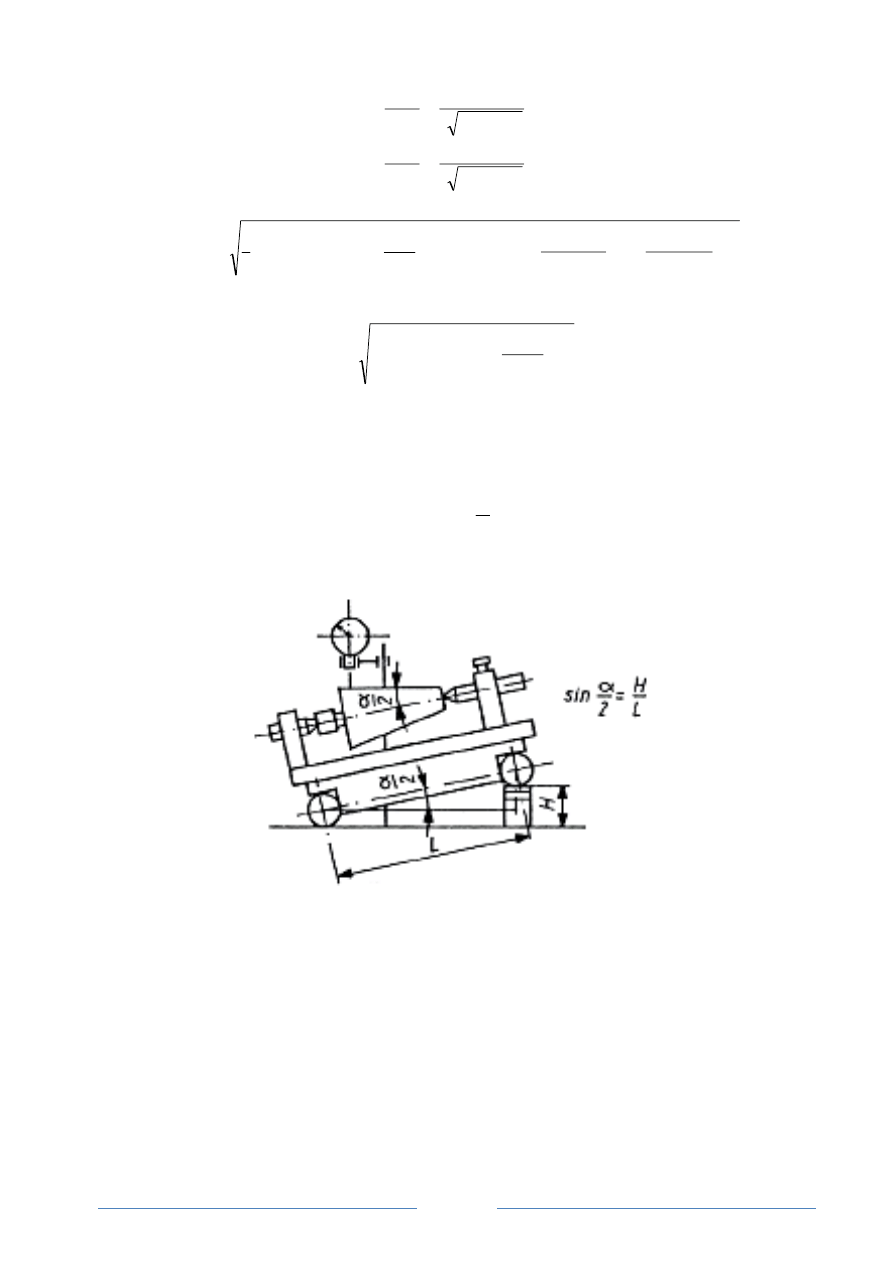
Pośrednie pomiary kątów i stożków z użyciem liniału sinusowego
Do pomiaru kąta liniałem sinusowym - oprócz liniału - używa się sprzętu pomocniczego, jak
płytek wzorcowych czujnika z podstawił oraz płyty pomiarowej. Liniał sinusowy składa się z
liniału opartego na dwóch walkach o jednakowej średnicy, których osie są równoległe do siebie i
leżą w płaszczyźnie równoległej do górnej płaszczyzny liniału. Odległość L między osiami
wałków wynosi 100 lub 200 mm. Pomiar kąta klina przy użyciu liniału sinusowego polega na
tym,

że po ustawieniu klina na liniale podstawia się pod jeden

z wałeczków stos płytek wzorcowych o takim wymiarze, aby górna płaszczyzna lub tworząca
mierzonego przedmiotu (klina lub stożka) była równoległa do płaszczyzny płyty pomiarowej, co
sprawdza się za pomocą czujnika. W przypadku spełnienia tego warunku różnica wskazań
czujnika (O

2

– O

1

) jest równa zero, a kąt klina

α

oblicza się ze wzoru (rys. 3)

L

H

=

α

sin

,

(1.11)

gdzie:
H - wysokość stosu płytek wzorcowych,
L - długość liniału wzorcowego.

Strona 3

Zakład TKUT

www.it.pw.edu.pl/ztkut

Laboratorium Metrologii

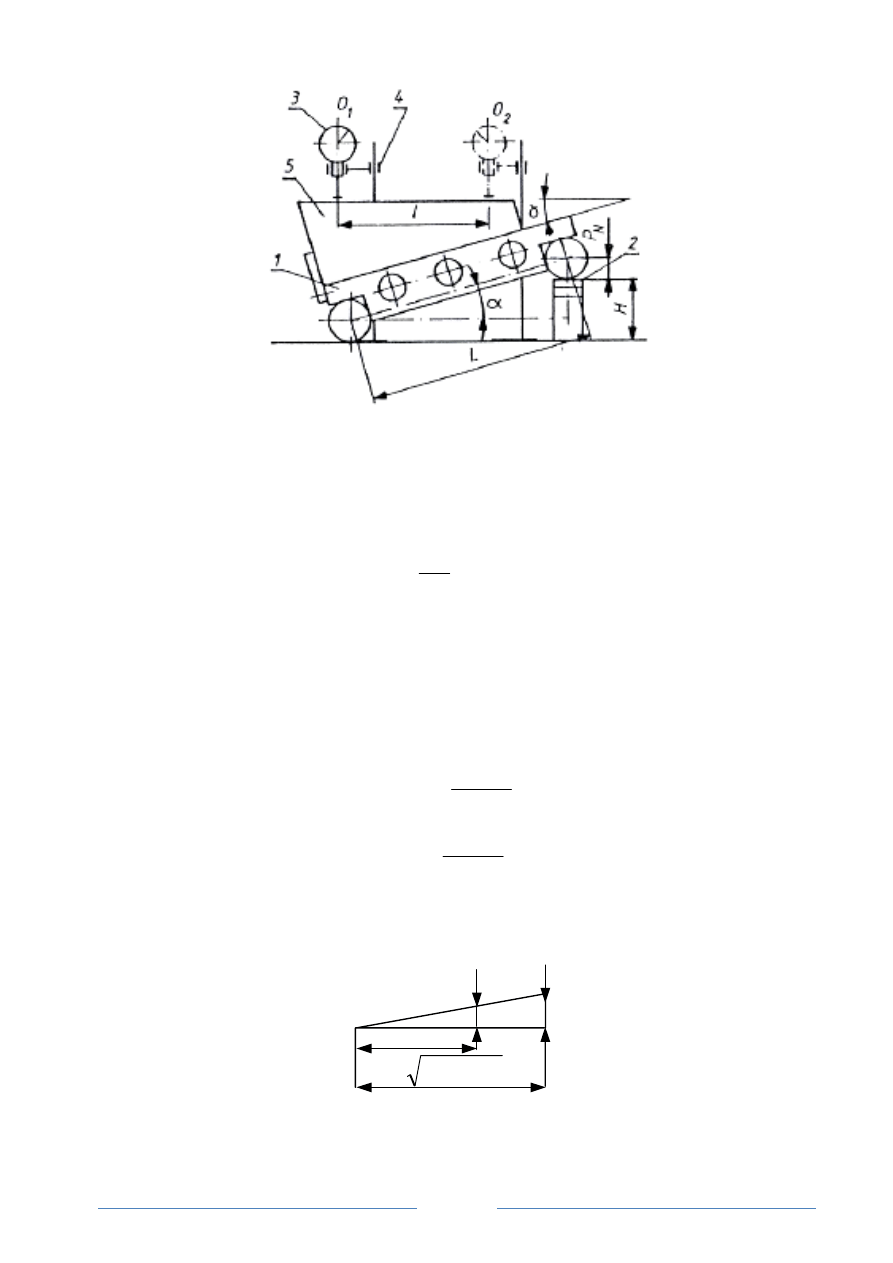
Rys.3 Schemat pomiaru kąta klina za pomocą liniału sinusowego: 1- liniał sinusowy,

2- płytki wzorcowe, 3- czujnik, 4 - statyw czujnika, 5 - przedmiot mierzony

Dobranie odpowiedniego stosu płytek wymaga przeprowadzenia wielu pracochłonnych

prób, ale i tak nie zawsze udaje się zestawić taki stos płytek, aby różnica wskazań czujnika w
skrajnych punktach mierzonego przedmiotu była równa zero. W tym przypadku należy do
obliczonego kąta dodać algebraicznie poprawkę, którą należy obliczyć ze wzoru

3438

l

W

∆

=

α

ρ

[min],

gdzie:
∆W = O

2

– O

1

- różnica wskazań czujnika [mm],

l

- odległość [mm] między skrajnymi położeniami czujnika, w których otrzymano
różnicę wskazań.

Znak poprawki

ρ

α

zależy od znaku różnicy wskazań czujnika

∆W.

Jeżeli

∆W > 0, to

ρ

α

< 0 i odwrotnie, jeżeli

∆

W < 0, to

ρ

α

> 0. W dokładnych pomiarach różnicę

wskazań czujnika uwzględnia się w postaci poprawki wysokości stosu płytek wzorcowych i
stosuje się następujący wzór na wynik pomiaru

L

P

H

H

+

=

α

sin

,

Skąd

L

P

H

H

+

= arcsin

α

, (1.12)

gdzie:
P

H

- poprawka do wysokości stosu płytek wzorcowych ze względu na różnicę wskazań

∆W

czujnika.

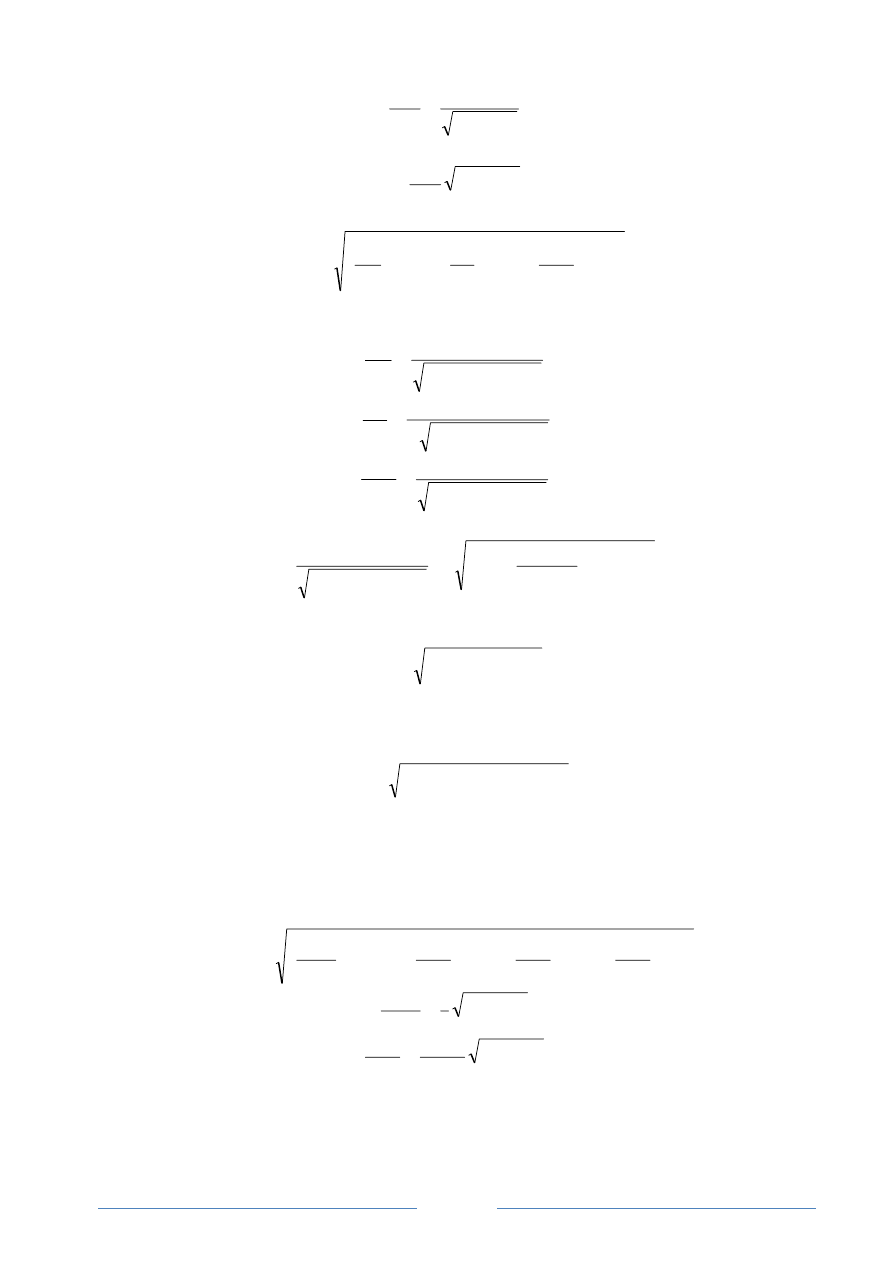
Wyznaczenie poprawki P

H

(rys.4)

l

2

2

H

L

−

∆

W

P

H

Rys. 4 Schemat do wyznaczania poprawki P

w

ze względu na różnicę wskazań czujnika W:

l – odległość punktów pomiaru czujnikiem, H – wymiar podstawionego pod liniał stosu płytek

wzorcowych.

Strona 4

Zakład TKUT

www.it.pw.edu.pl/ztkut

Laboratorium Metrologii

2

2

H

L

P

l

W

H

−

=

∆

,

skąd

2

2

H

L

l

W

P

H

−

∆

=

. (1.13)

Błąd graniczny pomiaru kąta za pomocą liniału na różnicę sinusowego oblicza się ze wzoru

2

2

2

2

2

2

H

P

H

L

H

e

P

e

L

e

H

e

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

+

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

+

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

±

=

α

α

α

α

,

który wynika z ogólnego wzoru na obliczanie błędów granicznych pomiarów pośrednich.
Różniczkując wzór (1.12), otrzymuje się

(

)

2

2

1

H

P

H

L

H

+

−

=

∂

∂

α

,

(

)

2

2

H

H

P

H

L

L

P

H

L

+

−

+

=

∂

∂

α

(

)

2

2

1

H

H

P

H

L

P

+

−

=

∂

∂

α

,

Skąd

(

)

2

2

2

2

2

2

1

H

P

L

H

H

H

H

e

e

L

P

H

e

e

P

H

L

e

+

⎟

⎠

⎞

⎜

⎝

⎛

+

+

+

−

±

=

α

. (1.14)

Błędy graniczne poszczególnych składników wynoszą:

a) e

H

- błąd graniczny wymiaru stosu płytek

,

2

2

2

1

K

+

+

=

N

N

H

e

e

e

gdzie:

K

2

1

,

N

N

e

e

- błędy graniczne wymiarów poszczególnych płytek;

b) e

L

- błąd graniczny długości liniału sinusowego

(

)

2

6

2

2

10

1

µm

2

tL

e

L

∆

⋅

+

±

=

−

,

L

t

t

−

=

∆

o

20

;

(odległość między osiami wałków liniału sinusowego wynosi 100 ± 0,002 mm

lub 100 ± 0,003 mm);
c)

H

P

e

- błąd graniczny wyznaczenia poprawki wysokości H na podstawie wskazań czujnika

oblicza się, różniczkując wzór (1.14)

2

2

2

2

2

2

2

2

H

H

L

H

L

H

W

H

P

e

H

P

e

L

P

e

L

P

e

W

P

e

H

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

+

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

+

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

+

⎟

⎠

⎞

⎜

⎝

⎛

∆

∂

∂

±

=

∆

,

2

2

1

H

L

l

W

P

H

−

=

∆

∂

∂

,

2

2

2

H

L

l

W

L

P

H

−

∆

−

=

∂

∂

,

Strona 5

Zakład TKUT

www.it.pw.edu.pl/ztkut

Laboratorium Metrologii

2

2

H

L

l

WL

L

P

H

−

∆

=

∂

∂

,

2

2

H

L

l

WH

H

P

H

−

∆

−

=

∂

∂

.

Po podstawieniu otrzymuje się

(

)

(

)

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2

1

H

L

l

W

P

e

H

L

H

W

e

H

L

L

W

e

H

L

l

W

e

H

L

l

e

H

−

∆

+

−

∆

+

−

⎟

⎠

⎞

⎜

⎝

⎛ ∆

+

−

±

=

∆

.

Ponieważ składniki trzeci i czwarty mają znikomy wpływ na wartość całego pierwiastka, mogą
być pominięte i ostateczny wzór przybiera postać

(

)

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

∆

+

−

±

≅

∆

2

2

2

2

2

2

l

W

P

e

l

W

e

H

L

e

H

. (1.15)

Praktycznie dla kątów mniejszych od 45° błąd graniczny pomiaru nie przekracza:

dla L = 100 mm ±15",
dla L = 200 mm ±8".

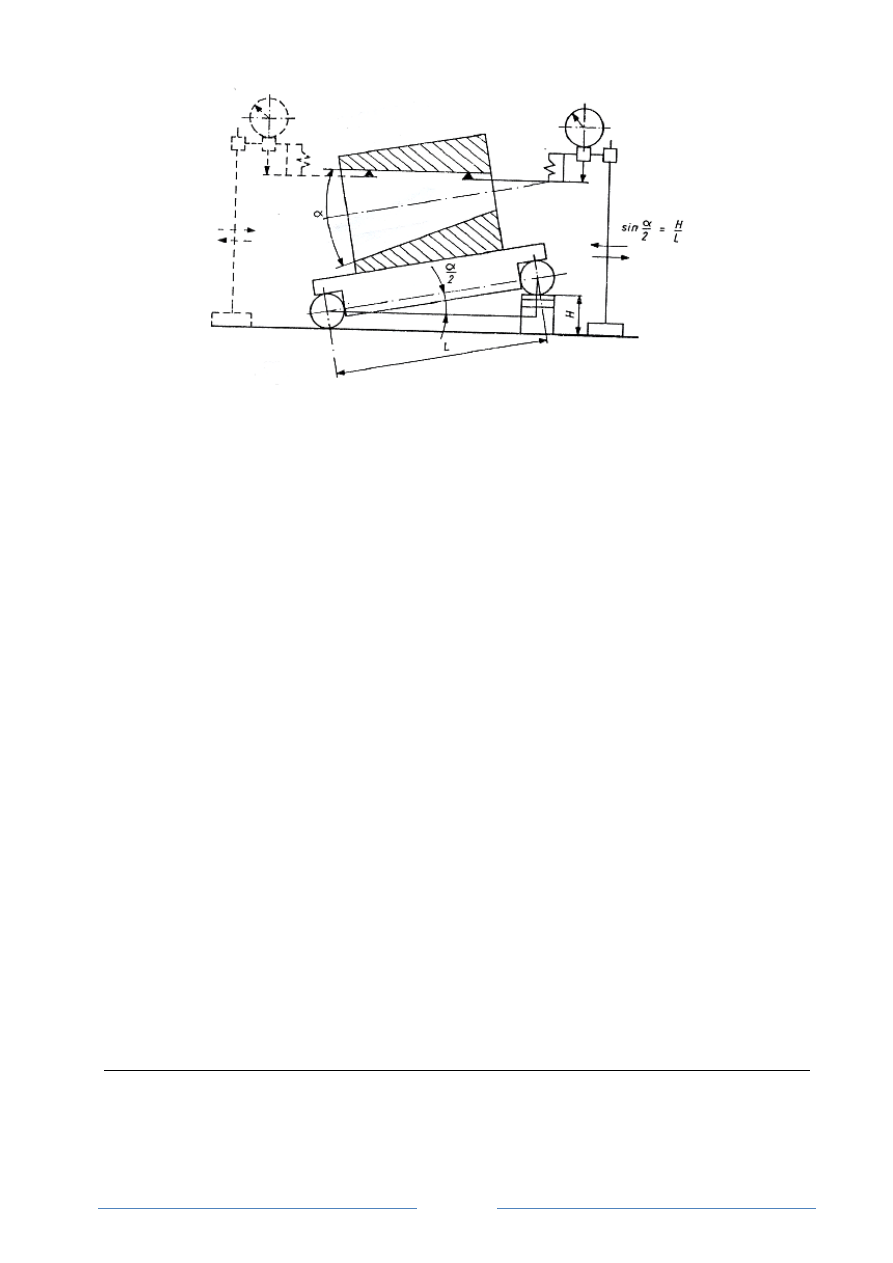
Przy pomiarze stożka zewnętrznego (mocowanego w kłach) za pomocą liniału sinusowego (rys.
5) zbieżność stożka oblicza się ze wzoru

2

tg

2

α

=

∆

,

gdzie:

α

/2 - połowa kąta wierzchołkowego stożka

Rys. 5 Schemat pomiaru stożka zewnętrznego za pomocą liniału sinusowego z uchwytem

kłowym

Pomiar stożka wewnętrznego wykonuje się zgodnie z zasadą pokazaną na rys. 6.

Strona 6

Zakład TKUT

www.it.pw.edu.pl/ztkut

Laboratorium Metrologii

Rys. 6 Schemat pomiaru stożka wewnętrznego za pomocą liniału sinusowego

5. Przebieg ćwiczenia

1. Pomiary kątów z użyciem kątomierza uniwersalnego.
2. Pomiary kątów z użyciem liniału sinusowego
3. Oszacowanie błędu wskazań pomiarów kątów za pomocą programu komputerowego

LPM2.

6. Wymagania dotyczące sprawozdania
Sprawozdanie powinno zawierać:

- opis wyników przebiegu ćwiczeń 1

÷3,

- wykresy błędów wskazań,
- wnioski końcowe.

7. Literatura
[l] Praca zbiorowa pod red. E. Ratajczyka: Laboratorium pomiarów wielkości geometrycznych.
Warszawa, WPW, 1976.
[2] Meller E., A.: Laboratorium metrologii warsztatowe,. Poznań, PWN, 1975.

Ostatnia aktualizacja dokumentu: 28.10.2008 rok.