G.4. Równanie wektorowe krzywej w przestrzeni

Funkcje wektorowe

Definicjea

Funkcję, która każdemu punktowi pewnego obszaru D przyporządkowuje określony wektor

nazywamy funkcją wektorową, a obszar D obszarem istnienia funkcji.

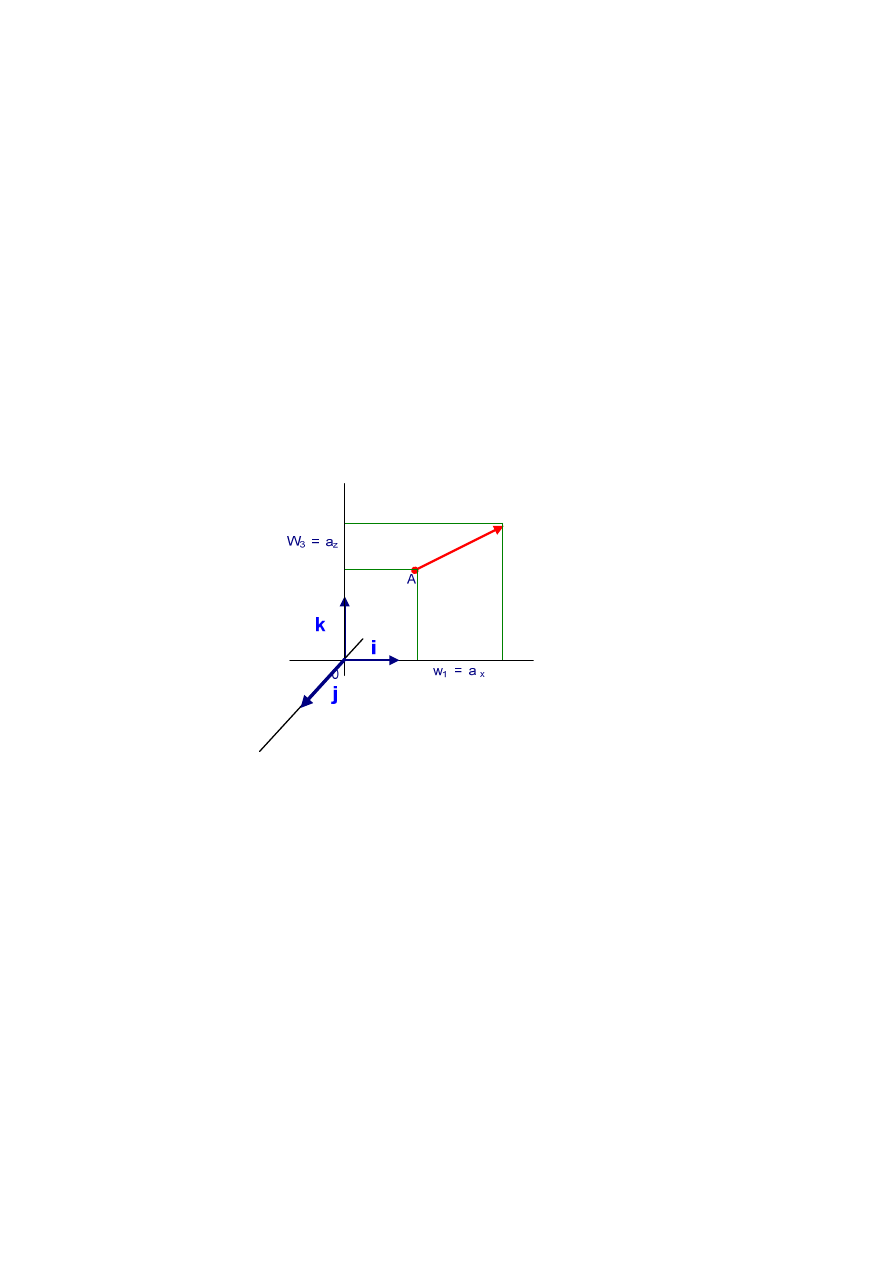
Załóżmy, że w trójwymiarowej przestrzeni kartezjańskiej Oxyz punkt A = (x, y, z) zaś

rzutami wektora

→

r

na oś x, oś y i oś z są odpowiednio funkcje – składowe wektora

→

r

:

w

1

= a

x

(x, y, z), w

2

= a

y

(x, y, z), w

3

= a

z

(x, y, z).

Tym samym wektor

→

r

jest wyznaczony przez podanie tych funkcji określonych w obsza-

rze D, co notujemy:

→

r

= [w

1

, w

2

, w

3

] = [a

x

(x, y, z); a

y

(x, y, z); a

z

(x, y, z)]

lub

→

r

= a

x

(x, y, z)

⋅

i + a

y

(x, y, z)

⋅

j + a

z

(x, y, z)

⋅

k.

gdzie i, j, k są wektorami jednostkowymi (wersorami) osi x, osi y i osi z.

W tym przypadku funkcje - składowe wektora

→

r

są funkcjami liczbowymi trzech zmien-

nych liczbowych (zmiennych x, y, z).

Przykład 1.

Funkcję wektorową definiujemy następująco:

→

r

= [3x – 2y; z – 1+ x; x + y + z].

Oznacza to, że:

a) punktowi A = (0, 1, -1) przyporządkowano wektor

→

A

r

= [-2, -2,0] = -2i -2j + 0 k,

b) punktowi B = (0, 0, 0) przyporządkowano wektor

→

B

r

= [0, -1,0] = -j.

Punktowi C = (2, 1, -3) nie jest przyporządkowany wektor

→

r

= [-1, -4,3] = -i -4j + 3k,

ponieważ -1

≠

3

⋅

2 - 2

⋅

1 = 4 .

Wektor

→

r

= [-1, -4,3] = -i -4j + 3k jest przyporządkowany takiemu punktowi

P = (x

0

,y

0

, z

0

), którego współrzędne spełniają układ równań 3x

0

– 2y

0

= -1 i z

0

– 1+ x

0

= -4

x

0

+ y

0

+ z

0

= 3. Jest to punkt P = (

3

13

−

, 6,

3

22

−

).

Przyjmijmy, że współrzędne punktu P = (x, y, z) są funkcjami parametru u

∈

[ a, b]

(czyli zależą tylko od u ). Czyli x = x(u) ; y = y(u) ; z = z(u).

Wiemy, że wartościami funkcji wektorowej w trójwymiarowej przestrzeni kartezjańskiej

Oxyz są wektory

→

r

= a

x

(x, y, z)

⋅

i + a

y

(x, y, z)

⋅

j + a

z

(x, y, z)

⋅

k. Skoro x = x(u) ; y = y(u);

z = z(u), więc także składowe wektora

→

r

są funkcjami jednej zmiennej liczbowej u

∈

[ a, b].

Oznaczmy: w

1

= a

x

(x, y, z) = a

x

(u); w

2

= a

y

(x, y, z) = a

y

(u); w

3

= a

z

(x, y, z) = a

z

(u).

Wtedy

→

r

= [a

x

(u); a

y

(u); a

z

(u)], dla u

∈

[ a, b]. Inaczej

→

r

= a

x

(u)i + a

y

(u)j + a

z

(u)k.

Oznacza to, że składowe wektora

→

r

będącego wartościami funkcji wektorowej

→

r

są

funkcjami liczbowymi jednej zmiennej liczbowej u.

Przykład 2.

Rozważmy funkcję wektorową

→

r

= r(u) = [3 - u; -4u+5; u

2

+ 3 u - 1] dla u

∈

[ -1, 3]

Wartościami tej funkcji są, na przykład, wektory:

a)

→

1

r

= [3, 5, -1] wyznaczony dla u = 0,

b)

→

2

r

= [2, 1, 3] wyznaczony dla u = 1,

c)

→

3

r

= [ 4, 9, -3] wyznaczony dla u = -1,

d)

→

4

r

= [1, -3, 9] wyznaczony dla u = 2.

Natomiast

→

5

r

= [ 0, -7, -1] nie jest wartością tej funkcji, ponieważ nie istnieje takie

u

∈

[ -1, 3], by jednoczenie 3 – u = 0 i -4u+5 = -7 i u

2

+ 3 u – 1 = -1.

Rozważmy te wartości funkcji wektorowej

= r(u) = [a

x

(u); a

y

(u); a

z

(u)] = a

x

(u) i + a

y

(u) j + a

z

(u) k dla u

∈

(a, b)

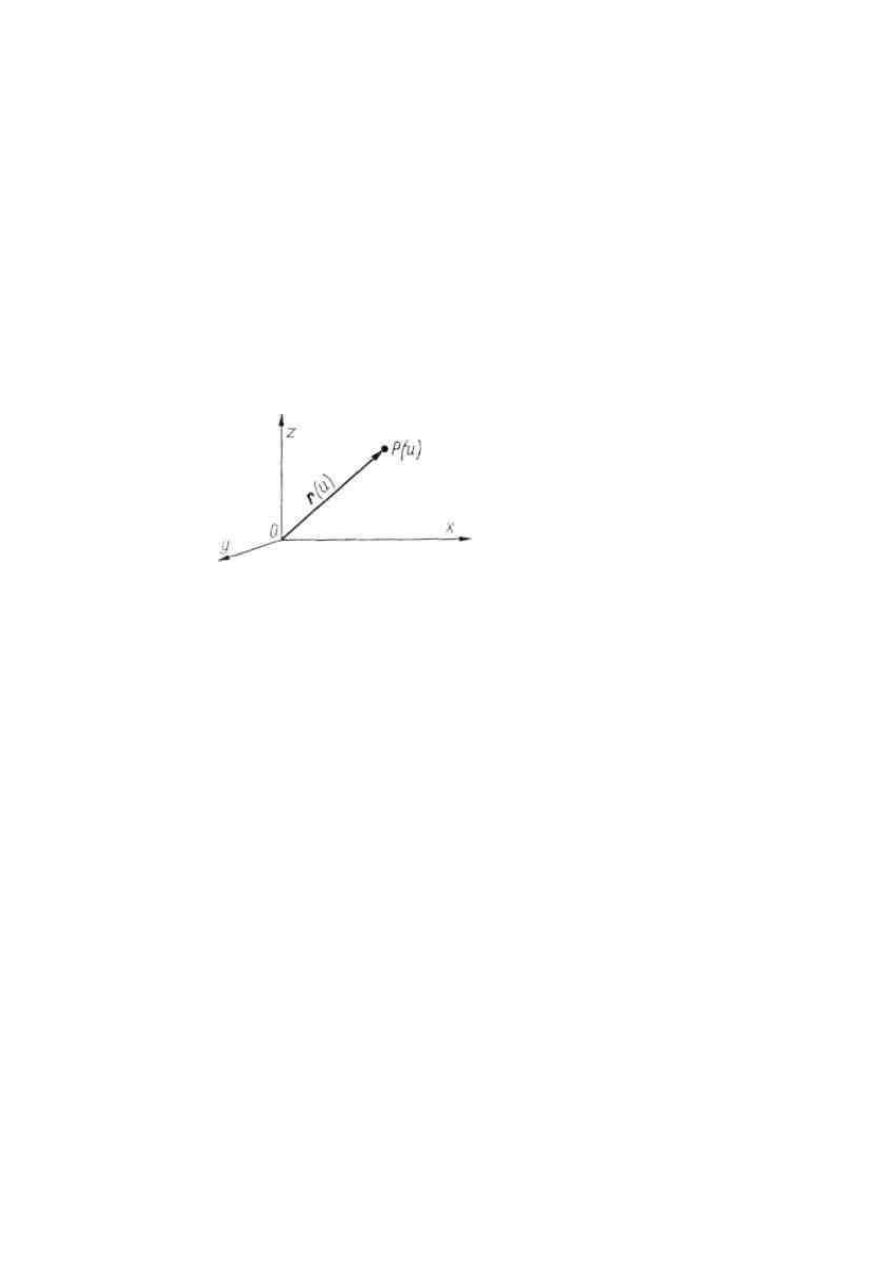
są reprezentowane „strzałkami” zaczepionymi w początku układu współrzędnych.

Rysunek przedstawia wektor r(u), gdzie u jest konkretnie wybraną liczbą z przedziału

(a, b), reprezentowany „strzałką”

→

OP

.

Mówimy, że wektor

→

r

= r(u) jest wektorem wodzącym punktu P(u) będącego końcem

wektora

→

r

= OP(u).

Gdy parametr u przebiega wszystkie wartości z przedziału (a, b), to zbiór punktów bę-

dących końcami wszystkich wektorów

→

r

= OP(u) - wektorów wodzących punktu P(u) - jest

określonym zbiorem punktów.

Przykład 3.

Wartościami funkcji wektorowej

→

r

= r(u) = [3u; -4u; u+1] = (3u) i + (-4u)j + (u+1) k , dla u

∈

[ -2, 4]

są, na przykład, wektory:

a)

→

1

r

= [0, 0, 1] wyznaczony dla u = 0,

b)

→

2

r

= [3, -4, 2] wyznaczony dla u = 1,

c)

→

3

r

= [ -3, 4, 0] wyznaczony dla u = -1,

d)

→

4

r

= [6, -8, 3] wyznaczony dla u = 2.

Niech O będzie początkiem układu współrzędnych. Rozważmy takie punkty A, B,

C, D, że wektory:

OA =

→

1

r

= [0, 0, 1] = 0 i + 0j + k = k ,

OB =

→

2

r

= [3, -4, 2] = 3 i -4j + 2 k,

OC =

→

3

r

= [ -3, 4, 0] = -3 i + 4j + 0 k = -3 i + 4j,

OD =

→

4

r

= [6, -8, 3] = 6 i -8j + 3 k.

Wektory OA, OB, OC, OD, jako wartości funkcji wektorowej

→

r

= (3u) i + (-4u)j + (u+1) k

dla argumentów u= 0, u= 1, u= -1, u= 2 są wektorami wodzącymi punktów A, B, C, D.

Równanie wektorowe krzywej. Wektor styczny.

Definicje

Załóżmy, że funkcja wektorowa

→

r

= r(u) = a

x

(u) i + a

y

(u) j + a

z

(u) k jest określona w prze-

dziale (a, b) parametru u. Załóżmy dalej, że funkcje w

1

= a

x

(u); w

2

= a

y

(u); w

3

= a

z

(u) są cią-

głe oraz ich funkcje pochodne w

1

’= a’

x

(u); w

2

’= a’

y

(u); w

3

’= a’

z

(u)] są ciągłe i nie są jedno-

cześnie równe 0.

a) Zbiór punktów P przestrzeni będących końcami wektorów wodzących

→

r

= OP nazywamy

krzywą, zaś

→

r

= r(u) nazywamy równaniem wektorowym tej krzywej.

b) Równania x = a

x

(u); y = a

y

(u); z = a

z

(u) nazywamy równaniami parametrycznymi tej

krzywej.

Przykład 4.

Wiemy, że układ równań x = 1 + 3t, y = -2 + 4t, z =5 – 7t, t

∈

R, opisuje prostą – nazwijmy ją

a - przechodzącą przez punkt A = (1, -2,5) równoległą do wektora w = [3, 4,-7].

Zgodnie z przyjętą umową równania x = 1 + 3t, y = -2 + 4t, z =5 – 7t, t

∈

R, są równa-

niami parametrycznymi prostej a. Jej równaniem wektorowym jest

→

r

= (1 + 3t) i + (-2 + 4t) j + (5 – 7t) k lub

→

r

= [1 + 3t, -2 + 4t, 5 – 7t] dla t

∈

R.

Definicja

Wektor

→

'

r

= r’ (u) = [a’

x

(u); a’

y

(u); a’

z

(u)] = a’

x

(u) i + a’

y

(u)j + a’

z

(u)k - jego składowymi są

pochodne funkcji w

1

= a

x

(u); w

2

= a

y

(u); w

3

= a

z

(u) - nazywamy wektorem stycznym do

krzywej L o równaniu

→

r

= r(u) = a

x

(u) i + a

y

(u) j + a

z

(u) k w punkcie P(u) krzywej L odpo-

wiadającym wartości u parametru z przedziału [a, b].

Twierdzenie - równanie stycznej

Jeżeli P(u

0

) jest danym punktem krzywej L, czyli P(u

0

) = ( a

x

(u

0

), a

y

(u

0

), a

z

(u

0

) ),

oraz r’ (u

0

) = a’

x

(u

0

) i + a’

y

(u

0

)j + a’

z

(u

0

)k jest wektorem stycznym do krzywej L w punkcie

P(u

0

), wtedy styczna - w układzie współrzędnych Oxyz – ma równania parametryczne

x

−

a

x

(u

0

) = t

⋅

a’

x

(u

0

); y

−

a

y

(u

0

) = t

⋅

a’

y

(u

0

), z

−

a

z

(u

0

) = t

⋅

a’

z

(u

0

) dla t

∈

R.

Przykład 5.

Dana jest krzywa o równaniu r(u) = u i + u

2

j - u

3

k dla u

∈

[ 0, 5].

a) Zbadaj, który z punktów A = (1, 3, -1), B = (0, 0, 0), C= ( -1, 1, 1), D = (3, 9, -27)

należy do tej krzywej.

b) Wyznacz wektor

→

s

styczny do tej krzywej w punkcie P = (2, 4, -8).

c) Napisz równanie prostej stycznej do tej krzywej w punkcie P = (2, 4, -8).

Rozwiązanie

a) Tylko punkt D należy do tej krzywej bowiem dla parametru u = 3 mamy

r(3) = 3 i + 9 j - 27 k.

b) Rozważamy funkcje f(u) = u, g(u) = u

2

, h(u) = - u

3

dla u

∈

[ 0, 5].

Mamy f’(u) = 1, g’(u) = 2u, h’(u) = - 3u

2

dla u

∈

[ 0, 5].

Punkt P jest końcem wektora OP, dla parametru u = 2.

Zatem: f’(2) = 1, g’(2) = 4 , h’(3) = - 12.

Poszukiwanym wektorem jest

→

s

= [1, 4, -12] = i + 4j – 12k.

c) Równanie stycznej jest następujące: x = -2 + t , y = -4 + 4t, z = 8 – 12 t dla t

∈

R.

Przykład 6.

W układzie współrzędnych kartezjańskich Oxyz prosta a dana jest układem równań parame-

trycznych

x = 2 + 3u, y = -3 + u, z = 4 - 5u

dla u

∈

R.

Punkt A = (2, 1, -5) należy do tej prostej. Aby się o tym przekonać wystarczy przyjąć,

że u = 0.

Jest ona równoległa do wektora [3, 1, -5].

Równanie r(u) = (2 + 3u) i + (-3 + u)j + (4 - 5u

)k dla u

∈

R jest równaniem wektorowym

tej prostej. Mówimy, że ta prosta jest sparametryzowana parametrem u.

Parametryzacja naturalna krzywej

Niech

→

r

= r(u), dla u

∈

[a, b], będzie równaniem wektorowym krzywej L; mówimy, że

krzywa ta jest sparametryzowana parametrem u.

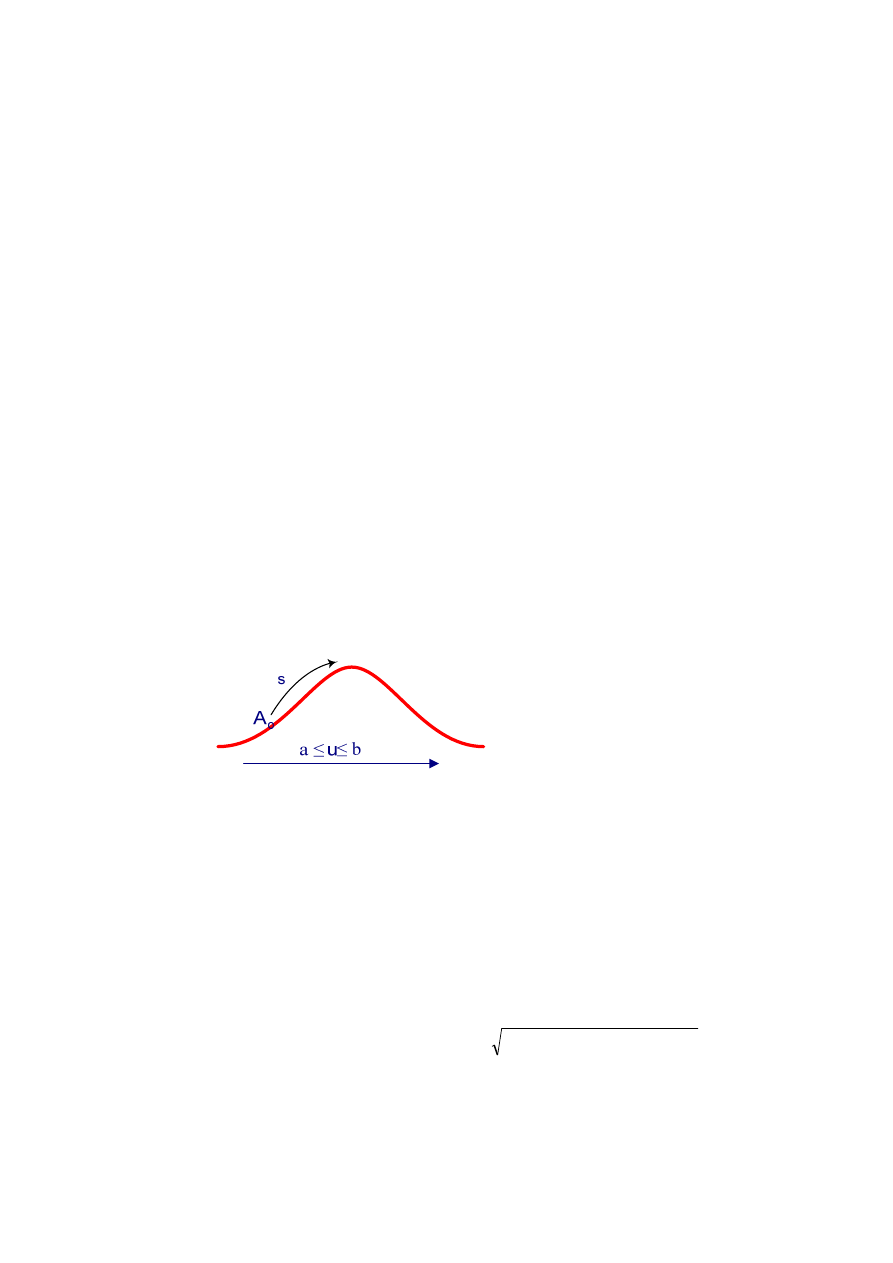
Wśród wszystkich możliwych parametrów krzywej można wybrać taki, który nazywa-

my parametrem naturalnym krzywej. Jest nim względna długość łuku krzywej, np. mierzona

od ustalonego jej punktu krzywej.

Na rysunku kolorem czerwonym przedstawiono krzywą L, parametr u

∈

[a, b], zaś parametr s

określa długość tej krzywej poczynając od punktu A krzywej L.

Przejścia od dowolnej parametryzacji do parametryzacji naturalnej dokonujemy następująco:

Przyjmijmy, że u

0

jest wartością parametru odpowiadającą ustalonemu punktowi P

0

krzy-

wej L o równaniu

→

r

= r(u) = a

x

(u) i + a

y

(u) j + a

z

(u) k, zaś u jest wartością parametru

odpowiadającą punktowi zmiennemu P, wtedy s =

∫

+

+

u

u

z

y

x

du

u

a

u

a

u

a

0

2

,

2

,

2

,

)]

(

[

)]

(

[

)]

(

[

.

Wzór ten określa długość s łuku jako ciągłą funkcję parametru u, wobec czego s = s(u).

Długość łuku krzywej od punktu P

0

, któremu od-

powiada wartość u

0

parametru do punktu P, które-

mu odpowiada wartość u parametru wyraża się

wzorem s =

∫

+

+

u

u

z

y

x

du

u

a

u

a

u

a

0

2

,

2

,

2

,

)]

(

[

)]

(

[

)]

(

[

.

Jeżeli pochodna

→

r

,

= r

,

(u) funkcji

→

r

= r(u) jest stale różna od zera, wtedy równanie

s = s(u) można napisać w postaci u = u(s), czyli jako funkcję długości s łuku. Wtedy równanie

→

r

= r(u) krzywej L można zapisać

→

r

= r[u(s)].

Jest to naturalna parametryzacja krzywej L; to równanie piszemy wówczas

→

r

= r(s),

gdzie s jest długością łuku mierzonego od punktu s = 0.

Przykład 7.

Dana jest krzywa L o równaniu r(u) = (2 + 3u) i + (-3 + u)j + (4 - 5u

)k dla u

≥

0 w układzie

współrzędnych kartezjańskich Oxyz. Napisz równanie krzywej L w parametryzacji natural-

nej.

Rozwiązanie

Niech P

0

będzie punktem tej krzywej odpowiadającym parametrowi u = 0, zaś P punktem

zmiennym odpowiadającym parametrowi u.

Długość łuku tej krzywej od P

0

do P wyraża się wzorem

s =

∫

−

+

+

−

+

+

u

du

u

u

u

0

2

,

2

,

2

,

]

)

5

4

[(

]

)

3

[(

]

)

3

2

[(

=

=

∫

−

+

+

u

du

0

2

2

2

]

5

[

]

1

[

]

3

[

=

∫

u

du

0

35

=

35

u.

Czyli s =

35

u. Stąd u =

35

1

s.

Zatem w parametryzacji naturalnej krzywa L ma następujące równanie

r(s) = (2 + 3

35

1

s) i + (-3 +

35

1

s)j + (4 - 5

35

1

s

)k dla s

≥

0.