
TRYGONOMETRIA SFERYCZNA
Zajmuje się obliczaniem trójkątów sferycznych. Trójkąt sferyczny to taki, który wierzchołki
ma na powierzchni kuli, a boki są krawędziami kół wielkich. Trójkąt „eulerowski” (boki i
kąty< 180°)
KĄT SFERYCZNY – powstaje tam gdzie przecinają się dwa boki kół wielkich.
MIARĄ KĄTA SFERYCZNEGO JEST:
1. Kąt płaski między dwoma stycznymi do boków kąta, które są łukami kół wielkich,
wystawionymi z wierzchołka kąta.
2. Kąt dwuścienny między dwoma płaszczyznami kół wielkich tworzących dany kąt
sferyczny.
3. Łuk zatoczony promieniem 90° z wierzchołka kąta miedzy jego ramionami.
BIEGUN ŁUKU KOŁA WIELKIEGO – nazywamy punkt odległy od niego o 90°. Równik
ma dwa bieguny północny i południowy. Każde koło wielki na kuli ma dwa bieguny leżące na
końcach jednej średnicy.

DWUKĄT SFERYCZNY – jego wierzchołki leżą na jednej średnicy, boki mają po 180°,
kąty są równe, można go podzielić na dwa trójkąty sferyczne
∆
ABC- trójkąt dany
∆
A’BC- trójkąt sprzężony
NAROŻE TRÓJŚCIENNE – powstaje po połączeniu trójkąta sferycznego ze środkiem kuli.
α
, β, γ - kąty płaskie = miary boków a, b, c
Zachodzą związki:
0
360
0
360
a b c
α β γ
° ≤
+ + ≤
°
° ≤ + + ≤
°
Suma kątów dwuściennych w narożu trójściennym jest mniejsza od 540° i większa od 180°
180 A
540
B C
° ≤
+ +
≤
° ←180° - przy zwiększeniu promienia kula dąży do powierzchni
płaskiej, i wtedy suma kątów jest minimalna
→
odejmuję 180° od obu stron
0 A
180 360
nadmiar sferyczny
=
180
B C
A B C
ε
° ≤
+ + −
° ≤
°
+ + −
°
NADMIAR SFERYCZNY – jest różnicą między sumą kątów sferycznych i sumą kątów
odpowiadającą figurze płaskiej.

TRÓJKĄTY WZAJEMNIE BIEGUNOWE I ICH WŁASNOŚCI
Trójkąt wewnętrzny jest
biegunowy wobec zewnętrznego.
Powstał przez zatoczenie wobec
wierzchołków łuków o promieniu
90°.
WŁASNOŚCI:
Wierzchołki jednego
trójkąta są biegunami boków
drugiego trójkąta ( i na odwrót)
A’
jest biegunem dla
a
B’
b
C’
c
A
a’
B
b’
C
c’
Suma kąta z małego trójkąta i boku naprzeciwległego z dużego trójkąta jest równa 180°
Dowód:
' 180
'
'
'
'
'
'
' 90 90 180 c.b.d.u.
A a
A KL
a B K KL LC
A a KL B K KL LC
A a
+ =
°
=
=
+
+
+ =
+
+
+
+ =
° +
°
=
°

PODSTAWOWE WZORY TRYGONOMETRII SFERYCZNEJ
Wzory cosinusowe dla boków
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
wyprowadzenie wzorów:
z trójkąta
i
2
cos
2
cos
2
cos
2
cos
podstawiam
2
cos
2
OKL AKL
KL
AK
AL
AK AL
A
KL OK
OL
OK OL
a
AK
AL
AK AL
A OK
OL
OK OL
a
OK
OA
AK
OL OA
AL
AK
AL
AK AL
A OA
AK
OA
AL
OK
=
+
−
⋅
⋅
=
+
−
⋅
⋅
+
−
⋅
⋅
=
+
−
⋅
⋅
=
+
=
+
+
− ⋅
⋅
⋅
=
+
+
+
− ⋅
⋅
2
cos
2
cos
2
cos
2
dzielę przez /2
cos
cos
WZORY Albataniego
Dla tr
cos cos cos sin sin cos
cos cos cos sin sin cos
cos cos cos sin sin cos
OL
a
OK OL
a
AK AL
A
OA
OK OL
OA OA AK AL
a
A
OK OL OK OL
a
b
c
b
c
A
b
a
c
a
c
B
c
a
b
a
b
C
⋅
⋅
⋅
⋅
= ⋅
⋅
⋅
+ ⋅
⋅
⋅
=
⋅
+
⋅
=
⋅
+
⋅
⋅
=
⋅
+
⋅
⋅
=
⋅
+
⋅
⋅
ójkąta biegunowego względem
cos ' cos ' cos ' sin ' sin ' cos '
podstawiam
' 180
' 180
' 180
' 180
cos
cos cos
sin sin cos
cos
cos cos
sin sin cos
cos
cos cos
sin sin co
ABC
a
b
c
b
c
A
a
A
b
B
c
C
A
a
A
B
C
B
C
a
A
B
C
B
C
a
B
A
C
A
C
=
⋅
+
⋅
⋅
=
°−
=
°−
=
°−
=
°−
−
=
⋅
−
⋅
⋅
=−
⋅
+
⋅
⋅
=−
⋅
+
⋅
⋅ s
cos
cos cos
sin sin cos
b
C
A
B
A
B
c
=−
⋅
+
⋅
⋅

Wzory sinusowe
sin
sin
sin
sin
sin
sin
a
b
c
A
B
C
=
=
Wzory 5 elementów (3 boki, 2 kąty)
2
wyprowadzenie wzorów:
do wzoru cosinusowego wstawiamy drugi cosinusowy innego boku
cos
cos cos sin sin cos
cos
cos cos sin sin cos / cos
wstawiamy za cos cos
cos
cos cos
sin
b
a
c
a
c
B
a
b
c
b
c
A
c
a
c
b
b
c
=
⋅
+
⋅
⋅
=
⋅
+
⋅
⋅
⋅
⋅
=
⋅
+
2
2
2
sin cos cos
sin sin cos
cos cos cos
sin sin cos cos
sin sin cos
cos (1 cos ) sin sin cos cos
sin sin cos / sin
sin
cos sin sin cos cos
sin cos
sin cos
si
b
c
c
A
a
c
B
b
b
c
b
c
c
A
a
c
B
b
c
b
c
c
A
a
c
B
c
c
b
c
b
c
A
a
B
a
B
⋅
⋅
⋅
+
⋅
⋅
−
⋅
=
⋅
⋅
⋅
+
⋅
⋅
−
=
⋅
⋅
⋅
+
⋅
⋅
÷
=
⋅
⋅
+
⋅
⋅
= n cos sin cos cos
sin cos
sin cos sin cos cos
c
b
b
c
A
b
A
c
a
a
c
B
−
⋅
⋅
⋅
=
−
⋅
⋅
Wzory 4 elementów (cotangensowe)
wyprowadzenie wzorów:
Do wzoru 5 elementów wstawiamy wzór sinusowy
sin cos
sin cos sin cos cos wz. 5 el.
sin sin
sin sin dzielimy stronami
sin
cos cos
sin
sin
sin
sin
b
A
c
a
a
c
B
b
A
a
B
c
c
B
ctgA ctga
B
B
ctgA
B
c ctga
⋅
=
−
⋅
⋅
⋅
=
⋅
⋅
=
−
⋅
=
⋅
−cos cos
sin
sin
cos cos
c
B
c ctga
B ctgA
c
B
⋅
⋅
=
⋅
+
⋅

PROSTOKĄTNY TRÓJKĄT SFERYCZNY
90 ponieważ cos90 0 to wzory się upraszczają
cos cos cos
cos
cos sin
sin
A
a
b
c
C
c
B
c ctgB tgb
=
°
°=
=
⋅
=
⋅
=
⋅
WYSOKOŚĆ TRÓJKĄTA SFERYCZNEGO
Wysokością nazywamy łuk koła wielkiego poprowadzony prostopadle z wierzchołka kąta do
boku przeciwległego.
sinh
sin a z trójkąta 1
sin
sin90
sinh
sin z trójkąta 2
sin
sin90
sinh sin sin sin sin
sinh sin sin / sin
sinh sin sin / sin
sinh sin
sin sin sin
sinh
b
b
b
b
a
b
a
c
A
a
C
A
c
a
C
a
C
b
b
C
a
b
a
b
C
=
←
°
=
←
°
=
⋅
=
⋅
−−−−−−−−−−−−−−−−−−−−−−
=
⋅
⋅
=
⋅
⋅
⋅
=
⋅
⋅
sin
sin sin sin
Tw. o wysokosciach w trójkącie sferycznym
sinh sin sinh sin sinh sin
a
a
b
C
a
b
c
a
c
b
⋅
=
⋅
⋅
⇒
⋅
=
⋅
=
⋅
TWIERDZENIE O WYSOKOŚCI W TRÓJKĄCIE SFERYCZNYM – iloczyn sinusa
boku i sinusa odpowiadającej mu wysokości jest wielkością stałą.
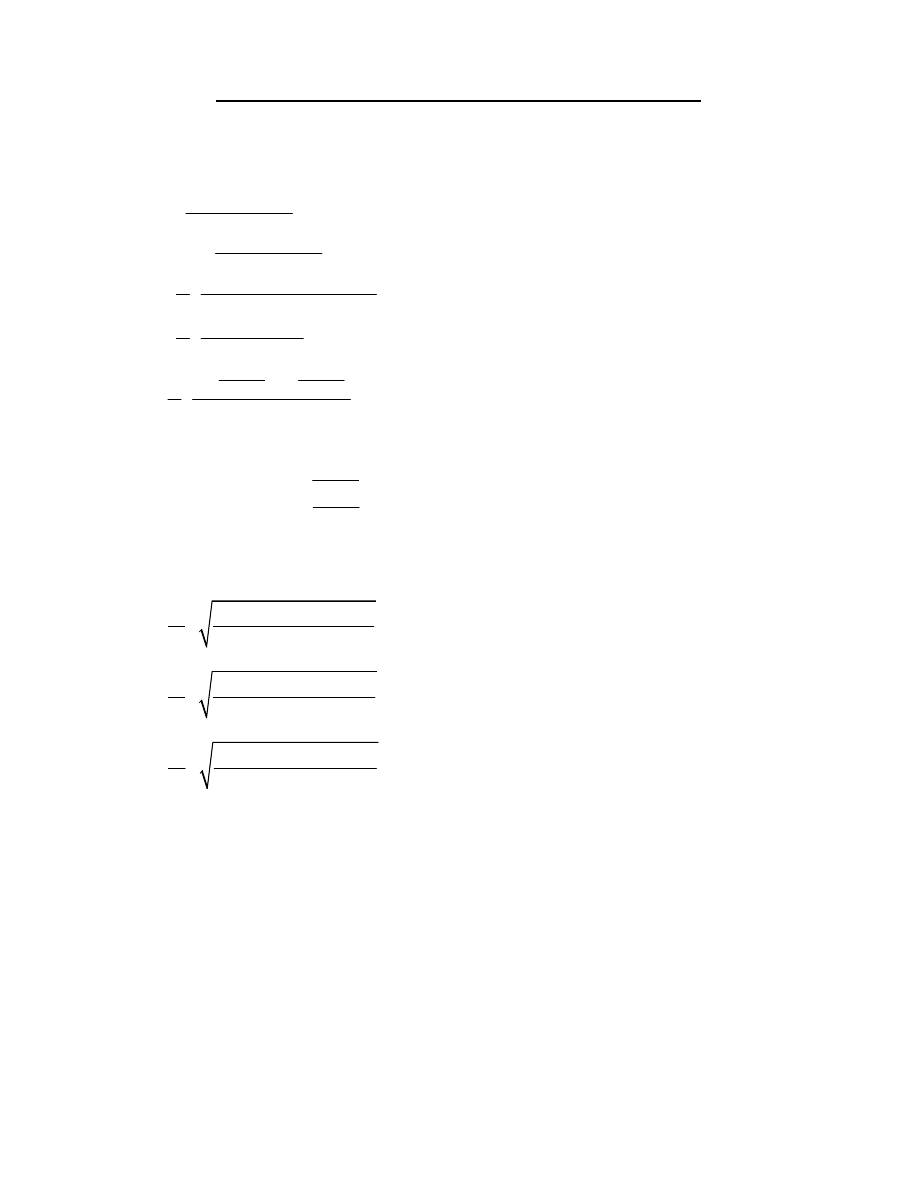
WZORY NA SINUSA KĄTA POŁÓWKOWEGO
2
2
wyprowadzenie wzorów:
cos
cos cos sin sin cos
cos cos cos
cos
sin sin
cos cos cos
1 cos
1
sin sin
sin sin cos cos cos
2sin
2
sin sin
cos(
) cos
2sin
różnica cosi
2
sin sin
a
b
c
b
c
A
a
b
c
A
b
c
a
b
c
A
b
c
b
c
b
c
a
A
b
c
b c
a
A
b
c
=
⋅
+
⋅
⋅
−
⋅
=
⋅
−
⋅
−
= −
⋅
⋅
+
⋅
−
=
⋅
− −
=
←
⋅
(
) (
)
2
nusów
sin
sin
2
2
sin
2
sin sin
wprowadzam oznaczenia
2
2
2
2
2
2
2
WZORY
sin(
) sin(
)
sin
2
sin sin
sin(
) sin(
sin
2
a b c
a b c
A
b
c
a b c
p
a b c
a b c
p
c
p c
a b c
a b c
p
b
p b
p b
p c
A
b
c
p a
p
B
+ −
− +
⋅
=
⋅
+ + =
+ −
+ − =
−
⇒
= −
+ +
− + =
−
⇒
= −
− ⋅
−
=
⋅
− ⋅
−
=
)
sin sin
sin(
) sin(
)
sin
2
sin sin
c
a
c
p a
p b
C
a
b
⋅
− ⋅
−
=
⋅

WZORY NA COSINUSA KĄTA POŁÓWKOWEGO
2
2
wyprowadzenie wzorów:
cos
cos cos sin sin cos
cos cos cos
cos
sin sin
cos cos cos
1 cos
1
sin sin
sin sin cos cos cos
2cos
2
sin sin
cos cos(
)
2cos
różnica cosi
2
sin sin
a
b
c
b
c
A
a
b
c
A
b
c
a
b
c
A
b
c
b
c
b
c
a
A
b
c
a
b c
A
b
c
=
⋅
+
⋅
⋅
−
⋅
=
⋅
−
⋅
+
= +
⋅
⋅
−
⋅
+
=
⋅
−
+
=
←
⋅
(
) (
)
2
nusów
sin
sin
2
2
cos
2
sin sin
wprowadzam oznaczenia
2
2
2
2
WZORY
cos
cos
sin sin(
)
2
sin sin
sin sin(
)
2
sin sin
sin sin(
)
sin
2
sin sin
a b c
b c a
A
b
c
a b c
p
b c a
b c a
p
a
p a
p
p a
A
b
c
p
p b
B
a
c
p
p c
C
a
b
+ +
+ −
⋅
=
⋅
+ + =
+ −
+ − =
−
⇒
= −
⋅
−
=
⋅
⋅
−
=
⋅
⋅
−
=
⋅
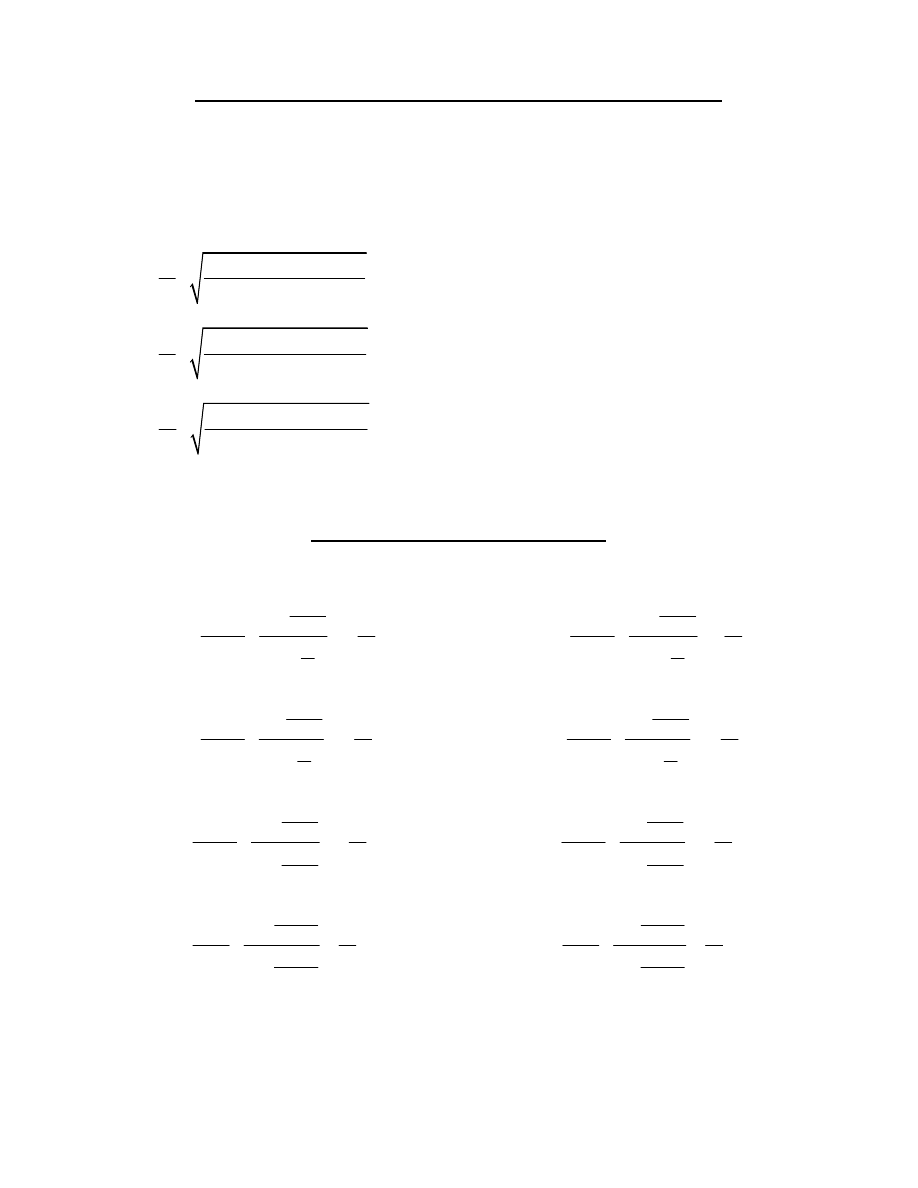
WZORY NA TANGENSA KĄTA POŁÓWKOWEGO
wyprowadzenie wzorów:
z wydzielenia wzorów sinusowych przez cosinusowe
otrzymujemy wzory na tangens
WZORY
sin(
) sin(
)
2
sin sin(
)
sin(
) sin(
)
2
sin sin(
)
sin(
) sin(
)
2
sin
tg
tg
tg
p b
p c
A
p
p a
p a
p c
B
p
p b
p a
p b
C
p
− ⋅
−
=
⋅
−
− ⋅
−
=
⋅
−
− ⋅
−
=
sin(
)
p c
⋅
−
WZORY Delambre’a i Nepera
cos
cos
2
2
sin
cos cos
sin
2
2
2
2
cos
cos
2
2
sin
sin
2
2
sin
cos cos
cos
2
2
2
2
sin
sin
2
2
cos
2
2
2
cos
2
a b
a b
C
C
A B
A B
c
c
a b
a b
C
C
A B
A B
c
c
a b
C
A B
tg
ctg
a b
−
+
+
+
=
=
−
+
−
−
=
=
−
+ =
+
sin
2
2
2
sin
2
cos
sin
2
2
2
2
2
2
cos
sin
2
2
a b
C
A B
tg
ctg
a b
A B
A B
a b
C
a b
C
tg
tg
tg
tg
A B
A B
−
− =
+
−
−
+
−
=
=
+
+
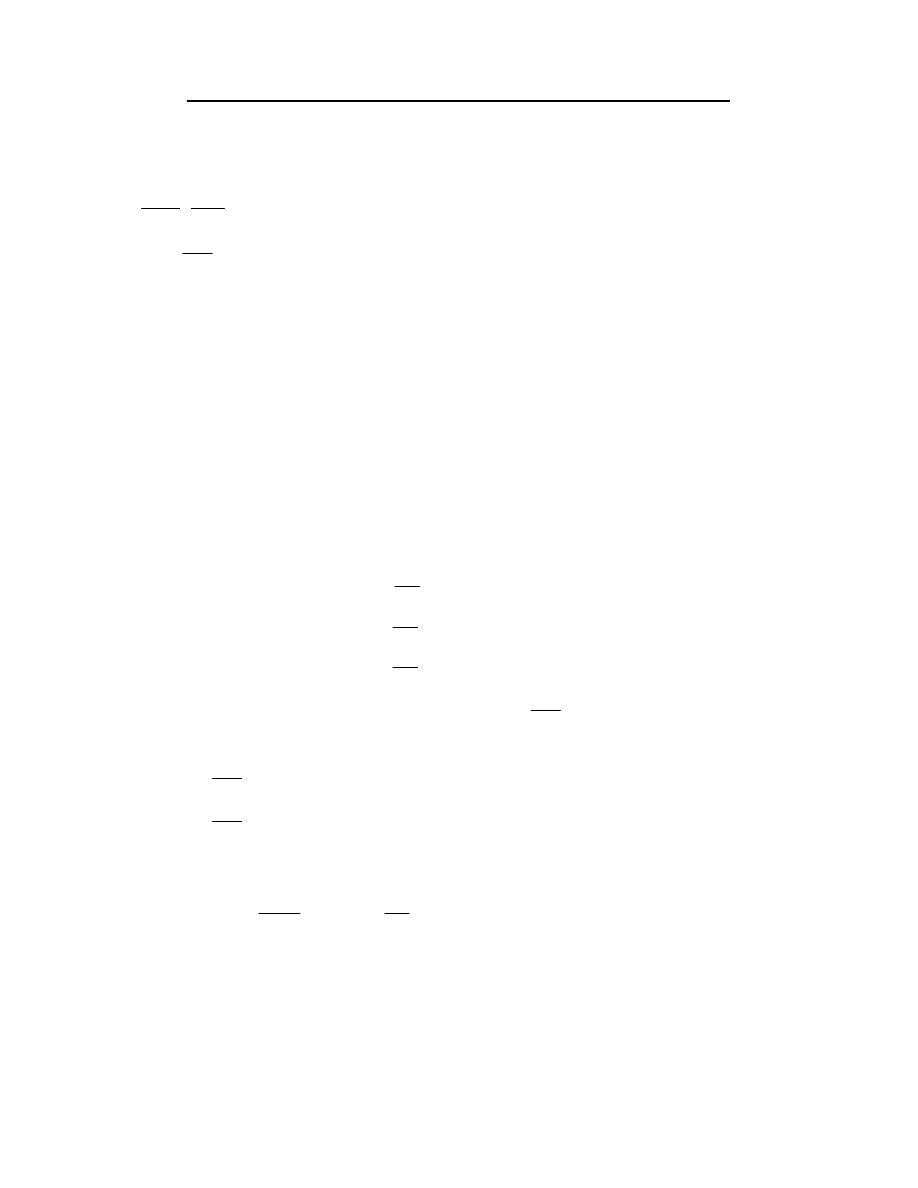
POLE POWIERZCHNI TRÓJKĄTA SFERYCZNEGO
1. Tw.pomocnicze dotyczące pola powierzchni dwukątna sferycznego
2
2
360
4
90
p
S
R
R
S p
π
π
°
=
°
= °⋅
°
2. Pole powierzchni trójkąta sferycznego (w oparciu o dwukąt)
' 180
' 180
' 180
' 180
'
' AC'=CA'
BC CB
CA AC
CB BC
AC CA
CB BC
+
=
°
+
=
°
+
=
°
+
=
°
⇓
⇓
=
1
2
3
2
1
2
2
kąty wierzchołkowe C=C'
' '
'
oznaczam powierzchnię dwukątów:
'
;
'
;
'
' '
90
'
A B C
ABC
ACBC S
ABA C S
ABCB S
C
S
ABC
A B C
R
S
ABC
A CB
R
π
π
⇓
∆
=∆
=
=
=
°
= ∆
+ ∆
=
⋅
°
= ∆
+ ∆
=
⋅
2
2
3
2
1
2
3
razem dają powierzchnię półkuli 2
90
'
90
2
' '
'
'
90
R
A
B
S
ABC
ACB
R
R
S S
S
ABC
ABC
A B C
A CB
ACB
π
π
π
=
°
°
°
= ∆
+ ∆
=
⋅
°
+−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
+ +
= ⋅∆
+∆
+∆
+∆
+∆
=
14444442444444
3
(
)
(
)
(
)
2
2
2
2
2
90
2
180
90
POLE POWIERZCHNI TRÓJKĄTA SFERYCZNEGO
2
2
S=
180
A
B
C
R
ABC
A
B
C
R
R
ABC
A
B
C
R
S
R
π
π
π
ε
π
ε
ε
ρ
°+ °+ °
°
⋅∆
=
°+ °+ ° −
°
⋅∆
=
°+ °+ °−
° ← °
°
°
=
⋅ °
⋅
°
°
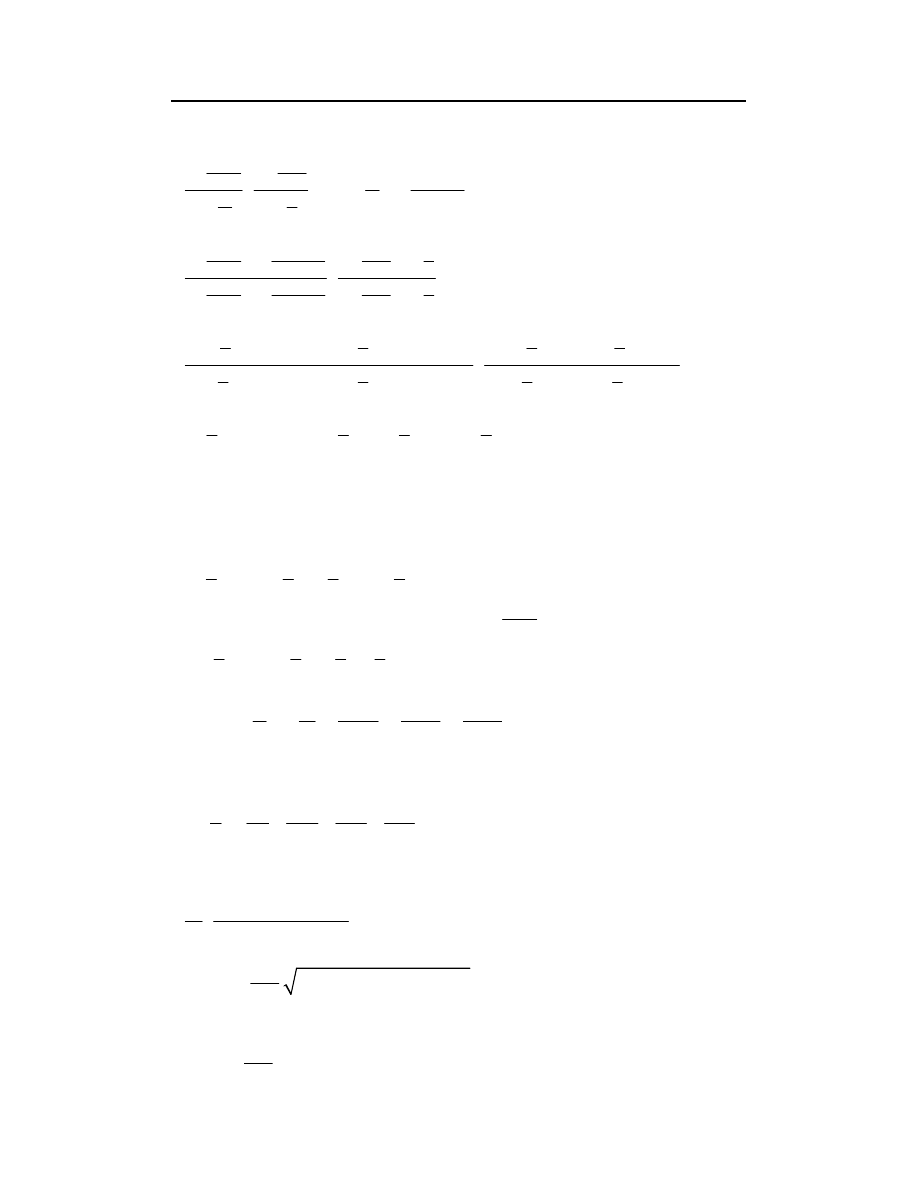
WZORY NA NADMIAR W TRÓJKĄCIE SFERYCZNYM
w zależności od boków (nie zawsze mamy dane kąty)
wychodzimy ze wzoru Delambr'a
sin
cos
180
2
2 cos
sin
2
2
cos
cos
2
2
180
sin
sin
cos
cos
2
2
2
2
180
sin
sin
cos
cos
2
2
2
2
1
2 cos
4
a b
A B
C
C
C
c
C
a b
c
A B
C
a b
c
A B
A
−
+
°−
=
=
°−
−
+ −
−
=
°−
−
+ +
+
⋅
+
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
1
1
1
180 sin
180
2 sin
sin
4
4
4
1
1
1
1
2 sin
180 cos
180
2 cos
cos
4
4
4
4
1
1
1
1
180
4
4
4
4
oznaczam
180
180 2
360
2
360
B C
A B C
a b c
a b c
A B C
A B C
a b c
a b c
ctg
A B C
tg
tg
a b c tg
a b c
A B C
A B C
C
C
a b c
ε
ε
− +
° ⋅
+ + −
°
− ⋅
− + ⋅
− −
=
⋅
+ − +
° ⋅
+ + −
°
⋅
− + ⋅
− −
+ − +
° ⋅
°=−
− + ⋅
− −
+ − +
°= + + −
°−
+
°= −
+
°
− +
(
)
(
)
(
)
(
)
(
)
(
)
(
)
2
2
1
1
1
1
2
I
4
4
2
2
wychodząc z innego wzoru Delambre'a na cos
otrrzymamy
2
1
1
1
1
2
II
4
4
2
2
mnożąc I II
2
1.
4
2
p b
a b c
p b
tg
C
tg
tg
p b tg
p a
A B
ctg
C
tg
tg p tg
p c
p
p
tg
tg
tg
ε
ε
ε
ε
ε
=
−
− − =−
−
− ⋅
=
− ⋅
−
+
− ⋅
=
⋅
−
⋅
−
=
⋅
2
wzór ścisły Luillera na nadmiar
można nim obliczać dowolnie duże trójkąty
WYPROWADZENIE WZORU NA R KULI
4
2
2
2
2
jeżeli boki trójkąta są małe w stosunku
2
2
2
p
p a
p b
p c
tg
tg
tg
tg
tg
R
R
R
R
a
p b
p c
tg
tg
ε
−
−
−
=
⋅
⋅
⋅
−
−
⋅
⋅
2
4
4
do promienia R, tg
tangensy zastępujemy samymi miarami boków w mierze łukowej
(
)(
)(
)
4
2
z odwrócenia wzoru na pole trójkąta sferycznego
"
2. "
(
)(
)(
)
2
S
3. =
2
x x
p p a p b p c
R
p p a p b p c
R
R
ε
ρ
ε
ε
ρ
≈
−
−
−
=
⋅
=
⋅
−
−
−
⋅ °
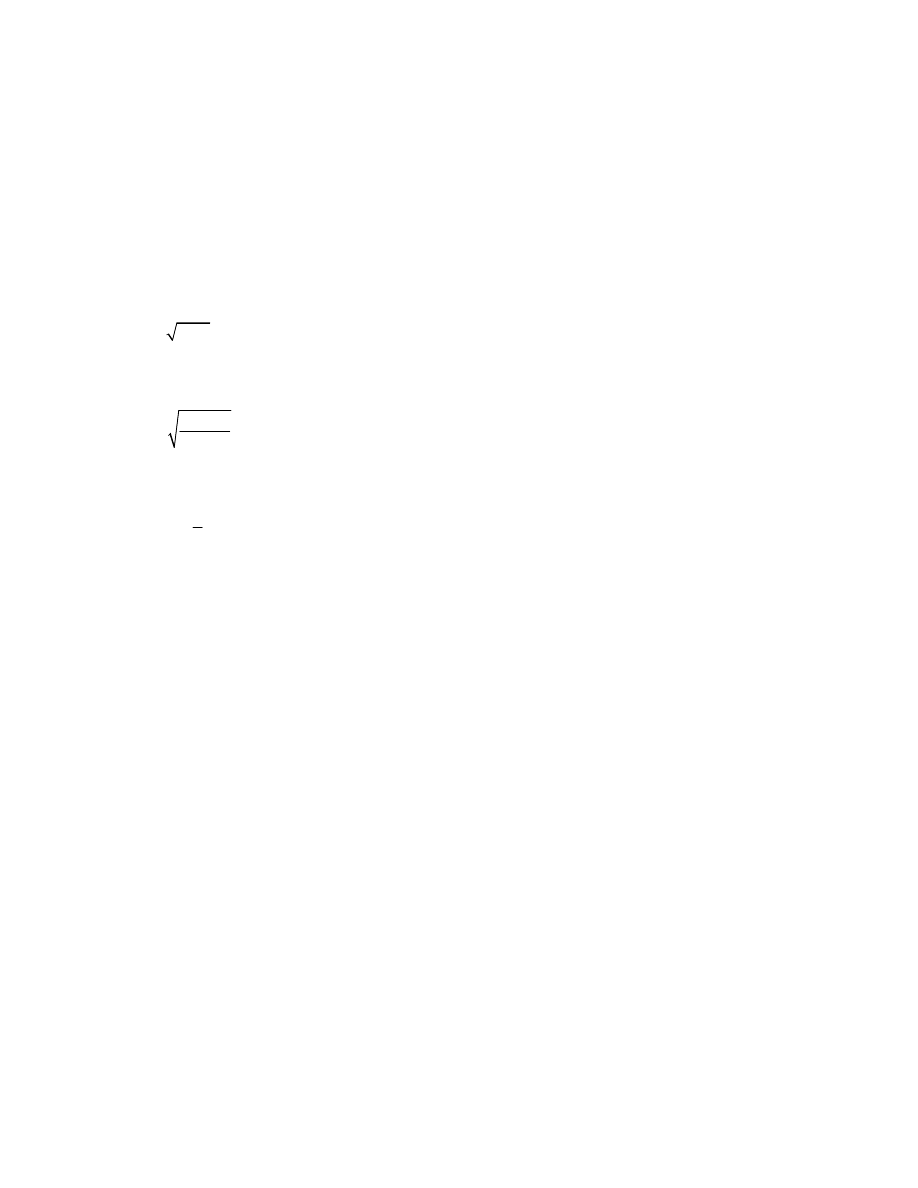
KARTOGRAFIA MATEMATYCZNA
ODWZOROWANIA KARTOGRAFICZNE
Przedstawienie powierzchni regularnych na płaszczyźnie jest przedmiotem kartografii
matematycznej.
KARTOGRAFIA KULI – jaki promień kuli?
1. Kula o objętości takiej samej jak objętość elipsoidy obrotowej
3
1
6370283 m (elipsoida Bessela)
R
a a b
=
⋅ ⋅ =
2. Kula o powierzchni równej powierzchni elipsoidy obrotowej
2
2
2
2
6370289 m (elipsoida Bessela)
3
a
b
R
+
=
=
3. Promień średni arytmetyczny
(
)
3
1
6370291 m (elipsoida Bessela)
3
R
a a b
=
+ + =
6370,3 km w skali 1: 40 mln
(21,3 km 0,5 mm)
w skali 1: 25000
(21,3 km 84 cm)
R
a b
a b
=
− ≈
−
− ≈
−
ODWZOROWANIEM KARTOGRAFICZNYM – nazywamy takie przedstawienie jednej
powierzchni matematycznej na drugiej, (ponieważ na płaszczyźnie), w którym głównym
warunkiem jest, aby każdemu punktowi oryginału odpowiadał jeden i tylko jeden punkt
obszaru, jak również każdemu punktowi obrazu odpowiadał jeden i tylko jeden punkt
oryginału.
(
)
(
)
1
2
,
,
x f
y f
ϕ λ
ϕ λ
=
=
UKŁADY WSPÓŁRZĘDNYCH NA KULI
(
)
(
)
(
)
90 90
,
współrzędne geograficzne
180 180
cos cos
cos sin
, ,
współrzędne prostokątne przestrzenne
sin
0 360
,
współrz
90 90
x R
y R
x y z
z R
p
p q
q
ϕ
ϕ λ
λ
ϕ
λ
ϕ
λ
ϕ
−
° ≤
≤
°
−
−
° ≤
≤
°
=
=
−
=
° ≤
≤
°
−
−
° ≤
≤
°
ę
dne sferyczne

(
) (
)
(
)
(
)
0
0
0
0
0
0
nowy biegun
, ;
,
0 360 -azymut
0 180 -odległość sferyczna
Związek między współrzędnymi azymutalnymi
i geograficznymi
cos
sin sin
cos cos cos
cos sin
sin
sin
M
M
P
ϕ λ
ϕ λ
α
δ
δ
ϕ
ϕ
ϕ
ϕ
λ λ
ϕ
λ λ
α
δ
−
°≤
≤
°
°≤
≤
°
=
⋅
+
⋅
⋅
−
⋅
−
=
TEORIA ZNIEKSZTAŁCEŃ
PIERWSZE TWIERDZENIE TISSOTA
Przy dowolnym regularnym odwzorowaniu jednej powierzchni regularnej na drugą musi
istnieć przynajmniej jedna siatka linii przecinających się pod kątem prostym, która
odwzorowuje się na drugiej powierzchni również jako siatka linii przecinających się pod
kątem prostym
ODWZOROWANIE REGULARNE – takie, w którym funkcje
(
)
(
)
1
2
,
,
x f
y f
ϕ λ
ϕ λ
=
=
Przynajmniej w pewnym zwartym obszarze kuli lub elipsoidy spełniają następujące warunki:
1. funkcje x i y mają ciągłe pochodne cząstkowe przynajmniej 2 rzędu
2. funkcje x i y są niezależne
Warunek 1. żąda aby obraz kuli nie miał przerw ani gwałtownych zagięć
Warunek 2. wyklucza wszystkie oddziaływania zdegenerowane tzn. takie, w których obrazem
punktu nie jest inny punkt tylko linia lub obszar.
DOWÓD GEOMETRYCZNY (Tissota)
1 2
,
90
,
przecinają się pod kątem prostym
l l
α β
→
°
→
' kąt ostry
' kąt rozwarty
β
β
α
α
→
→

Układ ABCD obracamy o 90° naokoło punktu P tak, że kąt β przejdzie w położenie BPC.
W odwzorowaniu kąt β’ przejdzie na kąt α’, zmieni się z ostrego na rozwarty. Ponieważ
założona była ciągłość odwzorowania, dlatego musi istnieć takie położenie układu (np.
A
1
,B
1
,C
1,
D
1
), któremu w odwzorowaniu odpowie układ prostokątny A
1
’,B
1
’,C
1
’
,
D
1
’
Kierunki wzajemnie prostopadłe nazywamy w kartografii KIERUNKAMI GŁÓWNYMI. Na
kuli jest to układ południków i równoleżników.
SKALE I ZNIEKSZTAŁCENIA ODWZOROWAWCZE
'
' skala liniowa
skal pól
dp
ds
k
p
ds
dp
=
=
ZNIEKSZTAŁCENIE – jest różnicą między skalą a jednością
'
1
-zniekształcenie liniowe
'
1
-zniekształcenie pól
i
p
ds ds
z k
ds
dp dp
z
p
dp
−
= − =
−
= − =
SKALE W KIERUNKACH GŁÓWNYCH
( ) ( )
( ) ( )
2
2
2
2
,
,
',
' kierunki główne
, skale w kierunkach głównych
'
'
'
'
'
'
'
'
OX OY OX OY
m n
r
x
y
x mx
y ny
r
mx
ny
y
x
m
n
x
y
−
−
=
+
=
=
=
+
=
=

SKALA W DOWOLNYM KIERUNKU
( )
2
2
2
2
'
2
2
2
2
cos
sin
y
x
r
k
m
n
r
r
r
k
m
n
β
β
β
β
= =
+
=
+
DRUGIE TWIERDZENIE TISSOTA
( )
( )
2
2
2
2
Równanie elipsy w układzie ( ', ') będzie
'
'
1
dla
oraz
oraz jednostkowego promienia 1
'
'
1
x y
y
x
a
b
a mr
b nr
r
y
a m
x
b n
m
n
+
=
=
=
=
=
+
=
=
Obszarem graficznym zniekształceń w punkcie jest elipsa, której półosie równają się skalą w
kierunkach głównych.
Elipsa ta nosi nazwę elipsy zniekształceń Tissota albo indykatrysy.
Gdy n=m elipsa będzie kołem. Obraz koła w oryginale daje odwzorowanie wiernokątne.
SKALA PÓL
2
2
2
a b
m n r
p
m n
R
R
p mn
π
π
π
π
⋅
⋅ ⋅
=
=
= ⋅
=
MAKSYMALNE ZNIEKSZTAŁCENIE KĄTÓW
Kula (koło o promieniu r)
płaszczyzna (elipsa)
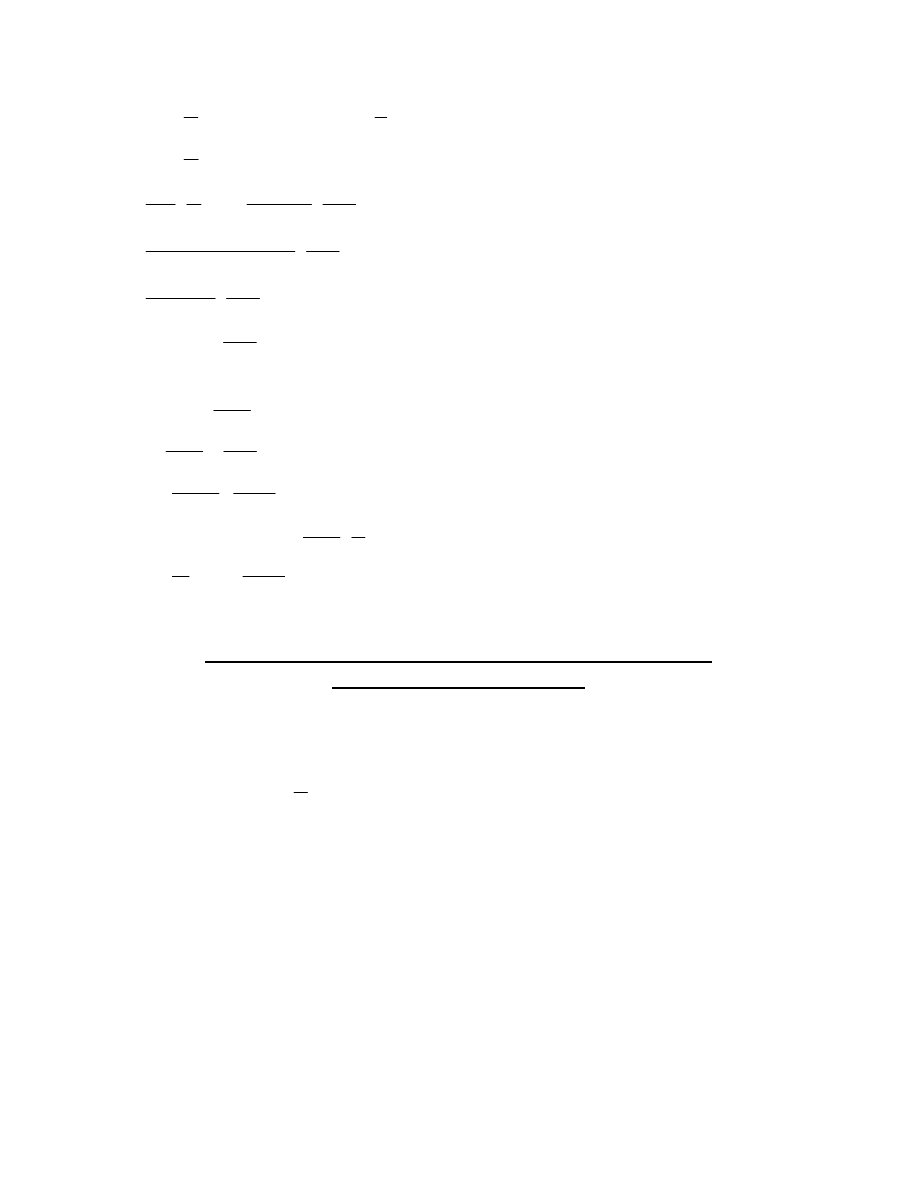
'
'
'
'
'
'
'
'
'
sin 'cos
sin cos '
sin 'cos
sin cos '
sin( '
)
sin( '
)
sin( '
)
sin( '
)
'
y
y
y n y
tg
tg
x m x
x
x
m
tg
tg
n
tg
tg
tg
n
n m
tg
m
tg
tg
n m
n m
n m
n m
n m
n m
n m
β
β
β
β
β
β
β
β
β
β
β
β
β
β
β
β
β
β
β β
β β
β β
β β
α
= ⋅
=
=
= ⋅
= ⋅
−
−
=
⇒
=
+
+
−
−
=
+
+
−
−
=
+
+
−
−
=
⋅
+
+
−
180 2 ' (180 2 )
'
( '
)
2
'
sin
sin( '
)
2
'
dla ( '
) 90 ozn.
max
2
2
sinus maksymalnego zniekształcenia kątów
'
sin
sin( '
)
2
sin max
2
n m
n m
m n
m n
m n
m n
α
β
β
α α
β β
α α
β β
α α ω
β β
α α
β β
ω
=
°−
−
°−
−
−
−
=
−
−
=−
⋅
+
+
−
−
=
°
=
−
−
=
⋅
+
+
−
= +
ZASADNICZE WŁAŚCIWOŚCI ODWZOROWAŃ
KARTOGRAFICZNYCH
ODWZOROWANIE WIERNOKĄTNE (równokątne, kątforemne)
1. gdy
to sin
0 =0
'
2
m n
ω
ω
α α
=
=
⇒
=
ODWZOROWANIE WIERNOPOLOWE (równopolowe)
2. gdy
1 skala pól
p m n
= ⋅ =
ODWZOROWANIE WIERNOODLEGŁOŚCIOWE (równoodległościowe, pośrednie)
3. gdy
1 1 wzdłuż południków
1 1 wzdłuż równoleżników
m
n
m
n
=
∧
≠
→
≠
∧
=
→
Pośrednie – nazwa pochodzi stąd, że zniekształcenia kątów są tutaj mniejsze niż w
odwzorowaniu wiernopolowym, a zniekształcenia pól mniejsze niż w wiernokątnym.

RODZAJE ODWZOROWAŃ KARTOGRAFICZNYCH
PŁASZCZYZNOWE
WALCOWE
STOŻKOWE

ODWZOROWANIE PŁASZCZYZNOWE
(w położeniu normalnym)
Siatka geograficzna
(
)
,
P
ϕ λ
=
Siatka kartograficzna
(
)
'
,
P
x y
=
( ) promień równoleżnika w odwzorowaniu
' długość geograficzna bez zmian
cos y
sin
BP
f y
x
ρ
λ λ
ρ
λ
ρ
λ
= =
−
=
= ⋅
= ⋅
SKALE W KIERUNKACH GŁÓWNYCH
2
1
2
2
1
2
1
cos
' '
dodatniemu przyrostowi po d
toważyszy skrócenie o d
' '
' '
cos
cos
PP Rd
PP R
d
P P
d
P P
P P
d
d
m
n
PP
Rd
PP
R
d
R
ϕ
ϕ λ
ρ
ϕ
ϕ
ρ
ρ
ρ
ρ λ
ρ
ϕ
ϕ λ
ϕ
=
=
=−
←
−
=
=
=
=
=
A.
Odwzorowania płaszczyznowe perspektywiczne
1.
Odwz. gnomoniczne (środek rzutu w środku kuli)
2
3
1
sin
cos
cos
1
sin
1 sin
sin
2
1 sin
1
2
sin
1
sin
3
cos
Rctg
R
d
d
Rd
Rd
Rctg
R
R
m n
m n
m n
m
n
p
ec
ρ
ϕ
ϕ
ϕ
ρ
ϕ
ϕ
ϕ
ρ
ϕ
ϕ
ϕ
ϕ
ω
ϕ
ϕ
ϕ
ϕ
=
−
−
⋅
−
=
=
=
=
=
=
= ⋅ =
=
−
−
=
=
+
+
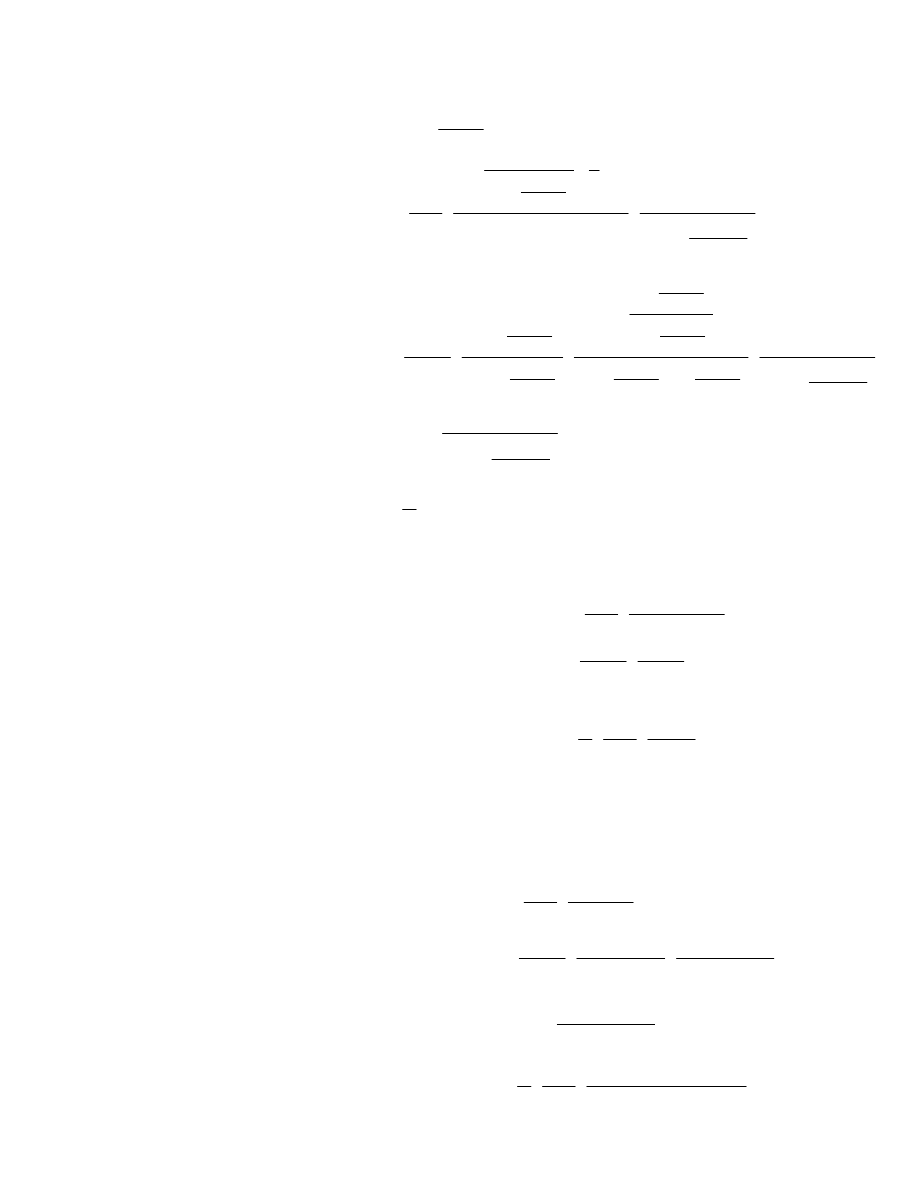
2.
Oddz.. stereograficzne (środek rzutu w przeciwległym biegunie)
3.
Odwz. ortograficzne (środek rzutu w nieskończoności)
(
)
cos
sin
cos
cos
cos
sin 1
sin
2
sin
1
sin
1
sin
R
R
d
d
Rd
Rd
R
R
R
m n
m n
m n
m
n
p
ρ
ϕ
ϕ ϕ
ρ
ϕ
ϕ
ρ
ϕ
ϕ
ϕ
ϕ
ω
ϕ
ϕ
ϕ
=
− −
⋅
−
=
=
=
=
=
=
= ⋅ =
−
−
=
=
+
+
B.
Odwzorowania płaszczyznowe nieperspektywiczne
4.
Rzut pośredni Postela
( )
2
90
2
2
1
1
2
2
90
cos
2
90
sin
2
2
90
90
2
cos
2
2
cos
90
90
90
sin2
sin
cos
2
2
2
1
90
2
cos
2
1
90
2
cos
2
1
c
Rtg
R
d
d
Rd
Rd
R
Rtg
R
R
R
m n
m
n
p
ϕ
ρ
ϕ
ϕ
ρ
ϕ
ϕ
ϕ
ϕ
ϕ
ρ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
°−
=
−
− ⋅
°−
−
=
=
=
°−
°−
°−
=
=
=
=
°−
°−
°−
= ⋅ =
°−
°−
sin
0
2
90
4
os
2
ω
ϕ
=
°−
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
1
90
90
cos
cos
sin 90
90
sin
2
sin 90
90
1
90
sin 90
90
sin 90
m
Rarc
R
d
d
Rd
Rd
Rarc
R
R
m n
arc
m n
m n
arc
m
arc
n
arc
p
ρ
ϕ
ϕ
ρ
ϕ
ϕ
ϕ
ρ
ϕ
ϕ
ϕ
ϕ
ω
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
=
=
°−
− ⋅ −
−
=
=
=
°−
=
=
=
= ⋅ =
°− −
°−
−
=
=
+
°− +
°−
°−
°−
°−
°−
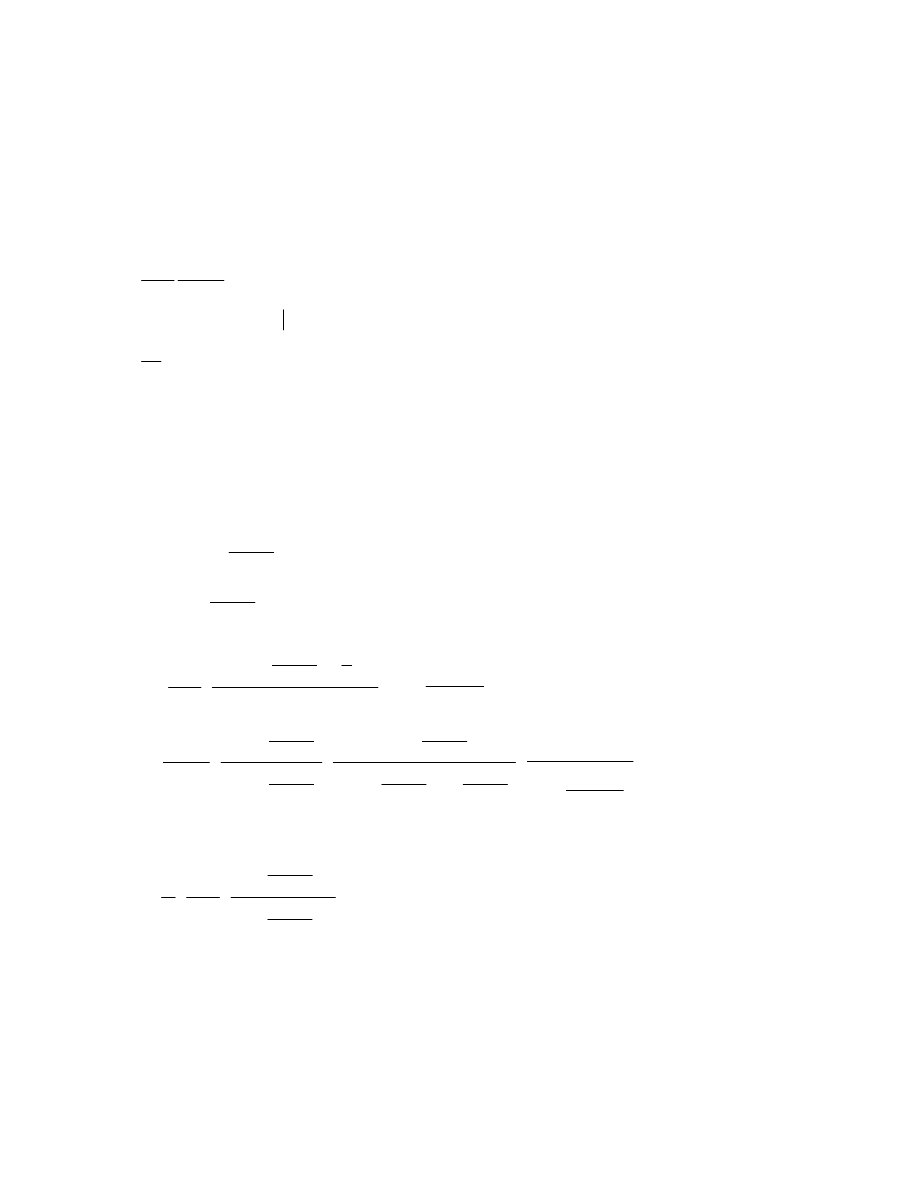
5.
Odwz. płaszczyznowe wiernopolowe Lamberta
(
)
2
2
2
2
2
2
2
2
2
2
2
2
1 warunek wiernopolowości
1
cos
cos
sin
2
2 sin
Podstawiam biegun (
90 ,
0 )
0
2 sin90
2
2
1 sin
90
4
sin
2
90
2 sin
2
m n
d
Rd
R
d
R
d
R
C
R
C
R
C
C
R
R
R
R
d
Rd
m
ρ
ρ
ϕ
ϕ
ρ ρ
ϕ ϕ
ρ
ϕ
ρ
ϕ
ϕ
ρ
ρ
ϕ
ϕ
ρ
ϕ
ρ
ρ
ϕ
⋅ =
−
⋅
=
⋅
=−
=−
+
=−
+
=
° = °
=−
°+
=
=
−
°−
=
°−
=
−
=
=
∫
( )
2
2
90
1
2 cos
2
2
90
90
2 sin
2 sin
2
2
cos
90
90
90
sin2
2 sin
cos
2
2
2
90
cos
1
2
sin
2
90
cos
90
cos
2
1
90
cos
2
1
R
d
Rd
R
R
R
R
R
m n
m n
m n
n
p
ϕ
ϕ
ϕ
ϕ
ϕ
ρ
ϕ
ϕ
ϕ
ϕ
ϕ
ω
ϕ
ϕ
ϕ
°−
−
⋅ −
=
°−
°−
=
=
=
=
°−
°−
°−
= ⋅ =
°−
−
−
=
=
+
°−
°−
°−
1
2
+

C.
Odwzorowania pseudoazymutalne
-powstają przez przekształcenie rzutów azymutalnych (płaszczyznowych)
1.
Rzut Aitowa
Podstawą jest rzut pośredni Postula w położeniu transwersalnym jako oś X został przyjęty
obraz równika, rzędne y zostały skrócone do połowy, a południki zagęszczone podwójnie tzn
ponumerowane zamiast od -90 do 90 liczbami podwójnymi od -180 do 180. W ten sposób
obraz półkuli zmienił się w obraz całej kuli. Siatka taka nazywa się PLANISFERĄ AITOWA
2.
Rzut Hammera
Jeżeli za podstawę jako siatkę pierwotną przyjmie się płaszczyznowy rzut wiernopolowy
Lamberta, to postępując z nim w sposób analogiczny jak wyżej, otrzyma się rzut
pseudoazymutalny Hammera dający obraz całej kuli zawarty w jednej elipsie.
ODWZOROWANIE WALCOWE
(w położeniu normalnym)
SKALE W KIERUNKACH GŁÓWNYCH
2
1
2
1
2
2
1
1
cos
' '
' '
' '
' '
1
cos
cos
PP Rd
PP R
d
P P
dx
P P dy Rd
P P
dx
m
PP
Rd
P P
Rd
n
PP
R
d
ϕ
ϕ λ
λ
ϕ
λ
ϕ λ
ϕ
=
=
=
=
=
=
=
=
=
=

A.
Odwzorowania walcowe normalne
1.
Karta kwadratów
dla
kwadraty
cos 1
sin
2
cos 1
1
1
cos
1
cos
x Rarc
y Rarc
Rd
dx
Rd
Rd
m n
m n
m n
m
n
p
ϕ
ϕ
λ
λ
ϕ
ϕ
ϕ
ϕ
ω
ϕ
ϕ
ϕ
=
∆ =∆
→
=
=
=
=
=
= ⋅ =
−
−
=
=
+
+
Wady: Rosną zniekształcenia w miarę oddalania się od równika
2.
Odwz. walcowe wiernopolowe Lamberta
2
2
1
1
1
cos
cos
/
sin
Podstawiamy równik (
0 , 0)
0
sin0
0
sin
cos
cos
1
sin
2
cos
1
cos
1
cos
1
m n
dx
Rd
dx R
d
x R
C
x
R
C
C
x R
R
d
dx
Rd
Rd
m n
m n
m n
m
n
p
ϕ
ϕ
ϕ ϕ
ϕ
ϕ
ϕ
ϕ ϕ
ϕ
ϕ
ϕ
ω
ϕ
ϕ
ϕ
⋅ =
⋅
=
=
=
+
= °
=
=
°+
=
=
=
=
=
=
= ⋅ =
−
−
=
=
+
+
∫
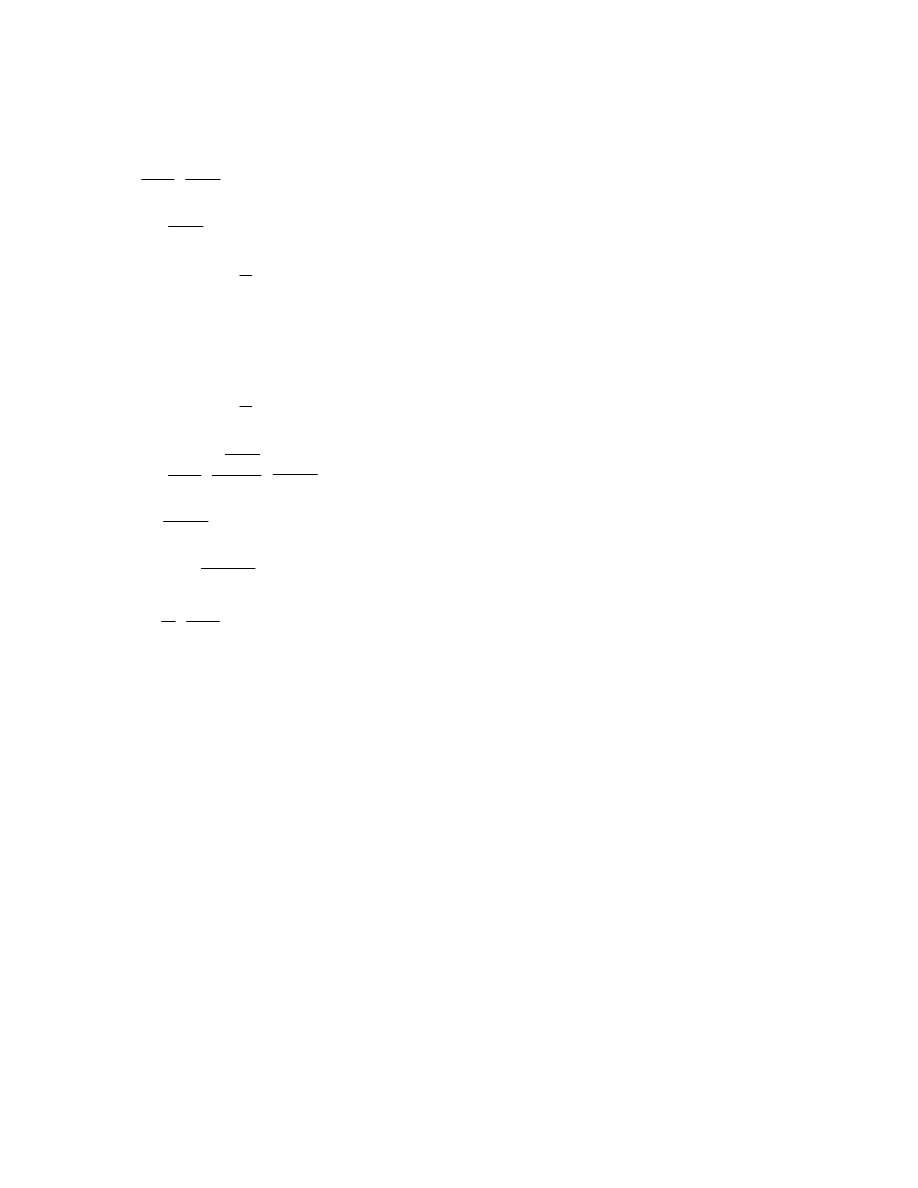
3.
Odwz. walcowe wiernokątne Mercatora (1569)
warunek
1
cos
/
cos
ln
45
2
Podstawiamy równik (
0 , 0)
0
ln 45
0
ln
45
2
cos
2
sin
0
2
1
cos
1
cos
1
cos
m n
dx
Rd
Rd
dx
x R tg
C
x
R tg
C
C
x R tg
d
R
dx
Rd
Rd
m n
m n
m n
m
n
p
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ω
ϕ
ϕ
ϕ
=
=
=
=
°+
+
= °
=
=
+
=
=
°+
=
=
=
=
= ⋅ =
−
=
=
+
∫
Własności: Obrazem loksodromy (krzywej przecinającej na kuli południki pod stałym kątem),
jest tutaj linia prosta przecinająca prostoliniowe obrazy południków pod tym samym kątem co
na kuli.
B.
Odwzorowanie walcowe poprzeczne (transwersalne) Cassini-Soldner (dla kuli)

1.
rzut walcowy poprzeczny wiernopolowy
( )
3
2
sin
6
x
y f
R
y
R
R
η
η
ξ
η
η
=
=
=
⇒
≅ −
2.
rzut walcowy poprzeczny wiernokątny
3
2
ln
4 2
6
x
y R tg
y
R
R
η
η
π
ξ
η
=
=
+
⇒
≅ +
3.
rzut walcowy poprzeczny wiernoodległościowy
x
y
ξ
η
=
=
współrzędne punktu P(
x
y
ξ
η
=
= )
(
)
(
)
(
)
(
)
(
)
(
)
0
0
0
0
'
90
' '
90
1
1
sin
1
sin
sin 1
sin
2
sin 1
związek między , , a , wznika y
cos
cos 90
cos90 sin 90
sin90 cos 90
cos
cos sin
osta
x OP
Rarc
y P P
Rarch Rarc
z
m
n
z
p m n
z
m n
z
m n
z
h z
BPG
z
z
α
ω
α
λ ϕ
ϕ
ϕ
λ λ
ϕ
λ λ
=
=
°+
=
=
=
°−
=
=
= ⋅ =
−
−
=
=
+
+
=
°+
°+
°+
°
°− −
=
−
(
)
(
)
0
0
2
2
2
2
2
2
tecznie
cos
arcsin cos sin
dla wąskich pasów południkowych można nieco uprościć wzory
1
cos
sec
sec
1
2
''
2 sin1'' 2
''
x Rarcctg ctg
y R
m
y
y
n
ecz
h
R
R
y
y
R
R
ϕ
λ λ
ϕ
λ λ
ω
ρ
=
−
=
−
=
=
=
=
= +
=−
=

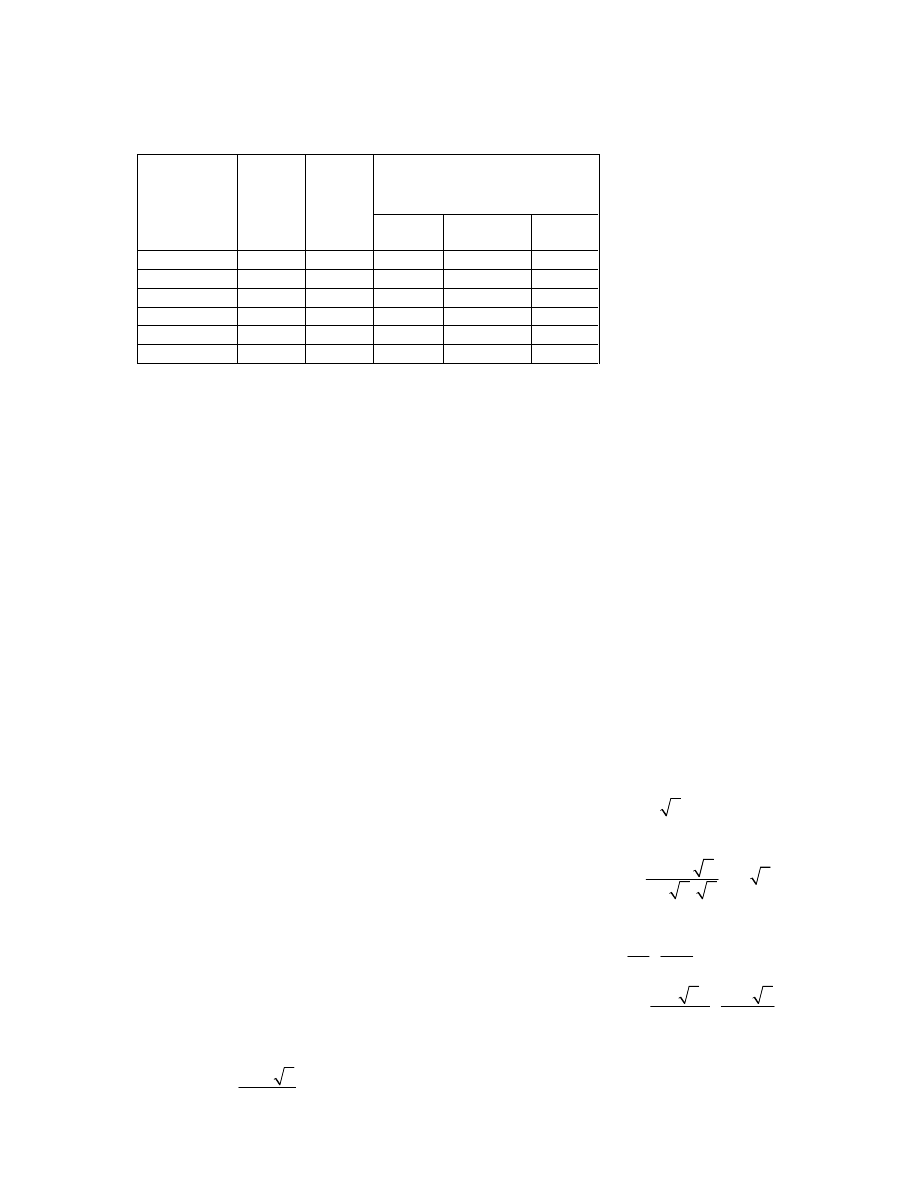
Odwzorowanie takie używane było do map katastralnych w Austrii (XVIII, XIX, XX w)
1. Kościół św. Stefana Wiedeń
2. Kopiec Unii Lubelskiej Lwów
Mapy opierały się na południkach przechodzących przez te punkty
przybliżone zniekształcenia
odległość od
południka
ś
rodkowego
m
n=p
na 1 km
długosci
na 1 km2
powierzchni
kąta
0
1
1,0000
0cm
0m2
0''
50
1
1,00003
3cm
30m2
6''
100
1
1,00012
12cm
123m2
2,5''
200
1
1,00049
49cm
492m2
1'48''
300
1
1,00111
111cm
1107m2
3'46''
325
1
1,0013
130cm
1302m2
4'28''
C.
Odwzorowania pseudowalcowe
1.
Odwz. Sansona-Flamsteeda (rzut sinusoidalny)
cos
jest funkcją dwóch zmiennych
dlatego odwz. pseudowalcowe
x Rarc
y R
arc
y
ϕ
ϕ
λ
=
=
−
2.
Odwz. Mollweidego (odwz. wiernopolowe)
Założenia: a. obraz półkuli – koło
b. obraz kuli – elipsa
c. obrazy południków elipsy
2
2
1
1
2
1 2
2
2
2
1
2
2
Ad.a.
2
2
Ad.b.
4
4
/ 2
2
2
2/ 2
2
Ad.c.
2
2
4
2
2
2
2
n
n
r
R
r R
rr
R
R
r
R
R
r
r
r
R
r
R
R
R
r
R
π
π
π
π
π
π
λ
π
λ
λ
π
π
=
=
=
=
=
=
=
=
=
Obrazy równoleżników są prostymi równoległymi do obrazu równika i przebiegają w
odległości
( )
2
2 cos ' '
R
x
f
λ
ϕ
ϕ
ϕ
π
⋅
=
=
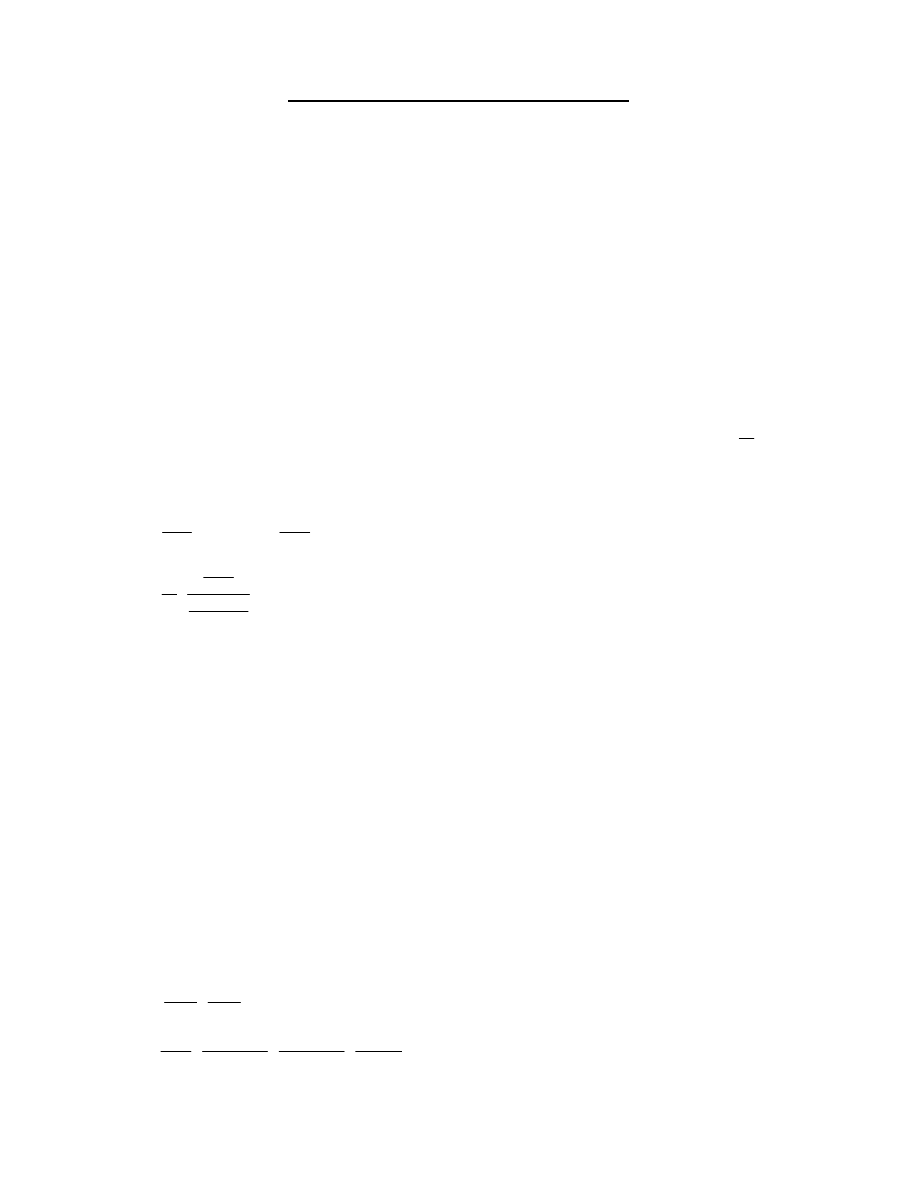
ODWZOROWANIE STOŻKOWE
Obrazy południków jako pęk prostych, kąty między nimi są mniejsze niż te, które znajdują się
na kuli.
Obrazy równoleżników to koła współśrodkowe.
( )
1
'
'( , ') =
' stała odwzorowania stożkowego -
cos '
sin '
wyznaczenie stałej
'
P
f
WP
c
c
x
y
c
AD
AD
A
AO
AW
λ
ρ λ
ρ
ϕ
λ
ρ
λ
ρ
λ
λ
λ
=
=
=
=
=
=
1
0
0
=
sin
'=
sin
sin
dyskusja stałej 0
1
. 0 sin
0
0 (q=0) odwz. walcowe
. 1 si
sin 0
O AW
q
AD
AW
q
AD
AW
q
c
c
I
c
II
c
c
λ
λ
ϕ
ϕ
ϕ
=
=
=
≤ ≤
=
⇒
=
⇒
=
⇒
=
⇒
0
0
n
1
90 (q=90 ) odwz. płaszczyznowe
WNIOSEK: odwzorowania stożkowe są najogólniejsze ponieważ zawierają w skrajnych
przypadkach zarówno odwz. walcowe jak i odwz. płaszcz
ϕ
ϕ
=
⇒
=
°
°
⇒
yznowe.
SKALE W KIERUNKACH GŁÓWNYCH
2
1
2
1
2
2
1
1
cos
' '
' '
'
'
'
' '
' '
'
cos
cos
PP Rd
PP R
d
P P
d
P P
d
c
d
c d
P P
d
m
PP
Rd
P P
d
c d
n
PP
R
d
R
d
ϕ
ϕ λ
ρ
ρ λ
λ
λ
λ
λ
ρ
ϕ
ρ λ
ρ λ
ϕ λ
ϕ
=
=
=−
=
= ⋅
= ⋅
−
=
=
=
=
=
cos
c
R
ρ
λ
ϕ
⋅
=

A.
Odwzorowania stożkowe normalne
1.
Odwz. stożkowe wiernokątne Lamberta-Gaussa
warunek
cos
/
cos
ln
ln
45
ln
2
45
2
Podstawiamy równik (
0 ) ,
stała jest promieniem koła przedstawiającego równik
45
2
założ
c
a
c
a
m n
d
c
Rd
d
cd
c tg
K
K tg
K
K
tg
ρ
ρ
ϕ
ϕ
ρ
ϕ
ρ
ϕ
ϕ
ρ
ϕ
ρ
ϕ
ρ
ϕ
ρ ρ
=
−
=
−
=
=
°−
+
= ⋅
°−
= °
=
= ⋅
°−
∫
enie: stożek styczny w
dla
,
45
2
45
2
popodstawieniu do wzoru na
45
cos
cos
sin
45
2
45
2
o
o
o
c
o
a
o
a
c
o
Rctg
tg
Rctg
tg
tg
o
m n
o
tg
Rctg o
o
tg
ϕ
ρ ρ
ϕ ϕ
ϕ
ϕ ρ
ϕ
ρ
ϕ
ρ
ϕ
ϕ
ϕ
ϕ
ρ
ϕ
ϕ
=
=
= ⋅
°−
=
°−
= =
°−
=
°−
( )
2
sin
2
45
2
1
dla
-małe
1
2
o
o
o
tg
m n
ϕ
ϕ
ϕ
ϕ ϕ
ϕ
ϕ
°−
°−
− =∆
= = + ∆
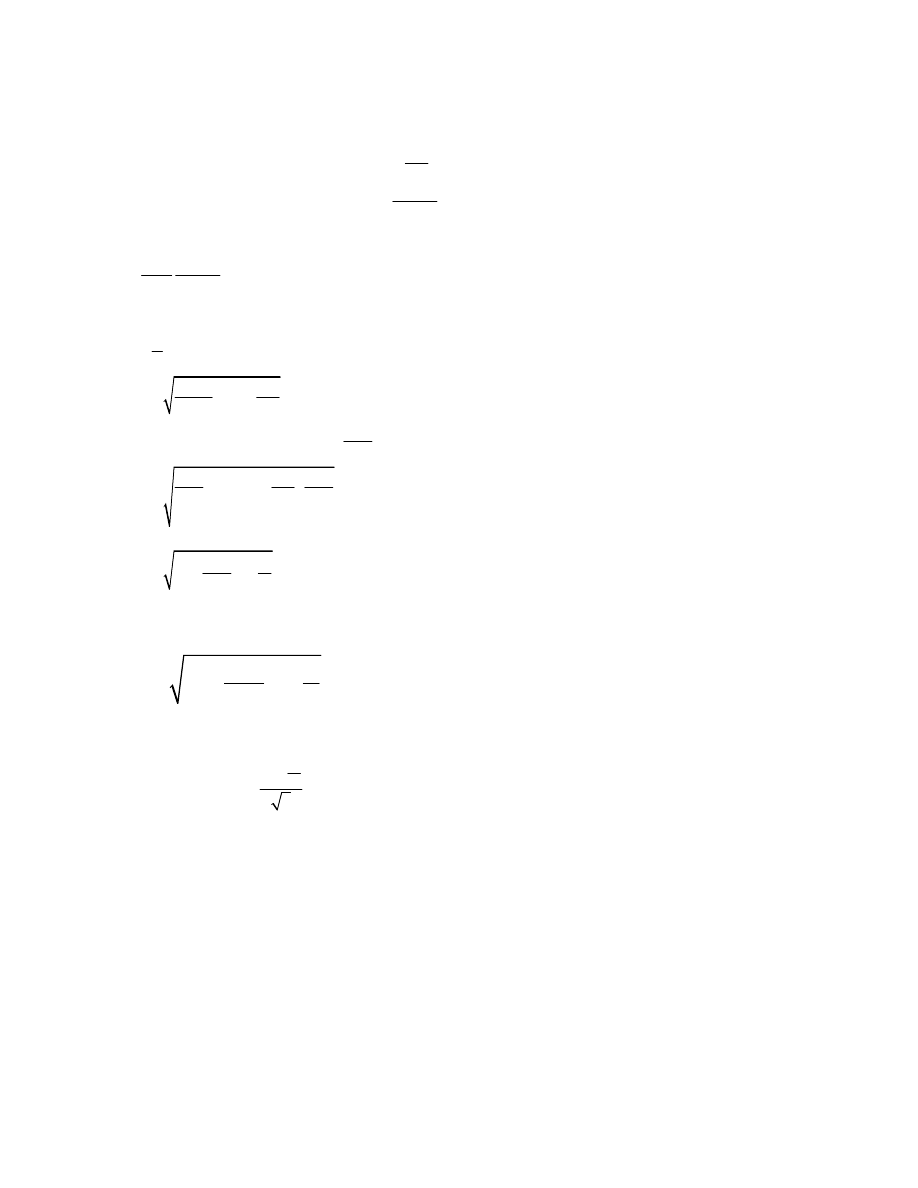
2.
Odwz. stożkowe wiernopolowe Lamberta
}
2
2
2
2
90
-odlegołość biegunowa
wtedy
sin
warunek wiernopolowości
1
1
sin
sin
/
1
cos
2
2
2
cos
pod pier
p
d
m
dp
d
dp
d
dp
c
n
R
p
m n
d
c
Rdp R
p
d
c
R
pdp
c
R
p C
C
R
p
c
c
ϕ
ρ
ϕ
ϕ
ρ
ρ
ρ
ρ ρ
ρ
ρ
=
°−
=
=−
=−
=
⋅ =
⋅
=
⋅
=
⋅
=−
+
−
=
+
∫
(
)
2
1
2
2
2
ozn.
2
2
2
1
1
1
2
w. dodaje i odejmuje
2
2
2
1 cos
4
sin
2
Podstawiamy biegun (p 0 )
stała jest promieniem koła oznaczająca biegun
gdy założymy, że obraz bi
2
2
2
4
sin
2
C
b
R
c
C
R
R
p
c
c
c
p
R
C
c
C
C
p
R
c
b
ρ
ρ
ρ
ρ
ρ
=
−
+
−
=
+
= °
=
=
+
1
424
3
2
eguna leży w punkcie W to
sin
2
0 oraz
2
b
p
R
c
ρ
ρ
=
=
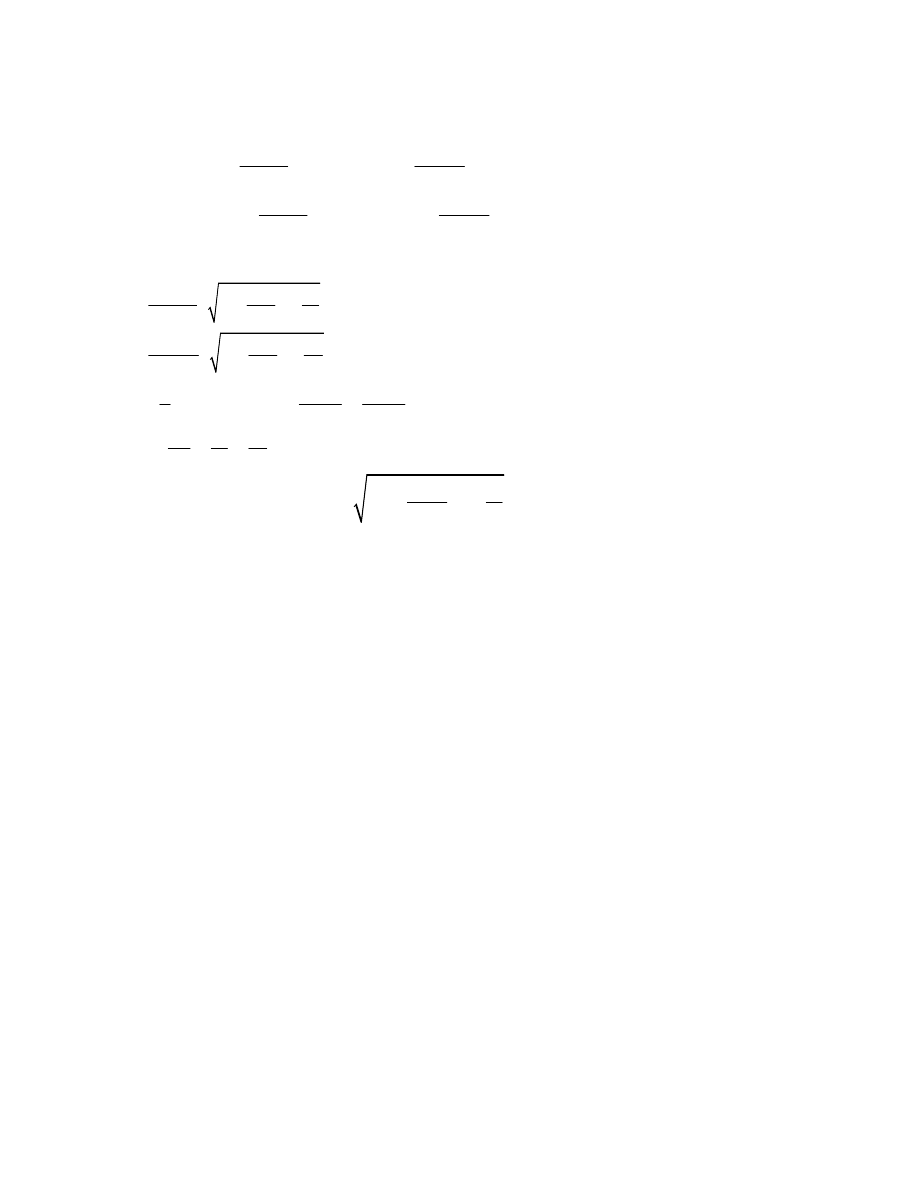
3.
Odwz. stożkowe wiernopolowe Alberta
1
2
1
2
1
2
1
2
1
2
założenie:
1
1
1
1
sin
sin
sin
sin
ponieważ
n
n
c
c
R
p
R
p
R
p
R
p
c
c
ρ
ρ
ρ
ρ
=
∧
=
=
∧
=
=
∧
=
(
)
2
2
2
1
1
2
2
2
2
2
1
2
1
2
1
2
1
2
odwzorownie musi pozostac wiernopolowym zachodzą związki:
sin
4 sin
2
sin
4
sin
2
1 cos cos
cos
sin
2
2
2
2 sin sin
2
2
Dowolny równoleżnik:
2
2 4
b
b
b
R
p
p
R
c
c
R
p
p
R
c
c
p
p
p
p
c
p
p
p
p
R
c
R
c
b
ρ
ρ
ρ
ρ
ρ
=
+
=
+
−
+
=
+
=
=
=
+
2
sin
2
p

4.
Odwz. stożkowe pośrednie Ptolemeusza
(
)
(
)
(
)
warunek:
1
1
/
dla
,
inny wzór na
90
cos
1
cos
sin
(
)
cos
o
o
o
o
o
o
b
m
d
Rd
d
Rd
Rarc
C
Rctg
Rarc
C
C Rctg
Rarc
Rarc
Rd
d
Rd
Rd
c
R
p
Rctg
Rarc
o
o
m
arc
o
o
o
n
ρ
ϕ
ρ
ϕ
ρ
ϕ
ρ ρ
ϕ ϕ
ϕ
ϕ
ϕ
ϕ
ρ
ρ ρ
ϕ
ϕ
ρ
ϕ
ϕ
ρ
ϕ
ρ
ϕ
ϕ ϕ
ϕ
ϕ
ϕ ϕ
ϕ
=
−
=
=−
=−
+
=
=
=−
+
=
+
=
+
°−
− −
−
=
=
=
=
=
=
∫
=
+
−
+
−
( )
( ) (
)
2
2
cos
cos
sin
(
)
sin
2
cos
cos
sin
(
)
dla
-małe
1
1
1
sin
1
2
2 4
o
o
o
o
o
o
o
o
m n n
arc
m n
m n
arc
p n
tg
ϕ
ϕ
ϕ
ϕ ϕ
ω
ϕ
ϕ
ϕ
ϕ ϕ
ϕ ϕ
ϕ
ω
ϕ
ϕ
ϕ ϕ
⋅ =
−
+
−
−
=
=
+
+
+
−
− =∆
= = + ∆
=
∆
+∆

5.
Odwz. Delisle’a – modyfikacja odwz. Ptolemeusza m=1
Dodatkowo dwarównoleżniki odwzorowane wiernie
(
)
(
)
(
)
(
)
1
1
1
1
1
1
2
2
2
2
2
2
cos
cos
1
90
2 równania
cos
2 niewiadome
cos
cos
,
1
90
cos
90
cos
90
cos
cos
2
1
1
2
2 1
b
b
b
c
R
R
Rarc
R
c
c
c
R
R
c
Rarc
R
c
c
c
R
b
arc
ρ
ϕ
ϕ
ρ
ρ
ϕ
ϕ
ρ
ϕ
ϕ
ρ
ρ
ρ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ρ
ϕ ϕ
=
⇒
=
⇒
=
+
°−
=
⇒
=
⇒
=
+
°−
°−
−
°
−
=
=
−
(
)
(
)
(
)
(
)
Promień dowolny równoleżnika
90
cos
90
cos
2
1
1
2
90
cos
cos
2
1
cos
1
2
cos
cos
2
1
R
ϕ
ϕ
ϕ
ϕ
ρ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
°−
−
°−
=
+
°−
−
−
−
6.
Odwzorowanie Tissota – modyfikacja odwz. Ptolemeusza
(
)
(
)
{
ozn. s
3
modyfikacja
Tissota
-odwz. Ptolemeusza
1
6
Rctg
Rarc
o
o
Rctg
Rarc
o
o
Rctg
s
s
o
ρ
ϕ
ϕ ϕ
ρ
ϕ
ϕ
ϕ
ρ
ϕ
=
+
−
=
−
−
=
− −
14243
wzór otrzymany drogą badania zniekształceń

B.
Odwzorowania Pseudostożkowe
1.
Rzut stożkowy zwykły zmodyfikowany – modyfikacja odwzorowania
Ptolemeusza
φ
1,
φ
2
odtwarza się wiernie i dzieli się na równe części jak na kuli. Aby uzyskać obrazy kuli
łączymy punkty podziału. Proste będące obrazami południków nie zejdą się w jednym
punkcie.
2.
Rzut Bonne’a – modyfikacja odwzorowania
Rezygnujemy z prostoliniowości obrazów południków żądając, aby wszystkie równoleżniki
były odwzorowane wiernie i podzielone tak jak na kuli. Promienie równoleżników
otrzymamy ze wzoru:
(
)
{
}
R ctg
Rarc
o
o
ρ
ϕ
ϕ ϕ
=
+
−
Obrazem bieguna jest jeden punkt, niepokrywający się ze środkiem kół obrazów
równoleżników. Mamy tylko jedną prostą – południk środkowy. Ważna własność to
wiernopolowość.
(
)
{
}
dla
0
rzut pseudowalcowy
Sansona - Flamsteeda
dla
90
rzut Wernera (Staba)
o
R ctg
Rarc
o
o
o
ϕ
ρ
ϕ
ϕ
ϕ
ϕ
= °⇒
=
+
−
⇒
=
°⇒

3.
Wielostożkowy rzut amerykański
Rzut ten otrzymuje się przyjmując dla każdego równoleżnika osobny stożek styczny i
rozwijając ten równoleżnik wiernie na płaszczyźnie.
{
}
2
'
sin '
, '
sin '
'
2
sin
2
Rctg
c
x Rctg
y R
ctg
ρ
ϕ
λ λ
ϕ
λ
λ
ρ λ
ϕ
λ
λ
ϕ
ϕ
=
=
=
=
=
+
powstała siatka nie jest ortogonalna, ale jest wierny podział. To odwzorowanie przy pewnych
modyfikacjach jest podstawą do tworzenia siatki w Międzynarodowej Mapie Świata w skali
1 : 000 000
4.
Wielostożkowy rzut angielski
Wprowadzono pewne modyfikacje i otrzymano obray południków i równoleżników
przecinających się pod kątem prostym.

KARTOGRAFIA ELIPSOIDY OBROTOWEJ
Odwzorowanie elipsoidy na płaszczyznę może być dokonane dwiema drogami:
1. Poprzez modyfikację poszczególnych wzorów
2. Przy zastosowaniu odwzorowań podwójnych (dwuetapowych), gdzie w
pierwszym etapie elipsoidę odwzorowujemy na kulę, a następnie obraz kuli
przenosimy na płaszczyznę poznanymi już metodami.
2
2
3
2
2
2
1
KULA ELIPSOIDA
(1
)
Łuk południka
(1
sin )
Łuk równoleżnika
B
B
a
e
s R
s
dB
e
B
p r
ϕ
λ
−
= ⋅∆
=
−
= ⋅∆
∫
1
2
2
2
2
2
2
cos
(1
sin )
a
B
p
L
e
B
a
b
e
a
=
∆
−
−
=
Odwzorowując kulę na elipsoidę mamy pięć możliwości:
1. Rzut środkowy elipsoidy na kulę
2. Rzut elipsoidy na kulę przy pomocy szerokości zredukowanych
3. Rzut wiernopolowy elipsoidy na kulę
4. Wiernokątny rzut Lagrange’a elipsoidy na kulę
5. Wiernokątny rzut Gaussa
1.
Odwz. Mufflinga
Jest to odwz. elipsoidy na wielościan nierozkładalny na płaszczyznę w sposób ciągły. Każdy
arkusz odpowiada czworobokowi sferycznemu na kuli a sferoidalnemu na elipsoidzie.
Ograniczony jest dwoma łukami odpowiednio dobranych południków i dwoma łukami
równoleżników.
Każdy z tych czworoboków będących trapezami sferoidalnymi odwzorowuje się na
płaszczyznę przechodzącą przez jego cztery wierzchołki (wielościan wpisany w elipsoidę) lub
styczną w środku (wielościan opisany na elipsoidzie).
Obrazem trapezu sferoidalnego będzie trapez płaski ograniczony dwoma prostoliniowymi
obrazami południków i dwoma krzywoliniowymi obrazami równoleżników.
Długości boków można otrzymać ze wzorów abo tablic.

2.
Odwz. Roussilhe’a = quasistereograficzne odwz. WIG
Jest wiernokątnym odwzorowaniem elipsoidy na płaszczyznę, odpowiada ono ukośnemu
odwz. stereograficznemu kuli o promieniu
o
o
R
M N
=
⋅
Mo, No – promień krzywizny głównych przekrojów elipsoidy obrotowej
W latach 1927-1930 w Polsce prof. L. Grabowski, przystosował to odwz. dla naszego kraju
przyjmując punkt główny
52
22
o
o
ϕ
λ
=
°
=
° , zmniejszono wymiary elipsoidy Bessela o
1 : 2000, co odpowiada odwz. na płaszczyznę sieczną.
Wewnątrz tego koła obraz ulegnie skurczeniu a na zewnątrz rozciągnięciu. Zniekształcenia w
tym odwz. są małe (2x mniejsze niż w walcowym, poprzecznym Gaussa i Lamberta – Gaussa)
Siatka kartograficzna przedstawi się jako zespół sieci krzywych bardzo zbliżonych do łuków
kół.

ROZPOZNAWANIE SIATEK
1.
Odszukać linie proste i zorientować się w ich ułożeniu
2.
Sprawdzamy gdzie znajdują się łuki kół a gdzie innych krzywych (wpisując cięciwy
równych długości)
3.
Badamy kształt południków (prostolinijne, krzywolinijne), równoleżników (odstępy
między nimi)
*rosnące odstępy nasuwają przypuszczenie o siatce wiernokątnej
*malejące – wiernopolowej
*równe odstępy – wiernoodległościowej
4.
Badamy bieguny ( punkty, linie)
-W ten sposób gromadzimy jak najwięcej informacji o siatce
-Stawiamy hipoteze
-Ostateczne rozstrzygniecie nie jest jednak do końca PEWNE
Wybór odpowiedniego rzutu
Błąd, dokładność położenia punktu na mapie szczegółowej 0,2mm-0,5mm na mapach
ś
ciennych 5mm. Przy wyborze rzutu kierujemy się następującymi zasadami:
1. Najprostszy rzut będzie zawsze najlepszym pod warunkiem, że zniekształcenia w nim
występujące nie przekroczą założonych wartości
2. Należy też zawsze tak dobierać powierzchnię odwzorowania aby jak najlepiej
przystawała do obszaru, który ma być odwzorowany.
globus 1 : 000 000
A=699,373 mm
pł. Postula (wiernopolowe)
A=699,373 mm
pł. Lamberta (wiernopolowe)
A=699,367 mm
pł. gnomoniczne
A=699,400 mm
pł. stereograficzne (wiernokątne)
A=699,379 mm
Dla obszarów okołorównikowych najlepsze są odwzorowania walcowe
Dla obszarów okołobiegunowych stosuje się odwzorowania płaszczyznowe
Dla obszarów umiarkowanych szerokości najlepiej wybrać odwzorowania stożkowe
Przy wyborze najkorzystniejszego odwzorowania kierujemy się odpowiedziami na dwa
pytania:
Do jakich celów ma służyć dana mapa?
Jaki jest rozmiar i kształt obszaru, który ma być przedstawiony na mapie?

UKŁADY WSPÓŁRZĘDNYCH I ODWZOROWANIA
STOSOWANE W POLSCE PO II WOJNIE ŚWIATOWEJ
1.
Układ „Borowa Góra” 1945-1955
-punkt triangulacji, od którego wyznaczano pozostałe
-oparty na elipsoidzie Bessela
-odwzorowanie Gaussa-Krugera (walcowe poprzeczne) w pasach 3
o
(15
o
, 18
o
, 21
o
, 24
o
)
- m
o
=1 południk bez zniekształceń
-zniekształcenia na skraju pasa 3
o
+14cm/km
2.
Układ „1942” 1955-do dziś
-oparty na elipsoidzie Krasowskiego
-punkt przyłożenia Pułków koło St. Petersburga
-odwzorowanie Gaussa-Krugera w dwóch wariantach
a. w strefach 3
o
(15
o
,
18
o
, 21
o
, 24
o
)
b. w strefach 6
o
(15
o
, 21
o
, 27
o
…..)
-zniekształcenia na skraju pasa 6
o
+60 cm/km
-od 1968 tylko dla potrzeb obronności kraju, gdyż okazał się bardzo wiernym ukladnem.
3.
Układ „1965”
-niejednolity: 5 stref odwzorowawczych
Strefy: 1-4 odwz. quasistereograficzne
m=0,9998 koło bez zniekształceń,
zniekształcenia liniowe +/- 25 cm
Strefa 5 odwz. Gaussa-Krugera
m=0,99983
Mankamentem jest trudność sporządzenia jednolitych i pełnowartościowych map na stykach
dwóch, trzech sąsiadujących stref. Dlatego że poszczególne strefy są przesunięte i skręcone.
Na granicach stref są też największe zniekształcenia. Trzeba wykonywać mapy podwójne.
4.
Układy „lokalne”
-stosuje się dla większych miast, ośrodków przemysłowych

5.
”GUGIK 80”
-jednostrefowe odwzorowanie quasistereograficzne
-koło bez zniekształceń 215 km
-elipsoida Krakowskiego
-zniekształcenia w punkcie głównym -0,29 m / km
-zniekształcenia na skraju +0,96m / km
Przykryto całą Polskę mapami w różnych skalach
6.
Układ „1992”
-elipsoida WGS 84 (World Geodetic System)
-odwz. Gaussa-Krugera w jednej strefie L
o
=19
o
południk środkowy
-współczynnik kurczenia na południku m
o
=0,9993
-zniekształcenia na południku środkowym -70 cm / km
-zniekształcenia na skraju strefy +90 cm / km
7.
Układ „2000”
-elipsoida WGS 84
-odwz. Gaussa-Krugera w czterech strefach (15
o
, 18
o
, 21
o
, 24
o
)
- m
o
=0,999923
-zniekształcenia na południku środkowym -7,7 cm / km
-zniekształcenia na skraju pasa +7 cm / km
Wykorzystywane dla odwzorowań kartograficznych wielkoskalowych

REDAKCJA MAP
1. Mapy można klasyfikować ze względu na
• PRZEZNACZENIE
• ZASIĘG TERYTORIALNY
• SKALĘ
a. Wielkoskalowe to mapy 1 : 10 000 i większe
b. Średnioskalowe 1 : 50 000, 1 : 25 000
c. Małoskalowe 1 : 100 000, 1 : 200 000, 1 : 500 000
W Polsce skala 1 : 10 000 jest najmniejszą, w której opracowuje się mapy w oryginale
• TREŚĆ
OGÓLNE-dają pełną charakterystykę przedstawionego terenu. Dzielimy je na:
a. topograficzne skala większa od 1 : 1 000 000
b. przeglądowo-topograficzne skala 1 : 1 000 000
c. przeglądowe skala mniejsza od 1 : 1 000 000
SPECJALNE- uwypuklają jeden lub kilka elementów mapy ogólnej lub eksponują na jej tle
inne zjawiska (np. przyrody). Do map specjalnych zaliczamy:
• mapy fizyczne lub przyrodnicze
• mapy społeczno-gospodarcze
• mapy techniczne
ze względu na główny element treści mapy:
d. hipsometryczne
e. geomorfologiczne
f. glebowe
g. klimatyczne
h. hydrograficzne
i. administracyjne
j. komunikacyjne
k. historyczne
l. demograficzne
m. przemysłowe

E
LEMENTY TREŚCI MAP DZIELĄ SIĘ NA TRZY ZASADNICZE GRUPY
:
I.
Elementy matematyczne
Jest to siatka południków i równoleżników we właściwym odwzorowaniu, skala mapy,
punkty nawiązania, a także ramka mapy z podziałem stopniowym i dokładniejszym, a na
niektórych ramka z podziałem kilometrowym.
Mapa musi posiadać orientację, strzałka- kierunek północy, układ ramek skierowany na
północ.
II.
Elementy geograficzne
*Zarys linii brzegowej mórz i jezior
*Sieć rzeczna
*Rzeźba powierzchni Ziemi
*Elementy glebowo roślinne
a także
*osiedla ludzkie
*sieć komunikacyjna
*zjawiska gospodarcze
*el. polityczne np. granice
Geograficzna treść przedstawia się za pomocą znaków i barw.
III.
Napisy na mapie i poza jej właściwą powierzchnią
Są to objaśnienia występujących na mapie obiektów oraz poza jej powierzchnią jako
informacje pomocnicze. Inf. Pomocnicze tworzą tzw. LEGENDĘ
*tytuł mapy
*instytucja wydawnicza
*skala mapy
*podziałka
*ROK wydania
*objaśnienia znaków i skrótów
*skala barw
Pismo ma cztery zasadnicze własności:
1. Harmonię
2. Czytelność
3. Wzajemną kontrastowość różnych pism na jednej i tej samej mapie
4. Zdatność do reprodukcji
Pismo powinno być możliwie proste (nie za bardzo ozdobne) prostota zwiększa czytelność
opisu. Czytelność z kolei zależy również od grubości pisma i stosunku barwy czarnej do
białego otoczenia. Badania wykazały, że optymalna grubość pisma na mapach ręcznych
powinna być 0,2-0,3 mm. (zbyt cienkie pismo też jest nie dobre bo męczy się oko podczas

czytania). Przeciętny stosunek wysokości do grubości w piśmie kartograficznym 6:1, a w
piśmie drukarskim 8:1. Wielkość pisma też ma znaczenie. Małe wymaga używania lupy, duże
zacienia mapę, zmniejsza czytelność.
Zwartość pisma wyraża się w rozstawie liter. Powinna wynosić 120%-130% grubości pisma.
Dobieramy kilka rodzajów czcionek w celu zróżnicowania, Nie za dużo tzn. dwa, trzy rodzaje.
Rozmieszczenie i położenie napisów na mapie w stosunku do opisywanych obiektów musi
spełniać dwa warunki:
1. Napis nie powinien zasłaniać ani rozrywać istotnych szczegółów mapy. Nie powinien
przecinać znaków linii kolejowych, szos oraz charakterystycznych szczegółów rzeźby
terenu.
2. Przynależność nazwy do określonego obiektu geograficznego nie powinna nasuwać
ż
adnych wątpliwości, czyli napis nie powinien się znajdować w dużej odległości od
obiektu, który określa.
Obiekty liniowe opisuje się zasadniczo wzdłuż ich osi, obiekty małe lub przedstawione
znakami umownymi opisuje się na mapach przeglądowych i w atlasach wzdłuż
równoleżników, a na mapach o większych skalach poziomo, na prawo od obiektu.
Obiekty zajmujące na mapie dużą powierzchnię (morze, jezioro) opisuje się wewnątrz ich
konturów, czasami rozsuwając litery napisu na osi największego rozprzestrzenienia obszaru.
Nazwy gór, dolin, rzek – opisuje się w kierunku wydłużenia obiektu. Napisy nie mogą być w
położeniu odwróconym do normalnego położenia mapy. Duże znaczenie ma właściwa ilość i
zagęszczenie napisów. Przy dużej ich ilości mapa staje się słabo czytelna. Gdy pomniejszamy
mapę trzeba usunąć napisy drugorzędne, czyli tzw. GENERALIZACJA MAPY.
ZNAKI KARTOGRAFICZNE
Na mapie mogą występować:
*znaki obrazowe-podobne do przedmiotów, w postaci szkiców, rzutów, kładów lub
schematów tych przedmiotów.
*znaki abstrakcyjne-nie podobne do przedmiotów, jako symbole geometryczne lub dowolne,
których znaczenia na mapie musi być objaśnione.
*znaki obrazowe lub abstrakcyjne w grupach
*znaki ruchu, wartości zmian natężenia zjawiska
*znaki diagramowi, wymierzalne wg oznaczeń zawartych w legendzie mapy
*znaki piśmiennicze tj. nazwy i skróty literowe lub litery
*znaki cyfrowe, charakteryzujące wielkość lub kolejność
ZESTAWIENIE PIERWORYSU MAPY
Można zestawić pierworys kilkoma sposobami:
1. Kartowanie bezpośrednie ze szkiców polowych
2. kartowanie z materiałów fotogrametrycznych (cyfrowe stacje fotogrametryczne).
Dokładność map wykonanych ze zdjęć lotniczych jest mniejsza niż ta za pomocą pomiarów
bezpośrednich. Dokładność położenia punktu przedmiotowego na mapie, pomierzonego
metodami geodezyjnymi 0,2 mm, ze zdjęć lotniczych 0,4mm.
3. Na drodze generalizacji mapy w skali większej niż opracowywana
4. Kartowanie kompilacyjne
5. Kartodiagramowanie w oparciu o materiał statystyczny lub opisowy

GENERALIZACJA KARTOGRAFICZNA
1. Generalizacja pierwotna-wykonywana już podczas pomiaru w terenie. (obserwując
różne formy w terenie trzeba je jakoś zmierzyć np. skarpa)
2. Wtórna stosowana przy przetwarzaniu map pierwotnych na mapy w skalach
mniejszych.
CELE GENERALIZOWANIA
1. Aby odpowiednia treść mapy zmieściła się na określonym formacie w żądanej skali
2. Aby uzyskać mapę specjalnie wyodrębniającą pewne elementy
3. Aby zwiększyć czytelność mapy
Dokonuje się generalizacji:
a. Elementów liniowych - do których zaliczamy: lnie kolejowe, drogi, rzeki, linie
brzegowe, warstwice.
-Najważniejszy jest warunek zgodności kątowej. Tj. wszystkie linie muszą się przecinać pod
tymi samymi kątami, co na mapie generalizowanej. Linia krzywa powinna posiadać wszystkie
zagięcia mapy generalizowanej. Jednak, jeśli zagięcia są < 0,2 mm i łuków krzywizny nie
dałoby się wykreślić swobodnie to jest obowiązek generalizowania takich miejsc.
b. Elementów powierzchniowych tj. osiedla, obszary wód, lasów, powierzchni
zamkniętych w granicach terytorialnych i innych znaków tworzących graficznie plamę.
-Warunkiem jest wiernopolowość i podobieństwo figury, obwodu w zmniejszonej skali.
c. Elementów punktowych, do których należą skupienia i rozproszenia drobnych plam i
punktów.
-Punkt albo zostaje albo się go usuwa. Czasem jeśli punkty pozostają w zespole, to można je
łączyć i zastąpić znakiem pojedynczym lub specjalnym.
d. Znaków specjalnych takich jak sygnatury, opisy, cieniowanie, kreskowanie.
-znaki te muszą być zmieniane i dopasowywane do nowej skali. Przykładem jest mapa
topograficzna, która ma ustalone różne znaki dla map w róznych skalach.
Pierwszym zadaniem przy generalizacji jest ustalenie celu mającej powstać mapy, co jest
związane z ustaleniem zakresu jej treści.

KARTOWANIE KOMPILACYJNE
Jest to kartowanie mapy na podstawie różnych map w różnych skalach. Dobrze jest
przetwarzać na podstawie osnowy geodezyjnej.
Kolejność opracowania:
1. Rozbudować osnowę geodezyjną
2. Obliczyć skurcz i ujednolicić mapę
3. Zaktualizować treść mapy przez pomiar bezpośredni z kontrolą styków
4. Montaż map zaktualizowanych na tle uzupełnionej osnowy i jednolitego
odwzorowania
PRZETWARZANIE MAPPODSTAWOWYCH NA MAPY W SKALACH
MNIEJSZYCH (POMNIEJSZANIE MAPY)
Mapy podstawowe powstają przez bezpośredni pomiar w terenie, mapy w skali mniejszej
przez opracowanie map podstawowych.
Jest wiele metod przetwarzania:
1. Metoda graficzna odręczna
2. Pantografowanie mechaniczne
3. Pantografowanie optyczne
4. Przetwarzanie fotograficzne
5. Przetwarzanie komputerów
AKTUALIZACJA – UNACZEŚNIANIE MAP
1. Aktualizację okresową map topograficznych wykonuj się w cyklu 5-10 letnim. Do
przeprowadzenia aktualizacji często trzeba wykonywać nowe zdjęcia lotnicze na
dużych obszarach lub w miejscach dużych przemian gospodarczych jakiegoś terenu.
2. Aktualizacja ciągła – podlegają jej wielkoskalowe mapy miejskie i rolnicze. Spośród
map miejskich należy utrzymać w ciągłej aktualizacji grupę map podstawowych,
ewidencyjnych, inwentaryzacyjnych i rejestracyjnych. Inne rodzaje map mogą być
aktualizowane okresowo. Z grupy map podstawowych dla danego miasta powinna być
wybrana jedna w skali 1 : 1 000 lub 1 : 500, która musi być aktualizowana na
podstawie pomiarów wykonanych natychmiast po wykonaniu budowy lub po każdej
zmianie sytuacji przedmiotów w trenie.
GRAFICZNE UPLASTYCZNIANIE MAP
Osiąga się przez stosowanie różnych barw, różnej intensywności barw, skali barw: przez
cieniowanie albo szrafowanie rzeźby terenu.
Właściwą intensywność można otrzymać przez zastosowanie odpowiedniego rastra.
RASTER- jest to przeźrocze na szkle lub błonie fotograficznej, którego rysunkiem jest
jednolity wzór utworzony z linii lub znaków równomiernie pokrywających daną
powierzchnię. Rastry mogą być: liniowe, kropkowe, kratkowe, wzorzyste.

PRZYDATNOŚĆ RASTRA W KARTOGRAFII
1. Charakter wzoru j.w.
2. Gęstość – ilość lini lub kropek na 1 cm długości
-b. gęste 60-80 / 1 cm
-rzadkie 20 linii /1 cm
3. Stopień zaczernienia
Raster 50% oznacza, że suma el. czarnych wzoru w 1 cm
2
wynosi 0,5 cm
2
reszta to białe pola.
GRAWEROWANIE OBRAZÓW KARTOGRAFICZNYCH
WARSTWORYTOWANIE
Podstawowa metoda wykonywania map do lat 80-tych. Są trzy rodzaje warstworytowania.
• POZYTYWOWE – arkusz folii pokryty warstwą rytowniczą.
Polega na tym, że po procesie rytowania, miejsca linii rysunkowych zostają zatrawione
w podłoże za pomocą lakieru zatrawiającego. Po usunięciu warstwy rytowniczej za pomocą
wody, otrzymuje się rysunek na folii lub płycie szklanej będącej DIAPOZYTEM
spełniającym rolę pierworysu lub czystorysu.
• NEGATYWOWE – polega na tym, że po procesie rytowania zabarwia się warstwę
rytowniczą roztworem specjalnego barwnika. Otrzymany w ten sposób negatyw,
używany jest do kopiowania diapozytywów, pozytywów oraz form druku offsetowego
czy sitowego.
• NEGATYWOWO-POZYTYWOWE – polega na rytowani odpowiedniej treści,
kopiowaniu jej na odpowiednie formy drukarskie, zaprawieniu, kolejnym rytowaniu i
kopiowaniu dalszych elementów. Po skopiowaniu całości treści mapy i zadrwieniu
ostatniej formy rysunku, zmywa się warstwę rytowniczą i uzyskuje zbiorczy
diapozytyw na folii.

SPOSOBY RYTOWANIA
1. Można wykonać na powierzchni arkusza rytowniczego, nałożonego na materiał
kartograficzny znajdujący się pod arkuszem rytowniczym. Materiałem takim może
być mapa, pierworys, foto-mapa, zdjęcia lotnicze. Rytowanie wykonuje się w
specjalnej kopioramie.
2. Polega na rytowaniu rysunku na powierzchni arkusza rytowniczego, na który
naniesiono rysunek. Może być to kopia srebrowa, błękitna, sepiowa, dwuazowa, druk
lub kopia kserograficzna.
REPRODUKCJA KARTOGRAFICZNA
To zespół czynności zmierzających do wykonania z oryginału większej ilości kopii
zgodnie z określonymi założeniami technicznymi. Wybór metody reprodukowania zależy
od okoliczności:
1. Graficznej postaci oryginału wydawniczego
2. Dokładności, z jaką ma być wykonana kopia
3. Ilości egzemplarzy
4. Od postaci graficznej żądanej reprodukcji lub jej podłoża
SPOSOBY DRUKOWANIA
DRUK WYPUKŁY – zlicza się tutaj drzeworyt, cynko-chemigafię i druk czcionkowy. W tej
technice drukują miejsca wypukłe. Drukuje się z blach cynkowych grubości 2mm. Druk
stosowany do szczególnie precyzyjnych oryginałów np. siatek kwadratów
DRUK WKLĘSŁY – drukują miejsca zagłębione, położone niżej niż elementy nie drukujące.
Zaliczamy tutaj: miedzioryt, staloryt, linoryt, rotograwiurę. Przykład miedziorytu. Rytuje się
tekst czy rysunek w blasze miedzianej. Na tak przygotowaną blachę wlewa się farbę. Farba
wypełnia zagłębienia, z pozostałych miejsc między rysunkowych należy ją usunąć. Na
zwilżoną blachę nakłada się papier i poddaje silnemu naciskowi w prasie miedziorytniczej.
DRUK PŁASKI – w tej technice miejsca drukujące i nie drukujące znajdują się na jednej
płaszczyźnie. (miejsca zatłuszczone i te które nie przyjmują tłuszczu, nawilżone). Istnieją dwa
rodzaje druku płaskiego:
1. Bezpośredni – uzyskuje się odbitkę przez dociśnięcie papieru do odbitki drukującej,
którą może być blacha cynkowa lub aluminiowa.

2. Pośredni – offsetowy – rysunek z blachy przenoszony jest na cylinder gumowy, skąd
następnie drukowany jest na papierze (stąd metoda pośrednia). Za pomocą walca
obraz przenoszony jest na papier.
Jest to najbardziej praktyczny druk z punktu widzenia reprodukcji małonakładowej. Druk
następuje z płaskich blach o grubości 06 – 0,7 mm.
Przygotowanie blachy do druku.
1. Ziarnowanie blachy – w maszynie zwanej ziarnówką, składającej się z żeliwnej
podstawy i skrzynki, na dno skrzynki wkłada się blachę, przymocowuje, pokrywa
drobnym pyłem kwarcowym. Skrapia się wodą i posypuje warstwą drobniutkich
kuleczek porcelanowych. Maszynę wprawia się w ruch na około 1 godzinę. Kulki
porcelanowe wcierają pył kwarcowy w blachę. Efektem jest zwiększenie powierzchni
porowatej 3 – 5 krotnie.
2. Na blachę wylewa się odpowiednio przygotowaną emulsję światłoczułą. Umieszcza
się w specjalnej wirówce, w celu równomiernego rozprowadzenia substancji na
powierzchni całej blachy.
3. Suszy się blachę za pomocą grzałek elektrycznych z dwustopniową regulacją
temperatury.
4. Przygotowaną, wysuszoną płytę mocuje się w kopioramie próżniowej. Umieszcza się
na niej diapozytyw foliowy lub negatyw. Pompa próżniowa jest zastosowana w celu
jak najdokładniejszego, ścisłego przylegania płyty i oryginału. Zapobiega to
pojawianiu się pęcherzyków powietrza. Naświetla się.
5. Po naświetlaniu, pokrywa się powierzchnię cienką warstwą farby kopiowej.
6. Następnie wywołuje się płytę poprzez zmycie woda warstwy emulsji w miejscach nie
naświetlonych. Miejsca naświetlone pozostają zabarwione.
7. Po wywołaniu zbiera się nadmiar wody, pokrywa blachę zakwaszoną gumą arabską.
Suszy i przekazuje do druku.
DRUK OFFSETOWY
1. Przed każdą kopią musi być nalana woda na całą powierzchnię blachy.
2. Za pomocą wałka nanosi się farbę drukarską. Farbę przyjmują tylko miejsca pokryte
wcześniej emulsją, czyli naświetlone.
3. Przenoszenie rysunku na walec gumowy, a z walca na papier, czyli druk pośredni.
Druk z jednej blachy może być powtarzany wielokrotnie, lecz czynności zwilżania i
nakładania farby, muszą być wykonywane każdorazowo.
KSEROGRAFIA
Wykorzystuje fizyczne właściwości półprzewodników takich jak selenu i pewnego rodzaju
ż
ywic. Wynalezione już w 1937 roku przez Carlosona. Wykonuje się kseropłyty, pokryte
warstwą półprzewodnika, które spełniają rolę półprzewodnika. Płyta naładowana potencjałem
elektrycznym w ciemności utrzymuje ładunek, a naświetlona traci go w miejscach
naświetlonych.
KSEROGRAFIA OPTYCZNA – można przeskalować kopię dzięki dodatkowemu układowi
soczewek.
KSEROGRAFIA STYKOWA – tylko 1:1

Aparatura składa się z urządzenia ładującego, z zasilaczem wysokiego napięcia, urządzenia
naświetlającego, urządzenia wywołującego oraz urządzenia wyświetlającego.
FAZY KSEROGRAFII
1. Założenie oryginału na ekran urządzenia
2. Nastawienie układu optycznego do żądnej skali reprodukcji
3. Naładowanie w procesorze płyty pokrytej półprzewodnikiem, w polu elektrycznym o
napięciu 6000 V
4. Naświetlenie płyty przez układ optyczny
5. Powstaje obraz utleniony na powierzchni płyty
6. Wywołanie kaskadowe przy użyciu pigmentu (toneru – proszku o ładunku
przeciwnym do ładunku płyty)
7. Przeniesienie obrazu z płyty na podkład (folię)
8. Utrwalenie kopii sposobem termicznym. Najczęściej toner zatapiany jest w podłoże w
temperaturze około 90° C
KOPIE DWUAZOWE
Kopie wykonywane z materiałów przezroczystych (matryc, diapozytywów, negatywów)
Metoda ta wykorzystuje światłoczułe właściwości związków dwuazowych. Warstwa
ś
wiatłoczuła składa się z dwóch składników: biernego i czynnego. Bardzo prosta i tania
metoda ozalidu. Na podłożu powstaje obraz przez naświetlanie matrycy. Wywołanie obrazu
odbywa się w parach amoniakalnych. Obraz występuje w postaci pozytywu
Kopiowanie dwuazowe suche – wywołanie w zimnych parach amoniaku, w specjalnych
drewnianych skrzynkach szczelnie zamkniętych.
Kopiowanie dwuazowe pół-mokre – wywołanie odbywa się przez delikatne zwilżenie emulsji,
specjalnym wywoływaczem. Pozwala to otrzymywać tony odcieni w kolorach od ciemnej
sepii do fioletów. Efekt jest kilka razy lepszy jednak droższy. Plusem jest też, że warstwy
ś
wiatłoczułe mogą być rozlewane na dowolne podłoże: papier, plansze kartograficzne,
materiały płócienne, folię plastikową.
FARBY REPRODUKCYJNE
Powstają przez zmieszanie trzech składników. Pigmentu (jest to substancja nieorganiczna,
nie rozpuszczalna w wodzie, znanych jest 25 pigmentów), substancji wiążącej (np. smoła,
olej, żywica- mają za zadnie równo rozłożyć pigment i przylepić go do powierzchni) i
substancji uzupełniającej- ma za zadanie podnieść właściwości farby: trwałość koloru,
przylepność, jakość, tłustość.
Właściwości farb:
*światłtrwałość
*odporność na wpływy atmosferyczne
*czysty i ładny ton
*zdolność mieszania się z innymi farbami
*zdolność schnięcia
*wydajność
*przyczepność
*zdolność rozprowadzania
*gęstość

KARTOMETRIA
Zajmuje się metodami przeprowadzania pomiarów na mapie i samymi pomiarami.
Od czego zależy dokładność wyników pomiarów na mapie?
1. Błędy techniczne, niedokładność przyrządów
2. Błędy kartograficzne wynikające z niedokładności mapy, na której wykonujemy
pomiary.
*niedokładność siatki
*zniekształcenia rysunku
*generalizacja
POMIAR NA MAPACH
1. Odcinki
*linie proste
*krzywe – można mierzyć za pomocą kroczka, sumując linie łamane, krzywomierzem
2. Pola powierzchni – mierzymy: planimetrem, polami siatki geograficznej
3. Objętość – na mapie warstwicowej
4. Spadki terenu i nachylenie
5. Powierzchnia topograficzna P’=P sec α
Wyszukiwarka
Podobne podstrony:
Elementy trygonometrii sferycznej, Kartografia matematyczna
TRYGONOMETRIA SFERYCZNA I
Trygonometria sferyczna ppt
podstawowe wzory trygonometrii sferycznej, Geodezja, studia III rok
TRYGONOMETRIA SFERYCZNA IIb
Trygonometria sferyczna
trygonometria sferyczna
TRYGONOMETRIA SFERYCZNA I
trygonometria 2
3 2 Ćwiczenie Obliczanie siatki kartograficznej Merkatora
6 KartograficzneSrodkiWyrazu (1)
45Załamania światła na powierzchni sferycznej
Decyzja w-z, Geodezja i Kartografia, II rok, PPPiPU
izolinie, semestr 1, kartografia
koszulka karto, AGH, Kartografia I, temat 1
Koło 2 Kartografia
więcej podobnych podstron