TRYGONOMETRIA

TRYGONOMETRIA

SFERYCZNA

SFERYCZNA

ORTODROMA I JEJ ELEMENTY

ORTODROMA I JEJ ELEMENTY

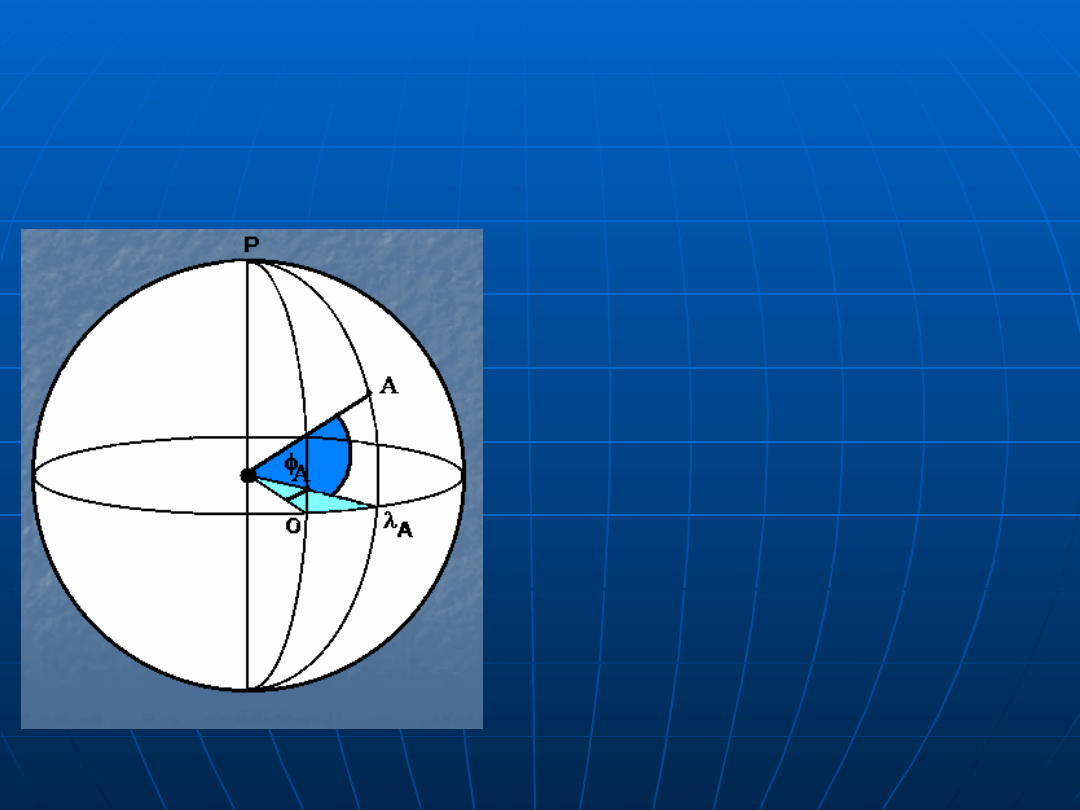
Dysponując współrzędnymi sferycznymi punktów

Dysponując współrzędnymi sferycznymi punktów

A

A

(

(

λ

λ

A

A

,

,

φ

φ

A

A

)

)

i

i

B

B

(

(

λ

λ

B

B

,

,

φ

φ

B

B

)

)

na powierzchni Ziemi, możemy obliczyć ich wzajemne odległości:

na powierzchni Ziemi, możemy obliczyć ich wzajemne odległości:

kątową i liniową.

kątową i liniową.

WSPÓŁRZĘDNE NA SFERZE

WSPÓŁRZĘDNE NA SFERZE

We

wzorach

korzystamy

z

konwencji w myśl której

szerokość

południowa

i

długość zachodnia

zapisywane są we wzorach jako
liczby ujemne.

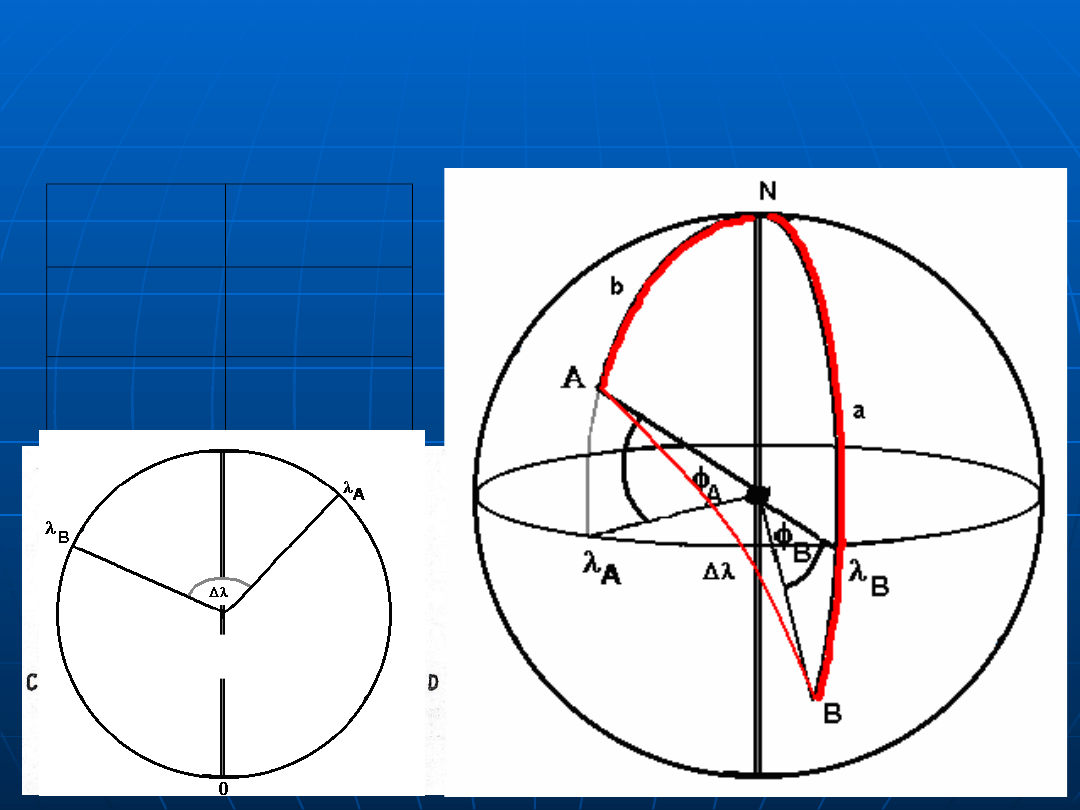
Elementy

dane

Elementy

szukane

a = 90

0

–

φ

B

A

b = 90

0

–

φ

A

B

C = |Δλ|

d (bok c)

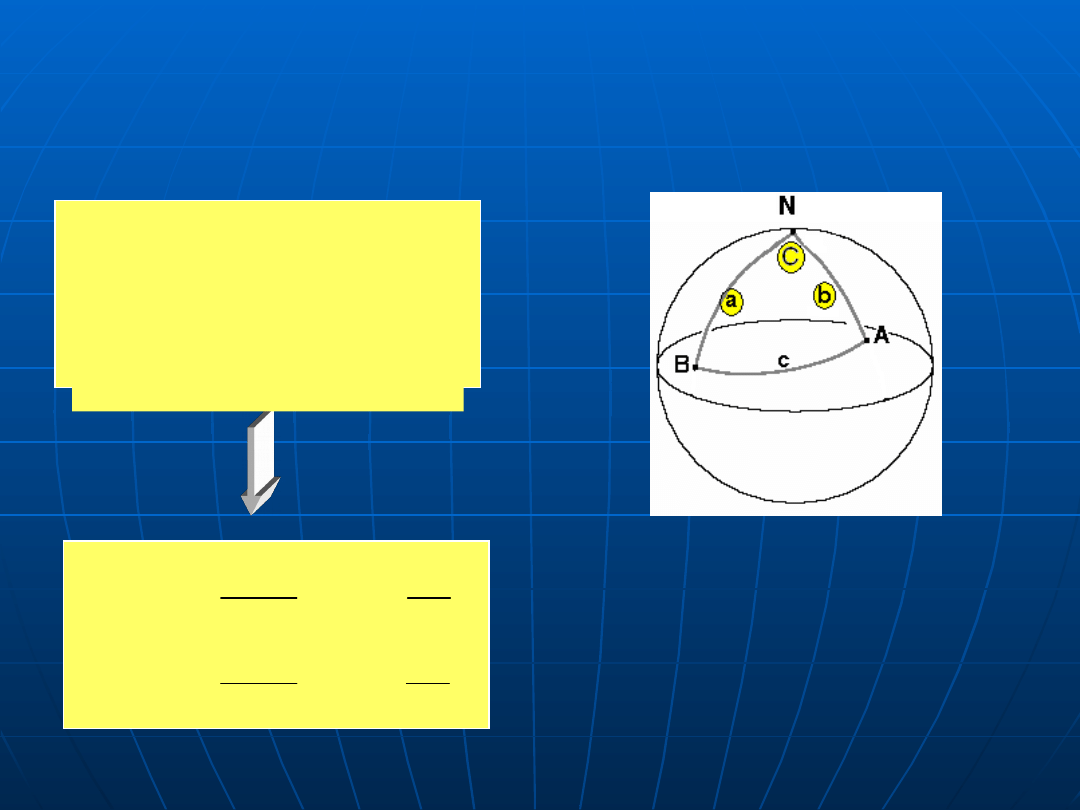
TRÓJKĄT PODSTAWOWY - ELEMENTY

TRÓJKĄT PODSTAWOWY - ELEMENTY

W przypadku

W przypadku

obliczeń nawigacyjnych

obliczeń nawigacyjnych

wykorzystujemy trójkąt

wykorzystujemy trójkąt

podstawowy

podstawowy

ABN

ABN

w którym dane są dwa boki (

w którym dane są dwa boki (

a

a

,

,

b

b

) i kąt zawarty

) i kąt zawarty

pomiędzy nimi (

pomiędzy nimi (

C

C

= |

= |









|

|

).

).

Δλ = λ

B

− λ

A

Gdy |Δλ| >
180º

C = 360º

−

|

Δλ|

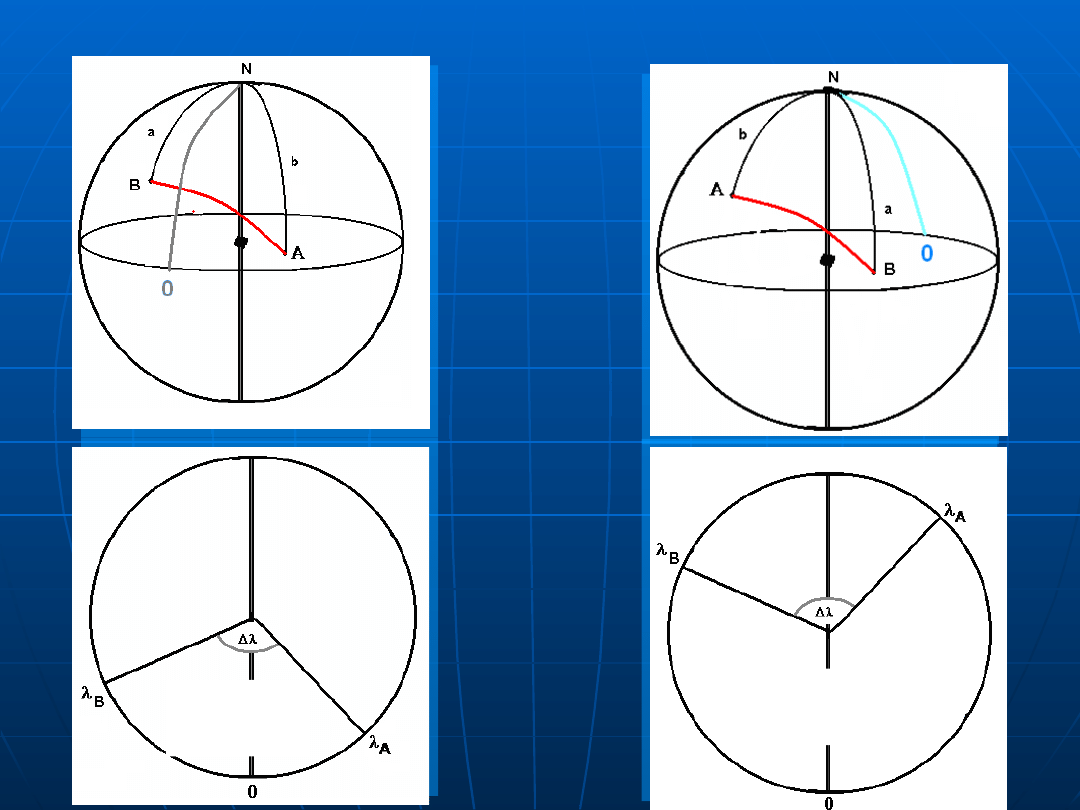
Trójkąt podstawowy - elementy

Trójkąt podstawowy - elementy

C = |λ

B

−

λ

A

|

C = 360º − |λ

B

− λ

A

|

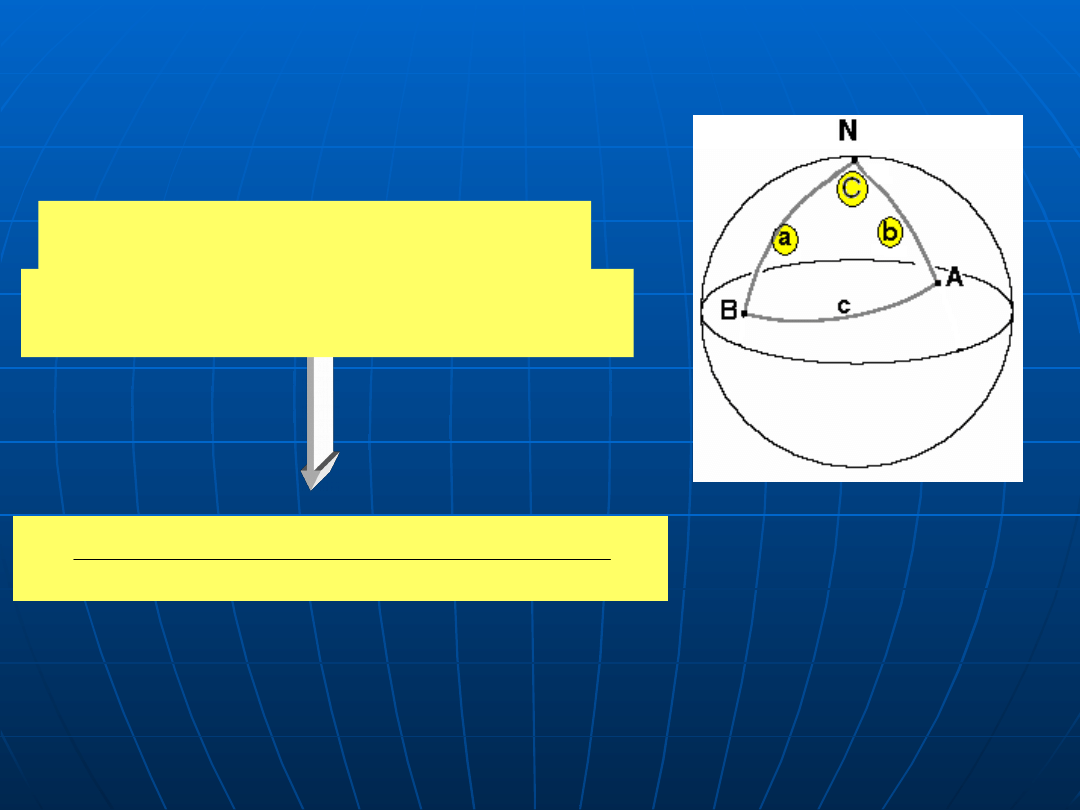
Twierdzenie cosinusów

Twierdzenie cosinusów

cos c = cos b cos a + sin b sin a

cos C

ODLEGŁOŚĆ ORTODROMICZNA – TRZECI BOK

ODLEGŁOŚĆ ORTODROMICZNA – TRZECI BOK

cos d = sin φ

A

sin φ

B

+ cos φ

A

cos φ

B

cos Δλ

60

180

)

cos

sin

cos

arccos(











C

a

inb

s

a

osb

c

d

Mm

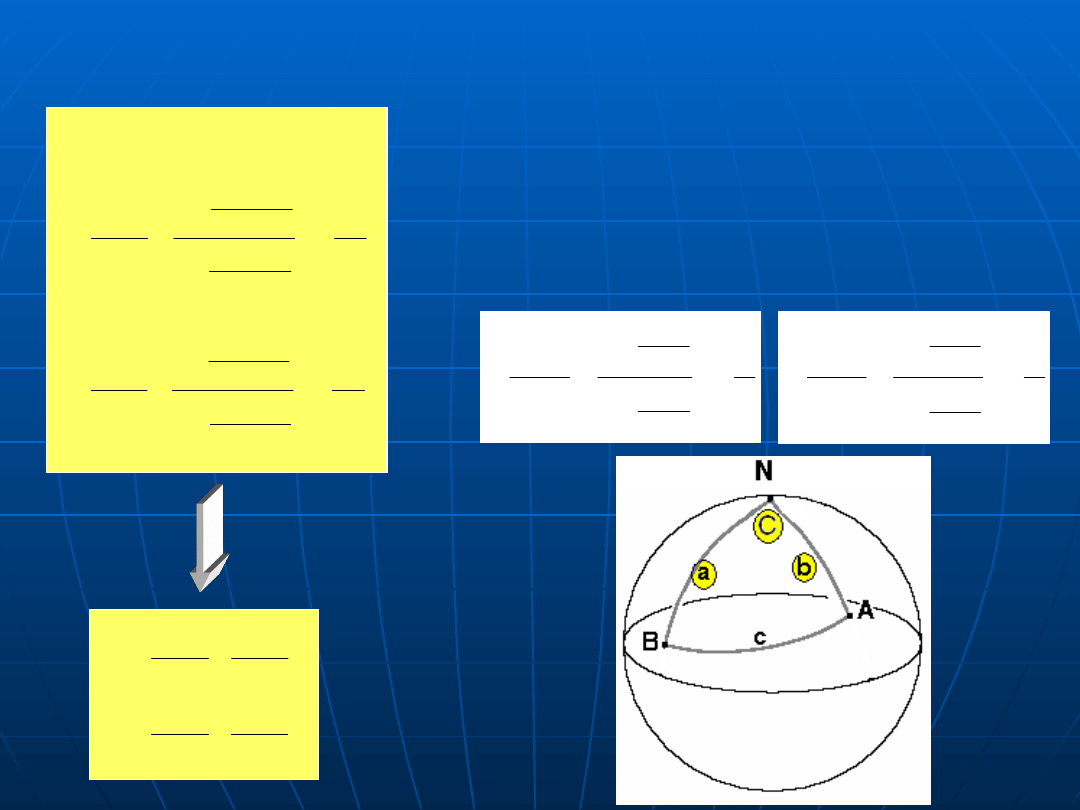
Twierdzenie sinusów

sin A / sin a = sin C /sin

c

sin B / sin b = sin C /sin

c



180

)

sin(

sin

)

sin(

arcsin



















a

c

C

A



180

)

sin(

sin

)

sin(

arcsin



















b

c

C

B

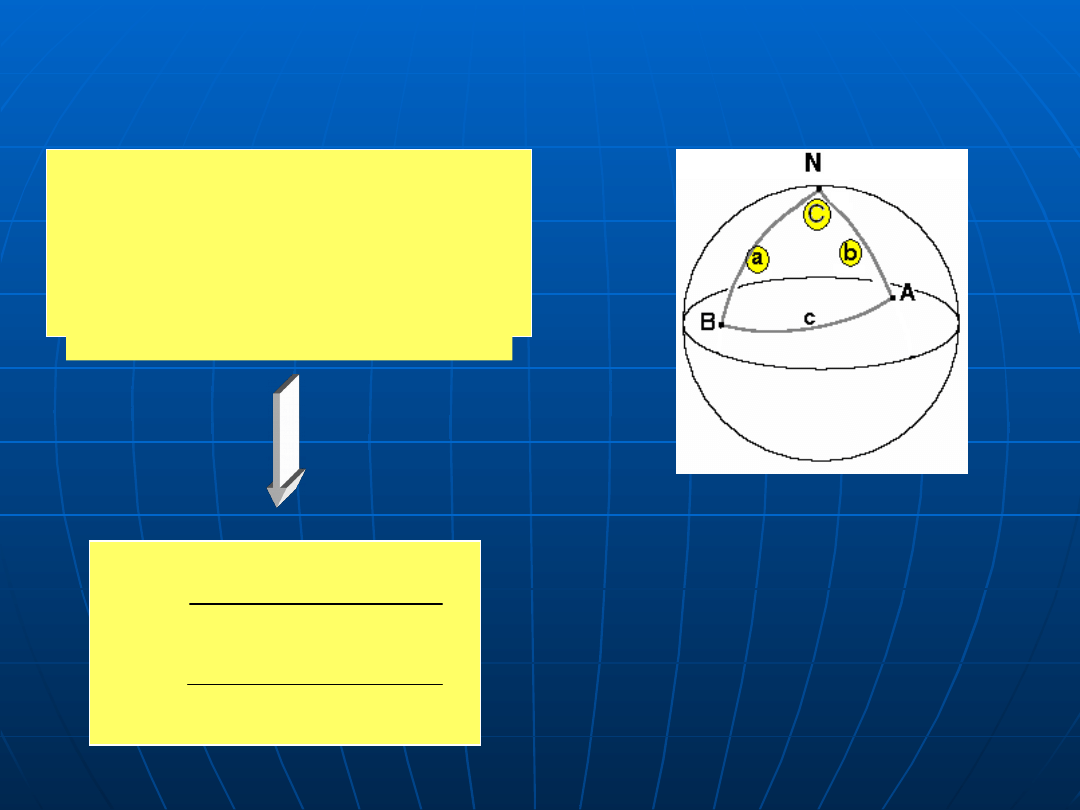
Aby znaleźć

Aby znaleźć

początkowy i końcowy kąt drogi

początkowy i końcowy kąt drogi

po ortodromie, należy

po ortodromie, należy

znaleźć kąty

znaleźć kąty

A

A

i

i

B

B

trójkąta podstawowego

trójkąta podstawowego

ABN

ABN

.

.

KĄT POCZĄTKOWY I KOŃCOWY DROGI – KĄTY I

KĄT POCZĄTKOWY I KOŃCOWY DROGI – KĄTY I

UWAGA:



Mankamentem

stosowania

twierdzenia

sinusów

jest

konieczność wyboru jednej z dwóch
odpowiedzi.

Analogie Nepera

2

2

sin

2

cos

2





















ctg

B

A

tg

B

A

B

A

2

2

cos

2

sin

2





















ctg

B

A

tg

B

A

B

A

2

2

B

A

B

A

A









2

2

B

A

B

A

B









KĄT POCZĄTKOWY I KOŃCOWY DROGI – KĄTY II

KĄT POCZĄTKOWY I KOŃCOWY DROGI – KĄTY II

UWAGI:

 Wygodniej jest skorzystać z analogii Nepera
lub twierdzenia cotangensów.
 Możemy skorzystać z twierdzenia cosinusów
dla kątów aby wybrać właściwą odpowiedź.

2

2

cos

2

cos

2

C

ctg

b

a

b

a

B

A

tg









2

2

sin

2

sin

2

C

ctg

b

a

b

a

B

A

tg









Twierdzenie cotangensów

sinb ctga – sinC ctgA =
cosb cosC

sina ctgb – sinC ctgB =
cosa cosC

C

C

b

ctga

b

ctgA

sin

cos

cos

sin









C

C

a

ctgb

a

ctgB

sin

cos

cos

sin









KĄT POCZĄTKOWY I KOŃCOWY DROGI – KĄTY III

KĄT POCZĄTKOWY I KOŃCOWY DROGI – KĄTY III

DEFINICJA 1.

DEFINICJA 1.

Początkowym kątem drogi

Początkowym kątem drogi

po ortodromie

po ortodromie

AB

AB

nazywamy kąt dodatni, którego początkowym ramieniem jest

nazywamy kąt dodatni, którego początkowym ramieniem jest

część południka łączącego punkt

część południka łączącego punkt

A

A

z biegunem północnym, a

z biegunem północnym, a

końcowym − ortodroma

końcowym − ortodroma

AB

AB

.

.

Końcowym kątem drogi

Końcowym kątem drogi

po ortodromie

po ortodromie

AB

AB

nazywamy kąt dodatni,

nazywamy kąt dodatni,

którego początkowym ramieniem jest część południka łączącego

którego początkowym ramieniem jest część południka łączącego

punkt

punkt

B

B

z biegunem północnym, a końcowym − przedłużenie

z biegunem północnym, a końcowym − przedłużenie

ortodromy poza punkt

ortodromy poza punkt

B

B

.

.

KĄT POCZĄTKOWY I KOŃCOWY

KĄT POCZĄTKOWY I KOŃCOWY

DROGI PO ORTODROMIE

DROGI PO ORTODROMIE

Obrotem dodatnim

Obrotem dodatnim

(a tym samym kątem dodatnim) nazywamy

(a tym samym kątem dodatnim) nazywamy

obrót zgodny z ruchem wskazówek zegara.

obrót zgodny z ruchem wskazówek zegara.

Kursem nazywamy kąt dodatni

Kursem nazywamy kąt dodatni

leżący na płaszczyźnie stycznej do

leżący na płaszczyźnie stycznej do

powierzchni Ziemi, którego wierzchołkiem jest obserwator O

powierzchni Ziemi, którego wierzchołkiem jest obserwator O

traktowany jako punkt, początkowym ramieniem jest półprosta

traktowany jako punkt, początkowym ramieniem jest półprosta

ON, biegnąca w kierunku geograficznego bieguna północnego, a

ON, biegnąca w kierunku geograficznego bieguna północnego, a

końcowym półprosta OD, zgodnie równoległa do wektora RD,

końcowym półprosta OD, zgodnie równoległa do wektora RD,

wyznaczonego przez rufę R i dziób D statku na jego podłużnej osi

wyznaczonego przez rufę R i dziób D statku na jego podłużnej osi

symetrii.

symetrii.

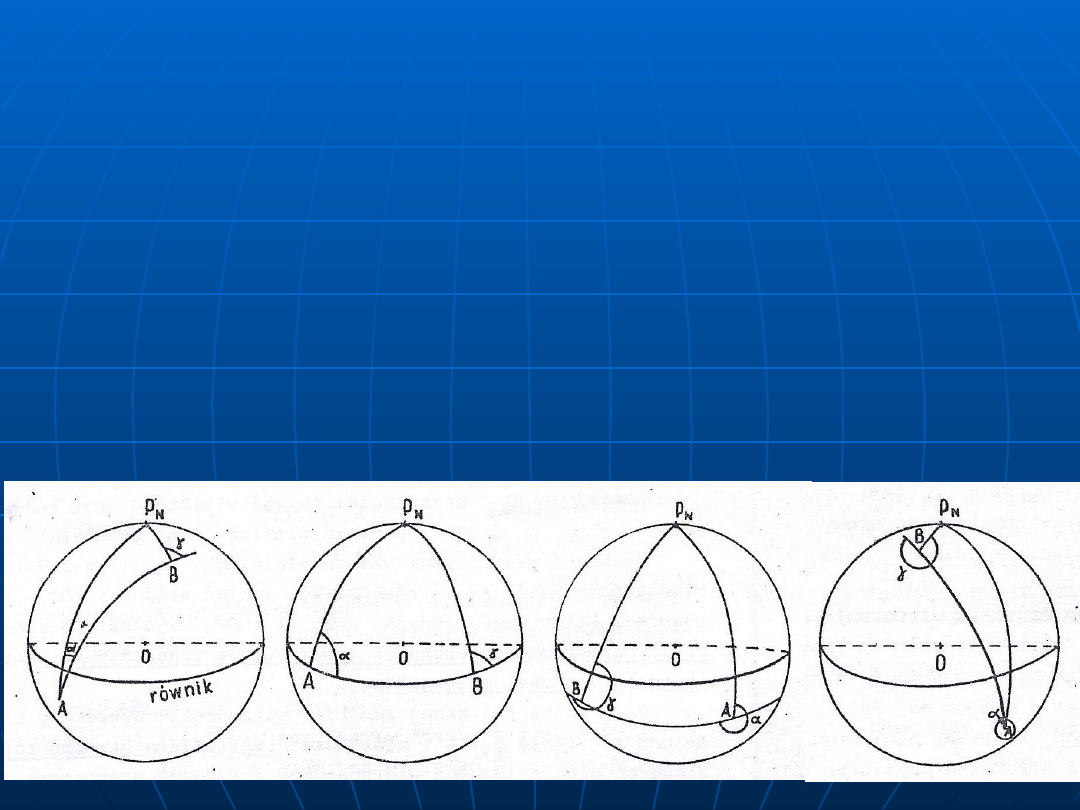
DEFINICJA 1.

DEFINICJA 1.

Początkowym kątem drogi

Początkowym kątem drogi

(ozn.

(ozn.

α

α

)

)

po ortodromie

po ortodromie

AB

AB

nazywamy kąt dodatni, którego początkowym ramieniem jest

nazywamy kąt dodatni, którego początkowym ramieniem jest

część południka łączącego punkt

część południka łączącego punkt

A

A

z biegunem północnym, a

z biegunem północnym, a

końcowym − ortodroma

końcowym − ortodroma

AB

AB

.

.

Końcowym kątem drogi

Końcowym kątem drogi

(ozn.

(ozn.

β

β

lub

lub

γ

γ

)

)

po ortodromie

po ortodromie

AB

AB

nazywamy

nazywamy

kąt dodatni, którego początkowym ramieniem jest część południka

kąt dodatni, którego początkowym ramieniem jest część południka

łączącego punkt

łączącego punkt

B

B

z biegunem północnym, a końcowym −

z biegunem północnym, a końcowym −

przedłużenie ortodromy poza punkt

przedłużenie ortodromy poza punkt

B

B

.

.

KĄT POCZĄTKOWY I KOŃCOWY

KĄT POCZĄTKOWY I KOŃCOWY

DROGI PO ORTODROMIE

DROGI PO ORTODROMIE